Как составить трехфакторную модель

Условие:
определить влияние численности персонала,
количества отработанных смен и выработки
в смену на одного работника на изменение
объема выпуска продукции (N_п).

Месяцы	Численность работников, чел.	Выработка в смену, шт.	Количество смен
1	24	1500	144
2	25	1505	146

Сделать вывод.

Алгоритм решения:

1. Факторная
   модель, описывающая взаимосвязь
   показателей, имеет вид: N
   = ч * См * В

2. Исходные
   данные – факторы и результирующий
   показатель представляются в аналитической
   таблице:

Показатели	Условные обозначения	Базисный период	Отчетный период	Отклонение	Темп изменения, %
1. Численность работников, чел.	ч	24	25	+1	104,2
2. Количество смен	См	144	146	+2	101,4
3. Выработка, штук	В	1500	1505	+5	100,3
4. Выпуск продукции, тыс. шт.	N	5184	5493,25	+309,25	106,0

1. Способы
   детерминированного факторного анализа,
   применяемые для решения трехфакторных
   моделей:

 цепной
подстановки;

 абсолютных
разниц;

 взвешенных
конечных разниц;

 логарифмический;

 интегральный.

1. Применение
   различных методов для решения типовой
   задачи:

   1. Способ
      цепной подстановки.
      Применение этого способа предполагает
      выделение количественных и качественных
      факторных признаков: здесь количественными
      факторами являются численность
      персонала и количество отработанных
      смен; качественный признак – выработка.

а)
N₁
= ч₀
* См⁰
* В⁰
=5184 тыс. шт.;

б)
N₂
= ч¹
* См⁰
* В⁰
=25 * 144 * 1500 =5400 тыс. шт.;

в)
N
(ч) = 5400 – 5184 = 216 тыс. шт.;

N₃
= ч¹
* См¹
* В⁰
=25 * 146 * 1500 =5475 тыс. шт.;

N(См)
= 5475 – 5400 = 75 тыс. шт.;

N₄
= ч¹
* См¹
* В¹
=25 * 146 * 1505 =5493,25 тыс. шт.;

N(В)
= 5493,25 – 5475 = 18,25 тыс. шт.;

N
=N(ч)
+N(См)
+N
(B) = 216 + 75 +18,25 = 309,25 тыс. шт.

4.2.
Способ
абсолютных разниц
также предполагает выделение количественных
и качественных факторов, определяющих
последовательность подстановки:

а)
N(ч)
=ч
* См⁰
* В⁰ =
1 * 14 * 1500 = 216 тыс. шт.;

б)
N(См)
=См
* ч¹
* В⁰
= +2 * 25 * 1500 = 75 тыс. шт.;

в)
N
(B) =B
* ч¹
* См¹
= +5 * 25 * 146 = 18,25 тыс. шт.;

N
=
N(ч)
+N(См)
+N
(B) = 309,25 тыс. шт.

1. Способ
   относительных разниц

а)
N(ч)
=тыс. шт.;

б)

N(См)
=тыс.
шт.;

в)
N(В)тыс.
шт.;

Общее
влияние факторов :
N
=N(ч)
+N(См)
+N
(B) = 309,3 тыс. шт.

4.4.
Способ
взвешенных конечных разностей
предполагает применение всех возможных
постановок на основе способа абсолютных
разниц.

Подстановка
1 производится в последовательности

результаты
определены в предыдущих расчетах:

N(ч)
= 216 тыс. шт.;

N(См)
= 75 тыс. шт.;

N
(B) = 18,25 тыс. шт.

Подстановка
2 производится в последовательности
:

а)+1
* 1500 * 144 = 216 тыс. шт.;

б)
+5
* 25 * 11 = 18 тыс. шт.;

в)
+2
* 25 *1505 = 75,5 тыс. шт.;

Подстановка
3 производится в последовательности
:

а)
2
* 24 * 1500 = 72 тыс. шт.;

б)
1
* 146 * 1500 = 219 тыс. шт.;

в)
+
5 * 25 * 146 = 18,25 тыс. шт.

Подстановка
4 производится в последовательности
:

а)
2
* 1500 *5 * 146 * 24 = 17,52 тыс. шт.;

б)
5
* 146 * 24 = 17,52 тыс. шт.;

в)
1
* 146 * 1515 = 219,73 тыс. шт.;

Подстановка
5 производится в последовательности
:

а)
5
* 144 * 24 = 17,28 тыс. шт.;

б)
2
* 1505 * 24 = 72,27 тыс. шт.;

в)
1
* 146 * 1505 = 219,73 тыс. шт.

Подстановка
6 производится в последовательности
:

а)
5
* 24 * 144 = 17,28 тыс. шт.;

б)
1
* 1505 * 144 = 216,72 тыс. шт.;

в)
2
* 1505 * 25 = 75,25 тыс. шт.

Влияние факторов
на результирующий показатель

Факторы	Размер влияния факторов при подстановке, тыс. шт.	Среднее значение влияния факторов
№ 1	№ 2	№ 3	№ 4	№ 5	№ 6
1. Численность	216	219	216	219,73	219,73	216,72	217,86
2. Сменность	75	72	75,25	72	72,27	75,25	73,63
3. Выработка	18,25	18,25	18,0	17,52	17,28	17,28	17,76
4. Итого:	309,25	309,25	309,25	309,25	309,25	309,25	309,25

4.5.
Логарифмический
способ
предполагает распределение отклонения
результирующего показателя пропорционально
доле каждого фактора в сумме отклонения
результата

а)
доля влияния каждого фактора измеряется
соответствующими коэффициентами:

б)
влияние каждого фактора на результирующий
показатель рассчитывается как произведение
отклонения результата на соответствующий
коэффициент:

309,25*0,706
= 218,33;

309,25*0,2438
= 73,60;

309,25*
0,056 = 17,32.

4.6.
Интегральный метод
предполагает применение стандартных
формул для расчета влияния каждого
фактора:

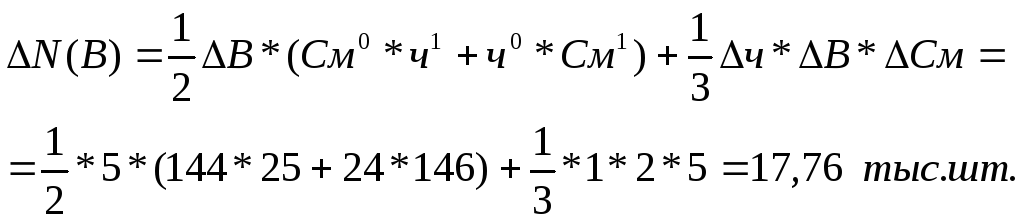
5. Результаты
расчетов каждого из перечисленных
способов объединяются в таблице
совокупного влияния факторов.

Совокупное
влияние факторов:

Факторы	Размер влияния, тыс. шт.	Способом относительных разниц	Размер влияния, тыс. шт.
Способом цепных подстановок	Способом абсолютных разниц	Способом взвешенных конечных разниц	Логарифм. способ	Интегральный способ
1. Численность	216	216	216,17	217,86	218,33	217,86
2. Количество смен	75	75	75,06	73,63	73,60	73,63
3. Выработка	18,25	18,25	18,07	17,76	17,32	17,76
4. Итого:	309,25	309,25	309,3	309,25	309,25	309,25

Сопоставление
результатов расчетов, полученных
различными способами (логарифмическим,
интегральным и взвешенных конечных
разниц), показывает их равенство.
Громоздкие расчеты способом взвешенных
конечных разниц удобно заменить
применением логарифмического и
интегрального методов, которые дают
более точные результаты по сравнению
с приемами цепной подстановки и абсолютных
разниц.

5.
Вывод:
Объем выпуска продукции возрос на 309,25
тыс. штук.

Положительное
влияние в размере 217,86 тыс. шт. оказал
рост численности персонала.

В результате
увеличения количества смен объем выпуска
возрос на 73,6 тыс. шт.

За счет увеличения
выработки объем выпуска продукции
увеличился на 17,76 тыс. шт.

Наиболее сильное
влияние на объем выпуска продукции
оказали экстенсивные факторы: рост
численности персонала и количества
отработанных смен. Совокупное влияние
этих факторов составили 94,26 % (70,45 +23,81).
На долю влияния фактора выработки
приходится 5,74 % роста выпуска продукции.

По
результатам анализа можно рекомендовать
предприятию разработать ряд мер, по
повышению производительности труда,
что при неизменности экстенсивных
фактора работы приведет к повышению
прибыли.

Примечание:
Применение рассмотренных приемов
аналогично в отношении мультипликативных
моделей любого количества факторов.
Однако использование приема взвешенных
конечных разниц к многофакторным моделям
ограничено необходимостью выполнения
большого количества расчетов, и это
нецелесообразно при наличии других,
более простых и рациональных приемов,
например, логарифмического.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Для расчета и анализа рентабельности собственного капитала (ROE), а также рентабельности активов (ROA) можно использовать модель (уравнение) Дюпона.

Данная модель позволяет проводить углубленный анализ показателя. Так как дает понять, за счет каких конкретных факторов происходило изменение рентабельности собственного оборотного капитала (ROE) или ROA.

А главное – данный анализ позволяет выявить, что нужно сделать, чтобы увеличить отдачу собственного капитала (или активов предприятия) или же, по крайней мере, сохранить ее на прежнем уровне.

Формула Дюпона

Модель Дюпона связывает несколько экономических показателей.

В зависимости от того сколько множителей входит в уравнение, модель может быть:

• двухфакторной ;

• трехфакторной;

• пятифакторной.

Двухфакторная модель Дюпона

В двухфакторной модели Дюпона устанавливается зависимость между ROA (рентабельностью активов) и коэффициентами рентабельности продаж (ROS) и оборачиваемости активов.

где ROS – рентабельность продаж, доли ед.;

КобА – коэффициент оборачиваемости активов, доли ед.

Проверить адекватность модели можно, расписав формулы, входящих в уравнение показателей. Как видно из формулы представленной ниже, равенство не нарушается.

Трехфакторная модель Дюпона

Формула расчета рентабельности собственного капитала по Дюпону имеет следующий вид:

где ROS – рентабельность продаж, доли ед.;

КобА – коэффициент оборачиваемости активов, доли ед.;

Ф_{независ.} – коэффициент финансовой независимости, руб./руб.

Распишем каждый множитель трехфакторной модели:

Как видно из формулы, равенство сохраняется.

Используя трехфакторную формулу Дюпона, можно оценить влияние на рентабельность собственного капитала трех ключевых аспектов деятельности предприятия:

• операционной эффективности;
• эффективности использования активов компании;
• финансового левериджа.

Трехфакторная модель Дюпона: пример расчета

Для проведения факторного анализа рентабельности собственного капитала (ROE) воспользуемся данными, приведенными в таблице.

Исходные данные для анализа показателей рентабельности

Для решения задачи на основании исходных данных необходимо определить все сомножители формулы Дюпона.

Решение:

1. найдем базисную величину ROE за предыдущий год:

ROE₁ = ROS₁ * K_обА₁ * Ф_{независ.1} = 0,144 * 1,1197 * 1,56 = 0,2515

Определение влияния рентабельности продаж на ROE

2. определим условную величину  ROE при изменении ROS:

ROE_ROS = ROS₂ * K_обА₁ * Ф_{независ.1} = 0,161 * 1,1197 * 1,56 = 0,2812

3. определим абсолютное изменение ROE при изменении ROS:

∆ROE_ROS = ROE_ROS – ROE₁ = 0,2812 – 0,2515 = 0,0298

4. найдем относительное изменение ROE при изменении ROS:

∆ROE_ROS / (ROE₂ – ROE₁) *100% = 0,0297 / 0,099 * 100% = 30,03 %

Определение влияния оборачиваемости активов на ROE

5. определим условную величину ROE при изменении K_обА:

ROE_{K_обА} = ROS₂ * K_обА₂ * Ф_{независ.1} = 0,161 * 1,4207 * 1,56 = 0,3568

Это значение рентабельности СК при условии, что изменилось два фактора: рентабельность продаж и оборачиваемость активов. Для выявления влияния только одного фактора произведем следующее действие.

6. рассчитаем абсолютное изменение ROE при изменении K_обА:

∆ROE_{K_обА} = ROE_{K_обА} – ROE_ROS = 0,3568 – 0,2812 = 0,0757

7. определим относительное изменение ROE  при изменении K_обА:

∆ROE_{K_обА} / (ROE₂ – ROE₁) * 100% = 0,0757 / 0,099 * 100% = 76,46 %

Определение влияния финансовой независимости на ROE

8. рассчитаем условную величину ROE  при изменении Ф_{независ.} или величину ROE  за отчетный год:

ROE₂ = ROS₂ * K_обА₂ * Ф_{независ.2} = 0,161 * 1,4207 * 1,53 = 0,35

9. найдем абсолютное изменение ROE  при изменении Ф_{независ.}:

∆ROE_{Фнезавис.} = ROE₂ – ROE_{K_обА} = 0,35 – 0,3568 = -0,0068

10. определим относительное изменение ROE  при изменении Ф_{независ.}:

∆ROE_{Фнезавис.} / (ROE₂ – ROE₁) * 100% = -0,0068 / 0,099 * 100% = -6,87 %

Проверка (баланс уравнений)

∆ROE_ROS + ∆ROE_{K_обА} + ∆ROE_{Фнезавис.} = 0,0298 + 0,0757 + (-0,0068) = 0,099

Полученное значение соответствует расчетам, приведенным в таблице (см. строка 6 таблицы).

∆ROE_ROS + ∆ROE_{K_обА} + ∆ROE_{Фнезавис.} = 30,03% + 76,46% + (-6,87%) ≈ 100%

Таким образом, проверка прошла успешно.

Вывод (трехфакторная модель Дюпона)

Рентабельность собственного капитала увеличилась на 9,9%.

На это повлияло 3 фактора:

1. рентабельность продаж;
2.  коэффициент оборачиваемости активов;
3. коэффициент финансовой независимости.

• За счет увеличения ROS с 0,144 до 0,161 произошло увеличение доходности собственного капитала на 0,0298, что составляет 30,03 % от изменения  между предыдущим и отчетным годами.

• За счет увеличения оборачиваемости активов с 1,1197 до 1,4207 произошёл рост показателя отдачи собственного капитала на 0,0757, что составляет 76,23 % от изменения  между предыдущим и отчетным годами.

• За счет уменьшение коэффициента финансовой независимости с 1,56 до 1,53 произошло уменьшение  на 0,006, что составляет -6,26 % от изменения  между предыдущим и отчетным годами.

Таким образом, наибольшее влияние на увеличение ROE оказало увеличение оборачиваемости активов. Увеличение величины  показывает, что один рубль собственного капитала стал отдавать большее количество рублей чистой прибыли, что является положительной тенденцией для развития предприятия.

Двухфакторная модель Дюпона: пример расчета

Для проведения факторного анализа рентабельности активов (ROA) воспользуемся данными из предыдущей задачи.

Исходные данные для анализа показателей рентабельности

Для решения задачи на основании исходных данных необходимо определить все сомножители формулы Дюпона.

Решение:

1. найдем базисную величину ROA за предыдущий год:

ROA₁ = ROS₁ * K_обА₁ = 0,144 * 1,1197 = 0,161

Определение влияния рентабельности продаж на ROA

2. определим условную величину ROA при изменении ROS:

ROA_ROS = ROS₂ * K_обА₁ = 0,161 * 1,1197 = 0,1803

3. определим абсолютное изменение ROA при изменении ROS:

∆ROA_ROS = ROA_ROS – ROA₁ = 0,1803 – 0,161 = 0,0193

4. найдем относительное изменение ROA при изменении ROS:

∆ROA_ROS / (ROA₂ – ROA₁) *100% = 0,0193 / 0,068 * 100% = 28,38 %

Определение влияния оборачиваемости активов на ROA

5. определим условную величину ROA при изменении K_обА:

ROA_{K_обА} = ROS₂ * K_обА₂ = 0,161 * 1,4207 = 0,2287

6. рассчитаем абсолютное изменение ROA при изменении K_обА:

∆ROA_{K_обА} = ROA_{K_обА} – ROA_ROS = 0,2287 – 0,1803 = 0,0484

7. определим относительное изменение ROE  при изменении K_обА:

∆ROA_{K_обА} / (ROA₂ – ROA₁) * 100% = 0,0484 / 0,068 * 100% = 71,18 %

Проверка (баланс уравнений)

∆ROA_ROS + ∆ROA_{K_обА} = 0,0193 + 0,0484 = 0,068

∆ROA_ROS = 0,068 * 100% = 6,8%

Полученное значение соответствует расчетам, приведенным в таблице (см. строка 6 таблицы).

∆ROA_ROS + ∆ROA_{K_обА} = 28,38% + 71,18% ≈ 100%

Таким образом, проверка прошла успешно.

Вывод (двухфакторная модель Дюпона)

Рентабельность активов увеличилась на 6,8%.

На это повлияло 2 фактора:

1. рентабельность продаж;
2.  коэффициент оборачиваемости активов.

• За счет увеличения рентабельности продаж с 0,144 до 0,161 произошло увеличение ROA на 1,93%, что составляет 28,38 % от изменения  между предыдущим и отчетным годами.

• За счет увеличения оборачиваемости активов с 1,1197 до 1,4207 произошёл рост показателя ROA на 4,84%, что составляет 71,18 % от изменения  между предыдущим и отчетным годами.

Таким образом, наибольшее влияние на увеличение ROA оказало увеличение оборачиваемости активов.

Также Вы можете по этой теме прочитать следующие статьи:

• Рентабельность собственного капитала ROE: Формула расчета. Примеры

Анализ DuPont разбивает ROE на составляющие компоненты, чтобы определить, какие из этих факторов наиболее ответственны за изменения ROE

Эта статья включена в раздел справки Budget-Plan Express – программного продукта для подготовки бизнес-планов в формате Word и Excel

Сегодня мы познакомимся с факторной моделью Дюпона. Мы рассмотрим 1-2-3 и 5-ти факторные модели, которые используются для анализа влияния различных факторов на рентабельность капитала. Отсюда и название модели – факторная модель.

В следующих статьях мы обязательно поговорим о современных факторных моделях, которые, кстати сказать, мало известны, и конечно же не идут ни в какое сравнение по популярности с факторной моделью Дюпона. Последовательный успех привел к тому, что модель #DuPont стала популярной во всех крупных корпорациях США. Сегодня анализ DuPont известен под многими другими названиями, включая DuPont Equation, DuPont Framework, DuPont Identity, DuPont Model, DuPont Method и т. д.

В следующих статьях мы обязательно поговорим о современных факторных моделях, которые, кстати сказать, мало известны, и конечно же не идут ни в какое сравнение по популярности с факторной моделью Дюпона. Последовательный успех привел к тому, что модель DuPont стала популярной во всех крупных корпорациях США. Сегодня анализ DuPont известен под многими другими названиями, включая DuPont Equation, DuPont Framework, DuPont Identity, DuPont Model, DuPont Method и т. д.

Название модели происходит от названия американской химической компании «DuPont». Но конечно же, у этой модели есть автор – Фрэнк Дональдсон Браун, и до того, как Фрэнк перешел в финансовый отдел в 1914 году, он работал в компании инженером-электриком и вряд ли мог тогда представить, что уже скоро войдет в историю как автор популярного метода финансового анализа…

Суть методики

Идея 20-х годов прошлого века, в основе которой была 2-х факторная модель, в дальнейшем была модифицирована в факторную модель в виде древовидной структуры, в основании которой – показатель рентабельности собственного капитала (ROE), разложенный по признакам, характеризующим операционную и финансовую деятельность. Проще говоря, факторы, влияющие на ROE, дробятся с целью выяснения: какие из них в большей или меньшей степени влияют на рентабельность собственного капитала. Формула рентабельность собственного капитала (return on equity, ROE), представляет индикатор отношения чистой прибыли к собственному капиталу:

Первое разложение ROE на два фактора представляется в виде формулы:

И здесь уже можно выделить рентабельность активов (return on assets , ROA), показатель характеризующий качество управления активами. Теперь в формуле ROE появился показатель, который учитывает все активы, а не только собственные средства:

Все эти манипуляции с показателями не имеют никакого математического смысла, ведь всегда можно добавить или удалить (сократить) любой показатель, и математический смысл от этого не изменится:

Важно другое, добавляя новый показатель, теперь мы его рассматриваем как фактор влияние на рентабельность собственного капитала. И в этом – вся суть и простота анализа Дюпона (DuPont analysis).

Теперь перейдем к 3-факторным и 5-факторным моделям.

Трехфакторная модель Дюпона

Следующая 3-факторная модель дает возможность оценить влияние структуры капитала на рентабельность собственного капитала. Легко понять, что рентабельность собственного капитала тем выше, чем ниже величина собственного капитала в структуре пассивов компании.

3-факторная модель представлена следующей формулой:

Здесь мы разложили ROE на 3 индекса, то есть построили трехфакторную модель ROE. Согласно анализу DuPont, рентабельность собственного капитала равна величине прибыли, умноженной на оборот активов, умноженной на финансовое плечо. Разделив ROE (#рентабельность собственного капитала) на три части, компании могут легче понять изменения в их ROE с течением времени.

Маржа прибыли – это показатель рентабельности. Это показатель ценовой стратегии компании и того, насколько хорошо компания контролирует расходы. Маржа прибыли рассчитывается путем нахождения чистой прибыли в процентах от общей выручки. Как одна из особенностей уравнения DuPont, если рентабельность компании увеличивается, каждая продажа приносит больше денег в чистую прибыль компании, что приводит к более высокой общей рентабельности капитала.

Пятифакторная модель Дюпона

Пятиэтапный анализ DuPont включает два дополнительных компонента, таким образом, развернутая 5-факторная модель представлена формулой:

Разложение рентабельности капитала на различные факторы представляет собой коэффициенты, полезные для компаний в фундаментальном анализе, где:

1. Бремя налогов (tax вurden ).
2. Бремя процентов (interest b urden).
3. Рентабельность продаж (return on sales).
4. Коэффициент оборачиваемости активов (asset turnover ratio).
5. Коэффициент капитализации или финансовый рычаг (leverage ratio).

Естественно, необходимо учитывать отраслевую специфику. Выраженную в процентах рентабельность капитала лучше всего использовать для сравнения компаний в одной отрасли.

Анализ очень важен для инвестора, поскольку он отвечает на вопрос, что на самом деле заставляет ROE быть тем, чем он является. Если есть увеличение маржи чистой прибыли без изменения финансового рычага, это показывает, что компания может увеличить свою прибыльность. Но если компания может увеличить рентабельность собственного капитала только за счет увеличения финансового рычага, это рискованно, поскольку компания может увеличивать свои активы за счет привлечения заемных средств.

Таким образом, нам нужно проверить, связано ли увеличение рентабельности собственного капитала компании с увеличением маржи чистой прибыли или коэффициента оборачиваемости активов (что является хорошим признаком) или только с кредитным плечом (что является тревожным сигналом).

Пример анализа DuPont с финансовым рычагом равным 1

Изучив новую концепцию DuPont, мы, должно быть, задаемся вопросом, проводится ли этот анализ также для компании, не имеющей долга? Будет ли этот анализ иметь такую ​​же полезность для компании, не имеющей долгов?

Пример разложения ROE на 5 факторов с финансовым рычагом равным 1:

Как видно из таблицы, DuPont одинаково полезен при анализе компании, не имеющей долгов. Вышеупомянутая формула остается той же, за одним исключением: компонент финансового рычага принимается равным 1, а остальное остается прежним. График показывает самый низкий показатель ROE в периоды с июня по август. Таким образом, анализ DuPont можно проводить по всем компаниям.

Читайте также:

Кредитные продукты. Методы и алгоритмы расчета

Типы и стоимость лицензий Budget-Plan Express

—–

Оригинал статьи смотрите на сайте www.strategic-line.ru. Этот материал вместе с другими примерами, смотрите разделе «Факторная модель Дюпона (DuPont model)».

Автор: Олег Мостовой (разработчик IT-проектов)

Модель Дюпона показывает, насколько эффективно работает собственный капитал для получения прибыли. Согласно этой методике, показатель рентабельности собственного капитала (ROE) раскладывается на составные части. Каждая последующая часть уравнения выражается через предыдущую. Для чего это нужно – будем разбираться в этой статье.

Как определяется рентабельность продаж – все хорошо знают. Но в оборотах участвуют также собственные и заемные средства. Можно, конечно, займы не привлекать – это зависит от того, как работают ваши собственные деньги и насколько эффективны ваши продажи.

Суть модели Дюпона – анализ ключевых показателей эффективности бизнеса по отдельности и в совокупности.

Что такое модель Дюпона

Итак, модель Дюпона описывает степень эффективности влияния нескольких факторов на рентабельность капитала компании. Чтобы было более понятно, приведу практический пример. Вы открываете бизнес, и на первоначальном этапе ваши вложения – 7 500 000 руб. (100 000 $ или 2 900 000 грн.). Ваша задача – определить, сколько прибыли принесут эти деньги. Сделать это можно, зная потенциальный объем продаж и величину заемного капитала (если таковой понадобится).

ROE (Return of equity) – это коэффициент рентабельности собственного капитала. Он показывает, сколько прибыли принесет каждый вложенный рубль. Мы помним, что аналогично определяется рентабельность продаж, которая считается как отношение прибыли к выручке. Ее расчет показывает, сколько прибыли приносит каждый заработанный рубль. Но, чтобы начать зарабатывать деньги, нужно вложить определенную сумму – из собственных средств или путем привлечения займа.

Вспоминаем, что такое оборотные средства. Это деньги, которые проходят через кассу или расчетный счет в целях расчетов с контрагентами. Иными словами, это средства, которые компания зарабатывает и тратит.

Оборотные активы – это материальные и товарные запасы, которые компания приобретает и расходует в течение жизненного цикла.

К оборотным активам не относятся основные средства (здания, оборудование, транспорт и др.), используемые в экономической деятельности предприятия.

Итак, в оборотном капитале участвуют:

• собственный и заемный капиталы;
• выручка.

Модель Дюпона позволяет проанализировать рентабельность каждого из этих показателей. То есть, рассчитать, сколько прибыли в отдельности приносит каждый источник образования оборотных средств. Этот метод был впервые применен компанией DuPont в начале XX столетия.

В чем ее смысл

Для начала следует определиться, сколько мы хотим зарабатывать. Понятно, что в первый год существования фирмы получать прибыль могут не все. Для начала нужно окупить вложения, а затем поставить цели.

Многие российские предприятия (речь идет о малом бизнесе) регистрируются с минимальным уставным капиталом. Таким образом, проанализировать его рентабельность часто бывает невозможно: как анализировать то, чего нет? Однако на начальном этапе учредитель так или иначе делает какие-то финансовые вложения – как минимум, чтобы открыть расчетный счет, заплатить за услуги банка и закупить первую партию товара. Чаще всего такая операция оформляется как беспроцентный заем учредителя, а средства играют роль финансового рычага.

Но со временем возможна закупка оборудования, транспортных средств и даже недвижимости, используемой в производственном процессе. Это довольно большие расходы, которые относятся к капиталовложениям. Задача модели Дюпона – определить, стоило ли приобретать такие дорогостоящие основные средства или проще было их арендовать. Иными словами, если компания увеличивает активы, значит, они должны приносить прибыль.

Прибыль рассчитывается через объем продаж, а степень эффективности использования активов – через коэффициент их оборачиваемости, обозначаемый как Коа.

Коа=Выручка/Активы.

Кто обращает внимание на эти показатели? Конечно же, инвесторы. В частности, изменение стоимости основных средств в большую сторону гарантирует инвестору получение своей доли в случае банкротства компании. Что касается ROE, то этот коэффициент важен на этапе развития деятельности, т.к. чем он выше, тем больший доход получит акционер.

Модель Дюпона определяет взаимосвязь между объемом продаж, стоимостью активов и размером собственных средств, а также влияние каждого из этих факторов на чистую прибыль предприятия.

Двухфакторная модель Дюпона: формула

Самая простая модификация модели Дюпона – двухфакторная. Ее формула включает две составляющие – рентабельность продаж и оборачиваемость активов.

Roa=ЧП/V*V/A, где:

Rоа – коэффициент рентабельности активов;

ЧП – чистая прибыль;

А – стоимость активов (используется усредненное значение за период с учетом начисленной амортизации);

V – объем продаж.

Если вы дружите с математикой, то несложно преобразовать эту формулу путем сокращения дробей. Полученный результат будет выглядеть так:
Rоа=ЧП/А.

Далее мы рассчитаем все показатели на примерах, а пока напомню, как рассчитывается чистая прибыль:

ЧП=V-Cconst-Cvar+ОД-ОР-НПР, где:

Cconst – постоянные расходы;

Cvar – переменные расходы;

ОД – операционные доходы;

ОР – операционные расходы;

НПР – налог на прибыль.

Трехфакторная модель Дюпона: формула

Трехфакторная модель используется наиболее часто и показывает зависимость между прибылью и собственными средствами через показатели продаж и размера активов.

ROE=ЧП/V*V/А*А/СК, где

СК – собственный капитал.

Последняя дробь в формуле (А/СК) представляет собой коэффициент капитализации.

Преобразовав эту формулу, получим:

ROE=ЧП/СК.

Напомню, что собственный капитал включает уставный, добавочный и резервный капиталы предприятия, целевые финансовые фонды и нераспределенную прибыль.

Пятифакторная модель Дюпона: модификация формулы

Формула, выраженная пятифакторной моделью Дюпона, содержит показатели операционной прибыли и прибыли до налогообложения:

ROE=ЧП/НОБ*НОБ/ПОД*ПОД/V*V/А*А/СК, где:

НОБ – налогооблагаемая база (т.е. прибыль до вычета налогов);

ПОД – прибыль от основной деятельности (без учета операционных доходов и расходов).

Преобразовав формулу, получаем:

ROE=ЧП/СК.

Вполне естественный вопрос: зачем нужны все эти показатели, если в процессе математических преобразований они сокращаются? Не проще ли взять только два показателя – чистую прибыль и собственный капитал, и получить верное, нужное нам значение?

Практическое значение и смысл модели Дюпона в том, чтобы до преобразований вычислить значение по каждой дроби в отдельности. Каждая составляющая формулы – это коэффициент, который необходимо учитывать и анализировать в динамике:

• ЧП/НОБ=TaxBurden – коэффициент налогового бремени;
• НОБ/ПОД=Interest Burden – коэффициент процентного бремени;
• ПОД/V – рентабельность продаж;
• V/A – коэффициент оборачиваемости активов;
• А/СК – коэффициент капитализации (финансового рычага).

Далее, на практическом примере мы будем рассчитывать все эти коэффициенты в отдельности для разных периодов и посмотрим, какой из них существенно влияет на рентабельность собственного капитала, рассчитываемый по модели Дюпона.

Практическое применение

Детальный анализ каждого коэффициента позволяет определить основные риски. Так, увеличение расходов на уплату процентов может свидетельствовать о таких факторах, как:

• увеличение кредитной нагрузки;
• повышение ставки рефинансирования;
• изменение кредитной политики банка.

Понятно, что на второй фактор (повышение ключевой ставки) мы повлиять никак не можем, а вот остальные вполне можно подкорректировать: сменить банк или направить все усилия на сокращение задолженности по кредиту.

Далее проанализируем коэффициент налогового бремени. Ставки налогов устанавливаются государством, и их мы менять не можем (если только компания имеет право на налоговые льготы, которыми стоит воспользоваться). Кроме того, можно пересмотреть расходы за счет чистой прибыли – возможно, какие-то из них компания вправе отнести на расходы, внеся изменения в учетную политику или прибегнув к помощи квалифицированных юристов. Так, дебиторскую задолженность с истекшим сроком исковой давности можно относить на расходы при наличии правильно оформленных документов. Резерв по сомнительным долгам также разрешается принимать в качестве расхода в налоговом учете.

Что касается оборачиваемости активов, то здесь есть один важный нюанс. В формуле Дюпона активы учитываются по балансовой стоимости, которая может существенно отличаться от рыночной. Подставлять в формулу значения рыночной стоимости основных средств некорректно. Но можно сравнить ROE, рассчитав для себя оба значения – по рынку и учетной стоимости. Эта дельта поможет вам оценить риски. К примеру, в самом неблагоприятном случае, если объекты основных средств придется продавать – сколько денег это нам принесет и насколько эффективно эти деньги можно использовать. И наоборот, если мы вдруг решим продать основное средство, сколько мы потеряем, лишившись единицы производственных мощностей.

Иными словами, имея все данные под рукой, специалист проводит сравнительный анализ влияния отдельных показателей на рентабельность капитала не только по модели Дюпона, но также с применением других методик, в том числе разработанных собственноручно.

Плюсы и минусы

Главным достоинством модели Дюпона является ее простота и гибкость – можно использовать двухфакторную, трехфакторную или пятифакторную формулу в зависимости от того, насколько глубокий анализ вам требуется.

Данные можно взять из показателей финансовой отчетности, которая находится в открытом доступе. Так что потенциальный инвестор может с легкостью провести необходимые расчеты.

Как и любая другая методика финансового анализа, модель Дюпона имеет и недостатки. В основном они относятся к анализу стоимости активов. Об одном недостатке мы уже упомянули – балансовая и рыночная стоимость активов – это небо и земля. К примеру, недвижимость учитывается на балансе по кадастровой стоимости, которая существенно отличается от фактической.

Если активы приобретены с использованием заемных средств, то правильнее учитывать в их стоимости проценты по кредитам банков. Этот момент моделью также не предусмотрен.

Кроме того, бухгалтерскую отчетность не всегда можно с уверенностью брать за основу для финансового анализа. Основная причина в том, что доходы и расходы в отчетности отражаются по методу начисления, что не всегда дает реальную картину. К примеру, в конце периода можно провести крупную сделку при минимальных расходах и ждать денег от покупателей не один месяц. Помимо этого, с целью сблизить налоговый учет с бухгалтерским, некоторые расходы нормируются и не отражены в полном объеме. Например, деньги по страховке за автомобиль заплачены сейчас, а на расходы эта сумма будет списываться целый год.

Тем не менее, модель Дюпона позволяет провести экспресс-анализ влияния отдельных факторов на рентабельность капитала компании.

Формула Дюпона: пример расчета

Сначала мы приведем пример расчета ROE по формуле Дюпона, используя пятифакторную модель, а затем перейдем к более реалистичным примерам из практики.

Итак, возьмем исходные данные из бухгалтерской отчетности. Отрасль деятельности компании – розничная торговля. Единица измерений – тыс. руб. Желтым цветом выделены нужные показатели.

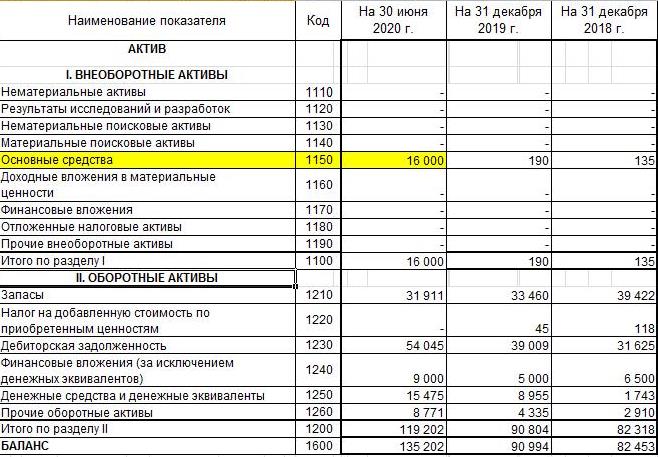
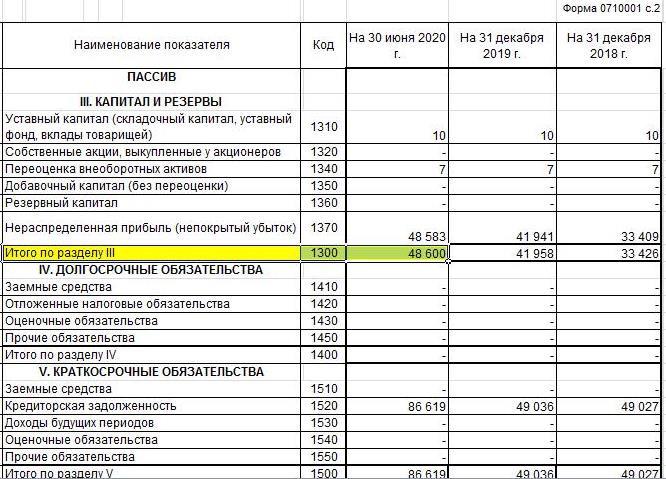
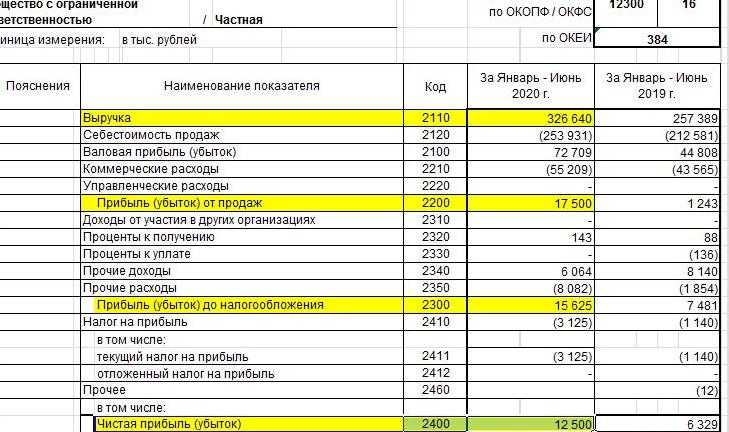
Занесем необходимые параметры в таблицу:

Показатель	Значение, тыс. руб.
Чистая прибыль (ЧП)	12500
Выручка (V)	326640
Стоимость активов (А)	16000
Собственный капитал (СК)	48600
Прибыль от основной деятельности (ПОД)	17500
Прибыль до вычета налогов (НОБ)	15625

Рассчитаем коэффициенты:

Наименование коэффициента	Формула	Решение	Результат
RoS (рентабельность продаж)	RoS=ПОД/V	17500/326640	0,0536
Коа (коэффициент оборачиваемости активов)	Коа=V/А	326640/16000	20,4150
LR (коэффициент капитализации)	LR=А/СК	16000/48600	0,3292
IB (коэффициент процентного бремени)	IB=НОБ/ПОД	15625/17500	0,8929
TB (коэффициент налогового бремени)	TB=ЧП/НОБ	12500/15625	0,8000
ROE (рентабельность собственного капитала)	ROE=Ros*Коа*LR*IB*TB	0,0536*20,4150*0,3292**0,8929*0,8000	0,2573

Если выразить ROE в процентах, то получим результат – 25,73%, что является нормой для розничной торговли.

Excel для расчета

Для быстрого расчета коэффициентов удобно использовать электронные таблицы Excel. Все составляющие, включая виды расходов, можно занести в ячейки из данных управленческой и бухгалтерской отчетности.

Приведем максимально развернутый пример расчета показателей эффективности работы компании по формуле Дюпона в Excel:

Наименование показателя	6 месяцев 2020	6 месяцев 2019
Выручка	326640	257389
Себестоимость товара	253931	212581
Валовая прибыль	72709	44808
Аренда помещения	14305	12520
Заработная плата	28383	21037
Налоги и отчисления	7521	6952
Расходы на логистику	2986	1800
Расходы на рекламу	1519	918
Амортизация	260	201
Услуги связи	180	111
Канцелярские товары	25	19
Хозяйственные расходы	30	7
Итого расходы	55209	43565
Прибыль от основной деятельности	17500	1243
Проценты по депозиту	143	88
Итого операционные доходы	143	88
Услуги банка	82	67
Проценты по кредиту		136
Итого операционные расходы	82	203
Премии поставщиков	6064	8140
Итого внереализационные доходы	6064	8140
Премии покупателям	8000	1787
Итого внереализационные расходы	8000	1787
Прибыль до вычета налогов	15625	7481
Налог на прибыль	3125	1152
Чистая прибыль	12500	6329
Активы	16000	190
Собственный капитал	48600	36672
RoS	0,0536	0,0048
Коа	20,4150	1354,6789
LR	0,3292	0,0052
IB	0,8929	6,0185
TB	0,8000	0,8460
ROE	0,2572	0,1726

Использование на реальном примере

Теперь, когда у нас есть все коэффициенты, рассчитанные за 2 периода, мы можем проанализировать их изменение и сделать выводы: что произошло с компанией за год.

Первое, что бросается в глаза, – это высокий коэффициент финансового рычага (LR), который, однако, снизился в 2020 году в связи с приобретением основных средств.

Финансовый рычаг Дюпона показывает, какая часть активов финансируется за счет собственного капитала. Не следует путать это понятие с определением финансового рычага как кредитного плеча, которое показывает соотношение собственного капитала и заемных средств.

В 2020 году стоимость основных фондов составляет примерно треть от собственного капитала, при этом нераспределенная прибыль увеличилась так же – примерно на треть (48600/36672*100%).

А вот коэффициент процентного бремени снизился. Это произошло за счет того, что в 2020 году прочие расходы (т.е. затраты, не относящиеся напрямую к основной деятельности), стали намного меньше влиять на прибыль до налогообложения. Сравните доход от продаж (1243 тыс. руб.) и прибыль до вычета налога (7481 тыс. руб.) за 2019 год. Мы видим, что львиную долю дохода компания получала не за счет выручки от реализации, а за счет премий, полученных от поставщиков. Такая ситуация может складываться, но с бонусами лучше быть осторожнее, т.к. они не облагаются НДС, что может послужить поводом для налоговой проверки. В 2020 году этот дисбаланс был ликвидирован.

Что касается коэффициента налогового бремени, то по данным бухгалтерской отчетности его значение всегда будет около 0,8, т.к. ставка по налогу на прибыль в РФ – 20%. В некоторых случаях в расчете этого показателя могут участвовать финансовые санкции (пеня и штрафы).

Таким образом, ROE по формуле Дюпона увеличился в результате факторов:

• увеличения стоимости основных фондов;
• повышения рентабельности продаж;
• снижения налогового бремени.

Заключение

Как видите, модель Дюпона помогла нам разобрать сильные и слабые стороны компании. Если бы рентабельность собственного капитала рассчитывалась через преобразованную формулу, полной картины бы не получилось.

Если ROE, рассчитанный по модели Дюпона, снижается, – это не обязательно должно быть поводом для беспокойства. Тому есть вполне объяснимые причины. Например, в первый год после покупки оборудования компания может применять ускоренную амортизацию. Это увеличит расходы и снизит стоимость основных фондов. Поэтому вполне возможно, что в 2021 году ROE начнет снижаться.

Чтобы получить максимально полное представление о том, что влияет на рентабельность капитала, следует использовать данные не только бухгалтерского, но также управленческого учета. Если данные берутся только из бухучета, рекомендуется запросить структуру затрат, как в разобранном нами примере. Это даст возможность проанализировать все статьи расходов, в частности, ту же амортизацию, которая по факту расходом не является, т.к. за нее не нужно платить, однако сумма начисленного износа влияет на стоимость активов.

Для российской экономики нормальный показатель ROE – примерно 15-20% (в нашем примере – 25,72%). На эту величину ориентируются инвесторы при покупке акций компании.

Необходимо учитывать и отраслевой фактор. Так, в капиталоемких отраслях (строительство, добыча ресурсов, промышленное производство и т.д.) ROE будет значительно выше, чем у ресурсоемких компаний (например, оказание услуг).

Трехфакторная модель Фама-Френча оценки доходности финансового инструмента (ценной бумаги), как продолжение однофакторной модели  Capital Asset Pricing Model (CAPM). Учет риска капитализации компании и стоимостного риска ее ее акций. Основные подходы формирования инвестиционного портфеля, исходя из трехфакторной модели. Многофакторный подход в инвестировании.

Содержание:

• Введение. Коровьев-Фагот, бином Ньютона и “Факторная модель экспоненты”
• Начало. CAPM, как 1F-модель
• Появление 3F-модели Фама-Френча
• Премия за размер, SMBP (Small Minus Big Premium)
• Премия за стоимость. HMLP (High Minus Low Premium)
• 3F-модель. Немного практики
• Достижения и значение 3F-модели. Повышение факторности
• Что дальше? Все выше и выше
• Примечания и ссылки
• Используемые сокращения

Введение. Коровьев-Фагот, бином Ньютона и “Факторная модель” экспоненты

“Ну да, неизвестно,- послышался все тот же дрянной голос из кабинета, 

– подумаешь, бином Ньютона!”

М. Булгаков “Мастер и Маргарита”

“Дрянной голос из кабинета” принадлежал Коровьеву-Фаготу, персонажу “Мастера и Маргариты” Михаила Булгакова, “гражданину престранного вида с глумливой физиономией”[1]. Общеизвестный факт. 

Вряд ли далеко неглупый Коровьев считал бином Ньютона чем-то уж слишком мудреным. В нем нет ничего сложного. Изучается  бином Ньютона еще в старших классах средней школы в курсе “Алгебра и основы математического анализа”[2]. 

Для тех, кто не в курсе, бином Ньютона – “формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных”[3]:

(формула 1)

биноминальные коэффициенты, n – целое неотрицательное число, n!=1*2*3*…*(n-1)*n – (факториал числа n).

Cn^k – число сочетаний из n по k.

Для частных случаев n=1, 2, 3 бином Ньютона приобретает привычный уже для школьника 5-6 класса вид:

(a+b)¹=a+b. первая степень суммы;

(a+b)²=a²+2ab+b², квадрат суммы;

(a+b)³=a³+3a²b+3ab²+b³, куб суммы.

Бином Ньютона – частный случай разложения функции (1+x)^r в ряд Тейлора:

(формула 2)

В свою очередь, используя второй замечательный предел[4]:

(формула 3)

где: e – число “e”, основание экспоненты и натурального логарифма, равное примерно 2,71828, можно вывести знаменитую формулу разложения экспоненты в степенной ряд:

(формула 4)

При x=1 формула 4 позволяет вычислить число “е” с любой степенью точности, добавляя новые члены степенного ряда. 

Результаты несложных вычислений сведем в следующую таблицу:

таблица 1

Здесь: n – число членов степенного ряда разложения экспоненты, 

n=1, имеем ряд из одного члена – 1;

n=2, два члена 1+1/1!=2;

n=3, три члена 1+1/1!+1/2!=2,5 и т.д.

При оценке числа “е” ориентируемся на его “точное” значение с пятью знаками после запятой 2,71828. Видно, что уже при n=4 получаем достаточно приличное приближение с относительной ошибкой в 1,90%, а при n=5 погрешность падает и вовсе до 0,37%.

Введем понятие “Факторной модели” для оценки числа “е” или, в общем, для разложения экспоненциальной функции e^x в степенной ряд с конечным числом членов (слагаемых). 

Так, разложение вида:e^x =1+x/1!=1+x, с двумя членами, содержащее х в первой степени (линейная зависимость), назовем “однофакторной моделью” для функции e^x . 

Соотношение e^x=1+x/1!+х²/2!=1+x+x²/2, с тремя членами, с х в квадрате, назовем “двухфакторной моделью”, e^x=1+x/1!+х²/2!+х³/3!=1+x+x²/2+x³/6, с четырьмя членами, содержащее х в кубе, назовем “трехфакторной моделью” экспоненты и т.д. В нашей таблице “факторность”=4, то есть имеем дело с четырехфакторной моделью оценки (в данном случае) числа “е”. 

Очевидно, что, чем выше факторность модели, тем точнее получается выражение для приближения экспоненциальной функции, и, как следствие, числа “е”.

Начало. CAPM, как 1F-модель

Перейдем от стройной, бесконечно красивой и предсказуемой математической вселенной к полному риска, угроз и подводных камней, миру реальных инвестиций и нервного трейдинга. 

В материале, посвященном Альфе-критерию в инвестировании подробно изложена суть CAPM модели (Capital Asset Pricing Model) для оценки доходности бумаги/портфеля. 

Напомним главную формулу CAPM с учетом Альфа-компоненты (α) :

E(R_i)=α+R_j+β_i*(E(R_m)-R_j)

(формула 5)

где: E(R_i) – ожидаемая (рассчитываемая) доходность i-ой акции;

R_j – безрисковая ставка доходности, допустим доходность гособлигаций;

E(R_m) – доходность рыночного портфеля R_m, обычно доходность фондового индекса (S&P500, Доу-Джонс и др.), часто говорят – “бенчмарк”;

β_i –  Бета-коэффициент  i-ой акции по рынку (индексу/бенчмарку) R_m.

Авторы концепции CAPM Уильм Шарп и Майкл Дженсен полагали, что доходность ценной бумаги определяется одним фактором – фактором рыночного риска, формализованным в премию за рыночный риск E(Rm)-Rj. В этом смысле, CAPM вполне имеет право именоваться однофакторной моделью (1F-моделью) оценки доходности финансового актива. 

Разными авторами были предприняты попытки исследовать временную динамику премии за рыночный риск. Один из графиков[5] имеет вид:

Премия за рыночный риск в годовом исчислении в 1965-2000 гг.

(график 1 по премиям)

Максимального значения в 20% за указанный период премия достигает дважды. Где-то между 1985 и 1990 годами, рядом с “черным понедельником” 19.10.1987, дня максимальной дневной волатильности индекса Доу-Джонса, потерявшего за одну сессию легендарные 22,61%. И ближе к краху доткомов 10 марта 2000 года. В 1970-1980 гг. премия находилась преимущественно в отрицательной области. 

Если доходность некоей i-ой акции отличается от суммы безрисковой ставки R_j и произведения премии за риск на бету в большую сторону, то по мысли “отцов” 1F-модели имеет место положительная Альфа. Значит инвестиционный менеджер большой молодец, он обыграл рынок. В противном случае – победа за бенчмарком. Таким образом, подобные отклонения регулируются и объясняются всего лишь Альфа-критерием.

Теория была стройна, изящна и объясняла многое. За труды в области CAPM с формулировкой “За вклад в теорию формирования цены финансовых активов” У. Шарп (совместно с Г Марковицем и М. Миллером) в 1990 г. удостаивается премии по экономике имени Альфреда Нобеля[6]. 

Но, как впоследствии выяснилось, 1F-модель CAPM не дает толкование некоторым сравнительно тонким вещам в инвестиционной деятельности. Списывать частые удачи (большую положительную Альфу) отдельного (и довольно) большого класса инвесторов на божественный дар управления инвестпортфелем удавалось с трудом. И чем дальше – тем больше. Назрела насущная потребность повысить факторность модели оценки доходности финансовых активов. 

Идея витала в воздухе. 

Появление 3F-модели Фама-Френча

В 1993 году[7] (по другим источникам в 1992 г.) Юджин Фама, Eugene F. Fama и Кеннет Френч, Kenneth R. French вводят трехфакторную модель, названную по их именам: “Трехфакторная модель Фама-Френча”, далее по тексту используется сокращение “3F-модель Фама-Френча” или просто “3F-модель”.

Несколько слов о “действующих лицах”. 

Юджин Фама (слева) и Кеннет Френч (справа)

Ю. Фама уже был подробно представлен на страницах нашего сайта, как экономист, оставивший существенный след в развитии гипотезы эффективного рынка (EMH). Прежде всего, как автор классификации форм рыночной эффективности (слабая, средняя и сильная). Представитель Чикагской экономической школы. Нобелевский лауреат 2013 года. Родился в 1939 г.

Кеннет Френч принадлежит к более молодому поколению ученых. Он на 15 лет моложе Фама (1954 г.р.). Работает в Tuck бизнес-школе Дартмутского колледжа, Ганновер, штат Нью-Гемпшир. Трехфакторная модель – пока его самое знаковое достижение.

В чем смысл новации от Фама и Френча? 

Повышение факторности модели оценки финансовых активов. Скачок от одно- к трехфакторности. Говоря языком физики, переход от финансово-экономического одномерного “пространства”, в котором “объект” (доходность акции) перемещается по прямой, к трехмерному континууму, в котором он имеет три степени свободы. 

Юджин Фама и Кеннет Френч расширяют базовую формулу CAPM для доходности акции, введя два новых члена:

E(R_i)=α+R_j+β_i*(E(R_m)-R_j) +γ*SMBP+φ*HMLP

(формула 6)

где: SMBP (Small Minus Big Premium) – “премия за размер”, обусловленная риском превышения в портфеле компаний малой капитализации над компаниями большой капитализации;

HMLP (High Minus Low Premium) – “премия за стоимость”, возникающая от наличия в портфеле недооцененных акций;

γ, φ – коэффициенты линейной регрессии по SMBP и HMLP соответственно. 

Формула 6 может быть интерпретирована, в том числе, и так. Доходность акции складывается из четырех видов доходности (премий):  доходности безрискового инструмента, общей скорелированной Бетой доходности фондового рынка и доходностей, обусловленных риском владения акциями малых компаний и недооцененными акциями. 

По-прежнему, первым слагаемым в формуле 6 от Фама-Френча, как и формуле 5 от Шарпа-Дженсена, идет Альфа-критерий (α). Но это разные Альфы. Большие α в формате Шарпа-Дженсена приписывают портфельным управляющим куда большее мастерство, чем у Фама-Френча. Из Альфы однофакторной модели Шарпа-Дженсена Фама и Френч вырезают большой кусок, введя два новых фактора. 

Профдеятельность инвестора и трейдера связана с большим количеством разнообразных рисков. Они в них “купаются”. Каждую минуту. Чем (помимо прочего) и отличаются от математика и физика. За что и получают вознаграждения на порядки больше.

CAPM работает с одним видом риска – риском рынка, market risk. 3F-модель добавляет риск размера, size risk, и риск стоимости (недооценки), value risk. Пропущенная через спектр size-value картина становится более объемной и многогранной. Становится более реальной. 

Тот, кто сознательно идет на дополнительные риски, отклоняя портфель от среднего положения, получает премии. Во всех смыслах. Инвестор не должен быть гением, уровня Леонардо в живописи, гоняясь за супер-Альфой в однофакторной CAPM-модели. Все гораздо “проще” – надо правильно учесть и корректно рассчитать дополнительные риски.

Премия за размер, SMBP (Small Minus Big Premium)

Двусмысленное изречение “Размер имеет значение” отлично работает на фондовом рынке, в смысле размера фирмы. Добавление в портфель акций компаний с низкой капитализацией повышает его волатильность и, при благоприятных условиях, может повысить его доходность. 

Общая идея вычисления премии за размер, SMBP состоит из трех этапов.

1. По определенной методике формируются  две группы компаний – с наибольшей и наименьшей капитализацией на данной торговой площадке, в корзине данного индекса и т.д. 
2. За выбранный период рассчитывается усредненная доходность по каждой группе. Пусть доходность акций крупнейших компаний составляет R(cap_max), а бумаг их небольших визави – R(cap_min).
3. Премия за размер выводится, как SMBP=R(cap_min)-R(cap_max).

Это крупными мазками, для ясности. Как всегда, возможно использование весов, усреднений, балансирующих и корректирующих коэффициентов и пр.

Источником информации для инвестора могут послужить профильные интернет-ресурсы. Например, базы данных сайта CRSP – Center for Research in Security Prices (Центр по изучению ценных бумаг). Наглядно увидеть масштаб разделения между крупными и малыми компаниями в режиме реального времени позволит Stock Screener от Finviz.

По уровню капитализации Finviz-скринер разбивает компании на шесть сегментов: от мега- до нано-компаний:

1. Mega (мега) от $200 млрд.
2. Large (крупные) $10-$200 млрд.
3. Mid (средние) $2-$10 млрд.
4. Small (небольшие) $0,3-$2 млрд.
5. Micro (микро) $50-$300 млн.
6. Nano (нано) до $50 млн.

Вот картинка по мега-компаниям на 25.12.2019. 

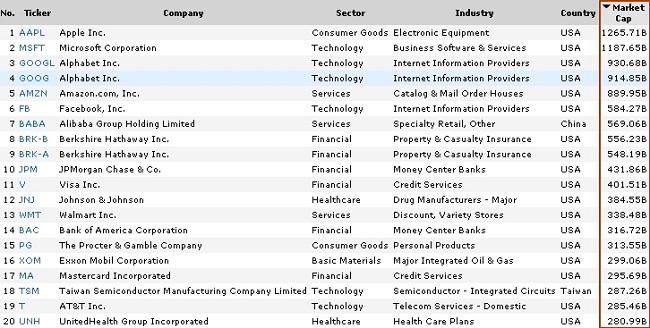
Первая двадцатка крупнейших по капитализации публичных компаний

Версия Finviz, 25.12.2019

Знакомые, у всех на слуху, мировые бренды. Лидеры – Apple, $1265 млрд и Microsoft, $1187 млрд. Прочие не дотягивают до триллиона долларов.

Самая маленькая у Finviz нано-компания на 25.12.2019 – Amira Nature Foods (ANFI) стоит “смешные” $0,8 млн.

Ниже приведен список двадцати публичных нано-компаний с наименьшей капитализацией. От меньшей – к большей.

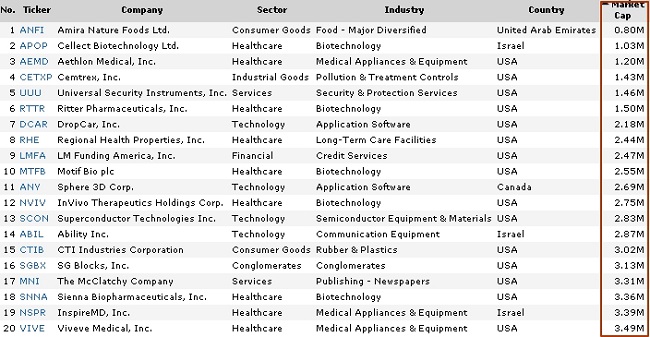
Первая двадцатка публичных компаний стоимостью до $50млн (по мере возрастания их капитализации)

Версия Finviz, 25.12.2019

25 декабря 2019 г. Apple Джобса и Кука стоит дороже арабских Amira Nature Foods в фантастические 1581250 (1,58 млн!) раз. Безусловно нет большого смысла комбинировать в одном портфеле такие позиции в ожидании супер-премии за размер SMBP. Тем более, что в данном конкретном случае, акции ANFI с апреля 2019 г. показывают отрицательную доходность, тогда как, бумаги AAPL неуклонно росли:

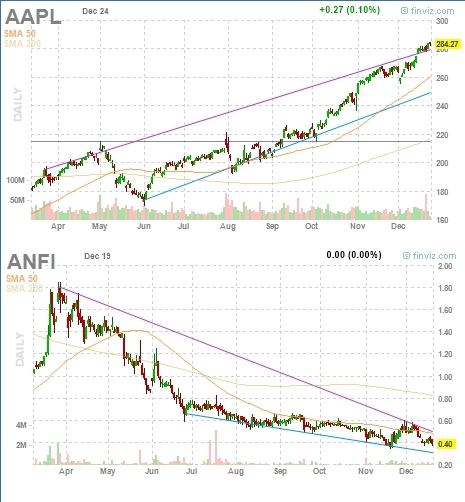
Более разумным представляется объединение не столь полярных категорий, а предположим, Large и Micro или Mid и Small. На практике часто используют медианный подход. Балансируют портфель из акций компаний, капитализация которых находится выше и ниже медианного уровня капитализации по выбранной бирже (индексу), допустим, по NYSE.

Цитируемый ранее источник[5] приводит следующую динамику премии за размер в последней трети прошлого века:

Премия за размер SMBP  в годовом исчислении в 1965-2000 гг.

(График 2 по премиям)

Тенденции совсем иные, нежели в премии за рыночный риск (см. график 1 по премиям). Максимум SMBP, чуть ниже 20%, приходится на 1970-ый и 1980-ый годы, тогда как в 1980 г. премия за market была в районе нуля. И, напротив, в период бурного роста премии за рыночный риск в 1995-2000 гг., SMBP неуклонно снижалась от крайне небольших положительных уровней, глубоко заходя в отрицательную область. 

Премия за стоимость. HMLP (High Minus Low Premium)

Рассмотрение стоимостных/недооцененных акций отсылает нас к истокам стоимостного анализа акций и стоимостного инвестирования, Value investing. 

Главный вопрос вокруг которого крутится все стоимостное инвестирование – истинная, внутренняя, фундаментальная стоимость акции (intrinsic/fundamental value) и ее соотношение с текущей рыночной ценой. Если рынок идет ниже внутренней стоимости, акция считается недооцененной, ниже – переоцененной. В первом случае бумагу берут в лонг, во втором – в шорт. Положительную разницу между внутренней и биржевой ценой называют “запасом прочности” или “пределом безопасности”, Margin of Safety. Чем выше запас прочности по акции, тем выше потенциальная премия, HMLP по ней.

В теории все ясно, даже банально. Тривиальность резко заканчивается непосредственно перед отбором стоимостных акций. Единого рецепта не существует. Цитата от многолетнего последовательного сторонника Value investing “Волшебника из Омахи” Уоррена Баффетта: “Для вычисления истинной стоимости не существует никакой формулы. Вы просто должны хорошо знать тот бизнес, в котором собираетесь покупать пакет акций”[8].

Простейшим критерием стоимостной оценки акции признается отношение P/B, рыночной цены бумаги к ее балансовой стоимости. Можно сказать и так: отношение рыночной капитализации компании к ее чистым активам (собственному капиталу)[9]. 

(Другим стоимостным индикатором служит P/E –  отношение рыночной цены акции к прибыли на одну акцию)

Традиционно принимают:

P/B<<1 существенно недооцененные акции;

P/B<1 недооцененные акции;

P/B>1 переоцененные акции;

P/B>>1 существенно переоцененные акции.

(Акции с P/B>1 и P/B>>1  называют растущими, growth акциями)

Finviz-скринер, отбирающий бумаги по фундаментальным показателям, классифицирует уровни P/B следующим образом:

P/B<1 – низкий (low);

P/B>5 – высокий (high).

Для более тонкой настройки по P/B введены десять категорий коэффициента класса Under (под, ниже): от Under 1 до Under 10; и класса Over (над, выше): от Over 1 до Over 10.

Задав low P/B<1 для нано-компаний, и отранжировав их по мере роста капитализации, получим такой список:

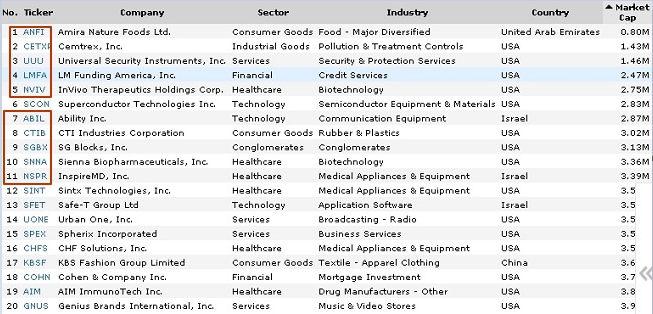
Первая двадцатка публичных компаний стоимостью до $50млн с P/B<1 (по мере возрастания их капитализации)

Версия Finviz, 25.12.2019

Нано-двадцатка с P/B<1 (двадцатка-2) заметно отличается от нано-двадцатки (двадцатки-1), не прошедшей через какой-либо фильтр, приведенной выше. Красными рамками выделены компании, попавшие в оба перечня. Очевидно, что за пределами двадцатки-2 остались ряд компаний начала и середины двадцатки-1 с капитализацией ниже $3 млн. По всей видимости, их P/B>1. 

Согласно источнику[5], премия за стоимость (недооцененность) в 1965-2000 годах вела себя следующим образом:

Премия за стоимость HMLP  в годовом исчислении в 1965-2000 гг.

(График 3 по премиям)

Максимумы HMLP приходятся на 1977/78 и 1986/87 годы. Интересно, что в районе 1980/81 гг. HMLP топталась возле нулевой отметки, тогда, как премия за размер, SMBP была на пике. К 2000 году и HMLP, и SMBP дружно нырнули под ноль, а market risk премия рванула вверх. 

3F-модель. Немного практики

Формирование портфеля на основе трехфакторной модели дает инвестору достаточно места для креатива и управленческой смекалки.

Общие этапы построения трехфакторного портфеля выглядят следующим образом.

1. За базу берется индекс. Проще говоря, инвестпортфель с той или иной степенью точности копирует выбранный индекс. Получаем индексный фонд. Это достигается различными путями. Если корзина индекса невелика, как у промышленного индекса Доу-Джонса с его 30 компаниями, не столь уж трудно самостоятельно приобрести все позиции, выдержав требуемый масштаб. 

Для S&P500 задачка выглядит потруднее. Здесь на помощь придут ценные бумаги взаимных индексных фондов, заточенных под S&P500, например из линейки Vanguard 500; торгуемых на бирже фондов (ETF), самый известный – SPDR S&P 500 ETF Trust (тикер SPY), а также фьючерсы на индекс.

2. Индексный портфель разбавляется (отклоняется) акциями компаний малой капитализации и/или недооцененными бумагами. Методики ввода акций, генерирующих HMLP и SMBP, множественны и разнообразны. Именно здесь – точка приложения мастерства и профессионализма инвестиционного управляющего.

Для оценки премий SMBP и HMLP по выбранному рынку/отрасли/стране создаются и анализируются группы теоретических портфелей.

Один из вариантов процедуры выглядит так.

1. Отбираются акции высокой и низкой капитализации. Обычно, по медианному методу  (см. выше). Результат – два инвестпортфеля. Назовем их ИП(cap_min) и ИП(cap_max).

2. Отбираются акции по коэффициенту P/B. Группируются три портфеля. В первый, ИП(P/B_min) войдут бумаги с минимальным P/B, P/B<<1, значительно недооцененные акции. Во второй, ИП(P/B_mid) – бумаги со средним P/B, допустим: 0,5<P/B<1,5. В третий, ИП(P/B_max), с высоким P/B, пусть с P/B>5, high-показатель по версии Finviz. Примем, что в ИП(P/B_min) – k штук акций, в ИП(P/B_mid) – m штук, в ИП(P/B_max) – v штук. Принятая пропорция: k/m/v=3/4/3. То есть, предположим, по 30, 40 и 30 позиций соответственно. 

3. Далее, путем пересечения сформированных ИП, выделяют шесть новых портфелей:

таблица 2

В ИП(S/L) попадают акции недооцененные акции небольших компаний, в ИП(B/H) – переоцененные бумаги компаний с большой капитализацией и т.д. “⋂” – знак пересечения.

На практике, портфели можно формировать пропуская базовые ИП(cap_min) и ИП(cap_max) через фильтры по P/B. Скринеры акций, подобные Finviz, прекрасно реализуют подобную опцию.

Оценкой для премии за размер SMBP будут разности усредненных доходностей портфелей ИП(S/L), ИП(S/M) и ИП(S/H) с одной стороны и портфелей ИП(B/L), ИП(B/M) и ИП(B/H) с другой: 

SMBP=1/3[R(ИП(S/L))+R(ИП(S/M))+R(ИП(S/H))]-

-1/3[R(ИП(B/L))+R(ИП(B/M))+R(ИП(B/H))]

(формула 7)

где: R(ИП(_/_) – доходности исходных инвестпортфелей.

В качестве ориентира премии за стоимость HMLP могут быть взяты разности средних доходностей портфелей ИП(S/L) и ИП(B/L) с одной стороны и ИП(S/H) и ИП(B/H) с другой:

HMLP=12[R(ИП(S/L))+R(ИП(B/L))]-1/2[R(ИП(S/H))+R(ИП(B/H))]

(формула 8)

Знаки у коэффициентов линейной регрессии γ, φ формулы 6 трехфакторной модели таковы. 

γ при SMBP положительны для портфелей, с акциями малой капитализации, и наоборот, для портфелей с “дорогими” компаниями γ<0. 

φ при HMLP положительны для портфелей, со стоимостными акциями (P/B<1), для портфелей с акциями, у которых P/B>1, φ<0.

Исторические данные по SMBP, HMLP и другим параметрам трехфакторной модели в различных секторах отдельных национальных экономик доступны на веб-странице Tuck бизнес-школы Дартмутского колледжа, постоянно обновляемой Кеннет Френчем. 

Достижения и значение 3F-модели. Повышение факторности

Трехфакторная модель Фама-Френча неплохо зарекомендовала себя после появления в начале 1990-х. В целом, она объясняет уровни доходностей 90% диверсифицированных, отклоненных от центра (от индекса) инвестиционных портфелей. Показатель “старой” однофакторной CAPM – 70%[10]. 

Многочисленные выкладки показали, что на длинных горизонтах премии за размер и за стоимость, SMBP и HMLP, демонстрируют устойчивые, и (что важно) предсказуемые значения по данным корзине, сектору и стране. Для каждого рынка существуют свои “трехфакторные” наборы параметров. 3F-Инвестор осознанно получает значительные конкурентные преимущества. 

Загадочная Альфа, занимающая в CAPM 30% доходности, сужается в 3F-модели до 10%. Значительный скачок, согласитесь. 

Тем не менее, работы у инвестора, по-прежнему, немало. Ключевая задача – поиск оптимального соотношения между тремя факторами риска (премий) для формирования портфеля заданной доходности или, просто, для ее максимизации. Главное – обогнать индекс.

Трехфакторная модель получила не только лавры, но и критику. В частности, она не всегда давала удовлетворительные результаты для развивающихся рынков, emerging markets. Стоимостной фактор работает неплохо, а вот фактор размера (капитализации) проваливается. В 2013 году Foye, Mramor и Pahor высказали идею замены SMBP.

Но магистральным путем любого приближения, от экспоненты до доходности финансового актива, остается не замещение или модернизация уже привычных и доказавших свою работоспособность компонентов формулы доходности, а добавление новых. Другими словами, повышение факторности модели. 

В 1997 году М. Кэрхарт, M.M. Carhart представляет на суд публике четырехфакторную модель (4F-модель). 

Новация М. Кэрхарта состояла в ведении компоненты инерции, момента (модель именуется также моделью Моментума/Моментум-эффекта) WMLP – Winners Minus Losers Premium. Название емкое и хлесткое – премия по фактору “победители минус проигравшие”. Рассчитывается, как разница средней доходности акций компаний, показавших лучшую динамику за предыдущие 11 месяцев (победителей), и средней доходности бумаг с худшими показателями (лузеров). 

Одна из формул для WMLP имеет следующий вид:

WMLP=1/2[R(Small_High)+R(Big_High)]-1/2[R(Small_Low)+R(Big_Low)]

(формула 9)

где: Small_High и Big_High – высокодоходные портфели акций компаний низкой и высокой капитализации соответственно.

Small_Low и Big_Low – низкодоходные портфели акций компаний низкой и высокой капитализации;

R – доходность портфеля.

Модель Кэрхарта можно дополнительно протестировать, оценивая, например, WMLP через высоко- и низкодоходные портфели, сгруппированные по стоимостному параметру (P/B) или по иным показателям.

Прогонка 4F-модели на разных рынках показала, что она весьма чувствительна к периодам наблюдений, что едва ли относится к ее сильным сторонам.

Наконец, совсем недавно, в 2015 г.[10]  все те же Ю. Фама и К. Френч повышают ставки (читай, факторность) до пяти. Они вводят пятифакторную 5F-модель, включающую два новых слагаемых, два фактора в формуле оценки финансового актива (ценной бумаги). 

Первый, RMWP – премия за рентабельность предприятия, представляющая разницу между доходностями  компаний с высокой и низкой операционной рентабельностью. Второй, CMAP – премия за инвестиционную направленность (стратегию). В данном случае – разность доходностей фирм, ведущих агрессивную инвестполитику и компаний с консервативной инвестстратегией. 

Исследования показали, что учет новых факторов 5F-модели делает излишним использование премии за стоимость  HMLP, все покрывают другие четыре фактора: премия за риск, за размер, за рентабельность и за инвестполитику. 

Что дальше? Все выше и выше

“Оставляя в горах, оставляя в горах своё сердце. 

Я себе уже всё доказал: 

Лучше гор могут быть только горы, 

На которых ещё не бывал”.

В. Высоцкий “Прощание с горами”

Пятифакторная модель Фама-Френча в очередной раз сделала попытку уменьшения Альфа, объясняя доходность если не всех, то большинства портфелей через новые факторы риска (премии за риск). 

Не получилось.

Сбой произошел на небольших фирмах, проводящих агрессивные инвестиции, при низкой рентабельности. Для выхода на реальные доходности их акций требовалось помощь в виде большой отрицательной Альфы. 

И вот, уже за введение очередного, шестого фактора в 5F-модель выступает бывший студент-аспирант Ю Фама (PhD student) Клиффорд Скотт Эснесс, Clifford Scott Asness, основатель и руководитель хедж-фонда  AQR Capital Managemen[11].

Эснесс не особенно оригинален. Он предлагает Моментум, фактор премии “чемпион-лузер”. 

Итог –  шестифакторная модель. 

Позвольте сделать прогноз, итог промежуточный. Обнулить Альфу и здесь не удастся. 

Будут (скорее всего, уже есть) новые эксперименты и, уверен, новые факторы №№ 7, 8 и т.д. 

Кстати, каждый инвестор может “жонглировать” факторами самостоятельно, не дожидаясь подарков от экономических светил с Нобелевским статусом и без него.

Очевидно, что этим давно занимаются крупнейшие игроки.

Вот такой, понимаете “бином Ньютона”…

Владимир Наливайский

При подготовке статьи использованы материалы порталов Long/Short и Studme.

Примечания и ссылки (источник – Википедия/Wikipedia или авторский комментарий, если не оговорено иное).

1. “Мастер и Маргарита”
2. Точно было в школьной программе по математике в СССР, когда среднюю школу заканчивал автор данной статьи.
3. “Бином Нютона”.
4. “Замечательные пределы”.
5. Бернстайн У. “Разумное распределение активов. Как построить портфель с максимальной доходностью и минимальным риском”.
6. “Список лауреатов премии по экономике памяти Альфреда Нобеля”.
7. Буренин А.Н. “Управление портфелем ценных бумаг”.
8. “Уоррен Баффетт”, Викицитатник.
9. В иностранной литературе широко используется также обратный коэффициент Book-To-Market (BTM). BTM=B/P=1/(P/B).
10. “Fama–French three-factor model”. 
11. “AQR Capital Management”.

Используемые сокращения

3F-модель (Фама-Френча) – трехфакторная модель Фама-Френча.

CAPM – Capital Asset Pricing Model,  Модель ценообразования капитальных активов или  Модель оценки финансовых <долгосрочных> активов, она же по тексту: 1F-модель CAPM.

4F-модель (Кэрхарта) – четырехфакторная модель М. Кэрхарта.

5F-модель (Фама-Френча) – пятифакторная модель Фама-Френча.

SMBP – Small Minus Big Premium, премия за размер в 3F-модели.

HMLP – High Minus Low Premium, премия за стоимость 3F-модели.

WMLP – Winners Minus Losers Premium, премия по фактору “победители минус проигравшие” в 4F-модели Кэрхарта (модели Моментума).

NYSE – New York Stock Exchange, Нью-Йоркская фондовая биржа.

ИП – инвестиционный портфель, инвестпортфель, коротко – портфель.

P/B – отношение рыночной цены к балансовой стоимости акции.