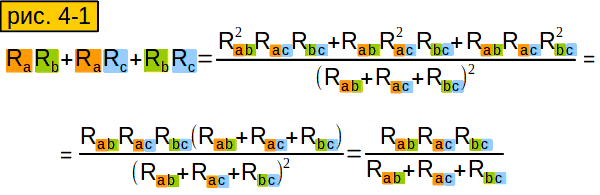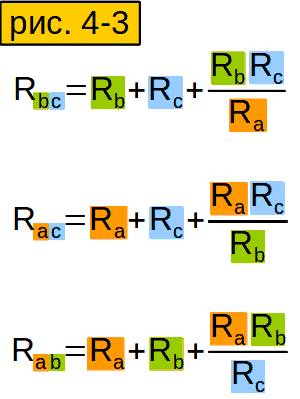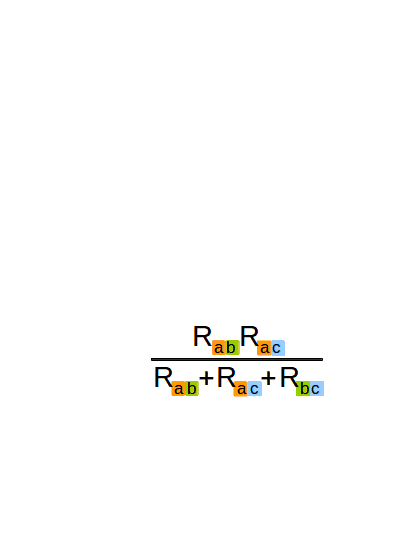Треугольники напряжений, сопротивлений и мощностей
Из векторной
диаграммы следует, что вектора напряжений
образуют треугольник напряжений, в
котором гипотенуза – входное напряжение
цепи U, катет, прилегающий
к углу φ – активная
составляющая напряжения UR,
второй катет UL
– UC
= UP
– реактивная составляющая напряжения
UR
= Ucosφ;
UP
= Usinφ;
Если в треугольнике
напряжений все стороны разделить на
ток I, то получим
треугольник сопротивлений, а если
умножить на I2
– треугольник мощностей.

Треугольник
сопротивлений
Треугольник мощностей
Из треугольника
сопротивлений
R
= Zcosφ;
X = Zsinφ;
Из
треугольника мощностей
P =
Scosφ; Q
= Ssinφ;
S =
Из треугольников
определяют
cosφ
= UR/U
= R/Z
= P/S.
Свое название cosφ
получил из треугольника мощностей –
коэффициент мощности
– важный показатель электрооборудования.
Определяет, какую часть от полной
мощности составляет активная мощность,
мощность, расходуемая на совершение
полезной работы.
Резонанс напряжений
Резонанс
– это явление в электрической цепи, при
котором ток и
напряжение
цепи совпадают по фазе.
Резонанс
напряжений возникает в цепи при
последовательном соединении элементов,
при XL
= XC.
Так как при этом Z
= R,
т. е. полное сопротивление имеет
минимальное значение, следовательно,
ток
цепи
будет максимальным. В этом режиме резко
возрастают напряжения на реактивных
элементах XL
и XC.
Происходит непрерывный обмен
энергии между магнитным полем катушки
и электрическим полем конденсатора.
Равенства ХL
и XC
можно добиться изменением L,
C, f. Изменение
I, UR,
UL,
UC,
U, φ при разных
ω показаны на рисунке.

Зависимость
напряжения и тока от частоты
Явление резонанса
широко используется в устройствах
радиотехники, телевидения, автоматики
и др

Векторная диаграмма для режима
резонанса напряжений
Если электрическая
цепь имеет такие L и
С, что резонансной для этой цепи
является ω0 =
,
то ток этой частоты f будет максимальным.
Изменяя индуктивность L
или емкость С, можно настроить контур
на эту частоту, т. е. усилить ток этой
цепи.
В электросиловых
устройствах это явление не нашло
применения, так как в режиме резонанса
напряжений резко увеличиваются UL
и UC,
что может привести к пробою изоляции.
Лекция №6. Цепь с параллельным соединением резистивного, индуктивного и емкостного элементов
При подаче напряжения
u =
Umахsinωt
в электрическую цепь с параллельным
соединением R, L,
C в ветвях создаются
токи iR
= ImахRsinωt
в ветви с R; iL
= ImахLsin(ωt
– π/2)
в ветви с L; iC
= ImахCsinωt(ωt
+ π/2) в ветви с С.

Схема электрической
цепи при параллельном соединении
элементов
с R,
L,
C
Действующие
значения токов в ветвях соответственно
будут равны
IR
=U/R=GU;
IL=U/XL
= BLU;
IC
= U/XC
= BCU.
где
G = 1/R;
BL
= 1/XL;
BC
= 1/XC,
Y = 1/Z
– активная, индуктивная, емкостная и
полная проводимости цепи.
Полный ток
I
= U/Z
=YU,
По I
ЗК для цепи
I
= İR
+ İL
+ İС .
В комплексной
форме записи: напряжение источника
питания
,
Полное сопротивление
цепи:
Z
экв = Z
R
Z
L
Z
c
/( Z
R
Z
L
+ Z
C
Z
L+
Z
R
Z
C
) = Z
эквejφ
где
Токи
İ =
/Z
экв.
= Ie
jψi,
I = U/Z
экв.;
ψi
= ψU
– φ
= – φ.
İR
=
/R
= Uej0°/Rej0°
= IRej0°=
IR;
İL
=
/ZL
= Uej0°/(XLe+j90°)
= U/XLe–j90°
=ILe
–j90°;
İC
=
/ZC
= Uej0°/(XCe–
j90°)
= ICe
+j90°.
При
построении векторной диаграммы цепи
за начальный вектор удобно принимать
вектор напряжения, а вектора токов
откладывать на комплексной плоскости
с учетом их сдвига по фазе по
отношению к вектору
напряжения. Вектор полного комплексного
тока İ определяют
геометрическим сложением векторов
токов İR,
İL,
и İС

Векторная диаграмма
цепи
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
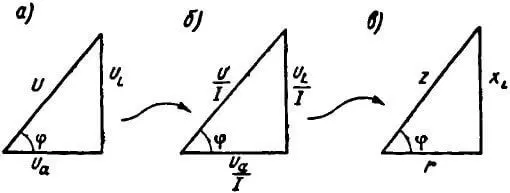
Если стороны треугольника напряжений (рисунок 1, а) разделить на ток I (рисунок 1, б), то углы треугольника от этого не изменятся, и мы получим новый треугольник, подобный первому – треугольник сопротивлений (рисунок 1, в).
Рисунок 1. Получение треугольника сопротивлений
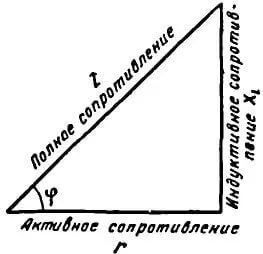
Рисунок 2. Треугольник сопротивлений
В треугольнике сопротивления, показанном отдельно на рисунке 2, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.
Из треугольника сопротивлений видно, что полное или кажущееся сопротивление z равно геометрической сумме активного r и индуктивного xL сопротивлений.
Применяя теорему Пифагора к треугольнику сопротивлений, получаем:
z2 = r2 + xL2 ,
откуда
Если одно из сопротивлений цепи (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко можно убедиться непосредственным расчетом.
Пример 1. Определить полное сопротивление цепи, в которой r = 9 Ом и xL = 12 Ом.
Было бы совершенно неправильно, если бы для определенного полного сопротивления были арифметически сложены оба сопротивления r и xL, так как
9 + 12 = 21 Ом.
Результат, как мы видим, в этом случае получается неверный.
Пример 2. Полное сопротивление обмотки электромагнита z = 25 Ом. Активное сопротивление обмотки r = 15 Ом. Определить индуктивное сопротивление.
Так как
z2 = r2 + xL2 ,
то
xL2 = z2 – r2 ,
откуда
Поэтому
Пример 3. Индуктивное сопротивление обмотки электродвигателя переменного тока равно 14 Ом. Полное сопротивление ее равно 22 Ом. Найти активное сопротивление.
Так как
z2 = r2 + xL2 ,
то
r2 = z2 – xL2 ,
Поэтому
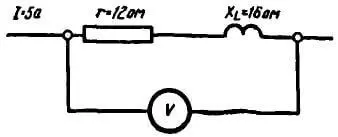
Пример 4. В цепи, изображенной на рисунке 3, определить показание вольтметра.
Рисунок 3. К примеру 4
Uа = I × r = 5 × 12 = 60 В.
UL = I × xL = 5 × 16 = 80 В.
Определим общее сопротивление:
Если умножить z на ток I, получим:
U = I × z = 5 × 20 = 100 В.
то есть тот же результат, что и выше.
Следовательно, если
Uа = I × r
и
UL = I × xL
то
U = I × z .
Источник: Кузнецов М. И., “Основы электротехники” – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560 с.
Из векторной диаграммы цепи с последовательным соединением имеем треугольник напряжений:
,
где cos j – коэффициент мощности, .
Согласно закону Ома ;
;
.
Делим каждую сторону треугольника напряжений на ток и получаем треугольник сопротивлений:
;
;
;
.
Умножаем каждую сторону треугольника напряжений на ток, и получаем треугольник мощностей:
;
;
;
,
здесь P – активная мощность [Вт]; S – полная мощность, вырабатываемая источником [ВА]; Q – реактивная мощность [ВАр].
Коэффициент мощности показывает, насколько эффективно и рационально используется энергия. Р характеризует ту часть энергетического процесса, в которой электрическая энергия потребляется приемником и преобразуется в другие виды энергии, т.е. в полезные дела. Q характеризует ту часть энергетического процесса, которая связана с изменением энергии электрического поля емкости или магнитного поля индуктивности. Реактивная мощность не совершает полезной работы, т.к. электрическая энергия не преобразуется в другие виды энергии.


Методы расчета резисторных схем постоянного тока
3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»
Рассматриваемый метод основан на том, что сложную схему, имеющую три вывода (узла), можно заменить другой, с тем же числом выводов (узлов). Замену следует произвести так, чтобы сопротивление участка между двумя любыми выводами новой схемы было таким же, как у прежней. В результате получится цепь, сопротивление которой эквивалентно сопротивлению данной по условию. Общее сопротивление обеих цепей будет одинаковым. Однако, поскольку в результате такого преобразования изменяются токи внутри цепи, такую замену можно проводить только в тех случаях, когда не надо находить распределение токов.
Подобные преобразования широко известны для случая двух выводов. Так, например, два резистора сопротивлениями R1 и R2, включенные последовательно, можно заменить одним резистором сопротивлением R1 + R2. Если резисторы включены параллельно, то их можно заменить одним резистором сопротивлением
$frac{R_1R_2}{R_1 + R_2}$
И в этих случаях распределение токов в цепи (или в части цепи) претерпевает изменения. Рассмотрим более сложное преобразование схем, имеющих три вывода (трехполюсников). Иначе это называется преобразованием «звезды» (рис. а) в «треугольник» (рис. б), и наоборот.
Сопротивления резисторов в схеме «звезда» обозначаются с индексом точки, с которой соединен этот резистор, например, резистор r1 соединен с точкой 1. В «треугольнике» индексы резисторов соответствуют точкам, между которыми они включены, например, резистор R13 подключен к точкам 1 и 3. Как отмечено выше, чтобы заменить одну из этих схем другой, нужно получить такие соотношения между их сопротивлениями, чтобы эквивалентные сопротивления между любыми точками были одинаковы для обеих схем (при условии сохранения числа этих точек). Так, в «звезде» сопротивление между точками 1 и 2 равно r1 + r2, в «треугольнике»
$frac{R_{12}(R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}$,
следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы выполнялось следующее равенство:
$r_1 + r_2 = frac{R_{12}(R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}$.
Аналогично для точек 2 и 3 и для точек 1 и 3:
$r_2 + r_3 = frac{R_{23}(R_{12} + R_{13})}{R_{12} + R_{13} + R_{23}}$,
$r_1 + r_3 = frac{R_{13}(R_{12} + R_{23})}{R_{12} + R_{13} + R_{23}}$.
Сложим все эти уравнения и, поделив обе части на 2, получим:
$r_1 + r_2 + r_3 = frac{R_{12}R_{13} + R_{12}R_{23} + R_{13}R_{23}}{R_{12} + R_{13} + R_{23}}$.
Вычитая из этого уравнения поочередно предыдущие, получим:
$r_1 = frac{R_{12}R_{13}}{R_{12} + R_{13} + R_{23}}$,
$r_2 = frac{R_{12}R_{23}}{R_{12} + R_{13} + R_{23}}$,
$r_3 = frac{R_{13}R_{23}}{R_{12} + R_{13} + R_{23}}$.
Эти выражения легко запомнить:
знаменатель в каждой формуле есть сумма сопротивлений всех резисторов «треугольника», а в числителе дважды повторяется индекс, стоящий слева:
$r_1 rightarrow R_{12}R_{13}, r_2 rightarrow R_{12}R_{23}, r_3 rightarrow R_{13}R_{23}$.
Аналогично получают и формулы обратного преобразования:
$R_{12} = frac{r_1r_2 + r_1r_3 + r_2r_3}{r_3}$,
$R_{13} = frac{r_1r_2 + r_1r_3 + r_2r_3}{r_2}$,
$R_{23} = frac{r_1r_2 + r_1r_3 + r_2r_3}{r_1}$.
Последние выражения также легко запомнить и проверить:
числитель у всех уравнений один и тот же, а в знаменателе стоит сопротивление резистора с индексом, которого не достает в левой части выражения.
Этот метод представляет собой наиболее универсальный подход к решению практически всех типов задач на разветвленные цепи.
Задача 27. Определите сопротивление цепи АВ (рис.), если R1 = R5 = 1 Ом, R2 = R6 = 2 Ом, R3 = R7 = 3 Ом, R4 = R8 = 4 Ом.
Решение. Преобразуем «треугольники» R1R2R8 и R4R5R6 в эквивалентные «звезды». Схема примет иной вид (рис.).
Сопротивления $r_1, r_2, …, r_6$ найдем по формулам:
$r_1 = frac{R_1R_8}{R_1 + R_2 + R_8} = frac{4}{7}$ Ом;
$r_2 = frac{R_1R_2}{R_1 + R_2 + R_8} = frac{2}{7}$ Ом;
$r_3 = frac{R_2R_8}{R_1 + R_2 + R_8} = frac{8}{7}$ Ом;
$r_4 = frac{R_4R_6}{R_4 + R_5 + R_6} = frac{8}{7}$ Ом;
$r_5 = frac{R_5R_6}{R_4 + R_5 + R_6} = frac{2}{7}$ Ом;
$r_6 = frac{R_4R_5}{R_4 + R_5 + R_6} = frac{4}{7}$ Ом.
Теперь нет никаких препятствий для расчета схемы, которая состоит из последовательно и параллельно соединенных резисторов (рис.). После простых расчетов получим
$R_{AB} = frac{47}{14}$ Ом
1.1. Шаговый (рекуррентный) метод
1.2. Метод преобразования
1.3. Метод равнопотенциальных узлов
1.3.1. Метод исключения «пассивных» участков цепи
1.3.2. Метод объединения равнопотенциальных узлов
1.3.3. Метод разделения узлов
1.3.4. Метод расщепления ветвей
1.4.1 Расчет эквивалентных сопротивлений линейных бесконечных цепей
1.4.2. Расчет эквивалентных сопротивлений плоскостных бесконечных цепей
1.4.3. Расчет эквивалентных сопротивлений объемных бесконечных цепей
2. Расчет цепей по правилам Кирхгофа
3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»

4 инструмента крутого Кирхгофщика
Внимание! Чтобы увидеть ответы на вопросы, кликните по ним. Кликать надо по тексту, а не по пустому месту. Чтобы сменить картинку, кликните по кнопке. Если ответ на вопрос вам не ясен, советую хорошо подумать, прежде чем смотреть ответ.
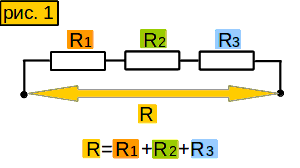
Инструмент 1. Вычисление сопротивления цепи из нескольких последовательно соединённых сопротивлений
Просто, как ….. Сложил все эти сопротивления и получил сопротивление цепи.
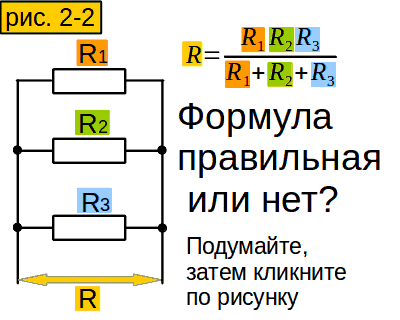
Инструмент 2. Вычисление сопротивления участка из нескольких параллельно соединённых сопротивлений
Рассмотрим участок с двумя параллельными одинаковыми сопротивлениями. Сопротивление его в два раза меньше, чем каждого сопротивления. Если сопротивлений три, сопротивление участка будет в три раза меньше.
Какую тут можно провести аналогию?
Несколько одинаковых дырок. Через них протечёт воды в столько раз больше, чем через одну дырку, сколько дырок имеется.
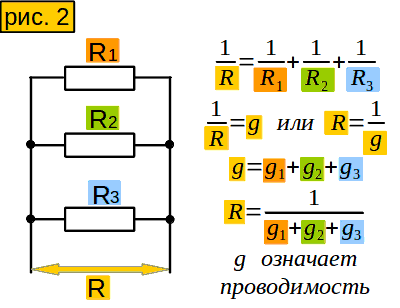
А как быть, если сопротивления не одинаковые? Есть такое понятие – проводимость. Оно означает величину, обратную сопротивлению. (рисунок 2)
Так если сопротивление больше, то проводимость что?
меньше
Чтобы вычислить проводимость нашего участка, надо сложить проводимости сопротивлений. Потом можно легко найти сопротивление участка.
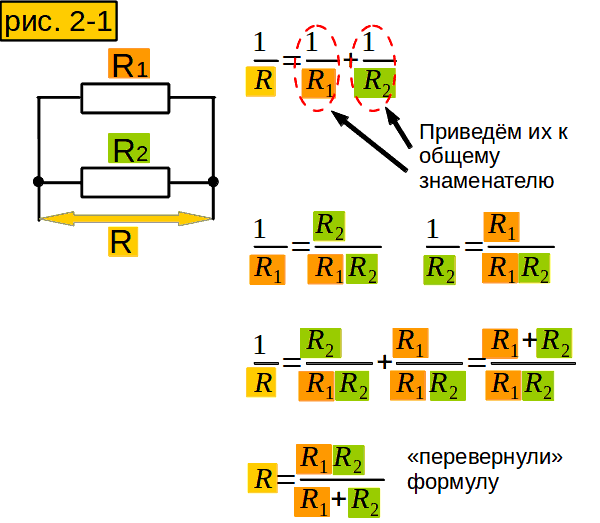
А нельзя ли вычислить сопротивление участка, не преобразуя сопротивления в проводимости, а потом обратно? Можно. Пусть у нас участок из двух параллельно соединённых сопротивлений (рис. 2-1). Проводимость его равна сумме проводимостей сопротивлений (1 строчка). Приведём проводимости сопротивлений к общему знаменателю (2 строчка). Сложим их и получим суммарную проводимость (3 строчка). “Переворачиваем” формулу (4 строчка) и получаем формулу для участка из двух параллельно соединённых сопротивлений. А если сопротивлений не два, а больше?

Сформулируйте своими словами формулу сопротивления участка из нескольких параллельных сопротивлений, чтобы лучше её запомнить.
Надо умножить все сопротивления, и разделить на сумму произведений этих сопротивлений, но в каждом этом произведнии одного сопротивления не хватает. Вы, может быть, и получше сформулируете.
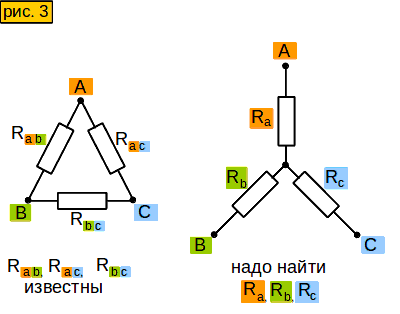
Инструмент 3. Преобразование “треугольника” в “звезду”
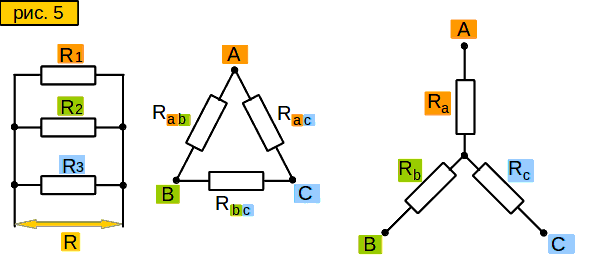
Пусть у нас в схеме есть вот такой участок цепи – “треугольник” (рис. 3, слева). Нам надо заменить его участком вот такого вида – “звездой” (рис. 3, справа), но чтобы сопротивления между сторонами “звезды” были такими же, как между соответствующими лучами “треугольника”. Зачем это нужно? Позже узнаете.
Смотрим на “звезду” на рис. 3. Допустим, мы знаем сопротивления между точками
A и B, то есть (Ra+Rb);
A и C, то есть (Ra+Rc);
B и C, то есть (Rb+Rc).
Чему будут равны сопротивления Ra, Rb, Rc ?
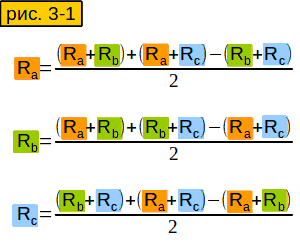
Зная все сопротивления между концами лучей “звезды”, мы можем вычислить сопротивление каждого отдельного луча.
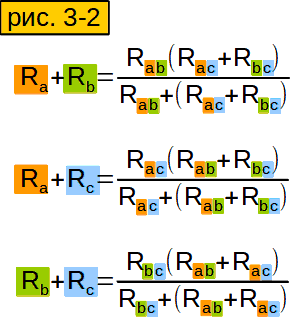
Теперь будем вычислять сопротивления между точками A, B, и C (звезды) через сопротивления треугольника, которые нам известны (рис. 3-2). Для начала вычислим сопротивление между точками A и B звезды (рис. 3-2 верхняя строчка). В нашем треугольнике мы имеем два параллельно включённых сопротивления – Rab и (Rac+Rbc). Вычислять их общее сопротивление мы умеем (ответы на вопросы 3 и 4). Вычисляем сопротивления между точками A и C, B и C (2 и 3 строчки). Обратите внимание, что во всех формулах знаменатель одинаковый.
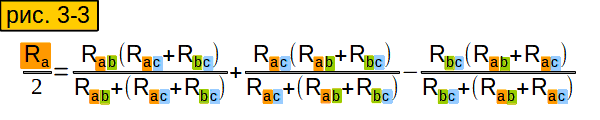
Теперь можно вычислить сопротивление отдельного луча (рис. 3-3). Формула получилась очень громоздкая, но мы её хорошенько подсократим.
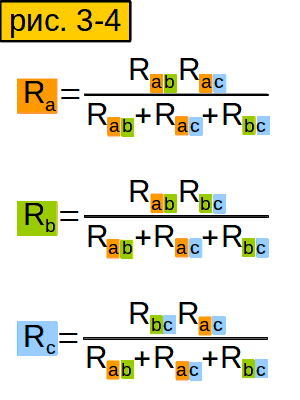
И получим вот такую стройную и изящную формулу (рис. 3-4, верхняя строчка). Аналогично вычисляем сопротивления других лучей звезды.
Сформулируйте своими словами формулу из рисунка 3-4, чтобы лучше её запомнить.
Чтобы найти сопротивление луча “звезды”, надо умножить сопротивления сторон “треугольника”, которые “прилегают” (“имеют ту же букву”), и разделить на сумму сопротивлений всех сторон “треугольника”.
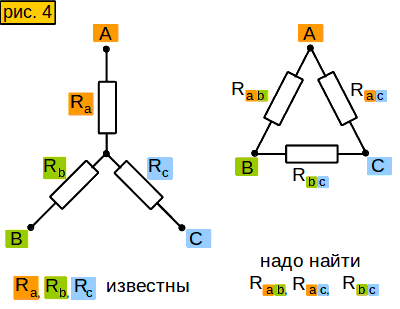
Инструмент 4. Преобразование “звезды” в “треугольник”
Иногда полезно делать обратное преобразование – “звезды” в “треугольник”. Нельзя ли вычислить сопротивление стороны “треугольника” через сопротивления эквивалентной “звезды”, используя формулы, которые мы уже вывели? Можно. Смотрим рисунок 3-4. Проделаем с формулами этого рисунка следующий трюк: попарно их перемножим и результаты сложим (смотрим рис. 4-1).
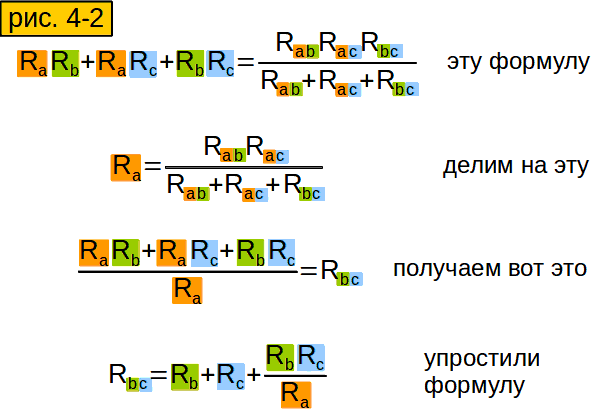
Затем результат разделим на верхнюю формулу рисунка 3-4. Получится у нас вот что: рисунок 4-2, третья сверху формула. Маленько её подсократим и получим нижнюю формулу.
Как раз то, что нам надо!
Сопротивления других сторон “треугольника” выводятся аналогично (рисунок 4-3).
Сформулируйте своими словами формулу из рисунка 4-3, чтобы лучше её запомнить.
Чтобы найти сопротивление стороны “треугольника”, надо сложить сопротивления соответствующих сторон “звезды” (у которых “те же буквы”), и ещё прибавить произведение тех же сторон “звезды”, делёное на оставшуюся сторону.
Зубрилка
об ошибках сообщайте по адресу obuchmat@mail.ru
Продолжение следует
На домашнюю страницу