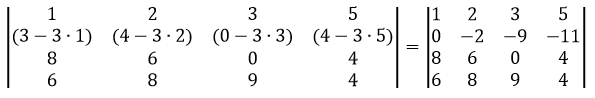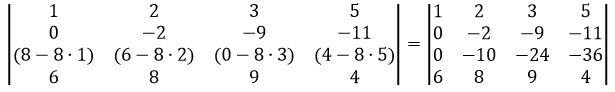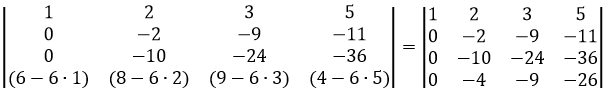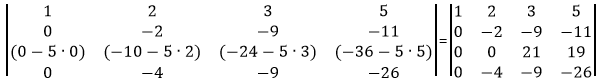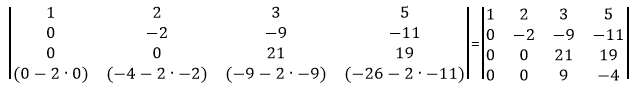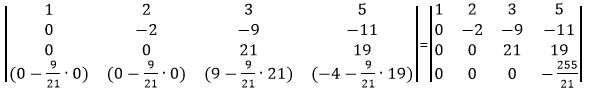Приведение матрицы к треугольному виду
Приведение матрицы к треугольному виду методом Гаусса и методом Барейса.
Ниже два калькулятора для приведения матриц к треугольному, или ступенчатому, виду. Первый использует для этого метод Гаусса, второй — метод Барейса. Описание методов и немного теории — под калькуляторами.
Приведение матрицы к треугольному виду (метод Гаусса)
Приведение матрицы к треугольному виду (метод Барейса)
Итак, для начала определимся с понятием треугольной, или ступенчатой матрицы:
Матрица имеет ступенчатый вид, если:
- Все нулевые строки матрицы стоят последними
- Первый ненулевой элемент строки всегда находится строго правее первого ненулевого элемента предыдущей строки
- Все элементы столбца под первым ненулевым элементом строки равны нулю (это впрочем следует из первых двух пунктов)
Пример ступенчатой матрицы:
1 0 2 5
0 3 0 0
0 0 0 4
Понятие треугольной матрицы более узкое, оно используется только для квадратных матриц (хотя я думаю, что это не строго), и формулируется проще: треугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю. Строго говоря, это даже определение верхнетреугольной матрицы, но мы будем использовать его. Понятно, что такая верхнетреугольная матрица является также и ступенчатой.
Пример треугольной (верхнетреугольной) матрицы:
1 0 2 5
0 3 1 3
0 0 4 2
0 0 0 3
Кстати, определитель треугольной матрицы вычисляется простым перемножением ее диагональных элементов.
Чем же так интересны ступенчатые (и треугольные) матрицы, что к ним надо приводить все остальные? — спросите вы.
У них есть замечательной свойство, а именно, любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.
Что же такое элементарные преобразования? — спросите вы.
Элементарными преобразованиями матрицы называют следующие операции:
- перестановка любых двух строк (столбцов) матрицы
- умножение любой строки (столбца) на призвольное, отличное от нуля, число
- сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.
И что? — спросите вы.
А то, что элементарные преобразования матрицы сохраняют эквивалентность матриц. А если вспомнить, что системы линейных алгебраический уравнений (СЛАУ) записывают как раз в матричной форме, то это означает, что элементарные преобразования матрицы не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Приведя матрицу системы линейных уравнений AX=B к треугольной форме A’X = B’, то есть, с соответствующими преобразованиями столбца B, можно найти решение этой системы так называемым «обратным ходом».
Чтобы было понятно, используем треугольную матрицу выше и перепишем систему уравнений в более привычной форме (столбец B я придумал сам):
Понятно, что сначала мы найдем , потом, подставив его в предыдущее уравнение, найдем и так далее — двигаясь от последнего уравнения к первому. Это и есть обратный ход.
Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют методом Гаусса. Метод Гаусса — классический метод решения систем линейных алгебраических уравнений. Также его еще называют Гауссовым исключением, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Теперь про сам метод.
Собственно, как можно занулить переменную во втором уравнении? Вычтя из него первое, домноженное на коэффициент
Поясним на примере:
Зануляем во втором уравнении:
Во втором уравнении больше не содержится
Обобщенно алгоритм метода Гаусса можно представить следующим образом:
где N — число строк,
— i-тая строка,
— элемент, находящийся в i-той строке, j-том столбце
И все бы ничего, да и метод отличный, но. Дело все в делении на , присутствующем в формуле. Во-первых, если диагональный элемент будет равен нулю, то метод работать не будет. Во-вторых, в процессе вычисления будет накапливаться погрешность, и чем дальше, тем больше. Результат будет отличаться от точного.
Для уменьшения погрешности используют модификации метода Гаусса, которые основаны на том, что погрешность тем меньше, чем больше знаменатель дроби. Эти модификации — метод Гаусса с выбором максимума в столбце и метод Гаусса с выбором максимума по всей матрице. Как следует из названия, перед каждым шагом исключения переменной по столбцу (всей матрице) ищется элемент с максимальным значением и проводится перестановка строк (строк и столбцов), таким образом, чтобы он оказался на месте .
Но есть еще более радикальная модификация метода Гаусса, которая называется методом Барейса (Bareiss).
Как можно избавиться от деления? Например, умножив перед вычитанием строку на . Тогда вычитать надо будет строку , домноженную только на , без всякого деления.
.
Уже хорошо, но возникает проблема с ростом значений элементов матрицы в ходе вычисления.
Барейс предложил делить выражение выше на и показал, что если исходные элементы матрицы — целые числа, то результатом вычисления такого выражения тоже будет целое число. При этом принимается, что для нулевой строки .
Кстати, то, что в случае целочисленных элементов исходной матрицы алгоритм Барейса приводит к треугольной матрице с целочисленными элементами, то есть без накопления погрешности вычислений — довольно важное свойство с точки зрения машинной арифметики.
Алгоритм Барейса можно представить следующим образом:
Алгоритм, аналогично методу Гаусса, также можно улучшить поиском максимума по столбцу(всей матрице) и перестановкой соответствующих строк (строк и столбцов).
Виды матриц. Ступенчатый вид матрицы. Приведение матрицы к ступенчатому и треугольному виду
Матрица – это особый объект в математике. Изображается в форме прямоугольной или квадратной таблицы, сложенной из определенного числа строк и столбцов. В математике имеется большое разнообразие видов матриц, различающихся по размерам или содержанию. Числа ее строк и столбцов именуются порядками. Эти объекты употребляются в математике для упорядочивания записи систем линейных уравнений и удобного поиска их результатов. Уравнения с использованием матрицы решаются посредством метода Карла Гаусса, Габриэля Крамера, миноров и алгебраических дополнений, а также многими другими способами. Базовым умением при работе с матрицами является приведение к стандартному виду. Однако для начала давайте разберемся, какие виды матриц выделяют математики.
Нулевой тип
Все компоненты этого вида матрицы – нули. Между тем, число ее строк и столбцов абсолютно различно.
Квадратный тип
Количество столбцов и строк этого вида матрицы совпадает. Иначе говоря, она представляет собой таблицу формы “квадрат”. Число ее столбцов (или строк) именуются порядком. Частными случаями считается существование матрицы второго порядка (матрица 2×2), четвертого порядка (4×4), десятого (10×10), семнадцатого (17×17) и так далее.
Вектор-стобец
Это один из простейших видов матриц, содержащий только один столбец, который включает в себя три численных значения. Она представляет ряд свободных членов (чисел, независимых от переменных) в системах линейных уравнений.
Вектор-строка
Вид, аналогичный предыдущему. Состоит из трех численных элементов, в свою очередь организованных в одну строку.
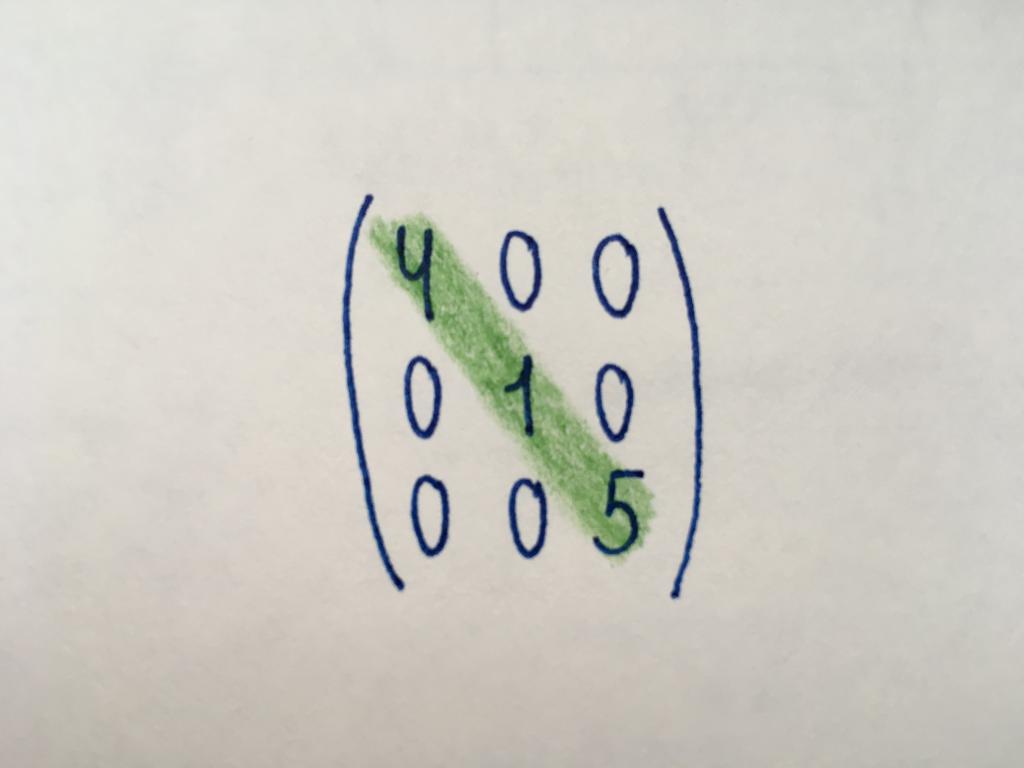
Диагональный тип
Числовые значения в диагональном виде матрицы принимают только компоненты главной диагонали (выделена зеленым цветом). Основная диагональ начинается с элемента, находящегося в левом верхнем углу, а заканчивается элементом в правом нижнем соответственно. Остальные компоненты равны нулю. Диагональный тип представляет собой только квадратную матрицу какого-либо порядка. Среди матриц диагонального вида можно выделить скалярную. Все ее компоненты принимают одинаковые значения.
Единичная матрица
Подвид диагональной матрицы. Все ее числовые значения являются единицами. Используя единичный тип матричных таблиц, выполняют ее базовые преобразования или находят матрицу, обратную исходной.
Канонический тип
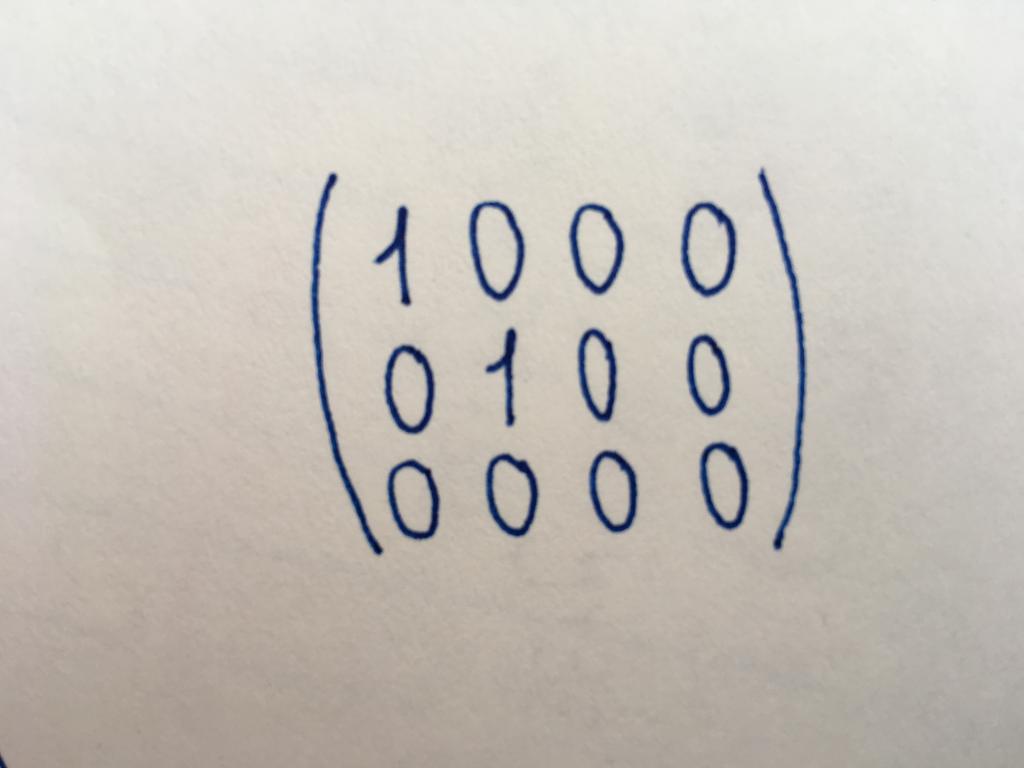
Канонический вид матрицы считается одним из основных; приведение к нему часто необходимо для работы. Число строк и столбцов в канонической матрице различно, она необязательно принадлежит к квадратному типу. Она несколько похожа на единичную матрицу, однако в ее случае не все компоненты основной диагонали принимают значение, равное единице. Главнодиагональных единиц может быть две, четыре (все зависит от длины и ширины матрицы). Или единицы могут не иметься вовсе (тогда она считается нулевой). Остальные компоненты канонического типа, как и элементы диагонального и единичного, равны нулю.
Треугольный тип
Один из важнейших видов матрицы, применяемый при поиске ее детерминанта и при выполнении простейших операций. Треугольный тип происходит от диагонального, поэтому матрица также является квадратной. Треугольный вид матрицы подразделяют на верхнетреугольный и нижнетреугольный.
В верхнетреугольной матрице (рис. 1) только элементы, которые находятся над главной диагональю, принимают значение, равное нулю. Компоненты же самой диагонали и части матрицы, располагающейся под ней, содержат числовые значения.
В нижнетреугольной (рис. 2), наоборот, элементы, располагающиеся в нижней части матрицы, равны нулю.
Ступенчатая матрица
Вид необходим для нахождения ранга матрицы, а также для элементарных действий над ними (наряду с треугольным типом). Ступенчатая матрица названа так, потому что в ней содержатся характерные “ступени” из нулей (как показано на рисунке). В ступенчатом типе образуется диагональ из нулей (необязательно главная), и все элементы под данной диагональю тоже имеют значения, равные нулю. Обязательным условием является следующее: если в ступенчатой матрице присутствует нулевая строка, то остальные строки, находящиеся ниже нее, также не содержат числовых значений.
Таким образом, мы рассмотрели важнейшие типы матриц, необходимые для работы с ними. Теперь разберемся с задачей преобразования матрицы в требуемую форму.
Приведение к треугольному виду
Как же привести матрицу к треугольному виду? Чаще всего в заданиях нужно преобразовать матрицу в треугольный вид, чтобы найти ее детерминант, по-другому называемый определителем. Выполняя данную процедуру, крайне важно “сохранить” главную диагональ матрицы, потому что детерминант треугольной матрицы равен именно произведению компонентов ее главной диагонали. Напомню также альтернативные методы нахождения определителя. Детерминант квадратного типа находится при помощи специальных формул. Например, можно воспользоваться методом треугольника. Для других матриц используют метод разложения по строке, столбцу или их элементам. Также можно применять метод миноров и алгебраических дополнений матрицы.
Подробно разберем процесс приведения матрицы к треугольному виду на примерах некоторых заданий.
Задание 1
Необходимо найти детерминант представленной матрицы, используя метод приведения его к треугольному виду.
Данная нам матрица представляет собой квадратную матрицу третьего порядка. Следовательно, для ее преобразования в треугольную форму нам понадобится обратить в нуль два компонента первого столбца и один компонент второго.
Чтобы привести ее к треугольному виду, начнем преобразование с левого нижнего угла матрицы – с числа 6. Чтобы обратить его в нуль, умножим первую строку на три и вычтем ее из последней строки.
Важно! Верхняя строка не изменяется, а остается такой же, как и в исходной матрице. Записывать строку, в четыре раза большую исходной, не нужно. Но значения строк, компоненты которых нужно обратить в нуль, постоянно меняются.
Далее займемся следующим значением – элементом второй строки первого столбца, числом 8. Умножим первую строку на четыре и вычтем ее из второй строки. Получим нуль.
Осталось только последнее значение – элемент третьей строки второго столбца. Это число (-1). Чтобы обратить его в нуль, из первой строки вычтем вторую.
detA = 2 x (-1) x 11 = -22.
Значит, ответ к заданию: -22.
Задание 2
Нужно найти детерминант матрицы методом приведения его к треугольному виду.
Представленная матрица принадлежит к квадратному типу и является матрицей четвертого порядка. Значит, необходимо обратить в нуль три компонента первого столбца, два компонента второго столбца и один компонент третьего.
Начнем приведение ее с элемента, находящегося в нижнем углу слева, – с числа 4. Нам нужно обратить данное число в нуль. Удобнее всего сделать это, умножив на четыре верхнюю строку, а затем вычесть ее из четвертой. Запишем итог первого этапа преобразования.
Итак, компонент четвертой строки обращен в нуль. Перейдем к первому элементу третьей строки, к числу 3. Выполняем аналогичную операцию. Умножаем на три первую строку, вычитаем ее из третьей строки и записываем результат.
Далее видим число 2 во второй строке. Повторяем операцию: умножаем верхнюю строку на два и вычитаем ее из второй.
Нам удалось обратить в нуль все компоненты первого столбца данной квадратной матрицы, за исключением числа 1 – элемента главной диагонали, не требующего преобразования. Теперь важно сохранить полученные нули, поэтому будем выполнять преобразования со строками, а не со столбцами. Перейдем ко второму столбцу представленной матрицы.
Снова начнем с нижней части – с элемента второго столбца последней строки. Это число (-7). Однако в данном случае удобнее начать с числа (-1) – элемента второго столбца третьей строки. Чтобы обратить его в нуль, вычтем из третьей строки вторую. Затем умножим вторую строку на семь и вычтем ее из четвертой. Мы получили нуль вместо элемента, расположенного в четвертой строке второго столбца. Теперь перейдем к третьему столбцу.
В данном столбце нам нужно обратить в нуль только одно число – 4. Сделать это несложно: просто прибавляем к последней строке третью и видим необходимый нам нуль.
После всех произведенных преобразований мы привели предложенную матрицу к треугольному виду. Теперь, чтобы найти ее детерминант, нужно только произвести умножение получившихся элементов главной диагонали. Получаем: detA = 1 x (-1) x (-4) x 40 = 160. Следовательно, решением является число 160.
Итак, теперь вопрос приведения матрицы к треугольному виду вас не затруднит.
Приведение к ступенчатому виду
При элементарных операциях над матрицами ступенчатый вид является менее “востребованным”, чем треугольный. Чаще всего он используется для нахождения ранга матрицы (т. е. количества ее ненулевых строк) или для определения линейно зависимых и независимых строк. Однако ступенчатый вид матрицы является более универсальным, так как подходит не только для квадратного типа, но и для всех остальных.
Чтобы привести матрицу к ступенчатому виду, сначала нужно найти ее детерминант. Для этого подойдут вышеназванные методы. Цель нахождения детерминанта такова: выяснить, можно ли преобразовать ее в ступенчатый вид матрицы. Если детерминант больше или меньше нуля, то можно спокойно приступать к заданию. Если же он равен нулю, выполнить приведение матрицы к ступенчатому виду не получится. В таком случае нужно проверить, нет ли ошибок в записи или в преобразованиях матрицы. Если подобных неточностей нет, задание решить невозможно.
Рассмотрим, как привести матрицу к ступенчатому виду на примерах нескольких заданий.
Задание 1. Найти ранг данной матричной таблицы.
Перед нами квадратная матрица третьего порядка (3×3). Мы знаем, что для нахождения ранга необходимо привести ее к ступенчатому виду. Поэтому сначала нам необходимо найти детерминант матрицы. Воспользуемся методом треугольника: detA = (1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) – (1 x 1 x 4) – (2 x 3 x 0) – (6 x 5 x 2) = 12.
Детерминант = 12. Он больше нуля, значит, матрицу можно привести к ступенчатому виду. Приступим к ее преобразованиям.
Начнем его с элемента левого столбца третьей строки – числа 2. Умножаем верхнюю строку на два и вычитаем ее из третьей. Благодаря этой операции как нужный нам элемент, так и число 4 – элемент второго столбца третьей строки – обратились в нуль.
Далее обращаем в нуль элемент второй строки первого столбца – число 3. Для этого умножаем верхнюю строку на три и вычитаем ее из второй.
Мы видим, что в результате приведения образовалась треугольная матрица. В нашем случае продолжить преобразование нельзя, так как остальные компоненты не удастся обратить в нуль.
Значит, делаем вывод, что количество строк, содержащих числовые значения, в данной матрице (или ее ранг) – 3. Ответ к заданию: 3.
Задание 2. Определить количество линейно независимых строк данной матрицы.
Нам требуется найти такие строки, которые нельзя какими-либо преобразованиями обратить в нуль. Фактически нам нужно найти количество ненулевых строк, или ранг представленной матрицы. Для этого выполним ее упрощение.
Мы видим матрицу, не принадлежащую к квадратному типу. Она имеет размеры 3×4. Начнем приведение также с элемента левого нижнего угла – числа (-1).
Прибавляем первую строку к третьей. Далее вычитаем из нее вторую, чтобы обратить число 5 в нуль.
Дальнейшие ее преобразования невозможны. Значит, делаем вывод, что количество линейно независимых строк в ней и ответ к заданию – 3.
Теперь приведение матрицы к ступенчатому виду не является для вас невыполнимым заданием.
На примерах данных заданий мы разобрали приведение матрицы к треугольному виду и ступенчатому виду. Чтобы обратить в нуль нужные значения матричных таблиц, в отдельных случаях требуется проявить фантазию и правильно преобразовать их столбцы или строки. Успехов вам в математике и в работе с матрицами!
Как привести матрицу к треугольному (ступенчатому) виду (метод Гаусса)?
Данная статья является первой частью серии статей под названием “Решение матриц”. Каждая часть сопровождается теорией, примерами и подробным описанием.
Если Вам нужно привести матрицу к треугольному (ступенчатому) виду, воспользуйтесь нашим онлайн калькулятором.
Содержание:
Введение
Эту задачу приходится решать очень часто, так как она используется во многих операциях над матрицами (решение систем линейных алгебраических уравнений (СЛАУ), вычисление определителя матрицы).
Что бы привести матрицу к треугольному виду, нужно воспользоваться методом Гаусса, который является простым в использовании и позволяет быстро прийти к конечному результату. Метод заключается в том чтобы исходную матрицу, путём элементарных преобразований привести к треугольному (ступенчатому) виду.
Описание алгоритма
Для приведения матрицы к треугольному виду, необходимо обнулить все элементы стоящие ниже главной диагонали.
Пусть дана матрица
.
Первым действием обнуляем первые элементы 2,3. n строки, для этого вычтем из этих строк первую строку умноженную на соответственно,
получим ,
где .
Теперь вычтем из 3,4. n строки вторую строку умноженную на , этим действием обнуляем вторые элементы этих строк, соответственно, получаем
,
где bij элементы получившиеся в результате этих преобразований. И так далее, пока не получим вид ,
где bij это элементы получившиеся в результате элементарных преобразований, это и есть матрица треугольного вида.
Пример приведения матрицы к треугольному виду
Заключение
Если Вам не понятен какой-либо шаг или у Вас есть вопросы по приведению матрицы к треугольному (ступенчатому) виду, вы всегда можете оставить свой комментарий ниже или решить её воспользовавшись нашим онлайн калькулятором.
Свои вопросы по данной статье, Вы всегда можете задать в комментариях.
[spoiler title=”источники:”]
http://fb.ru/article/373673/vidyi-matrits-stupenchatyiy-vid-matritsyi-privedenie-matritsyi-k-stupenchatomu-i-treugolnomu-vidu
http://rytex.ru/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F/%D0%9C%D0%B0%D1%82%D1%80%D0%B8%D1%86%D1%8B/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4-%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%B0
[/spoiler]
A matrix is defined as a rectangular array of numbers that are arranged in rows and columns. The size of a matrix can be determined by the number of rows and columns in it. A matrix is said to be an “m by n” matrix when it has “m” rows and “n” columns and is written as an “m × n” matrix. For example, a matrix of order “5 × 6” has five rows and six columns. We have different types of matrices, such as rectangular, square, triangular, symmetric, singular, etc.
What is a Triangular Matrix?
A triangular matrix is a special case of a square matrix, where all elements above or below the principal diagonal are zeros. An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros. A lower triangular matrix is a square matrix, whose all elements above the principal diagonal are zeros. The matrices in the image given below are upper triangular and lower triangular matrices of order “4 × 4.”
Types of Triangular Matrices
There are different types of matrices which are discussed below in this article:
- Upper Triangular Matrix: An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros.
- Lower Triangular Matrix: A lower triangular matrix is a square matrix, whose all elements above the principal diagonal are zeros.
- Strictly Triangular Matrix: A triangular matrix is referred to as a strictly triangular matrix if all the elements of the principal diagonal are zero.
- Strictly Lower Triangular Matrix: A lower triangular matrix is referred to as a strictly lower triangular matrix if all the elements of the principal diagonal are zero.
- Strictly Upper Triangular Matrix: An upper triangular matrix is referred to as a strictly upper triangular matrix if all the elements of the principal diagonal are zero.
- Unit Triangular Matrix: A triangular matrix is referred to as a unit triangular matrix if all the elements of the principal diagonal are one.
- Unit Lower Triangular Matrix: A lower triangular matrix is referred to as a unit lower triangular matrix if all the elements of the principal diagonal are one.
- Unit Upper Triangular Matrix: An upper triangular matrix is referred to as a unit upper triangular matrix if all the elements of the principal diagonal are one.
Upper Triangular Matrix
An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros. A square matrix “A = [aij]” is said to be an upper triangular matrix when aij = 0 for all i > j.
If Un,n is a square matrix of order “n × n” and uij represents an element in the ith row and jth column of the given matrix, then
Examples of Upper Triangular Matrix
The matrix given below is an upper triangular matrix of order “2 × 2.” We can see that the elements below the principal diagonal are zeros.
The matrix given below is an upper triangular matrix of order “3 × 3.”
Lower Triangular Matrix
A lower triangular matrix is a square matrix whose all elements above the principal diagonal are zeros. A square matrix “A = [aij]” is said to be a lower triangular matrix when aij = 0 for all i < j.
If L is a square matrix of order “n × n” and lij represents an element in the ith row and jth column of the given matrix, then the condition for the given matrix to be a lower triangular matrix is given as follows:
If L is a square matrix of order “n × n” and lij represents an element in the ith row and jth column of the given matrix, then the condition for the given matrix to be a lower triangular matrix is given as follows:
Examples of Lower Triangular Matrix
The matrix given below is a lower triangular matrix of order “2 × 2.”
The matrix given below is a lower triangular matrix of order “3 × 3.” We can see that the elements above the principal diagonal are zeros.
Properties of a Triangular Matrix
Various properties of the Triangular Matrix are discussed below in this article:
- The transpose of an upper triangular matrix is a lower triangular matrix, i.e., UT = L, and the transpose of a lower triangular matrix is an upper triangular matrix, i.e., LT = U.
- The determinant of a triangular matrix of any order is equal to the product of the principal diagonal elements.
- The inverse of a triangular matrix will also be a triangular matrix.
- A triangular matrix is invertible if and only if all elements of the principal diagonal are non-zero.
- When two triangular matrices are multiplied, the resultant matrix is also triangular.
- When two upper (lower) triangular matrices are multiplied, the resultant matrix is also an upper (lower) triangular matrix.
- When two upper (lower) triangular matrices are added, the resultant matrix is also an upper (lower) triangular matrix.
Also, Check
- Minors and Cofactors of Determinants
- Determinant of the Square Matrix
- Adjoint of the Square Matrix
Solved Examples on Triangular Matrix
Example 1: Calculate the determinant of the matrix given below.
Solution:
We can notice that the given matrix is an upper triangular matrix.
We know that the determinant of an upper triangular matrix of any order is equal to the product of the principal diagonal elements.
So, |A| = 1 × 7 × 8 = 56
Hence, the determinant of the given matrix is 56.
Example 2: Prove the inverse of the inverse of a lower triangular matrix will also be a lower triangular matrix.
Solution:
Let us consider a lower triangular matrix of order “2 × 2,” to prove the inverse of the inverse of a lower triangular matrix will also be a lower triangular matrix.
L-1 = Adj L/ |L|
|L| = 5 × 8
= 40
We can see the inverse matrix is also a lower triangular matrix.
Hence, proved.
Example 3: Prove that the transpose of an upper triangular matrix is a lower triangular matrix.
Solution:
To prove that the transpose of an upper triangular matrix is a lower triangular matrix, let us consider an upper triangular matrix.
Now,
We can notice that the resultant matrix is a lower triangular matrix.
Hence proved.
Example 4: Find the values of “a” and “b” in the given matrix P, if P is a unit lower triangular matrix.
Solution:
We know that a lower triangular matrix is referred to as a unit lower triangular matrix if all the elements of the principal diagonal are one.
So, 2a + 5 = 1
2a = 1 − 5 = −4
a = −4/2 = −2
3b − 2 = 1
3b = 1 + 2 = 3
b = 3/3
= 1Hence, the values of “a” and “b” are −2 and 1 respectively.
FAQs on Triangular Matrix
Question 1: What is meant by a triangular matrix?
Answer:
A triangular matrix is a special case of a square matrix where all elements above or below the principal diagonal are zeros.
Question 2: What is an upper triangular matrix?
Answer:
An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros. A square matrix “A = [aij]” is said to be an upper triangular matrix when aij = 0 for all i > j.
Question 3: What is the determinant of an upper triangular matrix?
Answer:
The determinant of an upper triangular matrix of any order is equal to the product of the principal diagonal elements.
Question 4: What is meant by a lower triangular matrix?
Answer:
A lower triangular matrix is a square matrix, whose all elements above the principal diagonal are zeros.
Question 5: What is the transpose of a unit upper triangular matrix?
Answer:
An upper triangular matrix is referred to as a unit upper triangular matrix if all the elements of the principal diagonal are one.
Last Updated :
09 Jan, 2023
Like Article
Save Article
Как привести матрицу к треугольному (ступенчатому) виду (метод Гаусса)?
Данная статья является первой частью серии статей под названием “Решение матриц”. Каждая часть сопровождается теорией, примерами и подробным описанием.
Если Вам нужно привести матрицу к треугольному (ступенчатому) виду, воспользуйтесь нашим онлайн калькулятором.
Содержание:
- Введение
- Описание алгоритма
- Примеры решения матриц
- Заключение
Введение
Эту задачу приходится решать очень часто, так как она используется во многих операциях над матрицами (решение систем линейных алгебраических уравнений (СЛАУ), вычисление определителя матрицы).
Что бы привести матрицу к треугольному виду, нужно воспользоваться методом Гаусса, который является простым в использовании и позволяет быстро прийти к конечному результату. Метод заключается в том чтобы исходную матрицу, путём элементарных преобразований привести к треугольному (ступенчатому) виду.
Описание алгоритма
Для приведения матрицы к треугольному виду, необходимо обнулить все элементы стоящие ниже главной диагонали.
Пусть дана матрица

Первым действием обнуляем первые элементы 2,3,…,n строки, для этого вычтем из этих строк первую строку умноженную на
соответственно,
получим

где

Теперь вычтем из 3,4…,n строки вторую строку умноженную на

этим действием обнуляем вторые элементы этих строк, соответственно, получаем

где bij элементы получившиеся в результате этих преобразований. И так далее, пока не получим вид

где bij это элементы получившиеся в результате элементарных преобразований, это и есть матрица треугольного вида.
Пример приведения матрицы к треугольному виду
Заключение
Если Вам не понятен какой-либо шаг или у Вас есть вопросы по приведению матрицы к треугольному (ступенчатому) виду, вы всегда можете оставить свой
комментарий ниже или решить её воспользовавшись нашим
онлайн калькулятором.
Свои вопросы по данной статье, Вы всегда можете задать в комментариях.
Преобразование матрицы до треугольной
Матрица – математический объект, записываемый в виде прямоугольной таблицы чисел и допускающий
алгебраические операции (сложение, вычитание, умножение) между ним и другими подобными объектами. К треугольному
виду можно привести даже не квадратную матрицу.
Введите количество строк:
Если после использования данного онлайн калькулятора
(Получение треугольной матрицы) у Вас возникли какие-то вопросы по работе сервиса или вопросы
образовательного характера, то Вы всегда можете задать их на нашем
форуме.
Вы поняли, как решать? Нет?
Рассчитайте цену решения ваших задач


Калькулятор
стоимости
Решение контрольной
от 300 рублей
*
* Точная стоимость будет определена после загрузки задания для исполнителя
+Загрузить файл
Файлы doc, pdf, xls, jpg, png не более 5 МБ.

Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду.
Рассмотрим приведение определителя матрицы к треугольному виду.
Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами. Для нахождения определителя нужно умножить все элементы на главной диагонали.
Пример
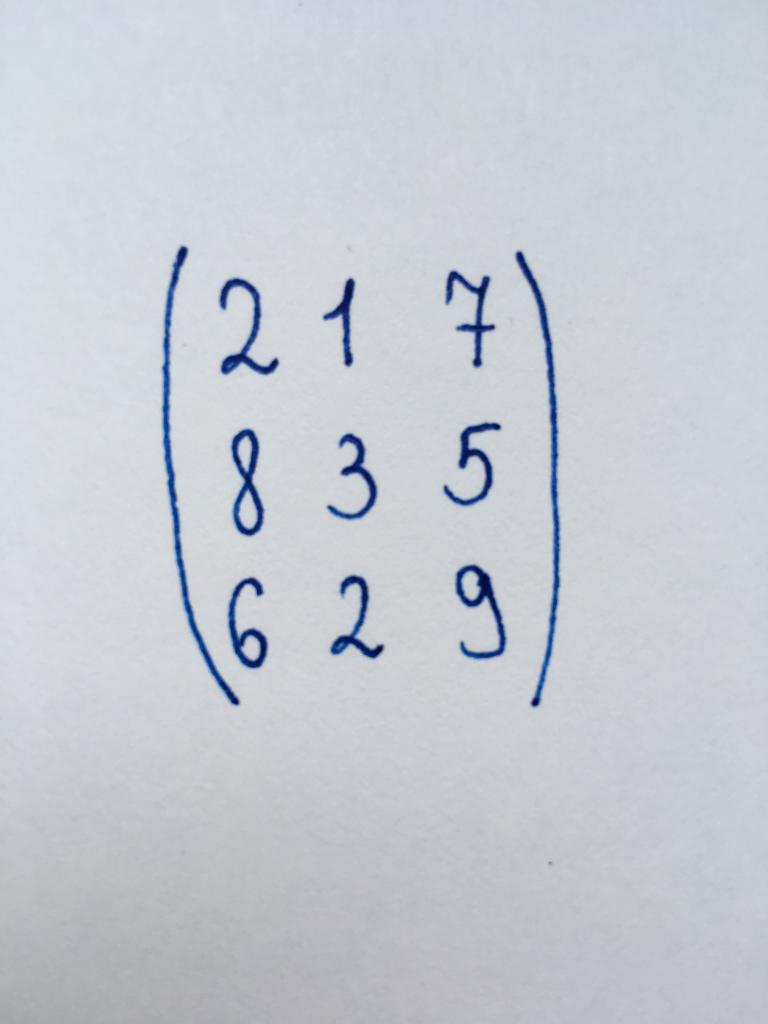
Найдем определитель матрицы четвертого порядка.

Сделаем элемент a2,1 равный нулю.
Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т.е. на 3
Сделаем элемент a3,1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8
Сделаем элемент a4,1 равный нулю.
Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6
Сделаем элемент a3,2 равный нулю.
Из строки №3 вычитаем строку №2, умноженную на 5
Сделаем элемент a4,2 равный нулю.
Из строки №4 вычитаем строку №2, умноженную на 2
Сделаем элемент a4,3 равный нулю.
Из строки №4 вычтем строку №3, умноженную на 9/21.
Умножим элементы матрицы находящиеся на диагонали.
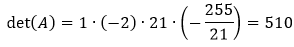



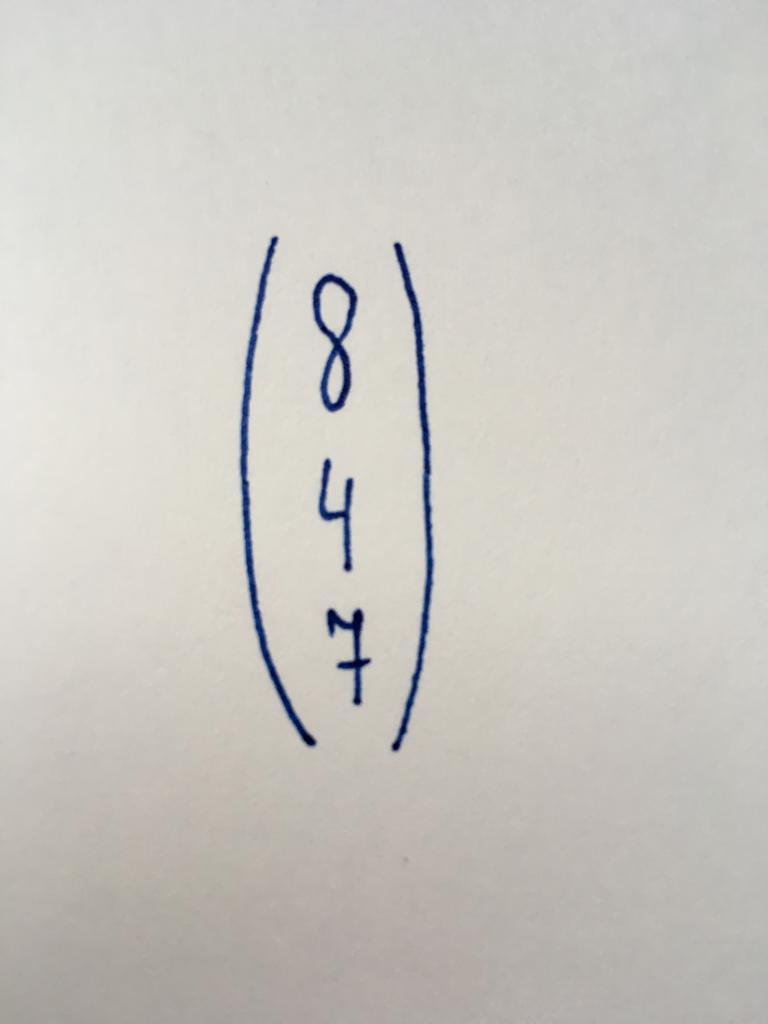
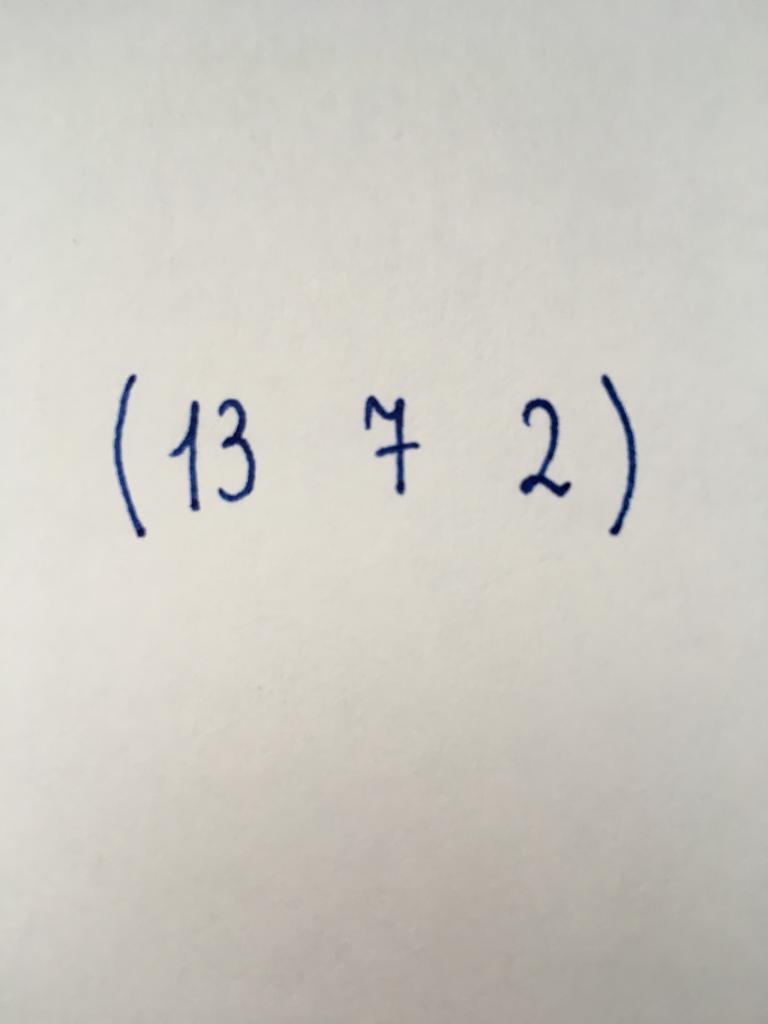

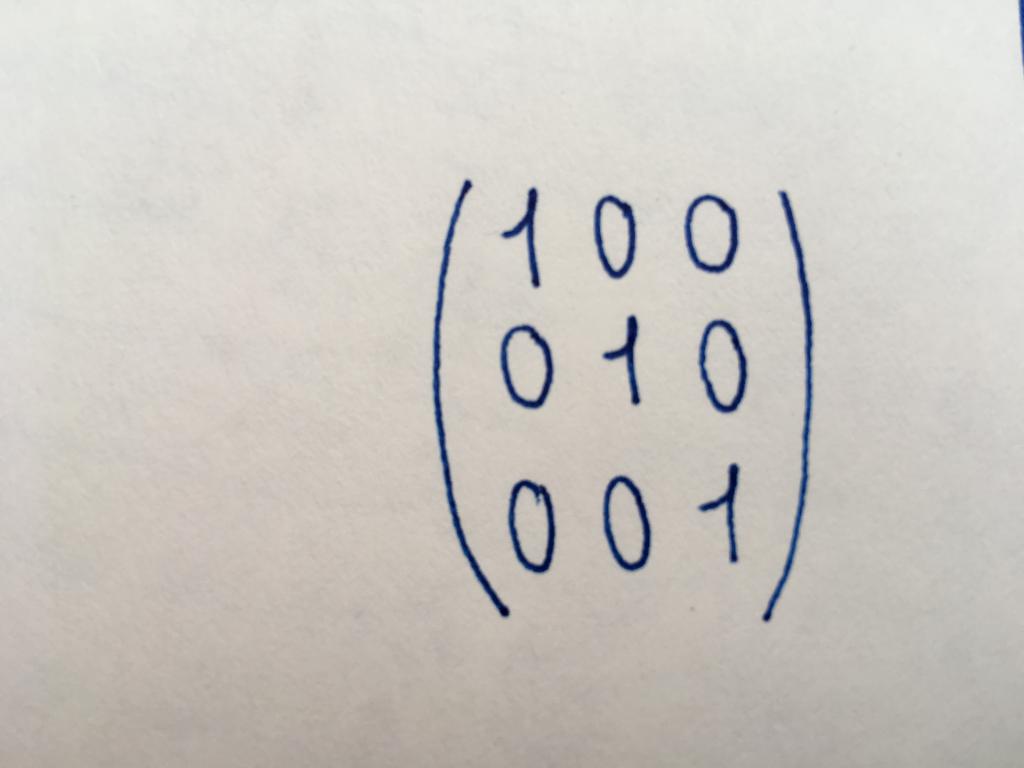


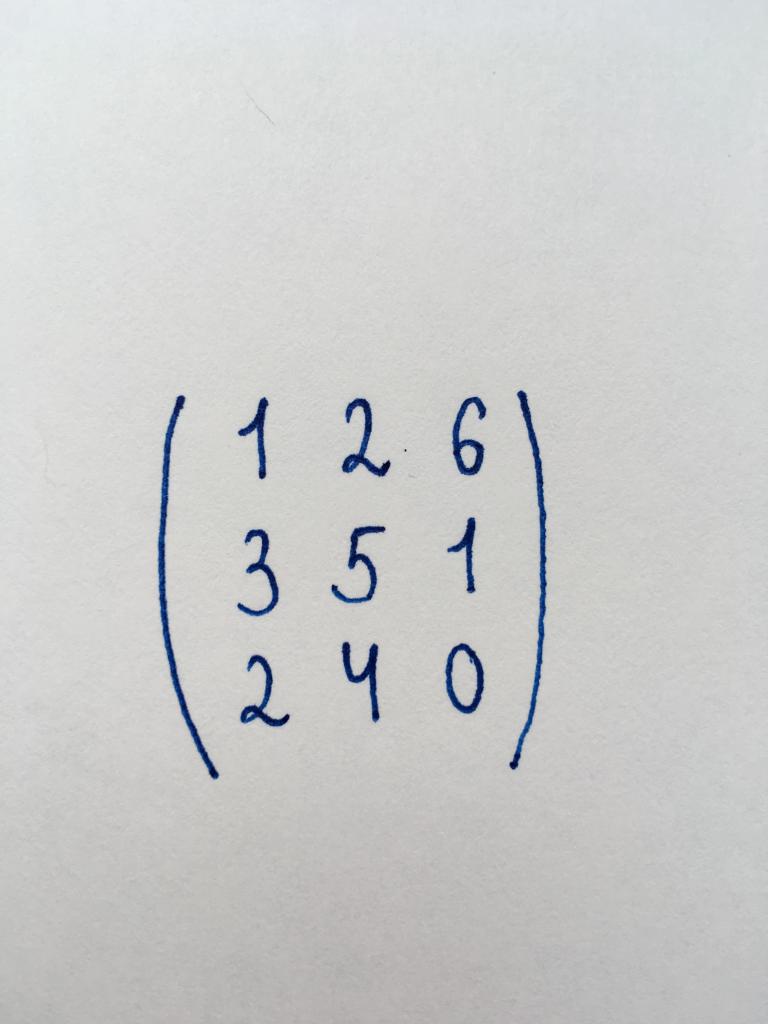
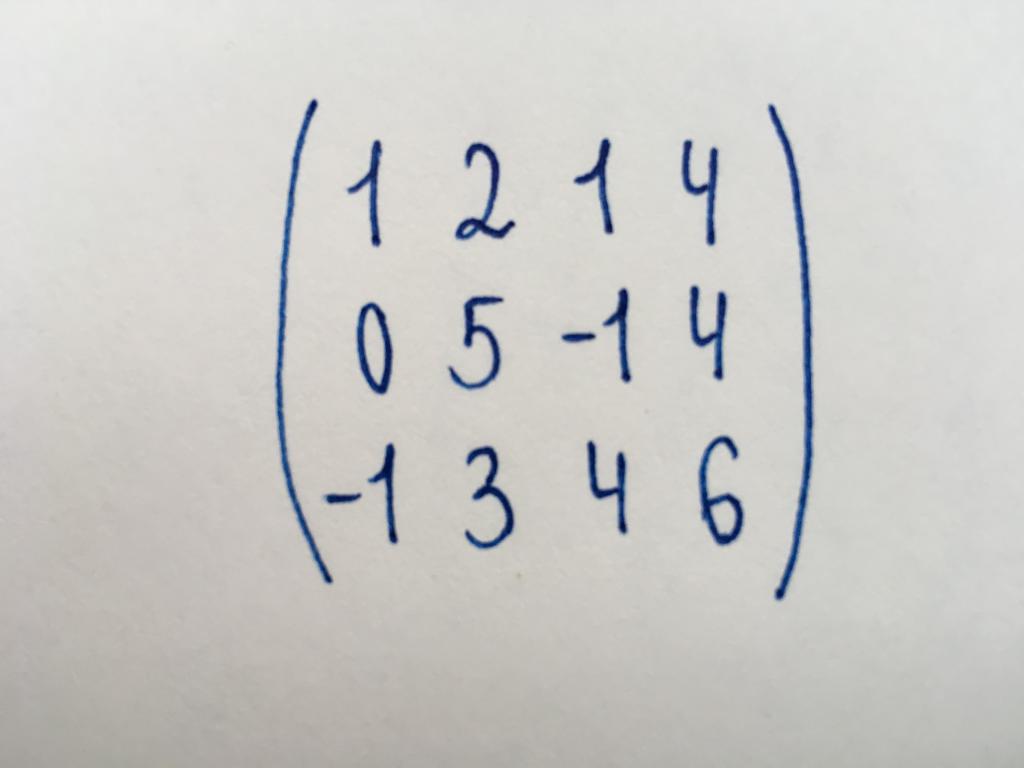

![Rendered by QuickLaTeX.com U = left[begin{array}{ccc} a & b & c\ 0 & d & e\ 0 & 0 & f end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f57401892f74026b58593d2dfe3441a_l3.png)
![Rendered by QuickLaTeX.com L = left[begin{array}{ccc} 1 & 0 & 0\ 2 & 3 & 0\ 4 & 5 & 6 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-056f46d28db4a56ddf93871e4fea1ab0_l3.png)
![Rendered by QuickLaTeX.com A = left[begin{array}{ccc} 0 & 0 & 0\ p & 0 & 0\ q & r & 0 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3ee2c530db96915b81e0829695d54d4_l3.png)
![Rendered by QuickLaTeX.com B = left[begin{array}{ccc} 0 & 12 & -7\ 0 & 0 & 9\ 0 & 0 & 0 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-debebebf8143fa1e944f2fe904cb55c0_l3.png)
![Rendered by QuickLaTeX.com P = left[begin{array}{ccc} 1 & 0 & 0\ 2 & 1 & 0\ 5 & 6 & 1 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-773f6bf5929c35225595f0378001cb90_l3.png)
![Rendered by QuickLaTeX.com Q = left[begin{array}{ccc} 1 & 21 & 19\ 0 & 1 & 17\ 0 & 0 & 1 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b90d279a11e4ec492757a56eb6f41638_l3.png)
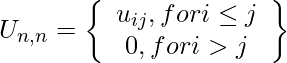
![Rendered by QuickLaTeX.com U_{2,2} = left[begin{array}{cc} 13 & 9\ 0 & 7 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4df88646c7887d0b19b67a7e576cc8c9_l3.png)
![Rendered by QuickLaTeX.com U_{3,3} = left[begin{array}{ccc} 3 & -8 & 6\ 0 & 5 & 11\ 0 & 0 & 4 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d11cb1a22b5a6f32dc0abe43730b9db_l3.png)

![Rendered by QuickLaTeX.com L = left[begin{array}{cc} 1 & 0\ 3 & 5 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a2ffe4102972378ff972938f189d41c6_l3.png)
![Rendered by QuickLaTeX.com L_{3,3} = left[begin{array}{ccc} 4 & 0 & 0\ 7 & 9 & 0\ -5 & 3 & 11 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a09f5929ef88e26ad0d969f5b268e6bd_l3.png)
![Rendered by QuickLaTeX.com A = left[begin{array}{ccc} 1 & 3 & -4\ 0 & 7 & 0\ 0 & 0 & 8 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54632ab91e02b4b8982d54d2a2f08361_l3.png)
![Rendered by QuickLaTeX.com L = left[begin{array}{cc} 5 & 0\ -7 & 8 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-488c092b3c44415879eca56956f93d43_l3.png)
![Rendered by QuickLaTeX.com Adj L = left[begin{array}{cc} 8 & 0\ 7 & 5 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-32116ad33d66c9897e724c9e927ae91c_l3.png)
![Rendered by QuickLaTeX.com L^{-1} = frac{1}{40} left[begin{array}{cc} 8 & 0\ 7 & 5 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3313a79008fabd1f9eec243acc95aeca_l3.png)
![Rendered by QuickLaTeX.com U^{T} = left[begin{array}{ccc} a & 0 & 0\ b & d & 0\ c & e & f end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3b011707a6685e3099e47af9bbe990a8_l3.png)
![Rendered by QuickLaTeX.com P = left[begin{array}{cc} 2a+5 & 0\ 5 & 3b-2 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a7e427df431b4afa33e25f11255b8d5_l3.png)