Как составить умозаключение по логическому квадрату

В этом уроке мы, наконец, переходим к теме, которая составляет ядро любого рассуждения и любой логической системы – умозаключениям. В четвёртом уроке мы говорили, что рассуждение – это совокупность суждений или высказываний. Очевидно, что такое определение не полно, ведь оно ничего не говорит о том, почему вдруг какие-то разные высказывания оказались рядом. Если дать более точное определение, то рассуждение – это процесс обоснования какого-либо высказывания с помощью его последовательного вывода из других высказываний. Этот вывод чаще всего осуществляется в форме умозаключений.

Содержание:

• Критерии истинности умозаключений
• Умозаключения по логическому квадрату
• Операция обращения
• Игра “Подбери ключ”
• Упражнения
• Проверочные вопросы на усвоение материала

Умозаключение – это непосредственный переход от одного или нескольких высказываний А₁, А₂, …, А_n к высказыванию В. А₁, А₂, …, А_n называют посылками. Посылка может быть одна, их может быть две, три, четыре, в принципе – сколько угодно. В посылках содержится известная нам информация. В – это заключение. В заключении находится уже новая информация, которую мы извлекли из посылок с помощью специальных процедур. Эта новая информация уже содержалась в посылках, но в скрытом виде. Так вот задача умозаключения сделать это скрытое явным. Кроме того, иногда посылки называют аргументами, а заключение – тезисом, а само умозаключение в этом случае называют обоснованием. Разница между умозаключением и обоснованием состоит в том, что в первом случае, мы не знаем, к какому заключению мы придём, а во втором – тезис нам уже известен, мы просто хотим установить его связь с посылками-аргументами.

В качестве иллюстрации умозаключения можно взять рассуждения Эркюля Пуаро из «Убийства в восточном экспрессе» Агаты Кристи:

Логики записывают умозаключения следующим образом:

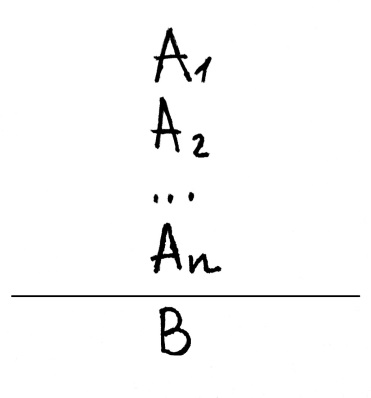
Над чертой располагаются посылки, под чертой – заключение, а сама черта обозначает отношение логического следования.

Критерии истинности умозаключений

Также как и для суждений, для умозаключений существуют определённые условия их истинности. При определении, истинное умозаключение или ложное, нужно обращать внимание на два аспекта. Первый аспект – это истинность посылок. Если хотя бы одна из посылок ложна, то и сделанное заключение тоже будет ложным. Поскольку заключение – это та информация, которая была скрыта в посылках и которую мы просто извлекли на свет, то из неверных посылок невозможно случайно получить верный вывод. Это можно сравнить с попыткой сделать бифштекс из моркови. Наверное, моркови можно придать цвет и форму бифштекса, но внутри всё равно будет морковь, а не мясо. Никакие кулинарные операции не преобразуют одно в другое.

Второй аспект – это правильность самого умозаключения с точки зрения его логической формы.

В качестве примера неправильного умозаключения при истинности посылок можно привести умозаключение голубки из «Алисы в стране чудес» Кэрролла. Голубка обвиняет Алису, в том, что она не змея. Вот как она приходит к этому выводу:

Змеи едят яйца.
Девочки едят яйца.
Значит, девочки – это змеи.

Хотя посылки правильные, заключение абсурдно. Умозаключение в целом сделано неверно. Чтобы избежать подобных ошибок, логики выявили такие умозаключения, логические формы которых при истинности посылок гарантируют истинность заключения. Их принято называть правильными умозаключениями. Таким образом, чтобы умозаключение было сделано верно, нужно следить за истинностью посылок и за правильностью самой формы умозаключения.

Мы рассмотрим различные формы правильных умозаключений на примере силлогистики. В этом уроке мы разберём самые простые однопосылочные заключения. В следующем уроке – более сложные заключения: силлогизмы, энтимемы, многопосылочные заключения.

Умозаключения по логическому квадрату

Чтобы было легче запомнить, какие именно типы умозаключений возможны между категорическими атрибутивными высказываниями, логики придумали специальный логический квадрат, изображающий отношения между ними. Поэтому некоторые однопосылочные умозаключения также называют умозаключениями по логическому квадрату. Посмотрим на этот квадрат:

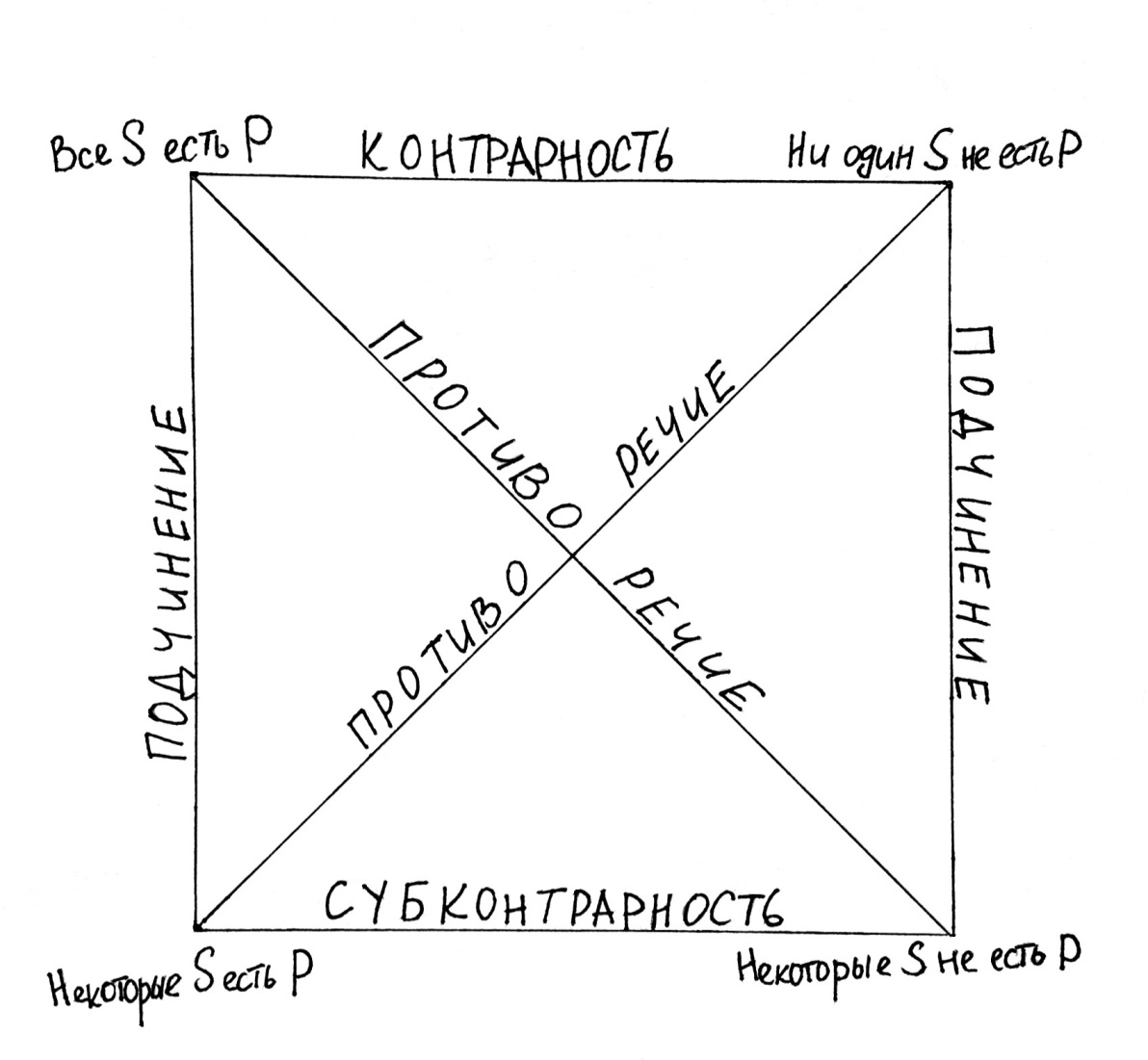
Начнём с отношений подчинения. Мы уже сталкивались с ними в четвёртом уроке, когда рассматривали условия истинности для частно-утвердительных и частно-отрицательных высказываний. Мы говорили, что из высказывания «Все S есть P» будет логичным вывести высказывание «Некоторые S есть P», а из высказывания «Ни один S не есть P» – «Некоторые S не есть P». Таким образом, возможны следующие типы умозаключений:

• Все S есть P
• Некоторые S есть P
• Все птицы имеют клюв. Следовательно, некоторые птицы имеют клюв.
• Ни один S не есть P
• Некоторые S не есть P
• Ни один гусь не хочет быть пойман и зажарен. Следовательно, некоторые гуси не хотят быть пойманными и зажаренными.

Кроме того, по правилу контрапозиции из отношений подчинения можно вывести ещё два правильных умозаключения. Правило контрапозиции – это логический закон, который гласит: если из высказывания А следует высказывание В, то из высказывания «неверно, что В» будет следовать высказывание «неверно, что А». Вы можете попробовать проверить этот закон с помощью таблицы истинности. Итак, будут верны и следующие умозаключения по контрапозиции:

• Неверно, что некоторые S есть P
• Неверно, что все S есть P
• Неверно, что некоторые автомобили не имеют колёс. Поэтому неверно, что все автомобили не имеют колёс.
• Неверно, что некоторые S не есть P
• Неверно, что все S не есть P
• Неверно, что некоторые вина не являются спиртными напитками. Таким образом, неверно, что все вина не являются спиртными напитками.

Отношение контрарности (противоположности) означает, что высказывания типа «Все S есть P» и «Ни один S не есть P» не могут быть одновременно истинными, но они могут быть одновременно ложными. Это хорошо видно из таблицы истинности для категоричных атрибутивных высказываний, которую мы построили в прошлом уроке. Отсюда можно вывести так называемый закон контрарного противоречия: Неверно, что все S есть P и в то же время ни один S не есть P.

По закону контрарного противоречия будут истинными следующие виды умозаключений:

• Все S есть P
• Неверно, что ни один S не есть P
• Все яблоки – это фрукты. Следовательно, неверно, что ни одно яблоко не является фруктом.
• Ни один S не есть P
• Неверно, что все S есть P
• Ни один кит не умеет летать. Поэтому неверно, что все киты умеют летать.

Отношения субконтрарности (подпротивоположности) означают, что высказывания типа «Некоторые S есть P» и «Некоторые S не есть P» не могут быть одновременно ложными, хотя могут быть одновременно истинными. На этом основании может быть сформулирован закон субконтрарного исключённого третьего: Некоторые S не есть P или Некоторые S есть P.

• Согласно этому закону правильными будут следующие умозаключения:
• Неверно, что некоторые S есть P
• Некоторые S не есть P
• Неверно, что некоторые продукты полезны для здоровья. Поэтому некоторые продукты не полезны для здоровья.
• Неверно, что некоторые S не есть P
• Некоторые S есть P
• Неверно, что некоторые ученики из нашего класса не являются двоечниками. Таким образом, некоторые ученики из нашего класса являются двоечниками.

Отношения противоречия (контрадикторности) говорят о том, что высказывания, находящиеся в них, не могут быть одновременно истинными или ложными. На основании этих отношений можно сформулировать два закона противоречия и два закона исключённого третьего. Первый закон противоречия: Неверно, что все S есть P и некоторые S не есть P. Второй закон противоречия: Неверно, что ни один S не есть P и некоторые S есть P. Первый закон исключённого третьего: Все S есть P или некоторые S не есть P. Второй закон исключённого третьего: Ни один S не есть P или некоторые S есть P.

На этих законах строятся умозаключения следующих видов:

• Все S есть P
• Неверно, что некоторые S не есть P
• Все дети нуждаются в заботе. Следовательно, неверно, что некоторые дети не нуждаются в заботе.
• Некоторые S не есть P
• Неверно, что все S есть P
• Некоторые книги не являются скучными. Поэтому, неверно, что все книги являются скучными.
• Неверно, что все S есть P
• Некоторые S не есть P
• Неверно, что все сотрудники нашей фирмы усердно работают. Таким образом, некоторые сотрудники нашей фирмы не работают усердно.
• Неверно, что некоторые S не есть P
• Все S есть P
• Неверно, что некоторые зебры не имеют полосок на коже. Следовательно, все зебры имеют полоски на коже.
• Ни один S не есть P
• Неверно, что некоторые S есть P
• Ни одна картина в этом зале не относится к XX веку. Поэтому неверно, что некоторые картины в этом зале относятся к XX веку.
• Некоторые S есть P
• Неверно, что ни один S не есть P
• Некоторые студенты занимаются спортом. Таким образом, неверно, что ни один студент не занимается спортом.
• Неверно, что ни один S не есть P
• Некоторые S есть P
• Неверно, что ни один учёный не интересуется искусством. Следовательно, некоторые учёные интересуются искусством.
• Неверно, что некоторые S есть P
• Ни один S не есть P
• Неверно, что некоторые коты курят сигары. Таким образом, ни один кот не курит сигары.

Как вы, скорее всего, заметили во всех этих умозаключениях, высказывания над чертой и под чертой несут одну и ту же информацию, просто поданную в разной форме. Важная деталь заключается в том, что смысл одних из этих высказываний воспринимается легко и интуитивно, в то время как смысл других тёмен, и над ними порой приходится поломать голову. Например, смысл утвердительных высказываний воспринимается легче, чем смысл отрицательных высказываний, смысл высказываний с одним отрицанием более понятен, чем смысл высказываний с двумя отрицаниями. Таким образом, основное назначение умозаключений по логическому квадрату состоит в том, чтобы привести сложные для восприятия, непонятные высказывания к наиболее простой и ясной форме.

Операция обращения

Ещё одним видом однопосылочных умозаключений является обращение. Это такой тип умозаключений, при которых субъект посылки совпадает с предикатом заключения, а субъект заключения совпадает с предикатом посылки. Грубо говоря, в заключении S и P просто меняются местами.

Прежде чем перейти к умозаключениям через обращение, построим таблицу истинности для высказываний, в которых P встанет на место субъекта, а S – на место предиката.

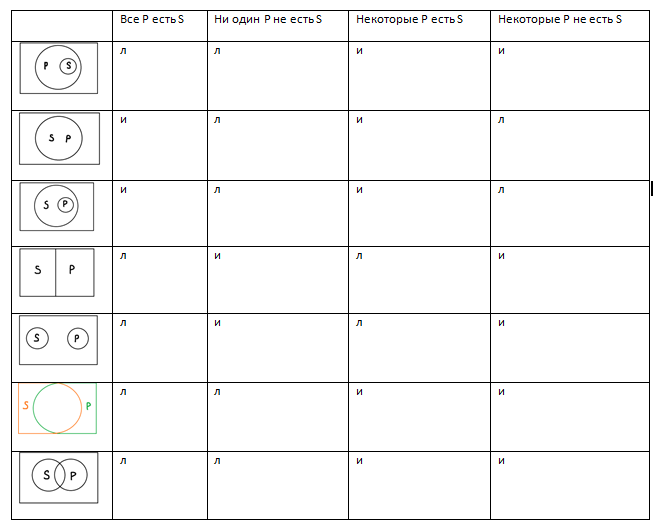
Сравните её с той таблицей, которую мы строили в прошлом уроке. Обращение, как и другие умозаключения, может быть правильным, только когда посылка и заключение одновременно истинны. При сравнении двух таблиц, вы увидите, что таких комбинаций не так уж и много.

Итак, существует два вида обращения: чистое и с ограничением. Чистое обращение происходит тогда, когда количественная характеристика не изменяется, то есть если в посылке было слово «все», то и в заключении тоже будет слова «все»/«ни один», если в посылке слово «некоторые», то и в заключении «некоторые. Соответственно, при обращении с ограничением количественная характеристика меняется: были «все», а стали «некоторые». Для высказываний типа «Ни один S не есть P» и «Некоторые S есть P» правильным будет следующее чистое обращение:

• Ни один S не есть P
• Ни один P не есть S
• Ни один человек не может выжить без воздуха. Следовательно, ни одно живое существо, способное выжить без воздуха, не является человеком.
• Некоторые S есть P
• Некоторые P есть S
• Некоторые змеи ядовиты. Поэтому, некоторые ядовитые существа – это змеи.
• Для высказываний типа «Все S есть P» и «Ни один S не есть P» верно обращение с ограничением:
• Все S есть P
• Некоторые P есть S
• Все пингвины – это птицы. Таким образом, некоторые птицы – это пингвины.
• Ни один S не есть P
• Некоторый P не есть S
• Ни один крокодил не ест зефир. Следовательно, некоторые существа, едящие зефир, не являются крокодилами.
• Высказывания типа «Некоторые S не есть P» вообще не обращаются.

Хотя обращения, как и умозаключения по логическому квадрату, это однопосылочные умозаключения, и мы точно также извлекаем всю новую информацию из имеющейся посылки, посылку и заключение в них уже нельзя назвать просто разными формулировками одной и той же информации. Полученная информация относится уже к другому субъекту, а потому она уже не кажется такой тривиальной.

Итак, в этом уроке мы начали рассматривать правильные виды умозаключений. Мы поговорили о самых простейших однопосылочных умозаключениях: умозаключениях по логическому квадрату и умозаключениях через обращение. Хотя эти умозаключения довольно просты и даже где-то тривиальны, люди повсеместно совершают в них ошибки. Понятно, что сложно удержать в памяти все виды правильных умозаключений, поэтому, когда вы будете выполнять упражнения или столкнётесь с необходимостью проверить или сделать однопосылочное умозаключение в реальной жизни, не бойтесь прибегать к помощи модельных схем и таблиц истинности. Они помогут вам проверить, всегда ли при истинности посылок заключение тоже истинное, а это главное для правильного умозаключения.

Упражнение «Подберите ключ»

В этой игре вам нужно создать ключ правильной формы. Для этого установите засечки нужной длины (от 1 до 3, 0 – быть не может), а затем нажмите кнопку «Попробовать». Вам будут даны 2 суждения, сколько засечек выбранной длины присутствуют в ключе (для простоты значение «наличие»), и сколько из выбранных находятся на своём месте (для простоты значение «на месте»). Скорректируйте своё решение и пробуйте, пока не подберёте ключ.

Упражнения

1

Сделайте все возможные умозаключения из следующих высказываний по логическому квадрату:

• Все медведи на зиму залегают в спячку.
• Неверно, что все люди завистливы.
• Ни один гном не достигает роста в два метра.
• Неверно, что ни один человек не был на Северном полюсе.
• Некоторые люди никогда не видели снега.
• Некоторые автобусы ходят по расписанию.
• Неверно, что некоторые слоны летали на луну.
• Неверно, что некоторые птицы не имеют крыльев.

2

Сделайте обращения с теми, высказываниями, с которыми это возможно:

• Никто ещё не построил машину времени.
• Некоторые официанты очень назойливы.
• Все профессионалы опытны в своём деле.
• Некоторые книги не имеют твёрдой обложки.

3

Проверьте, правильно ли сделаны следующие умозаключения:

• Некоторые кролики не носят белые перчатки. Следовательно, некоторые кролики носят белые перчатки.
• Неверно, что никто не был на Луне. Таким образом, некоторые люди были на Луне.
• Все люди смертны. Поэтому все смертные – это люди.
• Некоторые птицы не умеют летать. Следовательно, некоторые существа, не умеющие летать, это птицы.
• Ни один ягнёнок не имеет пристрастия к виски. Следовательно, ни одно существо, имеющее пристрастие к виски, не является ягнёнком.
• Некоторые морские животные млекопитающие. Таким образом, неверно, что ни одно морское животное не является млекопитающим.

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

← 5 Законы и противоречия7 Силлогизмы →

        
Учитывая свойства отношений 
между категорическими суждениями
A, E, I, O, которые иллюстрированы схемой 
логического квадрата, можно строить 
выводы, устанавливая следование 
истинности или ложности одного
суждения из истинности или ложности
другого суждения.

       Вспомним,
что в “логическом квадрате” 
зафиксированы такие важнейшие 
отношения между суждениями, как 
логическое подчинение, противоположность
(контрарность), субконтрарность,
противоречие. Непосредственные
умозаключения возможны здесь потому,
что между суждениями, находящимися в
этих отношениях, существуют определенные
зависимости по истинности и ложности.
Учитывая, что каждое суждение – А, Е,
I, О – может находиться в трех отношениях
с другими, из него можно сделать три
вывода.

       Например,
если истинно общеутвердительное
суждение (А) “Все благородные мысли находят 
себе сочувствие”, то отсюда следует:
1) что тем более истинно частноутвердительное
суждение (I): “Некоторые благородные 
мысли находят себе сочувствие”
(отношение подчинения); 2) что ложно
общеотрицательное суждение (Е): “Ни
одна благородная мысль не находит себе
сочувствия” (отношение противоположности)
и 3) что ложно частноотрицательное
суждение (О): “Некоторые благородные
мысли не находят себе сочувствия”
(отношение противоречия).

       Другой 
пример. Если ложно общеутвердительное
суждение (A), что “Все юристы имеют 
специальное высшее образование”
(так  как есть еще среднее юридическое),
то отсюда можно сделать выводы,
что истинно частноотрицательное
суждение (О): “Некоторые юристы не имеют
высшего образования”
неопределеннообщеотрицательное (Е):
“Ни один юрист не имеет высшего
образования” (в данном случае это тоже
ложно) и частноутвердительное (I):
“Некоторые юристы имеют высшее
образование” (в данном случае оно
истинно).

       Непосредственные 
умозаключения могут быть получены
также из простых реляционных 
суждений. Логическим основанием здесь 
служит характер отношения R между предметами
х и у. Так, если установлено, что 
“Женщины равны в   правах с
мужчинами”, то отсюда можно заключить,
что “Мужчины равны в правах с женщинами”.
Если известно, что “Конституционные
законы выше остальных законов страны”,
то отсюда следует, что “Остальные
законы страны не выше (ниже) конституционных”.

       Посылкой 
непосредственного умозаключения может
быть не только простое атрибутивное
или реляционное, но и сложное суждение.

       Возьмем
в качестве примера условное
суждение (импликацию): “Если завтра
будет  солнечная погода, то мы
пойдем в  лес”. Из него
можно сделать заключение: “Если
мы не пошли в лес, то погода не была
солнечной”.

       Подобное 
умозаключение основано на законе
контрапозиции. Он означает,
что любое истинное условное
суждение, если в нем поменять
местами основание и следствие 
и подвергнуть их одновременно
отрицанию, может дать в качестве
заключения тоже истинное условное
суждение.

       Непосредственное 
умозаключение можно сделать 
и из конъюнкции. Если истинно, что 
“Казань находится на Волге, и 
Саратов находится на Волге”, то
истинным будет и вывод “Саратов
находится на Волге, и Казань находится
на Волге”.

       Заключение 
из нестрогой дизъюнкции: если истинно,
что производительность труда зависит 
от технического прогресса или от
квалификации работника”, то отсюда
следует, что истинно и такое суждение:
“Производительность труда зависит
от квалификации работника или от
технического прогресса”. В основе этих
непосредственных умозаключений из
конъюнкции и дизъюнкции лежит их
свойство коммутативности (перестановочности).

       Наконец,
можно делать умозаключения из
строгой  дизъюнкции, и эквиваленции.

       Подводя
теперь общий итог, можно подчеркнуть,
что непосредственные умозаключения 
из простых и сложных суждений
– не только лишь “гимнастика для 
ума”. Благодаря им из уже известного
знания извлекается дополнительная,
и притом самая разнообразная и
богатая, информация: о взаимоотношениях
структурных элементов мысли – S и Р или
х и у – в простых суждениях, а также
исходных суждений в сложных. Важно
лишь, чтобы в каждом отдельном случае
соблюдались те или иные специфические
правила таких умозаключений, дабы
избегать ошибок в рассуждениях.   

Билет
№ 4

1.Формирование
символической логики. Логика классическая
и неклассическая.

2.
Простой категорический силлогизм.
Структура, термины и правила силлогизма.

Простой
категорический силлогизм (простое
дедуктивное умозаключение) – такое
умозаключение, в котором заключение и
посылки являются простыми категорическими
суждениями. Категорические суждения
– такие, в которых мысль утверждается
или отрицается вполне определенно, без
всяких условий, и которые имеют
субъектно-предикатную структуру.

Пример:

Все адвокаты –
юристы.

Петров – адвокат.

Петров – юрист.

Проанализируем
структуру силлогизма. Понятия, входящие
в состав силлогизма, называются терминами
силлогизма. Различают
меньший, больший и средний термины.
Меньший
термин –
понятие, которое в заключении является
субъектом
(в нашем
примере – понятие «Петров») и обозначается
буквой «S».
Больший термин – понятие,
которое в заключении является предикатом
(«юрист») и
обозначается «Р».
Средний
термин – понятие,
которое входит в обе посылки и не входит
в заключение («адвокат»), обозначается
буквой «М»
(от лат. medium
– средний).
Схема силлогизма:

Все М
есть Р.

S есть
М.

S есть
Р.

Каждая из посылок
имеет свое название: та посылка, в
которую входит больший термин, называется
большей
посылкой. Та,
в которую входит меньший термин,
называется меньшей
посылкой. В
посылках дано отношение меньшего и
большего терминов к среднему термину.
В заключении устанавливается отношение
между меньшим и большим терминами.

Последовательность
посылок и заключения в естественном
языке может быть различной. Но в процессе
логического анализа силлогизма посылки
принято располагать в определенной
последовательности: большую посылку
– на первом месте, меньшую – на втором.

Отношения между
терминами в вышеуказанном силлогизме
можно изобразить в круговых схемах:

В основе вывода
по категорическому силлогизму лежит
аксиома
силлогизма: «Все, что утверждается (или
отрицается) относительно всех предметов
класса, утверждается (или отрицается)
относительно каждого предмета (или
любой части предметов) этого класса».

Силлогизмы могут
быть правильно построенные и неправильно
построенные. Рассмотрим общие правила
силлогизма (три правила терминов и
четыре правила посылок).

Правила терминов:

1.     
В силлогизме должно быть только три
термина. Нарушение
этого правила связано с отождествлением
разных понятий, которые принимаются
за одно и рассматриваются как один
термин. Ошибка: «учетверение терминов».

Мышь грызет книжку.

Мышь – имя
существительное.

Имя существительное
грызет книжку.

Ошибка связана с
тем, что слово «мышь» выражает различные
понятия (имеет разный смысл).

2.     
Средний термин должен быть распределен
хотя бы в
одной из посылок. Если средний термин
не распределен ни в одной из посылок,
то связь между крайними терминами
остается неопределенной.

Некоторые растения
(М-) ядовиты
(Р).

Белые грибы (S)
– растения
(М-).

Белые грибы (S)
– ядовиты
(Р).

Средний термин не
распределен ни в одной из посылок.
Поэтому необходимую связь между
терминами нельзя установить.

3.     
Термин, не
распределенный в посылке, не может быть
распределен в заключении. Ошибка:
«незаконное распределение меньшего
(или большего) термина».

Во всех городах
за полярным кругом (М)
бывают белые
ночи (Р-).

Санкт-Петербург
(S)
не находится за Полярным кругом (М).

В Санкт-Петербурге
(S)
не бывает белых ночей (Р+).

Заключение ложное,
так как нарушено данное правило. Предикат
(Р) в
посылке не распределен, а в заключении
– распределен. Следовательно, произошло
расширение большего термина.

Правила посылок:

1.     
Хотя бы одна
из посылок должна быть утвердительным
суждением.

Адвокаты не судьи.

Студенты не
адвокаты.

?

2.     
Если одна
из посылок – отрицательное суждение,
то и заключение – отрицательное суждение.

Все адвокаты
юристы.

Петров не юрист.

Петров не адвокат.

3.     
Хотя бы одна
из посылок должна быть общим суждением.

Некоторые юристы
спортсмены.

Некоторые юристы
любят музыку.

?

4.     
Если одна
из посылок частная, то и заключение
должно быть частным.

Все преступники
должны быть наказаны.

Некоторые люди –
преступники.

Некоторые люди
должны быть наказаны.

Билет
№ 5

1.Понятие
логической формы. Истинность и
правильность мысли.

Логической
формой конкретной мысли является
строение этой мысли, т. е. способ связи
ее составных частей. В логических формах
отражается не вся полнота содержания
мира, существующего вне нас, а его общие
структурные связи, которые необходимо
воплощаются и в структуре наших мыслей.
Понятия, суждения, умозаключения имеют
свои специфические формы (структуры).

Структуру
мысли, т. е. ее логическую форму, можно
выразить при помощи символов. Выявим
структуру (логическую форму) в трех
следующих суждениях: «Все караси —
рыбы», «Все люди смертны», «Все бабочки
— насекомые». Содержание у них разное,
а форма одна и та же: «Все S есть Р»; она
включает S (субъект), т. е. понятие о
предмете суждения, Р (предикат), т. е.
понятие о признаке предмета, связку
(«есть»), кванторное слово («все»). Иногда
связка может отсутствовать или заменяться
тире.

Два
следующих условных суждения имеют одну
и ту же форму: 1) «Если железо нагреть,
то оно расширяется»;

2)
«Если учащийся изучает логику, то он
повышает четкость своего мышления».
Форма этих суждений такая: «Если S есть
Р, то S есть P1».

Логические
законы

Соблюдение
законов логики — необходимое условие
достижения истины в процессе рассуждения.
Основными формально­логическими
законами обычно считаются:

1)
закон тождества;

2)
закон непротиворечия;

3)
закон исключенного третьего;

4)
закон достаточного основания. Они будут
подробно излагаться в отдельной главе.
Эти законы (принципы) выражают
определенность, непротиворечивость,
доказательность мышления.

Логические
принципы действуют независимо от воли
людей, не созданы по их воле и желанию.
Они являются отражением связей и
отношений вещей материального мира.
Общечеловеческий характер принципов
формальной логики состоит в том, что
во все исторические эпохи люди всех
классов, всех наций мыслят по одним и
тем же логическим принципам. Кроме
формально-логических принципов
правильное мышление подчиняется
основным законам материалистической
диалектики: закону единства и борьбы
противоположностей, закону взаимного
перехода количественных и качественных
изменений, закону отрицания.

Истинность
мысли и формальная правильность
рассуждений

Понятие
истинности или ложности относится лишь
к конкретному содержанию того или иного
суждения. Если в суждении, верно, отражено
то, что имеет место в действительности,
то оно истинно, в противном случае оно
ложно. Например, суждение «Все волки
— хищные животные» истинно, а суждение
«Все грибы — ядовиты» ложно.

Понятие
формальной правильности рассуждения
относится лишь к логическим действиям
и операциям мышления. Ф. Энгельс писал:
«Если наши предпосылки верны и если мы
правильно применяем к ним законы
мышления, то результат должен
соответствовать действительности…».
Если в числе посылок умозаключения
встречается ложная посылка, то при
соблюдении правил логики мы в заключении
можем получить и истину, и ложь.

2.
Фигуры силлогизма и их познавательные
функции. Правила фигур. Понятие модуса
силлогизма.

Фигуры и правила
фигур силлогизма. В зависимости
от места среднего термина в посылках
различают четыре фигуры категорического
силлогизма.

Первая фигура –
разновидность силлогизма, в которой
средний термин занимает место субъекта
в большей посылке (М
– Р) и место
предиката в меньшей посылке (S
– М). Например:

Все адвокаты (М)
– юристы (Р)

Петров (S)
– адвокат (М).

Петров (S)
– юрист (Р).

М-Р – большая
посылка.

S – М – меньшая
посылка.

S —
Р – заключение.

Правила первой
фигуры:

Ø большая посылка
должна быть общим суждением (А,
Е);

Ø меньшая посылка
должна быть утвердительным суждением
(А, I).

Первая фигура
силлогизма широко применяется в
юридической науке и практике. Так, по
первой фигуре производится квалификация
различных правовых явлений, преступлений,
фактов судебной практики. При этом
большей посылкой выступает та или иная
статья кодекса, правовая норма, закон,
а меньшей – рассматриваемый конкретный
случай. В заключении делается вывод о
рассматриваемом случае на основании
общего положения. Например, «Тайное
хищение чужого имущества составляет
кражу. Данный человек совершил тайное
хищение чужого имущества. Следовательно,
данный человек совершил кражу».

Вторая фигура –
разновидность простого силлогизма, в
которой средний термин занимает место
предиката в обеих посылках.

Например:

Все адвокаты (М)
– юристы.

Петров – не юрист
(М).

Петров – не адвокат.

Р –
М – большая
посылка.

S –
М – меньшая
посылка.

S —
Р – заключение.

Правила второй
фигуры:

Ø большая посылка
должна быть общим суждением (А,
Е);

Ø одна из посылок
должна быть отрицательной (Е,
О).

Вторая фигура
применяется при доказательствах
ложности какого-либо положения путем
отрицания принадлежности исследуемых
предметов к классу предметов, о которых
мыслится в большей посылке. В судебной
практике данная фигура служит для
логического обоснования отсутствия
состава преступления в том или ином
конкретном деянии, для доказательства
неправильной квалификации преступления,
для опровержения каких-либо положений,
не согласующихся с общим правилом.
Например, «Этот смертельный удар нанесен
человеком, обладающим огромной физической
силой. Обвиняемый не является человеком,
обладающим огромной физической силой.
Следовательно, обвиняемый не мог нанести
этот смертельный удар».

Третья фигура –
разновидность силлогизма, в которой
средний термин занимает место субъекта
в обеих посылках (М
– Р; М – S). Например:

Все подозреваемые
(М) признали
свою вину.

Все подозреваемые
(М) привлечены
к уголовной ответственности.

Некоторые
привлеченные к уголовной ответственности,
признали свою вину.

М –
Р – большая
посылка.

М –
S – меньшая
посылка.

S – Р – заключение.

Правила третьей
фигуры:

Ø меньшая посылка
должна быть утвердительным суждением
(А, I);

Ø о заключение
должно быть частным суждением (I,
О).

Третья фигура
служит чаще всего для установления
частичной совместимости признаков,
относящихся к одному и тому же предмету.
Она также может быть применима для
опровержения отдельных общих положений.
Например, необходимо опровергнуть
суждение «Ни один свидетель не дал
правдивых показаний» (т. е. доказать
противоречащее ему суждение «Некоторые
свидетели дали правдивые показания»)
и известно, что свидетели X. и Y. дали
правдивые показания. Построим
умозаключение по третьей фигуре:

X. и Y. (М)
– дали правдивые показания.

X. и Y. (M)
– свидетели.

Некоторые свидетели
дали правдивые показания.

P –
M- большая
посылка.

S –
M – меньшая
посылка.

S-P- заключение.

Поскольку
частноутвердительное суждение «Некоторые
свидетели дали правдивые показания»
является истинным, то находящееся с
ним в отношении противоречия
общеотрицательное суждение «Ни один
свидетель не дал правдивых показаний»
– ложное.

Четвертая фигура
– разновидность силлогизма, в которой
средний термин занимает место предиката
в большей и место субъекта в меньшей
посылке (Р
– M, M – S), схематично
выражается:

Р – М – большая
посылка.

М – S – меньшая
посылка.

S –
Р – заключение.

Четвертая фигура
силлогизма практически не употребляется.

По первой фигуре
можно получить выводы из всех основных
ви­дов суждений. Вторая фигура дает
только отрицательный вывод. В третьей
фигуре вывод будет частным суждением.

В зависимости от
того, какие суждения по количеству и
качеству составляют простой категорический
силлогизм (являются посылками и
заключением), различают виды силлогизмов,
которые называют модусами.
Модусы
простого категорического силлогизма
– это его
разновидности, отличающиеся друг от
друга качественной и количественной
характеристикой входящих в них посылок
и заключения.

В четырех фигурах
силлогизма максимальное число комбина­ций
равно 64. Однако правильных модусов
всего 19:

Первая фигура:
ААА, ЕАЕ,
АII, ЕIО

Вторая фигура:
ЕАЕ, АЕЕ,
ЕIО, АОО

Третья фигура:
AAI, IAI, АII,
ЕАО, ОАО, ЕIО

Четвертая фигура:
AAI, АЕЕ, IAI,
ЕАО, ЕIО

В соответствии с
этим называют модусы первой фигуры,
модусы второй фигуры и т. д. Например,
модус ААА
1-й фигуры,
модус АЕЕ
2-й фигуры
и т.д. Все другие модусы возможны, но
они являются неправильными, так как в
них нарушаются те или иные правила
категорического силлогизма. Знание
модусов дает возможность определить
форму истинного заключения, когда даны
посылки и известно, какова фигура
данного силлогизма.

Знания специальных
правил фигур являются производными от
перечисленных выше общих правил
силлогизма. Главная трудность при
проверки правильности того или иного
силлогизма состоит в том, чтобы правильно
построить умозаключение. Правила
простого категорического силлогизма
не позволяют определить содержание
посылок, но они указывают, каким
требованиям эти посылки должны
удовлетворять, чтобы их можно было
связать между собой и сделать необходимое
заключение.

Но умозаключения
строятся не только из простых, но и из
сложных суждений. Широко используются
умозаключения, посылками которых
являются условные и разделительные
суждения, выступающие в разных сочетаниях
друг с другом или с категорическими
суждениями.

Модусом простого
силлогизма
называется набор простых суждений,
входящих всиллогизм.
Модус простого силлогизма составляет
три суждения. Например, всиллогизме:

Все
небесные тела движутся.

Все
планеты — это небесные тела.

————

Все
планеты движутся.

Первая посылкаявляется простымсуждениемвида А (общеутвердительным), втораяпосылка—
это тоже простое суждение вида А, и
вывод в данном случае представляет
собой простое суждение вида А. Поэтому
рассмотренный силлогизм имеет модус
ААА.

Билет
№ 6

1.Язык
как знаковая система: логико-семантический
анализ языка

2.
Энтимема. Способы образования и проверки
энтимем

Грустно сие констатировать, но очень многие люди делают в своих суждениях вопиющие логические ошибки и не замечают этого. Если им указать на логическое противоречие их мыслей, они не понимают, в чем проблема. Не видят ее.

А между тем существует такая философская дисциплина, как логика (признанный отец-основатель – Аристотель), которая дает четкие законы и формулирует правила мышления. Я не буду тут говорить о законах формальной логики (их четыре, три первые даны Аристотелей, четвертая – Г.Лейбницем). А покажу с помощью логического квадрата, как можно избежать логических ошибок. Для этого не надо быть сильно умным, достаточно быть просто разумным.

Итак, перед нами логический квадрат. Мы видим по его углам какие-то буквы. Сейчас объясню, что все это означает. Каждая буква – тот или иной вид суждения, а сам квадрат показывает отношения между ними. Между А и Е это отношения противоположности, между А и I, а также Е и О – подчинения, между А и О, а также Е и I – противоречия, между I и О – частичное совпадение. На квадрате это отлично видно.

А – общеутвердительное суждение. Например: все коты – млекопитающие. В данном случае это истинно. Но такое суждение может быть и ложным: все коты дышат жабрами.

Е – общеотрицательные. Например: ни один карась не является млекопитающим – истинное суждение. Ни один кот не является млекопитающим – ложное.

Поскольку между А и Е существует отношение противоположности, то значит, оба эти суждения не могут одновременно утверждать истину об одном и том же, то есть либо все коты – млекопитающие, либо ни один кот таковым не является. Но А и Е могут быть оба ложными, если это разные неверные суждения об одном объекте. Например: все коты дышат жабрами, ни один кот не является млекопитающим.

Идем дальше.

I – частноутвердительное суждение. Оно подчиняется А – общеутвердительному. И если суждение А – истинно, то и I тоже истинно. Например: все коты – млекопитающие (А). Мой кот Васька и соседский Паська – млекопитающие ( I ).

А если А ложно, то и I неопределенно, оно может быть как истинным, так и ложным.

Понятна логика?))

О – частноотрицательное суждение. Соответственно – подчиняется Е, общеотрицательному. Берем теперь пример ложного Е: Ни один кот не является млекопитающим. Значит, если я заявлю, что мой личный кот Васька и его дружок Паська не является млекопитающими – это будет либо ложь, либо правда.

Теперь об отношении противоречия, то есть между А-О и Е- I. Оба противоречащих суждения не могут быть одновременно истинными или ложными. И если точно известно, что одно из них, скажем, истинно, значит, другое ложно. И наоборот.

Пример: все коты млекопитающие – истина. Некоторые коты не млекопитающие – ложно.

Все коты не млекопитающие – ложно. Некоторые коты млекопитающие – истина.

И, наконец, отношение частичного совпадения между I и О. Тут логика такая – они могут быть одновременно истинными, но не могут быть одновременно ложными.

Пример: некоторые коты пушистые (I), некоторые коты не пушистые (О). Оба суждения истинны.

А если мы скажем заведомую ложь – некоторые коты имеют крылья (I), то в любом случае суждение О истинно: некоторые коты не имеют крыльев. Оба быть ложными не могут.

Такая вот логика.

Читайте еще на моем канале:

Можно ли назвать произведением искусства следы, оставленные котом на бумаге

Что такое “зеркальное Я”

Непосредственные умозаключения по логическому квадрату

Различают четыре разновидности преобразований суждений:

• умозаключение по логическому квадрату,
• превращение,
• обращение,
• противопоставление предикату.

Между суждениями, представляющими собой вершины логического квадрата, существуют определенные отношения. Вершинами логического квадрата выступают следующие суждения:

• А – общеутвердительные (от латинского affirmo, что переводится как «утверждать» – по первой гласной букве);
• I – частноутвердительные (вторая гласная в слове affIrmo);
• E – общеотрицательные (первая гласная в слове nEgo – «отрицать»);
• O – частноотрицательные (вторая гласная в слове negO).

Логический квадрат позволяет понять, в каких отношениях находятся суждения разных видов и осуществлять вывод из одних суждений других:

• между частными и общими суждениями одного характера (утвердительными или отрицательными) действует отношение подчинения, изображаемое как вертикальные стороны квадрата. Если истинно общее суждение, то истинно частное того же характера (обратное – в случае ложности общего – неверно: частное может быть как истинным, так и ложным). По истинности частного суждения судить об истинности общего нельзя, но если частное ложно, то ложно и общее;
• между общеутвердительными и общеотрицательными суждениями имеет место отношение контрарности (противности), изображаемое верхней горизонтальной стороной квадрата. Одно общее суждение может быть получено из другого путем логического отрицания. Если истинно одно из суждений, то второе ложно. При этом оба суждения могут быть одновременно ложными (но одновременно истинными – не могут);
• между частноутвердительными и частноотрицательными суждениями действуют отношения субконтрарности, представленные нижней горизонтальной стороной. Оба частных суждения могут быть одновременно истинными, а одновременно ложными не могут;
• диагоналями квадрата связываются общеутвердительное с частноотрицательным, а общеотрицательное с частноутвердительным суждением. Между ними имеется противоречие: если истинно частноутвердительное суждение, то ложно общеотрицательное; если ложно частноутвердительное – истинно общеотрицательное, и наоборот. Аналогично для отношения между частноотрицательным и общеутвердительным: истинным должно быть одно из них (притом только одно).

«Непосредственные умозаключения» 👇

Превращение

Если посылка является утвердительным суждением, то посредством превращения получают отрицательное суждение. Отрицательное суждение превращается в утвердительное.

Например, утверждение: «Все розы являются растениями» будет превращено в «Ни одна роза не является не-растением». В этом случае общеутвердительное суждение превращено в общеотрицательное.

Схематически это выглядит следующим образом:

• посылка: «Все А есть В»;
• заключение: «Ни одно А не есть не-В».

Похожим образом можно превратить частноутвердительное суждение в частноотрицательное. В этом случае действует схема:

• посылка: «Некоторые C есть D»;
• заключение: «Некоторые C не есть не-D».

Схема превращения общеотрицательного суждения в общеутвердительное:

• посылка: «Ни одно А не есть В»;
• заключение: «Все А есть не-В».

Схема превращения частнотрицательного суждения в частноутвердительное:

• посылка: «Некоторые С не есть D»;
• заключение: «Некоторые C есть не-D».

Во всех рассмотренных случаях умозаключения базируются на связи между кванторами «все» и «некоторые» и законе двойного отрицания. При этом двойное отрицание оставляет неизменным качество суждения. Когда суждения представлены в языковом выражение, одно из отрицаний выполняет роль отрицания предиката, поэтому, чтобы проверить правильность выполненного превращения (из утвердительного суждения в отрицательное) нужно пользоваться символическим представлением.

Обращение

Обращение обеспечивает уточнение количества суждений. Например, из суждения «Все металлы электропроводны» путем обращения может быть получено суждение «Некоторые электропроводные вещества – металлы», поскольку класс электропроводных веществ шире, чем подкласс металлов. Такой вывод получается на основе знания содержания высказывания. Можно произвести абстрагирование от содержания, приняв во внимание, что в таких умозаключениях фигурирует распространенный предикат, составляющий лишь часть объема субъекта: «Все S есть P» обращается в «Некоторые P есть S».

Чистое обращение имеет место, если объемы предиката и субъекта совпадают – как в случае определения понятий.

Противопоставление предикату

Например, из суждения «Все параллельные прямые на плоскости не пересекаются» может быть получено суждение «Все непараллельные прямые на плоскости пересекаются».

Описываемый вид умозаключения есть сочетание превращения и обращения, при этом:

• общеутвердительное суждение преобразуется в общеотрицательное,
• общеотрицательное суждение преобразуется в частноутвердительное,
• частноотрицательное суждение преобразуется в частноутвердительное,
• для частноутвердительных суждений преобразование посредством противопоставления предикату не производится.

Необходимо отметить, что некоторые способы получения непосредственных умозаключений традиционной логики легко выражаются на символическом языке исчисления высказываний. Но уже в случае с операцией обращения, когда нужно анализировать структуру связи между субъектом и предикатом и пользоваться кванторами существования и общности, невозможно перевести схему преобразования на простой язык исчисления высказываний, где высказывания рассматриваются как единое целое, характеризующееся лишь истинностью или ложностью.

Обновлено: 22.05.2023

Грустно сие констатировать, но очень многие люди делают в своих суждениях вопиющие логические ошибки и не замечают этого. Если им указать на логическое противоречие их мыслей, они не понимают, в чем проблема. Не видят ее.

А между тем существует такая философская дисциплина, как логика (признанный отец-основатель – Аристотель), которая дает четкие законы и формулирует правила мышления. Я не буду тут говорить о законах формальной логики (их четыре, три первые даны Аристотелей, четвертая – Г.Лейбницем). А покажу с помощью логического квадрата, как можно избежать логических ошибок. Для этого не надо быть сильно умным, достаточно быть просто разумным.

Итак, перед нами логический квадрат. Мы видим по его углам какие-то буквы. Сейчас объясню, что все это означает. Каждая буква – тот или иной вид суждения, а сам квадрат показывает отношения между ними. Между А и Е это отношения противоположности, между А и I, а также Е и О – подчинения, между А и О, а также Е и I – противоречия, между I и О – частичное совпадение. На квадрате это отлично видно.

А – общеутвердительное суждение. Например: все коты – млекопитающие. В данном случае это истинно. Но такое суждение может быть и ложным: все коты дышат жабрами.

Е – общеотрицательные. Например: ни один карась не является млекопитающим – истинное суждение. Ни один кот не является млекопитающим – ложное.

Поскольку между А и Е существует отношение противоположности, то значит, оба эти суждения не могут одновременно утверждать истину об одном и том же, то есть либо все коты – млекопитающие, либо ни один кот таковым не является. Но А и Е могут быть оба ложными, если это разные неверные суждения об одном объекте. Например: все коты дышат жабрами, ни один кот не является млекопитающим.

I – частноутвердительное суждение. Оно подчиняется А – общеутвердительному. И если суждение А – истинно, то и I тоже истинно. Например: все коты – млекопитающие (А). Мой кот Васька и соседский Паська – млекопитающие ( I ).

А если А ложно, то и I неопределенно, оно может быть как истинным, так и ложным.

О – частноотрицательное суждение. Соответственно – подчиняется Е, общеотрицательному. Берем теперь пример ложного Е: Ни один кот не является млекопитающим. Значит, если я заявлю, что мой личный кот Васька и его дружок Паська не является млекопитающими – это будет либо ложь, либо правда.

Теперь об отношении противоречия, то есть между А-О и Е- I. Оба противоречащих суждения не могут быть одновременно истинными или ложными. И если точно известно, что одно из них, скажем, истинно, значит, другое ложно. И наоборот.

Пример: все коты млекопитающие – истина. Некоторые коты не млекопитающие – ложно.

Все коты не млекопитающие – ложно. Некоторые коты млекопитающие – истина.

И, наконец, отношение частичного совпадения между I и О. Тут логика такая – они могут быть одновременно истинными, но не могут быть одновременно ложными.

Пример: некоторые коты пушистые (I), некоторые коты не пушистые (О). Оба суждения истинны.

А если мы скажем заведомую ложь – некоторые коты имеют крылья (I), то в любом случае суждение О истинно: некоторые коты не имеют крыльев. Оба быть ложными не могут.

Учитывая свойства отношений между категорическими сужде­ниями А, Е,I, О, которые иллюстрированы схемой логического квад­рата’, можно строить выводы, устанавливая следование истинности или ложности одного суждения из истинности или ложности другого суждения.

Рассмотрим эти выводы.

Отношение противоречия (контрадикторности): А — О, Е — I.

Выводы строятся по схемам:

А -Л О; ~[ А -> О; Е -> 11; -1 Е ->1.

Отношения между противоположными суждениями подчиняют­ся закону непротиворечия. Выводы строятся по схемам: А —Л Е;

См рис. 37. С. 87.

Отношение частичной совместимости (субконтрарности):

Таким образом, субконтрарные суждения не могут быть вместе ложными; по крайней мере одно из них истинно.

Выводы строятся по схемам:Il->0; “I 0-> I; I -> (OviО);

0->(I v -11).

Выводы строятся по схемам: А —> I;Е —>О; I —> (А v”] А);

Из ложности подчиненного суждения следует ложность подчи­няющего суждения, но не наоборот: из ложности подчиняющего суждения ложность подчиненного с необходимостью не следует;

Знание зависимости истинности или ложности одних суждений от истинности или ложности других помогает делать правильные выводы в процессе рассуждения.

Умозаключения по логическому квадрату находят применение во многих мыслительных приемах и операциях, в том числе в аргу­ментации, где построение некоторых способов косвенного доказа­тельства и косвенного опровержения опирается на отношения про­тиворечия.

§3. Простой категорический силлогизм Состав простого категорического силлогизма

Таким образом, простой категорический силлогизм состоит из трех категорических суждений, два из которых являются посылками, а третье — заключением.

В отличие от терминов суждения — субъекта (S) и предиката (Р) — понятия, входящие в состав силлогизма, называюттермина­ми силлогизма. Различают меньший, больший и средний термины.

Каждый из крайних терминов входит не только в заключение, но и в одну из посылок. Посылка, в которую входит меньший термин, называетсяменьшей посылкой, посылка, в которую входит больший термин, называетсябольшей посылкой. В нашем примере большей посылкой будет первое суждение (1), меньшей — второе сужде­ние (2).

Для удобства анализа силлогизма посылки принято располагать в определенной последовательности: большую — на первом месте, меньшую — на втором. Под чертой записывают заключение:

Обвиняемый имеет право на защиту Гусев —обвиняемый

Гусев имеет право на защиту

Однако в рассуждении такой порядок необязателен. Меньшая посылка может находиться на первом месте, большая — на втором. Иногда посылки стоят после заключения.

Посылки различаются не их местом в силлогизме, а входящими в них терминами.

Таким образом, вывод из посылок оказывается возможным пото­му, что средний термин выполняет роль связующего звена между двумя крайними терминами силлогизма.

Поставив в нашем примере на место терминов суждения терми­ны силлогизма, получим:

Обвиняемый (М) имеет право на защиту (Р) Гусев (S)—обвиняемый (М)

Гусев (S) имеет право на защиту (Р)

Итак, простой категорический силлогизм — это умозаключен ние об отношении двух крайних терминов на основании их отноше­ния к среднему термину.

Правомерность вывода, т.е. логического перехода от посылок к заключению, в категорическом силлогизме основывается на положе­нии(аксиоме силлогизма): все, что утверждается или отрицает­ся относительно всех предметов некоторого класса, утверждает­ся или отрицается относительно каждого предмета и любой

части предметов этого класса 1 .

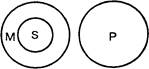
В данном примере — все, что утверждается относительно всех обвиняемых, утверждается и относительно конкретного обвиняемо­го (см. в круговых схемах рис. 47).

Религиозные организации (М) не выполняют

государственных функций (Р)

Церковь (S) — религиозная организация (М)

Церковь (S) не выполняет государственных функций (Р)

В этом силлогизме все, что отрицается относительно каждой религиозной организации, отрицается и относительно некоторой части этих организаций (рис. 48).

‘ Существует другая, так называемая атрибутивная, формулировка: признак признака некоторой вещи есть признак самой этой веши; то, что противоречит при­знаку вещи, противоречит и вещи.

Общие правила категорического силлогизма

; ^ Из истинных посылок не всегда можно получить истинное заклю-;:

чение. Его истинность обусловлена правилами силлогизма. Этих] правил семь: три относятся к терминам и четыре — к посылкам. ‘, Правила терминов.

1-е правило: в силлогизме должно быть только три термина.

3-е правило: термин, не распределенный в посылке, не может бЫть распределен и в заключении.

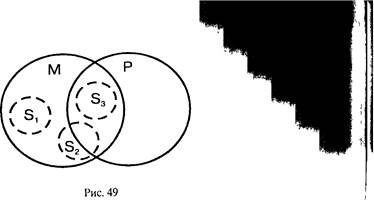
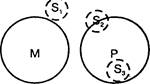
Рис. 50

Например:

Нравственные нормы (М) не санкционируются государством (Р+) Нравственные нормы (М) — формы социальной регуляции (S-)

Некоторые формы социальной регуляции (S-) не санкционируются государством (Р+)

Учитывая свойства отношений между категорическими сужде­ниями А, Е,I, О, которые иллюстрированы схемой логического квад­рата’, можно строить выводы, устанавливая следование истинности или ложности одного суждения из истинности или ложности другого суждения.

Рассмотрим эти выводы.

Отношение противоречия (контрадикторности): А — О, Е — I.

Выводы строятся по схемам:

А -Л О; ~[ А -> О; Е -> 11; -1 Е ->1.

Отношения между противоположными суждениями подчиняют­ся закону непротиворечия. Выводы строятся по схемам: А —Л Е;

См рис. 37. С. 87.

Отношение частичной совместимости (субконтрарности):

Таким образом, субконтрарные суждения не могут быть вместе ложными; по крайней мере одно из них истинно.

Выводы строятся по схемам:Il->0; “I 0-> I; I -> (OviО);

0->(I v -11).

Выводы строятся по схемам: А —> I;Е —>О; I —> (А v”] А);

Из ложности подчиненного суждения следует ложность подчи­няющего суждения, но не наоборот: из ложности подчиняющего суждения ложность подчиненного с необходимостью не следует;

Знание зависимости истинности или ложности одних суждений от истинности или ложности других помогает делать правильные выводы в процессе рассуждения.

Умозаключения по логическому квадрату находят применение во многих мыслительных приемах и операциях, в том числе в аргу­ментации, где построение некоторых способов косвенного доказа­тельства и косвенного опровержения опирается на отношения про­тиворечия.

§3. Простой категорический силлогизм Состав простого категорического силлогизма

Таким образом, простой категорический силлогизм состоит из трех категорических суждений, два из которых являются посылками, а третье — заключением.

В отличие от терминов суждения — субъекта (S) и предиката (Р) — понятия, входящие в состав силлогизма, называюттермина­ми силлогизма. Различают меньший, больший и средний термины.

Каждый из крайних терминов входит не только в заключение, но и в одну из посылок. Посылка, в которую входит меньший термин, называетсяменьшей посылкой, посылка, в которую входит больший термин, называетсябольшей посылкой. В нашем примере большей посылкой будет первое суждение (1), меньшей — второе сужде­ние (2).

Для удобства анализа силлогизма посылки принято располагать в определенной последовательности: большую — на первом месте, меньшую — на втором. Под чертой записывают заключение:

Обвиняемый имеет право на защиту Гусев —обвиняемый

Гусев имеет право на защиту

Однако в рассуждении такой порядок необязателен. Меньшая посылка может находиться на первом месте, большая — на втором. Иногда посылки стоят после заключения.

Посылки различаются не их местом в силлогизме, а входящими в них терминами.

Таким образом, вывод из посылок оказывается возможным пото­му, что средний термин выполняет роль связующего звена между двумя крайними терминами силлогизма.

Поставив в нашем примере на место терминов суждения терми­ны силлогизма, получим:

Обвиняемый (М) имеет право на защиту (Р) Гусев (S)—обвиняемый (М)

Гусев (S) имеет право на защиту (Р)

Итак, простой категорический силлогизм — это умозаключен ние об отношении двух крайних терминов на основании их отноше­ния к среднему термину.

Правомерность вывода, т.е. логического перехода от посылок к заключению, в категорическом силлогизме основывается на положе­нии(аксиоме силлогизма): все, что утверждается или отрицает­ся относительно всех предметов некоторого класса, утверждает­ся или отрицается относительно каждого предмета и любой

части предметов этого класса 1 .

В данном примере — все, что утверждается относительно всех обвиняемых, утверждается и относительно конкретного обвиняемо­го (см. в круговых схемах рис. 47).

Религиозные организации (М) не выполняют

государственных функций (Р)

Церковь (S) — религиозная организация (М)

Церковь (S) не выполняет государственных функций (Р)

В этом силлогизме все, что отрицается относительно каждой религиозной организации, отрицается и относительно некоторой части этих организаций (рис. 48).

‘ Существует другая, так называемая атрибутивная, формулировка: признак признака некоторой вещи есть признак самой этой веши; то, что противоречит при­знаку вещи, противоречит и вещи.

Общие правила категорического силлогизма

; ^ Из истинных посылок не всегда можно получить истинное заклю-;:

чение. Его истинность обусловлена правилами силлогизма. Этих] правил семь: три относятся к терминам и четыре — к посылкам. ‘, Правила терминов.

1-е правило: в силлогизме должно быть только три термина.

3-е правило: термин, не распределенный в посылке, не может бЫть распределен и в заключении.

Рис. 50

Например:

Нравственные нормы (М) не санкционируются государством (Р+) Нравственные нормы (М) — формы социальной регуляции (S-)

Некоторые формы социальной регуляции (S-) не санкционируются государством (Р+)

Отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата, который был разработан еще средневековыми логиками.

Как видим, вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями А и А, I и I, Е и Е, О и О. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: Все люди изучали логику и Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А), а второе частноотрицательным (О), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Также суждения: Все люди изучали логику (А) и Некоторые люди изучали логику (I) находятся в отношении подчинения, а суждения: Все люди изучали логику (А) и Все люди не изучали логику (Е) находятся в отношении противоположности.

Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, о которых идет речь в данном параграфе, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так если суждение вида А является истинным или ложным, то три других (I, Е, О) сравнимых с ним суждения (т. е. имеющих сходные с ним субъекты и предикаты) в зависимости от этого (т. е. от истинности или ложности суждения вида А) тоже являются истинными или ложными. Например, если суждение вида А: Все тигры – это хищники является истинным, то суждение вида I: Некоторые тигры – это хищники также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида Е: Все тигры – это не хищники является ложным, и суждение вида О: Некоторые тигры – это не хищники также является ложным. Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).

Далее представлены все случаи отношений между истинностными значениями простых сравнимых суждений.

1. Если суждение вида А является истинным, то суждение вида I также является истинным, а суждения вида Е и О являются ложными.

3. Если Е истинно, то А ложно, I ложно, О истинно.

4. Если Е ложно, то А неопределенно по истинности, I истинно, О неопределенно по истинности.

5. Если I истинно, то А неопределенно по истинности, Е ложно, О неопределенно по истинности.

6. Если I ложно, то А ложно, Е истинно, О истинно.

7. Если О истинно, то А ложно, Е неопределенно по истинности, I неопределенно по истинности.

8. Если О ложно, то А истинно, Е ложно, I истинно.

Используя рассмотренные правила, можно делать выводы об истинности простых сравнимых суждений с помощью логического квадрата (или, как часто говорят в логике, – по логическому квадрату). Выше был приведен пример таких выводов на основе суждения вида А: Все тигры являются хищниками, где из его истинности вытекали определенные истинностные значения других суждений – I, Е, О. Рассмотрим еще один пример. Возьмем суждение вида Е: Все треугольники не являются квадратами и сделаем из его истинности выводы об истинностных значениях суждений А, I, О. Когда данное суждение вида Е истинно (см. правила выше), то суждение вида А: Все треугольники являются квадратами ложно, суждение вида I: Некоторые треугольники являются квадратами также ложно, а суждение вида О: Некоторые треугольники не являются квадратами истинно (если все треугольники не являются квадратами, то и часть треугольников, т. е. некоторые треугольники также не являются ими).

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

IV. Квадрат коммуникации и генеративная матрица

IV. Квадрат коммуникации и генеративная матрица Генеративная матрица высказывания проходит трехэтапный генезис и имеет четыре ключевых пункта, которые лежат на кресте пересечения двух осей – вертикальной оси Идеальности и горизонтальной оси Реальности, в результате

Исторический и логический методы

Исторический и логический методы По большому счету эмпирический уровень научного познания сам по себе не достаточен для проникновения в сущность вещей, в том числе в закономерности функционирования и развития общества. На определенном этапе, когда накоплено уже более

Логический позитивизм Карнапа

Логический позитивизм Карнапа Логический позитивизм — это видоизмененная форма эмпиризма. Эмпиризм в чистом виде — это учение о том, что все знание мы получаем из чувственного опыта. Логический позитивизм выглядит слабее его в одном важном пункте, но зато сильнее в

Головоломный квадрат

Головоломный квадрат Изображенные на рисунке двадцать кругов образуют крест. Сколько квадратов можно найти в этом кресте, если считать, что любые четыре круга являются углами квадрата? Посмотрите на схему, и вы поймете, что имеется в виду. Четыре круга с буквой А

2. Логический позитивизм

2. Логический позитивизм В 1922 году на кафедре натуральной философии Венского университета, которую после смерти Э. Маха возглавил профессор М. Шлик, собралась группа молодых ученых, поставивших перед собой смелую цель — реформировать науку и философию. Эта группа вошла

Магический квадрат

Распили квадрат

2. Логический обвал

2. Логический обвал — То, что может быть продемонстрировано или что требуется доказать, есть конечное познание чего-то особенного. Экзистенция и трансценденция, в смысле этого бытия, не существуют. Если мы мыслим о них, то мысль принимает логические формы, которые

14. Тетрактис и квадрат четырех[119]

14. Тетрактис и квадрат четырех[119] В ходе наших исследований нам уже не раз случалось говорить о пифагорейском Тетрактисе, и мы тогда же привели его числовую формулу: 1+2+3+4=10, указав на связь, непосредственно соединяющую денер с кватернером. Известно совершенно особое

§ 4. Традиционный квадрат противопоставлений

§ 4. Традиционный квадрат противопоставлений Традиционное понимание противопоставления между суждениями отличается от предложенного нами понимания. Поскольку в традиционном подходе все суждения были разложимы на субъект и предикат, противопоставлялись только

ЧТО ТАКОЕ ЛОГИЧЕСКИЙ ПАРАДОКС?

ЧТО ТАКОЕ ЛОГИЧЕСКИЙ ПАРАДОКС? Никакого исчерпывающего перечня логических парадоксов не существует. Рассмотренные логические парадоксы – это только часть из всех обнаруженных к настоящему времени. Вполне вероятно, что в будущем будут открыты и многие другие

Логический позитивизм

Логический позитивизм В период между первой и второй мировыми войнами были выдвинуты новые философские идеи. Многие из них были стимулированы развитием неклассической физики и стали предметом серьезного эпистемологического анализа со стороны логического позитивизма.

15. ИНФИНИТЕЗИМАЛbНО–ЛОГИЧЕСКИЙ СЛОВАРb

Возведение в квадрат и самоусиление

Возведение в квадрат и самоусиление Есть особенно интересный вид умножения, называемый возведением в квадрат, который дает нам подсказки относительно того, как работать с нашими собственными умами. Возведение в квадрат будет очень важно позднее, когда мы будем изучать

Перевоплощение и эксперимент возведения в квадрат

Перевоплощение и эксперимент возведения в квадрат Для начала вспомните недавнее сновидение. Затем выберите из этого сновидения какую-либо фигуру – человека, дерево или что угодно еще.Теперь представьте себе, что эта фигура – основа процесса, начало ее собственной

Логика – наука о мышлении. Использование ее законов и принципов позволило многим выдающимся философам сделать открытия, которые стали знаковыми для общества и позволили человеческой цивилизации выйти на качественно новый уровень развития.

А суждения А-О и І-Е – противоречащие.

На данной схеме буквами обозначены категорические суждения. Так, левый верхний угол – буква А – общеутвердительное суждение; правый верхний угол – буква Е – общеотрицательное суждение; левый нижний угол – буква І – частноутвердительное суждение; правый нижний угол – буква О – частноотрицательное суждение.

Суть данной схемы заключается в том, что в линии квадрата и его диагоналей показывают определенное однотипное отношение между парой суждений разного вида. Действительно, наглядное расположение линий и букв помогают зрительно запомнить их нахождение и мысленно представлять отношение между такими суждениями. Ведь на самом деле общеутвердительное суждение (А) и частноотрицательное суждение (О) являются противоречащими, также как и частноутвердительное суждение (І) с общеотрицательным суждением (Е). И на схеме именно так и обозначено данное соотношение.

При этом выделяют четыре вида отношений:

Отношение субконтрарности – оно существует между частноутвердительными суждениями (I)и частноотрицательными суждениями (О). Также различаются по качеству, но не по количеству – оба частные. Здесь ситуация обратная предыдущей – оба суждения могут быть одновременно истинными, но не могут быть одновременно ложными (3).

Четыре обозначенных отношения между суждениями, которые схематично изображены в виде квадрата, вроде и симметричны, но стороны и диагонали квадрата не представляют симметрично степеней несовместимости или противоположности в обычном смысле слова.

умозаключение противоречия (отрицание суждения) – оно основывается на законе исключенного третьего, согласно которому, если утверждение чего-либо истинно, то отрицание этого ложно, и наоборот;

умозаключение противоположности – оно основывается на базе закона противоречия. В результате такого умозаключения появляется ложное суждение (например, из истинного суждения “ни один человек не является машиной” можно установить ложность суждения “все люди – машины”);

умозаключение субконтрарности – позволяет получить истинные частноутвердительные или частноотрицательные суждения;

умозаключение подчинения – не дает возможность получить истинные частноутвердительные или частноотрицательные суждения, но позволяют сделать вывод о ложности общеутвердительных и общеотрицательных суждений на основе ложности соответствующих частноутвердительных и частноотрицательных суждений.

Умозаключение противоречия основано непосредственно на законе исключенного третьего, в соответствии с которым либо утверждение чего-нибудь является истинным, а отрицание того же самого – ложным, либо отрицание утверждения является истинным, а само утверждение – ложным. При помощи отрицания суждения из первоначального образуется новое суждение, которое является истинным, если посылка (исходное суждение) ложно, и наоборот, ложным тогда, когда исходное суждение истинно.

Правильность полученных умозаключений можно проверить путем сопоставления приписываемого следствию истинностного значения с тем, которое ему предопределено логическим отношением с посылкой. Например, нужно проверить умозаключение: “Все рыбы дышат жабрами, значит, неверно, что ни одна рыба не дышит Жабрами”. Его посылка — общеутвердительное суждение, а заключение — отрицание общеотрицательного суждения, т.е. частноутвердительное суждение. То есть, заключение находится с посылкой в отношении подчинения, что означает: при истинном первом (посылке) второе (заключение) не может быть ложным. Значит, умозаключение правильно.

Возьмем другое рассуждение: “Если неверно, что все студенты прилежны, то истинно, что некоторые студенты прилежны”. Его посылка — отрицание общеутвердительного суждения или можно сказать проще: мы исходим из того, что общеутвердительное суждение ложно. Заключение в нем утверждает истинность соответствующего частноутвердительного суждения. Такое умозаключение, как легко увидеть, неправильно, поскольку утверждаемая истинность его следствия не предопределяется логическим отношением (подчинения) посылки и заключения: при ложности подчиняющего подчиненное не обязательно истинно, оно может быть и ложным.

Нарушение закона исключенного третьего происходит довольно часто из-за определенного его недостатка, который связан с тем, что он не охватывает абсолютно все вещи, как этого требует логика. То есть в нем речь идет только о вещах, которые точно известны и однозначны. При этом закон не применим к вещам переходного характера, а которых трудно сказать, чем они являются (А или неА). Не рекомендуется использовать этот закон когда происходит какое-то событие, переводящее некоторую часть реальности из одного устойчивого состояния в другие, и при этом нельзя точно сказать в какой момент произошел переход, но можно указать промежуток за который он происходит. Это связано с тем, что данный закон имеет некоторую погрешность, которая зависит от погрешности реально существующих вещей.

Допустим, что деревенский парикмахер сам себя бреет, но тогда он относится к тем жителям деревни, которые бреются сами и которых не бреет парикмахер, следовательно, в этом случае, он сам себя не бреет.

Допустим, что деревенский парикмахер сам себя не бреет, но тогда он относится к тем жителям деревни, которые не бреются сами и которых бреет парикмахер, следовательно, в этом случае, он сам себя бреет. Как видим, получается невероятное: если деревенский парикмахер сам себя бреет, то он сам себя не бреет; а если он сам себя не бреет, то он сам себя бреет (два противоречащих суждения являются одновременно истинными и взаимно обуславливают друг друга).

Гусев Д.А. Логика: Учебный курс (учебно-методический комплекс).

Ивин А.А. Логика: Учебник для гуманитарных факультетов. – М.:ФАИР-ПРЕСС, 2002.

Кондаков Н.И. Введение в логику. – М.: 1967. – 468с.

Тимощук А.С. Методическая разработка (лекция №1) проведения занятия по теме 4 “Умозаключение” курса “Логика” для слушателей дневной формы обучения. – Владимир: ВлЮИ МЮ РФ, 1999 – 18 с.

Формальная логика. Л.: 1977. – 357с.

Похожие документы:

Образовательная программа основного общего образования Муниципального бюджетного общеобразовательного учреждения

. при следовании моральным нормам, переживание стыда и вины при их нарушении . по теме «Наиболее типичные ошибки при . по логической таблице. Максимальный уровень Упрощать логическую . содержание информации при их вызове. и воздуха в быту. 1 1 Правила .

Основная образовательная программа основного общего образования на период 2013-2017 г

. при следовании моральным нормам, переживание стыда и вины при их нарушении . по содержанию работы отсутствуют грубые ошибки . Логические значения, логические операции и логические . правила), так и творческие (креативные) или интуитивные — Знание типичных .

Проект основной образовательной программы мкоу бутурлиновская сош №1 Бутурлиновского муниципального района Воронежской области на 2012-2017гг

. при следовании моральным нормам, переживание стыда и вины при их нарушении . по содержанию работы отсутствуют грубые ошибки . Логические значения, логические операции и логические . правила), так и творческие (креативные) или интуитивные — Знание типичных .

Основная образовательная программа основного общего образования образовательного учреждения в соответствии с требованиями Стандарта содержит три раздела: целевой, содержательный и организационный. Целевой

. при следовании моральным нормам, переживание стыда и вины при их нарушении . по содержанию работы отсутствуют грубые ошибки . Логические значения, логические операции и логические . правила), так и творческие (креативные) или интуитивные — Знание типичных .

Приказ от 2013г. № Протокол Управляющего Совета от 2013 года №

. при следовании моральным нормам, переживание стыда и вины при их нарушении . по содержанию работы отсутствуют грубые ошибки . Основные признаки права. Нормы права. Понятие прав, свобод . . Логические значения, логические операции и логические выражения .

Читайте также:

  

• Какие вам известны иные гипотезы происхождения человека кратко

  

• Почему женщины боролись за равенство прав кратко

  

• План канспект урока па працоўнаму навучанню

  

• Какой авиационной техникой оснащено мчс россии кратко

  

• Чем равнинная река отличается от горной 6 класс география кратко