 В этом уроке мы, наконец, переходим к теме, которая составляет ядро любого рассуждения и любой логической системы – умозаключениям. В четвёртом уроке мы говорили, что рассуждение – это совокупность суждений или высказываний. Очевидно, что такое определение не полно, ведь оно ничего не говорит о том, почему вдруг какие-то разные высказывания оказались рядом. Если дать более точное определение, то рассуждение – это процесс обоснования какого-либо высказывания с помощью его последовательного вывода из других высказываний. Этот вывод чаще всего осуществляется в форме умозаключений.
В этом уроке мы, наконец, переходим к теме, которая составляет ядро любого рассуждения и любой логической системы – умозаключениям. В четвёртом уроке мы говорили, что рассуждение – это совокупность суждений или высказываний. Очевидно, что такое определение не полно, ведь оно ничего не говорит о том, почему вдруг какие-то разные высказывания оказались рядом. Если дать более точное определение, то рассуждение – это процесс обоснования какого-либо высказывания с помощью его последовательного вывода из других высказываний. Этот вывод чаще всего осуществляется в форме умозаключений.
Содержание:
- Критерии истинности умозаключений
- Умозаключения по логическому квадрату
- Операция обращения
- Игра “Подбери ключ”
- Упражнения
- Проверочные вопросы на усвоение материала
Умозаключение – это непосредственный переход от одного или нескольких высказываний А1, А2, …, Аn к высказыванию В. А1, А2, …, Аn называют посылками. Посылка может быть одна, их может быть две, три, четыре, в принципе – сколько угодно. В посылках содержится известная нам информация. В – это заключение. В заключении находится уже новая информация, которую мы извлекли из посылок с помощью специальных процедур. Эта новая информация уже содержалась в посылках, но в скрытом виде. Так вот задача умозаключения сделать это скрытое явным. Кроме того, иногда посылки называют аргументами, а заключение – тезисом, а само умозаключение в этом случае называют обоснованием. Разница между умозаключением и обоснованием состоит в том, что в первом случае, мы не знаем, к какому заключению мы придём, а во втором – тезис нам уже известен, мы просто хотим установить его связь с посылками-аргументами.
В качестве иллюстрации умозаключения можно взять рассуждения Эркюля Пуаро из «Убийства в восточном экспрессе» Агаты Кристи:
Перебрав в уме еще раз показания пассажиров, я пришел к весьма любопытным результатам. Для начала возьмем показания мистера Маккуина. Первая беседа с ним не вызвала у меня никаких подозрений. Но во время второй он обронил небезынтересную фразу. Я сообщил ему, что мы нашли записку, в которой упоминается о деле Армстронгов. Он сказал: «А разве…» – осекся и, помолчав, добавил: «Ну это самое… неужели старик поступил так опрометчиво?…»
Но я почувствовал, что он перестроился на ходу. Предположим, он хотел сказать: «А разве ее не сожгли?» Следовательно, Маккуин знал и о записке, и о том, что ее сожгли, или, говоря другими словами, он был убийцей или пособником убийцы.
Логики записывают умозаключения следующим образом:
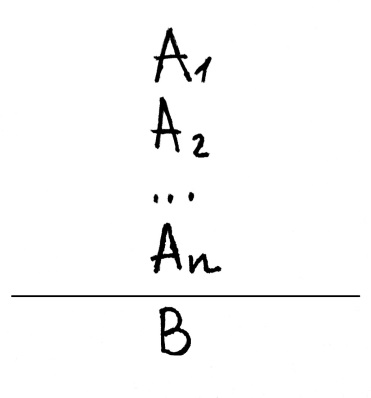
Над чертой располагаются посылки, под чертой – заключение, а сама черта обозначает отношение логического следования.
Критерии истинности умозаключений
Также как и для суждений, для умозаключений существуют определённые условия их истинности. При определении, истинное умозаключение или ложное, нужно обращать внимание на два аспекта. Первый аспект – это истинность посылок. Если хотя бы одна из посылок ложна, то и сделанное заключение тоже будет ложным. Поскольку заключение – это та информация, которая была скрыта в посылках и которую мы просто извлекли на свет, то из неверных посылок невозможно случайно получить верный вывод. Это можно сравнить с попыткой сделать бифштекс из моркови. Наверное, моркови можно придать цвет и форму бифштекса, но внутри всё равно будет морковь, а не мясо. Никакие кулинарные операции не преобразуют одно в другое.
Второй аспект – это правильность самого умозаключения с точки зрения его логической формы.
В качестве примера неправильного умозаключения при истинности посылок можно привести умозаключение голубки из «Алисы в стране чудес» Кэрролла. Голубка обвиняет Алису, в том, что она не змея. Вот как она приходит к этому выводу:
Змеи едят яйца.
Девочки едят яйца.
Значит, девочки – это змеи.
Хотя посылки правильные, заключение абсурдно. Умозаключение в целом сделано неверно. Чтобы избежать подобных ошибок, логики выявили такие умозаключения, логические формы которых при истинности посылок гарантируют истинность заключения. Их принято называть правильными умозаключениями. Таким образом, чтобы умозаключение было сделано верно, нужно следить за истинностью посылок и за правильностью самой формы умозаключения.
Мы рассмотрим различные формы правильных умозаключений на примере силлогистики. В этом уроке мы разберём самые простые однопосылочные заключения. В следующем уроке – более сложные заключения: силлогизмы, энтимемы, многопосылочные заключения.
Умозаключения по логическому квадрату
Чтобы было легче запомнить, какие именно типы умозаключений возможны между категорическими атрибутивными высказываниями, логики придумали специальный логический квадрат, изображающий отношения между ними. Поэтому некоторые однопосылочные умозаключения также называют умозаключениями по логическому квадрату. Посмотрим на этот квадрат:
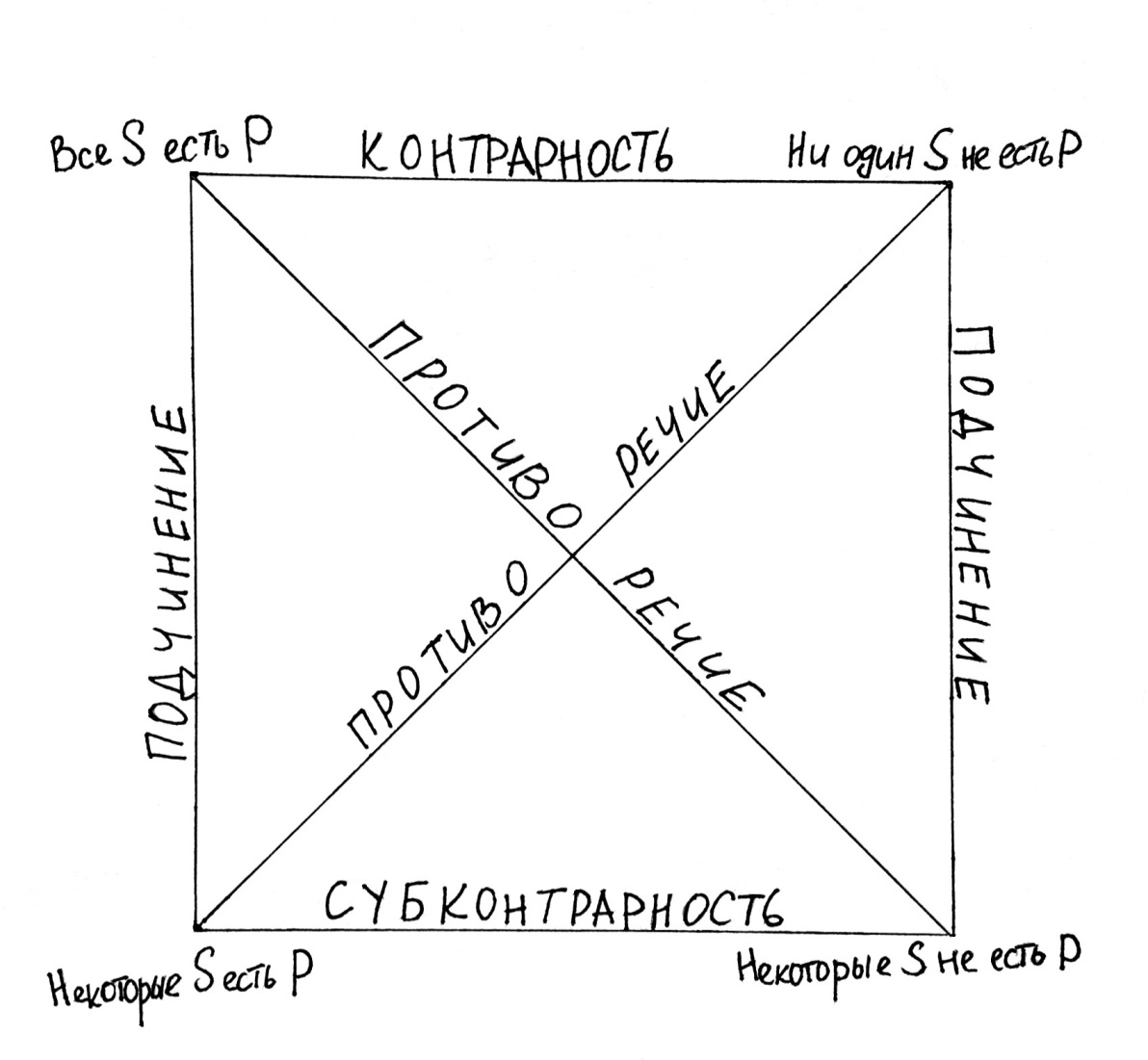
Начнём с отношений подчинения. Мы уже сталкивались с ними в четвёртом уроке, когда рассматривали условия истинности для частно-утвердительных и частно-отрицательных высказываний. Мы говорили, что из высказывания «Все S есть P» будет логичным вывести высказывание «Некоторые S есть P», а из высказывания «Ни один S не есть P» – «Некоторые S не есть P». Таким образом, возможны следующие типы умозаключений:
- Все S есть P
- Некоторые S есть P
- Все птицы имеют клюв. Следовательно, некоторые птицы имеют клюв.
- Ни один S не есть P
- Некоторые S не есть P
- Ни один гусь не хочет быть пойман и зажарен. Следовательно, некоторые гуси не хотят быть пойманными и зажаренными.
Кроме того, по правилу контрапозиции из отношений подчинения можно вывести ещё два правильных умозаключения. Правило контрапозиции – это логический закон, который гласит: если из высказывания А следует высказывание В, то из высказывания «неверно, что В» будет следовать высказывание «неверно, что А». Вы можете попробовать проверить этот закон с помощью таблицы истинности. Итак, будут верны и следующие умозаключения по контрапозиции:
- Неверно, что некоторые S есть P
- Неверно, что все S есть P
- Неверно, что некоторые автомобили не имеют колёс. Поэтому неверно, что все автомобили не имеют колёс.
- Неверно, что некоторые S не есть P
- Неверно, что все S не есть P
- Неверно, что некоторые вина не являются спиртными напитками. Таким образом, неверно, что все вина не являются спиртными напитками.
Отношение контрарности (противоположности) означает, что высказывания типа «Все S есть P» и «Ни один S не есть P» не могут быть одновременно истинными, но они могут быть одновременно ложными. Это хорошо видно из таблицы истинности для категоричных атрибутивных высказываний, которую мы построили в прошлом уроке. Отсюда можно вывести так называемый закон контрарного противоречия: Неверно, что все S есть P и в то же время ни один S не есть P.
По закону контрарного противоречия будут истинными следующие виды умозаключений:
- Все S есть P
- Неверно, что ни один S не есть P
- Все яблоки – это фрукты. Следовательно, неверно, что ни одно яблоко не является фруктом.
- Ни один S не есть P
- Неверно, что все S есть P
- Ни один кит не умеет летать. Поэтому неверно, что все киты умеют летать.
Отношения субконтрарности (подпротивоположности) означают, что высказывания типа «Некоторые S есть P» и «Некоторые S не есть P» не могут быть одновременно ложными, хотя могут быть одновременно истинными. На этом основании может быть сформулирован закон субконтрарного исключённого третьего: Некоторые S не есть P или Некоторые S есть P.
- Согласно этому закону правильными будут следующие умозаключения:
- Неверно, что некоторые S есть P
- Некоторые S не есть P
- Неверно, что некоторые продукты полезны для здоровья. Поэтому некоторые продукты не полезны для здоровья.
- Неверно, что некоторые S не есть P
- Некоторые S есть P
- Неверно, что некоторые ученики из нашего класса не являются двоечниками. Таким образом, некоторые ученики из нашего класса являются двоечниками.
Отношения противоречия (контрадикторности) говорят о том, что высказывания, находящиеся в них, не могут быть одновременно истинными или ложными. На основании этих отношений можно сформулировать два закона противоречия и два закона исключённого третьего. Первый закон противоречия: Неверно, что все S есть P и некоторые S не есть P. Второй закон противоречия: Неверно, что ни один S не есть P и некоторые S есть P. Первый закон исключённого третьего: Все S есть P или некоторые S не есть P. Второй закон исключённого третьего: Ни один S не есть P или некоторые S есть P.
На этих законах строятся умозаключения следующих видов:
- Все S есть P
- Неверно, что некоторые S не есть P
- Все дети нуждаются в заботе. Следовательно, неверно, что некоторые дети не нуждаются в заботе.
- Некоторые S не есть P
- Неверно, что все S есть P
- Некоторые книги не являются скучными. Поэтому, неверно, что все книги являются скучными.
- Неверно, что все S есть P
- Некоторые S не есть P
- Неверно, что все сотрудники нашей фирмы усердно работают. Таким образом, некоторые сотрудники нашей фирмы не работают усердно.
- Неверно, что некоторые S не есть P
- Все S есть P
- Неверно, что некоторые зебры не имеют полосок на коже. Следовательно, все зебры имеют полоски на коже.
- Ни один S не есть P
- Неверно, что некоторые S есть P
- Ни одна картина в этом зале не относится к XX веку. Поэтому неверно, что некоторые картины в этом зале относятся к XX веку.
- Некоторые S есть P
- Неверно, что ни один S не есть P
- Некоторые студенты занимаются спортом. Таким образом, неверно, что ни один студент не занимается спортом.
- Неверно, что ни один S не есть P
- Некоторые S есть P
- Неверно, что ни один учёный не интересуется искусством. Следовательно, некоторые учёные интересуются искусством.
- Неверно, что некоторые S есть P
- Ни один S не есть P
- Неверно, что некоторые коты курят сигары. Таким образом, ни один кот не курит сигары.
Как вы, скорее всего, заметили во всех этих умозаключениях, высказывания над чертой и под чертой несут одну и ту же информацию, просто поданную в разной форме. Важная деталь заключается в том, что смысл одних из этих высказываний воспринимается легко и интуитивно, в то время как смысл других тёмен, и над ними порой приходится поломать голову. Например, смысл утвердительных высказываний воспринимается легче, чем смысл отрицательных высказываний, смысл высказываний с одним отрицанием более понятен, чем смысл высказываний с двумя отрицаниями. Таким образом, основное назначение умозаключений по логическому квадрату состоит в том, чтобы привести сложные для восприятия, непонятные высказывания к наиболее простой и ясной форме.
Операция обращения
Ещё одним видом однопосылочных умозаключений является обращение. Это такой тип умозаключений, при которых субъект посылки совпадает с предикатом заключения, а субъект заключения совпадает с предикатом посылки. Грубо говоря, в заключении S и P просто меняются местами.
Прежде чем перейти к умозаключениям через обращение, построим таблицу истинности для высказываний, в которых P встанет на место субъекта, а S – на место предиката.
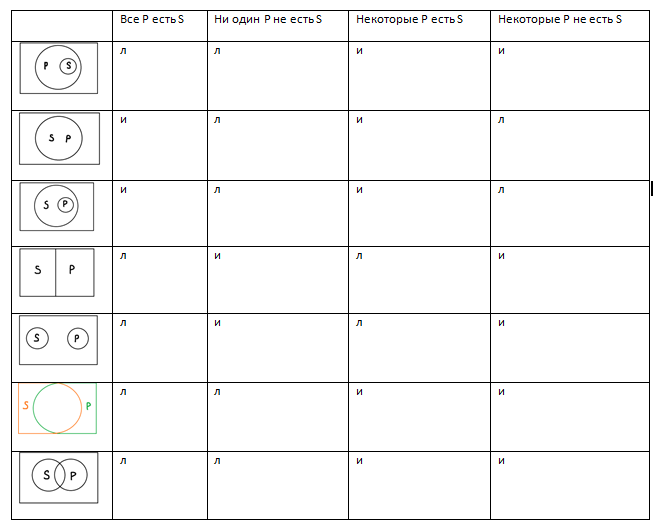
Сравните её с той таблицей, которую мы строили в прошлом уроке. Обращение, как и другие умозаключения, может быть правильным, только когда посылка и заключение одновременно истинны. При сравнении двух таблиц, вы увидите, что таких комбинаций не так уж и много.
Итак, существует два вида обращения: чистое и с ограничением. Чистое обращение происходит тогда, когда количественная характеристика не изменяется, то есть если в посылке было слово «все», то и в заключении тоже будет слова «все»/«ни один», если в посылке слово «некоторые», то и в заключении «некоторые. Соответственно, при обращении с ограничением количественная характеристика меняется: были «все», а стали «некоторые». Для высказываний типа «Ни один S не есть P» и «Некоторые S есть P» правильным будет следующее чистое обращение:
- Ни один S не есть P
- Ни один P не есть S
- Ни один человек не может выжить без воздуха. Следовательно, ни одно живое существо, способное выжить без воздуха, не является человеком.
- Некоторые S есть P
- Некоторые P есть S
- Некоторые змеи ядовиты. Поэтому, некоторые ядовитые существа – это змеи.
- Для высказываний типа «Все S есть P» и «Ни один S не есть P» верно обращение с ограничением:
- Все S есть P
- Некоторые P есть S
- Все пингвины – это птицы. Таким образом, некоторые птицы – это пингвины.
- Ни один S не есть P
- Некоторый P не есть S
- Ни один крокодил не ест зефир. Следовательно, некоторые существа, едящие зефир, не являются крокодилами.
- Высказывания типа «Некоторые S не есть P» вообще не обращаются.
Хотя обращения, как и умозаключения по логическому квадрату, это однопосылочные умозаключения, и мы точно также извлекаем всю новую информацию из имеющейся посылки, посылку и заключение в них уже нельзя назвать просто разными формулировками одной и той же информации. Полученная информация относится уже к другому субъекту, а потому она уже не кажется такой тривиальной.
Итак, в этом уроке мы начали рассматривать правильные виды умозаключений. Мы поговорили о самых простейших однопосылочных умозаключениях: умозаключениях по логическому квадрату и умозаключениях через обращение. Хотя эти умозаключения довольно просты и даже где-то тривиальны, люди повсеместно совершают в них ошибки. Понятно, что сложно удержать в памяти все виды правильных умозаключений, поэтому, когда вы будете выполнять упражнения или столкнётесь с необходимостью проверить или сделать однопосылочное умозаключение в реальной жизни, не бойтесь прибегать к помощи модельных схем и таблиц истинности. Они помогут вам проверить, всегда ли при истинности посылок заключение тоже истинное, а это главное для правильного умозаключения.
Упражнение «Подберите ключ»
В этой игре вам нужно создать ключ правильной формы. Для этого установите засечки нужной длины (от 1 до 3, 0 – быть не может), а затем нажмите кнопку «Попробовать». Вам будут даны 2 суждения, сколько засечек выбранной длины присутствуют в ключе (для простоты значение «наличие»), и сколько из выбранных находятся на своём месте (для простоты значение «на месте»). Скорректируйте своё решение и пробуйте, пока не подберёте ключ.
Упражнения
1
Сделайте все возможные умозаключения из следующих высказываний по логическому квадрату:
- Все медведи на зиму залегают в спячку.
- Неверно, что все люди завистливы.
- Ни один гном не достигает роста в два метра.
- Неверно, что ни один человек не был на Северном полюсе.
- Некоторые люди никогда не видели снега.
- Некоторые автобусы ходят по расписанию.
- Неверно, что некоторые слоны летали на луну.
- Неверно, что некоторые птицы не имеют крыльев.
2
Сделайте обращения с теми, высказываниями, с которыми это возможно:
- Никто ещё не построил машину времени.
- Некоторые официанты очень назойливы.
- Все профессионалы опытны в своём деле.
- Некоторые книги не имеют твёрдой обложки.
3
Проверьте, правильно ли сделаны следующие умозаключения:
- Некоторые кролики не носят белые перчатки. Следовательно, некоторые кролики носят белые перчатки.
- Неверно, что никто не был на Луне. Таким образом, некоторые люди были на Луне.
- Все люди смертны. Поэтому все смертные – это люди.
- Некоторые птицы не умеют летать. Следовательно, некоторые существа, не умеющие летать, это птицы.
- Ни один ягнёнок не имеет пристрастия к виски. Следовательно, ни одно существо, имеющее пристрастие к виски, не является ягнёнком.
- Некоторые морские животные млекопитающие. Таким образом, неверно, что ни одно морское животное не является млекопитающим.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
← 5 Законы и противоречия7 Силлогизмы →
Е.А. Иванов
Раздел третий. Умозаключение
Еще более сложной формой мышления, чем суждение, является умозаключение. Оно содержит в своем составе суждения (следовательно, и понятия), но не сводится к ним, а предполагает еще их определенную связь. Благодаря этому и образуется качественно особая форма с ее специфическими функциями в мышлении.
Формально-логический анализ этой формы означает ответ на следующие основные вопросы: в чем сущность умозаключений и какова их роль и структура; что представляют собой их основные типы; в каких взаимоотношениях между собой они находятся; наконец, какие логические операции с ними возможны.
Значение подобного анализа определяется тем, что именно в умозаключениях (и основанных на них доказательствах) сокрыта «тайна» принудительной силы речей, которая поражала людей еще в древности и с постижения которой началась логика как наука. Именно умозаключения обеспечивают то, что мы называем в настоящее время «силой логики». Вот почему нередко логику именуют «наукой о выводном знании». И в этом есть значительная доля истины. Ведь весь предшествующий анализ понятий и суждений, хотя и важный сам по себе, в полной мере раскрывает все свое значение лишь в связи с их логическими функциями по отношению к умозаключениям (а значит, и доказательствам).
Теория умозаключений – наиболее тщательно и глубоко разработанная часть логики. Когда на экзамене по логике одной из отвечающих был задан вопрос: «Что больше всего Вам понравилось в логике?», она ответила: «Умозаключение. Это очень красивая теория. Здесь одно вытекает из другого». И она права. Добавим от себя, что это еще очень практичная теория, дающая нам в руки могущественное орудие познания и общения.
Глава I. Общая характеристика умозаключения
Придерживаясь избранного в предыдущих разделах принципа, рассмотрим умозаключения в двух соотношениях: 1) как форму отражения действительности и 2) как форму мышления тоже так или иначе воплощающуюся в языке. В целях большей стройности изложения, учитывая бесконечное многообразие проявления этой формы, рассмотрим здесь же типологию умозаключений, чтобы последующие главы посвятить уже анализу каждого из их типов в отдельности.
1. Умозаключение и взаимосвязь (взаимоотношение) предметов
Происхождение и сущность умозаключения. Чтобы уяснить происхождение и сущность умозаключения, необходимо сопоставить два рода знаний, которыми мы располагаем и пользуемся в процессе своей жизнедеятельности, – непосредственные и опосредованные.
Непосредственные знания – это те, которые получены нами с помощью органов чувств: зрения, слуха, обоняния и т.д. Таковы, например, знания, выраженные суждениями типа: «Дерево зеленое», «Снег бел», «Птица поет», «Сосновый лес пахнет смолой». Они составляют значительную часть всех наших знаний и служат их базой.
Однако далеко не обо всем на свете мы можем судить непосредственно. Например, никто никогда не наблюдал, что в районе Москвы некогда бушевало море. А знание об этом есть. Каким образом? Оно получено из других знаний. Дело в том, что в Подмосковье обнаружены большие залежи белого камня, из которого и строилась белокаменная. Он образовался из скелетов бесчисленных мелких морских организмов, которые могли накапливаться лишь на дне моря. Так был сделан вывод о том, что примерно 250 – 300 млн лет назад Русскую равнину, на которой расположена и Московская область, заливало море. Подобные знания, которые получены не прямо, непосредственно, а опосредованно, путем выведения из других знаний, называются опосредованными (или выводными). Логической формой их приобретения и служит умозаключение. В самом общем виде под ним разумеется форма мышления, посредством которой из известного знания выводится новое знание.
Существование такой формы в нашем мышлении, как и понятия и суждения, обусловлено самой объективной действительностью. Если в основе понятия лежит предметный характер действительности, а в основе суждения – связь (отношение) предметов, то объективную основу умозаключения составляют более сложная, взаимная связь предметов, их взаимные отношения. Так, если один класс предметов (А) входит целиком в другой (В), но не исчерпывает его объема, то это означает необходимую обратную связь: более широкий класс предметов (В) включает в себя менее широкий (А) как свою часть, но не сводится к нему. Это видно из схемы:

Например: «Все космонавты – мужественные люди». Это означает: «Некоторые мужественные люди – космонавты». Или более сложный случай взаимосвязи предметов мысли: если один класс предметов (А) входит в другой (В), а этот, в свою очередь, входит в третий (С), то отсюда следует, что первый (А) входит в третий (С). На схеме:

Пример. «Если А.Леонов – космонавт, а все космонавты – мужественные люди, то А.Леонов – мужественный человек».
Такова объективная возможность умозаключений: это структурный слепок с самой действительности, но в идеальной форме, в форме структуры мысли. А их объективная необходимость, как и понятий и суждений, тоже связана со всей практикой человечества. Удовлетворение одних потребностей людей и возникновение на этой основе других требует прогресса общественного производства, а он, в свою очередь, немыслим без прогресса знаний. Необходимым связующим звеном в осуществлении этого прогресса и выступают умозаключения как одна из форм перехода от известных знаний к новым.
Роль умозаключений и их структура. Умозаключения – весьма распространенная форма, используемая в научном и повседневном мышлении. Этим определяется их роль в познании и практике общения людей. Значение умозаключений состоит в том, что они не только связывают наши знания в более или менее сложные, относительно законченные комплексы – мыслительные конструкции, но и обогащают, усиливают эти знания.
Вместе с понятиями и суждениями умозаключения преодолевают ограниченность чувственного познания. Они оказываются незаменимыми там, где органы чувств бессильны: в постижении причин и условий возникновения какого-либо предмета или явления, его сущности и форм существования, закономерностей развития и т.д. Они участвуют в образовании понятий и суждений, которые нередко выступают как итог умозаключений, чтобы стать средством дальнейшего познания.
Умозаключения используются как способ познания прошлого, которое непосредственно наблюдать уже нельзя. Например, с их помощью получены фундаментальные знания о «большом взрыве»
Вселенной, который произошел 10 – 20 млрд лет назад; о становлении крупномасштабной структуры Вселенной (галактик и их скоплений); о возникновении Солнечной системы и образовании Земли; о происхождении и сущности жизни на Земле; о возникновении и этапах развития человеческого общества. Историки общества по отдельным фрагментам, доступным нам, восстанавливают облик прошедших поколений людей, их образ жизни. Теоретики общества по бесчисленным проявлениям общественной жизни познают глубинные закономерности ее экономического, социального, политического и духовного развития.
Умозаключения тем более важны для понимания будущего, которое наблюдать еще нельзя. В общественной жизни предвидения, прогнозы, цели человеческой деятельности тоже невозможны без определенных выводов – о тенденциях развития, действовавших в прошлом и действующих в настоящее время, прокладывающих путь в будущее.
На каждом шагу умозаключения производятся в повседневной жизни. Так, выглянув утром в окно и заметив мокрые крыши домов, мы делаем вывод о прошедшем ночью дожде. Увидев, что день солнечный, мы заключаем, что сосновый лес теперь пахнет смолой. Наблюдая вечером багрово-красный закат, мы предполагаем на завтра ветреную погоду. Заметив на площади множество людей со знаменами, транспарантами, плакатами, мы умозаключаем, что идет митинг.
Особую роль играют умозаключения в юридической практике. В своих знаменитых записках о Шерлоке Холмсе А.Конан Дойл дал классический образ сыщика, который блестяще, в совершенстве владел искусством умозаключений и на их основе распутывал самые сложные и невероятные криминальные истории. В современной юридической литературе и практике умозаключениям тоже принадлежит огромная роль. Так, предварительное следствие с точки зрения логики есть не что иное, как построение всевозможных умозаключений о предполагаемом преступнике, о механизме образования следов преступного деяния, о мотивах, побудивших к его совершению, и о последствиях совершенного для общества. Самый суд есть не что иное, как анализ фактов с целью получения определенного вывода. Наконец, обвинительное (или оправдательное) заключение есть лишь одна из форм умозаключения вообще.
Умозаключение – целостное мыслительное образование. Но подобно тому как, например, вода, будучи целостным качественно определенным агрегатным состоянием вещества, разлагается на химические элементы – водород и кислород, находящиеся в определенном соотношении между собой, так и всякое умозаключение имеет свою структуру. Она обусловлена природой этой формы мышления и ее ролью в познании и общении. В структуре любого умозаключения различаются два основных более или менее сложных элемента: посылки (одна или несколько) и заключение, между которыми, конечно, тоже существует определенная связь.
Посылки – это исходное, и притом уже известное, знание, служащее основанием заключения.
Заключение (или вывод) – производное, притом новое, знание, полученное из посылок и выступающее их следствием.
Связь между посылками и заключением есть необходимое отношение между ними, делающее возможным переход от одного к другому, – отношение логического следования. Это основной закон всякого умозаключения, позволяющий раскрыть его самый глубокий и сокровенный «секрет» – принудительность вывода. Если мы признали какие-либо посылки, то хотим мы этого или не хотим, но вынуждены признать и заключение – именно из-за определенной связи между тем и другим. Этот закон, в основе которого лежит объективное соотношение самих предметов мысли, проявляется во многих особых правилах, которые специфичны для разных форм умозаключений и которые будут раскрываться в последующих главах.
Выше говорилось, какую роль играют умозаключения в образовании понятий и суждений. А какую роль играют понятия и суждения в умозаключениях? Поскольку они входят в структуру умозаключений, важно установить здесь их логические функции. Так, нетрудно понять, что суждения выполняют функции либо посылок, либо заключения. Понятия же, будучи терминами суждения, выполняют здесь функции терминов умозаключения. Если рассматривать познание диалектически, как процесс перехода с одной ступени знания на другую, более высокую, то не составит труда уяснить себе относительность деления суждений на посылки и заключение. Одно и то же суждение, будучи результатом (выводом) одного познавательного акта, становится исходным пунктом (посылкой) другого. Этот процесс можно уподобить строительству дома: один ряд бревен (или кирпичей), положенный на уже имеющееся основание, превращается тем самым в основание для другого, последующего ряда.
Аналогично обстоит дело и с понятиями – терминами умозаключения: одно и то же понятие может выступать то в роли субъекта, то в роли предиката посылки или заключения, то в роли посредствующего звена между ними. Так осуществляется бесконечный процесс познания.
Подобно всякому суждению заключение может быть истинным и ложным. Но то и другое определяется здесь, как и в сложных суждениях, непосредственно отношением не к действительности, а прежде всего к посылкам и их связи.
Заключение будет истинным при наличии двух необходимых условий: 1) если посылки истинны по содержанию и 2) если умозаключение правильно по своей форме (строению). Например:
Все художники тонко чувствуют природу.
И. Левитан – художник.
Следовательно, И.Левитан тонко чувствовал природу.
Здесь обе посылки истинны, а умозаключение построено правильно, что явствует из следующей схемы:

где А – И. Левитан, В – художники, С – тонко чувствующие природу.
И наоборот, заключение может быть ложным, если: 1) хотя бы одна из посылок ложна или 2) строение умозаключения неправильное. Пример:
Все свидетели правдивы.
Сидоров – свидетель.
Следовательно, Сидоров правдив (?)
Здесь одна из посылок ложная. Вот почему определенного вывода сделать нельзя. А о том, насколько важно правильное строение умозаключения, свидетельствует известный в логике шутливый пример, когда из обеих истинных посылок вывод следует нелепый:
Все дикари носят перья.
Женщины тоже носят перья.
Следовательно, все женщины – дикари (?)
О том, что определенный вывод при подобной конструкции умозаключения невозможен, свидетельствует круговая схема:

где А – женщины, В – дикари, С – носящие перья.
Из ложных посылок или при неправильном строении умозаключения истинный вывод может получиться чисто случайно. Например:
Стекло не проводит электричества.
Железо – не стекло.
Следовательно, железо проводит электричество.
При подобном строении умозаключения достаточно вместо «железа» подставить «резину», чтобы понять случайность верного вывода. Связь между посылками и заключением должна быть не случайной, а необходимой, однозначной, обоснованной: одно должно действительно следовать, вытекать из другого. Если же связь случайна или многозначна и в отношении вывода, как говорят при обмене квартир, «возможны варианты», то такой вывод делать нельзя. Иначе неизбежна ошибка, которая в логике называется «поп sequitur» («не следует»). Продолжая начатое выше сравнение со строительством дома, можно сказать: нельзя построить добротный дом, если материал негодный (например, бревна гнилые); но и дом из хорошего материала может развалиться, если строить его неправильно, не соблюдая законов механики.
2. Умозаключение и связь предложений
Как и любая другая форма мышления, умозаключение так или иначе воплощается в языке. Если понятие выражается отдельным словом (или словосочетанием), а суждение – отдельным предложением (или сочетанием предложений), то умозаключение всегда есть связь нескольких (двух или более) предложений, хотя не всякая связь двух или более предложений – непременно умозаключение (вспомним сложные суждения).
В русском языке эта связь выражается словами: «следовательно», «значит», «таким образом» и др., либо словами: «потому что», «так как», «ибо» и т.п. Употребление тех или иных языковых средств не произвольно, а определяется порядком расположения посылок и заключения. Дело в том, что в живой речи в отличие от учебника логики этот порядок тоже является относительным. Умозаключение может завершаться заключением (выводом), но может и начинаться с него; наконец, вывод может находиться в середине умозаключения – между его посылками. И это естественно: ведь новизна заключения не психологическая, а логическая. Она не носит характера какой-то «приятной неожиданности» или «счастливой случайности», когда из произвольного сочетания каких-то суждений вдруг что-то получилось. И она, конечно, не заложена изначально ни в одном из элементов исходного знания в отдельности, но потенциально, скрыто содержится во всей структуре этого знания в целом и проявляется лишь во взаимодействии ее элементов. Это можно сравнить с тем, что огонь не заключен ни в спичке, ни в коробке, взятых порознь, а вспыхивает лишь от трения одной о другую. Как здесь, чтобы получить новое явление, требуется определенное действие, так и в мышлении, чтобы получить новое знание, требуется определенное умственное усилие: это и достигается посредством умозаключения.
Общее правило языкового выражения умозаключения таково: если заключение стоит после посылок, то перед ним ставятся слова «следовательно», «значит», «поэтому», «итак», «отсюда следует» и т. п. Если же заключение стоит перед посылками, то после него ставятся слова «потому что», «так как», «ибо», «оттого что» и др. Если же, наконец, оно располагается между посылками, то и перед ним, и после него употребляются соответствующие слова одновременно.
Воспользуемся приведенным выше примером с художниками. Здесь возможны следующие логические, а следовательно, и языковые конструкции:
1) «Все художники тонко чувствуют природу, а И. Левитан – художник, следовательно, он тонко чувствовал природу» (заключение в конце);
2) «И. Левитан тонко чувствовал природу, потому что он – художник, а все художники тонко чувствуют природу» (заключение в начале);
3) «Все художники тонко чувствуют природу, следовательно, И. Левитан тонко чувствовал природу, потому что он художник» (заключение в середине).
Совсем не трудно догадаться, что мы не исчерпали всех возможных вариантов (в данном случае их шесть). Их важно знать, чтобы в потоке живой речи – письменной или устной – уметь выделить более или менее устойчивые мыслительные конструкции, дабы подвергнуть их строгому логическому анализу во избежание возможных или допущенных ошибок и недоразумений.
3. Типология умозаключений
Выступая в качестве более сложной, чем понятие и суждение, формы мышления, умозаключение представляет собой в то же время более богатую по своим проявлениям форму. И в этом есть определенная закономерность.
Обозревая практику мышления, можно обнаружить великое множество самых разнообразных видов и разновидностей умозаключений. Они различаются числом посылок – одна, две и более; типом суждений – простое или сложное; видом суждений – атрибутивное или реляционное; характером заключения – достоверное или вероятное и т. д. и т. п. Какой же из признаков положить в основу деления умозаключений на типы? Думается, мы поступим разумно, если будем исходить прежде всего из самой глубокой сущности этой формы мышления. Поскольку всякое умозаключение вообще, безотносительно к его формам, представляет собой логическое следование одних знаний из других, то в зависимости от характера этого следования, от направленности хода мысли в умозаключении можно выделить три коренных, фундаментальных типа, которые и будут положены в основу всего последующего анализа выводного знания. Это дедукция, индукция и традукция.
Дедукция (от лат. deductio – выведение) – умозаключение от более общего знания к менее общему. Типичный пример дедукции, идущий от древности:
Все люди смертны.
Сократ – человек.
Следовательно, Сократ смертен.
Индукция (от лат. inductio – наведение) – умозаключение от менее общего знания к более общему. Например: наблюдая за движением каждой из планет Солнечной системы, можно сделать общий вывод: «Все планеты движутся с запада на восток».
Традукция (от лат. traductio – перевод, перемещение, перенос) – умозаключение, в котором посылки и заключение – одной и той же степени общности.
Пример: «На Земле, где есть атмосфера, смена дня и ночи, времен года, есть также и жизнь. На Марсе подобно Земле есть атмосфера, смена дня и ночи, смена времен года. Возможно, что на Марсе тоже есть жизнь» (вывод, как будет показано в главе VI настоящего раздела пока не подтвердился).
В подобной типологии – отправной пункт для понимания всего многообразия умозаключений.
В современной логике придается особое значение также делению всех умозаключений по характеру самого вывода (заключения). Дедукция дает логически необходимые, а значит достоверные, т. е. истинные выводы. Индукция и традукция, наоборот, в огромном числе случаев приводят лишь к вероятным (правдоподобным) заключениям.
Каждый из основных типов, в свою очередь, имеет особые виды и разновидности. К их последовательному рассмотрению мы и переходим.
Глава II. Дедукция. Непосредственные умозаключения
В зависимости от числа посылок, из которых можно сделать тот или иной вывод, дедуктивные умозаключения подразделяются прежде всего на непосредственные и опосредованные. Учитывая, что эти выражения уже употреблялись нами в предыдущей главе при характеристике умозаключений в целом, подчеркнем во избежание недоразумений: там речь шла о непосредственном и опосредованном знании, а в настоящей главе речь идет о непосредственном и опосредованном умозаключении, т.е. о видах исключительно выводного, опосредованного знания. Этим и исчерпываются неудобства данной терминологии.
Непосредственные умозаключения – это такие, которые делаются из одной посылки.
Опосредованные – те, которые делаются из нескольких (двух и более) посылок.
Перейдем к их конкретной характеристике.
1. Непосредственные умозаключения из простых суждений
Непосредственные умозаключения можно получать прежде всего из простых суждений – как атрибутивных, так и реляционных. Применительно к атрибутивным суждениям это достигается двояким путем: 1) через преобразование суждений и 2) через отношение суждений (в «логическом квадрате»).
Непосредственные умозаключения через преобразование суждений. Как отмечалось выше, преобразование суждений происходит в формах обращения и превращения, на основе сочетания которых возможны противопоставление субъекту и противопоставление предикату.
В силу чего возможно здесь умозаключение? В силу того, что нам известно отношение субъекта (S) суждения к предикату (Р). На этой основе можно вывести новое знание о целой гамме других отношений этих структурных элементов суждения – Р к S, S к не-Р, Р к не-S, не-Р к S.
Общее правило непосредственного умозаключения гласит: термин, не распределенный в посылке, не может быть распределен и в заключении.
В умозаключении через обращение суждения мы, зная отношение S к Р, выясняем обратное отношение – Р к S. Приведем пример такого умозаключения, где посылка – общеутвердительное суждение (А):
Все поэты – впечатлительные люди.
Следовательно, некоторые впечатлительные люди – поэты.
Логическая схема такого умозаключения: «Все S есть Р. Следовательно, некоторые Р есть S». Выразим эти взаимоотношения S и Р графически:

где S – поэты, Р – впечатлительные люди.
Непосредственные умозаключения на основе обращения могут быть получены также из общеотрицательных (Е) и частноутвердительных (I) суждений. Что же касается частноотрицательных суждений (О), то они, как подчеркивалось, не обращаются, поэтому умозаключения из них сделать нельзя. Иначе будет нарушено общее правило распределенности терминов: субъект, не распределенный в посылке, окажется распределенным в заключении.
В непосредственном умозаключении через превращение суждения наше знание об отношении S к Р позволяет сделать вывод об отношении S к не-Р (поскольку оно находится в отношении противоречия к Р).
Вот пример такого умозаключения, где посылка – общеутвердительное суждение (А):
Все поэты – впечатлительные люди.
Следовательно, ни один поэт не является невпечатлительным человеком.
Логическая формула такого умозаключения: «Все S есть Р. Следовательно, ни одно S не есть не-Р». Вспомним круговую схему:

где S – поэты, Р – впечатлительные люди, не-Р – невпечатлительные люди.
Аналогично можно сделать умозаключения из общеотрицательных (Е), частноутвердительных (I) и частноотрицательных (О) суждений.
Непосредственные умозаключения на основе противопоставления субъекту или предикату сделать нетрудно, если вспомнить, что сами эти логические операции есть лишь то или иное сочетание обращения и превращения.
Приведем лишь примеры. Вот пример умозаключения на основе противопоставления субъекту:
Все поэты – впечатлительные люди.
Следовательно, некоторые впечатлительные люди не могут быть не поэтами.
Пример умозаключения через противопоставление предикату:
Все поэты – впечатлительные люди.
Следовательно, ни один невпечатлительный человек не поэт.
Непосредственные умозаключения через отношение суждений (в «логическом квадрате»). Вспомним, что в «логическом квадрате» зафиксированы такие важнейшие отношения между суждениями, как логическое подчинение, противоположность (контрарность), субконтрарность, противоречие. Непосредственные умозаключения возможны здесь потому, что между суждениями, находящимися в этих отношениях, существуют определенные зависимости по истинности и ложности. Учитывая, что каждое суждение – А, Е, I, О – может находиться в трех отношениях с другими, из него можно сделать три вывода.
Например, если истинно общеутвердительное суждение (А), что «Все благородные мысли находят себе сочувствие», то отсюда следует: 1) что тем более истинно частноутвердительное суждение (I): «Некоторые благородные мысли находят себе сочувствие» (отношение подчинения); 2) что ложно общеотрицательное суждение (Е): «Ни одна благородная мысль не находит себе сочувствия» (отношение противоположности) и 3) что ложно частноотрицательное суждение (О): «Некоторые благородные мысли не находят себе сочувствия» (отношение противоречия).
Другой пример. Если ложно общеутвердительное суждение (А), что «Все юристы имеют специальное высшее образование» (так как есть еще среднее юридическое), то отсюда можно сделать выводы, что истинно частноотрицательное суждение (О): «Некоторые юристы не имеют высшего образования» и неопределенны общеотрицательное (Е): «Ни один юрист не имеет высшего образования» (в данном случае это тоже ложно) и частноутвердительное (I): «Некоторые юристы имеют высшее образование» (в данном случае оно истинно).
Непосредственные умозаключения могут быть получены также из простых реляционных суждений. Логическим основанием здесь служит характер отношения R между предметами х и у. Так, если установлено, что «Женщины равны в правах с мужчинами», то отсюда можно заключить, что «Мужчины равны в правах с женщинами». Если известно, что «Конституционные законы выше остальных законов страны», то отсюда следует, что «Остальные законы страны не выше (ниже) конституционных».
2. Непосредственные умозаключения из сложных суждений
Посылкой непосредственного умозаключения может быть не только простое – атрибутивное или реляционное, но и сложное суждение.
Возьмем в качестве примера условное суждение (импликацию): «Если завтра будет солнечная погода, то мы пойдем в лес». Из него можно сделать заключение: «Если мы не пошли в лес, то погода не была солнечной».
Подобное умозаключение основано на законе контрапозиции. Он означает, что любое истинное условное суждение, если в нем поменять местами основание и следствие и подвергнуть их одновременно отрицанию, может дать в качестве заключения тоже истинное условное суждение.
Непосредственное умозаключение можно сделать и из конъюнкции. Если истинно, что «Казань находится на Волге, и Саратов находится на Волге», то истинным будет и вывод: «Саратов находится на Волге, и Казань находится на Волге».
Заключение из нестрогой дизъюнкции: если истинно, что «Производительность труда зависит от технического прогресса или от квалификации работника», то отсюда следует, что истинно и такое суждение: «Производительность труда зависит от квалификации работника или от технического прогресса». В основе этих непосредственных умозаключений из конъюнкции и дизъюнкции лежит их свойство коммутативности (перестановочности).
Наконец, можно делать умозаключения из строгой дизъюнкции и эквивалентности.
Подводя теперь общий итог, можно подчеркнуть, что непосредственные умозаключения из простых и сложных суждений – не только лишь «гимнастика для ума». Благодаря им из уже известного знания извлекается дополнительная, и притом самая разнообразная и богатая, информация: о взаимоотношениях структурных элементов мысли – S и Р или х и у – в простых суждениях, а также исходных суждений в сложных. Важно лишь, чтобы в каждом отдельном случае соблюдались те или иные специфические правила таких умозаключений, дабы избегать ошибок в рассуждениях.
Глава III. Дедукция. Опосредованные умозаключения из простых суждений
Опосредованные умозаключения, состоящие из нескольких (двух и более) посылок, тоже бывают различных видов.
Прежде всего выделяются опосредованные умозаключения из простых суждений (им и посвящена настоящая глава) и опосредованные умозаключения из сложных суждений (им будет посвящена следующая глава).
Опосредованные умозаключения из простых суждений, в свою очередь, подразделяются на умозаключения из атрибутивных (категорических) суждений и умозаключения из суждений об отношениях (реляционных).
И наконец, умозаключения из атрибутивных суждений в зависимости от числа посылок – двух или более – делятся на простой категорический силлогизм и сложный (тоже категорический) силлогизм.
1. Простой категорический силлогизм
Наиболее распространенной и важной формой опосредованного умозаключения из простых атрибутивных суждений выступает простой категорический силлогизм (от греч. syllogismos – умозаключение, выведение). Приводившийся выше пример с Сократом и есть классический пример такого силлогизма.
Структура простого категорического силлогизма. Он называется простым именно потому, что состоит всего из двух посылок, особым образом связанных между собой, и заключения.
В свою очередь, посылки и заключение, будучи суждениями, состоят из терминов, тоже определенным образом соотносящихся друг с другом. Принципиально важно отметить, что их всего три: меньший, больший и средний.
Меньшим термином называется субъект заключения. Поэтому он обозначается буквой «S».
Бóльшим термином именуется предикат заключения (буква «Р»).
Средний термин не входит в заключение, но входит в обе посылки, обеспечивая логическую связь между ними, выступая их посредствующим звеном и тем самым делая возможным само заключение. Обозначается буквой «М» (от лат. medius – средний).
Посылка, в которую входит больший термин, называется большей.
Посылка, включающая в себя меньший термин, – меньшая.
Вся эта структура может быть наглядно представлена на примере:
Все люди (М) смертны (Р). (Бóльшая посылка)
Сократ (S) – человек (М). (Меньшая посылка)
Следовательно, Сократ (S) смертен (Р). (Заключение)
Заметим, что все значение подобного силлогизма, который кажется ученически тривиальным и который люди до поры до времени не склонны относить к себе, обнаруживается (как это с огромной художественной силой показал Л.Толстой в повести «Смерть Ивана Ильича») лишь на смертном одре.
Аксиома силлогизма. Отражением многовековой практики мышления людей, миллиардного повторения одной и той же мыслительной конструкции служит аксиома силлогизма. В зависимости от того, рассматриваются ли посылки в объемном или содержательном плане, различаются две ее формулировки.
1. Dictum de omni et de nullo (буквально: сказанное обо всем и ни об одном): все, что утверждается или отрицается о классе предметов в целом, утверждается или отрицается и о части или отдельном элементе этого класса.
2. Nota notae est nota rei (признак признака есть признак самой вещи).
В современной логической литературе обе формулировки подвергаются критике; последняя считается даже элементарно ошибочной; но сама аксиома в целом сохраняет известный рациональный смысл. Более того, она составляет исходную логическую основу, на которой выстраивается грандиозное и стройное здание всей силлогистики.
Общие правила простого категорического силлогизма. Построение простого категорического силлогизма подчиняется ряду общих правил, без соблюдения которых даже из истинных посылок нельзя с логической необходимостью получить истинное заключение. Всего таких правил семь: три из них – это правила терминов, а четыре – правила посылок.
Каковы прежде всего правила терминов?
1. В силлогизме должно быть только три термина (S, Р и М). Нарушение этого правила ведет к логической ошибке, которая называется «quaternio terminorum» («учетверение терминов»). Так, из того, что «Собака бегает по двору», а «Кошка сидит на заборе», никакого вывода не получится. Здесь налицо четыре разных термина – два субъекта и два предиката. Среднего термина, который связывал бы оба суждения, нет.
Логическая ошибка «учетверение терминов» часто носит завуалированный характер. Это может быть связано с употреблением омонимов (т.е. одного и того же слова в разных значениях). Например, слово «закон» означает и объективную связь между предметами, и юридическое установление. Поэтому если мы построим силлогизм, где это слово выражает средний термин, то вытекающего отсюда с логической необходимостью вывода не получится.
Например:
Все законы объективны, т.е. не зависят от людей.
Конституция России – закон.
Следовательно, Конституция России не зависит от людей.
Нелепость получается именно из-за «учетверения терминов».
2. Средний термин должен быть распределен хотя бы в одной из посылок. Если это правило нарушается, то связь между большим и меньшим терминами будет неопределенной. Значит, и вывод из посылок не может следовать с логической необходимостью.
Все художники (Р) тонко чувствуют природу (М).
Петров (S) тонко чувствует природу (М).
Следовательно, Петров (S) – художник (P).
Вывод неопределенный, так как Петров может и не быть художником. Причина неопределенности в том, что средний термин (М), занимающий место предиката и в большей, и в меньшей посылках, не распределен, так как обе они утвердительные, а в утвердительных суждениях предикат, как правило, не распределен. Покажем соотношение терминов на круговой схеме:

3. Если больший или меньший термины не распределены в посылках, то они не могут быть распределены и в заключении.
Например:
Все учебники (М) полезны (Р).
Все учебники (М) – книги (S).
Следовательно, некоторые книги (S) полезны (Р).
А почему в этом случае нельзя сказать, что «Все книги полезны»? Суть в том, что субъект заключения («книги»), занимающий место предиката в меньшей посылке, не распределен, так как эта посылка утвердительная, а в утвердительных суждениях предикат, как правило, не распределен. Поэтому он не может быть взят во всем объеме и в заключении. См. круговую схему:

Нетрудно догадаться, что по этой же причине не распределен и предикат заключения.
Таковы правила терминов. А теперь о правилах посылок.
1. Из двух отрицательных посылок определенного вывода сделать нельзя. Хотя бы одна из них должна быть утвердительным суждением. Например:
Стекло (М) не проводит электричества (Р).
Резина (S) – не стекло (М).
Следовательно, резина (S) проводит электричество (P).
Вывод ложный. Если же вместо «резины» подставить, например, «железо», то он окажется истинным. В чем причина неопределенности вывода? В том, что при отрицательных посылках средний термин не может связать субъект и предикат. См. схему:

2. Если одна из посылок отрицательная, то и вывод будет отрицательным. Например:
Всякое преступление (Р) есть правонарушение (М).
Моральный проступок (S) не есть правонарушение (М).
Следовательно, моральный проступок (S) не есть преступление (Р).
См. схему:

3. Из двух частных посылок определенного вывода сделать нельзя. Хотя бы одна из посылок должна быть общим суждением.
Например:
Некоторые депутаты Госдумы (М) – юристы (Р).
Некоторые артисты (S) – депутаты Госдумы (М).
Следовательно, некоторые артисты (S) – юристы (Р)
А может быть, «ни один»? А почему не «все»?
См. схему:

4. Если одна из посылок частная, то и вывод будет частным. Например:
Некоторые пенсионеры (Р) – работающие (М).
Все работающие (М) получают заработную плату (S).
Следовательно, некоторые получающие заработную плату (S) – пенсионеры (Р).
См. схему:

Фигуры и модусы простого категорического силлогизма. Простой категорический силлогизм имеет свои разновидности, которые называются фигурами силлогизма. Они различаются положением среднего термина (М) в посылках. Таких фигур четыре.
Первая фигура характеризуется тем, что средний термин занимает место субъекта в большей посылке и место предиката – в меньшей. Приведем соответственно ее графическое изображение и пример.

Всякое преступление (М) есть правонарушение (Р).
Кража (S) есть преступление (М).
Следовательно, кража (S) есть правонарушение (Р).
Во второй фигуре средний термин занимает место предиката в большей и меньшей посылках.

Все юристы (Р) знают логику (М).
Павлов (S) не знает логики (М).
Следовательно, Павлов (S) – не юрист (Р).
Третья фигура отличается тем, что средний термин занимает здесь место субъекта в большей и меньшей посылках.

Все учебники (М) полезны (Р).
Все учебники (М) – книги (S).
Следовательно, некоторые книги (S) полезны (Р).
Четвертой фигуре свойственно то, что средний термин занимает здесь место предиката в большей посылке и место субъекта – в меньшей.

Некоторые пенсионеры (Р) – работающие (М).
Все работающие (М) получают зарплату (S).
Следовательно, некоторые получающие зарплату (S) – пенсионеры (Р).
Каждая фигура тоже имеет свои разновидности, которые называются модусами (от лат. modus – способ, образ). Они различаются количеством и качеством суждений, составляющих посылки. Каждая из посылок может быть общеутвердительной (А), общеотрицательной (Е), частноутвердительной (I) и частноотрицательной (О). Поэтому в одной фигуре возможно 16 модусов (4×4). Так, если большая посылка – общеутвердительная (А), то могут быть следующие модусы: АА, АЕ, AI, АО. Если большая посылка – общеотрицательная (Е), то возможны модусы ЕА, ЕЕ, EI, ЕО. Если большая посылка – частноутвердительная (I), то модусы будут IA, IE, II, IO. Наконец, если большая посылка – частноотрицательная (О), то могут быть модусы ОА, ОЕ, OI, OO.
Таким образом, в четырех фигурах соответственно будет 64 модуса (16×4). Но правильные из них – только 19 модусов.
Запишем их вместе с заключениями:
по первой фигуре – AAA, ЕАЕ, АII, ЕIO;
по второй фигуре – ЕАЕ, АЕЕ, ЕIO, АОО;
по третьей фигуре – AAI, IAI, АII, ЕАО, ОАО, ЕIO
и, наконец, по четвертой – AAI, АЕЕ, IAI, ЕАО, ЕIO.
Почему только эти 19 модусов являются правильными? Потому что именно они подчиняются общим правилам простого категорического силлогизма. Остальные же так или иначе не подчиняются. Например, модус ЕЕ – неправильный, так как обе посылки отрицательные, а из них определенного вывода сделать нельзя. Или модус II: в нем обе посылки частные.
Специальные правила фигур силлогизма. Каждая из фигур имеет особые, специальные правила, вытекающие из общих.
Правила первой фигуры. Большая посылка должна быть общим суждением, меньшая посылка – утвердительным. Начнем с меньшей. Если меньшая посылка – отрицательная, то и вывод, согласно одному из общих правил силлогизма, будет отрицательным. Но в отрицательных суждениях предикат всегда распределен. Следовательно, согласно одному из правил терминов, он должен быть распределен и в большей посылке. А он может быть распределен в ней лишь в том случае, если эта посылка отрицательная. Но это противоречит одному из общих правил о том, что из двух отрицательных посылок определенного вывода сделать нельзя. Значит, меньшая посылка не может быть отрицательной. Значит, она должна быть утвердительным суждением.
А почему большая посылка должна быть непременно общей? Если, как установлено, меньшая посылка – утвердительная, то средний термин, занимающий в ней место предиката, не распределен. Следовательно, согласно одному из общих правил терминов, он должен быть распределен в большей. А так как он занимает в ней место субъекта, то, значит, она должна быть общим суждением.
Вспомним, что в первой фигуре возможны следующие модусы:
АА ЕА ІА ОА
АЕ ЕЕ ІЕ ОЕ
АІ ЕІ ІІ ОІ
АО ЕО ІО ОО
Вычеркнем вначале все те, которые не соответствуют первому правилу первой фигуры, а затем те, которые не соответствуют второму правилу. Какие же останутся? АА, ЕА, AI, EI. А какие будут заключения? В соответствии с общими правилами силлогизма – ААА, ЕАЕ, АII, ЕIO.
Какое значение имеют умозаключения по первой фигуре простого категорического силлогизма? Без преувеличения – огромное. Это наиболее распространенная и богатая форма силлогизма. На ее основе происходит типичное для дедукции применение какого-либо общего положения к частному (или единичному) случаю. Вспомним классическое: «Все люди смертны. Сократ – человек». Первая фигура дает самые различные заключения: А, Е, I, О.
Ее часто используют в юридической практике, когда на основании общей нормы, – статьи какого-либо кодекса – делается вывод о конкретном факте. Например: «Хищение в особо крупных размерах наказывается по статье такой-то. Данное хищение – в особо крупном размере. Следовательно, оно наказывается по статье такой-то».
Правила второй фигуры. Большая посылка должна быть общим суждением, одна из посылок – отрицательным. Естественно, что по второй фигуре заключение всегда носит отрицательный характер. Значение умозаключений по второй фигуре тоже велико. Она используется в тех случаях, когда частный случай не подходит под общее правило. Например, в юридической практике – когда требуется доказать чью-либо невиновность.
Правила третьей фигуры. Меньшая посылка должна быть утвердительным суждением, заключение – частным. Третья фигура – сравнительно редкая в практике мышления.
Правила четвертой фигуры. Если большая посылка – утвердительное суждение, то меньшая посылка должна быть общим. Если одна из посылок отрицательное суждение, то большая должна быть общим. Заключение по четвертой фигуре носит в значительной мере искусственный характер. Вспомним пример с работающими пенсионерами:
Некоторые пенсионеры (Р) – работающие (М).
Все работающие (М) получают зарплату (S).
Следовательно, некоторые получающие зарплату (S) – пенсионеры (Р).
Естественнее было бы, конечно, сказать: «Некоторые пенсионеры получают зарплату».
Рассмотренные выше качественные различия между фигурами силлогизма на самом деле относительны. При определенных условиях силлогизм одной фигуры может превращаться в силлогизм другой.
Особое значение имеет здесь логическая операция, которая называется сведением всех фигур силлогизма к первой фигуре, поскольку она является наиболее употребительной и важной. Покажем это на примере силлогизма третьей фигуры, уже приводившемся нами:
Все учебники (М) полезны (Р).
Все учебники (М) – книги (S).
Следовательно, некоторые книги (S) полезны (Р).
Подвергнем меньшую посылку операции обращения: «Все учебники – книги» – «Некоторые книги – учебники». В итоге получим то же самое заключение, но уже по первой фигуре:
Все учебники (М) полезны (Р).
Некоторые книги (S) – учебники (М).
Следовательно, некоторые книги (S) полезны (Р).
Сокращенная форма простого категорического силлогизма. Энтимема. Простой категорический силлогизм может быть полным и сокращенным.
В практике мышления далеко не всегда он может облекаться в полную, т. е. развернутую, языковую форму – с большей и меньшей посылками, заключением.
Нередко он принимает сокращенную форму, т. е. в нем опускается либо одна из посылок, либо заключение. Такой сокращенный категорический силлогизм называется энтимемой (от греч. «в уме»).
Существует три разновидности энтимемы:
1) силлогизм с пропущенной большей посылкой. Например: «Петров – адвокат. Следовательно, он юрист». Здесь подразумевается очевидная большая посылка: «Все адвокаты – юристы», поэтому она опускается;
2) энтимема с пропущенной меньшей посылкой. Например: «Все адвокаты – юристы. Следовательно, Петров юрист». Предполагается, что «Петров – адвокат»;
3) энтимема с пропущенным заключением. Например: «Все адвокаты – юристы. Петров – адвокат». Предполагается, что «следовательно, он юрист».
Значение энтимем состоит в том, что с их помощью достигается краткость, лаконичность речи. Кроме того, они побуждают слушателя или читателя мыслить, думать. Вот почему энтимемы довольно широко используются в устной и письменной речи. Так, древний афоризм: «Юпитер, ты сердишься, значит, ты неправ» – это энтимема. Здесь подразумевается, а поэтому опущена, большая посылка: «Всякий, кто сердится, неправ». Восстановим весь силлогизм полностью:
Всякий, кто сердится, неправ.
Юпитер сердится.
Следовательно, Юпитер неправ.
Подобную энтимему представляет замечательно краткое и сильное высказывание А. Пушкина о Е. Баратынском: «Оригинален, ибо мыслит». Здесь тоже опущена большая посылка. Восстановим полный силлогизм:
Тот, кто мыслит, оригинален.
Баратынский мыслит.
Следовательно, Баратынский оригинален.
Еще пример. «Все это говорят, а что говорят все, должно быть правдой». Пропущено заключение: «Следовательно, это правда».
Или как сказано у поэта: «Я где боль: а боль – везде». Восстановим полностью силлогизм:
Боль везде.
Я – где боль.
Следовательно, я везде.
Для чего необходимо восстанавливать полный силлогизм из энтимемы? Чтобы проверить ее правильность. Как это делается? Покажем всю процедуру на примере: «Он, должно быть, очень невежественный человек, поскольку отвечает на все вопросы, которые ему задают». Сначала находим заключение. Оно, как мы помним, стоит после слова «следовательно» и ему подобных либо перед словами «потому что» и их аналогами. В нашем примере заключением будет: «Он, должно быть, очень невежественный человек», так как стоит перед словом «поскольку». Определяем структуру этого суждения, т.е. находим в нем субъект и предикат. Субъект – «он», предикат – «невежественный человек». По субъекту или предикату заключения устанавливаем характер имеющейся налицо посылки: «Он отвечает на все вопросы…» В ней находится субъект заключения, следовательно, это меньшая посылка. По предикату заключения и среднему термину, который входит в меньшую посылку, восстанавливаем опущенную большую посылку: «Тот, кто отвечает на все вопросы, должно быть, очень невежественный человек». Получаем полный силлогизм:
Тот, кто отвечает на все вопросы, невежественный человек.
Он отвечает на все вопросы, которые ему задают.
Следовательно, он невежественный человек.
Проверим правильность этого силлогизма. Он построен по первой фигуре, оба правила этой фигуры (см. выше) соблюдены. Значит, этот силлогизм правильный. Его можно проверить также с помощью круговой схемы:

2. Сложный категорический силлогизм
Умозаключение из атрибутивных (категорических) суждений далеко не всегда облекается в форму простого силлогизма, включающего лишь две посылки. Оно может принимать форму и сложного категорического силлогизма, состоящего из нескольких силлогизмов, определенным образом связанных между собой. Такое умозаключение называется полисиллогизмом (от греч. poly – много) или сложным силлогизмом. Например:
Все растения – живые организмы.
Все цветы – растения.
Следовательно, все цветы – живые организмы.
Заключение этого силлогизма может быть, в свою очередь, использовано в качестве большей посылки нового силлогизма:
Все цветы – живые организмы.
Роза – цветок.
Следовательно, роза – живой организм.
Нетрудно заметить, что первое (промежуточное) заключение может быть опущено. И тогда все умозаключение в целом примет следующий вид:
Все растения – живые организмы.
Все цветы – растения.
Роза – цветок.
Следовательно, роза – живой организм.
Такой силлогизм называется соритом (от греч. soros – куча). Он используется в тех случаях, когда необходимо обозреть более или менее длинную цепочку зависимостей между классами предметов.
Наконец, может быть полисиллогизм, в котором обе посылки – энтимемы, т.е. сокращенные простые силлогизмы. Такой полисиллогизм называется эпихейремой. Используем в качестве большей посылки известное философское положение Р. Декарта: «Cogito, ergo sum» («Я мыслю, следовательно, я существую»). Справедливости ради заметим, что сам Декарт пытался доказать, будто это не умозаключение, а нечто непосредственно, интуитивно данное, а потому, безусловно, истинное. Но по форме это все же энтимема.
В качестве меньшей посылки используем афоризм древних: «Dum spiro, spero» («Пока дышу, надеюсь»), несколько перефразировав его.
Таким образом, из двух энтимем получается эпихейрема: «Я мыслю, следовательно, я существую, а пока существую, надеюсь».
Развернем ее в полный сложный силлогизм:
Тот, кто мыслит, существует.
Я мыслю.
Следовательно, я существую.
Тот, кто существует, надеется.
Я существую.
Следовательно, я надеюсь.
Обладая свойствами простого категорического силлогизма в его энтимематической форме, эпихейремы нередко применяются в дискуссиях, спорах и т. д., поскольку позволяют сложное и полное умозаключение представить в виде простого и сокращенного.
Разумеется, мы не исчерпали всех форм простого и сложного категорического силлогизма. Но и сказанного достаточно, чтобы сделать общий вывод о богатстве силлогистических форм, а следовательно, о развитости человеческого мышления, обладающего таким разнообразным арсеналом логических средств.
3. Несиллогистические дедуктивные опосредованные умозаключения (из суждений об отношениях)
Помимо силлогистических существуют еще несиллогистические дедуктивные опосредованные умозаключения. Если первые есть выводы из простых атрибутивных (категорических) суждений, то вторые – это выводы из суждений об отношениях. Несомненно, у них может быть определенное сходство с силлогизмами. Например:
B. Маяковский – современник М. Горького.
C. Есенин – современник В. Маяковского.
Следовательно, С. Есенин – современник М. Горького.
Как и в силлогизме, здесь налицо две посылки, из которых с логической необходимостью следует определенный вывод. По своему строению это умозаключение напоминает первую фигуру силлогизма.
Однако это не силлогизм в строгом смысле этого слова. За внешним сходством с ним кроются существенные различия. И обусловлены они характером посылок: в них выражается не принадлежность (или непринадлежность) того или иного свойства предмету, а отношение между предметами. Поэтому здесь нет обычного среднего термина силлогизма. Понятие «В. Маяковский» в первой посылке и «современник В. Маяковского» во второй – это совершенно разные понятия: одно выражает конкретное лицо, другое – отношение к нему. Поэтому и вывод делается не на основании среднего термина, как в силлогизме, а иначе. Да и сами посылки не делятся здесь на большую и меньшую.
Что же в таком случае лежит в основе умозаключения? Объективным, а значит, и логическим основанием здесь служит наличие одного и того же отношения, обладающего одним и тем же свойством (в данном случае – свойством симметричности): одновременность жизни известных лиц.
Во многих науках – об истории Земли, о жизни на Земле, истории человечества – делаются подобного рода умозаключения, поскольку речь идет о сосуществовании каких-то объектов, одновременности явлений, событий, исторических деятелей.
Могут быть умозаключения и о других отношениях – пространственных (дальше – ближе), временны́х (раньше – позже), количественных (равно, больше – меньше), семейных, моральных, правовых и др. Известный пример:
Эльбрус выше Монблана.
Эверест выше Эльбруса.
Следовательно, Эверест выше Монблана.
Несиллогиетические умозаключения из суждений об отношениях так или иначе используются в юридической теории и практике: например, в расследовании преступлений, в решении трудовых и имущественных споров. Так, при расторжении брака и разделе имущества учитывается, приобретено ли оно до брака или совместно нажито, ибо отсюда вытекают разные правовые последствия для супругов.
Глава IV. Дедукция. Опосредованные умозаключения из сложных суждений
Наряду с опосредованными умозаключениями из простых суждений существуют еще опосредованные умозаключения из сложных суждений. Логическое следование заключения из посылок определяется в них не субъектно-предикатными отношениями, как в умозаключениях из простых суждений, а лишь логической связью между составляющими сложного суждения.
В зависимости от характера этой связи выделяются такие виды опосредованных умозаключений из сложных суждений, как условное и разделительное.
1. Условное умозаключение
Условным называется умозаключение, в котором, по крайней мере, одна из посылок представляет собой условное суждение. В зависимости от того, одна или обе посылки являются условными, различают две разновидности условных умозаключений – условно-категорические и чисто условные.
Условно-категорическое умозаключение. Оно состоит из одной условной и одной категорической посылки. Заключение в этом случае – категорическое суждение. Логическим основанием для такого умозаключения служит определенная связь между основанием и следствием (антецедентом и консеквентом).
В условно-категорическом умозаключении мысль, вообще говоря, может протекать по следующим четырем направлениям:
1) от утверждения основания к утверждению следствия;
2) от отрицания основания к отрицанию следствия;
3) от утверждения следствия к утверждению основания;
4) от отрицания следствия к отрицанию основания.
Поэтому в зависимости от хода мысли теоретически возможны четыре разновидности, или модуса, условно-категорического умозаключения. Однако подобно тому, как в простом категорическом силлогизме из 64 возможных модусов правильны лишь 19, так и здесь из 4 правильны лишь 2 модуса.
Первый – это modus ponens – утверждающий модус, когда мысль движется от утверждения основания к утверждению следствия. Пример:
Если день солнечный, то сосновый лес пахнет смолой.
День – солнечный.
Следовательно, сосновый лес пахнет смолой.
Формула:

В символической записи:

Еще пример:
Если решение суда обжаловано в кассационном порядке, то оно еще не вступило в законную силу.
Решение суда обжаловано в кассационном порядке.
Следовательно, оно еще не вступило в законную силу.
Второй – modus tollens – отрицающий модус, когда мысль протекает от отрицания следствия к отрицанию основания. Пример:
Если день солнечный, то сосновый лес пахнет смолой.
Сосновый лес не пахнет смолой.
Следовательно, день не солнечный.
Или:
Если решение суда обжаловано в кассационном порядке, то оно еще не вступило в законную силу.
Решение суда вступило в законную силу.
Следовательно, оно не обжаловано в кассационном порядке.
Формула:

Символическая запись:
A→B, ˥В
˥A
Почему правильными являются только эти два модуса? В конечном счете их правильность определяется объективными взаимоотношениями между причиной и следствием в действительности, отражением которых прежде всего и выступают условные суждения. Если есть причина, то есть и следствие, а если нет следствия, то нет и причины.
Почему же два других возможных модуса неправильны? Потому что взаимоотношения причины и следствия неоднозначны. Одно и то же следствие может быть результатом действия многих причин (это так называемая «множественность причин»), А одна и та же причина может вызывать много следствий (так называемая «множественность следствий»).
Вот почему если нет данной причины, то это еще не значит, что не может быть и данного следствия: оно может оказаться следствием совсем другой причины. Например:
Если я простужусь, то заболею.
Я не простудился.
Следовательно, я не заболею.
Нет, такой вывод из посылок не следует с логической необходимостью. Я могу заболеть, если заражусь, отравлюсь и т. д. С другой стороны, если есть данное следствие, то это еще не означает, что оно вызвано именно данной причиной. Например:
Если я простужусь, то заболею.
Я заболел.
Следовательно, я простудился.
Но подобный вывод тоже не обязателен. Я мог заболеть потому, что заразился, отравился и т. п.
Отсюда вытекают следующие четыре правила условно-категорического умозаключения, соблюдение которых при истинности посылок обеспечивает истинность вывода.
1. Можно идти от утверждения основания к утверждению следствия.
2. Можно идти от отрицания следствия к отрицанию основания.
3. Нельзя идти от отрицания основания к отрицанию следствия.
4. Нельзя идти от утверждения следствия к утверждению основания.
В двух последних случаях можно получить лишь вероятные выводы. Если, однако, речь идет о выделяющем условном суждении, то вывод будет достоверным. Все дело в том, что в таком суждении связь основания и следствия взаимнооднозначна. Так, «Если лицо совершило правонарушение, то оно несет юридическую ответственность». Это означает, что «Оно несет юридическую ответственность только в том случае, если совершило правонарушение».
Символическая логика подводит более прочную, чем традиционная логика, базу под объяснение выводов в условно-категорических умозаключениях, а главное, под проверку их истинности или ложности. С помощью таблиц (матриц) импликации и конъюнкции можно показать, почему, например, утверждающий и отрицающий модусы являются правильными.
Чисто-условное умозаключение. Оно отличается от условно-категорического умозаключения тем, что обе его посылки – условные суждения. Поэтому и заключение – тоже условное суждение. Например:
Если данное деяние – мошенничество, то оно – преступление.
Если оно – преступление, то карается по закону.
Следовательно, если данное деяние – мошенничество, то оно карается по закону.
Схематически это умозаключение выглядит так:
Если А, то В.
Если В, то С.
Следовательно, если А, то С.
В символической записи:

Здесь действует правило: следствие следствия есть следствие основания.
2. Разделительное умозаключение
Разделительным называется такое умозаключение, в котором хотя бы одна из посылок – разделительное суждение (дизъюнкция). В зависимости от характера другой посылки различаются три основные его разновидности: разделительно-категорическое, разделительно-условное и чисто разделительное.
Разделительно-категорическое умозаключение. Оно состоит из разделительной и категорической посылок. Заключение – категорическое суждение.
В зависимости от хода мысли выделяются два модуса разделительно-категорического умозаключения:
1) модус ponendo tollens – утверждающе-отрицающий модус, когда мысль направляется от утверждения одного из мыслимых вариантов к отрицанию другого. Например:
Формами соучастия в преступлении признаются соучастие с разделением ролей или соучастие без разделения ролей.
Данное соучастие осуществлено с разделением ролей.
Следовательно, оно не было соучастием без разделения ролей.
Формула:

В символической записи:
А∨В, А
˥В
2) модус tollendo ponens – отрицающе-утверждающий модус, в котором мысль следует от отрицания одного к утверждению другого варианта. Например:
Формами соучастия в преступлении признаются соучастие с разделением ролей или соучастие без разделения ролей.
Данное соучастие не было осуществлено с разделением ролей.
Следовательно, оно осуществлено без разделения ролей.
Формула:

В символической записи:
А∨В, ˥А
В
Разделительно-категорическое умозаключение подчиняется определенным правилам:
а) суждение должно быть строго разделительным, т.е. мыслимые варианты (члены деления) должны исключать друг друга. Если это правило нарушается, то возможны логические ошибки. Пример:
Книги бывают полезными или интересными.
Эта книга полезна.
Следовательно, эта книга неинтересна.
Вывод не следует здесь с логической необходимостью, так как дизъюнкция – не строгая, а слабая: книги могут быть и полезными и интересными одновременно;
б) строго разделительное суждение должно быть исчерпывающим. Нарушение этого правила тоже ведет к ошибке. Например:
Власть может быть законодательной или исполнительной.
Данная власть – не законодательная.
Следовательно, она исполнительная.
Этот вывод тоже логически не необходимый, ибо власть может оказаться судебной, но этот вариант не был предусмотрен в дизъюнкции;
в) в строго разделительном суждении не должно быть «лишних» членов.
Политики нашей страны могут быть дестабилизаторами, нормализаторами или стабилизаторами.
Данный политик – нормализатор.
Следовательно, он не стабилизатор и не дестабилизатор.
Получается бессмыслица, ибо политики исчерпываются двумя основными противоречащими понятиями: «стабилизаторы» или «дестабилизаторы»; «нормализаторы» здесь лишний член.
Разделительно-условное суждение. Оно называется иначе еще «дилемма» (от двух греч. слов: dis – дважды, lemma – предположение, посылка). Одна посылка в нем – условное суждение, другая – разделительное. Заключение может быть категорическим или разделительным.
В зависимости от направления мысли различаются две основные разновидности дилеммы: конструктивная (созидательная) и деструктивная (разрушительная).
1. Конструктивная дилемма характеризуется тем, что мысль переходит в ней от утверждения вариантов в основании к утверждению следствия. Например:
Если вред причинен личности гражданина, то он подлежит возмещению в полном объеме (лицом, причинившим вред).
Если вред причинен имуществу гражданина, то он тоже подлежит возмещению в полном объеме.
Но вред может быть причинен или личности гражданина, или его имуществу.
Следовательно, в любом случае он подлежит возмещению в полном объеме.
Формула:

Символически:

2. Деструктивная дилемма. Она отличается тем, что мысль направляется в ней от отрицания следствий, вытекающих из основания, к отрицанию самого основания. Например:
Если у меня будет достаточно свободного времени, то я буду работать над книгой и писать картину.
Я не работал над книгой или не писал картину.
Следовательно, у меня не было достаточно свободного времени.
Формула:

Символическая запись

Правила, которым подчиняется условно-разделительное суждение, складываются из правил других условных и разделительных умозаключений.
Чисто-разделительное умозаключение. Обе посылки в нем – разделительные суждения, заключение – тоже разделительное.
Пример:
Политические институты бывают государственными или негосударственными.
Негосударственные – в свою очередь, это партийные или непартийные (профсоюзы, молодежные, женские и т. д.) организации.
Следовательно, все политические институты бывают государственными или партийными или непартийными.
Основные правила здесь, по существу, те же, что и в разделительно-категорическом силлогизме.
Мы рассмотрели вначале простые формы дедуктивных опосредованных умозаключений из сложных суждений. Но так же как, например, есть сложные категорические силлогизмы из простых суждений, так и есть сложные формы дедуктивных опосредованных умозаключений из сложных суждений. Приведем лишь примеры.
С древних времен дошло до нас предостережение, которое сделала жительница Афин своему честолюбивому сыну, собиравшемуся прославиться посредством ораторского искусства:
«Если ты будешь говорить правду, то тебя возненавидят богатые и знатные. Если ты будешь лгать, то тебя возненавидит простой народ. Но ты должен или говорить правду, или лгать. Значит, тебя возненавидят богатые и знатные или тебя возненавидит простой народ».
А вот как ответил сын матери:
«Если я буду говорить правду, то меня прославит простой народ. Если я буду лгать, то меня прославят богатые и знатные. Значит, меня прославит простой народ или прославят богатые и знатные».
Это примеры сложного умозаключения из условных (с конъюнкцией) и разделительных посылок с выводами в виде разделительных суждений (с конъюнкцией).
Еще пример, который мы находим у Цицерона:
«Для блага республики надо было или повиноваться сенату, или учредить другой законодательный совет, или действовать по своему усмотрению; учреждать другой совет было бы высокомерно, действовать по своему усмотрению дерзко, поэтому надо было следовать решению сената».
Это сложное разделительно-категорическое умозаключение с конъюнкцией.
Современный пример:
«Если меняется характер собственности в стране, то неизбежно меняются взаимоотношения профсоюзов с администрацией предприятий, а если меняются эти взаимоотношения, то неизбежно должны меняться содержание деятельности профсоюзов, их организационное строение, формы и методы работы. Следовательно, если меняется характер собственности в стране, то неизбежно должны меняться содержание деятельности профсоюзов, их организационное строение, формы и методы работы».
Здесь сложное умозаключение, включающее несколько условных суждений с конъюнкцией.
Опосредованные умозаключения из сложных суждений, особенно в их сложной форме, используются главным образом в научной литературе, а также средствах массовой информации – всегда, когда требуются более или менее тщательный, подробный и глубокий анализ условий возникновения, существования или развития предмета или явления, перебор возможных вариантов чего-либо, альтернатив развития.
В судебно-следственной практике оба основных вида таких умозаключений применяются, например, при отработке версий.
Обобщая сказанное в гл. И–IV о дедукции, необходимо подчеркнуть следующее. Заслуга традиционной формальной логики состояла в том, что она выявила и исследовала великое множество форм дедуктивных умозаключений – как непосредственных, так и опосредованных, как из простых суждений, так и из сложных, как простых по своему строению форм, так и весьма сложных, разветвленных. В каждом отдельном случае она выработала соответствующие правила, позволяющие отличить правильные формы от неправильных. Но она, к сожалению, не дала единого принципа их анализа и проверки. И в этом состоит ее основной недостаток.
Символическая логика – логика высказываний и логика предикатов – в значительной мере преодолевает этот недостаток традиционной логики. Недаром она нередко определяется как наука о методах дедуктивной формализации содержательных теорий. Современная теория вывода позволяет выражать структуру тех или иных умозаключений, пусть даже очень сложных, в символической форме, а на этой основе осуществлять их проверку. Для этого выработана особая логическая процедура, правда, сама по себе довольно сложная и громоздкая, требующая специальной подготовки. Ее анализ выходит за пределы задач данного пособия.
В диалектической логике предпринимаются попытки найти и проанализировать диалектические формы умозаключений, например силлогизмов. Однако существенных результатов они пока не дали.
Глава V. Индукция
Другой, кроме дедукции, наиболее общий тип умозаключений – это индукция. В ней заключено глубокое своеобразие, и она находится в тесных взаимоотношениях с дедукцией. В реальной практике мышления ее сущность проявляется тоже в многообразных видах.
Значение изучения индукции обусловлено тем, что она неразрывно связана с практикой, жизнью и служит важным средством получения эмпирического, опытного знания. Вот почему ею так широко пользуются в естественных науках, основанных на опыте, в конкретных социальных исследованиях, включая правовые.
1. Природа, роль и структура индукции
Происхождение и сущность индукции. Индукция возникает в процессе практической деятельности людей из настоятельной потребности в обобщении, т. е. получении знаний о более или менее общих свойствах предметов и явлений окружающего мира, а также в раскрытии закономерных связей и отношений между самими предметами и явлениями. Эти общие знания, отвлеченные от единичного, конкретного, случайного, необходимы в качестве мыслительного средства более успешного воздействия на природу, на организацию общественной жизни и управление ею.
Объективную основу возникновения и существования индукции как особого типа умозаключения составляет прежде всего диалектика общего и отдельного в самой действительности. Отдельное не существует вне общего, а общее – вне отдельного. Отдельное связано с другого рода отдельным через общее. Общее, в свою очередь, проявляется лишь в отдельном, через отдельное. Это обстоятельство делает возможным познание общего на основе познания отдельного – конкретных единичных предметов.
Индукция возможна также как отражение объективных связей и отношений между предметами и явлениями, прежде всего причинно-следственных. Сравнение и сопоставление отдельных предметов и явлений позволяет вскрывать в них общие связи и отношения, определять одно как причину, другое – как следствие, или наоборот.
Как тип умозаключения индукция существенно отличается от дедукции, и в этом проявляется ее наиболее глубокая природа. Если в дедуктивных умозаключениях мысль движется от более общего знания к менее общему, то в индуктивных – наоборот: от менее общего знания к более общему. В дедукции общее знание предполагается «готовым», существующим. В индукции раскрывается «механизм» его образования. Поэтому если в дедукции общее знание служит исходным пунктом умозаключения, то в индукции оно выступает как результат.
Познавательное значение индукции и ее структура. Наиболее общее познавательное значение индукции состоит в том, что она дает новое знание – в виде более или менее существенных обобщений отдельных фактов на основе наблюдений, экспериментов и т. д. Причем диапазон обобщений здесь весьма широк: от простейших, чисто эмпирических обобщений, которые делаются в процессе повседневной практической деятельности, до самых глубоких и общих – научного и философского характера.
Правда, если в дедуктивных умозаключениях при наличии истинных посылок и правильном строении вывод всегда достоверный, то в индуктивных умозаключениях он может быть как достоверным, так и вероятным (правдоподобным). При этом степень вероятности здесь может быть самой различной – от маловероятных, самых приближенных и грубых обобщений до более или менее точных, определенных, почти достоверных.
Какова структура индуктивных умозаключений?
Исходные суждения здесь, как и в дедукции, называются посылками. Разница, однако, в том, что в дедукции ими служат общие (или частные) суждения, а здесь характерны единичные суждения, поскольку в них выражено знание об отдельных предметах (хотя может быть знание и об их отдельных группах).
Суждение, выведенное логическим путем из исходных, называется тоже заключением (или выводом). Но существенное отличие состоит в том, что по своему характеру оно главным образом общее (хотя может быть и частным, о части предметов какого-либо класса), тогда как в дедукции оно может быть и частным, и единичным.
Логическим основанием вывода в индуктивном умозаключении служит тоже отношение логического следования между посылками и заключением, в котором отражается объективная связь между отдельным и общим, причиной и следствием и т. д. и которая делает возможным перенос знания с отдельных предметов на классы или с одних, менее общих классов на другие, более общие.
Однако в отличие от дедукции логическое следование с индукции не строгое, а «ослабленное». Она лишь «наводит» на истину. Поэтому во многих случаях ее выводы и носят вероятный характер.
Единство индукции и дедукции. В системе умозаключений индукция не стоит особняком. Она неразрывно связана с дедукцией. Эту связь можно выразить положением: «Нет дедукции без индукции, и наоборот, нет индукции без дедукции». И действительно, если бы не было общих знаний, полученных индуктивным путем, то были бы невозможными дедуктивные умозаключения, основанные на этих знаниях. В свою очередь, дедуктивные умозаключения, давая знания о частном и единичном, так или иначе создают основу для дальнейшего индуктивного исследования отдельных предметов или их групп, а следовательно, для получения нового общего знания. Более того, вне дедуктивного знания было бы невозможным объяснить самый процесс индукции, ее механизм как логической формы.
Можно смело сказать, что прогресс человеческих знаний немыслим без тесного взаимодействия индукции и дедукции. Вот почему оказались неосновательными и бесплодными попытки преувеличения роли одного из этих видов умозаключений и умаления другого. Когда Ф. Бэкон сравнивал силлогизмы с «бесплодными девственницами», он, конечно, был глубоко не прав. Но и не правы те, кто превозносил роль дедуктивного познания.
Поэтому и здесь нельзя задаваться вопросом: «Что возникло раньше – индукция или дедукция?» Как основные типы умозаключения они оформлялись в процессе развития человеческого познания одновременно. Основа этой одновременности коренится в том, что отдельное не существует раньше общего или наоборот; что связи и отношения не существуют раньше самих предметов или наоборот.
Также, как в дедукции, виды индукции многообразны. Наиболее общими из них являются полная и неполная. Поскольку всякая индукция представляет собой обобщение, то их различие обусловлено главным: изучены ли для этого обобщения элементы того или иного класса полностью или же частично.
2. Полная индукция
Полной индукция получается в том случае, если, во-первых, исследованы все элементы класса предметов и, во-вторых, если установлено, что каждому из них принадлежит (или не принадлежит) одно и то же общее свойство (отношение).
В простейшем случае это выглядит так. Например, мы ежедневно ведем запись наблюдений за погодой и фиксируем солнечные дни в течение такого отрезка времени, как неделя. Мы можем констатировать, что каждый из дней был солнечным. Это дает возможность сделать общий вывод, что вся неделя в целом была солнечной. На этом примере можно убедиться, что индуктивное умозаключение принимает особую форму, отличную от дедуктивного. В учебных целях ее можно представить так:
Понедельник – солнечный день.
Вторник – солнечный день.
………..
День n – солнечный день.
Понедельник, вторник … день n исчерпывают все дни недели.
Следовательно, неделя была солнечной.
Более сложный случай представляет собой пример индукции, приводившийся в самом начале раздела «Умозаключение», – о том, что «Все планеты Солнечной системы движутся с запада на восток». Этот общий вывод может быть сделан путем непосредственных астрономических наблюдений за каждой планетой в отдельности.
Нетрудно установить, что в обоих случаях умозаключение имеет одинаковую структуру. Она может быть представлена следующей формулой:
S1 – P
S2 – P
…..
Sn – P
S1, S2 … Sn … исчерпывают класс S.
Следовательно, все S – Р.
В символической записи это выглядит так:

Каково познавательное значение вывода в форме полной индукции? На первый взгляд кажется, что по сравнению с посылками он не дает никакого нового знания или что его значение ничтожно. К сожалению, такого рода взгляды высказывались и в истории науки. В действительности полная индукция дает новое знание. Если в посылках содержится знание лишь об отдельных элементах какого-либо класса предметов, то в выводе речь идет об этом классе в целом. Следовательно, он познается и оценивается под новым углом зрения: в нем выявляется некая сущность, а соответственно и закономерность. И это естественно: ведь понятия «общее», «сущность», «закономерность» – однопорядковые. Так, выявление того общего, что «Все планеты Солнечной системы движутся с запада на восток», открывает возможности для более глубокого познания причин и сущности планетообразования, закономерностей развития всей Солнечной системы.
Особо ценно, что полная индукция, как и дедукция, способна давать достоверные знания.
Разумеется, заключение в полной индукции может быть истинным и ложным. Оно будет истинным, если, во-первых, все посылки истинны по содержанию и, во-вторых, если между ними и заключением есть отношение логического следования: в данном случае если исчерпаны все элементы исследуемого класса и каждый обладает (или не обладает) тем или иным свойством.
Заключение может оказаться ложным, если хотя бы одно из этих условий не соблюдено. Например, вывод, что «Все бывшие союзные республики СССР объявили о своей независимости», – истинный; а вывод, что «Все бывшие союзные республики СССР вступили в СНГ» – ложный.
Посредством полной индукции могут быть получены важные научные знания более или менее общего характера: «Все планеты Солнечной системы вращаются вокруг своей оси», «На всех планетах происходит смена времен года», «Все планеты светят отраженным светом». Если же установлено, что не все элементы какого-либо класса (или виды рода) обладают данным общим свойством, то обобщение может быть облечено в форму частного суждения. Например: «Некоторые металлы легче воды», «Некоторые металлы – жидкие тела».
Обобщение может принимать форму не только утвердительного, но и отрицательного суждения. Например: «На некоторых планетах нет жизни», «Некоторые планеты не имеют спутников», «Некоторые металлы не являются твердыми телами» и др.
Характерно, что подобные суждения – определенно-частные. Кванторное слово «некоторые» употребляется здесь в смысле «только некоторые» («Только некоторые металлы легче воды»), но не в смысле «некоторые, а может быть и все».
На первый взгляд кажется, что сфера применения полной индукции весьма ограниченна, что она может использоваться лишь там, где число элементов класса нетрудно сосчитать. В действительности полная индукция довольно широко применяется в науках, даже если число исследуемых случаев чрезвычайно велико. Таковы, например, обобщения о динамике численности населения в стране, о соотношении мужчин и женщин в составе населения, об особенностях численности различных возрастных групп и т. д., получаемые на основе сплошных переписей населения. Таковы обобщения ежегодных данных состояния экономики, собираемых государственными статистическими органами. Так, статистическим путем получено обобщение о падении рождаемости в стране за 90-е годы.
При достаточно большом числе статистических данных четко проявляются определенные закономерности. Вспомним в этой связи о «законе больших чисел». Так, рождение мальчика или девочки в отдельной семье – случайность. Но если провести полный статистический анализ родившихся за год в масштабе более или менее крупного региона, то выявится интересная общая закономерность: число мальчиков превышает число девочек на вполне определенную величину. Например: на 100 девочек рождается 106 мальчиков.
Полная индукция применяется и в юридической практике. Юристы нередко пользуются статистикой преступлений, чтобы выявить определенные зависимости, тенденции и выработать соответствующие практические меры. Полную индукцию можно использовать и в раскрытии отдельного преступления. Так, следствие по какому-либо делу может быть завершено, если собран необходимый и достаточный материал обо всех участниках преступления. В противном случае какое-либо дело может быть выделено в отдельное производство.
Однако в целом пределы применения полной индукции обусловлены наличием классов с известным, поддающимся счету числом элементов (так называемых «закрытых классов»). За этими пределами она оказывается неприменимой.
3. Неполная индукция
Неполной индукцией называется умозаключение обо всем классе предметов в целом на основе изучения лишь части предметов данного класса.
Формула неполной индукции:
S1 – P
S2 – P
…..
Sn – P
S1, S2 … Sn … составляют часть класса S.
Следовательно, все S – Р.
В символической записи:

Посредством неполной индукции преодолевается недостаток полной индукции. Она применяется прежде всего там, где число элементов исследуемого класса неопределенно, неограниченно или бесконечно. Таковы так называемые «открытые классы». Правда, она может применяться и там, где это число ограниченно и его нетрудно сосчитать («закрытые классы»), однако надобности в исследованиях всех без исключения элементов почему-либо нет. Так была установлена, например, электропроводность металлов на основе знания лишь о некоторых металлах, хотя число их определенно.
Возможность заключения в форме неполной индукции обусловлена тем, что если некоторое общее свойство принадлежит более или менее значительной части класса, то в силу его большей или меньшей существенности оно может принадлежать и всему классу в целом.
Познавательное значение неполной индукции по сравнению с полной в известном смысле более важно и велико. Как отмечалось, в полной индукции заключение не распространяется на другие предметы, кроме изученных, хотя весь их класс в целом и рассматривается с новой стороны. В заключении же неполной индукции осуществляется логический перенос знания с изученной части класса на всю остальную его часть.
Однако в этом достоинстве неполной индукции содержится и ее существенный недостаток. В отличие от полной индукции сам вывод здесь – даже при истинности всех посылок – может давать в принципе лишь вероятное знание, способное в большей или меньшей степени приближаться к достоверному. Обобщение, содержащееся в нем, может обеспечивать и твердое, достоверное знание, но лишь в том случае, если оно облекается в форму частного суждения. Однако кванторное слово – по сравнению с полной индукцией – употребляется здесь в ином смысле: «Некоторые, а может быть и все». Следовательно, сами такие обобщения носят характер неопределенного частного суждения.
Неполная индукция имеет две основные разновидности: это популярная индукция и научная индукция.
Популярная индукция (или индукция через простое перечисление). Ее полное наименование: «индукция через простое перечисление, когда не встречается противоречащий случай» («inductio per enumerationem simplicem, ubi non reperitur instantia contradictoria»). Повседневная жизнь людей дает массу примеров такой индукции. Так, люди не раз наблюдали, что ласточки перед дождем летают низко над землей. На этой основе был сделан вывод: «Всегда ласточки перед дождем летают низко над землей». Подобных примет, сделанных на основе непосредственных наблюдений, зафиксировано народной мудростью немало. Вот почему они получили название «народные приметы», а сама индукция – наименование «популярная» («народная»). Однако такие выводы носят характер лишь вероятного знания. Достаточно встретиться противоречащему случаю, чтобы заключение оказалось ложным. Вспомним классическую историю с лебедями. На основе бесчисленных наблюдений издавна был сделан вывод, что «Все лебеди белы». Однако со временем в Австралии были обнаружены черные лебеди, которых теперь можно видеть и в других местах. То же самое с выводом: «Все березы белы». Оказывается, есть и черные березы. С подобной проблемой столкнулась знаменитая «курица Рассела». У Б. Рассела есть такая притча. В курятнике живет курица. Ежедневно приходит хозяин, приносит ей поклевать зернышек. Курица, естественно, делает отсюда вывод: с появлением хозяина связано появление зернышек. Но вот однажды хозяин является не с зернышком, а с ножом… Это и есть «противоречащий случай»!
Степень вероятности получения истинного вывода на основе популярной индукции зависит от двух важнейших условий: 1) количества обозреваемых случаев; 2) качества признака, т. е. степени его существенности для данного класса предметов.
Однако и это не в состоянии устранить основные недостатки популярной индукции. Один из них состоит в том, что дается простое перечисление случаев повторяемости одного и того же признака и не делается сознательного отбора типичных фактов и их специального анализа. Другой – в том, что обобщение производится на основе простого наблюдения случайно попавшейся совокупности предметов класса и не исследуется причина самого явления. Вот почему наряду со многими верными народными приметами есть немало ложных обобщений, лежащих в основе суеверия, поверий, заклинаний и т. п., – о «пустых ведрах», «черной кошке», «сглазе», «заговоре» и пр.
Научная индукция. Отмеченные выше недостатки популярной индукции преодолеваются так называемой «научной индукцией» (хотя правильно называть ее неполной научной индукцией, так как научной может быть и полная). С ее помощью не просто наблюдаются отдельные случаи, а исследуется природа самого явления и дается ответ на вопрос: «Почему так, а не иначе?» Например, достаточно понять, что ласточки перед дождем летают низко над землей потому, что низко летают мошки, за которыми они охотятся; а те летают низко потому, что перед дождем у них набухают крылышки. Благодаря этому степень вероятности получения истинного вывода в неполной индукции значительно повышается.
Другой пример. В результате популярной индукции было установлено, что металлы при нагревании расширяются. Но все или только некоторые? И лишь молекулярная теория, раскрыв механизм этого расширения, сделала общий вывод, и притом вывод достоверный.
Если в популярной индукции важно обозреть как можно большее число случаев, то для научной индукции это не имеет принципиального значения. Легенда гласит, что Ньютону для открытия фундаментального закона всемирного тяготения достаточно было наблюдать один случай – падение яблока. Это легенда. Но вот факт. Известно, что исходным пунктом для открытия Р. Майером другого фундаментального закона – закона сохранения и превращения энергии послужили наблюдения над цветом крови людей в разных климатических поясах. Открытие многих законов в естественных и общественных науках так или иначе связано с индукцией, зачастую неполной.
Конечно, в разных науках неполная индукция проявляется по-разному. Так, в познании микромира, где действуют преимущественно статистические закономерности, широко используется статистическая индукция. Она нередко применяется в социологических исследованиях: например, при выявлении рейтинга того или иного политического деятеля, вероятности избрания того или иного человека на какой-либо государственный пост и при других опросах общественного мнения. Однако в любой разновидности научной индукции действуют общие закономерности, исследуемые формальной логикой.
4. Методы индуктивного исследования
Для вскрытия причинной (или иной) связи между предметами и явлениями используются различные методы индуктивного исследования. В формальной логике обычно выделяются методы сходства, единственного различия, сопутствующих изменений и остатков.
Метод сходства. Его суть состоит в сопоставлении различных фактов и выявлении в них сходства в том или ином отношении. Например, мы пытаемся выяснить причину радуги и для этого наблюдаем ряд случаев ее появления: во время дождя, на утренней росе, в водяной пыли у водопада, при прохождении солнечного луча через стеклянную призму и т. д. Мы замечаем, что, несмотря на все различия между ними, они сходны в одном – прохождении солнечного луча через прозрачное тело определенной формы. Это и дает логическое основание сделать вывод о причине радуги во всех случаях ее появления. Вот формула индуктивного исследования на основе метода сходства:
АВС … – а
АСД … – а
AEI … – а
А причина а
Познавательное значение метода сходства велико. Он часто используется в науках, где применяются опыты, наблюдения, и дает серьезное приращение знания.
Однако достоверного знания этот метод может и не дать. Почему? Может оказаться так, что не все явление «А», а лишь его часть вызывает следствие «а». Например, в народной медицине долгое время считалось, что мышьяк лишь в совокупности с заклинанием излечивает лихорадку. А потом обнаружилось, что мышьяк сам по себе способен излечить болезнь.
Метод единственного различия. Сходные во многих отношениях предметы или явления в чем-то могут и различаться между собой, а с этим различием может быть связано наличие или отсутствие тех или иных следствий. Так, если под колокол воздушного насоса поместить живое существо, например мышь, то оно живет. Если оставить те же условия, но выкачать воздух, – гибнет. Значит, наличие воздуха – условие или причина сохранения живого. Формула:
АВС … – а
ВС … – не имеет а
А причина а
Пример-шутка. К врачу приходит пациент. Жалуется, что всякий раз, когда он пьет чай, у него болит глаз. Врач, внимательно выслушав больного, посоветовал: «Попробуйте, когда пьете чай, вынуть из стакана ложку». Он предложил здесь применить метод единственного различия.
Познавательное значение метода единственного различия более велико, чем метода сходства. Почему? Потому, что здесь имеет место уже не наблюдение, а эксперимент, дающий возможность создавать специальные условия. Отпадает надобность наблюдать массу случаев, не надо учитывать фактор множественности причин и др.
Но вероятность вывода остается и в этом случае. Причиной «а» может быть не «А» само по себе, а в сочетании с чем-то другим, например с «В». Так, колокольчик под куполом воздушного насоса дает звук, когда воздух есть, и не дает, когда воздуха нет. Но причиной звука является не сам по себе воздух, а в сочетании с колокольчиком.
Метод сопутствующих изменений. Само название говорит о сути этого метода: изменяя одно обстоятельство, мы наблюдаем, какие изменения ему сопутствуют. Так, если удлинить маятник, то его движение замедлится, удлинить еще – движение замедлится еще более. Значит, определенная длина маятника является причиной определенной скорости его движения. Формула:
А1ВС … – а1
A2BC … – а2
A3BC … – а3
А причина а
Метод сопутствующих изменений тоже довольно широко используется в практике мышления. Однако вывод и по этому методу – вероятный. Ведь причиной замедления движения маятника может быть не только длина, но и увеличение его тяжести вместе с длиной.
Метод остатков. Схематическое выражение индуктивного рассуждения по этому методу:
АВС … – авс
ВС … – вс
…..
А причина а
Например, с помощью этого метода была открыта планета Нептун. Началось с установления факта, что движение планеты Уран не соответствует точно вычисленной орбите этой планеты. Оказалось, что величина отклонения орбиты планеты больше, чем та, которую могли вызвать другие планеты. Остаток, следовательно, должен был иметь причину. Леверье вычислил положение возможной планеты, а Галле обнаружил эту планету в телескоп. Ею и был Нептун.
По своей доказательной силе метод остатков может быть приравнен к методу единственного различия. Но вывод и по этому методу – лишь вероятный. Ведь «А» может быть единственной причиной «а», частью причины или, наоборот, содержать в себе причину.
В практике научных эмпирических исследований рассмотренные методы могут применяться и в отдельности, и в их различных сочетаниях. Так, нередко метод сходства соединяется с методом единственного различия. Поэтому в логике это сочетание иногда выделяется в качестве самостоятельного метода.
Естественно, что любое сочетание методов способно лишь усилить их познавательные возможности.
Надо только подчеркнуть, что в любом случае – это лишь элементарные, «исходные» методы индуктивного исследования и ими далеко не исчерпывается все многообразие методов эмпирического познания.
5. Основные ошибки в индуктивных умозаключениях
Как и в любом другом рассуждении, в индукции возможны свои логические ошибки. Наиболее распространенными из них выступают две: отождествление причинной и временной последовательности явлений и «поспешное обобщение».
Отождествление причинной и временнóй последовательности явлений. В логике эта ошибка получила специальное наименование «post hoc, ergo propter hoc» («после этого – значит, по причине этого»). Она происходит тогда, когда причинная связь явлений неправомерно отождествляется с простой последовательностью их во времени. Не учитывается, что хотя всякая причинная связь есть связь во времени (одно предшествует другому), но не всякая связь во времени есть непременно причинная связь. Так, день следует за ночью, но это еще не значит, что ночь – причина дня (как, впрочем, и наоборот). Или: раз ласточки прилетели и наступила весна, значит, прилет ласточек – причина наступления весны.
Подобная ошибка нередко допускается в следственной практике. Предположим, что один угрожал другому поджечь дом. Через некоторое время дом действительно загорелся. Можно ли отсюда сделать вывод, что преступление совершил непременно угрожавший? Тут могло быть простое совпадение во времени, а причина пожара оказаться совсем иной.
«Поспешное обобщение». Подобная ошибка происходит тогда, когда человек на основании лишь нескольких, иногда случайных фактов устанавливает общее положение. Например, мы обнаружили, что наш собеседник не читал газет раз, другой, третий… и на этом основании сделали вывод: «Он вообще не читает газет». Но вывод может оказаться поспешным, так как по каким-то причинам (из-за болезни, особой занятости и т. д.) в чтении газет был перерыв.
В народе недаром говорят: «Поспешишь – людей насмешишь». Но это в практических делах. А поспешишь в рассуждениях – можешь допустить серьезную логическую ошибку.
Чтобы избежать подобной ошибки, следует взять для анализа и обобщения как можно больше случаев, желательно в самых различных обстоятельствах; посмотреть, насколько типично предполагаемое следствие, и т. д.
«Поспешное обобщение» особенно опасно в решении трудовых, имущественных споров, расследовании уголовных дел. Ведь за допущенной ошибкой может стоять судьба человека.
Проблемы индукции во всем их объеме исследуются так называемой индуктивной логикой. Ныне она выделилась в относительно самостоятельную отрасль логического знания. Хотя основным объектом изучения в ней остается индуктивный вывод, само понятие такого вывода толкуется теперь более широко, чем прежде. Так, если в классической логике Ф. Бэкона – Дж. Милля задача ограничивалась изучением индуктивного следования, то теперь анализируются и другие виды отношения, например подтверждения. В целях формализации индуктивной логики используется аппарат теории вероятностей, а сама вероятностная логика иногда считается ее современной формой. В рамках индуктивной логики раскрываются методы обоснования и подтверждения индуктивных умозаключений. Она тоже претерпевает новое интенсивное развитие.
Глава VI. Традукция (аналогия)
Богатство форм умозаключений не исчерпывается многообразными видами дедукции и индукции. Третий из основных типов умозаключения наряду с этими двумя – традукция, которая, в свою очередь, тоже имеет различные формы. Ее наиболее распространенная и важная форма – это умозаключения по аналогии или сокращенно – аналогия (от греч. analogia – соответствие, сходство). Она и будет рассмотрена ниже с точки зрения ее сущности и значения, структуры и видов.
Актуальность и важность темы обусловлена местом и ролью аналогии в процессе познания действительности и практической деятельности людей, ее особым значением для юристов.
1. Сущность и назначение аналогии, ее структура
Происхождение и сущность аналогии. Аналогия – одна из самых древних мыслительных операций. Она возникает из объективного противоречия между потребностью познания человеком качественного многообразия мира и наличными знаниями о нем. Ее назначение – быть одним из средств разрешения этого противоречия.
И в самом деле, первобытный человек, не зная действительных свойств множества окружавших его предметов и явлений, их связей и отношений, пытался объяснить их по сходству с уже известными, доступными ему; распространять на них или – как мы теперь говорим – «экстраполировать» свои, пусть еще скудные, ограниченные знания. Так, в частности, возникли антропоморфизм и анимизм – уподобление человеку и его душе. Уподобление было одной из предпосылок возникновения мифологии и религии.
Как тип умозаключения аналогия возможна в мышлении прежде всего потому, что сами предметы и явления, будучи качественно определенными, а следовательно, отличными друг от друга, в то же время имеют объективное сходство между собой. А так как в мире все взаимосвязано, то сходство в одном отношении может быть необходимым образом связано со сходством в других отношениях. Это и служит объективным основанием для соответствующего умозаключения. Миллиарды раз повторяясь в мышлении, подобная операция приобрела характер устойчивой логической формы и получила специальное название – «аналогия».
Необходима же аналогия в первую очередь потому, что в процессе практической деятельности нередко нельзя познать предмет иначе, как в сравнении с другими, или же потому, что сравнение, сопоставление, уподобление позволяет получить знание о нем проще, быстрее и легче.
Всякая аналогия вообще независимо от форм ее проявления представляет собой умозаключение, посредством которого из сходства предметов в одних признаках выводится их сходство в других признаках.
Например, между теплотой и электричеством есть сходство в способе распространения. Это и дало возможность в свое время перенести уравнения для теплоты на область электрических явлений. Другой пример. Известно, что вторжение войск Наполеона в Россию в силу ряда факторов привело к тому, что он потерпел поражение. Отсюда можно было умозаключить, что поражение Гитлера неизбежно.
Конечно, проявлений аналогии – великое множество: от самой слабой и смутной догадки о сходстве двух предметов до самых глубоких и общих предположений о сходстве закономерностей микро-, макро- и мегамира с вытекающими отсюда научными и философскими последствиями.
Как умозаключение аналогия обладает общими признаками всякого умозаключения вообще. В то же время она значительно отличается от дедукции и индукции, представляя собой особый тип – традуктивного умозаключения. Главное ее отличие состоит в том, что мысль перетекает в ней от единичного к единичному, от частного к частному, от общего к общему, т. е. получаемое знание имеет ту же степень общности, что и исходное.
Вместе с тем аналогия связана с дедукцией и индукцией. С одной стороны, она опирается на те знания, которые добыты дедуктивным и индуктивным путем. А с другой – сама доставляет им материал для новых умозаключений.
Значение и структура аналогии. Диапазон оценок аналогии весьма велик: от нигилистических до чрезмерных, преувеличенных. В действительности же аналогия обладает значительной эвристической ценностью, но у нее есть и свои специфические недостатки. Подобно другим типам умозаключения, она способна давать и дает новое знание, однако это знание не только достоверное, но и зачастую вероятное. О важности аналогии свидетельствует то, что на ее основе сделаны многие глубокие выводы в философии, открытия в частных науках, изобретения в технике. Даже самая слабая догадка иногда оказывала великую услугу человечеству.
Так, древнегреческий философ Гераклит, уподобив мир, окружающий нас, реке, высказал фундаментальное диалектическое положение о мире как процессе: «все течет, все изменяется», говорил он, подобно водам реки. Нельзя войти дважды в воды одной и той же реки, потому что это будут уже иные воды.
Другой древнегреческий философ и естествоиспытатель Демокрит, уподобив мельчайшие частицы материи – атомы пылинкам в солнечном луче, сделал вывод об их движении и взаимодействии в самих предметах, состоящих из них.
В новое время в физике на основе сходства света с распространением звуковых волн Гюйгенс сделал вывод о волновой природе света. Посредством умозаключения по аналогии Франклин высказал положение об электрической природе молнии. В биологии Дарвин на основе аналогии с искусственным отбором растений и животных в домашнем хозяйстве ввел понятие «естественный отбор» и с его помощью объяснял эволюцию растительного и животного мира.
В современной астрономии аналогия с обычным взрывом имела определенное значение для формирования представления о «большом взрыве» Вселенной, ее последующей эволюции.
В сравнительно новой науке – кибернетике используется аналогия между функциями управления в живых организмах и технических устройствах. Новейшая наука – бионика основана на применении принципов строения живых организмов к строению различных сооружений.
С аналогией тесно связано моделирование, получающее все более широкое распространение в технике и науке (строительство зданий, железных дорог, космических кораблей, моделирование экономических процессов, даже моделирование мышления). В космонавтике вывод о возможности полетов человека в космос был сделан на основе аналогии с запуском животных (Белки и Стрелки).
Аналогии используются и в изучении общественной жизни: например, в истории, где проводятся исторические параллели между эпохами, событиями, лицами с соответствующими выводами; в социологии; в юридических науках.
Аналогия имеет довольно широкую область применения в юридической практике. Интересно отметить, что и здесь она возникает из объективного противоречия, в данном случае – между наличием общественных отношений, требующих правового регулирования, и отсутствием соответствующих прямых норм. В праве отражением этого противоречия является понятие «пробел», а аналогия выступает в определенном смысле средством разрешения такого противоречия.
В зависимости от характера пробела юридическая аналогия принимает две специфические формы: аналогии закона и аналогии права.
Аналогия закона применяется в тех случаях, когда требуется правовое регулирование тех или иных общественных отношений, прямо не предусмотренных законом или предусмотренных не полностью, но когда существуют правовые нормы, регулирующие сходные отношения.
Аналогия права используется в тех случаях, когда нет сходных правовых норм. Тогда приходится руководствоваться общими началами и смыслом соответствующей отрасли права или законодательства страны в целом.
Применение аналогии закона и аналогии права в нашей стране строго ограничено и регулируется соответствующими законодательными актами. Так, то и другое закреплено в Гражданском процессуальном кодексе России (См. ст. 6. Применение гражданского законодательства по аналогии).
Значение аналогии определяется здесь тем, что она расширяет сферу применения существующих норм права и тем самым служит укреплению существующего правопорядка. Благодаря ей открывается возможность для дальнейшей разработки правовых норм. В то же время ее применение не означает создания новой нормы права. Решение конкретного вопроса по аналогии носит индивидуальный характер и не имеет обязательной силы по отношению к другим сходным случаям. Вместе с тем применение аналогии в соответствующих случаях обязательно. Суд не может уклониться от решения вопроса, если нет соответствующей нормы или она страдает неполнотой.
Аналогия может применяться в известных пределах также в трудовом и административном праве. В уголовном праве нашей страны аналогия не используется. В других странах уголовный закон применяется и по аналогии, если есть так называемый «прецедент».
Следует учитывать, что аналогия в юридической сфере носит весьма специфический характер и ее применение в судебной практике – сложная процедура, включающая не только чисто логические, но и правовые, и даже политические аспекты.
Аналогия обладает структурой, сходной со структурой других типов умозаключения. Здесь тоже налицо посылки и заключение, находящиеся в определенной логической связи между собой. Но есть и особенности.
Посылки в аналогии – это суждения о двух предметах или группах предметов, имеющих не тождественные, а лишь сходные признаки, которые называются «уподобляемыми». Один из предметов в этом случае называется «моделью», а другой – «прототипом» или «оригиналом». Причем известно, что у модели есть еще признак, относительно которого неизвестно, обладает им оригинал или не обладает.
Заключение (или вывод) и есть суждение, в котором утверждается наличие этого признака. Он называется «переносимым».
Логическим основанием заключения выступает наличие логической связи между посылками – отношение сходства их по содержанию, отражающего объективное сходство самих предметов.
Структуру аналогии можно представить схематически следующим образом:
S1 есть Р1, Р2 … Рn
S2 сходен с S1 (Р1, Р2 …)
Следовательно, S2 есть Рn
Бросается в глаза прежде всего определенное сходство аналогии с силлогизмом. Здесь как будто бы тоже три термина, но нельзя сказать, что один из них больший, а другой меньший; средний же термин не тождественный, а лишь сходный. Поэтому и вывод несет с собой как достоверное, так и вероятное знание.
Есть некоторое сходство и со строением индукции, поскольку аналогия основана на единичных суждениях (хотя могут быть и частные, и даже общие). Но в выводе речь идет не о классе в целом, а о том или ином отдельном признаке предмета или группы предметов, хотя и здесь и там неизбежна вероятность вывода. Разумеется, и в аналогии степень этой вероятности может быть весьма различной: от смутной догадки до почти твердо установленного положения.
Поскольку заключение в аналогии принимает форму суждения, а оно может быть истинным и ложным, то и аналогия может давать как истинное, так и ложное знание.
Истинной аналогия оказывается в том случае, если сходство предметов в одних признаках действительно влечет за собой сходство в других. Вот почему многие аналогии, особенно в науке и технике, оказались истинными. Таковы, например, аналогии между распространением теплоты и электричеством, между искусственным и естественным отбором и др. Ложной бывает аналогия, не соответствующая действительному сходству предметов. Так, аналогия Марса с Землей в отношении возможной жизни на нем (которую любили приводить в учебниках логики еще столетие назад) в результате полета космических кораблей к этой планете не подтвердилась. Признаков жизни там пока не обнаружено.
Точно так же оказались ложными аналогия между организмом и обществом, аналогия между сообществами животных (пчел, муравьев и т. д.) и человеческим обществом.
На ложной аналогии основаны многие суеверия, гороскопы, приметы и т. п. Например, рассыпалась соль – к ссоре; найдена монета «решкой» вверх – к тратам, проигрышу; родился под знаком Скорпиона – энергетический вампир и пр.
Степень вероятности вывода по аналогии зависит от ряда условий, основными из которых являются следующие:
1) качество общих признаков (т. е. степень их общности и существенности);
2) количество (число) таких признаков;
3) соотношение между сходными и различными признаками.
Аналогия имеет пределы своей применимости, за которыми она оказывается неэффективной или вредной. Она неприменима, если в исследуемом предмете есть признаки, исключающие возможность переносимого признака. В противном случае аналогия будет ложной. Так, Земля и Луна как космические объекты одной Солнечной системы в некоторых отношениях сходны. Но отсюда нельзя умозаключать, что на Луне возможна жизнь, так как там нет ни воды, ни атмосферы, без которых живое существовать не может. Нельзя пользоваться аналогией, если различия слишком велики. Особенно осторожно следует использовать ее в общественной жизни. Общественные явления, поразительно аналогичные, но относящиеся к разным историческим эпохам, могут приводить к совершенно разным результатам, а следовательно, делать аналогию ложной. Так, наемный труд, характерный для капитализма, существовал и в условиях рабовладельческого общества. Но там он носил спорадический характер и не влиял сколь-нибудь существенно на общественную жизнь, а при капитализме он становится господствующей системой труда и определяет облик самого общества. Поэтому проводить аналогию между современным рабочим и наемным работником эпохи рабовладения – дело рискованное.
2. Виды аналогии
Аналогия, как и другие типы умозаключения, – многоликое явление. Поэтому в зависимости от признака, положенного в основу деления, виды аналогии будут различными.
Виды аналогии по характеру сходства предметов. Если исходить прежде всего из сущности всякой аналогии как умозаключения на основе сходства предметов, то в зависимости от того, о каком логическом сходстве идет речь – в свойствах предметов или в отношениях между самими предметами, можно выделить два ее основных вида: аналогию свойств и аналогию отношений.
Аналогия свойств предметов характеризуется тем, что два предмета (или две группы предметов) имеют некоторые сходные свойства. На этом основании делается вывод, что они могут быть сходными и в некоторых других свойствах. Так, упоминавшаяся выше аналогия света со звуком в свое время показала, что свет тоже обладает свойствами распространяться прямолинейно, отражаться, преломляться и т. д. Но звук обладает еще свойством волнового процесса. На этом основании было сделано умозаключение, что и свет есть волновой процесс. Другие примеры, приводившиеся выше, – с атомом, электричеством, естественным отбором – это примеры аналогии свойств.
Аналогия отношений между предметами отличается тем, что уподобляемые предметы сами могут не обладать сходными свойствами, а быть даже совершенно различными, в известном смысле «несравнимыми», но у них есть сходные отношения. По этому признаку и возможно соответствующее умозаключение. Так, сравнение отношения между ядром атома и электронами, вращающимися вокруг него, с отношением между Солнцем и планетами позволило Резерфорду построить планетарную модель атома. Хотя очевидно, что атом и Солнечная система – это, как говорят в Одессе, «две большие разницы».
Или, например, между математикой и логикой имеются весьма существенные различия, поскольку различны сами объекты той и другой науки. Одна исследует пространственные формы и количественные соотношения в реальном мире, а другая – мышление. Но есть удивительное сходство в отношениях между низшей и высшей математикой, с одной стороны, формальной и диалектической логикой – с другой. То и другое есть отношение постоянного и переменного, устойчивого и текучего, покоящегося и движущегося, «готового» и развивающегося. На этом основании, зная другие особенности отношения низшей математики к высшей (не исключают друг друга, одна дополняет другую и пр.), можно умозаключить о соответствующих особенностях отношений формальной и диалектической логики.
Виды аналогии по степени сходства предметов. Сходство между свойствами предметов или во взаимоотношениях предметов, в свою очередь, может иметь различные степени. Поэтому и аналогия способна принимать разные формы – быть строгой или нестрогой.
Строгая (или сильная) аналогия (она называется еще нередко «научной») особенно распространена в науках. Для нее характерно то, что переносимый признак необходимым образом связан с другими, сходными признаками (будучи, например, их следствием или, наоборот, причиной). В этом случае и вывод может стать достоверным.
Нестрогая (слабая) аналогия (называется иногда «популярной» – по сходству с популярной индукцией) имеет особенно широкую область применения. Она используется там, где переносимый признак непосредственно не связан со сходным, но может иметь место. Разумеется, такая аналогия дает чаще всего вероятное знание, а нередко бывает ложной, ошибочной.
Как и другие виды умозаключения, например индукция, аналогия может быть полной и неполной. В полной сходство превосходит различия, уподобляемые явления имеют ближайший род. В неполной – сходство лишь в некоторых отношениях.
Аналогия может быть, как и силлогизм, развернутой и свернутой (энтимематической). Многие сравнения-уподобления, которые не считаются аналогией, в скрытом виде могут содержать вывод или открывать для него возможность. Например: «Закон, что дышло: куда повернул, туда и вышло». Здесь содержится мысль о влиянии субъективных интересов на исполнение законов и т. д., об осуждении такого отношения к закону общественным мнением.
Иногда в качестве особого вида выделяют еще ложную аналогию, поскольку есть и истинная. Но так же как нет особых, специальных видов суждений по истинности и ложности (это их сущностная характеристика), так нет особой, всегда ложной аналогии. Ложной, как было показано, мЬжет оказаться и строгая, и нестрогая аналогия, и аналогия свойств, и аналогия отношений. Истинность и ложность вывода по аналогии, равно как и та или иная степень его вероятности, входят в сущностную характеристику познавательного значения аналогии и не имеют прямого отношения к делению ее на виды.
Конечно, все рассмотренные виды аналогии имеют лишь относительные различия. Так, выделяя аналогию свойств предметов, необходимо учитывать, что свойства проявляются в отношениях между предметами, а говоря об аналогии отношений – считаться с тем, что эти отношения сходны, а следовательно, уподобляются по своим свойствам. Поэтому в результате умозаключения по аналогии свойств может быть получена новая информация об отношениях предмета к другим и наоборот. Один пример. Аналогия электричества с распространением теплоты – это аналогия свойств двух физических явлений. Но перенос на электричество уравнений, разработанных для теплоты (а уравнение есть отношение), говорит о том, что тут вскрыта и аналогия отношений.
В заключение подчеркнем методологически важное положение: о каких бы конкретно видах аналогии ни шла речь, ее наибольшая эффективность достигается лишь во взаимодействии с другими формами умозаключений, в тесной связи с другими формами и методами познания.
Сводная таблица

Источник: Логика: учебник для студентов юридических вузов и факультетов / Е. А. Иванов. – Изд. 3-е, перераб. и доп. – Москва: Волтерс Клувер, 2007. – 405 с. – (Библиотека студентв).; ISBN 5-466-00105-8
Комментарии для сайта Cackle
I.
Умозаключение
как форма мышления Структура и виды
умозаключений.
II.
Дедуктивные
умозаключения.
-
Непосредственные
умозаключения.
Превращение. Обращение.
Противопоставление субъекту ,
противопоставление предикату.
Практическое использование непосредственных
умозаключений в силлогистике.
-
Простой
категорический силлогизм,
его структура и правила. Фигуры и модусы
силлогизма. Сложные и сложносокращенные
силлогизмы (энтимема, полисиллогизм,
сорит, эпихейрема) Алгоритмы решения
задач.
-
Умозаключения
логики суждений.
Условно-категорические и чисто условные
умозаключения. Разделительно-категорические
умозаключения. Конструктивные и
деструктивные дилеммы. Возможные
ошибки. Алгоритмы решения задач.
I. Умозаключение как форма мышления.
На
предыдущих лекциях мы познакомились с
такими формами мышления как понятие и
суждение. Следующей более сложной формой
мышления является умозаключение.
Умозаключения лежат в основе наших
рассуждений и позволяют из одного знания
выводить другое.
Умозаключение
– это форма мышления, посредством
которой из одного или нескольких суждений
выводится новое суждение .
Если
суждение – это мысль, то умозаключение
– это последовательность мыслей.
Последовательность мыслей – это более
сложный объект исследования, следовательно
для его исследования нам понадобится
все, что мы знали о суждении и понятии.
Умозаключениями пользуемся мы в различных
видах деятельности.: следователь при
обосновании версии, ученик при
доказательстве теоремы, при обосновании
аргументов в споре , просто, для получения
нового знания путем рассуждений.
Умозаключение
имеет устойчивую структуру:
-
посылки
– исходные суждения, из которых выводится
новое знание.
Например. а) « Преступление совершено
умышленно или по неосторожности» б) «
Данное преступление совершено умышленно»
2)
Заключение
– новое суждение, полученное логическим
путем из
посылок.
Например, Следовательно, неверно, что
преступление совершено по неосторожности.
Перед заключением всегда стоят слова:
следовательно, значит, получается… Это
позволяет отделить заключение от
посылок.
3)Вывод
– логическая
процедура, посредством которой из
посылок
выводится заключение.
В нашем случае мы воспользовались
утверждающе – отрицательным модусом
разделительно- категорического
умозаключения, его формула
Преступление
совершено умышленно (p)
— 1 посылка
или
по неосторожности (q)
p
v
q
p
v
q
Данное
преступление совершено умышленно
p p
Следовательно,
неверно, что оно осуществлено ~q ~q
по
неосторожности
Существует
несколько классификаций умозаключений
по разным основаниям:
-
По
строгости правил вывода умозаключения
делятся на
А)
НЕОБХОДИМЫЕ. В
них заключение с
необходимостью
следует из посылок, т.е. логическое
следование ( из истинного суждения не
может быть получено ложное ) представляет
собой логический закон.
В)
ПРАВДОПОДОБНЫЕ.Правила
вывода в них обеспечивают лишь вероятное
следование заключения из посылок.
-
По
направленности логического следования
умозаключения делятся на:
А)
ДЕДУКТИВНЫЕ. В этих умозаключениях
мысль движется от общего к частному.
Они не расширяют наших знаний о
действительности путем присоединения
новых фактов, но гарантируют истинность
заключения при истинности посылок и
соблюдении логических законов.Здесь
посылки и заключение всегда находятся
в ситуации логического следования. К
дедуктивным умозаключениям относятся
выводы из категорических суждений
(непосредственные умозаключения и
силлогизмы) , а также выводы из сложных
высказываний.
В)
НЕДЕДУКТИВНЫЕ. Они
не обладают логической надежностью
дедуктивных,
но они позволяют обобщать новые факты,
мысли двигаться от частного к общему,
расширять объем наших знаний. К
ним относятся
индуктивные умозаключения и умозаключения
по аналогии.
Дедуктивные
умозаключения можно разделить на:
а)
Непосредственные
(заключение
выводится из одной посылки) – превращение,
обращение, умозаключения по логическому
квадрату и противопоставление субъекту
и предикату)
б)
опосредованные,
в которых заключение выводится из двух
посылок. Это простой категорический
силлогизм, умозаключение из суждений
с отношениями, умозаключения из сложных
суждений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема
4: УМОЗАКЛЮЧЕНИЕ КАК ФОРМА МЫСЛИ.
Учебные вопросы:
1. Общая характеристика
умозаключения, его структура и типы.
2. Непосредственное
умозаключение и его преобразования.
3. Структура, общие
правила, фигуры и модусы простого категорического силлогизма.
4. Сокращенные и сложные
силлогизмы.
5. Умозаключения из
сложных суждений.
6. Индуктивные
умозаключения.
7. Умозаключения по
аналогии.
Введение
Познавая окружающую действительность, мы
приобретаем новые знания. Некоторые из них – непосредственно, при помощи
органов чувств; другие же опосредованно, на основании логического мышления,
путем выведения новых знаний из знаний, уже имеющихся. Эти знания называются
выводными. Логической формой получения выводных знаний является умозаключение.
В зависимости от способа получения выводных знаний различают дедуктивные,
индуктивные и традуктивные (по аналогии) умозаключения.
Цель лекции: сформировать
представление об умозаключении, его структуре и основных видах, приобрести
навыки непосредственных выводов; усвоить и научиться применять на практике
правила силлогизма, выработать навыки правильного рассуждения, умение отличать
правильные рассуждения от неправильных; научиться определять виды умозаключений
в форме выводов из сложных суждений, приобрести навыки правильного рассуждения
в такой форме; сформировать представление о недедуктивных умозаключениях,
усвоить виды этих умозаключений и требования, повышающие степень вероятности их
выводов; научиться определять вид недедуктивного умозаключения и характер его
вывода, а также приобрести навыки рассуждения в форме индуктивного
умозаключения и по аналогии.
Ключевые
понятия:
Умозаключение, силлогизм, посылки,
заключение, вывод, дедуктивные умозаключения, индуктивные умозаключения,
умозаключения по аналогии, непосредственные умозаключения, превращение,
обращение, противопоставление предикату, термины силлогизма, меньший термин,
больший термин, средний термин, аксиома силлогизма, фигура силлогизма, модус
силлогизма, правильный модус, неправильный модус, чисто условное умозаключение,
условно-категорическое умозаключение, разделительно-категорическое
умозаключение, условно-разделительное умозаключение, дилемма, энтимема,
эпихейрема, сорит, просиллогизм, эписиллогизм, индуктивные методы установления
причинных связей.
1. Общая
характеристика умозаключения, его структура и типы.
В процессе познания действительности мы приобретаем новые
знания.
Некоторые из них – непосредственно, в
результате воздействия предметов внешнего мира на органы чувств. Но большую
часть знаний мы получаем путем выведения новых знаний из знаний уже имеющихся.
Эти знания называются выводными.
Логической формой получения выводных знаний является
умозаключение.
Умозаключение – это форма мысли,
в которой из одного или нескольких суждений выводится новое суждение, с
необходимостью или определённой степенью вероятности следующее из них.
Суждения, из которых делается вывод, называются посылками
умозаключения.
Суждение, являющееся выводом из посылок, называется заключением.
Внутренняя связь между посылками и
заключением называется логическим следованием, или выводом.
Отношение логического следования между
посылками и заключением предполагает связь между посылками по содержанию.
Если посылки между собой не связаны по
содержанию, то вывод из них сделать невозможно.
Например, из следующих двух посылок никакого вывода не
следует:
Все планеты – это небесные тела.
Все
сосны являются деревьями.
?
Исходные посылки должны быть истинными
суждениями и должны быть связаны между собой.
Если хотя бы одна из посылок ложна, то и вывод ложен.
Например:
Все птицы – это млекопитающие животные.
Все
воробьи – это птицы.
Все воробьи – это млекопитающие животные.
В приведенном примере ложность первой посылки приводит к
ложному выводу.
Если нарушается указанное выше условие,
то говорят, что «заключение делается из ложных посылок».
Кроме того, необходимо соблюдать правила
вывода, которые обусловливают формальную правильность умозаключения. Если это
условие нарушается, то говорят, что истинное заключение «не вытекает из данных
посылок» («не следует»).
Примером служит следующее умозаключение:
Все люди не имеют крыльев.
Собака
не имеет крыльев.
Собака – человек.
Обе посылки истинные, но из них не следует истинное
заключение.
Вывод не следует с необходимостью, так как нарушено
правило силлогизма.
Умозаключения можно классифицировать по нескольким
основаниям.
Во-первых, в зависимости от строгости
правил вывода выделяются:
–
демонстративные (необходимые) умозаключения,
которые с необходимостью следуют из посылок; демонстративные
умозаключения содержат необходимое логическое следование: в них связь посылок и
заключения такова, что при истинных суждениях в посылках заключение будет
достоверно истинным. Например: «Люди не ангелы. Я человек. Следовательно, я не
ангел»;
–
недемонстративные (правдоподобные) – обеспечивают
лишь вероятностное следование заключения из посылок; вероятностные
умозаключения содержат ослабленное логическое следование: в них истинность
посылок не гарантирует истинного заключения. Например: «У подъезда дома карета
«скорой помощи», следовательно, кто-то из жильцов болен».
Во-вторых, по направленности
логического следования, т.е. по характеру связи между знанием различной
степени общности, выраженному в посылках и заключении.
По направленности логического следования
все умозаключения делятся на дедуктивные, индуктивные и традуктивные выводы.
Дедуктивное умозаключение – это
вывод от знания большей степени общности к знанию меньшей степени общности. В
посылках дедуктивного умозаключения содержится некоторое общее правило, которое
применяется к частному случаю в заключении. Достоверные дедуктивные выводы
называются силлогизмами. Впервые теория силлогизма была разработана
Аристотелем. В современной математической логике дедукцией называют
демонстративные выводы. Пример дедуктивного умозаключения: «Все люди смертны.
Сократ – человек. Следовательно, Сократ смертен».
Индуктивные умозаключения – это
выводы от знания меньшей степени общности к знания большей степени общности, от
фактов к обобщениям. Название «индуктивные умозаключения» происходит от
латинского слова «inductio» («наведение»). В посылках индукции
рассматриваются частные случаи, в заключении из них выводится общее правило или
даже закон. Поскольку большинство индуктивных выводов (неполная индукция)
являются вероятностными, в математической логике индуктивными выводами называют
вероятностные умозаключения. Пример индуктивного вывода: «Алюминий, медь и
железо проводят электричество. Следовательно, все металлы электропроводны».
Традуктивные умозаключения по
направленности логического следования не могут быть однозначно отнесены ни к
дедуктивным, ни к индуктивным выводам. Например: «Иван – брат Петра. Пётр –
отец Андрея. Следовательно, Иван – родственник Андрея». Самое известное
традуктивное умозаключение – это умозаключение по аналогии.
Аналогия (от греческого слова «analogia»
(«соответствие», «сходство») – это вывод, в котором на основании сходства
двух классов (предметов), делается заключение о какомто свойстве одного из них.
Схема аналогии может быть такой: «Предмет А обладает свойствами a, b, c.
Предмет В обладает свойствами a, b. Следовательно, предмет В, возможно,
обладает свойством с». Аналогии различны по своей форме, но большинство из них
имеет вероятностный характер.
В-третьих, умозаключения бывают
простыми и сложными. Простое умозаключение содержит одно логическое
следование, сложное – два или несколько логических следований.
Сложные умозаключения – это полисиллогизмы, сориты и
эпихейремы.
Особую группу умозаключений составляют
выводы логики высказываний, то есть выводы, посылки которых являются сложными
суждениями. Самыми востребованными из умозаключений логики высказываний
являются условно-категорические силлогизмы, разделительно-категорические
силлогизмы и дилеммы.
По количеству суждений в посылках
умозаключения делятся на непосредственные (в посылках содержится одно
простое суждение) и опосредованные ( в посылках – два или более суждений)
2. Непосредственное
умозаключение и его преобразования.
Непосредственные умозаключения
– такие, в которых заключение выводится из одной посылки посредством
преобразования.
Например, из суждения «Все боксеры –
спортсмены» можно получить новое суждение «Некоторые спортсмены – боксеры».
К способам преобразования
непосредственных умозаключений относятся:
превращение, обращение, противопоставление предикату,
умозаключение по логическому квадрату.
Превращение –это преобразование
исходного суждения в непосредственном умозаключении, в котором изменяется
связка на противоположную, а предикат – на противоречащее понятие.
Например: «Все люди – разумные существа,
следовательно, ни один человек не является неразумным».
Превращение – это непосредственное
умозаключение, основанное на правиле: двойное отрицание равносильно
утверждению.
Превращению подвергаются все виды простого категорического
суждения А,Е,I,О.
Схемы превращений:
► ( А
) Все S есть Р.
 (Е)
(Е)
Ни одно S не есть не-Р.
► ( Е
) Ни одно S не есть Р.
(А) Все S есть не-Р.
► ( I
) Некоторые S есть Р.
(О) Некоторые S не есть не-Р.
![]() ► ( О ) Некоторые S
► ( О ) Некоторые S
не есть Р.
(I) Некоторые S есть не-Р.
Обращение – это такое
преобразование исходного суждения в непосредственном умозаключении, в котором
происходит перестановка субъекта и предиката при сохранении качества суждений.
Различают:
–
обращение с ограничением объема – применимо для суждений
А; ведет к изменению исходного суждения по количеству (из общего исходного
получается новое частное суждение): (А)«Все студенты – учащиеся.
Следовательно, некоторые учащиеся – это студенты».
–
обращение без ограничения объема: применяется для
суждений Е, I; не ведет к изменению исходного суждения по
количеству:
(Е) «Ни один студент нашей группы не
является неуспевающим. Следовательно, ни один не успевающий не является
студентом нашей группы»
(I)«Некоторые студенты – учащиеся.
Следовательно, некоторые учащиеся – это студенты».
Частноотрицательное суждение «О» обращению не
подвергается.
Схемы обращений:
►
( А ) Все S есть Р.
 ( I )
( I )
Некоторые Р есть S.
► ( Е ) Ни одно S не есть Р.
(Е) Ни одно Р не есть S.
►
( I ) Некоторые S есть Р.
(I) Некоторые Р есть S.
Противопоставление предикату (контрапозиция) – такое
преобразование в результате которых: субъектом заключения становится понятие,
противоречащее предикату исходного суждения, а предикатом – субъект исходного
суждения; и при этом меняется качество суждения.
Противопоставление предикату – результат
двух последовательных операций: сначала с посылкой производится
превращение, затем полученное суждение обращается.
►Общеутвердительное
суждение (А) преобразуется в общеотрицательное (Е).
«Все студенты являются учащимися.
Следовательно, ни один не учащийся не является студентом».
►
Общеотрицательное суждение (Е) преобразуется в частноутвердительное
(I).
►Частноотрицательное
суждение (О) преобразуется в частноутвердительное (I).
► Частноутвердительное суждение не
подвергается противопоставлению предикату по закону обращения.
Схемы противопоставления предикату:
► ( А ) Все S
есть Р.
 (Е)
(Е)
Ни одно не-Р не есть S.
► ( О ) Некоторые S не есть Р.
(I) Некоторые не-Р есть S.
► ( Е
) Ни одно S не есть Р.
(I) Некоторые не-Р есть S.
Умозаключение по логическому квадрату
по своему смыслу состоит в том, что знание зависимости истинности
или ложности одних суждений от истинности или ложности других помогает делать
правильные выводы в процессе рассуждения.
Например, имеем общеутвердительное суждение
«Всякое правонарушение есть противоправное деяние» (А). Допустим, оно
истинно.
Из него выведем противоположное, противоречивое и
подчиненное суждения:
1)
противоположное: «Ни одно правонарушение не является
противоправным деянием». Если А – истинно, то Е – ложно.
2)
противоречивое: «Некоторые правонарушения не являются
противоправным деянием». Если А – истинно, то О – ложно.
3)
подчиненное: «Некоторые правонарушения есть противоправные
деяния». Если А – истинно, то I – истинно.
Другой пример: имеем общеотрицательное
суждение «Ни один свидетель не говорит правду» (Е). Необходимо
вывести из него противоположное, противоречащее и подчиненное суждения и
установить их истинность или ложность: 1) противоположное: «Все
свидетели говорят правду» (А); 2) противоречащее: «Некоторые
свидетели говорят правду» (I); 3) подчиненное: «Некоторые свидетели не
говорят правду» (О).
Установим их истинность или ложность.
Если Е – истинно, то: А – ложно; I – ложно; О
– истинно.
Если Е – ложно, то: А – либо
истинно, либо ложно; I – истинно; О – либо истинно, либо ложно.
3. Структура, общие правила, фигуры и модусы простого
категорического силлогизма.
Простой категорический силлогизм
состоит из трех категорических суждений, два из которых являются посылками,
а третье — заключением.
Силлогизм происходит от
греческого syllogismos (сосчитывание, выведение следствия).
Например:
1. Обвиняемый имеет
право на защиту.
2. Бобров —
обвиняемый.
3. Бобров имеет право на
защиту.
В простом категорическом силлогизме посылки
и заключение являются простыми категорическими суждениями.
Категорические суждения – такие,
в которых мысль утверждается или отрицается вполне определенно, без всяких
условий и которые имеют субъектнопредикатную логическую форму.
![]() Логическая
Логическая
структура простого категорического силлогизма.
В отличие от терминов суждения —
субъекта (S) и предиката (Р) понятия, входящие в состав силлогизма, называются терминами
силлогизма.
Различают меньший, больший и средний термины.
► Меньший термин силлогизма – понятие,
которое в заключении является субъектом («Бобров»).
► Больший термин силлогизма – понятие,
которое в заключении является предикатом («имеет право на защиту»).
► Средний термин силлогизма – понятие,
входящее в обе посылки и отсутствующее в заключении («обвиняемый»).
Меньший и больший термины
называются крайними и обозначаются соответственно латинскими
буквами S (меньший термин) и Р (больший термин).
Средний термин обозначается латинской
буквой М (от латинского medius — «средний»).
Посылка, в которую входит меньший
термин, называется меньшей посылкой, посылка в которую входит больший
термин, называется большей посылкой.

Средний термин связывает два крайних
термина. Отношение крайних терминов (субъекта и предиката) устанавливается
благодаря их отношению к среднему термину.
Итак, простой категорический
силлогизм – это умозаключение об отношении
двух крайних терминов на основании их отношения к среднему термину.
Силлогизмы бывают правильно построенные и неправильно
построенные.
Иногда достаточно сравнить умозаключение
с аксиомой, чтобы убедиться в его правильности либо ложности.
Аксиома силлогизма – это
логический закон, обосновывающий правомерность вывода из посылок
категорического силлогизма.
Аксиома силлогизма имеет две формулировки: по объему и по
содержанию.
►Аксиома по объему: всё, что утверждается
(или отрицается) относительно всего класса предметов, действительно и
относительно части этого класса.
► Аксиома по содержанию: признак
признака вещи есть признак самой вещи. Если Р – признак М,
а М – признак S, то, следовательно, Р – признак S.
Например:
Все представители семейства кошачьих (М) имеют
втяжные когти (Р).
![]() Рысь ( S ) – представитель семейства кошачьих ( М).
Рысь ( S ) – представитель семейства кошачьих ( М).
Следовательно, рысь (S) имеет втяжные когти (Р).
В этом примере больший термин в
посылке является признаком среднего термина, а средний термин –
признаком меньшего термина.

Общие правила
силлогизма.
Помимо аксиомы силлогизма для проверки
правильности построения силлогизма применяются установленные правила. Они
подразделяются на две группы: правила терминов и правила посылок.
а)
правила терминов:
Правило 1: В каждом силлогизме
должно быть только три термина – большой, меньший и средний. Это правила
требует не только соответствующего количества терминов в построении силлогизма,
но и смысловой однозначности среднего термина в обеих посылках. В
противном случае он может потерять свою однозначность, и тогда правильный вывод
получить будет невозможно, ибо не будет связующего звена между крайними
терминами. Так получается в следующем силлогизме: «Труд – основа жизни.
Изучение логики – труд. Следовательно, изучение логики – основа жизни».
Понятие труд в каждой посылке взято не однозначно: в первом случае оно означает
деятельность как общую форму бытия человека, во втором – как конкретный вид
работы ума.
Правило 2: Средний термин
должен быть распределен (взят в полном объеме) хотя бы в одной из посылок.
Для этого он должен быть или субъектом общего суждения, или предикатом
отрицательного суждения. Если же средний термин взят не в полном объеме в обеих
посылках, то выполнить свою роль связующего звена он не сможет, и точный вывод
получить невозможно. Например, в посылках «Некоторые студенты – мастера
спорта» и «Все старосты учебных групп – студенты» средний термин
«студенты» не распределен, поэтому сделать вывод, есть ли мастера спорта среди
старост групп не представляется возможным (см.: рис. 1).

Рис.
1
Из рисунка 1 видно, что объем субъекта
(«все старосты учебных групп») может перекрещиваться с объемом большего термина
(«мастера спорта»), но может находиться и вне его.
Правило 3: Термин, не
распределенный в посылках, не может быть распределен в заключении. Из общих
суждений-посылок: «Все птицы летают с помощью крыльев» и «Все птицы –
теплокровные животные» нельзя получить в качестве вывода общее суждение.
Меньший термин «теплокровные животные» стоит на месте предиката в
утвердительной посылке и поэтому не распределен. Следовательно, в выводе его
нужно брать не в полном объеме (см. рис. 2).

б)
правила посылок:
Правило 1: Из двух частных
посылок невозможно сделать вывод. В этом случае нельзя установить объемные
отношения между терминами силлогизма, поэтому определенный вывод не получается.
Например, из посылок: «Некоторые члены Академии наук (М)- химики» (S)
«Некоторые биологи (P) – члены Академии наук» (М) никакой определенный
вывод не следует. Объем субъекта («некоторые биологи») может
перекрещиваться в какой-то мере с объемом предиката («химики»), но может
находиться и вне его, как показано на рисунке 3.
.

Рис.
3
Правило 2: Если одна посылка частная, то вывод
будет частным.
Из посылок: «Все участники кросса –
спортсмены» и «Некоторые студентыотличники – участники кросса» общий
вывод невозможен. Нельзя утверждать, что все студенты-отличники – спортсмены,
так как речь идет только о части объема меньшего термина.
Правило 3: Из двух отрицательных посылок нельзя
сделать вывод.
В этом случае все термины исключают друг
друга, устраняя всякую объемную взаимосвязь между ними. Из посылок: «Ни одна
планета не светит собственным светом» и «Искусственный спутник не есть
планета» – никакого вывода не следует.
Правило 4: Если одна посылка отрицательная, то вывод будет
отрицательным.
Например: «Всякое пребывание на
свежем воздухе полезно». «Пребывание на свежем воздухе при низкой
температуре опасно». Следовательно, «пребывание на свежем воздухе при
низкой температуре может принести вред здоровью» (см.: рис. 4).

Рис.4
Простые категорические силлогизмы бывают
различными по своей структуре. Разновидности силлогизма называются фигурами и
модусами.
Фигурами называются формы
силлогизма, различающиеся по положению среднего термина в посылках.
Существует четыре фигуры простого категорического
силлогизма.
В силлогизмах первой фигуры средний
термин является субъектом большей посылки и предикатом меньшей.
Во второй фигуре средний термин – предикат обеих посылок.
В третьей фигуре средний тремин является
субъектом как большей, так и меньшей посылки.
В четвёртой фигуре средний термин –
предикат большей посылки и субъект меньшей. Фигуры можно представить в виде
следующих схем: 1 фигура:

Например:
Все газы (М) – это химические элементы
(Р).
Гелий (S) – это газ (М).
Гелий (S) – это химический элемент (Р).
Вторая фигура силлогизма – это
такое расположение его терминов, при котором и первая, и вторая посылки
заканчиваются средним термином.

Например:
Все рыбы (Р) дышат жабрами (М).
Все киты (S) не дышат жабрами (М).
Все киты (S) не рыбы (Р).
Третья фигура силлогизма – это
такое расположение его терминов, при котором и первая, и вторая посылки
начинаются со среднего термина.

Например:
Все тигры (М) – это млекопитающие (Р).
Все тигры (М) – это хищники (S).
Некоторые хищники (S) – это млекопитающие
(Р).
Четвёртая фигура силлогизма – это
такое расположение его терминов, при котором первая посылка заканчивается
средним термином, а вторая начинается с него.

Например:
Все квадраты (Р) – это прямоугольники
(М).
Все прямоугольники (М) – это не
треугольники (S). Все треугольники (S) – это не
квадраты (Р).
![]() Силлогизмы каждой
Силлогизмы каждой
фигуры подчиняются особым правилам фигур . Правила первой фигуры.
|
общее |
|
|
утвердительное суждение. |
|
Большая посылка (Р) –
Меньшая посылка (S) –
Первая фигура дает любые заключения: общеутвердительные,
общеотрицательные, частноутвердительные и частноотрицательные. Другими словами,
в заключениях первой фигуры представлены все виды простого категорического
суждения.
Правила
второй фигуры.
Большая посылка должна быть общим суждением.
Одна из посылок и заключение – отрицательными.
Правила
третьей фигуры.
 Меньшая посылка
Меньшая посылка
должна быть утвердительным суждением.
Заключение – частным.
Правила
четвёртой фигуры.
–
Не дает общеутвердительных заключений
Вывод по четвертой фигуре имеет необходимый характер при
соблюдении следующих правил:
–
Если большая посылка утвердительная, то меньшая должна быть общей. –
Если одна из посылок отрицательная, то большая посылка должна быть общей; –
Если меньшая посылка утвердительная, то заключение должно быть частным.
Иногда правила фигур нарушаются. В этих случаях
логическое следование теряет необходимый характер, мы получаем вероятностное
умозаключение. Например: «Аудитории нуждаются в проветривании. Эта комната
не является аудиторией, следовательно, её можно не проветривать». Здесь
вывод строится по первой фигуре с отрицанием в меньшей посылке.
Нарушение правила фигур всегда
сопровождается нарушением какого-либо общего правила. В данном силлогизме
произошло «незаконное расширение большего термина».
Часто встречающейся ошибкой является
утвердительное заключение по второй фигуре. Например: «Бриллианты
великолепны. Этот камень очень хорош, следовательно, этот камень – бриллиант».
В этом выводе присутствует ошибка – «средний термин не связывает».
Модусы простого
категорического силлогизма – это его разновидности, определяемые количеством и
качеством образующих его суждений.
Модус выражается набором простых суждений, входящих в
силлогизм.
Например:
Все небесные тела движутся.
Все
планеты – это небесные тела.
Все планеты движутся.
В данном силлогизме:
– первая посылка является
простым суждением вида A (общеутвердительным); – вторая посылка –
простое суждение вида A;
– заключение в данном
случае – простое суждение вида A.
Таким образом, рассмотренный силлогизм имеет модус AАA.
Второй пример:
Все журналы – это периодические издания (А)
Все книги не
являются периодическими изданиями (Е) Все книги не являются журналами (Е) Силлогизм
имеет модус AEE.
Правильные
и неправильные модусы силлогизма.
В каждой фигуре 64 модуса.
Всего модусов во всех четырёх фигурах,
т. е. возможных комбинаций простых суждений в силлогизме, – 256.
Модусы силлогизмов бывают правильными
(при истинности посылок всегда дают истинное заключение) и неправильными.
Правильные модусы соответствуют
правильным умозаключениям, неправильные – неправильным умозаключениям.
Отделить правильные модусы от неправильных
можно простым способом: исключить комбинации посылок, не соответствующие
общим правилам простого категорического силлогизма, а также исключить посылки,
которые не соответствуют правилам фигур.
Правильные модусы силлогизма (их всего
19) – это те формы, которые удовлетворяют правилам простого категорического
силлогизма.

Правильные модусы имеют специально
сконструированные имена. Гласные буквы, входящие в имя, образуют сам модус.
По первой фигуре образуются
следующие правильные модусы: Barbara, Celarent, Darii, Ferio.
По
второй фигуре образуются модусы: Cesare, Camestres, Festino, Baroko.
Третья фигура имеет правильные модусы: Darapti,
Disamis, Datisti, Felapton, Bokardo, Ferison.
Четвёртая
фигура имеет модусы: Bramantip, Camenes, Dimaris, Fesapo, Fresison.
Самым действенным, доступным способом
проверки строгости дедуктивного вывода является проверка его по фигурам и
модусам. Со времён Аристотеля модусы первой фигуры считаются самыми лучшими,
так как образцово соответствуют аксиоме силлогизма. В традиционной логике было
принято сводить модусы второй, третьей и четвёртой фигур к модусам первой
фигуры. Эта операция считалась дополнительной проверкой строгости вывода и
хорошим логическим упражнением.
Правило сведения к модусам первой фигуры.
► Первая буква имени модуса указывает
на то, к какому модусу первой фигуры он может быть сведён: В, С, D, F,
начальные согласные названий, показывают модусы фигуры 1, получающиеся от
сведения.
Так Cesare, Camestres и Camenes фигур 2 и 4 можно свести к
Celarent фигуры 1;
Darapti, Disamis фигуры 3 можно свести к Darii;
Fresison — к Ferio;
Bramantip может быть сведён только к Barbara.
►Если в имени модуса есть буква s, то
посылка, стоящая перед s должна быть подвергнута простому обращению. Например,
Datisti сведётся к Darii путём чистого обращения меньшей посылки.
►Если
в имени модуса есть буква р, то его сведение осуществится через обращение с
ограничением стоящей перед р посылки. Например, сведение Felapton к Ferio
происходит через обращение с ограничением меньшей посылки.
►Если в имени модуса есть буква m, то
следует поменять местами его посылки и обратить заключение.
►Если в имени модуса есть буква к, то
модус к первой фигуре не сводим, но может быть проверен при помощи модуса
Barbara методом сведения к абсурду.
Рассмотрим несколько примеров сведения.
Модус Darapti сводится к Daril
фигуры 1 и именно следующим образом. Меньшую посылку нужно преобразовать
посредством обращения, т. е. из суждения «Все М суть S» должно
получиться суждение; «некоторые S суть M».
3 фигура
(Darapti) 1 фигура (Darii)
Все кошки красивы. Все
кошки красивы.
Все кошки – животные. Некоторые
животные – кошки.
 Некоторые
Некоторые
животные красивы. Некоторые животные красивы.
Bramantip сводится к Barbara путем перестановки посылок:
4
фигура (Bramantip) 1 фигура (Barbara)
Все P суть M все
M суть S
Все M суть S все
P суть M
Некоторые
S суть P все P суть S
Пример:
A Все металлы суть материальные вещества
A Все материальные вещества суть тяжелые тела
I Некоторые тяжелые тела есть суть металлы
A Все материальные вещества суть тяжелые тела A Все металлы
суть материальные вещества I Некоторые тяжелые тела суть металлы.
4. Сокращённые
и сложные силлогизмы
В мышлении и речи обычно используется не
простой силлогизм, а его различные сокращённые разновидности. Сокращенный
силлогизм называется энтимемой (от гр. enthymema «то, что в уме»).
Энтимема – это простой
силлогизм, в котором пропущена одна из посылок или вывод.
В зависимости от того, какая из частей
силлогизма не выражена, различают три вида энтимем:
1) с пропущенной большей посылкой; 2) с пропущенной меньшей
посылкой; 3) с пропущенным заключением.
Для иллюстрации возьмем следующий силлогизм:
Все металлы электропроводны.
Железо
– это металл.
Железо электропроводно.
Из данного силлогизма следуют три энтимемы:
►«Железо электропроводно, так как оно является металлом
(пропущена большая посылка)»,
►«Железо
электропроводно, потому что все металлы электропроводны
(пропущена меньшая посылка)»,
►«Все
металлы электропроводны, а железо – это металл (пропущен вывод)».
Проблема энтимемы в том, что для
проверки её логической правильности энтимему приходится восстанавливать до
полной формы.
Чтобы восстановить энтимему в полный
силлогизм, можно применить следующий алгоритм действий:
Во-первых, необходимо найти заключение и
так его сформулировать, чтобы меньший и больший термины были чётко выражены.
Для этого стоит обратить внимание на союзные слова: заключение обычно
помещается после слов «следовательно», «значит», «поэтому» или перед словами
«так как», «ибо», «потому что». Если в энтимеме союзное слово отсутствует («В
хоккей играют настоящие мужчины, трус не играет в хоккей»), это союзное слово
надо восстановить, опираясь на содержание суждений.
Во-вторых, нужно установить характер
сохранившейся посылки. Если она содержит больший термин, то она большая; если в
ней присутствует меньший термин, то – меньшая. Сохранившуюся посылку следует
сформулировать так, чтобы средний термин был чётко выражен.
В-третьих, восстанавливая недостающую посылку надо
попытаться построить правильный модус, и только в том случае, если мы
убедились, что правильный модус восстановить невозможно, следует считать
энтимему ложной.
Еще один вид сокращённых силлогизмов, который называется
эпихейремой.
Эпихейрема (от др.-греч.
ἐπιχείρημα — довод, аргумент) – это полисиллогизм, состоящий из энтимем.
Если расположить эти две энтимемы друг
за другом, то они станут посылками нового, третьего силлогизма, который и будет
эпихейремой:
«Социальная несправедливость – это зло,
так как оно приводит общество к бедствиям» (первая энтимема).
«Частная собственность – это социальная
несправедливость, так как она способствует обогащению одних за счёт обнищания
других» (вторая энтимема).
Следовательно, «частная собственность – это зло».
Сложные силлогизмы называются полисиллогизмами.
Они строятся таким образом, что заключение одного силлогизма является посылкой
для другого. Тот силлогизм, который предшествует, называется просиллогизмом,
а тот, который следует после, называется эписиллогизмом.
Есть два типа полисиллогизмов. В первом
умозаключение идет от более общего к менее общему, во втором, наоборот,
умозаключение идёт от менее общего к более общему. Первый тип называется
прогрессивным, второй — регрессивным.
В прогрессивном полисиллогизме
заключение предшествующего простого силлогизма становится большей посылкой
следующего. Вот схема прогрессивного полисиллогизма, состоящего из общих
суждений:
Все А суть В.
Все С суть А.
Следовательно, все С суть В. Все D суть С.
![]()
Все D суть В.
Пример прогрессивного полисиллогизма: «Все
позвоночные имеют красную кровь.
Все млекопитающие суть позвоночные.
Все млекопитающие имеют красную кровь.
Все млекопитающие имеют красную кровь.
Все хищные суть млекопитающие.
Все хищные имеют красную кровь.
Все хищные имеют красную кровь.
Тигры суть хищные животные.
Тигры имеют красную кровь».
Здесь умозаключение идёт от более общего
к менее общему (позвоночные, млекопитающие, хищные, тигры), т. е. шествует
вперёд по отношению к содержанию, так как в частных понятиях содержание больше.
В регрессивном полисиллогизме
заключение предшествующего вывода становится меньшей посылкой последующего. Вот
схема регрессивного полисиллогизма:
Все А суть В.
Все С суть А.
Следовательно, все С суть В.
Все
В суть D.
Все С суть D.
Пример регрессивного полисиллогизма:
«Позвоночные суть животные.
Тигры суть позвоночные. Тигры суть животные.
Животные суть организмы.
Тигры суть животные.
Тигры суть организмы.
Организмы разрушаются.
Тигры
суть организмы.
Тигры разрушаются».
Здесь умозаключение идёт от менее общего
к более общему (позвоночное, животное, организм, разрушимое).
Для проверки логической строгости
полисиллогизма следует проверить по фигурам и модусам каждый из составляющих
его простых силлогизмов.
Прогрессивный и регрессивный полисиллогизмы чаще
применяются в сокращенной форме – в виде соритов (от греч. soros
— куча). Существует два вида соритов.
Прогрессивный (гоклениевский) сорит
получается из прогрессивного полисиллогизма путём отбрасывания промежуточных
заключений, они же являются большими посылками. Прогрессивный сорит начинается
с посылки, содержащей предикат заключения, и заканчивается посылкой, содержащей
субъект заключения.
Регрессивный (аристотелевский) сорит
получается из регрессивного полисиллогизма путём отбрасывания промежуточных
заключений, которые являются меньшими посылками. Регрессивный сорит начинается
с посылки, содержащей субъект заключения, а заканчивается посылкой, содержащей
предикат заключения.
1.Аристотелевский сорит: Буцефал есть лошадь.
Лошадь есть четвероногое.
Четвероногое есть животное.
Животное
есть субстанция.
Буцефал есть субстанция.
Если бы этому сориту мы придали полную
форму, т. е. восстановили бы опущенные посылки, то у нас получилось бы
следующих три силлогизма:
1)
Лошадь есть четвероногое.
Буцефал есть лошадь.
Буцефал есть четвероногое.
2)
Четвероногое есть животное.
(Буцефал
есть четвероногое).
Буцефал есть животное.
3)
Животное есть субстанция.(Буцефал есть животное). Буцефал есть
субстанция 2. Гоклениевский сорит.
Животное есть субстанция.
Четвероногое есть животное.
Лошадь есть четвероногое.
Буцефал
есть лошадь.
Буцефал есть субстанция.
Это есть гоклениевский сорит, потому что выпущены большие
посылки.
Если бы мы восстановили пропущенные
посылки, то у нас получился бы следующий ряд силлогизмов:
1)
Животное есть субстанция. Четвероногое есть животное.
Четвероногое естьсубстанция.
2)
[Четвероногое есть субстанция]. Лошадь есть четвероногое. Лошадь
естьсубстанция.
3)
[Лошадь есть субстанция]. Буцефал есть лошадь. Буцефал есть
субстанция.
![]() 5. Умозаключения из сложных
5. Умозаключения из сложных
суждений.
Специфика выведения заключения в
умозаключениях из сложных суждений состоит в том, что оно определяется не
отношениями между понятиями (терминами умозаключения), а характером логической
связи между исходными суждениями.
При соблюдении установленных формальной
логикой правил истинности посылок гарантируется и истинность заключения.
Сложные
условные умозаключения.
К этой группе дедуктивных умозаключений
относят чисто условное и условнокатегорическое умозаключения.
Чисто условным![]() называется
называется
умозаключение, обе посылки которого являются условными суждениями.
Вот схема простейшего чисто условного умозаключения:
А→В
В→С
А→С
Например:
«Кто умеет владеть собою (А), тот может повелевать людьми
(В)» (Вольтер).
«Кто способен управлять женщиной (В)
/женщина — человек/, тот способен управлять государством (С)» (Бальзак).
Следовательно, кто умеет владеть собою
(А), тот способен управлять государством (С).
В приведенном примере обе посылки – условные суждения,
причем:
–
следствие первой посылки является основанием второй (В),
из которого, в свою очередь, вытекает некоторое следствие (С).
–
Общая часть двух посылок (В) позволяет связать
основание первой (А) и следствие второй (С). Поэтому заключение также
выражается в форме условного суждения. – Вывод в чисто условном умозаключении
основывается на правиле: следствие следствия есть следствие основания.
Условно-категорическое
умозаключение — умозаключение,
в котором одна из посылок — условное суждение, а другая посылка и
заключение — категорические суждения.
Различают четыре фигуры условно-категорического
умозаключения:
2 правильные: утверждающий модус
(modus ponens), отрицающий модус (modus tollens);
2 неправильные: вероятностные модусы.
Утверждающий и отрицающий модусы являются правильными
фигурами.
Вероятностные относятся к неправильным.
Логические схемы правильных фигур:

Логические схемы неправильных фигур:
![]()
Комбинации суждений называются модусами
условно-категорического умозаключения.
В двух из них рассуждение построено на
утверждениях основания или следствия, — это утверждающие модусы (1
и 3).
В двух других — на отрицаниях основания
или следствия, — это отрицающие модусы (2 и 4).

В содержательном выражении рассуждения по этим модусам
выглядят так:
1) «Когда
народ глуп (А), им легко управлять (В). Народ глуп (А).
Им легко управлять» (В).
Мысль движется здесь от утверждения
основания (А) к утверждению следствия (В). Это правильный
утверждающий модус. Он называется модус поненс (лат. modus ponens).
Утверждающий модус дает достоверные выводы.
2) «Когда
народ глуп (А), им легко управлять (В).
Народ не глуп (┐А).
Народом нелегко управлять» (┐В).
Мысль движется от отрицания основания (┐А)
к отрицанию следствия (┐В). Это неправильный
отрицающий модус. Такой ход рассуждения не гарантирует достоверности
выводного знания из истинных посылок.
Неправильный отрицающий модус (2), дает
лишь правдоподобные выводы. В корректной форме рассуждение должно выглядеть
так:
Когда народ глуп (А), им легко управлять (В). Народ не глуп
(-А).
Вероятно, что им нелегко управлять (-В);
3) «Когда
народ глуп (А), им легко управлять (В).
Народом легко управлять (В).
Народ глуп» (А).
Мысль движется от утверждения следствия (В)
к утверждению основания (А). Это неправильный
утверждающий модус, не обеспечивающий достоверных заключений из
истинных посылок. Народом легко управлять не только тогда, когда он оглуплен,
но и когда он, будучи просвещенным, консолидирован — объединен, сплочен в
борьбе за общие цели. Соответственно в заключении для корректности уместны слова
«вероятно»,
«видимо», «наверное» и т.п.;
4) «Когда
народ глуп (А), им легко управлять (В).
Народом нелегко управлять (┐В).
Народ не глуп (┐А)».
Мысль движется от отрицания следствия (┐В)
к отрицанию основания (┐А). Это правильный отрицающий модус, и
называется он модус толленс (лат. modus tollem).
![]() Рассмотрим отличие
Рассмотрим отличие
качества выводов из рассуждений по правильным модусам условно-категорического
умозаключения от выводов из неправильных фигур.
В качестве первой посылки во всех
четырех модусах следующее суждение «Если идет дождь (р), то на асфальте должны
быть лужи (q)».
1.
Рассуждаем по первой фигуре: «Если идет дождь (р), то на асфальте
должны быть лужи (q). Сейчас идет дождь (р). Значит, на асфальте должны быть
лужи (q)». Вывод правильный, так как рассуждение ведется от истинного
основания к утверждению истинности следствия по утверждающему модусу (modus
ponens).
2.
Рассуждаем по второй фигуре: «Если идет дождь (р), то на асфальте
должны быть лужи (q). На асфальте луж нет (┐q). Следовательно, сейчас дождь не
идет (┐р)». Вывод правильный, так как рассуждение ведется от отрицания
следствия к отрицанию основания по отрицающему модусу (modus tollens).
3.
Рассуждаем по третьей фигуре: «Если идет дождь (р), то на
асфальте должны быть лужи (q). Сейчас на асфальте лужи (q). Следовательно, идет
дождь (р)». Вывод не всегда правильный, так как рассуждение ведется по
правдоподобному модусу (лужи на асфальте могут появляться и по другим
причинам).
4.
Рассуждаем по четвертой фигуре: «Если идет дождь (р), то
на асфальте должны быть лужи (q). Сейчас дождь не идет (┐р). Следовательно, на
асфальте не должно быть луж (┐q)». Вывод неправильный, так как рассуждение
ведется по правдоподобному модусу (лужи могли остаться со вчерашнего дня).
![]() Чисто разделительное
Чисто разделительное
умозаключение — такое, в котором посылки и заключение являются
разделительными суждениями.
Вот его схема:
А˅В
А1˅А2
А1˅А2˅В Например:
-Управлять можно либо человеческими
ресурсами (А), либо техническими или иными системами (В).
–
В работе с людьми понятие брака не применимо: либо высший уровень
работы (А1), либо нам придется расстаться (А2) / из постулатов
менеджмента.
–
Следовательно, либо высший уровень работы (А1), либо нам придется
расстаться (А2) (в работе с людьми), либо возможен брак в
управлении техническими или иными системами (В).
Разделительно-категорическое умозаключение![]() состоит
состоит
из двух посылок и заключения:
–
первая (большая) посылка – разделительное суждение,
–
меньшая посылка и заключение являются категорическими суждениями.
Различают только две фигуры разделительно-категорического
умозаключения:
●
утверждающе-отрицающий модус (modus ponendo-tollens) ● и отрицающе-утверждающий (modus
tollendo-ponens).
Оба модуса правильные.
Логическая схема утверждающе-отрицающего модуса (modus
ponendo-tollens):
А˅В
А
┐В
Например: Стиль лидерства может быть
демократическим (А) или автократичным (В). Стиль
данного лидера демократический (А). Значит, он не является
автократичным (┐ В).
Следует иметь в виду, что данный модус
даст достоверное заключение только в том случае, когда возможности в
разделительной посылке исключают друг друга (строгая дизъюнкция).
► Логическая схема отрицающе-утверждающего модуса
(modus tollendo-ponens):
А˅В
┐А
В
Например: Стиль лидерства может быть демократическим (А)
или автократичным
(В). Стиль данного лидера не демократический (┐А).
Значит, он является автократичным
(В).
Необходимо учитывать, что этот модус
дает достоверное заключение только в том случае, когда в разделительной посылке
перечислены все возможности![]() (закрытая дизъюнкция).
(закрытая дизъюнкция).
Особую группу умозаключений из сложных
суждений составляют такие, которые имеют в своем составе и разделительные, и
условные посылки.
Условно-разделительное
умозаключение — это
умозаключение, в котором одна посылка состоит из двух или более условных
суждений, а другая представляет собой разделительное суждение.
Условно-разделительное умозаключение еще
называют леммой (от греч. lemma — предположение).
Такое название обусловлено тем, что в
этих умозаключениях рассматриваются различные предположения и их следствия.
Условно-разделительные умозаключения по
количеству альтернатив в разделительной посылке бывают следующих видов:
дилеммы (две альтернативы); трилеммы (три
альтернативы); полилеммы (четыре альтернативы и более).
Как правило, на практике используются дилеммы.
Существует четыре вида дилемм:
– две простые (конструктивная и деструктивная); – две
сложные (конструктивная и деструктивная).
► Дилемма считается конструктивной (утверждающей, созидающей),
если в заключение ее входят следствия условных посылок.
► Дилемма считается деструктивной (отрицающей, разрушительной),
если в заключение ее входят отрицания оснований условных посылок.
► Дилемма считается простой, если заключение
представляет собой простое категорическое суждение.
► Дилемма считается сложной, если
заключение является сложным разделительным суждением.
Запишем схемы дилемм.
1. Простая конструктивная дилемма:
А→В
С→В
А˅С
В Например:
-Если наставлять приказами (А), то
люди будут стараться обойти запреты и потеряют чувство стыда (В).
-Если насаждать порядок наказаниями (С),
то люди будут стараться обойти запреты и потеряют чувство стыда (б)»
(Конфуций).
-Но правитель обычно наставляет
приказами (А) или насаждает порядок наказаниями (С).
Следовательно, люди будут стараться обойти запреты и
потеряют чувство стыда
(В).
2. Простая деструктивная дилемма:
А→В
А→С
┐В
˅ ┐С
┐ А Например:
-Если наставлять добродетелью и
поддерживать порядок посредством ритуала (А), то люди будут
знать, что такое стыд (В) или будут вести себя пристойно (С)”
(Конфуций).
-Но люди не знают, что такое стыд (┐В) и не
ведут себя пристойно (┐С).
Значит, правитель не наставляет
добродетелью и не поддерживает порядок посредством ритуала (┐А).
3.Сложная конструктивная дилемма:
А→В
С→Д
А
˅ С В ˅ Д Например:
–
Если наставлять приказами и насаждать порядок наказаниями (А),
то люди будут стараться обойти запреты и потеряют чувство стыда (В).
–
Если наставлять добродетелью и поддерживать порядок посредством
ритуала (С), то люди будут знать, что такое стыд и будут вести
себя пристойно (Д).
–
Но правитель либо наказывает (А), либо подает пример
добродетельногоповедения (С).
Значит, люди, обходя запреты, теряют
чувство стыда (В), либо ведут себя пристойно (Д).
4. Сложная деструктивная дилемма:
А→В
С→Д
┐В
˅ ┐С ┐А ˅ ┐С Например:
–
Когда верхи чтят ритуал (А), никто из простолюдинов
не посмеет быть непочтительным (В).
–
Когда верхи чтят долг (С), никто из простолюдинов не посмеет быть
непокорным(Д) /Конфуций.
–
Простолюдины непочтительны (┐В) и непокорны Значит,
верхи не чтят ни долг (┐С), ни ритуал (┐А).
Выводы:
Самые распространенные виды
умозаключений из сложных суждений — это чисто условное, чисто разделительное,
условно-категорическое, разделительно-категорическое и условно-разделительное
умозаключения.
Условно-категорическое умозаключение
имеет два правильных модуса (две разновидности): утверждающий и отрицающий.
Разделительно-категорическое
умозаключение также имеет два правильных модуса: утверждающе-отрицающий и
отрицающе-утверждающий.
Условно-разделительное (лемматическое)
умозаключение чаще всего используется в виде дилеммы. Известны четыре вида
дилемм: простая конструктивная, простая деструктивная, сложная конструктивная и
сложная деструктивная.
6. Индуктивные
умозаключения.
Логический переход от знания об отдельных явлениях к знанию
общему совершается в форме индуктивного умозаключения, или индукции
(от латинского inductio — «наведение»).
Индукция есть процесс мышления,
посредством которого мы выводим, что истинное в частных случаях будет истинным
и во всех случаях, сходных с предыдущими.
Посылками индуктивного умозаключения являются суждения, в
которых фиксируется информация о повторяемости признака Р у ряда явлений — S1,
S2 , …, Sn, принадлежащих одному и тому же классу К.
В зависимости от полноты и законченности
эмпирического исследования различают два вида индуктивных умозаключений: полную
индукцию и неполную индукцию.
1). Полная индукция — это
умозаключение, в котором на основе принадлежности определенного признака
каждому элементу класса делают вывод о его принадлежности классу в целом.
Индуктивные умозаключения такого типа
применяются лишь в тех случаях, когда имеют дело с закрытыми классами, число
элементов в которых является конечным и легко обозримым. Например, число
государств в Европе, количество промышленных предприятий в данном регионе,
число субъектов федерации в данном государстве и т. п.
Вывод в умозаключении полной индукции
носит демонстративный характер. Это означает, что при истинности посылок
заключение будет необходимо истинным.
Схема умозаключения полной индукции:
Посылки:
1) S1 имеет признак Р.
S2 имеет признак Р.
Sn имеет признак Р.
2) ![]() S1, S2, …, S n —
S1, S2, …, S n —
составляют класс К.
Заключение:
Всем предметам класса К присущ признак Р.
Применение полной индукции определяется
возможностью перечисления множества явлений. Если охватить весь класс предметов
невозможно, обобщение строится в форме неполной индукции.
2) Неполная индукция — это умозаключение, в
котором на основе принадлежности признака некоторым элементам класса делают
вывод о его принадлежности к классу в целом.
Схема неполной индукции:
Посылки:
1) S1 имеет
признак Р.
S2 имеет признак Р.
Sn имеет признак Р.
2) S1, S2 ……Sn
— принадлежат классу К.
Заключение: Классу К, вероятно, присущ признак Р.
Индуктивный переход от некоторых ко
всем не может претендовать на логическую необходимость, т. к.
повторяемость признака может оказаться результатом простого совпадения.
На этом основании неполную индукцию относят
к правдоподобным (недемонстративным) умозаключениям.
По способу отбора различают два вида неполной индукции:
– индукцию путем перечисления, получившую
название популярной индукции, – научную индукцию.
Популярной индукцией называют
обобщение, в котором путем перечисления устанавливают принадлежность признака
некоторым предметам и на этой основе проблематично заключают о его
принадлежности всему классу.
Обоснованность выводов в популярной
индукции определяется главным образом количественным показателем:
соотношением исследованного подмножества предметов (образца или выборки) ко
всему классу (популяции). Чем ближе исследованный образец ко всему классу, тем
основательнее, а значит, и вероятнее будет индуктивное обобщение.
В условиях, когда исследуются лишь
некоторые представители класса, не исключается возможность поспешного
обобщения.
Научной индукцией называют
умозаключение, в котором обобщение строится путем отбора необходимых и
исключения случайных обстоятельств. В зависимости от способов исследования
различают:
(1) индукцию методом отбора (селекции) и (2)
индукцию методом исключения (элиминации).
Индукция методом отбора или
селективная индукция, — это умозаключение, в котором вывод о принадлежности
признака классу (множеству) основывается на знании об образце (подмножестве),
полученном методичным отбором явлений из различных частей этого класса.
Индукция методом исключения или
элиминативная индукция — это система умозаключений, в которой выводы о причинах
исследуемых явлений строятся путем обнаружения подтверждающих обстоятельств и
исключения обстоятельств, не удовлетворяющих свойствам причинной связи.
Познавательная
роль элиминативной индукции – анализ причинных связей.
Причинной называют такую связь между
двумя явлениями, когда одно из них причина – предшествует и вызывает другое
действие.
Важнейшими свойствами причинной связи
являются: (1) всеобщность, (2) последовательность во времени, (3) необходимость
и (4) однозначность.
Причинная связь между явлениями определяется посредством
четырёх методов, исследование которых
восходит ещё к Фр.Бэкону и Дж.Ст. Миллю. Некоторые из этих методов можно
выразить схематически.

Вероятно, А является причиной а. Если
наблюдаемые случаи какого-либо явления имеют общим лишь одно предшествующее
обстоятельство, то оно и есть, очевидно, причина данного явления. Метод
сходства применяется в наблюдениях. Например, составление «пищевого дневника»
аллергика. Метод различия.

Вероятно, А является причиной а.
Если случаи, при которых явление, соответсвенно, наступает
или не наступает, различаются только одним предшествующим обстоятельством, а
все другие обстоятельства тождественны, то именно это единственное
обстоятельство и есть причина данного явления.
Метод различий иногда применяют вместе с методом сходства
(пример с аллергиком), хотя он может применятся и отдельно от метода сходства
(например, досмотр в аэровокзале). Метод различий применяется в экспериментах. Метод
сопутствующих изменений.

Вероятно, А является причиной а.
Если изменение одного предшествующего
обстоятельства всегда сопровождается пропорциональным изменением наблюдаемого
явления, а все прочие обстоятельства при этом остаются неизменными, то,
вероятно, изменяющееся обстоятельство есть причина явления. Метод сопутствующих
изменений применяется нечасто. Он уместен в тех случаях, когда причина и
следствие теснейшим образом связаны и не могут рассматриваться по отдельности.
Метод остатков.
Пусть изучаемое явление К распадается на
несколько составляющих: a, b, c, d. Установлено, что ему предшествовали
обстоятельства А, В, С. Известно, что А является причиной а, В является
причиной b, С – причина с. Мы имеем право предположить, что некое
обстоятельство D, сходное с обстоятельствами А, В, С, является причиной d. При
помощи метода остатков была открыта планета Нептун.
7. Умозаключения
по аналогии
Термин «аналогия» означает сходство двух
предметов (или двух групп предметов) в каких-либо свойствах или отношениях.
Умозаключение по аналогии — один из самых древних видов умозаключения, присущий
человеческому мышлению.
Аналогия — умозаключение о
принадлежности предмету определенного признака (т. е. свойства или отношения)
на основе сходства в признаках с другим предметом. В форме такого умозаключения
осуществляется приписывание предмету свойства или перенос отношений. Посредством
аналогии осуществляется перенос информации с одного предмета (модели) на другой
(прототип). Посылки относятся к модели, заключение – к прототипу. В аналогии
между Землей (модель) и Марсом (прототип), зная, что на Земле существует жизнь,
делаем вывод о том, что и на Марсе, вероятно, есть жизнь.
В зависимости от характера информации,
переносимой с одного предмета на другой, аналогия делится на два вида: аналогия
свойств и аналогия отношений.
В аналогии свойств рассматриваются два единичных
предмета (или два множества однородных предметов, два класса), а переносимыми
признаками являются свойства этих предметов. Схема аналогии свойств в
традиционной логике такова:
Предмет А обладает свойствами а, b, с, d, e,f.
Предмет В обладает свойствами а, b, с, d.
___________________________________________ Вероятно, предмет В обладает
свойствами е, f.
Аналогии, как умозаключению, свойственны некоторые
специфические черты.
Во-первых, она представляет собой
определенное правдоподобие исследуемого предмета (или явления) и выражает
знание с внутренне скрытой вероятностью. Вот почему аналогия весьма широко применяется
не только в научном познании, но и в практической деятельности.
Во-вторых, процесс формирования и
широкого распространения аналогии начался с обыденного сознания, и она
непосредственным образом связана с повседневной жизнью людей, их бытовыми условиями.
В-третьих, выводы по аналогии носят
весьма проблематичный характер, они, как правило, не представляют доказательной
силы. Поэтому в развитии познания следует переходить от вывода по аналогии к
заключению по необходимости.
Поскольку в объективной действительности
каждый вновь обнаруженный признак конкретного предмета не возникает независимо
от других его свойств, а определенным образом связан с ними, то, обнаружив в
другом предмете такую же совокупность признаков, заключают о существовании у
него нового признака.
Логический переход от известного к новому
знанию регулируется в выводах по аналогии следующим правилом: если два
единичных предмета сходны в определенных признаках, то они могут быть сходны и
в других, обнаруженных в одном из сравниваемых предметов, признаках.
Заключения аналогии не являются
достоверно истинными при истинности посылок, а только вероятностно истинными.
Вероятность истинности заключений выводов по аналогии низка даже по сравнению с
популярной индукцией. Поэтому в науке аналогия редко используется как средство
обоснования или доказательства суждений.
Но умозаключения по аналогии играют
важную эвристическую роль в научном познании. Аналогия – один из основных
способов формирования научных гипотез, источник догадок и предположений,
которые затем проходят проверку более строгими дедуктивными и индуктивными
методами. На первых этапах исследования незнакомых явлений ученый ищет среди
уже известных ему явлений какие-то аналогии для нового.
Помимо этого, умозаключения по аналогии
– одна из составляющих метода моделирования. В силу использования
умозаключений по аналогии результаты моделирования всегда носят вероятностный
характер.
В умозаключениях по аналогии используются следующие
понятия:
–
образец аналогии – объект, признак которого переносится на
другой объект;
–
субъект аналогии – объект, на который переносится признак;
–
термины аналогии – это образец и субъект аналогии;
–
переносимый признак – признак, который переносится с
образца на субъект;
–
основание аналогии – признак, одновременно присущий обоим
терминам аналогии и служащий основанием для переноса интересующего нас
признака.
Переносимый признак обычно является простым,
а основание аналогии – сложным признаком.
В структуру аналогии входят следующие суждения:
1)
суждение о наличии основания аналогии у образца;
2)
суждение о наличии основания аналогии у субъекта;3) суждение о наличии
переносимого признака у образца; 4) суждение о наличии переносимого признака у
субъекта.
Первые три суждения являются посылками
умозаключения по аналогии, а четвертое – его заключением
Кроме деления на два вида — аналогия
свойств и аналогия отношений — по характеру выводного знания (по степени
достоверности заключения) умозаключения по аналогии можно разделить на три
вида: 1) строгая аналогия, дающая достоверное заключение; 2) нестрогая аналогия,
дающая вероятное заключение; 3) ложная (вульгарная) аналогия, дающая ложное
заключение.
Строгая аналогия.
Характерным признаком, отличающим
строгую аналогию от нестрогой и ложной, является наличие необходимой связи
общих признаков с переносимым признаком. Схема строгой аналогии такова:
Предмет А обладает признаками а, b, с, d, e.
Предмет В обладает признаками а, b, с, d.
Из совокупности признаков а, b, с, d необходимо следует е.
______________________________________________ Предмет В обязательно обладает
признаком е.
Если из совокупности признаков М={а, b,
с, d} закономерно, необходимо следует признак е, то эту зависимость можно
записать так:
![]()
Структура строгой аналогии подобна
структуре правила modus ponens условнокатегорического умозаключения и поэтому
дает достоверный, а не правдоподобный вывод.
Строгая аналогия применяется в научных
исследованиях, в математических доказательствах. Так, например, формулировка
признаков подобия треугольников основана на строгой аналогии. «Если три утла
одного треугольника равны трем углам другого треугольника, то эти треугольники
подобны» (подобие — вид аналогии).
На свойствах умозаключения по строгой
аналогии основан метод моделирования. Научные аналогии позволяют использовать
имеющийся к настоящему времени опыт, при этом кроме формально-логических
принципов проведения аналогий необходимо учитывать и методологическое
требование конкретности истины, рассмотрения явления в конкретно-исторической
обстановке.
При овладении управляемой термоядерной
реакцией и создании термоядерной энергетики люди получат практически
неограниченные топливные ресурсы. В природе высокотемпературная плазма в
естественном виде существует в атмосфере звезд. «Для управляемого термоядерного
синтеза необходимо необычное в земных условиях солнечное вещество — водородная
плазма с температурой около ста миллионов градусов. На Солнце она удерживается
гравитационным полем, а на Земле ее можно держать в повиновении магнитным
полем. Но ведь по воздействию на частицы плазмы магнитное поле совершенно не
похоже на гравитационное…»
Ученые нашей страны предложили способ
решения этой проблемы. Созданная ими теория равновесия и устойчивости плазмы
уже используется при проектировании термоядерных установок.
Нестрогая аналогия.
В отличие от строгой аналогии нестрогая
аналогия дает не достоверное, а лишь вероятное заключение. Если ложное суждение
обозначить через 0, а истину — через 1, то степень вероятности заключений по
нестрогой аналогии лежит в интервале от 1 до 0, т. е.
1>Р(а)>0, где Р (а) — обозначение вероятности
заключения по нестрогой аналогии.
Примерами нестрогой аналогии являются, в
частности, следующие: испытание модели корабля в бассейне и заключение о том,
что настоящий корабль будет обладать теми же характеристиками, испытание
прочности моста на модели, затем построение настоящего моста. При строгом
выполнении всех правил построения и испытания модели этот способ умозаключения
может приближаться к строгой аналогии и давать достоверное заключение, однако
чаще заключение бывает вероятным. Разница в масштабах, между моделью и
прототипом (самим сооружением) иногда бывает не только количественной, но и
качественной. Так же не всегда можно учесть различие между лабораторными
условиями испытания модели и естественными условиями работы самого сооружения, в
результате чего возникают ошибки.
Для повышения степени вероятности
заключений по нестрогой аналогии следует выполнить ряд условий:
1)
число общих признаков должно быть возможно большим;
2)
сходные признаки должны быть существенными. Аналогия на основе
сходстванесущественных признаков типична для ненаучного и детского мышления.
Например, дети могут съесть ядовитые ягоды на основе их внешнего сходства со
съедобными;
3)
общие признаки должны быть по возможности более разнородными;
4)
необходимо учитывать количество и существенность пунктов
различия. Еслипредметы различаются в существенных признаках, то заключение по
аналогии может оказаться ложным;
5)
переносимый признак должен быть того же типа, что и сходные
признаки.
Ложная аналогия.
При нарушении указанных выше правил
аналогия может дать ложное заключение, т. е. стать ложной. Вероятность
заключения по ложной аналогии равна 0 (Р (а) = 0). Ложные аналогии иногда
делаются умышленно, с целью ввести противника в заблуждение, и тогда они
являются софистическим приемом, в других случаях они делаются случайно, в
результате незнания правил построения аналогий или отсутствия фактических
знаний относительно предметов А и В и их свойств, на основании которых осуществляется
аналогия.
Подобную ошибку совершали в XIX в.
сторонники вульгарного материализма Л. Бюхнер, К. Фохт и Я. Молешотт, которые,
проводя аналогию между печенью и мозгом, утверждали, что мозг выделяет мысль
так же, как печень выделяет желчь.
Обобщим сказанное о строгой, нестрогой и ложной аналогиях.
Если Р (а)=1, т. е.
заключение получается достоверным, то это будет строгая
аналогия. Если 1 > Р (а) > 0, т. е. заключение будет вероятным, то это
будет нестрогая аналогия. Если Р (а) = 0, т. е. заключение – ложное суждение,
то это будет ложная аналогия.
Заключение
Таким образом, дедуктивное
умозаключение играет большую роль в мыслительной деятельности человека.
Рассуждения принимают форму дедукции в том случае, когда частное явление
подводится к общему знанию. Однако на практике очень часто появляется
необходимость движения мысли не только от общего знания к частному, но и,
наоборот, от частного знания к знанию общему. Вот почему нельзя ограничиваться
использованием только дедукции.
Но общее, существенное, повторяющееся и
закономерное в предметах познается через изучение единичного, и одним из
средств такого познания выступает индукция. Опираясь на свойства причинной
связи, дедукция выступает логическим средством исключения случайных
обстоятельств, тем самым она логически корректирует и направляет индуктивное
обобщение.
Специалисты часто обращаются к
умозаключению по аналогии. Поэтому возникает необходимость теоретического
усвоения логической сущности, особенностей, структуры и правил этого вида
умозаключения, что поможет правильной оценке и использованию тех результатов,
которые могут быть получены с его помощью.
При изучении данной темы
рекомендуется более детально остановится на изучении структуры
умозаключения, специфики его видов, выявить взаимосвязь индукции и дедукции в
познании, уяснить особенности аналогии и её видов, а также, используя задачи и
упражнения, предлагаемые в заданиях для самостоятельной работы, разобраться,
как используются различные виды умозаключений в различных отраслях
профессиональной деятельности, научиться делать выводы на основе существующих
правил, определять истинность или ложность умозаключений.
Литература:
а) основная литература:
1.
Гетманова А.Д. Логика: учебник для бакаловров. – М.: Изд-во: Омега-Л. Серия: Бакалавр – магистр, 2018. – 357 с.
2.
Демидов И.В. Логика: Учебник для бакалавров. – М.:Дашков и К,
2017.— 348 с.
3.
Кириллов В.И., Старченко А.А. Логика: Учебник для бакалавров. 6-е
изд. – М.: Изд-во Проспект, 2018. – 240 с.
б) дополнительная литература:
1.
Рузавин Г.И. Основы логики и аргументации [Электронный ресурс]:
учебноепособие для студентов вузов, обучающихся по гуманитарно-социальным
специальностям/ Рузавин Г.И.— Электрон. текстовые данные.— М.: ЮНИТИ-ДАНА,
2017.— 320 c.— Режим доступа: http://www.iprbookshop.ru/8109.— ЭБС «IPRbooks»,
по паролю
2.
Ивлев Ю.В. Логика: Учебник.4-е изд. ГРИФ: Рекомендовано
Министерствомобразования Российской Федерации в качестве учебника для студентов
высших учебных заведений, обучающихся по специальностям 020100 «Философия»,
021100
«Юриспруденция». – М.: «Проспект», 2017.- 304 с.
3.
Лаврикова И.Н. Логика. Учимся решать:. Уч.пос. для студ. ВУЗов,
обучающихсяпо соц.-гуманит. специальностям. – М.: ЮНИТИ-Дана, 2016.
4.
Светлов В.А. Логика [Электронный ресурс]: учебное пособие/
Светлов В.А.—Электрон. текстовые данные.— М.: Логос, 2017.— 432 c.— Режим
доступа: http://www.iprbookshop.ru/9134.— ЭБС «IPRbooks», по паролю
5.
Бочаров В.А., Маркин В.И. Введение в логику: Учебник. – М.:
Издательство: Инфра-М, Форум. Серия: Высшее образование, 2016. – 560 с.
Вопросы
для самопроверки:
1.
Как можно определить понятие умозаключения?
2.
Какие виды умозаключений выделяются в формальной логике?
3.
Как различаются демонстративные и недемонстративные
умозаключения?
4.
Что представляют собой непосредственные умозаключения?
5.
Как осуществляется операция превращения?
6.
Как производится обращение?
7.
Каким образом осуществить преобразование противопоставлением
предикату?
8.
Что представляет собой силлогизм?
9.
Какова логическая структура силлогизма?
10.
Что такое фигура силлогизма?
11.
Что представляет собой модус силлогизма?
12.
Какие модусы являются правильными, а какие неправильными?
13.
Что такое энтимема и какие виды энтимем выделяются в формальной
логике?
14.
Что такое эпихейрема?
15.
Что такое полисиллогизм?
16.
Что такое просиллогизм и эписиллогизм?
17.
Какое различие между просиллогизмом прогрессивным и регрессивным?
18.
Что такое сорит?
19.
Какое различие между соритом аристотелевским и гоклениевским?.
20.
Какие силлогизмы называются условными и какие существуют типы
условных силлогизмов?
21.
Какие силлогизмы мы называются разделительными?
22.
Какие силлогизмы называются условно-разделительными?
23.
Какие четыре типа их мы различаем и чем они отличаются друг от
друга?
24.
Что такое дилемма, трилемма?
25.
От чего зависит достоверность лемматического умозаключения?
26.
Какие умозаключения являются индуктивными?
27.
На какие виды делятся индуктивные умозаключения?
28.
Что представляют собой умозаключения по аналогии?
Правила логических умозаключений.
Умозаключение – это форма абстрактного мышления, посредством которой из ранее имевшейся информации выводится новая. При этом не задействуются органы чувств, т. е. весь процесс умозаключения проходит на уровне мышления и независим от получаемой в данный момент извне информации. Визуально умозаключение отражается в виде столбца, в котором присутствует как минимум три элемента. Два из них – это посылки, третье называют заключением. Друг от друга посылки и заключение принято отделять горизонтальной чертой. Заключение всегда пишется снизу, посылки – сверху. И посылки, и заключение представляют собой суждения. Причем эти суждения могут быть как истинными, так и ложными. Например:
Все млекопитающие – животные.
Все кошки – млекопитающие.
Все кошки – животные.
Это умозаключение является истинным.
Умозаключение имеет ряд преимуществ перед формами чувственного познания и опытными исследованиями. Так как процесс умозаключения проходит только в области мышления, он не затрагивает реальных предметов. Это очень важное свойство, так как зачастую у исследователя нет возможности получить для наблюдения или опытов реальный предмет в силу его дороговизны, размеров или удаленности. Некоторые предметы на данный момент вообще можно считать недоступными для прямого исследования. Например, к такой группе предметов можно отнести космические объекты. Как известно, исследование человеком даже ближайших к Земле планет представляется проблематичным.
Другим преимуществом умозаключений является то, что они позволяют получить достоверную информацию об изучаемом объекте. Например, именно посредством умозаключения Д. И. Менделеев создал свою периодическую систему химических элементов. В области астрономии зачастую положение планет определяется без любого видимого контакта, исходя только из уже имеющейся информации о закономерностях положения небесных тел.
Недостатком умозаключения можно назвать то, что зачастую заключения характеризуются абстрактностью и не отражают многих конкретных свойств предмета. Это не относится, например, к упомянутой выше периодической таблице химических элементов. Доказано, что при ее помощи были открыты элементы и их свойства, которые на тот момент еще не были известны ученым. Однако так бывает не во всех случаях. Например, при определении положения планеты астрономами свойства ее отражаются лишь приблизительно. Также зачастую нельзя говорить о правильности заключения до тех пор, пока оно не прошло проверку на практике.
Умозаключения могут быть истинными и вероятностными. Первые с достоверностью отражают реальное положение вещей, вторые носят неопределенный характер. Видами умозаключения являются: индукция, дедукция и заключение по аналогии.
Умозаключение – это прежде всего выведение следствий, оно применяется повсеместно. Каждый человек в своей жизни независимо от профессии строил умозаключения и получал следствия из этих заключений. И здесь встает вопрос истинности таких следствий. Человек, который не знаком с логикой, пользуется ею обывательским уровнем. То есть судит о вещах, строит умозаключения, делает выводы, исходя из того, что накопил в процессе жизни.
Несмотря на то что практически каждый человек проходит обучение основам логики в школе, учится у родителей, обывательский уровень знания нельзя считать достаточным. Конечно, в большинстве ситуаций достаточно и этого уровня, но есть процент случаев, когда логической подготовки просто не хватает, хотя именно в таких ситуациях она больше всего нужна. Как известно, существует такой вид преступлений, как мошенничество. Чаще всего мошенники пользуются простыми и проверенными схемами, однако некоторый процент их занимается высококвалифицированным обманом. Такие преступники знают логику едва ли не в совершенстве и, кроме того, обладают способностями в области психологии. Поэтому им зачастую ничего не стоит обмануть человека, который не подготовлен. Все это говорит о необходимости изучения логики как науки.
Выведение следствия – очень распространенная логическая операция. По общему правилу, для получения истинного суждения необходимо, чтобы и посылки были истинны. Однако данное правило не относится к доказательству от обратного. В этом случае намеренно берутся заведомо ложные посылки, которые необходимы, чтобы через отрицание их определить необходимый объект. Другими словами, ложные посылки в процессе выведения следствия отбрасываются.
Умозаключение – это способ получения нового знания на основе некоторого имеющегося.
Умозаключение состоит из посылок и заключения.
Посылки – это высказывания, содержащие исходное знание.
Заключение – это высказывание, содержащее новое знание, полученное из исходного.
Как правило, заключение отделяется от посылок с помощью слов «следовательно», «значит». Умозаключение с посылками р1, р2, …, рn и заключением Р будем записывать в виде: ![]() или (р1, р2, …, рn)
или (р1, р2, …, рn) ![]() Р.
Р.
Примеры умозаключений: а) Число а = b. Число b = с. Следовательно, число а = с.
b) Если в дроби числитель меньше знаменателя, то дробь правильная. В дроби ![]() числитель меньше знаменателя (5. Следовательно, дробь
числитель меньше знаменателя (5. Следовательно, дробь ![]() – правильная.
– правильная.
с) Если идет дождь, то на небе есть тучи. На небе есть тучи, следовательно, идет дождь.
Умозаключения могут быть правильными и неправильными.
Умозаключение называется правильным, если формула, соответствующая его структуре и представляющая собой конъюнкцию посылок, соединенная с заключением знаком импликации тождественно истинна.
Для того чтобы установить, является ли умозаключение правильным, поступают следующим образом:
1) формализуют все посылки и заключение;
2) записывают формулу, представляющую конъюнкцию посылок, соединенную знаком импликации с заключением;
3) составляют таблицу истинности для данной формулы;
4) если формула тождественно-истинна, то умозаключение правильное, если нет – то умозаключение неправильное.
В логике считают, что правильность умозаключения определяется его формой и не зависит от конкретного содержания входящих в него утверждений. И в логике предлагаются такие правила, соблюдая которые, можно строить дедуктивные умозаключения. Эти правила называют правилами вывода или схемами дедуктивных рассуждений.
Правил много, но наиболее часто используются следующие:
1. ![]() – правило заключения;
– правило заключения;
2. ![]() – правило отрицания;
– правило отрицания;
3. ![]() – правило силлогизма.
– правило силлогизма.
Приведем пример умозаключения, выполненного по правилу заключения: «Если запись числа х оканчивается цифрой 5, то число х делится на 15. Запись числа 135 оканчивается цифрой 5. Следовательно, число 135 делится на 5».
В качестве общей посылки в этом умозаключении выступает утверждение «если А(х), то В(х)», где А(х) – это «запись числа х оканчивается цифрой 5», а В(х) – «число х делится на 5». Частная посылка представляет собой высказывание, которое получилось из условия общей посылки при
х = 135 (т.е. А(135)). Заключение является высказыванием, полученным из В(х) при х = 135 (т.е. В(135)).
Приведем пример умозаключения, выполненного по правилу отрицания: «Если запись числа х оканчивается цифрой 5, то число х делится на 5. Число 177 не делится на 5. Следовательно, оно не оканчивается цифрой 5».
Видим, что в этом умозаключении общая посылка такая же как и в предыдущем, а частная представляет собой отрицание высказывания «число 177 делится на 5» (т.е. ![]() ). Заключение – это отрицание предложения «Запись числа 177 оканчивается цифрой 5» (т.е.
). Заключение – это отрицание предложения «Запись числа 177 оканчивается цифрой 5» (т.е. ![]() ).
).
И наконец, рассмотрим пример умозаключения, построенного по правилу силлогизма: «Если число х кратно 12, то оно кратно 6. Если число х кратно 6, то оно кратно 3. Следовательно, если число х кратно 12, то оно кратно 3».
В этом умозаключении две посылки: «если А(х), то В(х)» и «если В(х), то С(х)», где А(х) – «число х кратно 12», В(х) – «число х кратно 6» и С(х) – «число х кратно 3». Заключение представляет собой высказывание «если А(х), то С(х)».
Проверим, правильны ли следующие умозаключения:
1) Если четырехугольник – ромб, то его диагонали взаимно перпендикулярны. АВСD – ромб. Следовательно, его диагонали взаимно перпендикулярны.
2) Если число делится на 4, то оно делится на 2. Число 22 делится на 2. Следовательно, оно делится на 4.
3) Все деревья являются растениями. Сосна – дерево. Значит, сосна – растение.
4) Все учащиеся данного класса ходили в театр. Петя не был в театре. Следовательно, Петя – учащийся не данного класса.
5) Если числитель дроби меньше знаменателя, то дробь правильная. Если дробь правильная, то она меньше 1. Следовательно, если числитель дроби меньше знаменателя, то дробь меньше 1.
Решение: 1) Для решения вопроса о правильности умозаключения выявим его логическую форму. Введем обозначения: С(х)– «четырехугольник х – ромб», В(х) – «в четырехугольнике х диагонали взаимно перпендикулярны». Тогда первую посылку можно записать в виде:
С(х) ![]() В(х), вторую – С(а), а заключение В(а).
В(х), вторую – С(а), а заключение В(а).
Таким образом, форма данного умозаключения такова: ![]() . Оно построено по правилу заключения. Следовательно, данное рассуждение правильное.
. Оно построено по правилу заключения. Следовательно, данное рассуждение правильное.
2) Введем обозначения: А(х) – «число х делится на 4», В(х) – «число х делится на 2». Тогда первую посылку запишем: А(х) ![]() В(х), вторую В(а), а заключение – А(а). Умозаключение примет форму:
В(х), вторую В(а), а заключение – А(а). Умозаключение примет форму: ![]() .
.
Такой логической формы среди известных нет. Легко заметить, что обе посылки истинны, а заключение ложно.
Значит, что данное рассуждение неправильное.
3) Введем обозначения. Пусть А(х) – «если х дерево», В(х) – «х растение». Тогда посылки примут вид: А(х)![]() В(х), А(а), а заключение В(а). Наше умозаключение построено по форме:
В(х), А(а), а заключение В(а). Наше умозаключение построено по форме: ![]() – правила заключения.
– правила заключения.
Значит, наше рассуждение построено верно.
4) Пусть А(х) – «х – учащиеся нашего класса», В(х) – «учащиеся х ходили в театр». Тогда посылки будут следующими: А(х)![]() В(х),
В(х), ![]() , а заключение
, а заключение ![]() .
.
Данное умозаключение построено по правилу отрицания:
![]() – значит оно верное.
– значит оно верное.
5) Выявим логическую форму умозаключения. Пусть А(х) – «числитель дроби х меньше знаменателя». В(х) – «дробь х – правильная». С(х) – «дробь х меньше 1». Тогда посылки примут вид: А(х)![]() В(х), В(х)
В(х), В(х) ![]() С(х), а заключение А(х)
С(х), а заключение А(х) ![]() С(х).
С(х).
Наше умозаключение будет следующей логической формы: ![]() – правило силлогизма.
– правило силлогизма.
Значит, данное умозаключение верно.
Дедуктивные умозаключения.
Как и многое в классической логике, теория дедукции обязана своим появлением древнегреческому философу Аристотелю. Он разработал большую часть вопросов, связанных с этим видом умозаключений.
Согласно работам Аристотеля дедукция – это переход в процессе умозаключения от общего к частному. Другими словами, дедукцией является постепенная конкретизация более абстрактного понятия. Она проходит через несколько ступеней, каждый раз выводя следствие из нескольких посылок.
Необходимо сказать, что в процессе дедуктивного умозаключения должно получаться истинное знание. Такой цели можно добиться только при соблюдении необходимых условий, правил. Правила вывода бывают двух видов: правила прямого и правила косвенного вывода. Прямой вывод означает получение из двух посылок заключения, которое будет истинным при условии соблюдения правил прямого вывода.
Так, должны быть истинны посылки и соблюдены правила получения следствий. При соблюдении этих правил можно говорить о правильности мышления относительно взятого предмета. Это означает, что для получения истинного суждения, нового знания не обязательно иметь всю информацию. Часть сведений может быть воссоздана логическим путем и закреплена. Закрепление необходимо, так как без него сам процесс получения новой информации становится бессмысленным. Ни передать такую информацию, ни как-либо иначе использовать ее не представляется возможным. Естественно, что такое закрепление происходит посредством языка (разговорный, письменный, язык программирования и т. д.). Закрепление в логике происходит прежде всего при помощи символов. Например, это могут быть символы конъюнкции, дизъюнкции, импликации, буквенные выражения, скобки и др.
Дедуктивными являются следующие типы умозаключений: выводы логических связей и субъектно-предикатные выводы.
Также дедуктивные умозаключения бывают непосредственными.
Они делаются из одной посылки и называются превращением, обращением и противопоставлением предикату, отдельно рассматриваются умозаключения по логическому квадрату. Выводятся такие умозаключения из категорических суждений.
Рассмотрим эти умозаключения. Превращение имеет схему:
S есть Р
S не есть не-Р.
По этой схеме видно, что посылка только одна. Это категорическое суждение. Превращение характеризуется тем, что при изменении качества посылки в процессе вывода не происходит изменения ее количества, а предикат следствия отрицает предикат посылки. Есть два способа превращения – двойное отрицание и замена отрицания в предикате отрицанием в связке. Первый случай отражен на схеме, приведенной выше. Во втором превращение отражается на схеме как S есть не-Р – S не есть Р.
В зависимости от типа суждения превращение можно выразить следующим образом.
Все S есть Р – Ни одно S не есть не-Р. Ни одно S не есть Р – Все S есть не-Р. Некоторые S есть Р – Некоторые S не есть не-Р. Некоторые S не есть Р – Некоторые S есть не-Р. Обращение – это умозаключение, в котором при перемене мест субъекта и предиката качество посылки не меняется.
То есть в процессе вывода субъект встает на место предиката, а предикат – на место субъекта. Соответственно, схему обращения можно изобразить как S есть Р – Р есть S.
Обращение бывает с ограничением и без ограничения (его еще называют простое или чистое). Это разделение основывается на количественном показателе суждения (имеется в виду равенство или неравенство объемов S и Р). Это выражается в том, изменилось ли кванторное слово или нет и распределены ли субъект и предикат. Если такое изменение происходит, то имеет место обращение с ограничением. В обратном случае можно говорить о чистом обращении. Напомним, что кванторное слово – это слово – показатель количества. Так, слова «все», «некоторые», «ни один» и другие являются кванторными словами.
Противопоставление предикату характеризуется тем, что связка в следствии меняется на противоположную, субъект противоречит предикату посылки, а предикат эквивалентен субъекту посылки.
Необходимо сказать, что непосредственное умозаключение с противопоставлением предикату невозможно вывести из частноутвердительных суждений.
Приведем схемы противопоставления в зависимости от типов суждений.
Некоторые S не есть Р – Некоторые не-Р есть S. Ни одно S не есть Р – Некоторые не-Р есть S. Все S есть Р – Ни одно Р не есть S.
Объединяя сказанное, можно рассматривать противопоставление предикату как продукт сразу двух непосредственных умозаключений. Первым из них производится превращение. Его результат подвергается обращению.
Условные и разделительные умозаключения.
Говоря о дедуктивных умозаключениях, нельзя не обратить внимания на условные и разделительные умозаключения.
Условные умозаключения называются так потому, что в качестве посылок в них используются условные суждения (если а, то b). Условные умозаключения можно отразить в виде следующей схемы.
Если а, то b. Если b, то с. Если а, то с.
Выше указана схема умозаключений, являющихся видом условных. Для таких умозаключений характерно, что все их посылки являются условными.
Другим видом условных умозаключений являются условно-категорические суждения. Соответственно названию в этом умозаключении не обе посылки являются условными суждениями, одна из них – простое категорическое суждение.
Необходимо также упомянуть о модусах – разновидностях умозаключений. Существуют: утверждающий модус, отрицающий модус и два вероятностных модуса (первый и второй).
Утверждающий модус имеет самое широкое распространение в мышлении. Это связано с тем, что он дает достоверное заключение. Поэтому правила различных учебных дисциплин строятся в основном на основе утверждающего модуса. Можно отобразить утверждающий модус в виде схемы.
Если а, то b.
а.
b.
Приведем пример утверждающего модуса.
Если топор упадет в воду, он утонет.
Топор упал в воду.
Он утонет.
Два истинных суждения, которые являются посылками этого суждения, преобразуются в процессе вывода в истинное суждение. Отрицающий модус выражается по следующей схеме. Если а, то b. Не-b. Не-а.
Это суждение строится на основе отрицания следствия и отрицания основания.
Умозаключения могут давать не только истинные, но и неопределенные суждения (неизвестно, истинны они или ложны).
В связи с этим следует сказать о вероятностных модусах.
Первый вероятностный модус на схеме отображается следующим образом.
Если а, то b.
b.
Вероятно, а.
Как ясно из названия, следствие, выводимое из посылок при помощи этого модуса, является вероятным.
Если дует сильный ветер, то яхту кренит набок.
Яхту кренит набок.
Вероятно, дует сильный ветер.
Как мы видим, от утверждения следствия к утверждению основания невозможно вывести истинное умозаключение.
Второй вероятностный модус в виде схемы можно изобразить так.
Если а, то b. Не-а.
Вероятно, не-b. Приведем пример.
Если человек лежит под солнцем, он загорит.
Этот человек не лежит под солнцем.
Он не загорит.
Как видно из приведенного примера, производя умозаключение от отрицания основания к отрицанию следствия, мы получим не истинное, а вероятностное следствие.
Формулы утверждающего и отрицающего модусов являются законами логики, в то время как формулы вероятностных – не являются.
Разделительные умозаключения делятся на простые разделительные и разделительно-категорические умозаключения. В первом случае разделительными являются все посылки. Соответственно, разделительно-категорические суждения имеют в качестве одной из посылок простое категорическое суждение.
Таким образом, разделительным считается умозаключение, все или часть посылок которого являются разделительными суждениями. Структура простого разделительного умозаключения отражается следующим образом.
S есть А или В, или С.
А есть А1 или А2.
S есть А1 или А2, или В, или С.
Примером такого умозаключения является следующее.
Путь бывает прямым или окружным.
Окружный путь бывает с одной пересадкой или с несколькими пересадками.
Путь бывает прямым или с одной пересадкой, или с несколькими пересадками.
Разделительно-категорические умозаключения можно представить в виде схемы.
S есть А или В. S есть А (В). S не есть В (А). Например:
Выстрел бывает точным и неточным. Этот выстрел является точным. Этот выстрел не является неточным.
Здесь необходимо упомянуть об условно-разделительных умозаключениях. От указанных выше умозаключений они отличаются посылками. Одна из них – это разделительное суждение, что не является особенным, однако вторая посылка таких суждений состоит из двух или нескольких условных суждений.
Условно-разделительное суждение может быть или дилеммой, или трилеммой. В дилемме условная посылка состоит из двух членов. При этом разделительная подразумевает наличие выбора. Другими словами, дилемма – это выбор одного из двух вариантов.
Дилемма бывает простой конструктивной и сложной конструктивной, а также простой и сложной деструктивной. Первая имеет две посылки, одна из которых утверждает одинаковый исход двух предложенных ситуаций, другая говорит о том, что возможна одна из этих ситуаций. Следствие резюмирует утверждение первой посылки (условного суждения).
Если нажать на карандаш, он сломается; если согнуть карандаш, он сломается.
Можно нажать на карандаш или согнуть карандаш.
Карандаш сломается.
Сложная конструктивная дилемма предполагает более тяжелый выбор между альтернативами.
Трилемма состоит из двух посылок и следствия и предлагает выбор из трех вариантов или констатирует три факта.
Если спортсмен вовремя нанесет удар, то он победит; если спортсмен правильно распределит силы, то он победит; если спортсмен выполнит прыжок чисто, то он победит.
Спортсмен вовремя нанесет удар или правильно распределит силы на дистанции, или выполнит прыжок чисто.
Спортсмен победит.
Бывают случаи, когда в условных, разделительных или условно-разделительных умозаключениях пропускаются заключение или одна из посылок. Такие умозаключения называют сокращенными.
Понятие силлогизма. Простой категорический силлогизм
Слово «силлогизм» произошло от греческого syllogysmos, что означает «вывод». Очевидно, что силлогизм – это выведение следствия, заключения из определенных посылок. Силлогизм бывает простым, сложным, сокращенным и сложносокращенным.Силлогизм, посылками в котором являются категорические суждения, называется, соответственно, категорическим. Посылок в силлогизме две. Они содержат три термина силлогизма, обозначаемые буквами S, P и М. Р – это больший термин, S – меньший, а М – средний, связующий. Другими словами, термин Р шире по объему (хотя уже по содержанию) как М, так и S. Самый узкий по объему термин силлогизма – это S. При этом больший термин содержит предикат суждения, меньший – его субъект. S и Р связаны между собой средним понятием (М).
Пример категорического силлогизма.
Все боксеры – спортсмены.
Этот человек – боксер.
Этот человек – спортсмен.
Слово «боксер» здесь является средним термином, первая посылка – больший термин, вторая – меньший. Во избежание ошибок заметим, что в данном силлогизме имеется в виду данный, конкретный человек, а не все люди. В противном случае, конечно, вторая посылка была бы намного шире по объему.
Категорический силлогизм имеет четыре формы в зависимости от положения в его структуре среднего термина.
В первом случае большая посылка должна быть общей, а меньшая – утвердительной. Вторая форма категорического силлогизма дает отрицательное заключение, и одна из его посылок также отрицательна. Большее понятие, как и в первом случае, должно быть общим. Заключение третьей формы должно быть частным, меньшая посылка – утвердительной. Четвертая форма категорических силлогизмов наиболее интересна. Из таких умозаключений нельзя вывести общеутвердительное заключение, а между посылками существует закономерная связь. Так, если одна из посылок отрицательная, большая должна быть общей, при этом меньшая должна быть общей, если большая – утвердительна.
Для того чтобы избежать возможных ошибок, при построении категорических силлогизмов следует руководствоваться правилами терминов и посылок. Правила терминов следующие.
Распределенность среднего термина (М). Означает, что средний термин, связующее звено, должен быть распределен хотя бы в одном из двух других терминов – большем или меньшем. При нарушении данного правила заключение получается ложным.
Отсутствие лишних терминов силлогизма. Означает, что категорический силлогизм должен содержать только три члена – термины S, M и Р. Каждый термин должен рассматриваться только в одном значении.
Распределенность в заключении. Для того чтобы быть распределенным в заключении, термин должен быть распределен и в посылках силлогизма.
Правила посылок.
1. Невозможность вывода из частных посылок. То есть, если обе посылки являются частными суждениями, из них невозможно сделать вывод. Например:
Некоторые машины – пикапы.
Некоторые механизмы – машины.
Из этих посылок нельзя сделать заключение.
2. Невозможность вывода из отрицательных посылок. Отрицательные посылки не дают возможности сделать вывод. Например:
Люди не птицы.
Собаки не люди.
Вывод невозможен.
3. Следующее правило гласит, что если одна из посылок силлогизма частная, то и его следствие тоже будет частным. Например:
Все боксеры – спортсмены.
Некоторые люди – боксеры.
Некоторые люди – спортсмены.
4. Существует еще одно правило, которое говорит о том, что, если только одна из посылок силлогизма является отрицательной, вывод возможен, однако также будет отрицательным. Например:
Все пылесосы – бытовая техника.
Эта техника не является бытовой.
Эта техника не пылесос.
Задания
Задание 7. Сделайте вывод (если это возможно) путем превращения:
7.1. Некоторые приговоры суда не являются обвинительными 7.2. Все дороги ведут в Рим 7.3. Шила в мешке не утаить
Решение:
7.1. Некоторые приговоры суда (S) не являются обвинительными (P) Имеем дело с частноотрицательным суждением
Схема: Некоторые S не есть Р.
Схема превращения: Некоторые S есть не-Р
Некоторые приговоры (S) есть не обвинительными (не-Р)
7.2. Все дороги(S) ведут в Рим (Р)
Имеем дело с общеутвердительным суждением
Схема : Все S есть Р Схема превращения: Ни одно S не есть не-P
Ни одна дорога не является ведущей не в город Рим
7.3. Шила в мешке не утаить
Запишем суждение так: Ни одно шило в мешке не утаить
Имеем дело с общеотрицательным суждением.
Схема: Ни одно S не есть Р
Схема превращения: Все S суть не-P.
Любое шило можно в мешке утаить
Задание 8. Сделайте вывод (если это возможно) путем обращения:
8.1. Лица, занимающиеся контрабандой, привлекаются к уголовной ответственности
8.2. Некоторые преподаватели вузов не являются юристами
8.3. не всякий генерал от природы полный (Козьма Прутков)
Решение:
8.1. Лица, занимающиеся контрабандой(S), привлекаются к уголовной ответственности (P)
Схема: Все S есть Р (общеутвердительное суждение)
Схема обращения: Некоторые Р есть S.
Некоторые, привлекаемые к уголовной ответственности,(P) являются лицами, занимающимися контрабандой (S)
8.2. Некоторые преподаватели вузов (S) не являются юристами (P)
Схема: Некоторые S не есть Р (частноотрицательное суждение)
Обращения для частноотрицательного суждения нет.
8.3. не всякий генерал(S) от природы полный (Р) (Козьма Прутков)
Схема: Некоторые S есть Р (частноутвердительное суждение)
Схема обращения: Все Р есть S. Все от природы полные(Р) являются генералами(S)
Задание 9. Сделайте вывод (если это возможно) путем противопоставления предикату: 9.1. Все следователи – юристы 9.2. Некоторые птицы – перелетные
Решение: 9.1. Все следователи(S) – юристы (P)
Схема: Все S есть Р (общеутвердительное суждение)
Схема противопоставления предикату: Ни одно не – Р не есть S.
Ни один не юрист(не-Р) не является следователем(S)
9.2. Некоторые птицы(S) – перелетные (P)
Схема: Некоторые S есть Р (частноутвердительное суждение)
Для частноутвердительного суждения нельзя сделать противопоставление предикату.
Дополнительные вопросы:
1. Чем умозаключение как форма мышления отличается от суждения? Чем умозаключение отличается от понятия? Что объединяет все три формы? Какова роль умозаключений в познании мира?
О: Умозаключение является более сложной формой мышления, в отличии от суждения. В состав умозаключения входит суждение, значит и понятия. Но умозаключение нельзя свести к понятию, оно показывает их определенную связь. Так, именно в умозаключениях кроется «тайна» принудительной силы речей. Именно с постижения этих тайн, зарождалась наука логика. За счет многообразных видов умозаключений, люди имеют новые знания в нашей жизни и научных теориях, без умозаключений процесс мышления был бы невозможен.
«Умозаключение – это форма мышления, посредством которой осуществляется переход от известного (имеющегося) знания к новому знанию. В структуре умозаключения часто выделяется:
1.посылки – это исходное знание, которое и есть основание для умозаключения.
2.заключение – производное, то есть новое знание, которое получается из посылок.
3.Логическая связь между посылками и заключением, которая выражает отношение между ними.
Умозаключения весьма распространенная форма, используемая в научном и повседневном мышлении. Роль умозаключений в познании мира этим и определяется. Значение умозаключений – не только связывать, наши знания в более или менее сложные знания и в относительно законченные комплексы – мыслительные конструкции. А также обогащать и усиливать эти знания.
3. Решите практические задания:
a. Укажите, в каких отношениях находятся следующие пары понятий: «город» и «деревня», «небесное тело» и «звезда». Используя круги Эйлера, изобразите взаимное положение объемов указанных пар понятий.
О: обозначим данные понятия: Г – город, Д – деревня, Н – небесное тело, З – звезда.
изобразив данные понятия, с помощью кругов Эйлера, получим:
b. Дайте логическую характеристику понятию «ненависть».
О: понятие «ненависть» является общим, абстрактным, отрицательным, безотносительным.
c. Совершите операции ограничения и обобщения объемов следующих понятий: «знаменитый артист», «ураган», «сборная России».
О:
операция обобщения:
«Знаменитый артист» – « Знаменитый человек» – « Человек «
«Ураган» – «Атмосферный вихрь, больших размеров» – « Атмосферный вихрь»
«сборная России» – «сборная страны Восточной Европы» – « сборная страны»
операция ограничения:
«Знаменитый артист» – « Знаменитый Шаляпин» – « Знаменитый Федор Иванович Шаляпин»
«Ураган» – «Ураган, затронувший Ямайку» – «Ураган Сэнди»
«сборная России» – « женская сборная России» – «женская сборная России по легкой атлетике»
d. Дайте пример генетического определения.
О: Круг – это кривая, образуемая движением на плоскости точки, которая сохраняет равное расстояние от центра”
e. Приведите пример суждения вида А, в котором субъект распределен, а предикат – нераспределен.
О:
суждение вида А – общеутвердительное суждение
схема : Все S+ есть Р-
пример: Все студенты любят закрывать сессию
субъект S – «студенты» распределен
предикат Р – «любящие закрывать сессию» не распределен
4. Выполните практические задания:
a. Какое правило определения понятий нарушено: «Количество – это характеристика предмета с его количественной стороны»?
О:
нарушено правило определения : определение содержит тавтологию.(понятие количество раскрывается через количественную сторону), т.е. «масло масленое» – та же самая тавтология.
b. Преобразуйте следующее суждение путем превращения, обращения и противопоставления предикату: «Все автомобили являются средствами передвижения».
О:
(А):Все автомобили являются средствами передвижения
схема: Все S есть Р
Общая схема превращения:
A Все S суть P……………………E ни одно S не есть не-P
Общая схема обращения:
A Все S суть P……………………I некоторые Р есть S
Общая схема противопоставления предикату:
A Все S суть P…………………… ни одно не-P не есть S
превращение: Ни один автомобиль не является не средством передвижения
обращение: Некоторые средства передвижения являются автомобилями
противопоставление предикату: Ни одно не средство передвижения не является автомобилем
c. Установите с помощью логического квадрата, в каком отношении находятся суждения «Ни одно существо не бессмертно» и «Некоторые существа бессмертны».
О:
(Е): Ни одно существо не бессмертно
(I): Некоторые существа бессмертны
рассмотрим логический квадрат
видно, что данные суждения находятся в отношении противоречия.
8
