§ 17. Цилиндр
17.1. Определение цилиндра и его элементов
Определение. Тело, которое образуется при вращении прямоугольника вокруг прямой, содержащей его сторону, называется цилиндром (рис. 141).
Круги, образованные вращением сторон прямоугольника, перпендикулярных оси вращения, называются основаниями цилиндра (верхним и нижним). Так как противоположные стороны прямоугольника равны, то основаниями цилиндра являются равные круги.
Рис. 141
Поверхность, образованная вращением стороны прямоугольника, параллельной оси вращения, называется боковой поверхностью цилиндра, а её площадь — площадью боковой поверхности цилиндра и обозначается Sбок. Объединение боковой поверхности цилиндра и двух его оснований называется полной поверхностью цилиндра, а её площадь обозначается Sполн. Таким образом,
Sполн = Sбок + 2Sосн.(1)
Высотой цилиндра называется перпендикуляр, проведённый из какой-либо точки одного основания цилиндра к плоскости другого. Длину этого перпендикуляра также называют высотой цилиндра. Отрезок, соединяющий точки окружностей оснований и перпендикулярный к их плоскостям, называется образующей цилиндра вращения. Отрезок оси вращения, заключённый внутри цилиндра, называется осью цилиндра.

Если основания прямого кругового цилиндра подвергнуть сжатию так, чтобы окружность основания преобразовалась в эллипс, то получим цилиндр, который называется эллиптическим цилиндром (рис. 142, б).
Так как окружность при параллельном проектировании изображается эллипсом, то изображения кругового и эллиптического цилиндров совпадают.
Цилиндр, образующие которого не перпендикулярны плоскостям его оснований, называется наклонным цилиндром (рис. 142, в).
Рис. 142
Рис. 143
Нам предстоит изучать лишь прямой круговой цилиндр, поэтому слова «прямой круговой» опускаем.
Поверхность, образованную вращением прямой, параллельной оси вращения, называют цилиндрической поверхностью вращения (рис. 143).
Уравнение x2 + y2 = r2 (r > 0) задаёт цилиндрическую поверхность вращения с осью вращения Oz и радиусом основания r. Из этого уравнения следует, что цилиндрическая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» в конце этой книги.)
17.2. Свойства цилиндра
а) Сечения цилиндра плоскостью. Так как цилиндр является телом вращения, то любое его перпендикулярное сечение есть круг, а перпендикулярное сечение боковой поверхности цилиндра — окружность; центры этих окружностей и кругов — точки пересечения секущих плоскостей и оси цилиндра (рис. 144).
Рис. 144
Рис. 145
Рис. 146
Рис. 147
Рис. 148
Если секущая плоскость пересекает ось цилиндра и не перпендикулярна ей, то в сечении может получиться эллипс (рис. 145) или его некоторая часть (рис. 146, 147). Это следует из того, что параллельной проекцией окружности на плоскость, не параллельную плоскости окружности, является эллипс. (Вспомните: наклонив цилиндрический стеклянный сосуд с водой, вы видите на поверхности воды эллипс или его часть.)
Сечение цилиндра плоскостью, проходящей через ось, называется осевым сечением цилиндра. Так как поворот пространства вокруг прямой на угол 180° является осевой симметрией относительно оси вращения, то ось прямого кругового цилиндра является его осью симметрии. Значит, осевым сечением цилиндра вращения является прямоугольник, стороны которого равны диаметру основания и образующей цилиндра (рис. 148). При этом все осевые сечения цилиндра — равные между собой прямоугольники.
Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром (рис. 149).
Так как все образующие цилиндра равны и параллельны друг другу, то любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра (рис. 150).
б) Изображение цилиндра. Чтобы построить изображение цилиндра, достаточно построить: 1) прямоугольник AВB1A1 и его ось OO1 (рис. 151); 2) два равных эллипса, центрами которых являются точки O и O1 и осями — отрезки АВ и A1В1. Выделив штрихами невидимые линии, получаем искомое изображение цилиндра.
Рис. 149
Рис. 150
Рис. 151
в) Касательная плоскость к цилиндру.
Определение. Плоскость, проходящая через образующую цилиндра перпендикулярно плоскости осевого сечения, проведённой через эту образующую, называется касательной плоскостью к цилиндру (рис. 152).
Рис. 152
Говорят, что плоскость α касается цилиндра (цилиндрической поверхности) по образующей DD1, каждая точка образующей DD1 является точкой касания плоскости α и данного цилиндра.
Через любую точку боковой поверхности цилиндра проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности цилиндра можно провести лишь одну плоскость, касательную к данному цилиндру в этой точке.
17.3. Развёртка и площадь поверхности цилиндра
Следует заметить, что развёртка поверхности вращения — понятие в определённой мере интуитивное. К тому же не для каждой поверхности тела вращения можно построить её развёртку. Иными словами, не каждую поверхность можно «развернуть» на плоскости. Например, не существует развёртки сферы (см. раздел «Дифференциальная геометрия» в конце этой книги).
Рис. 153
Развёртку цилиндра мы также введём на интуитивном уровне.
Пусть R — радиус основания, h — высота цилиндра.
Рис. 154
Рис. 155
Полная поверхность цилиндра состоит из его боковой поверхности и двух оснований — равных кругов. Если эту поверхность «разрезать» по образующей DD1 (рис. 153) и по окружностям оснований, затем боковую поверхность развернуть на плоскости, то получим развёртку полной поверхности цилиндра (рис. 154), состоящую из прямоугольника и двух равных кругов, касающихся противоположных сторон этого прямоугольника (рис. 155).
Попробуйте изготовить развёртку цилиндра и склеить из неё цилиндр.
За площадь боковой поверхности цилиндра принимается площадь её развёртки, т. е. площадь боковой поверхности цилиндра равна площади прямоугольника, у которого одна сторона равна длине окружности основания цилиндра, а другая сторона — высоте цилиндра:
Sбок = 2πRh.
Таким образом, доказана следующая теорема.
Теорема 26. Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту. ▼
Площадь круга радиуса R равна πR2, поэтому Sосн = πR2. Тогда для нахождения площади полной поверхность цилиндра справедливо:
Sполн = Sбок + 2Sосн = 2πRh + 2πR2 = 2πR(R + h).
Следствие. Пусть цилиндр образован вращением прямоугольника ABCD вокруг его высоты AD (рис. 156). Тогда
Sбок = 2πDC•BC. (1)
Рис. 156
Если EF — серединный перпендикуляр к образующей BC, проведённый из точки F оси l цилиндра, то EF = CD. Учитывая, что ВС = AD, получаем: Sбок = 2πEF•AD, т. е. боковая поверхность цилиндра равна произведению высоты цилиндра на длину окружности, радиус которой равен длине серединного перпендикуляра его образующей, проведённого из точки оcu цилиндра.
Это следствие найдёт своё применение в п. 19.7.
17.4. Призмы, вписанные в цилиндр и описанные около цилиндра
Нам предстоит решать задачи, в которых рассматриваются многогранники, вписанные в фигуры вращения и описанные около них.
Для правильного и наглядного изображения конфигураций из таких многогранников и фигур вращения необходимо верно изображать правильные многоугольники, вписанные в окружность (круг) или описанные около неё.
Определение. Призма называется вписанной в цилиндр, если основания призмы вписаны в основания цилиндра (рис. 157).
Рис. 157
Цилиндр в этом случае называют описанным около призмы.
Боковые рёбра призмы соединяют соответственные вершины её оснований, вписанных в основания цилиндра. Эти вершины лежат на окружностях оснований цилиндра. Образующие цилиндра соединяют соответственные точки окружностей его оснований и параллельны боковым рёбрам призмы. Следовательно, боковые рёбра вписанной в цилиндр призмы — образующие цилиндра.
Определение. Призма называется описанной около цилиндра, если основания призмы описаны около оснований цилиндра.
Рис. 158
Цилиндр при этом называют вписанным в призму (рис. 158).
Так как соответственные стороны оснований призмы параллельны друг другу и перпендикулярны радиусам оснований цилиндра, проведённым в точки касания, то плоскости боковых граней призмы являются касательными плоскостями к цилиндру: эти плоскости касаются поверхности цилиндра по образующим, соединяющим точки, в которых стороны оснований призмы касаются окружностей оснований цилиндра.
При изображении правильных призм, вписанных в цилиндр, следует руководствоваться алгоритмами построений изображений правильных многоугольников, вписанных в окружность.
Итак, для построения изображения правильной призмы, вписанной в цилиндр: 1) строим изображение цилиндра; 2) строим изображение правильного многоугольника, вписанного в верхнее основание цилиндра; 3) через вершины построенного вписанного многоугольника проводим образующие цилиндра; 4) в нижнем основании цилиндра последовательно соединяем концы этих образующих; 5) выделяем видимые и невидимые линии (отрезки) изображаемых фигур.
Рис. 159
На рисунке 159 изображены вписанные в цилиндр: призма, в основании которой прямоугольный треугольник (рис. 159, а); правильная четырёхугольная призма (рис. 159, б); правильная треугольная призма (рис. 159, в); правильная шестиугольная призма (рис. 159, г).
ЗАДАЧА (3.029). Диагональ осевого сечения равностороннего цилиндра равна a
Рис. 160
Решение. Рассмотрим случай а). Пусть в равносторонний цилиндр вписана правильная призма ABCA1B1C1 (рис. 160); CDD1C1 — осевое сечение; OO1 = h — высота цилиндра; ОС = R — радиус основания цилиндра.
Так как цилиндр — равносторонний, то CDD1C1 — квадрат, значит, высота цилиндра равна диаметру его основания. Тогда в квадрате СDD1С1 находим CD = 
Далее, △ АВС — правильный, вписанный в основание, радиус которого R = 





Sосн = 

S
бок = 3SABB1A1 = 3AB•BB1 = 3•

Тогда
Sполн = Sбок + 2Sосн = 


Ответ: a) 

Рис. 161
ЗАДАЧА (3.032). В равносторонний цилиндр, высота которого равна a, вписана правильная призма. Найти расстояние и угол между диагональю боковой грани призмы и осью цилиндра, если призма: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решение. Рассмотрим случай б). Пусть ABCDA1B1C1D1 — вписанная в цилиндр правильная призма (рис. 161). Найдём расстояние и угол между осью OO1 цилиндра и скрещивающейся с ней (почему?) диагональю АB1 боковой грани ABB1A1 данной призмы.
Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведёнными через эти прямые.
Если точка Е — середина отрезка AD, то расстояние между скрещивающимися прямыми AB1 и OO1 равно расстоянию между плоскостью грани ABB1A1 и параллельной ей (почему?) плоскостью сечения EFF1E1. Это расстояние равно длине отрезка ОK (где точка K — середина АВ), так как OK ⟂ (ABB1) и (ABB1) || (EFF1).
Поскольку данный цилиндр — равносторонний, то BDD1B1 — квадрат со стороной BD = ВВ1 = a. Тогда АВ = 



Обозначим ∠ (OO1; AB1) = ϕ, M = AB1 ∩ A1B. Для нахождения угла ϕ проведём в грани ABB1A1 прямую KK1 || OO1. Тогда ϕ = ∠ (OO1; AB1) = ∠ (KK1; AB1). Так как KK1 || OO1, OO1 ⟂ (ABC), то MK ⟂ AB. Поэтому △ АKМ — прямоугольный. В этом треугольнике АK = 




Ответ: б) 


Действительно, Sбок. пов. призм = h•Pосн. призм, где Росн. призм — периметр основания призмы, h — длина её высоты. Для правильных вписанных в цилиндр призм h — постоянная величина, равная длине высоты цилиндра, а предел последовательности периметров правильных многоугольников, вписанных в окружность (основание цилиндра), равен длине этой окружности. Таким образом, мы вновь получаем: Sбок = 2πRh.
17.5. Объём цилиндра
Напомним принятое нами соглашение, основанное на принципе Кавальери.
«Пусть даны два тела и плоскость. Если каждая плоскость, параллельная данной плоскости и пересекающая одно из данных тел, пересекает также и другое, причём площади сечений, образованных при пересечении обоих тел, относятся как m : n, то и объёмы этих тел относятся как m : n».
Рис. 162
Расположим цилиндр, имеющий высоту h и радиус основания R, и прямоугольный параллелепипед с рёбрами h, R, R так, чтобы их основания находились на двух параллельных плоскостях, расстояние между которыми равно h (рис. 162). Каждая плоскость, параллельная данным плоскостям и пересекающая цилиндр, пересекает также прямоугольный параллелепипед, причём площади образованных при пересечении обоих тел сечений относятся как π•R2 : R2 = π : 1. Тогда и для объёмов этих тел справедливо: Vцил : Vпарал = π : 1 или Vцил : (R2•h) = π : 1, откуда
Vцил = π•R2•h.
Если цилиндр высотой h пересечь плоскостью, параллельной его оси, то этот цилиндр разобьётся на два тела (рис. 163). Объёмы этих тел относятся как площади сегментов, образовавшихся в основании цилиндра (докажите это на основании принципа Кавальери). Следовательно, объём каждого из этих тел может быть вычислен по формуле
V = Sсегм•h.
Рис. 163
Рис. 164
Любая плоскость, проведённая через середину оси цилиндра, разбивает этот цилиндр на два равновеликих тела (рис. 164), объём V каждого из которых равен половине объёма данного цилиндра, т. е. V = 
Попробуйте, исходя из этой формулы, доказать, что в таком случае объём каждой части цилиндра (см. рис. 164) может быть вычислен по формуле:
V= 
где a и b — длины отрезков, на которые образующая цилиндра делится секущей плоскостью.
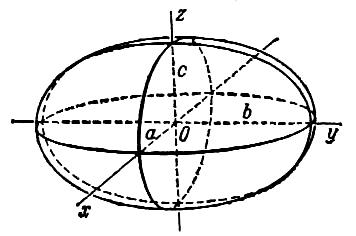
Эллипсоидом
называется поверхность, которая в некоторой
системе декартовых прямоугольных координат
определяется уравнением
(1).
Уравнение (1) называется каноническим
уравнением эллипсоида. Величины a,
b, c суть полуоси эллипсоида (рис. 1). Если все
они различны, эллипсоид называется трехосным; в
случае, когда какие-нибудь две из них одинаковы,
эллипсоид называется вытянутым, при a=b>c – сжатым. В случае, когда a=b=c, эллипсоид представляет
собой сферу.
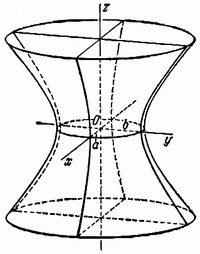
Гиперболоидами называются
поверхности, которые в некоторой системе
декартовых прямоугольных координат
определяются уравнениями
, (2)
. (3)
Гиперболоид, определяемый уравнением
(2), называется однополостным (рис. 2); гиперболоид,
определяемый уравнением (3), – двуполостным (рис. 3);
уравнения (2) и (3) называются каноническими
уравнениями соответствующих гиперболоидов.
Величины a, b, c называются
полуосями гиперболоида. В случае однополостного
гиперболоида, заданного уравнением (2), только
первые из них (а и b) показаны
на рис. 2. В случае двуполостного гиперболоида,
заданного уравнением (3), одна из них (именно, с)
показана на рис. 3. Гиперболоиды, определяемые
уравнениями (2) и (3), при a=b
являются поверхностями вращения.
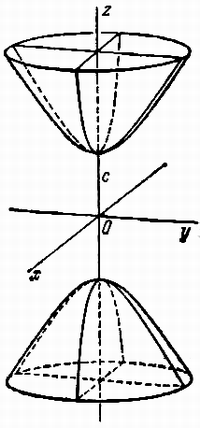
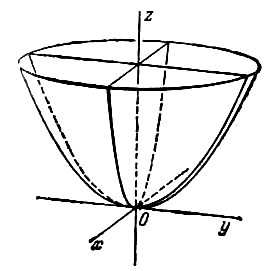
Параболоидами называются поверхности,
которые в некоторой системе декартовых
прямоугольных координат определяются
уравнениями
, (4)
, (5)
где p и q – положительные числа,
называемые параметрами параболоида. Параболоид,
определяемый уравнением (4), называется
эллиптическим (рис. 4); параболоид, определяемый
уравнением (5), – гиперболическим (рис. 5). Уравнения
(4) и (5) называют каноническими уравнениями
соответствующих параболоидов. В случае, когда p=q, параболоид, определяемый
уравнением (4), является поверхностью вращения
(вокруг Oz).
Рассмотрим теперь преобразование
пространства, которое называется равномерным
сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость;
обозначим ее буквой
. Зададим, кроме
того, некоторое положительное число q. Пусть М – произвольная точка
пространства, не лежащая на плоскости
,
– основание
перпендикуляра, опущенного на плоскость
из точки М. Переместим точку М по прямой
в
новое положение
так, чтобы имело
место равенство
и чтобы после перемещения точка
осталась с той же стороны от плоскости
,
где она была первоначально (рис. 6). Точно так же мы
поступим со всеми точками пространства, не
лежащими на плоскости
; точки, которые
расположены на плоскости
, оставим на своих
местах. Таким образом, все точки пространства, за
исключением тех, что лежат на плоскости
,
переместятся; при этом расстояние от каждой
точки до плоскости
изменится в
некоторое определенное число раз, общее для всех
точек. Описываемое сейчас перемещение точек
пространства называется его равномерным сжатием
к плоскости
; число q
носит название коэффициента сжатия.
Пусть дана некоторая поверхность F; при равномерном сжатии
пространства точки, которые ее составляют,
переместятся и в новых положениях сотавят
поверхность F’. Будем
говорить, что поверхность F’
получено из F в результате
равномерного сжатия пространства. Оказывается,
что многие поверхности второго порядка (все,
кроме гиперболического параболоида) можно
получить в результате равномерного сжатия из
поверхностей вращения).
ПРИМЕР. Доказать, что произвольный
трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных
равномерных сжатий пространства к координатным
плоскостям: к плоскости Oxy с
коэффициентом сжатия
и к плоскости Oxz с коэффициентом сжатия
.
ДОКАЗАТЕЛЬСТВО. Пусть производится
равномерное сжатие пространства к плоскости Oxy с коэффициентом
и
пусть
– точка, в которую переходит при этом
точка
. Выразим координаты x’,
y’, z’ точки М’ через координаты x, y, z точки М. Так как прямая MM’ перпендикулярна к плоскости Oxy, то x’=x, y’=y.
С другой стороны, так как расстояние от точки М’
до плоскости Oxy равно
расстоянию от точки М до этой плоскости,
умноженному на число
, то
.
Таким образом, мы получаем искомые
выражения:
,
,
(6)
или
,
,
(7)
Предположим, что M(x; y; z)
– произвольная точка сферы
.
Заменим здесь x, y, z
их выражениями (7); получим
,
откуда
.
Следовательно, точка M’(x’;
y’; z’) лежит на эллипсоиде вращения.
Аналогично, мы должны осуществить сжатие
пространства к плоскости Oxz
по формулам
,
,
;
тогда получим трехосный эллипсоид и
именно тот, уравнение которого дано в условии
задачи.
Отметим еще, что однополостный
гиперболоид и гиперболический параболоид суть
линейчатые поверхности, то есть они состоят из
прямых; эти прямые называются прямолинейными
образующими указанных поверхностей.
Однополостный гиперболоид
имеет две системы прямолинейных
образующих, которые определяются уравнениями:
,
;
,
,
где
и
– некоторые
числа, не равные одновременно нулю.
Гиперболический параболоид
также имеет две системы прямолинейных
образующих, которые определяются уравнениями
,
;
,
.
Конической поверхностью, или конусом,
называется поверхность, которая описывается
движущейся прямой (образующей) при условии, что
эта прямая проходит через постоянную точку S и пересекает некоторую
определенную линию L. Точка S называется вершиной конуса;
линия L – направляющей.
Цилиндрической поверхностью, или
цилиндром, называется поверхность, которая
описывается движущейся прямой (образующей) при
услвоии, что эта прямая имеет постоянное
направление и пересекает некоторую определенную
линию L (направляющую).
6.2. Цилиндрические поверхности
Или цилиндры. Под цилиндром также понимают геометрическое тело.
И это не совсем то, что обычно подразумевает обыватель – класс цилиндрических поверхностей не ограничивается чёрным цилиндром на голове:
Задача 167
Построить поверхность, заданную уравнением
…что за дела?! Не опечатка ли здесь? Вроде как дано уравнение эллипса…

Нет, здесь не опечатка и все дела происходят именно в пространстве! Исследуем предложенную поверхность тем же методом, что использовали для плоскостей. Перепишем уравнение в виде , из которого следует, что «зет» принимает любые значения. Зафиксируем
и построим в плоскости
эллипс
. Так как «зет» принимает все значения, то построенный эллипс непрерывно «тиражируется» вверх и вниз до бесконечности.
Данная поверхность называется эллиптическим цилиндром. Эллипс (на любой высоте) называется направляющей цилиндра, а параллельные прямые, проходящие через каждую точку эллипса называются образующими цилиндра (которые в прямом смысле слова его и образуют).
Ось является осью симметрии поверхности (но не её частью!).
Координаты любой точки, принадлежащей данной поверхности, обязательно удовлетворяют уравнению .
Пространственное неравенство задаёт «внутренность» бесконечной «трубы», включая саму цилиндрическую поверхность, и, соответственно, противоположное неравенство
определяет множество точек вне цилиндра.
В практических задачах наиболее популярен частный случай, когда направляющей цилиндра является окружность:
Задача 168
Построить поверхность, заданную уравнением
Бесконечную «трубу» изобразить невозможно, поэтому художества ограничиваются, как правило, «обрезком».

Сначала удобно построить окружность радиуса в плоскости
, а затем ещё пару окружностей сверху и снизу.
Полученные окружности (направляющие цилиндра) аккуратно соединяем 4 параллельными прямыми (образующими цилиндра):
Не забываем использовать пунктир для невидимых нам линий!
Координаты любой точки, принадлежащей данному цилиндру, удовлетворяют уравнению . Координаты любой точки, лежащей строго внутри «трубы», удовлетворяют неравенству
, а неравенство
задаёт множество точек внешней части. Для лучшего понимания рекомендую рассмотреть несколько конкретных точек пространства и убедиться в этом самостоятельно.
Часто эту поверхность некорректно называют круговым цилиндром. Круглым! Круговой цилиндр, строго говоря – есть тело, по той причине, что его направляющей является круг. И тело, кстати, определяется неравенством .
Задача 169
Построить поверхность и найти её проекцию на плоскость
Перепишем уравнение в виде , из которого следует, что «икс» принимает любые значения. Зафиксируем
и в плоскости
изобразим окружность
– с центром в начале координат, единичного радиуса. Так как «икс» непрерывно принимает все значения, то построенная окружность порождает цилиндр с осью симметрии
. Рисуем ещё одну окружность (направляющую цилиндра) и аккуратно соединяем их прямыми (образующими цилиндра). Местами получились накладки, но что делать, такой уж наклон:

На этот раз я ограничился кусочком цилиндра на промежутке и это не случайно. На практике зачастую и требуется изобразить лишь небольшой фрагмент поверхности.
Тут, к слову, получилось 6 образующих – две дополнительные прямые «закрывают» поверхность с левого верхнего и правого нижнего углов.
Теперь разбираемся с проекцией цилиндра на плоскость . Многие читатели понимают, что такое проекция, но, тем не менее, проведём очередную физкульт-пятиминутку:
Пожалуйста, встаньте и склоните голову над чертежом так, чтобы остриё оси смотрело перпендикулярно вам в лоб. То, чем с этого ракурса кажется цилиндр – и есть его проекция на плоскость
. А кажется он бесконечной полосой, заключенным между прямыми
, включая сами прямые. Данная проекция – это в точности область определения функций
(верхний «жёлоб» цилиндра),
(нижний «жёлоб»).
Давайте заодно проясним ситуацию и с проекциями на другие координатные плоскости. Пусть лучи солнца светят на цилиндр со стороны острия и вдоль оси . Тенью (проекцией) цилиндра на плоскость
является аналогичная бесконечная полоса – часть плоскости
, ограниченная прямыми
(
– любое), включая сами прямые.
А вот проекция на плоскость несколько иная. Если смотреть на цилиндр из острия оси
, то он спроецируется в окружность (не круг!) единичного радиуса
, с которой мы начинали построение.
Задача 170
Построить поверхность и найти её проекции на координатные плоскости
Это задача для самостоятельного решения. Если условие не очень понятно, возведите обе части в квадрат и проанализируйте результат – выясните, какую именно часть цилиндра задаёт функция . Используйте методику построения, неоднократно применявшуюся выше. Краткое решение, чертёж и комментарии в конце книги.
Цилиндрические поверхности могут быть смещены относительно координатных осей, например:
– данное уравнение (по знакомым мотивам линий 2-го порядка) задаёт цилиндр единичного радиуса с линией симметрии, проходящей через точку
параллельно оси
.
Однако на практике подобные цилиндры попадаются довольно редко, и совсем уж невероятно встретить «косую» относительно координатных осей цилиндрическую поверхность.
Параболические цилиндры
Как следует из названия, направляющей такого цилиндра является парабола.
Задача 171
Построить поверхность и найти её проекции на координатные плоскости.
Не мог удержаться от этого примера =)
Решение: идём проторенной тропой. Перепишем уравнение в виде , из которого следует, что «зет» может принимать любые значения. Зафиксируем
и построим обычную параболу
на плоскости
, предварительно отметив тривиальные опорные точки
. Поскольку «зет» принимает все значения, то построенная парабола непрерывно «тиражируется» вверх и вниз до бесконечности. Откладываем такую же параболу, скажем, на высоте (в плоскости)
и аккуратно соединяем их параллельными прямыми (образующими цилиндра):
Напоминаю полезный технический приём: если изначально нет уверенности в качестве чертежа, то линии сначала лучше прочертить тонко-тонко карандашом. Затем оцениваем качество эскиза, выясняем участки, где поверхность скрыта от наших глаз, и только потом придаём нажим грифелю.
Теперь вторая часть задания, отыскание проекций:
1) Проекцией цилиндра на плоскость является парабола
.
2) Проекция цилиндра на плоскость представляет собой полуплоскость
, включая ось
3) И, наконец, проекцией цилиндра на плоскость является вся плоскость
.
Тренируемся самостоятельно:
Задача 172
Построить параболические цилиндры:
а) , ограничиться фрагментом поверхности в ближнем полупространстве;
б) на промежутке
В случае затруднений не спешим и рассуждаем по аналогии с предыдущими примерами, благо, технология досконально отработана. Не критично, если поверхности будут получаться немного корявыми – важно правильно отобразить принципиальную картину.
Я и сам особо не заморачиваюсь над красотой линий – если получился сносный чертёж «на троечку», обычно не переделываю. В образце решения, кстати, использован ещё один приём, позволяющий улучшить качество чертежа 😉
Гиперболические цилиндры
Направляющими таких цилиндров являются гиперболы.

Этот тип поверхностей, по моим наблюдениям, встречается значительно реже, и поэтому я ограничился единственным схематическим чертежом гиперболического цилиндра .
Принцип рассуждения здесь точно такой же – обычная «школьная» гипербола из плоскости
непрерывно «размножается» вверх и вниз до бесконечности.
Переходим к следующей поверхности:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Цилиндры второго порядка их уравнения
3.5.6. Цилиндры второго порядка
В заключение обзора поверхностей второго порядка отметим еще случай, когда в уравнении отсутствует какая-нибудь координата. Такое уравнение определяет Цилиндрическую поверхность второго порядка (или Цилиндр) с образующими, параллельными той оси, координата которой в уравнении отсутствует.
Так, поверхность, заданная уравнением
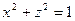
Является цилиндром с образующими, параллельными оси OY. Сечением цилиндра плоскостью XOZ является окружность с центром в начале координат и радиусом, равным единице
(рис. 16). Заметим, что уравнение цилиндра не отличается от уравнения окружности, называемой Направляющей для данного цилиндра.
Среди цилиндров, образующие которых параллельны оси OZ различают цилиндры следующих типов:

При 
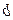
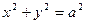
Б) гиперболический цилиндр

В) параболические цилиндры
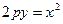
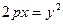
Тип цилиндра зависит от вида направляющей цилиндра в плоскости XOY (рис. 17)
Цилиндры второго порядка их уравнения
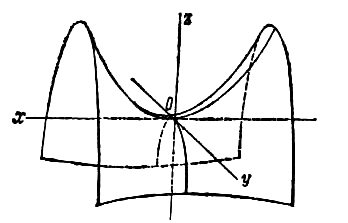
С помощью векторов мы ввели понятие пространства и его размерности, в частности трехмерного. Рассмотрим в нем поверхности, которые «похожи» на поверхности, образованные вращением кривой второго порядка вокруг ее оси симметрии. Например, сфера может быть получена вращением окружности вокруг диаметра. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d. Наряду с такими поверхностями мы встретимся и с более сложными случаями.
Пусть в пространстве задана прямоугольная декартова система координат.
Поверхность второго порядка – геометрическое место точек, декартовы прямоугольные координаты которых, удовлетворяют уравнению вида
в котором хотя бы один из коэффициентов 
Уравнение (2.48) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую поверхность второго порядка. В зависимости от значений коэффициентов общего уравнения (2.48) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из канонических видов, каждому из которых соответствует определённый класс поверхностей второго порядка. Среди них выделяют пять основных классов поверхностей: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из этих поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением.
Перечисленные поверхности второго порядка относятся к так называемым нераспадающимся поверхностям второго порядка. Можно говорить о случаях вырождения – распадающихся поверхностях второго порядка, к которым относятся: пары пересекающихся плоскостей, пары мнимых пересекающихся плоскостей, пары параллельных плоскостей, пары мнимых параллельных плоскостей, пары совпадающих плоскостей.
Наша цель – указать канонические уравнения для поверхностей второго порядка и показать, как выглядят эти поверхности.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется эллипсоидом (рис. 2.22) .
1. Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что 
· центральной симметрией относительно начала координат,
· осевой симметрией относительно координатных осей,
· плоскостной симметрией относительно начала координат.
3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс (см. рис. 2.22).

Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей.
Примечание. Сфера является частным случаем эллипсоида при а= b =с. Тогда все равные полуоси обозначают R и уравнение (2.49) после умножения на R 2 принимает вид 
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется эллиптическим параболоидом (рис. 2.23) .
1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.
2. Эллиптический параболоид обладает
· осевой симметрией относительно оси 0z ,
· плоскостной симметрией относительно координатных осей 0xz и 0yz .
3. В сечении эллиптического параболоида плоскостью, ортогональной оси 0z , получается эллипс, а плоскостями, ортогональными осям 0x и 0y –парабола. (см. рис. 2.23).
Можно получить эллиптический параболоид симметричный относительно оси 0х или 0у, для чего нужно в уравнении (2.50) поменять между собой переменные х и z или у и z соответственно.
Если полуоси равны a = b , то параболоид называется параболоидом вращения и может быть получен вращением параболы вокруг ее оси симметрии. При этом в сечении параболоида вращения плоскостью, перпендикулярной оси 0z , получается окружность.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется гиперболическим параболоидом (рис . 2.24).
Свойства гиперболического параболоида.
1. Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
2. Гиперболический параболоид обладает
· осевой симметрией относительно оси 0z ,
· плоскостной симметрией относительно координатных плоскостей 0xz и 0yz .
4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.
5. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется однополостным гиперболоидом (рис. 2.25) .
Свойства однополостного гиперболоида.
1. Однополостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
2. Однополостный гиперболоид обладает
· центральной симметрией относительно начала координат,
· осевой симметрией относительно всех координатных осей,
· плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z , получается эллипс, а плоскостями, ортогональными осям 0x и 0y, – гипербола (см. рис. 2.25).
Если в уравнении (2.52) a = b , то сечения однополостного гиперболоида плоскостями, параллельными плоскости ху, являются окружностями. В этом случае поверхность называется однополостным гиперболоидом вращения.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется двуполостным гиперболоидом (рис. 2.26) .
1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что | z |≥ c и неограничен сверху.
2. Двуполостный гиперболоид обладает
· центральной симметрией относительно начала координат,
· осевой симметрией относительно всех координатных осей,
· плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z , при | z |> c получается эллипс, при | z |= c – точка, а в сечении плоскостями, перпендикулярными осям 0x и 0y , – гипербола (см. рис. 2.26).
Если в уравнении (2.53) a = b , то сечения двуполостного гиперболоида плоскостями, параллельными плоскости ху, являются окружностями. В этом случае поверхность называется двуполостным гиперболоидом вращения.
Примечание. Если уравнение поверхности в прямоугольной системе координат имеет вид: F ( x 2 + y 2 ; z )=0, то эта поверхность – поверхность вращения с осью вращения 0z. Аналогично: F ( x 2 + z 2 ; y )=0 – поверхность вращения с осью вращения 0у, F ( z 2 + y 2 ; x )=0 – с осью вращения 0х
С учетом данного примечания могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси 0х или 0у.
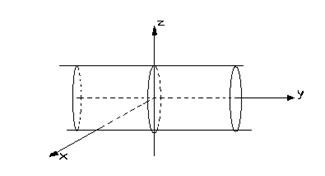
Цилиндрическая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и остающейся параллельной своему исходному положению. Множество прямолинейных образующих представляет собой непрерывный каркас цилиндрической поверхности. Через каждую точку поверхности проходит одна прямолинейная образующая. Неподвижная кривая, по которой скользит образующая, называется направляющей. Если направляющая линия является кривой второго порядка, то и цилиндрическая поверхность – второго порядка.
Если уравнение поверхности не содержит в явном виде какой–либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.
Достаточно нарисовать на плоскости ху направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси 0z. Для наглядности следует построить также одно–два сечения плоскостями, параллельными плоскости ху. В каждом таком сечении получим такую же кривую, как и исходная направляющая. Аналогично поступают, рассматривая направляющую в плоскости хz или уz.
Цилиндрическая поверхность является бесконечной в направлении своих образующих. Часть замкнутой цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется цилиндром, а фигуры сечения – его основаниями. Сечение цилиндрической поверхности плоскостью, перпендикулярной ее образующим, называется нормальным. В зависимости от формы нормального сечения цилиндры бывают:
1) эллиптические – нормальное сечение представляет собой эллипс (рис. 2.27а), каноническое уравнение
2) круговые – нормальное сечение круг, при a = b = r уравнение
3) гиперболические – нормальное сечение гипербола (рис. 2.27б), каноническое уравнение
4) параболические – нормальное сечение парабола (рис. 2.27в), каноническое уравнение
5) общего вида – нормальное сечение кривая случайного вида.
Если за основание цилиндра принимается его нормальное сечение, цилиндр называют прямым (рис. 2.27). Если за основание цилиндра принимается одно из косых сечений, цилиндр называют наклонным. Например, наклонные сечения прямого кругового цилиндра являются эллипсами. Наклонные сечения прямого эллиптического цилиндра в общем случае – эллипсы. Однако его всегда можно пересечь плоскостью, наклонной к его образующим, таким образом, что в сечении получится круг.
Конической поверхностью называется поверхность, производимая движением прямой, перемещающейся в пространстве так, что она при этом постоянно проходит через неподвижную точку и пересекает данную линию. Данная прямая называется образующей, линия – направляющей, а точка – вершиной конической поверхности (рис. 2.28).
Конусом называется тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины, и плоскостью, пересекающей все образующие по ту же сторону от вершины. Часть конической поверхности, ограниченная этой плоскостью, называется боковой поверхностью, а часть плоскости, отсекаемая боковой поверхностью, – основанием конуса. Перпендикуляр, опущенный из вершины на плоскость основания, называется высотой конуса.
Конус называется прямым круговым, если его основание есть круг, а высота проходит через центр основания. Такой конус можно рассматривать как тело, происходящее от вращения прямоугольного треугольника, вокруг катета как оси. При этом гипотенуза описывает боковую поверхность, а катет – основание конуса.
В курсе геометрии общеобразовательной школы рассматривается только прямой круговой конус, который для краткости называется просто конусом.
Если вершина конуса расположена в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат, то уравнение эллиптического конуса имеет вид:
При а = b конус становится круговым.
Примечание. По аналогии с коническими сечениями (аналогично теореме 2.1) существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x 2 = 0 описывается пара совпадающих плоскостей, уравнением x 2 = 1 – пара параллельных плоскостей, уравнением x 2 – y 2 = 0 – пара пересекающихся плоскостей. Уравнение x 2 + y 2 + z 2 = 0 описывает точку с координатами (0;0;0). Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии
Поверхности второго порядка: их виды, уравнения, примеры
Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат
Общее уравнение поверхности второго порядка имеет вид
Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:
Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:
В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.
Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому
I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.
Эллипсоид
Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.
После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

Тогда полуоси эллипсоида будут



Поэтому каноническое уравнение эллипсоида имеет вид

Мнимый эллипсоид
Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:




Мнимый конус
Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:




Однополостный гиперболоид
Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:




то каноническое уравнение однополостного гиперболоида будет иметь вид

Двуполостный гиперболоид
Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.
Конус
Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.
Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

известном как каноническое уравнение конуса.
II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический параболоид
Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.
Общее уравнение можно переписать в виде:

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая


получим каноническое уравнение эллиптического параболоида:

Гиперболический параболоид
Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.
Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем 



получим каноническое уравнение гиперболического параболоида:

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический цилиндр
Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



получим каноническое уравнение эллиптического цилиндра:

Мнимый эллиптический цилиндр
Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.
Мнимые пересекающиеся плоскости
Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



получим каноническое уравнение мнимых пересекающихся плоскостей:

Гиперболический цилиндр
Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



Таким образом, каноническое уравнение гиперболического цилиндра:

Пересекающиеся плоскости
Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



Таким образом, пересекающихся плоскостей:

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.
Параболический цилиндр
Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:


Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:


Параллельные плоскости
Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

перепишем его в виде

Мнимые параллельные плоскости
Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

перепишем его в виде

Совпадающие плоскости
Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

Решение примеров на определение вида поверхности второго порядка
Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :

I 1 = 1 + 5 + 1 = 7 ,
Следовательно, данная поверхность — однополостный гиперболоид.

Составляем и решаем характеристическое уравнение:






Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :


Следовательно, общее уравнение определяет эллиптический параболоид.

I 1 = 2 + 2 + 3 = 7 .
Решаем характеристическое уравнение:





Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением



I 1 = 5 + 2 + 5 = 12 .
Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.


Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение
Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Поверхности второго порядка. Цилиндрические поверхности.
Поверхность S называется цилиндрической поверхностью с образующей 
этой поверхности прямая, проходящая через эту точку параллельно образующей 
Теорема (об уравнении цилиндрической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность 
уравнение f(x,y)=0, то S — цилиндрическая поверхность с образующей, параллельной оси OZ.
Кривая, задаваемая уравнением f(x,y)=0 в плоскости z=0, называется направляющей цилиндрической
поверхности.
Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность
называется цилиндрической поверхностью второго порядка.
источники:
http://function-x.ru/surfaces_of_the_second_order.html
http://www.calc.ru/Poverkhnosti-Vtorogo-Poryadka-Tsilindricheskiye-Poverkhnosti.html