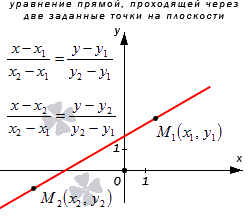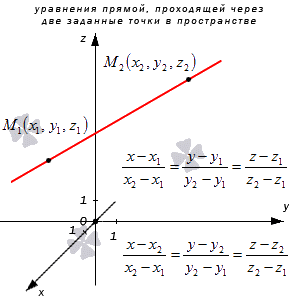Уравнение прямой, которая проходит через две заданные точки: примеры, решения
Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.
Уравнение прямой, проходящей через две заданные точки на плоскости
Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.
Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.
Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.
В каноническом уравнении прямой на плоскости, имеющего вид x — x 1 a x = y — y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .
Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .
Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 — x 1 , y 2 — y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 .
Рассмотрим рисунок, приведенный ниже.
Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ .
Рассмотрим подробней на решении нескольких примеров.
Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 — 5 , 2 3 , M 2 1 , — 1 6 .
Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . По условию задачи имеем, что x 1 = — 5 , y 1 = 2 3 , x 2 = 1 , y 2 = — 1 6 . Необходимо подставить числовые значения в уравнение x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . Отсюда получим, что каноническое уравнение примет вид x — ( — 5 ) 1 — ( — 5 ) = y — 2 3 — 1 6 — 2 3 ⇔ x + 5 6 = y — 2 3 — 5 6 .
Ответ: x + 5 6 = y — 2 3 — 5 6 .
При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.
Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .
Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x — 1 4 — 1 = y — 1 2 — 1 ⇔ x — 1 3 = y — 1 1 .
Приведем каноническое уравнение к искомому виду, тогда получим:
x — 1 3 = y — 1 1 ⇔ 1 · x — 1 = 3 · y — 1 ⇔ x — 3 y + 2 = 0
Ответ: x — 3 y + 2 = 0 .
Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x — x 1 = 0 .
Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .
Для этого найдем k = y 2 — y 1 x 2 — x 1 b = y 1 — y 2 — y 1 x 2 — x 1 · x 1 или k = y 2 — y 1 x 2 — x 1 b = y 2 — y 2 — y 1 x 2 — x 1 · x 2 .
С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 1 или y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 2 .
Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.
Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .
Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( — 7 , — 5 ) и M 2 ( 2 , 1 ) .
Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что — 5 = k · ( — 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему — 5 = k · — 7 + b 1 = k · 2 + b и решим.
При подстановке получаем, что
— 5 = k · — 7 + b 1 = k · 2 + b ⇔ b = — 5 + 7 k 2 k + b = 1 ⇔ b = — 5 + 7 k 2 k — 5 + 7 k = 1 ⇔ ⇔ b = — 5 + 7 k k = 2 3 ⇔ b = — 5 + 7 · 2 3 k = 2 3 ⇔ b = — 1 3 k = 2 3
Теперь значения k = 2 3 и b = — 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x — 1 3 .
Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.
Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( — 7 , — 5 ) , имеющее вид x — ( — 7 ) 2 — ( — 7 ) = y — ( — 5 ) 1 — ( — 5 ) ⇔ x + 7 9 = y + 5 6 .
Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x — 1 3 .
Ответ: y = 2 3 x — 1 3 .
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.
Имеем, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .
Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , в свою очередь параметрические x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ z = z 1 + ( z 2 — z 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ z = z 2 + ( z 2 — z 1 ) · λ .
Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.
Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , — 3 , 0 ) и M 2 ( 1 , — 3 , — 5 ) .
Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 .
По условию имеем, что x 1 = 2 , y 1 = — 3 , z 1 = 0 , x 2 = 1 , y 2 = — 3 , z 2 = — 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:
x — 2 1 — 2 = y — ( — 3 ) — 3 — ( — 3 ) = z — 0 — 5 — 0 ⇔ x — 2 — 1 = y + 3 0 = z — 5
Ответ: x — 2 — 1 = y + 3 0 = z — 5 .
Как составить уравнение диагонали по заданным точкам
Неверно введено число.
Точки должны быть разными.
Уравнение прямой по двум точкам
Введите координаты точек:
Количество знаков после разделителя дроби в числах:
Общее уравнение прямой:
Теория
Уравнение прямой, проходящей через две заданные точки (x1,y1) и (x2,y2), имеет вид:
или в общем виде
Т.е. получили общее уравнение прямой линии на плоскости в декартовых координатах:
Составить уравнение диагоналей квадрата ABCD, заданного точками A(1 ; 1), B(4 ; 2), C(5 : — 1), D(2 ; — 2)?
Математика | 10 — 11 классы
Составить уравнение диагоналей квадрата ABCD, заданного точками A(1 ; 1), B(4 ; 2), C(5 : — 1), D(2 ; — 2).
Диагонали прямоугольника ABCD пересекаются в точке О?
Диагонали прямоугольника ABCD пересекаются в точке О.
Найдите угол между диагоналями, если угол АВО = 30 градусам.
В прямоугольнике ABCD известно, что АВ = а, ВС = b, О — точка пересечения диагоналей?
В прямоугольнике ABCD известно, что АВ = а, ВС = b, О — точка пересечения диагоналей.
Начерти квадрат ABCD со стороной 4 см 5 мм проведи его диагонали точку пересечения диагоналей обозначь буквой о?
Начерти квадрат ABCD со стороной 4 см 5 мм проведи его диагонали точку пересечения диагоналей обозначь буквой о!
Точки а ( — 3 3) и в (4 1) — вершины квадрата abcd?
Точки а ( — 3 3) и в (4 1) — вершины квадрата abcd.
Периметр квадрата равен :
Записать координаты вершин А, В, С параллелограмма ABCD, найти координаты вершины D и точки О (пересечения диагоналей параллелограмма)?
Записать координаты вершин А, В, С параллелограмма ABCD, найти координаты вершины D и точки О (пересечения диагоналей параллелограмма).
Записать уравнение стороны АВ и высоты СН.
Из точки O пересечения диагоналей квадрата ABCD к его плоскости восстановлен перпендикуляр OM так, что угол OBM равен 60 градусов?
Из точки O пересечения диагоналей квадрата ABCD к его плоскости восстановлен перпендикуляр OM так, что угол OBM равен 60 градусов.
Найдите косинус угла ABM.
В параллелограмме abcd точка e середина стороны bc отрезок ae пересекает диагональ bd в точке f?
В параллелограмме abcd точка e середина стороны bc отрезок ae пересекает диагональ bd в точке f.
Сторона квадрата равна 4 сантиметра точка равноудалена от всех вершин квадрата находится на расстоянии 6 сантиметров от точки пересечения диагоналей Найдите расстояние от точки до вершины квадрата?
Сторона квадрата равна 4 сантиметра точка равноудалена от всех вершин квадрата находится на расстоянии 6 сантиметров от точки пересечения диагоналей Найдите расстояние от точки до вершины квадрата.
Две противоположные вершины квадрата находятся в точках А( — 1 ; 1) С(5 ; 3) Составьте уравнение сторон и диагоналей этого квадрата АВСД Решите плизз?
Две противоположные вершины квадрата находятся в точках А( — 1 ; 1) С(5 ; 3) Составьте уравнение сторон и диагоналей этого квадрата АВСД Решите плизз.
Диагоналей прямоугольника ABCD пересекаются в точке О угол ABO равен 40° найдите углы между диагоналями?
Диагоналей прямоугольника ABCD пересекаются в точке О угол ABO равен 40° найдите углы между диагоналями.
Вы перешли к вопросу Составить уравнение диагоналей квадрата ABCD, заданного точками A(1 ; 1), B(4 ; 2), C(5 : — 1), D(2 ; — 2)?. Он относится к категории Математика, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
0. 4 * 1000 = 400. Т. к. В 1 километре содержится 1000 метров.
1 км = 1000 м 1000 м : 5·2 = 200·2 = 400 м или 1000 м · ² / ₅ = 400 м.
Условие 1ширина — 8 см 1длина — ? На1 см меньше 2ширина — ? 2 длина — ? S1 — ? S2 — ? P1 = p2 решение 8 — 1 = 7 см длина 1 (8 + 7) * 2 = 30 см p1 = p2 30 : 4 = 7, 2 см стороны 2 30 * 30 = 900 см s1 7, 2 * 7, 2 = 5184 см s2.
1 дм = 10 см. Длина прямоугольника — 10 + 8 = 18(см) Перимети прямоугольника — (18 + 8)×2 = 52(см) Сторона квадрата — 52 : 4 = 13(см) Площадь прямоугольника — 18×8 = 144(см2) Площадь квадрата — 13×13 = 169(см2) Если удовлетворил ответ, прошу постави..
Мода = 2. 1 мода = 3, 5 мода = НИЧЕГО мода = 6. 1 и 7. 5 мода 0. 6.
1) 1. 7 — 1 = 6 2. 3 1 / 5 — 1 / 5 = 3 3. 15. 9 — 0. 6 = 15. 3 4. 20 — 0. 4 = 19. 6 2) 1. Мода = 2. 1 ; 2. Мода = 3. 5 ; 3. Моды нет ; 4. Мода = 7. 5 ; 5. Мода = 0. 6 ;..
57 : 3 • 4 = 76 1. 57 : 3 = 19 ; 2. 19 • 4 = 76 Ответ : 76 24 • 3 : 6 = 12 1. 24 • 3 = 72 ; 2. 72 : 6 = 12 Ответ : 12.
57 : 3 * 4 = 76 ; 24 * 3 : 6 = 12 ;..
S = ab 2дм = 40см. 4дм = 40 см. S = 20 * 40 = 800.
источники:
http://www.math.by/geometry/eqline.html
http://matematika.my-dict.ru/q/1722212_sostavit-uravnenie-diagonalej-kvadrata-abcd-zadannogo/
igycousceved290
Вопрос по математике:
Составить уравнение диагоналей квадрата ABCD, заданного точками A(1;1), B(4;2), C(5:-1), D(2;-2).
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
kinglychery647
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
<span>Тигр например-треугольник,слон-квадрат,собаки-круг и все они животные-овал.В овале находится внутри круг,квадрат и треугольник.Подмножествами являются круг,квадрат и треугольник.
Я думаю так</span>
1) 300-110=190 кг свеклы продали
2) 200-70=130 кг лука продали
3) 190-130=60 кг свеклы продали больше чем лука
4*2=8 см равен диаметр
1)9*8/5=14,4(кг) мёда
2)15*8/5=24(кг)мёда
Если не ошибаюсь вроде так com=64
Решение типового варианта контрольной работы. Аналитическая геометрия.
Задача №1.
Даны три последовательные вершины параллелограмма А(2;-3), В(5;1),С(3;-4). Не находя координаты вершины D, найти:
1) уравнение стороны AD;
2) уравнение высоты BK, опущенной из вершины В на сторону AD;
3) длину высоты BK;
4) уравнение диагонали BD;
5) тангенс угла между диагоналями параллелограмма.
Записать общие уравнения найденных прямых. Построить чертеж.
Решение.
Сначала построим чертеж. Построим в прямоугольной декартовой системе координат точки ,
,
. Построим отрезки
и
.
Рис. 1
Достроим полученный рисунок до параллелограмма и нанесем на чертеж высоту BK.
Рис. 2
1) Составим уравнение прямой AD.
А) Предварительно найдем уравнение прямой BС. Уравнение прямой, проходящей через точки и
, имеет вид
(3.1)
По условию ,
. Подставим координаты точек
и
в уравнение (3.1):
, т. е.
.
Запишем полученное уравнение в общем виде, то есть в виде . Для этого в последнем уравнении избавимся от знаменателей
и проведем преобразования, перенося все слагаемые в левую часть равенства:
или
.
Из этого уравнения выразим :
;
. Получили уравнение вида
– уравнение с угловым коэффициентом.
Б) Воспользуемся тем фактом, что противоположные стороны параллелограмма параллельны. Составим искомое уравнение прямой AD как уравнение прямой, проходящей через точку параллельно прямой
.
Уравнение прямой, проходящей через данную точку в данном направлении, имеет вид
(3.2)
Где направление определяется угловым коэффициентом .
Условие параллельности двух прямых и
имеет вид
(3.3)
По условию задачи , прямая
. Подставим координаты точки
в уравнение (3.2):
. Так как прямая
параллельна прямой
, то в силу формулы (3.3) их угловые коэффициенты совпадают. Угловой коэффициент прямой
равен
, следовательно, уравнение прямой
имеет вид
.
Запишем уравнение прямой в общем виде. Для этого раскроем скобки и все слагаемые перенесем в левую часть равенства:
. Умножим обе часть равенства на (-2) и получим общее уравнение прямой
:
.
Запишем уравнение прямой в виде с угловым коэффициентом. Для этого выразим
из общего уравнения:
.
2) Составим уравнение высоты , проведенной из вершины
на сторону
как уравнение прямой, проходящей через точку
перпендикулярно прямой
.
Условие перпендикулярности двух прямых и
имеет вид
(3.4)
Подставим координаты точки в уравнение (3.2):
. Так как высота
перпендикулярна прямой
, то их угловые коэффициенты связаны соотношением (3.4). Угловой коэффициент прямой
равен
, следовательно, угловой коэффициент высоты
равен
и уравнение прямой
имеет вид
. Запишем уравнение высоты
в общем виде:
. Запишем это же уравнение в виде с угловым коэффициентом:
.
3) Найдем длину высоты как расстояние от точки
до прямой
.
Расстояние от точки
до прямой
представляет собой длину перпендикуляра, опущенного из точки на прямую и определяется формулой
(3.5)
Так как перпендикулярна
, то длина
может быть найдена с помощью формулы (3.5). По условию
, прямая
определяется уравнением
. В силу формулы (3.5) длина высоты
равна

.
4) Найдем уравнение диагонали как уравнение прямой, проходящей через точки
И
, где
– середина отрезка
.
А) Если и
, то координаты точки
– середины отрезка
, определяются формулами
(3.6)
По условию ,
. В силу формул (3.6) имеем:
,
. Следовательно
.
Б) Так как точка пересечения диагоналей является их серединой, то точка (середина отрезка
) является точкой пересечения диагоналей и диагональ
проходит через точку
.
Воспользуемся уравнением (3.1). По условию ,
. В силу формулы (3.1) уравнение прямой
(диагонали
) имеет вид:


. Запишем это же уравнение в виде с угловым коэффициентом:
.
5) Найдем тангенс угла между диагоналями и
.
А) Найдем уравнение диагонали как уравнение прямой, проходящей через две данные точки.
Воспользуемся уравнением (3.1). По условию ,
. Следовательно,
. Общее уравнение диагонали
имеет вид
, уравнение с угловым коэффициентом – вид
, угловой коэффициент
прямой
равен
.
Б) Уравнение диагонали имеет вид
, ее угловой коэффициент
.
В) Тангенс угла между прямыми
и
определяется формулой
Следовательно, 
.
Задача №2.
Условие задачи №2 несколько различается в зависимости от номера варианта контрольной работы. Приведем решения простейших задач, входящих в это задание.
1) Составить уравнение плоскости, проходящей через точки ,
,
.
Решение.
Уравнение плоскости, проходящей через точки ,
,
имеет вид:

Тогда уравнение плоскости в силу уравнения (3.7) имеет вид


Запишем полученное уравнение в общем виде, т. е. в виде . Для этого раскроем определитель по первой строке
. После преобразований получим:
.
2) Найти нормальный вектор плоскости .
Решение.
Нормальный вектор – это вектор, перпендикулярный плоскости. Если плоскость задана общим уравнением
, то нормальный вектор имеет координаты
.
Рис. 3
Для плоскости нормальным является вектор
=
.
Отметим, что любой вектор, коллинеарный вектору =
так же является нормальным вектором плоскости
. Таким образом, при каждом ненулевом
вектор с координатами
будет являться нормальным вектором рассматриваемой плоскости.
3) Найти косинус угла между плоскостями и
.
Решение.
Угол между двумя плоскостями
и
представляет собой угол между их нормальными векторами и определяется равенством
Для плоскости координаты нормального вектора
определяются равенствами
,
,
. Для плоскости
– равенствами
,
,
. Следовательно,
=
.
4) Составить уравнение плоскости , проходящей через точку
параллельно плоскости
:
.
Решение.
Уравнение плоскости, проходящей через точку , имеет вид
(3.8)
Подставим в уравнение (3.8) координаты точки :
.
Условие параллельности плоскостей и
имеет вид
(3.9)
Так как плоскости и
параллельны, то в качестве нормального вектора
Плоскости
можно взять нормальный вектор
плоскости
, т. е. в формуле (3.9) отношение
можно принять равным единице. Следовательно, уравнение плоскости
примет вид
. Запишем это уравнение в общем виде:
.
5) Найти расстояние от точки до плоскости
:
.
Решение.
Расстояние от точки
до плоскости
представляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой
(3.10)
Для плоскости координаты нормального вектора
определяются равенствами
,
,
. Следовательно,

6) Составить канонические уравнения прямой, проходящей через точки и
.
Решение.
Уравнения прямой, проходящей через точки и
имеют вид
(3.11)
Так как ,
, то в силу (3.11) получим уравнения
или
.
7) Найти направляющий вектор прямой .
Решение.
Направляющий вектор – это вектор, параллельный прямой.
Если прямая задана каноническими уравнениями , то направляющий вектор
имеет координаты
.
Рис. 4
Для рассматриваемой прямой направляющим вектором является вектор
.
Отметим, что любой вектор, коллинеарный вектору так же является направляющим вектором прямой
. Таким образом, при каждом ненулевом
вектор с координатами
будет являться направляющим вектором рассматриваемой прямой.
8) Найти косинус угла между прямыми и
.
Решение.
Угол между двумя прямыми
и
представляет собой угол между их направляющими векторами и определяется равенством
Для прямой координаты направляющего вектора
определяются равенствами
,
,
. Для прямой
– равенствами
,
,
. Значит,
.
9) Составить канонические уравнения прямой , проходящей через точку
параллельно прямой
:
.
Решение.
Канонические уравнения прямой имеют вид . Здесь
– координаты точки, через которую проходит прямая.
В канонические уравнения прямой подставим координаты точки
. Получим:
.
Условие параллельности прямых и
имеет вид
(3.12)
Так как прямые и
параллельны, то в качестве направляющего вектора
прямой
можно взять направляющий вектор
прямой
, т. е. в формуле (3.12) отношение
можно принять равным единице. Следовательно, уравнение прямой
примет вид
.
10) Найти угол между прямой :
и плоскостью
:
.
Решение.
Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. Угол между прямой и плоскостью равен
, где
– угол между направляющим вектором
прямой и нормальным вектором
плоскости.
Рис. 5
Угол между прямой
и плоскостью
определяется формулой
Для плоскости :
координаты нормального вектора
определяются равенствами
,
,
. Для прямой
:
координаты направляющего вектора
– равенствами
,
,
. Синус угла между прямой и плоскостью равен
=
. Следовательно,
.
11) Составить уравнение плоскости , проходящей через точку
перпендикулярно прямой
:
.
Решение.
Уравнение плоскости, проходящей через данную точку, имеет вид .
Подставим в указанное уравнение координаты точки . Получим:
.
Условие перпендикулярности плоскости и прямой
имеет вид
(3.13)
Так как искомая плоскость перпендикулярна прямой
, то в качестве нормального вектора
плоскости можно взять направляющий вектор
прямой
, т. е. в формуле (3.13) отношение
можно принять равным единице. Следовательно, уравнение плоскости
примет вид
. Запишем это уравнение в общем виде:
.
12) Составить канонические уравнения прямой , проходящей через точку
перпендикулярно плоскости
:
.
Решение.
Канонические уравнения прямой, проходящей через данную точку, имеют вид .
Подставим в эти уравнения координаты точки . Получим:
Условие перпендикулярности прямой и плоскости
имеет вид
.
Так как прямая перпендикулярна плоскости
, то в качестве направляющего вектора
прямой
можно взять нормальный вектор
плоскости
, т. е. в формуле (3.13) отношение
можно принять равным единице. Следовательно, уравнение прямой
примет вид:
.
13) Найти координаты точки пересечения прямой :
и плоскости
:
.
Решение.
Координаты точки пересечения прямой

представляют собой решение системы

Запишем параметрические уравнения прямой :

в уравнение плоскости
:
. Отсюда
;
. Подставим найденное значение
в параметрические уравнения прямой
:

.
Задача №3.
К кривым второго порядка относятся эллипс (рис.6), гипербола (рис. 7 и 8), парабола (рис. 9-12). Приведем рисунки и канонические уравнения этих кривых.
Эллипс
Рис. 6
Гипербола Гипербола
.
Рис. 7 Рис. 8
Парабола Парабола
Рис. 9
Рис. 10
Парабола Парабола
Рис. 11
Рис. 12
Приведем примеры решения задачи №3.
Пример 1. Привести уравнение кривой второго порядка к каноническому виду и построить кривую.
Решение.
Для приведения уравнения кривой второго порядка к каноническому виду применяют метод выделения полного квадрата.
Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при и
вынесем за скобки:
.
Выделим полный квадрат: . Отсюда
. Разделим обе части равенства на 25:
. Запишем полученное уравнение в каноническом виде:

Выполним параллельный перенос осей координат по формулам 
, уравнение эллипса принимает канонический вид
.
В нашем примере ,
,
,
.
Итак, рассматриваемое уравнение определяет эллипс с центром в точке и полуосями
и
.
Рис. 13
Пример 2. Привести уравнение кривой второго порядка к каноническому виду и построить кривую.
Решение.
Как и в предыдущем примере, сгруппируем слагаемые, содержащие текущие координаты: .
В скобках выделим полный квадрат: ;
. Отсюда
.
Выполним замену переменных 
, вершина параболы в системе координат
расположена в точке
.
Рис. 14
Задача №4.
Кривая задана в полярной системе координат уравнением .
Требуется:
1) найти точки, лежащие на кривой, давая значения через промежуток, равный
, начиная от
до
;
2) построить полученные точки;
3) построить кривую, соединив построенные точки (от руки или с помощью лекала);
4) составить уравнение этой кривой в прямоугольной декартовой системе координат.
Решение.
Сначала построим таблицу значений и
:
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,00 |
1,92 |
1,71 |
1,38 |
1,00 |
0,62 |
0,29 |
0,08 |
0,00 |
0,08 |
0,29 |
0,62 |
1,00 |
1,38 |
1,71 |
1,92 |
Построим эти точки в полярной системе координат. Полярная система координат состоит из начала координат (полюса) и полярной оси
. Координаты точки
в полярной системе координат определяются расстоянием
от полюса (полярным радиусом) и углом
между направлением полярной оси и полярным радиусом (полярным углом). Для того, чтобы построить точку
, необходимо построить луч, выходящий из точки
под углом
к полярной оси; отложить на этом луче отрезок длиной
.
Рис. 15
Построим все точки, определенные в таблице и соединим их плавной линией
Рис. 16
Запишем уравнение рассматриваемой кривой в прямоугольной декартовой системе координат. Для этого воспользуемся формулами перехода от декартовой к полярной системе координат.
Если полюс совпадает с началом координат прямоугольной декартовой системы координат, полярная ось – с осью абсцисс, то между прямоугольными декартовыми координатами и полярными координатами
существует следующая связь:
,
Откуда
Рис. 17
Итак, в уравнении исходной кривой ,
. Поэтому уравнение
принимает вид
. После преобразований получим уравнение
.
Задача №5.
Построить на плоскости геометрическое место точек, определяемое неравенствами
1)
2)
Решение.
Для того, чтобы решить неравенство на плоскости, надо построить график линии
. Кривая
разбивает плоскость на части, в каждой из которых выражение
сохраняет свой знак. Выбирая пробную точку в каждой из этих частей, найдем часть плоскости, являющуюся искомым решением неравенства.
1) Построим прямые и
, заштрихуем область, в которой
. Затем построим параболу
и заштрихуем область, содержащую ось симметрии параболы (расположенную внутри параболы); построим прямую
и заштрихуем область, лежащую выше прямой. Пересечение всех заштрихованных областей и определит множество точек, представляющих решение рассматриваемой системы.
Рис. 18
2) Построим линию, определяемую уравнением . Эта линия представляет собой ту часть окружности
или
, на которой
. Далее построим прямую
(
). Решением рассматриваемого двойного неравенства является часть плоскости, расположенная между нижней половиной окружности
с центром в точке
радиуса
прямой
.
Рис. 19
| < Предыдущая | Следующая > |
|---|
Решение: согласно условия задачи нужно найти уравнение прямых, на которых лежат диагонали параллелограмма. Уравнения прямых будем искать по формуле уравнения прямой, проходящей через две заданные точки, т.е. нужно найти все четыре вершины параллелограмма.
1. Известна одна вершина с координатами A(3,-1), проверим принадлежит ли она данным прямым:
A(3,-1) ( l_1: quad 2x-y+3 = 0 => 2*3 – (-1)+3 ne 0 )
A(3,-1) ( l_2: quad x+3y-2 = 0 => 3 + 3(-1)-2 ne 0 )
Получили, что точка не принадлежит прямым.
Согласно условия задачи, две стороны параллелограмма лежат на двух прямых ( l_1: quad 2x-y+3=0 ) и ( l_2: quad x+3y-2=0), определим взаимное расположение этих прямых.
Прямые могут быть коллинеарными или пересекающимися
Проверяем прямые на коллинеарность
Две прямые называются коллинеарными, если они параллельны или совпадают
Прямые (l_1: quad A_1x+B_1y+C_1=0 ) и (l_2: quad A_2x+B_2y+C_2=0) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число ( lambda ne 0) , что (A_1 = lambda A_2), (B_1 = lambda B_2) , но ( C_1 ne lambda C_2).
По другому это условие можно записать $$l_1||l_2: quad frac{A_1}{A_2} =frac{B_1}{B_2} ne frac{C_1}{C_2} $$
Прямые (l_1, l_2) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны: (A_1 = lambda A_2), (B_1 = lambda B_2) , ( C_1 = lambda C_2).
По другому это условие можно записать $$ l_1≡ l_2: quad frac{A_1}{A_2} =frac{B_1}{B_2} = frac{C_1}{C_2} $$
Проверяем на коллинеарность прямые ( l_1: quad quad 2x-y+3=0) и ( l_2: quad x+3y-2=0). $$ frac{2}{1} ne frac{-1}{3} ne frac{3}{-2} $$
Вывод: прямые не являются коллинеарными.
2. Найдем вторую вершину – точку пересечения прямых ( l_1: quad 2x-y+3=0 ) и ( l_2: quad x+3y-2=0)
Составим систему уравнений $$ begin{cases}2x-y+3=0 \ x+3y-2=0end{cases} => begin{cases} 2x-y+3=0 \ 2x+6y-4=0 end{cases} => begin{cases}x=-1\ y=1end{cases}$$
Получили точку пересечения С(-1;1)
Вывод: точка пересечения двух сторон – вершина параллелограмма С(-1;1).
Получили две вершины, которые лежат на одной диагонали A(3;-1) и C(-1;1).
Найдем уравнение первой диагонали, проходящей через две заданные точки по формуле ( frac{x-x_1}{x_2-x_1} = frac{y-y_1}{y_2-y_1}).
Подставляем координаты вершин A(3;-1) и C(-1;1) в уравнение и получим искомое уравнение диагонали $$ frac{x-3}{-1-3} = frac{y+1}{1+1} => y = frac{1}{2} – frac{1}{2}x$$
Ответ: получили первое уравнение прямой, на которой лежит диагональ ( y = frac{1}{2} – frac{1}{2}x )
3. Найдем третью вершину.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Получаем, что через вершину C проходит две прямые, параллельные известным, найдем их, для этого применим формулу уравнения прямой, проходящей через заданную точку в заданном направлении. Направление – угловой коэффициент прямой (y – y_0 = k(x-x_0)). Для параллельных прямых известно свойство – угловые коэффициенты параллельных прямых равны (k_1=k_2).
Рассмотрим прямую ( l_1: quad quad 2x-y+3=0 ) преобразуем канонической уравнение прямой в уравнение прямой с угловым коэффициентом ( y = kx+b)
( l_1: quad quad 2x-y+3=0 => y = 2x+3 => k=2)
Найдем искомое уравнение прямой, для точки A(3;-1) с угловым коэффициентом ( k =2), получаем (y+1 = 2(x-3) => y = 2x-7)
найдем точку пересечения полученной прямой ( y = 2x-7 ) и ( l_2: quad x+3y-2 = 0 ). Составим и решим систему уравнений $$ begin{cases}y = 2x-7 \ x+3y-2 = 0end{cases} => begin{cases}y = 2x-7 \ 2x+6y-4 = 0end{cases} => begin{cases}y = – frac{3}{7} \ x = frac{23}{7} end{cases}$$
Получили координаты искомой вершины (B( frac{23}{7}; – frac{3}{7} ))
Рассмотрим прямую ( l_2: quad x+3y-2 = 0 ) преобразуем канонической уравнение прямой в уравнение прямой с угловым коэффициентом ( y = kx+b)
( l_2: quad quad x+3y-2 = 0 => y = frac{2}{3} – frac{1}{3}x => k = – frac{1}{3})
Найдем искомое уравнение прямой, для точки A(3;-1) с угловым коэффициентом ( k = – frac{1}{3}), получаем (y+1 = – frac{1}{3}(x-3) => y = – frac{1}{3}x )
4. Найдем четвертую вершину.
Найдем точку пересечения полученной прямой ( y = – frac{1}{3}x ) и ( l_1: quad 2x-y+3 = 0 ). Составим и решим систему уравнений $$ begin{cases} y = – frac{1}{3}x \ 2x-y+3 = 0 end{cases} => begin{cases} y = frac{3}{7} \ x = -frac{9}{7} end{cases} $$
Получили координаты искомой вершины (D( -frac{9}{7}; frac{3}{7} ))
Найдем уравнение второй диагонали, проходящей через две заданные точки по формуле ( frac{x-x_1}{x_2-x_1} = frac{y-y_1}{y_2-y_1}).
Подставляем координаты вершин (B( frac{23}{7}; – frac{3}{7} )) и (D( -frac{9}{7}; frac{3}{7} )) в уравнение и получим искомое уравнение диагонали $$ frac{x-frac{23}{7}}{- frac{9}{7}-frac{23}{7}} = frac{y+ frac{3}{7}}{frac{3}{7}+ frac{3}{7}} => y = -frac{3}{16}x + frac{3}{16}$$
Ответ: получили второе уравнение прямой, на которой лежит диагональ ( y = -frac{3}{16}x + frac{3}{16} )
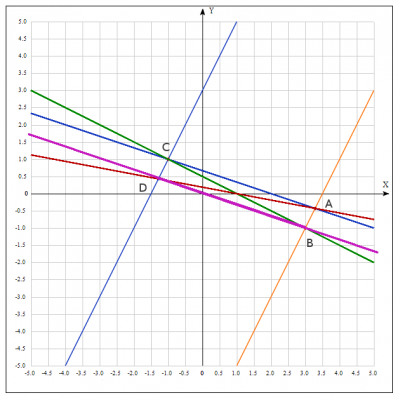
Ответ: уравнения диагоналей параллелограмма ( y = frac{1}{2} – frac{1}{2}x ) и ( y = -frac{3}{16}x + frac{3}{16} )
Строим рисунок: