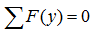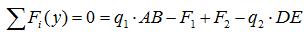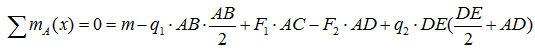Как составить уравнение для балки в статике

iSopromat.ru

Для плоской системы нагружения, при определении опорных реакций и внутренних силовых факторов исходя из условия равновесия системы, можно составить только три уравнения статики.

Ранее были показаны примеры составления уравнений равновесия для пространственной и плоской систем сил.

При плоском поперечном изгибе можно записать только два уравнения. Это частный случай плоского нагружения. В этом случае все силы приложенные к балке расположены нормально к ее оси, т. е. не дают проекций на ось балки.

В результате имеем следующие уравнения статики:

1. Сумма проекций всех сил на вертикальную ось равна нулю
   
2. Сумма моментов относительно любой точки системы тоже равна нулю.
   

Эти уравнения являются уравнениями равновесия рассматриваемой балки находящейся под действием комплекса нагрузок.

Рассмотрим пример плоского поперечного изгиба, когда все внешние силы имеют исключительно вертикальное направление.

Уравнения статики

Сумма проекций всех сил на ось Y:

Здесь силы и нагрузки записаны в соответствии с правилом знаков для проекций сил.

Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.

Проекции сил на ось Z в данном случае равны нулю:

Сумма моментов всех нагрузок, например, относительно точки A :

Дополнительные материалы

• Порядок определения момента от распределенной нагрузки.
• Правила знаков при составлении уравнений статики для систем находящихся в равновесии.

Совместное решение системы полученных уравнений позволяет определить величину и направление двух неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

– Рамки A4 для учебных работ
– Миллиметровки разного цвета
– Шрифты чертежные ГОСТ
– Листы в клетку и в линейку

Как определить реакции в опорах?

Привет! В этой статье, предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции в опорах, и этому уделяют особое внимание на термехе. А курс термеха, по традиции, читают до сопромата. Для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Что такое реакция опоры?

Реакция опоры – это та сила, которая возникает в опоре от действия внешней нагрузки. В зависимости от конструкции опоры и ее назначения, в ней может появляться разное количество реакций, это может быть как сила, так и момент.

В начале этой статьи, расскажу о том, что должен уже уметь читатель, для успешного освоения данного урока. Если у Вас есть проблемы по поднятым вопросам на старте статьи, переходите по ссылкам на другие материалы на нашем сайте, после чего возвращайтесь к нам на чай реакции. Во второй части статьи, посмотрим, как вычисляются реакции на простейшем примере – балки, загруженной по центру сосредоточенной силой. Тут я покажу, как пользоваться уравнениями равновесия статики, как их правильно составлять. Дальше по плану, научу учитывать распределенную нагрузку, на примере той же балки. И завершать данный урок, будет пример определения реакций для плоской рамы, загруженной всевозможными типами нагрузок. Где применим уже все фишки, о которых я буду рассказывать по ходу урока. Что же, давайте начнем разбираться с реакциями!

Что вы должны уже уметь?

В этом блоке статье, я расскажу, как и обещал, что Вы должны УЖЕ уметь, чтобы понять то, что я буду докладывать дальше, про реакции опор.

Должны уметь находить сумму проекций сил

Да, это то, что Вам когда-то рассказывали на термехе, как собственно, и опорные реакции. Если Вы шарите немного в этих проекциях, то можете смело переходить к следующему пункту. Если же нет, то специально на этот случай, у меня есть другая статья, про проекции сил. Переходите, просвещайтесь, после чего, обязательно, возвращайтесь сюда!

Должны уметь составлять сумму моментов относительно точки

Немного теории! Познакомимся для начала с самим понятием момент силы. Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр. Проиллюстрирую написанное:

На изображении показано, как определить момент силы F, относительно точки O.

Так же, для моментов, нужно задаться каким-то правилом знаков. Сила относительно точки может поворачивать как по часовой стрелке, так и против нее. Я в своих уроках буду придерживаться такого правила:

• Если сила относительно точки крутит ПРОТИВ часовой стрелке, то момент положительный.
• Если она крутит ПО часовой стрелки, то соответственно момент отрицательный.

Причем, это правило условно! Какое правило Вы будете использовать совсем не важно, результат получите тот же самый. В теоретической механике, к примеру, делают также как я рассказываю.

Должны разбираться в основных видах опор

Теперь поговорим о самих опорах. В этой статье, будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

Шарнирно-подвижная опора препятствует вертикальному перемещению элементу конструкции, в связи с чем, в ней, под действием внешней нагрузки возникает вертикальная реакция. Обозначают ее обычно как R_i, где i — точка крепления опоры.

Шарнирно-неподвижная опора имеет две реакции: вертикальную и горизонтальную. Так как препятствует перемещению в этих двух направлениях.

Вообще-то способов закрепления элементов конструкций и их условных обозначений достаточно много, но в рамках этой статьи их рассматривать не будем.

Примеры определения сил реакций опор

Вроде, всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнем с простейшей расчетной схемы балки.

Определение реакций опор для балки

Возьмем балку на двух опорах, длиной 2 метра. Загрузим ее, посередине пролета, сосредоточенной силой:

Для этой расчетной схемы, выгодно записать такое условие равновесия:
То есть, будем составлять две суммы моментов относительно опорных точек, из которых можно сразу выразить реакции в опорах. В шарнирно-неподвижной опоре горизонтальная реакция будет равна нулю, ввиду того, что горизонтальные силы отсутствуют. Последним уравнением, взяв сумму проекций на вертикальную ось, сможем проверить правильность нахождения опорных реакций, это сумма должна быть равна нулю.

Введем систему координат, пустим ось х вдоль балки, а ось y вертикально. Обозначим реакции в опорах как R_A и R_B:

Запишем уравнение моментов, относительно точки А. Сила F поворачивает ПО часовой стрелки, записываем ее со знаком МИНУС и умножаем на плечо. Сила R_B поворачивает ПРОТИВ часовой стрелки, пишем ее со знаком ПЛЮС и умножаем на плечо. Все это приравниваем к нулю:

Из полученного уравнения выражаем реакцию R_B.

Первая реакция найдена! Вторая реакция находится аналогично, только теперь уравнение моментов записываем относительно другой точки:

После нахождения реакций, делаем проверку:

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно свернуть до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Определение опорных реакций для плоской рамы

Теперь, после освоения азов по расчету реакций, предлагаю выполнить расчет плоской рамы. Для примера, возьмем раму, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:

• заменяем опоры на реакции;
• сворачиваем распределенную нагрузку до сосредоточенной силы;
• вводим глобальную систему координат x и y.

Для такой расчетной схемы, лучше использовать следующую форму условий равновесия:

Составив первое уравнение, относительно точки A, сразу найдем реакцию в опоре B:

Записав второе уравнение, сумму проекций на ось х, найдем горизонтальную реакцию H_A:

И, наконец, третье уравнение, позволит найти реакцию R_A:

Не пугайтесь отрицательного значения реакции! Это значит, что при отбрасывании опоры, мы не угадали с направлением этой силы.

Расчет же показал, что R_A, направленна в другую сторону:

В итоге, получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумму будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!

На этом заканчиваю данный урок. Если у Вас остались какие-то вопросы по нахождению опорных реакций, смело задавайте их в комментариях к этой статье. Обязательно на все отвечу!

Спасибо за внимание! Если понравилась данная статья, расскажите о ней своим одногруппникам, не жадничайте 🙂

Также рекомендую подписаться на наши соц. сети, чтобы быть в курсе обновлений материалов проекта.

Определение реакций опор балки – решение задачи

Как определить реакции опор балки

Пример решения задачи на определение реакций опор балки

Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и B, вызываемые указанными нагрузками.

Дано:
P = 20,2 Н ; G = 22,6 Н ; q = 2 Н/м ; M = 42,8 Н·м ; a = 1,3 м ; b = 3,9 м ; α = 45° ;

Решение задачи

Проводим оси x и y системы координат. Начало системы координат поместим в точку A . Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас. На рисунке она не указана.

Силы, действующие на балку.

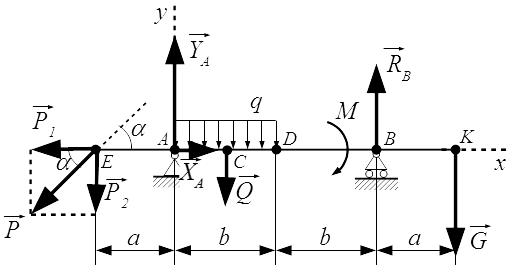
Отбрасываем опоры и заменяем их силами реакций.
В шарнире A , разложим силу реакции на составляющие и вдоль осей координат.
Реакция , в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.

Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
Н .
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD :
AC = CD = b/2 = 1,95 м .

Уравнения равновесия для сил

Определяем проекции сил на оси координат.

Разложим силу на составляющие вдоль координатных осей:
.
Абсолютные значения составляющих:
.
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
.

Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
;
;
;
;
.

Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
;
;
;
(П1) .

Сумма проекций всех сил на ось y равна нулю:
;
;
;
(П2) .

Уравнения равновесия для моментов

Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и . Чтобы их определить, нам нужно составить еще одно уравнение.

Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A , перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.

Находим моменты сил относительно выбранной оси.
Силы , и пересекают ось. Поэтому их моменты равны нулю:
; ; .

Сила перпендикулярна плечу AB . Ее момент:
.
Поскольку, относительно оси A , сила направлена против часовой стрелки, то ее момент положительный.

Сила перпендикулярна плечу AK . Поскольку, относительно оси A , эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
.

Аналогичным способом находим моменты остальных сил:
;
.
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
.

Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
;

;
;
(П3) .

Решение уравнений равновесия

Итак, для трех неизвестных величин, мы получили три уравнения:
(П1) .
(П2) .
(П3) .

Решаем эти уравнения. Вычисляем расстояния.
м;
м;
м;
м.

Из уравнения (П1) находим:
Н.
Из уравнения (П3) находим:

Н.
Из уравнения (П2) имеем:
Н.
Абсолютное значение реакции опоры в точке A :
Н.

Проверка правильности решения

Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.

Возьмем ось, проходящую через точку E . Вычисляем сумму моментов сил относительно этой оси:

.
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н . Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм . Мы получили значение -0,03 Нм . Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.

Второй способ решения

Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.

Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
.
Вычисляем моменты сил относительно оси B .
; ; ;
;
;
;
;
.

Сумма моментов сил относительно оси B равна нулю:
;

;
;
(П4) ;

Итак, вторым способом, мы также имеем три уравнения:
(П1) .
(П3) ;
(П4) .

Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее. Находим силу из уравнения (П4):

Н.

Значение реакции совпало со значением, полученным первым способом из уравнения (П2).

Автор: Олег Одинцов . Опубликовано: 14-10-2017 Изменено: 28-12-2021

[spoiler title=”источники:”]

http://ssopromat.ru/statika/kak-opredelit-reaktsii-v-oporah-dlya-balki/

http://1cov-edu.ru/mehanika/statika/opredelenie-reaktsij-opor-balki/

[/spoiler]

Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.

В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.

Что такое реакция опоры?

Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.

Виды связей и их реакции

Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.

 В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.

Жёсткая заделка

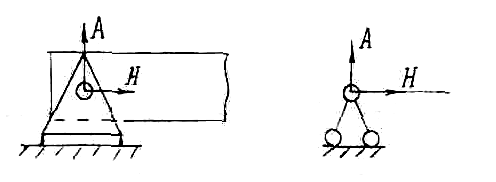
Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (R_A), горизонтальная (H_A) и момент (M_A).

Шарнирно-подвижная и шарнирно-неподвижная опора

В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.

Что такое момент силы?

Также необходимо разобраться с понятием момент силы.

Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.

Проиллюстрирую написанное:

Правило знаков для моментов

Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:

• если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;

• если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.

Определение реакций для двухопорной балки

Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как H_A, R_A и R_B:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.

В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы

Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.

Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.

Уравнения равновесия

Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций

Запишем первое уравнение — уравнение проекций для оси x.

В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — H_A. Так как H_A направлена против положительного направления оси x, в уравнение её нужно записать с минусом:

Тогда H_A будет равна:

Поздравляю, первая реакция найдена!

Уравнения моментов

А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.

Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.

Так как сила R_B поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:

Из полученного уравнения выражаем реакцию R_B:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций

Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.

Составим дополнительное уравнение проекций для оси y и подставим все численные значения:

Как видишь, реакции опор найдены правильно.

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Расчёт реакций для консольной балки

Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30^°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:

Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:

Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что M_A, направлена не по часовой стрелке, а против.

В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.

У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.

Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:

Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:

Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:

Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.

Реакции опор для плоской рамы

Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:

• заменяем опоры на реакции;
• сворачиваем распределенную нагрузку до сосредоточенной силы;
• вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции R_A:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!

Лекция №3

Тема: «Внутренние
усилия в поперечных сечениях стержня»

Вопросы:

1. Опоры и
опорные реакции, и их определение

2. Поперечная
сила и изгибающий момент

3. Взаимосвязь
между изгибающим моментом, поперечной
силой и интенсивностью распределенной
нагрузки

1. Опоры
и опорные реакции, и их определение

При
расчете конструкций в основном встречаются
элементы, испытывающие изгиб.
Стержни,
работающие преимущественно
на изгиб, называют балками. Для того
чтобы балка
могла
испытывать
нагрузку и передавать ее на основание,
она должна
быть соединена с ним опорными связями.
На практике применяют
несколько типов опорных связей, или,
как говорят, несколько
типов опор.

Различают три
основных типа опор:

а)
шарнирно-подвижная опора:

б)
шарнирно-неподвижная опора:

в)
жесткая заделка.

Рис. 1

На
рис. 1 показана шарнирно-подвижная
опора, такая опора позволяет
балке свободно поворачиваться и
перемещаться в горизонтальном
направлении. Поэтому реакция в опоре
будет одна 
вертикальная сила. Условное обозначение
такой опоры показано справа.

Рис. 2

На
рис. 2 показана шарнирно-неподвижная
опора. Такая опора
позволяет балке свободно поворачиваться,
но перемещаться она
не может. Поэтому могут возникать две
реакции – вертикальная и горизонтальная
силы. Их можно сложить и получить одну
результатирующую
силу, но нужно знать угол, под которым
oна
будет
направлена. Более удобно будет пользоваться
вертикальной и горизонтальной
составляющими реакции.

На
рис. 3 показана жесткая заделка. Она
не позволяет балке ни поворачиваться,
ни перемещаться. Поэтому могут возникать
три опорные
реакции: момент, вертикальная и
горизонтальная силы. Если балка не имеет
на конце опоры, то эта часть ее называется
консолью.

Рис. 3

Определим
реакции опор для балки (см. рис. 4).

Рис.4

В опоре
А горизонтальная реакция равна нулю,
так как распределенная
нагрузка q
и сосредоточенная сила F
имеют
вертикальное
направление. Реакции опор

направим
вверх.
Составим два уравнения статического
равновесия сил. Сумма моментов относительно
каждой из опор равна нулю. Уравнения
моментов нужно составлять относительно
опор, так как в этом случае получаются
уравнения с одним неизвестным. Если
составить уравнения
относительно точек В и С, то получим
уравнения с двумя неизвестными,
а их решать сложнее. Моменты против
часовой стрелки будем считать
положительными, по часовой 
отрицательными.

где


момент от равномерно распределенной
нагрузки.

Произведение
q
на расстояние, на котором она приложена,
из условия
равновесия системы равно сосредоточенной
силе, приложенной
посредине отрезка. Поэтому момент

равен:

– момент силы F

Внешний
момент m
на плечо не умножается, так
как
это
пара сил, т.е. две равные по величине,
противоположно направленные силы,
имеющие постоянное плечо.

или

.

Проверка:
Сумма всех сил на вертикальную ось Y
должна быть равна
нулю:

.

Момент
m
в условие статического равновесия

не записывают,
так как момент 
это две равные по величине, противоположно
направленные силы и в проекции на любую
ось они дадут
ноль.

30-20-2-40+50=0:

80-80=0.

Реакции
определены правильно.

2. Поперечная
сила и изгибающий момент

Пусть
на балку действуют силы
,
реакции опор
.
Определим внутренние усилия в сечении,
расположенном на расстоянии от нулевого
конца (см. рис.5).

Рис. 5

Поскольку
все внешние силы действуют вертикально,
то горизонтальной составляющей у реакции
опоры А
не будет. Балка не будет сжиматься или
растягиваться, т.е. продольная сила в
поперечных сечениях равна нулю. Можно
было взять пример, когда
силы

были бы не вертикальными по направлению.
Тогда бы в опоре А
была бы и вторая реакция 
горизонтальная сила, а в сечениях балки

продольная сила N.
В этом случае балка испытывала бы изгиб
с растяжением (сжатием), т.e.
был бы случай сложного сопротивления.
Его мы будем изучать позднее. Вначале
рассматривают более простые задачи и
идут к более сложным, а не наоборот.

Поскольку
внешние силы

лежат в одной плоскости,
проходящей через ось бруса, то возможно
возникновение
тpex
внутренних усилий: изгибающею момента
М,
поперечной силы Q
и
продольной силы N,
которая, как мы отмечали, равна нулю.
Значения М
и Q
определим
из уравнения статического равновесия
левой
части балки:

.

Вывод:
поперечная сила в сечении численно
равна алгебраической
сумме всех внешних сил, а изгибающий
момент 
сумме
всех моментов, вычисленных относительно
сечения и приложенных
к рассматриваемой части балки.

Для
поперечных сил и изгибающих моментов
приняты обязательные
правила знаков (см. рис. 6).

Если
сила пытается повернуть рассматриваемую
часть балки по часовой
стрелке, то она вызывает положительную
поперечную силу, и, наоборот, если
действует против часовой стрелки 
то поперечная
сила
отрицательная. На рис. 5
сила

вызывает положительное
Q,
а


отрицательное. Следует отметить, что
направление силы положительное для
левой части будет отрицательным для
правой части.
Это вызвано тем, что внутренние силы,
действующие на правую
и левую часть балки обязательно должны
быть равны и противоположно
направлены.

Если
внешняя сила или внешний момент изгибают
балку выпуклостью
вниз, то возникающий изгибающий момент
положительный
и, наоборот, выпуклостью вверх 
отрицательный.

Рис. 6

3. Взаимосвязь
между изгибающим моментом,

поперечной силой
и интенсивностью распределенной нагрузки

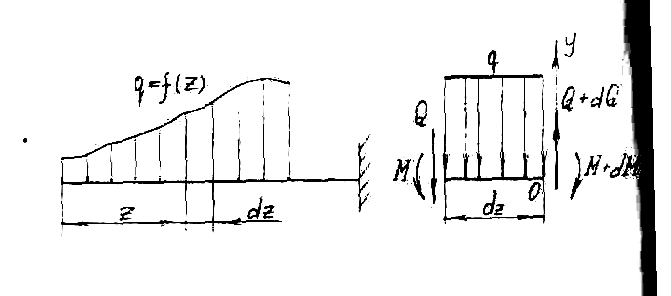
Пусть
на консольную балку (см. рис. 7)
действует
распределенная
нагрузка, изменяющаяся по длине балки.
На расстоянии z
от левого конца возьмем бесконечно
малый отрезок dz.

Рис. 7

Тогда
распределенную нагрузку на нем можно
рассматривать как постоянную.
В левой части рассматриваемого отрезка
будут внутренние усилия Q
и
М,
в правой 
с учетом приращения внутренних
усилий Q+dQ
и
M+dM.

Составим
уравнения статического равновесия для
отрезка балки:

(1)

Третьим
членом можно пренебречь, как бесконечно
малой величиной
более высокого порядка, т.е.:

После преобразований
получим:

(2)

т.е. первая
производная от изгибающего момента по
абсциссе (длине балки) есть поперечная
сила.

Если
в формулу (1) подставить значение Q
из
формулы (2),
то
получим:

, (3)

т.е. вторая
производная от изгибающего момента
есть интенсивность распределенной
нагрузки.

Как рассчитать неразрезную балку. Уравнение 3-х моментов.

Неразрезная балка нагружена во всех пролетах. Построить эпюры Q и M для неразрезной балки.

1. Определяем степень статической неопределимости балки по формуле:

n= Соп -3= 5-3 =2, где Соп – число неизвестных реакций, 3 – число уравнений статики. Для решения данной балки требуется два дополнительных уравнения.

2. Обозначим номера опор с нулевой по порядку (0,1,2,3)

3. Обозначим номера пролетов с первого по порядку (ι_1,ι_2,ι₃)

4. Каждый пролет рассматриваем как простую балку и строим для каждой простой балки эпюры Q и M. То, что относится к простой балке, будем обозначать с индексом «0», то, что относится к неразрезной балке, будем обозначать без этого индекса. Таким образом,  — это поперечная сила и изгибающий момент для простой  балки.

Рассмотрим балку 1^го пролета

Определим фиктивные реакции для балки первого пролета по табличным формулам (см.таблицу «Фиктивные опорные реакции….»)

Балка 2^го пролета

Балка 3^го пролета

5. Составляем уравнение 3^х моментов для двух точек ­­– промежуточных опор ­– опора 1 и опора 2.  Это и будут два недостающих уравнения для решения задачи.

Уравнение 3х моментов в общем виде:

Для точки (опоры) 1 (n=1):

Для точки (опоры) 2 (n=2):

Подставляем все известные величины, учитываем, что момент  на нулевой опоре и на третьей опоре равны нулю,  M₀=0; M₃=0

Тогда получим:

Поделим первое уравнение на сомножитель 4 при M₂ 

Второе уравнение поделим на сомножитель 20 при M₂   

Решим эту систему уравнений:

Из первого уравнения вычтем второе, получим:

Подставляем это значение в любое из уравнений и находим M₂

Итак, нашли опорные моменты:

1. Построение эпюры поперечной силы Q для неразрезной балки

Формула для определения Q в любом сечении неразрезной балки:, где n – пролет

1) Построение эп. Q в первом пролете:

Эта запись означает, что поперечная сила в неразрезной балке в первом пролете будет такая же, как в простой балке с разницей ординат на – 9 . 

На эпюрах должны прослеживаться скачки на величину сил.

2) Построение эп. Q во втором пролете:

Поперечная сила в неразрезной балке во втором пролете будет такая же, как в простой балке с разницей ординат на – 9,5.    

3)Построение эп. Q в третьем пролете:

Поперечная сила в неразрезной балке в третьем пролете будет такая же, как в простой балке с разницей ординат на +15,3.  

Строим эпюру поперечных сил для неразрезной балки. 

7.  Построение эпюры изгибающего момента для неразрезной балки. Сначала откладываем на опорах значения опорных моментов,   соединяем их линией опорных моментов. Это эпюра опорных моментов.

Эпюру М для неразрезной балки можно построить:

1 вариант – методом «подвешивания».  К эпюре опорных моментов  “подвешиваем”  эпюру M⁰  по разницам ординат. К примеру, в середине первого пролета на эпюре M⁰  ордината равна 90,  а на эпюре опорных моментов -27. В итоге получим 90-27=63. Это значение и откладываем.

2 вариант – формула для определения изгибающего M в любом сечении неразрезной балки:

, где n-пролет , x — расстояние.

Для той же точки первого пролета, которую рассматривали в методе «подвешивания»:

Построение эп. М во 2^ом пролете, загруженном равномерно распределенной нагрузкой

Определим положения т. К. по эпюре Q — это точка экстремума.

Определим М неразрезной балки во 2^ом пролете в этой точке: Теперь нужно определить в этой точке К изгибающий момент М в простой балке:

Таким образом, момент в точке К для неразрезной балки:

Строим эпюру М.

8. Выполним проверку опорных реакций. Покажем реакции   на схеме балки на опорах, направив их вверх. Значения этих реакций определим по скачкам эпюры Q. Таким образом получим:

Спроецируем все силы, приложенные к балке, и реакции на вертикальную ось, выполним проверку.

Подставим значения, получим 340-340=0

Проверка верна.