Как составить уравнение других сторон прямоугольника

Задача 36077 Помогите, пожалуйста, с задачей. Даны.

Условие

Помогите, пожалуйста, с задачей. Даны уравнения сторон прямоугольника 3х-4у+5=0, 4х+3у-7=0 и одна из его вершин А(-2;1). Составить уравнения двух других сторон прямоугольника.

Решение

Очевидно, что точка А не принадлежит ни одной из данных сторон, подставляем ее координаты в уравнение и убеждаемся, что координаты не удовлетворяют ни первому , ни второму уравнению
3*(-2)-4*1+5=0- неверно
4*(-2)+3*1-7=0 -неверно

Так как прямые
3х–4у+5=0 и 4х+3у–7=0
пересекаются под прямым углом, то дальнейшее решение видно из рисунка.
На рисунке проводим через точку А две прямые, перпендикулярные данным ( или параллельные данным как хотите)
Можно и так и так.

Находим уравнение прямой перпендикулярной
3х–4у+5=0
y=(3/4)x+(5/4)
k=3/4

Значит k=-4/3 – угловой коэффициент перпендикулярной прямой

y=(-4/3)x+b
Чтобы найти b подставляем координаты точки А
1=(-4/3)*2+b
b=11/3
y=(-4/3)x+(11/3)
[b]4x+3y-11=0[/b]

Находим уравнение прямой перпендикулярной
4х+3у–7=0
y=(-4/3)x+(7/3)
k=-4/3

Значит k=3/4 – угловой коэффициент перпендикулярной прямой

y=(3/4)x+b
Чтобы найти b подставляем координаты точки А
1=(3/4)*2+b
b=-1/2
y=(3/4)x+(-1/2)
[b]3x-4y-1=0[/b]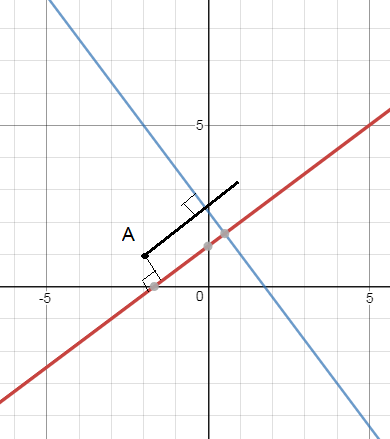

Стороны прямоугольника – вертикальные и горизонтальные, формула вычисления

В этой статье мы разберем в подробностях, как найти каждую из сторон прямоугольника. Посмотрим, какие ситуации возможны в задачах и разберем самые трудные и интересные из задач.

Длины прямоугольника

Очень часто понятия длины и ширины путаются. Некоторые источники утверждают, что вертикальные стороны прямоугольника – это ширина. Но это редкость, обычно длиной называется большая сторона прямоугольника, а шириной меньшая.

Для лучшего восприятия стоит располагать фигуру так, чтобы длина находилась в основании, а боковые стороны имели размеры ширины. Так будет проще решать задачи.

Перед тем, как перейти непосредственно к решению задач, нужно повторить несколько фактов, которые облегчат решение:

• Диагонали прямоугольника равны.
• Диагонали точкой пересечения делятся пополам.
• Диагонали прямоугольника делят прямоугольник на 4 равнобедренных треугольника, которые равны между собой.

Рис. 1. Прямоугольник

Примеры решения задач

Решим задачу, связанную с формулами вычисления сторон прямоугольника. Рассмотрим несколько вариантов нахождения длин сторон при различных известных параметрах.

Задача 1

• Известно, что площадь прямоугольника равна 21, а периметр 20. Найти стороны прямоугольника.

Такая задача содержит две неизвестных. Величины сторон a и b. Чтобы найти оба значения необходимо составить систему уравнений:

$(a+b)*2=P$ (уравнение нахождения периметра как суммы сторон фигуры)

$a*b=S$ (уравнение для нахождения площади)

При наличии двух неизвестных для решения системы необходимо наличие двух уравнений. Поэтому невозможно найти стороны прямоугольника, зная только площадь или только периметр.

Продолжим решение. Выразим значение a из первого выражения системы.

Подставим получившееся выражение в уравнение нахождения площади:

Это квадратное уравнение. Решим его с помощью теоремы Виета. Такое уравнение будет иметь два корня. Сумма корней будет равна 10, а произведение 21. Такое возможно при значении корней 3 и 7, так как это единственные числа, подходящие под данные условия.

Значит, при $b=3$, $а=10-3=7$

При $b=7$, $a=10-7=3$. То есть в любом случае, стороны будут равны 7 и 3. Это и есть ответ задачи.

Задача 2

• Известно, что сторона прямоугольника равна 16, а диагональ 20. Найти другую сторону прямоугольника.

Рис. 2. Рисунок к задаче.

Задача решается теоремой Пифагора. Диагональ делит прямоугольник на два равных прямоугольных треугольника. В таком треугольнике нам известна гипотенуза (20) и катет (16).

Сумма квадратов катетов равняется квадрату гипотенузы. Искать будем сторону а, предположив, что известная нам сторона это сторона b.

Корень квадратный из 144 равен 12. Это и есть ответ к задаче.

Задача 3

• Известно, что прямоугольник представляет собой ромб. Площадь ромба равна 25, необходимо найти все стороны четырехугольника.

У прямоугольника все углы прямые, а у ромба все стороны между собой равны. Значит, четырехугольник, который одновременно является и ромбом, и прямоугольником это фигура с 4 прямыми углами и сторонами, равными между собой. Такой фигурой может быть только квадрат.

Стороны квадрата равны, значит нас интересует одно значение. Площадь квадрата это значение стороны, возведенное в квадрат.

Что мы узнали?

Мы узнали, как найти длины прямоугольника. Рассмотрели различные типовые ситуации и научились решать задачи, связанные с нахождением длин прямоугольника.

Учитель физики, информатики и вычислительной техники. Победитель конкурса лучших учителей Российской Федерации в рамках Приоритетного Национального Проекта “Образование”.

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

• 1. Стороны прямоугольника являются его высотами.
• 2. Все углы прямоугольника прямые.
• 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
• 4. Диагонали прямоугольника равны.
• 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

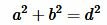(1)

Из равенства (1) найдем d:

.

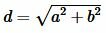(2)

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

( small R=frac<large d> <large 2>)

(3)

Подставляя (3) в (2), получим:

( small R=frac<large sqrt> <large 2>)

(4)

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

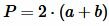(5)

где ( small a ) и ( small b ) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

(6)

(7)

Из формулы (7) найдем ( small b ) и подставим в (6):

(8)

(9)

Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):

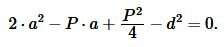(10)

Вычислим дискриминант квадратного уравнения (10):

Сторона прямоугольника вычисляется из следующих формул:

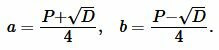(12)

После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

( frac< P><2>>d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*).

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

[spoiler title=”источники:”]

http://kupuk.net/uroki/matematika-uroki/storony-priamoygolnika-vertikalnye-i-gorizontalnye-formyla-vychisleniia/

http://matworld.ru/geometry/pryamougolnik.php

[/spoiler]

Даны уравнения двух сторон прямоугольника и точка пересечения его диагоналей. Составить уравнения двух других его сторон

артем сытник

Ученик

(249),
закрыт

8 лет назад

Прямые х – 3у + 6 =
0 и 3х + у – 12 = 0 являются сторонами прямоугольника, а точка Р (7; 2 ) – точкой пересечения его диагоналей.
Составить уравнения двух других сторон прямоугольника.

Площадь – 56 квадратных см. Периметр – 30 см. Сторона А=7, сторона В=8 S=AxB P=2A+2B S=56 P=30 автор вопроса выбрал этот ответ лучшим Можно попробовать решить данную задачу, составив систему уравнений. Периметр прямоугольника равен: p=2a+2b; Площадь прямоугольника равна: s=a*b; Так как мы знаем периметр и площадь, то сразу подставляем числа: 30=2a+2b; 56=a*b; Выражаем b через a во втором уравнении: b=56/a; И подставляем 56/a вместо b в первое уравнение: 30=2a+2(56/a); 15=a+56/a; Домножаем обе части на a: 15a=a²+56; Получаем квадратное уравнение: a²-15a+56=0; Находим корни этого квадратного уравнения: (15±√(15²-4*1*56))/2*1 = (15±√(225-224))/2 = (15±√1)/2 = (15±1)/2 Получилось, что корни этого уравнения: a1=(15+1)/2=16/2=8; a2=(15-1)/2=14/2=7; Получается, что у нас 2 возможных варианта прямоугольников. Вспомним, что мы выразили: b=56/a; Отсюда находим возможные b: b1=56/a1=56/8=7; b2=56/a2=56/7=8; Как оказалось эти два разных прямоугольника – это один и тот же, просто достигнуть периметра в 30 при площади в 56 можно: Если a=7 и b=8. Либо наоборот: a=8 и b=7. То есть в сущности у нас один и тот же прямоугольник, просто в одном варианте вертикальная сторона больше горизонтальной, а в другом наоборот – горизонтальная больше вертикальной. Ответ: одна сторона 7 сантиметров, а вторая 8 сантиметров. Oleg7­4 [202K] 9 лет назад  Если периметр прямоугольника Р = 30 см, а его площадь S = 56 см, то его стороны будут равны : а – одна сторона, в – другая сторона прямоугольника. S = а * в P = 2а + 2в Решив эту систему, приходим к тому, что сторона а будет равна 7 см, а сторона в будет равна 8 см. а = 7 см в = 8 см. Чтобы решить поставленную задачу, нужно составить систему уравнений и решить ее S = а*b P = 2(а+b) получим квадратное уравнение, которое легко решается, если подставить в него значения периметра и площади Дискриминант равен 1 и уравнение имеет два корня 7 и 8, следовательно одна из сторон равна 7 см, другая 8 см или наоборот. Я специально выписал здесь дискриминант, так как по нему очень хорошо ориентироваться если в условии задачи на нахождение сторон прямоугольника значение периметра и площади заданы так, что этот дискриминант больше ноля, тогда мы имеем прямоугольник; если дискриминант равен нолю – тогда имеем квадрат (P=30, S=56,25, квадрат со стороной 7,5); если дискриминант меньше ноля, то тогда такой прямоугольник не существует (P=20, S=56 – решения нет) Galin­a7v7 [120K] 7 лет назад  Дано: S = 56 см Р = 30 см Стороны=? Решение: Пусть стороны прямоугольника a и b. Тогда: площадь S = a * b , периметр Р=2*(a + b), Получим систему уравнений: {a*b=56 ? {ab=56 {2(a+b)=30, {a+b=15 ,выражая b через а получим квадратное уравнение: b=15-a, a^2 -15a +56 =0 ,решая которое ,получим : a1=7, a2=8, b1=8, b2=7. То есть стороны прямоугольника: a=7,b=8 ,или наоборот:a=8,b=7. Zolot­ynka [551K] 7 лет назад  Нашла еще такое решение, Известно, что периметр прямоугольника 30 а площадь 56, далее: периметр = 2*(длина + ширина) или 2L + 2W площадь= длина * ширина или L * W 2L + 2W = 30 (делим обе части на 2) L + W = 15 L * W = 56 L * (15 – L) = 56 Честно говоря, не совсем поняла решение, но думаю, тот, кто не совсем подзабыл математику, разберется. Azama­tik [55.3K] 7 лет назад  Вспоминаем школьную геометрию: Периметр прямоугольника – это будет сумма длин всех сторон, а площадь прямоугольника – это уже произведение двух смежных его сторон (длину на ширину). В данном случае нам известны и Площадь и Периметр прямоугольника. Они равны 56 см^2 и 30 см соответственно. Итак, решение: S – площадь = а x b; 56 = a x b; Р – периметр = а + b + a + b = 2a + 2b; 30 = 2 (а + b); 15 = a + b; a = 15 – b; Делаем подставление: 56 = (15 – b) x b; 56 = 15 b – b^2; b^2 – 15b + 56 = 0. Получили квадратное уравнение, решая которое получаем: b1 = 8, b2 = 7. Находим и другую сторону прямоугольника: a1 = 15 – 8 = 7; a2 = 15 – 7 = 8. Ответ: стороны прямоугольника равны 8 и 7 см или же 7 и 8 см. Зная формулы периметра прямоугольника и его площади, стороны ищутся в виде решения системы двух уравнений. Для начала выражаем значение одной стороны через другую и например площадь.Это выглядит так А=S/В=56/В Затем подставляем это выражение вместо буквы А в уравнении для периметра: Р=2(56/В + В)=30 Получаем что 56/В+В=15 В этом уравнении даже решать его не надо – любому человеку знакомому с таблицей умножения сразу видно, что 56 это произведение 7 и 8, а поскольку и сумма этих цифр как раз 15, то они и есть нужные нам значения сторон прямоугольника. Хелен­очка [61.9K] 8 лет назад  Обозначим одну сторону буквой Х, другую – буквой Y. Площадь прямоугольника вычисляется умножением длин сторон, следовательно, мы можем составить первое уравнение: Х*Y=56 Периметр – это сумма длин сторон, следовательно, второе уравнение такое: 2Х+2Y=30 Получаем систему двух уравнений. По первому уравнению выделяем Х: Х=56:Y, подставляем это во второе уравнение: 2*56:Y+2Y=30 Отсюда уже легко найти значение Y: Y=7, тогда Х=8. Lilec­hka [36.5K] 9 лет назад  Периметр 30, площадь 56. Назовем стороны прямоугольника а и с. Тогда можем составить такие уравнения: (а+c)х2=30 ахс=56 Далее решаем систему уравнений и находим, что стороны прямоугольника составляют 7 и 8 см. morel­juba [62.5K] 7 лет назад  Итак, для начала рассмотрим формулы для нахождения площади и периметра: 1) S = a * b = 56 см2; 2) Р = 2а + 2b = 30 см. Ведь мы знаем, что прямоугольник имеет по две одинаковых стороны. Таким образом нам требуется решить систему из двух уравнений: a * b = 56 2а + 2b = 30 Отсюда получаем, что одна сторона равна 7, а другая 8. Знаете ответ?

Воспользуемся тем что прямая, которая проходит через точку $%(x_0;y_0)$% и параллельно прямой $%ax+by+c=0,$% имеет фурмулу $%a(x-x_0)+b(y-y_0)=0,$% а прямая, которая проходит через точку $%(x_0;y_0)$% и пепендикулярно прямой $%ax+by+c=0,$% имеет формулу $%b(x-x_0)-a(y-y_0)=0.$%

Точки $%(-2;1)$% и $%(5;7)$% находятся на разные стороны прямой $%2x+3y-6=0,$% значит точка$%(-2;1)$% принадлежит прямой, которая перпендикулярна $%2x+3y-6=0.$% уравнение этой стороны будет $%3(x+2)-2(y-1)=0 Leftrightarrow 3x-2y=-8.$%
А уравнение прямой которое проходит через точку $%(5;7)$% и перпендикулярно $%2x+3y-6=0,$% будет $% 3(x-5)-2(y-7)=0Leftrightarrow 3x-2y=1.$%

Параллельные прямие $%3x-2y=-8$% и $% 3x-2y=1$% пересекают ос $%Oy$% в точках $%(0;4)$% и $%(0;-0,5)$% расстояние которых $%4,5$%.По теореме Фалеса продолжение второй стороны которая параллельна $%3x-2y=-8,$% пересекает $%Oy$% в точке $%(0;-5)$%, следовательно её уравнение будет $%3x-2(y+5)=0Leftrightarrow 3x-2y=10.$%

Через точку $%(5;7)$% проведем еще одну вспомогательную прямую параллельно $%2x+3y-6=0,$%её уравнение $% 2(x-5)+3(y-7)=0Leftrightarrow 2x+3y=31.$%

Параллельные прямые $%2x+3y=6$% и $% 2x+3y=31$% пересекают ос $%Oy$% в точках $%(0;2)$% и $%(0;31/3)$% расстояние которых $%25/3$%.По теореме Фалеса продолжение второй стороны, которая параллельна $%2x+3y=6,$% пересекает $%Oy$% в точке $%(0;56/3)$%, следовательно её уравнение будет $%2x+3(y-56/3)=0Leftrightarrow 2x+3y=56.$%

Ответ. $% 3x-2y=-8,3x-2y=10,2x+3y=6,2x+3y=56$%

210

Определить, какие из точек M₁(3; 1), M₂(2; 3), M₃(6; 3), M₄(-3;
-3), M₅(3; -1), M₆(-2; 1) лежат
на прямой и какие на ней не лежат. 211 Точки P₁,
P₂, P₃, P₄, P₅ расположены
на прямой ; их абсциссы соответственно равны
числам 4; 0; 2; -2; -6. Определить ординаты этих точек. 212 Точки Q₁,
Q₂, Q₃, Q₄, Q₅ расположены
на прямой ; их ординаты соответственно равны
числам 1; 0; 2; -1, 3. Определить абсциссы этих точек. 213 Определить точки
пересечения прямой с координатными
осями и построить эту прямую на чертеже. 214 Найти точку
пересечения двух прямых , . 215 Стороны АВ, ВС и АС
треугольника АВС даны соответственно
уравнениями , , . Определить
координаты его вершин. 216 Даны уравнения двух
сторон параллелограмма , и уравнение одной из
его диагоналей .
Определить координаты вершин
этого параллелограмма. 217 Стороны
треугольника лежат на прямых , , . Вычислить его площадь S. 218 Площадь
треугольника S=8, две его вершины суть точки А(1; -2),
В(2; 3), а третья вершина С лежит на прямой . Определить координаты вершины С. 219 Площадь
треугольника S=1,5, две его вершины суть точки А(2;
-3), В(3; -2), центр масс этого треугольника лежит на
прямой .
Определить координаты третьей
вершины С. 220 Составить
уравнение прямой и построить прямую на чертеже,
зная ее угловой коэффициент k и отрезок b,
отсекаемый ею на оси Oy: 220.1 k=2/3, b=3; 220.2 k=3, b=0; 220.3 k=0, b=-2; 220.4 k=-3/4, b=3; 220.5 k=-2, b=-5; 220.6 k=-1/3, b=2/3. 221 Определить угловой
коэффициент k и отрезок b, отсекаемый на оси Oy, для
каждой из прямых: 221.1 ; 221.2 ; 221.3 ; 221.4 ; 221.5 . 222 Дана прямая . Определить угловой коэффициент k
прямой: 222.1 Параллельной
данной прямой; 222.2 Перпендикулярно к
данной прямой. 223 Дана прямая . Составить уравнение прямой,
проходящей через точку М₀(2; 1): 223.1 Параллельно данной
прямой; 223.2 Перпендикулярно
данной прямой. 224 Даны уравнения двух
сторон прямоугольника , и одна из его вершин
А(2; -3). Составить уравнения двух других сторон
этого прямоугольника. 225 Даны уравнения двух
сторон прямоугольника , и уравнение одной из
его диагоналей .
Найти вершины прямоугольника. 226 Найти проекцию
точке Р(-5; 13) относительно прямой . 227 Найти точку Q,
симметричную точке Р(-5; 13) относительно прямой . 228 В каждом из
следующих случаев составить уравнение прямой,
параллельной двум данным прямым и проходящей
посередине между ними: 228.1 , ; 228.2 , ; 228.3 , ; 228.4 , ; 228.5 , . 229 Вычислить угловой
коэффициент k прямой, проходящей через две данные
точки: 229.1 M₁(2;
-5), M₂(3; 2); 229.2 P(-3, 1), Q(7; 8); 229.3 A(5; -3), B(-1; 6). 230 Составить
уравнения прямых, проходящих через вершины
треугольника A(5; -4), B(-1; 3), C(-3; -2) параллельно
противоположным сторонам. 231 Даны середины
сторон треугольника M₁(2; 1), M₂(5;
3), M₃(3; -4). Составить
уравнение его сторон. 232 Даны две точки P(2; 3),
Q(-1; 0). Составить уравнение прямой, проходящей
через точку Q перпендикулярно к отрезку . 233 Составить
уравнение прямой, если точка P(2; 3) служит
основанием перпендикуляра, опущенного из начала
координат на эту прямую. 234 Даны вершины
треугольника M₁(2; 1), M₂(-1; -1),
M₃(3; 2). Составить уравнения
его высот. 235 Стороны
треугольника даны уравнениями , , . Определить точку пересечения его
высот. 236 Даны вершины
треугольника A(1; -1), B(-2; 1), C(3; 5). Составить
уравнение перпендикуляра, опущенного из вершины
А на медиану, проведенную из вершины В. 237 Даны вершины
треугольника A(2; -2), B(3; -5), C(5; 7). Составить
уравнение перпендикуляра, опущенного из вершины
С на биссектрису внутреннего угла при вершине А. 238 Составить
уравнения сторон и медиан треугольника с
вершинами A(3; 2), B(5; -2), C(1; 0). 239 Через точки M₁(-1; 2), M₂(2; 3) проведена
прямая. Определить точки пересечения этой прямой
с осями координат. 240

Доказать,
что условие, при котором три точки M₁(x₁,
y₁), M₂(x₂, y₂), M₃(x₃,
y₃) лежат на одной прямой,
может быть записано в следующем виде:

241

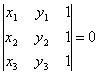
Доказать,
что уравнение прямой, проходящей через две
данные точки M₁(x₁, y₁),
M₂(x₂, y₂), может
быть записано в следующем виде:

242 Даны
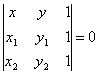
последовательные вершины выпуклого
четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2; -6).
Определить точку пересечения его диагоналей. 243 Даны две смежные
вершины A(-3; -1), B(2; 2) параллелограмма ABCD и точка Q(3;
0) пересечения его диагоналей. Составить
уравнения сторон этого параллелограмма. 244 Даны уравнения двух
сторон прямоугольника , и уравнение его
диагонали . Составить уравнения остальных
сторон и второй диагонали этого прямоугольника. 245 Даны вершины
треугольника A(1; -2), B(5; 4), C(-2; 0). Составить
уравнения биссектрис его внутреннего и внешнего
углов при вершине А. 246 Составить
уравнение прямой, проходящей через точку P(3; 5) на
одинаковых расстояниях от точек A(-7; 3) и B(11; -15). 247 Найти проекцию
точки P(-8; 12) на прямую, проходящую через точки A(2;
-3), B(-5; 1). 248 Найти точку M₁, симметричную точке М₂(8;
-9) относительно прямой,
проходящей через точки А(3; -4), B(-1; -2). 249 На оси абсцисс
найти такую точку P, чтобы сумма ее расстояний до
точек M(1; 2), N(3; 4) была наименьшей. 250 На оси ординат
найти такую точку P, чтобы сумма ее расстояний до
точек M(-3; 2), N(2; 5) была наибольшей. 251 На прямой найти такую точку Р, сумма
расстояний которой до точек A(-7; 1), B(-5; 5) была бы
наименьшей. 252 На прямой найти такую точку Р, разность
расстояний которой до точек A(4; 1), B(0; 4) была бы
наибольшей. 253 Определить угол между двумя прямыми: 253.1 , ; 253.2 , ; 253.3 , ; 253.4 , . 254 Дана прямая . Составить уравнение прямой,
проходящей через точку M₀(2; 1) под углом 45⁰ к данной прямой. 255 Точка А(-4; 5)
является вершиной квадрата, диагональ которого
лежит на прямой . Составить
уравнения сторон и второй диагонали этого
квадрата. 256 Даны две
противоположные вершины квадрата A(-1; 3), C(6; 2).
Составить уравнения его сторон. 257 Точка E(1; -1) является
центром квадрата, одна из сторон которого лежит
на прямой . Составить уравнения
прямых, на которых лежат остальные стороны этого
квадрата. 258 Из точки M₀(-2; 3) под углом к оси
Ox направлен луч света. Известно, что . Дойдя
до оси Ox, луч от нее отразился. Составить
уравнения прямых, на которых лежат падающий и
отраженный лучи. 259 Луч света направлен
по прямой , луч от нее отразился.
Составить уравнение прямой, на которой лежит
отраженный луч. 260 Даны уравнения
сторон треугольника , , . Доказать, что этот треугольник
равнобедренный. Решить задачу при помощи
сравнения углов треугольника. 261 Доказатть, что
уравнение прямой, проходящей через точку M₁(x₁; y₁) параллельно
прямой , может быть записано в виде . 262 Составить
уравнение прямой, проходящей через точку М₁(2: -3) параллельно
прямой: 262.1 ; 262.2 ; 262.3 ; 262.4 ; 262.5 . 263 Доказать, что
условие перпендикулярности прямых ; может быть записано
в следующем виде: . 264 Установить, какие
из следующих пар прямых перпендикулярны. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых. 264.1  , ; 264.2 , ; 264.3 , ; 264.4 , ; 264.5 , ; 264.6 , . 265

Доказать,
что формула для определения угла между
прямыми , может
быть записана в следующей форме:

266 Определить угол , образованный двумя прямыми. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых. 266.1 , ; 266.2  , ; 266.3  , . 267 Даны две вершины
треугольника M₁(-10; 2), M₂(6; 4);
его высоты пересекаются в точке
N(5; 2). Определить координаты третьей вершины M₃. 268 Даны две вершины A(3;
-1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения
его высот. Составить уравнения сторон этого
треугольника. 269 В треугольнике АВС
даны: уравнение стороны АВ: , уравнения
высот АМ: и BN: . Составить уравнения двух
других сторон и третьей высоты этого
треугольника. 270 Составить
уравнения сторон треугольника АВС, если даны
одна из его вершина А(1; 3) и уравнения двух медиан , . 271 Составить
уравнения сторон треугольника, сли даны одна из
его вершин B(-4; -5) и уравнения двух высот , . 272 Составить
уравнения сторон треугольника, зная одну из его
вершин A(4; -1) и уравнения двух биссектрис , . 273 Составить
уравнения сторон треугольника, зная одну из его
вершин B(2; 6), а также уравнения высоты и
биссектрисы , проведенных из одной вершины. 274 Составить
уравнения сторон треугольника, зная одну его
вершину B(2; -1), а также уравнения высоты и биссектрисы , проведенных из
различных вершин. 275 Составить
уравнения сторон треугольника, зная одну его
вершину C(4; -1), а также уравнения высоты и медианы , проведенной из
одной вершины. 276 Составить
уравнения сторон треугольника, зная одну его
вершину B(2; -7), а также уравнения высоты и медианы , проведенных из
различных вершин. 277 Составить
уравнения сторон треугольника, зная одну его
вершину C(4; 3), а также уравнения биссектрисы и медианы , проведенных из
одной вершины. 278 Составить
уравнения сторон треугольника, зная одну его
вершину A(3; -1), а также уравнения биссектрисы и медианы , проведенных из
различных вершин. 279 Составить
уравнение прямой, которая проходит черезначало
координат и вместе с прямыми , образует
треугольник с площадью, равной 1,5. 280 Среди прямых,
проходящих через точку P(3; 0), найти такую, отрезок
которой, заключенный между прямыми , , делится в точке Р
пополам. 281 Через точку Р(-3; -1)
проведены всевозможные прямые. Доказать, что
отрезок каждой из них, заключенный между прямыми , , делится
в точке Р пополам. 282 Через точку Р(0; 1)
проведены всевозможные прямые. Доказать, что
среди них нет прямой, отрезок которой,
заключенный между прямыми , , делился бы в точке Р
пополам. 283 Составить
уравнение прямой, проходящей через начало
координат, зная, что длина ее отрезка,
заключенного между прямыми , , равна . 284 Составить
уравнение прямой, проходящей через точку С(-5; 4),
зная, что длина ее отрезка, заключенного между
прямыми , , равна 5.