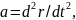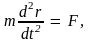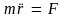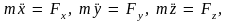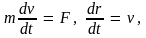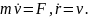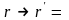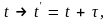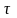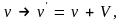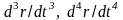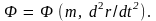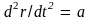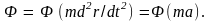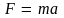Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.
Имеет смысл говорить только о движении в некоторой системе отсчета.
Система отсчета. Системы координат
Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.
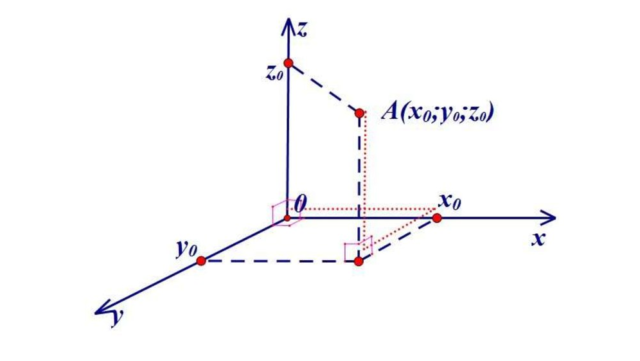
В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x, y, z – ее координат. Могут быть применены другие:
- сферическая система с положением точек и ее радиус-вектором, определенных координатами r, υ, φ;
- цилиндрическая система с координатами p, z, α;
- на полярной плоскости с параметрами r, φ.
В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.
Кинематическое уравнение движения материальной точки
Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.
При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.
Это возможно при использовании кинематического уравнения движения:
r¯=r¯(t) (1).
Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.
Ее перемещение по уравнению (1) определено, если имеется указанное положение в любой момент времени t. Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:
x(t)=x, y(t)=y, z(t)=z (2).
Прямоугольные декартовы координаты x, y, z – это проекции радиус-вектора r¯, проведенного из начала координат. Очевидно, что длину и направление r¯ можно найти из соотношений, где a, β, γ являются образованными радиус-вектором углами с координатными осями.
Равенства (2) считают кинематическими уравнениями движения материальной точки в декартовых координатах.
Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости Оху, тогда применимы полярные координаты r, φ, относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:
r=r(t), φ=φ(t) (3).
Кинематическое уравнение движения точки в криволинейных координатах q1, q2, q3, связанных с декартовыми преобразованиями вида x=x(q1, q2, q3), y=y(q1, q2, q3), z=z(q1, q2, q3) (4), записывается как
q1=q1(t), q2=q2(t), q3=q3(t) (5).
Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями (2), (5). Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.
Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:
s=s(t).
Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.
Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.
Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.
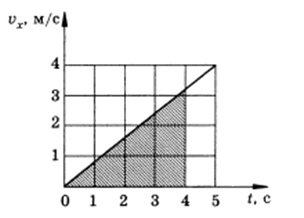
Дано уравнение движения материальной точки x=0,4t2. Произвести запись формулы зависимости υx(t), построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.
Дано: x=0,4t2, t=4c
Найти: υx(t), S – ?
Решение
При решении необходимо учитывать зависимость скорости от времени:
υx=υ0x+axt.
Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:
x=x0+υ0xt+axt22, x=0,4t2.
Очевидно, что x0=0, υ0x=0, ax=0,8 м/с2.
После подстановки данных в уравнение:
υx=0,8t.
Определим точки, изобразим график:
υx=0, t=0, υx=4, t=5
Рисунок 1
Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:
S=0,4t2=6,4 м.
Ответ: S=6,4 м.
Роман Алексеевич Лалетин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Система отсчета. Системы координат
Под движением материальной точки в пространстве понимают изменение ее положения относительно некоторых тел с течением времени. В связи с этим можно говорить только о движении в некоторой системе отсчета.
Сами по себе точки пустого пространства неразличимы между собой, поэтому говорить о той или иной точке пространства можно, если в ней находится материальная точка. Ее положение и определяется относительно тела отсчета с помощью измерений, для чего с телом (телами) отсчета жестко связывается некоторая система координат; в ней и измеряются пространственные координаты. Например, на поверхности Земли это географическая широта и долгота точки.
В теоретических рассуждениях часто наиболее удобна декартова прямоугольная система координат, в которой положение точки определяется радиус-вектором $overline{r}$ с тремя проекциями $x,y,z$ — координатами точки. Но возможно и использование других систем координат, например:
- сферической, где положение точки и ее радиус-вектор определены координатами $r,vartheta ,varphi $;
- цилиндрической: с координатами $p,z,alpha $;
- на плоскости – полярной: $r,varphi $.
В теоретических рассуждениях часто не принимают во внимание реальную систему отсчета, сохраняя только систему координат, которая и служит математической моделью системы отсчета, применяемой при измерениях на практике.
Кинематическое уравнение движения материальной точки
Итак, в любой системе отсчета и системе координат имеется возможность определить координаты материальной точки в любой момент времени.
Если положение материальной точки в каждый момент времени определено в данной системе отсчета, то движение ее задано или описано.
Это задание достигается в виде кинематического уравнения движения:
$overline{r}=overline{r}(t)$ (1)
Аналитически положение точки всегда определяется совокупностью трех независимых между собой чисел. Этот факт выражают словами: свободная точка имеет три степени свободы движения.
«Уравнение движения материальной точки» 👇
Движение точки согласно уравнению (1) полностью определено, если указано ее положение в любой момент времени $t$. Для этого достаточно задать декартовы координаты точки как однозначные и непрерывные функции времени:
$x(t)=x$, $y(t)=y$, $z(t)=z$. (2)
Прямоугольные декартовы координаты $x,y,z$ являются проекциями радиус-вектора $overline{r}$, проведенного в точку из начала координат, т.е.:
Длина и направление вектора $overline{r}$находятся из известных соотношений:
Здесь, $alpha ,beta ,gamma $ – углы, образованные радиус-вектором с координатными осями.
Равенства (2) являются кинематическими уравнениями движения материальной точки в декартовых координатах. Но уравнения могут быть записаны в любой другой системе координат, связанной с декартовой взаимно однозначным преобразованием. При движении точки в плоскости Оху часто бывает удобно пользоваться полярными коордиинатами $r,varphi $, связанными с декартовыми преобразованием:
В этом случае кинематические уравнения движения точки имеют следующий общий вид:
$r=r(t),varphi =varphi (t)$. (3)
В криволинейных координатах $q_{1} ,q_{2} ,q_{3} $ связанных с декартовыми преобразованием:
$x=x(q_{1} ,q_{2} ,q_{3} )$, $y=y(q_{1} ,q_{2} ,q_{3} )$, $z=z(q_{1} ,q_{2} ,q_{3} )$, (4)
кинематические уравнения движения точки запишутся так:
$q_{1} =q_{1} (t),q_{2} =q_{2} (t),q_{3} =q_{3} (t)$. (5)
(Это могут быть сферические, цилиндрические и другие координаты).
Годограф радиус-вектора точки, т.е. кривая, описываемая концом вектора $overline{r}$при движении точки, совпадает с траекторией движения этой точки. Уравнение траектории в параметрической форме, когда параметром служит время $t$, дано кинематическими уравнениями движения (2), (5). Для получения уравнения траектории в координатной форме достаточно исключить из кинематических уравнений время.
Движение точки может быть определено по-другому: заданием траектории и мгновенным положением точки на ней. Положение точки на кривой определяется указанием только одной величины — расстояния, измеряемого вдоль кривой от некоторой начальной точки. При этом должно быть указано положительное направление кривой. Тогда мгновенное положение точки на заданной кривой определяется функцией:
Это уравнение является уравнением движения точки по траектории. Такой способ задания движения называется естественным или траекторным.
Координатный и естественный способы задания движения точки физически (в смысле фиксации ее положения в пространстве)
эквивалентны. Что же касается математической стороны дела, то в одних задачах оказывается проще применение координатного, а в другом — естественного метода.
Закон движения точки по траектории может быть задан аналитически, графически или в виде таблицы. Оба последних способа широко применяются на транспорте (например, графики и расписания движения поездов).
Пример 1
Уравнение движения материальной точки имеет вид $x=0,4t^{2} $. Написать формулу зависимости $v_{x} (t)$ и построить график зависимости скорости точки от времени. Показать на графике площадь, численно равную пути, пройденному точкой за 4 секунды, и вычислить этот путь.
end{enumerate}
Дано: $x=0,4t^{2} $, $t=4$с.
Найти: $v_{x} (t)$, $S$-?
Решение: Зависимость скорости от времени имеет вид:
[v_{x} =v_{0x} +a_{x} t.]
Запишем уравнение зависимости координаты от времени и сравним его с данным:
[x=x_{0} +v_{0x} t+frac{a_{x} t^{2} }{2} , x=0,4t^{2} .]
Из сравнения видно, что $x_{0} =0$, $v_{0x} =0$, $a_{x} =0,8$м/с2.
Подставим полученные данные в уравнение скорости и получим:
[v_{x} =0,8t.]
Определим точки и построим график:
[v_{x} =0,t=0; v_{x} =4,t=5.]
Рисунок 1.
Путь, пройденный телом, численно равный площади фигуры, ограниченной графиком и может быть найден по следующей формуле:
$S=0,4t^{2} =6,4$м.
Ответ: $S=6,4$ м.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Уравнение движения точки

4.5
Средняя оценка: 4.5
Всего получено оценок: 68.
Обновлено 22 Июля, 2021
4.5
Средняя оценка: 4.5
Всего получено оценок: 68.
Обновлено 22 Июля, 2021
Кинематика — это раздел физики, который изучает движение без исследования его причин. С помощью кинематических закономерностей движения можно рассчитать, в каком месте будет находиться тело в тот или иной момент времени. Эти закономерности описываются с помощью математических формул, называемых «уравнения движения». Рассмотрим эту тему более подробно.
Движение материальной точки
Материальная точка — это тело, имеющее массу, размерами которого в данный момент можно пренебречь. Понятие материальной точки очень удобно в кинематике и динамике, поскольку позволяет исключить несущественные стороны исследуемого движения и сосредоточиться на основных параметрах.
Материальная точка находится в некоторой системе отсчёта, поэтому ей можно приписать некоторые координаты — одну, две или три, в зависимости от числа координатных осей.
Движение материальной точки состоит в том, что некоторые из координат меняются с течением времени. Следовательно, для описания движения необходимо сопоставить каждому моменту времени соответствующие координаты. Сделать это можно различными способами, например, просто составив таблицу, в первом столбце которой стоят моменты времени, а в остальных столбцах — соответствующие координаты. Однако удобнее найти математическую формулу, в которой в качестве исходной независимой переменной берётся время, а результатом формулы является координата.
Уравнения движения точки
Математические формулы, с помощью которых можно найти координаты точки в любой момент времени, называются уравнениями движения материальной точки.
Примером самого простого уравнения движения точки является формула:
$$x(t)=0$$
Несмотря на крайнюю простоту, эта формула обладает всеми чертами уравнения движения. В ней есть координата $x$, и, подставляя разные моменты времени, можно её найти. В данном случае, какой бы момент времени не взять, координата всегда будет равна нулю, то есть точка покоится в начале координат.
Возьмём пример немного сложнее. Если точка движется с постоянной скоростью, то, как известно к 9 классу, умножив скорость на время движения, мы получаем пройденное расстояние. В виде формулы это выразится, например, следующим образом:
$$x(t)=5t$$
С помощью этой формулы мы можем выяснить, что в начальный момент времени точка находилась в начале координат (подставив нулевое время, мы получим нулевую координату). Подставляя другие значения времени, мы найдём соответствующую координату. Кроме того, из формулы можно получить и скорость, с которой движется материальная точка — 5 метров в секунду, или других единиц, принятых в системе отсчёта.
Если в начальный момент точка имела некоторую координату, допустим, 1 (метр), то её уравнение движения примет вид:
$$x(t)=5t+1$$
Часто в кинематических уравнениях движения используются буквы-обозначения, а для определения конкретных координат они заменяются конкретными числами. В последнем примере скорость можно заменить буквой $v$, а начальную координату — $x_0$. Уравнение движения примет вид:
$$x(t)=vt+x_0$$
Наконец, в системе отсчёта может быть не одна, а несколько координатных осей. В этом случае движение материальной точки описывается системой уравнений. Например:
$$begin{cases}x=2t+1\y=3t+3\z=6t+5 end{cases}$$
В данном случае описывается движение в трёхмерном пространстве точки, которая в начальный момент имела координаты (1; 3; 5) и скорость которой равна 7.
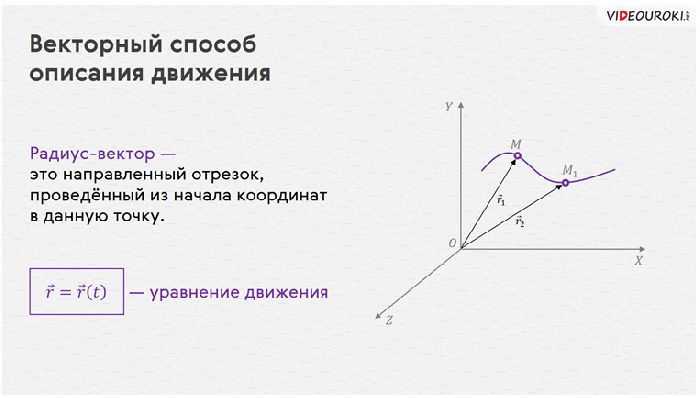
Для описания движения в системе отсчёта с несколькими координатами нередко используется векторный способ описания, когда все переменные в уравнении являются векторами. Записи получаются более компактными, хотя описывают те же самые координаты и движения.
Что мы узнали?
Уравнения движения точки — это математические формулы, связывающие время в принятой системе отсчёта с координатами точки в ней. Подставляя в эти уравнения различные моменты времени, можно получить положения точки в эти моменты. Кроме того, из уравнений движения можно получить скорость, с которой движется точка.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.5
Средняя оценка: 4.5
Всего получено оценок: 68.
А какая ваша оценка?
Основной закон
динамики материальной точки можно
записать в виде дифференциального
уравнения. Заменяя в выражении (3.2) вектор
ускорения кинематическим соотношением
получим
(3.9)
При
этом сила, действующая на материальную
точку, может зависеть как от положения
материальной точки (r)
и времени (t),
но и от ее относительной скорости v:
F = F(r,
t,
v).
Если эта функция известна, говорят, что
задан закон действия силы.
Линейное
дифференциальное уравнение второго
порядка (3.9) и называется уравнением
движения материальной точки в векторной
форме. Запишем его также в более компактном
виде:
(3.10)
Проецируя
векторы, входящие в это уравнение, на
координатные оси X,
Y,
Z,
получим уравнения движения материальной
точки в координатной форме
(3.11)
где
Fx,
Fy
и Fz
– проекции вектора силы, действующей
на материальную точку, на координатные
оси X,
Y
и Z
соответственно. В математическом
отношении уравнение (3.9) (или (3.10)) является
дифференциальным уравнением относительно
векторной функции r(t),
а уравнения (3.11) – уравнениями относительно
скалярных функций x(t),
y(t)
и z(t).
Уравнения движения
позволяют решить две основные задачи
динамики материальной точки.
1. Зная массу
материальной точки и ее закон движения,
т.е. зависимость радиус-вектора точки
или ее координат от времени, r
= = r(t),
найти действующую
на точку силу.
2. По заданной массе
m
точки и закону, действующей на нее силы
определить закон движения материальной
точки.
Решение первой
задачи сводится к двукратному
дифференцированию по времени векторной
функции r(t)
или скалярных функций x(t).
y(t),
z(t)
и последующему умножению полученного
результата на массу тела m.
Вторая задача
решается путем двух последовательных
интегрирований по времени либо векторного
уравнения (3.9), если сила задана в векторной
форме, либо уравнений (3.11), если заданы
компоненты силы
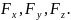
Рассмотрим случай,
когда сила задана в векторной форме. В
этом случае закон движения ищется в
векторной форме, т.е. определяется
функция r = r(t)
с помощью уравнения (3.9). При этом уравнение
(3.10) удобно заменить двумя векторными
уравнениями, являющимися дифференциальными
уравнениями первого порядка:
(3.12)
или
(в компактной форме)
(3.13)
Поэтому
решение задачи можно разбить на два
этапа: сначала, проинтегрировав первое
уравнение (3.12), получим функцию v(t),
а затем, подставив эту функцию во второе
уравнение (3.12) и проинтегрировав его,
найдем закон движения r(t).
При интегрировании каждого из уравнений
(3.12) появляются по одной неопределенной
постоянной C1
и C2
– постоянные векторы. Эти постоянные
интегрирования войдут в общее решение
уравнения (3.9), вследствие чего это общее
решение будет иметь вид r
= r(t,
C1,
C2).
Чтобы довести решение каждой конкретной
задачи до конца, надо определить значения
постоянных C1
и C2.
Для определения этих векторов уравнение
движения (3.9) следует дополнить двумя
условиями, в качестве которых берут
значение скорости точки и ее радиус-вектора
в какой-либо момент времени t0
(обычно в момент начала действия силы,
который принимают за начальный (t0
= 0), т.е. указывают
значение скорости v
и радиус-вектора r
при t0
= 0: v(0)
= v0,
r(0) = r0.
Эти условия называются начальными
условиями. Следовательно, закон движения
материальной точки с помощью уравнения
(3.9) можно определить, если во 1-х,
известна сила, действующая на точку и
во 2-х, если заданы начальные условия.
Мы видим, что
задание силы еще не определяет однозначно
движение материальной точки, а определяет
целый класс однотипных движений,
различающихся между собой характеристическими
параметрами – векторами C1
и C2.
Действующая сила определяет только
ускорение движущейся точки, а скорость
и положение точки на траектории (и сама
траектория) могут зависеть еще от
скорости, которая сообщена точке в
начальный момент, и от начального
положения точки. Так, например, материальная
точка, двигаясь вблизи поверхности
земли под действием силы тяжести, имеет
ускорение g,
если не учитывать сопротивление воздуха.
Но точка будет иметь различные скорости
и положения в пространстве в один и тот
же момент времени и различную форму в
зависимости от того, из какой точки
пространства началось движение и с
какой по величине и направлению начальной
скоростью. Для выделения конкретного
вида движения точки и задают ее начальные
условия.
Движущаяся
материальная точка характеризуется в
каждый момент времени координатами и
проекциями скорости (или импульса). Эти
величины называются механическими
параметрами точки. Если эти параметры
заданы, говорят, что определено
механическое состояние материальной
точки.
Как мы видели,
уравнения движения позволяют определить
положение и скорость материальной точки
– механическое состояние точки в данный
момент времени t
по известным силам , действующим на
точку , и ее состоянию в начальный,
вообще любой предшествующий момент
времени t0
< t.
Этот факт выражает собой принцип
причинности в классической механике.
Считается, что состояние материальной
точки в момент времени t0
является
причиной ее состояния в последующий
момент времени t.
Уравнения движения позволяют решить
задачу о движении точки не только для
момента времени t
> t0,
но и для момента времени t
< < t0.
Другими словами, с помощью уравнений
движения, зная состояние материальной
точки в данный момент времени, можно не
только предсказать дальнейшее движение
точки, но ретросказать ее движение, т.е.
восстановить ее движение в предшествующие
моменты времени. Все сказанное относится
не только к одной материальной точке,
но и к системе материальных точек.
Сила, действующая
на материальную точку, одинакова во
всех движущихся друг относительно друга
системах отсчета. Это следует из того,
что сила зависит от расстояния между
взаимодействующими материальными
точками (и, может быть, от относительной
скорости), а эти расстояния (и относительные
скорости) в ньютоновской механике
считаются одинаковыми во всех инерциальных
системах отсчета. Таким образом, F
= F′,
где F
и F′
– силы, действующие на материальную
точку в системах отсчета S
и S′
соответственно. Ускорения и масса тела
также одинаковы во всех инерциальных
системах отсчета. Поэтому если ma
= F
– в системе отсчета S,
то ma′
= F′
– в системе отсчета S′.
Это означает, что уравнения движения
классической механики являются
инвариантными по отношению к преобразованиям
Галилея.
Покажем, что
уравнение движения классической механики
в форме (3.9) является следствием
существования инерциальных систем
отсчета и принципа относительности.
Предположим, что
уравнение движения материальной точки
выражается некоторой вектор-функцией
Ф, зависящей
от радиус-вектора r
материальной точки, времени t
и производных радиус-вектора по времени
первого, второго, третьего и т.д. порядков.
Принцип относительности и свойства
симметрии пространства и времени
накладывают ограничения на число
переменных, входящих в функцию Ф.
Поскольку уравнение движения должно
быть инвариантным относительно
преобразования сдвига в пространстве
r + a,
где a
= const
– вектор трансляции (сдвига), то оно не
должно содержать радиус-вектор r
материальной точки, иначе это уравнение
при указанном преобразовании изменит
свой вид. Точно также, инвариантность
уравнения движения по отношению к
преобразованию сдвига во времени,
где
= const
(сдвиг во времени), исключает явную
зависимость уравнения движения от
времени t.
Инвариантность уравнения движения по
отношению к преобразованию скорости
где
–
скорость движения системы отсчета, т.е.
принцип относительности, требует
исключения из числа аргументов первую
производную радиус-вектора по времени
(скорость материальной точки).
Следует учесть
также уникальность инерциальных систем
отсчета. Этот класс систем отсчета
определяется исключительно только их
скоростью V
и не зависит от высших производных
b
и т.д. Поэтому функция Ф
не может
зависеть от производных более высокого
порядка, чем вторая.
Предположим теперь,
что существует один параметр m,
характеризующий материальную точку.
Тогда функция Ф
запишется в виде
Сделав простейшее допущение, что этот
параметр и производная
входят в функцию Ф
в виде произведения (мультипликативно),
получим
Определив, далее, произведение
как силу, действующую на материальную
точку, придем ко второму закону динамики
и к уравнению (3.9).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Механика твердого тела
Чтобы иметь возможность описать движение тела в математических терминах, мы должны сначала понять тип движения, которому оно подвергается. Используемый вид уравнения движения материальной точки будет варьироваться в зависимости от рассматриваемой ситуации.
Линейное движение
Существует три общих случая линейного движения, характеризующихся типом ускорения, которому оно подвергается. Виды линейного движения:
• прямолинейное равномерное;
• равноускоренное;
• переменное ускорение;
Если положение объекта изменяется по отношению к контрольной точке, то считается, что он находится в движении. Если точка не изменяется, то она находится в состоянии покоя. Для лучшего понимания или для решения различных ситуаций покоя и движения мы выводим некоторые стандартные уравнения, связывающие термины: расстояние, перемещение, скорость материальной точки уравнения движения и ускорение тела с помощью уравнений, называемых — уравнениями движения.
Прямолинейное равномерное движение
Если скорость объекта постоянно фиксирована, то объект не испытывает никакого ускорения или замедления. Его скорость будет оставаться постоянной с течением времени. На него могут действовать или не действовать силы, но нет чистой силы, заставляющей его ускоряться.
Формула
Уравнение движения, используемое в этом случае, простое, в виде:
[v=frac{s}{t}]
Где: v: скорость (в м/с), s: пройденное расстояние или перемещение (в метрах), t: время, необходимое для прохождения этого расстояния (в секундах).
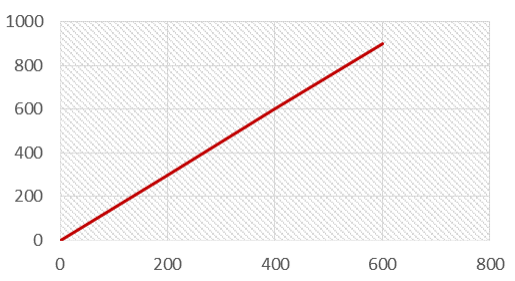
Пример 1. Человеку требуется 10 минут, чтобы дойти от точки А до точки Б. Вычислите расстояние, разделяющее две точки, предполагая, что он все время идет с постоянной скоростью 1,5 м/с.
Ответ: Во-первых, затраченное время необходимо перевести в секунды, чтобы оно соответствовало единицам измерения. Включив значения в уравнение, мы получим расстояние 900 м.
График зависимости расстояния от времени
Равноускоренное движение
В этом случае тело ускоряется с постоянной скоростью на протяжении всего своего движения. Поэтому скорость, с которой оно движется, будет меняться с течением времени.
Типичные графики для этого типа движения приведены ниже.
В случае движения с равномерным или постоянным ускорением (с одинаковым изменением скорости за равный промежуток времени) мы выводим три стандартных уравнения движения, которые также известны как законы постоянного ускорения. Эти уравнения содержат величины перемещения(s), скорости (начальной и конечной), времени(t) и ускорения(a), которые управляют движением тела. Уравнения могут быть применены только в том случае, когда ускорение тела постоянно, а движение является прямой линией.
[v=u+a t]
[
s=u t+frac{1}{2} a t^{2}
]
[
v^{2}=u^{2}+2 a c text {, где }
]
v: конечная скорость (м/с)
u: начальная скорость (м/с)
a: скорость ускорения. Если тело замедляется, то используйте знак минус (м/с2)
t: затраченное время (c)
s: пройденное расстояние (м)
Пример 2. Объект удерживается в состоянии покоя на высоте 12 м над землей. Объект освобождается вовремя t = 0с и свободно падает под действием силы тяжести. Учитывая, что ускорение под действием силы тяжести составляет [9,81 mathrm{м} / mathrm{c}^{2}], найдите его скорость на полпути между начальной точкой и землей.
Ответ: Используем третью формулу движения [left(v^{2}=u^{2}+2 a cright) text { при } mathrm{a}=9,81 mathrm{~m} / mathrm{c}^{2}, mathrm{~s}=6 mathrm{M}, mathrm{u}=0 mathrm{~m} / mathrm{c}]; затем мы получаем ответ 10,85 м/с.
Нет времени решать самому?
Наши эксперты помогут!
Переменное ускорение
Каждый объект, подвергающийся этому типу движения, будет иметь определенное уравнение, описывающее его перемещение, скорость и ускорение в определенные моменты времени. Зная одно из этих уравнений, можно определить другие, интегрируя или дифференцируя их по времени. Для этого типа движения важно иметь в виду следующее:
Скорость (v) — скорость изменения расстояния (s) со временем (t) или в терминах исчисления: [frac{d s}{d t}].
Ускорение (a) — это скорость изменения скорости (v) со временем (t) или в терминах исчисления: [frac{d^{2} s}{d t^{2}}].
Пример 3. Тело движется в пространстве со скоростью, заданной уравнением [v=4 t^{2}+6]. Найдите его скорость, пройденное расстояние и ускорение за время t = 5 с.
Ответ: Скорость можно легко найти, включив t = 5 с в приведенное выше уравнение, что дает v = 506 м/с. Ускорение также можно найти, дифференцируя v и используя t = 5 с. Чтобы определить пройденное расстояние, нам нужно интегрировать v используя пределы t = 0 с и t = 5 с.
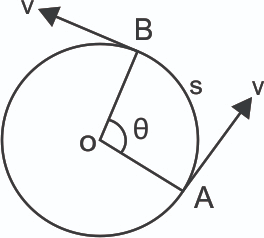
Движение по окружности
Рассмотрим тело, которое движется по окружности вокруг точки O, как показано ниже.
Если телу потребуется время t чтобы сделать угол θ в точке O, то мы можем найти ее угловую скорость, используя:
[omega=frac{theta}{t}]
Период T для завершения объектом полного оборота задается формулой:
[T=frac{2 pi}{w}]
Пройденное расстояние s рассчитывается:
[s=r theta]
Линейную скорость также можно найти, разделив последнее уравнение на затраченное время t:
[frac{s}{t}=r frac{theta}{t}]
[v=r omega]
Чтобы тело оставалось в круговом движении, необходима сила, притягивающая его к центру. В противном случае объект сойдет с орбиты по прямой линии в соответствии с Первым законом Ньютона. Эта сила также известна как центростремительная сила, и она вызывает ускорение тела. Направление ускорения направлено к центру, которое совпадает с направлением центростремительной силы. Центростремительное ускорение может быть рассчитано как:
[a=frac{u^{2}}{r}]
[a=r omega^{2}]
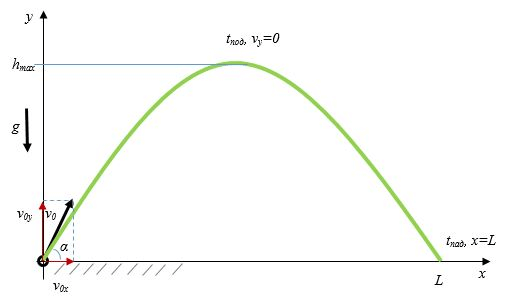
Движение снаряда
Рассмотрим движение снаряда, брошенного под углом x. Градусы относительно земли показаны ниже.
Вектор скорости u может быть разложен на 2 компонента [u_{x} text { и } u_{y} .]
[u_{x}=u cos x]
[u_{y}=u sin x]
Как только снаряд будет выпущен, его траектория будет зависеть от двух вещей: его начальной скорости и ускорения, вызванного гравитацией.