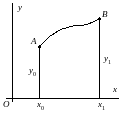
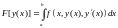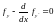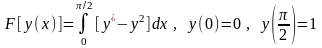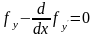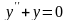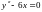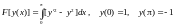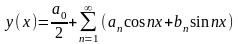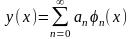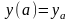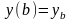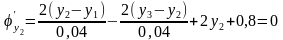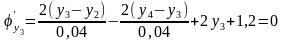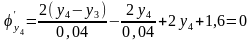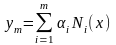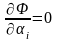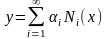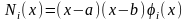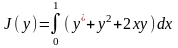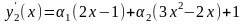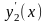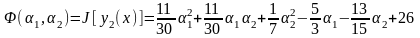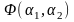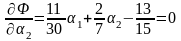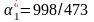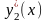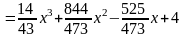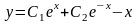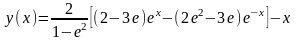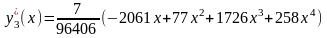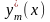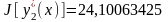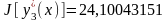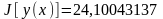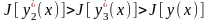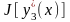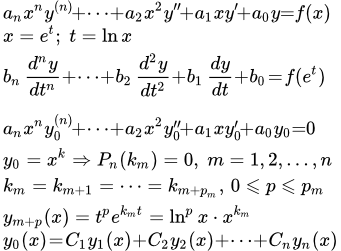Исследуем на экстремум функционал
,
(6.1)
причем граничные
точки допустимых кривых закреплены:
y(a)=y0
и y(b)=y1.
Будем полагать, что
подынтегральная функция имеет непрерывные
частные производные до 2-го порядка
включительно по всем своим аргументам.
Пусть множество M
образовано гладкими (т.е. y(x)c1[a,b])
кривыми, проходящими через точки A
и B (см. рис.).
Простейшая задача вариационного
исчисления состоит в отыскании на
множестве M той кривой,
на которой функционал (6.1) достигает
экстремума.
М
ожно
показать, что необходимое условие
экстремума этого функционала приводит
к уравнению
,
называемому
уравнением Эйлера. Таким образом, для
того чтобы функционал достигал на
некоторой функции y(x) экстремума,
необходимо, чтобы эта функция удовлетворяла
уравнению Эйлера.
Уравнение Эйлера в общем случае является
дифференциальным уравнением 2-го порядка.
Его интегральные кривые y=y(x,C1,C2)
называются экстремалями. Только на
экстремалях может достигаться экстремум
функционала (6.1).
Для нахождения
кривой, реализующей экстремум функционала
(1), следует проинтегрировать уравнение
Эйлера и из условий на границе
y(a)=y0
и y(b)=y1
определить обе произвольные постоянные
С1 и С2, входящие
в общее решение этого уравнения. Только
на удовлетворяющих этим условиям
экстремалях может реализоваться
экстремум функционала. Однако для того
чтобы установить, реализуется ли на них
в действительности экстремум, и притом
максимум или минимум, нужно воспользоваться
достаточными условиями экстремума,
которые приведены в специальной
литературе.
Краевая задача

как известно, не всегда имеет
решение, а если решение существует, то
оно может быть не единственным. Заметим,
что во многих вариационных задачах
существование решения очевидно из
физического или геометрического смысла
задачи.
Пример
1. На каких
кривых может достигать экстремума
функционал
?
Имеем
.
Составляем
уравнение Эйлера
:
.
Общее решение:
y=С1cosx+С2sinx.
Из граничных условий: y(0)=С11+С20=0,
y(/2)=С10+С21=1С1=0,
С2=1.
Следовательно, экстремум может достигаться
лишь на кривой y=sinx.
Пример 2.
.
Уравнение Эйлера:
y(x)=x3+С1x+С2,
y(0)=С2=0;
y(1)=1+С1=1
С1=0.
Ответ: y=x3.
Пример 3.
.
Экстремали данной задачи определяются
уравнением y(x)=С1cosx+С2sinx
(см. пример 1). В граничных точках:
y(0)=С1=1,
y()=–С1=–1.
Таким образом, граничные условия
определяют лишь постоянную
С1, а
константа С2 может
выбираться произвольно. Итак, искомая
функция имеет вид y(x)=cosx+Сsinx
(С – произвольная постоянная), т.е.
задача имеет бесконечное множество
решений.
6.3 О прямых методах вариационного исчисления
Дифференциальные уравнения (Эйлера)
вариационных задач интегрируются в
конечном виде лишь в исключительных
случаях. В связи с этим естественно
возникает потребность в иных методах
решения этих задач. Основная идея так
называемых прямых методов заключается
в том, что вариационная задача
рассматривается как предельная для
некоторой задачи на экстремум функции
конечного числа переменных. Эта задача
на экстремум функции конечного числа
переменных решается обычными методами
математического анализа и алгебры.
Функционал F[у(х)]
можно рассматривать как функцию
бесконечного множества переменных. Это
утверждение становится совершенно
очевидным, если предположить, что
допустимые функции могут быть разложены
в степенные ряды
y(x)
= a0
+ a1
x + a2
x2 +
… + an
xn
+…,
или в ряды
Фурье
,
или вообще в
какие-нибудь ряды вида
,
(6.2)
где (x)
— заданные функции. Для задания
функции у(x), представимой в виде
ряда (6.2), достаточно задать значения
всех коэффициентов {an },
и, следовательно, значение функционала
F[y(x)] в этом случае определяется
заданием бесконечной последовательности
чисел a0, a1, a2,
… , an, …, т. е. функционал
является функцией бесконечного множества
переменных:
F[y(x)]=
(a0,
a1, … , an,
…).
Следовательно, различие между вариационными
задачами и задачами на экстремум функций
конечного числа переменных состоит в
том, что в вариационном случае приходится
исследовать на экстремум функции
бесконечного множества переменных.
Л. Эйлер для решения
вариационных задач применял метод,
называемый теперь конечно-разностным
прямым методом. Пусть, к примеру, требуется
найти решение простейшей задачи
вариационного исчисления:
;
,
.
Идея конечно-разностного метода
заключается в том, что значения функционала
F[y(x)]
рассматриваются не на произвольных,
допустимых в данной вариационной задаче,
кривых, а лишь на ломаных, составленных
из заданного числа п прямолинейных
звеньев с заданными абсциссами вершин:
a+x,
a+2x,
… , a+(n–1)x,
где
.
На таких ломаных
функционал F[y(x)]
превращается в функцию (y1,y2,…,yn–1)
ординат y1,y2,…,yn–1
вершин ломаной, так как ломаная вполне
определяется этими ординатами.
Итак, разбивая отрезок [a,
b] на n
равных частей точками
функционал
F(y)
можно приблизить на основе какой-либо
квадратурной формулы, например
прямоугольников, выражением
,
x=(b–a)/n,
yiy(a+ix),
так что задача
оптимизации теперь имеет место для
функции n–1
переменной y1, … , yn–1.
Выбираем ординаты y1,
y2,…,
yn–1 так, чтобы функция
(y1,y2,…,yn–1)
достигала экстремума, т.е. определяем
y1, y2,…,
yn–1 из системы
уравнений
,
,
…,
.
В пределе при
n→
с учетом некоторых ограничений, налагаемых
на функцию f,
получим точное решение вариационной
задачи. Удобнее, однако, не совершать
предельного перехода и значение
функционала F(y)
на указанных ломаных вычислять
приближенно.
Пример 4. Найти экстремум функционала
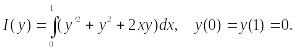
Решение. Отрезок
[0, 1] разбивается на пять отрезков:
Тем самым получаем приближенную задачу
на нахождение экстремума функционала
,
которая решается
методами дифференциального исчисления:
;
;
;
.
В табл. 6.1 сравниваются yi,
полученные на основе данного приближения,
с точными значениями y(0,2i)
(округленными до четвертого знака).
Таблица 6.1
|
i |
yi |
y(0,2i) |
|
1 2 3 4 |
–0,0286 –0,0503 –0,0580 –0,0442 |
–0,0287 –0,0505 –0,0583 –0,0444 |
Ниже приводится листинг программы для
пакета Maple, с помощью которой легко
выполнить указанные вычисления.
> restart;
> a:=0;
b:=1; ya:=0; yb:=0; n:=5; #
исходные
данные
>
h:=evalf((b-a)/n);
#
шаг
x
> g:=diff(y(x),x)^2+y(x)^2+2*x*y(x);
#
подынтегральная
функция в функционале
>
s1:=subs(diff(y(x),x)=(y1-y0)/h,y(x)=y0,
x=a,g);
#
вычисление
функции g
в узловых точках xi
>
s2:=subs(diff(y(x),x)=(y2-y1)/h,y(x)=y1,x=a+h,g);
>
s3:=subs(diff(y(x),x)=(y3-y2)/h,y(x)=y2,x=a+2*h,g);
>
s4:=subs(diff(y(x),x)=(y4-y3)/h,y(x)=y3,x=a+3*h,g);
>
s5:=subs(diff(y(x),x)=(y5-y4)/h,y(x)=y4,x=a+4*h,g);
>
F:=s1+s2+s3+s4+s5;
#
функционал
>
eqns:={diff(F,y1)=0,diff(F,y2)=0,diff(F,y3)=0,
diff(F,y4)=0,
y0=ya,y5=yb};
#
система
уравнений
>
rez:=solve(eqns,{y0,y1,y2,y3,y4,y5});
#
решение
rez
:= {y3
= –.05808400444,
y2
= –.05033254335,
y4
= –.04415882571,
y1
= –.02859438400,
y0
= 0, y5
= 0}
Метод Эйлера не имеет никаких преимуществ
перед другим прямым методом – методом
Ритца, а часто даже уступает ему из-за
более низкой точности и слишком большого
числа неизвестных параметров и поэтому
на практике используется редко.
Идея метода Ритца заключается в
том, что значения некоторого функционала
F[y(x)] рассматриваются не на
произвольных допустимых кривых данной
вариационной задачи, а лишь на всевозможных
линейных комбинациях вида
с постоянными коэффициентами, составленных
из m первых функций
некоторой выбранной последовательности
функций, называемых координатными или
базисными,
N1(x),
N2(x),
…, Nm(x),
….
Функции
должны быть допустимыми в рассматриваемой
задаче, что налагает некоторые ограничения
на выбор последовательности функций
Ni(x).
На таких линейных комбинациях функционал
F[y(x)] превращается в функцию
(1,
2, …, m)
коэффициентов 1,
2, …, m
. Эти коэффициенты выбираются так,
чтобы функция (1,
2, …, m)
достигала экстремума; следовательно,
1, 2,
…, m
должны быть определены из системы
уравнений
,
i = 1, 2,…, m.
Совершая предельный переход при m,
получим в случае существования предела
функцию
,
являющуюся точным решением рассматриваемой
вариационной задачи. Если не совершать
предельного перехода, а ограничиться
лишь m первыми членами,
то получим приближенное решение
вариационной задачи.
Если таким методом определяется
абсолютный минимум функционала, то
приближенное значение минимума
функционала находится с избытком. При
нахождении тем же методом максимального
значения функционала получим приближенное
значение максимума функционала с
недостатком.
Выбор последовательности функций N1,
N2…, Nm
сильно влияет на степень сложности
дальнейших вычислений, и поэтому от
удачного выбора базисной системы функций
в значительной мере зависит успех
применения этого метода.
Для того чтобы функции
были допустимыми, прежде всего, необходимо
удовлетворить граничным условиям
(конечно, не следует забывать и о других
ограничениях, которые могут быть наложены
на допустимые функции, например,
требованиях, касающихся их непрерывности
или гладкости, а также полноты).
Рассмотрим подходы к решению простейшей
задачи вариационного исчисления методом
Ритца. В этой задаче граничные условия
1-го рода y(a)=y0,
y(b)=y1
обычно играют роль главных условий.
Поэтому множество допустимых функций,
на которых ищется экстремум, приходится
ограничивать только теми функциями,
которые априори удовлетворяют этим
условиям. Применительно к методу Ритца
это означает выбор такой аппроксимации
,
которая заведомо удовлетворяет указанным
условиям вне зависимости от того, какие
значения принимают параметры {i}.
Если граничные условия однородны, т.е.
y(a)=y(b)=0,
то проще всего в качестве базисных
функций выбрать функции, удовлетворяющие
этим граничным условиям: Ni(a)=Ni(b)=0,
i=1,
2, …, m. Например,
,
где i(x)
– какие-нибудь непрерывные функции,
или
(k=1,
2, …).
Очевидно, что при этом и аппроксимация
при любых i
будет удовлетворять тем же однородным
граничным условиям.
Если условия неоднородны, т.е. у(a)=y0,
у(b)=y1,
где хотя бы одно из чисел y0
или y1 отлично от нуля, то
решение вариационной задачи можно
искать в виде
,
(6.3)
где (x)
удовлетворяет заданным граничным
условиям: (a)=y0,
(b)=y1
, а функции Ni(x)
удовлетворяют соответствующим однородным
граничным условиям, т.е. в рассматриваемом
случае Ni(a)=Ni(b)=0.
Очевидно, что при таком выборе при любых
i функции
ym(x)
удовлетворяют заданным граничным
условиям. В качестве функций (x)
можно выбрать, например, линейную функцию
.
(6.4)
Пример 5. Найти экстремаль функционала
;
y(0)=4,
y(1)=5.
Решение.
Здесь граничные условия неоднородные,
поэтому в аппроксимации (3) функция (x)
отлична от нуля и удовлетворяет этим
условиям. В качестве (x)
согласно (4) возьмём (x)=x+4
(проверьте для a=0,
b=1,
y0=4,
y1=5).
В качестве базисных функций выбираем
Nk(x)=xk+1–xk,
k=1,
2, 3, … . Эти функции удовлетворяют
однородным граничным условиям
Nk(0)=Nk(1)=0.
Для m=2
имеем
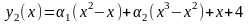
и
.
После подстановки
и
в функционал J и
интегрирования получим
.
Воспользовавшись необходимыми условиями
экстремума функции
,
находим
,
.
Решив систему, получим
,
.
Следовательно, приближенное выражение
для экстремали y(x)
имеет вид
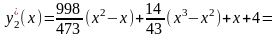
.
В данном случае существует точное
решение поставленной задачи. Действительно,
составляя уравнение Эйлера, получим
,
которое является линейным неоднородным
дифференциальным уравнением с постоянными
коэффициентами. Его общее решение
.
С учетом краевых условий y(0)=4,
y(1)=5,
находим
.
Сравним полученное методом Ритца
приближенное решение
и
точное при некоторых значениях аргумента
(табл. 6.2).
Таблица 6.2
|
x |
0,0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
|
y(x) |
4,000 |
3,85074 |
3,86405 |
4,04850 |
4,41951 |
5,000 |
|
4,000 |
3,85199 |
3,86235 |
4,04673 |
4,42073 |
5,000 |
|
|
|
0,000 |
3,85075 |
3,86409 |
4,04847 |
4,41949 |
0,000 |
Сравнение показывает, что точное и
приближенное решение совпадают с
точностью до 0,002. Это число может служить
характеристикой погрешности
аппроксимации.
Представленные шаги решения данной
задачи могут быть реализованы в пакете
компьютерной математики Maple с помощью
команд:
> restart;
> z:=x->((a1+a2*x)*x*(x-1)+x+4);
#
аппроксимация решения
>
F:=int((diff(z(x),x))^2+z(x)^2+2*x*z(x),
x=0..1);
#
функционал
>
eqns:={diff(F,a1)=0,diff(F,a2)=0};
#
система
уравнений
>
r:=solve(eqns,{a1,a2});
evalf(“);
#
решение
системы
>
phi:=x->subs(r,z(x)):
phi(x); collect(phi(x),x);
>
t:=dsolve({diff(diff(y(x),x),x)-y(x)=x,
y(0)=4,y(1)=5},y(x));
#
получение точного решения
> for
t
from
0 by
0.2 to
1 do
printf(`x=%3.1g
z=%7.5g
u=%7.5gn`,t,phi(t),u(t));
od;
#
табулирование
найденного приближенного и точного
решений
Если в сумме
взять три слагаемых, то получим
трехэлементную аппроксимацию
.
Путем аналогичного применения процедуры
Ритца получим
.
В приведенном тексте Maple-программы для
этого нужно поменять соответствующие
строки:
>
z:=x->((a1+a2*x+a3*x^2)*x*(x-1)+x+4);
>
eqns:={diff(F,a1)=0,diff(F,a2)=0,diff(F,a3)=0};
>
r:=solve(eqns,{a1,a2,a3});
Из табл. 6.2 видно, что данное приближенное
решение отличается от точного решения
уже не более чем на 410–5.
Таким образом, трехэлементная аппроксимация
дает на два порядка лучший результат,
чем двухэлементная аппроксимация. Если
с увеличением числа параметров (элементов)
аппроксимации 1,
2, …, m
приближенное решение
стремится к точному решению y(x),
то говорят, что имеется сходимость
аппроксимации. Скорость сходимости
является характеристикой процесса
сходимости, позволяющей судить о том,
как быстро
приближается к y(x)
c увеличением m.
В рассмотренном примере сходимость,
очевидно, имеет место, а скорость
сходимости достаточно высокая: добавление
одного элемента аппроксимации привело
к добавлению как минимум одной верной
значащей цифры. Еще можно сказать о
хороших аппроксимирующих
свойствах функций Ni(x)=xi+1–xi,
i=1,2,…,
поскольку всего первые три такие функции
обеспечивают четыре верных знака в
значениях искомой функции.
Всем приведенным характеристикам можно
дать строгие определения, используя
различные метрики конечномерных
функциональных пространств. Подробное
изложение этого вопроса, выходит за
рамки данных методических указаний.
Для иллюстрации факта, что в методе
Ритца минимальное значение функционала
определяется с избытком, вычислим три
числа:
;
;
.
Видно, что
,
т.е. приближенные значения функционала
стремятся к точному значению сверху.
Отметим характерную для прямых методов
особенность: с увеличением числа
элементов аппроксимации ошибка вычисления
функционала уменьшается быстрее, чем
ошибка вычисления функции
.
В рассматриваемом случае при переходе
от
к
имеем у функционала
три новых верных значащих цифры, в то
время как значения самой функции
стали точнее лишь на одну-две цифры.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение эйлера для функционала примеры
Пример 2.1. Рассмотрим пример, который легко решить аналитически. Требуется найти экстремум функционала
при граничных условиях
Найдём частные производные и
Вычислим полную производную по x от
Составляем дифференциальное уравнение Эйлера вида
или, после упрощений
Его общее решение имеет вид
Для нахождения произвольных постоянных C1 и C2 подставим решение (2.16) в граничные условия (2.11):
Видно, что система (2.17) имеет единственное решение. Решая эту систему, найдём значения C1 и C2:
и тогда уравнение экстремали имеет вид:
Действительно ли на этой кривой достигается экстремум? И если да, то какой: минимум или максимум? Далее, в главе 13, мы рассмотрим достаточные условия экстремума . В частности, мы выведем условие Лежандра: если на экстремали выполняется условие а на функциях, близких к экстремали, для произвольных y‘ имеет место то достигается сильный минимум. В нашем случае это выполняется:
и, следовательно, на нашей экстремали достигается сильный минимум. Проверим этот результат: вычислим на нескольких функциях вида Эти функции удовлетворяют граничным условиям (2.11) и, следовательно, являются допустимыми. Для вычислений применим MATLAB.
Действительно, полученный результат не противоречит выводу о том, что на функции достигается минимум. Но, конечно же, проведенная проверка не доказывает этот факт. Ведь мы проверили только несколько из бесконечного числа функций, графики которых проходят через точки и Доказательством могут служить необходимые и достаточные условия экстремума функционала.
Пример 2.2. Найти экстремаль функционала
при граничных условиях
Выводим уравнение Эйлера вида (2.9). Частные производные:
Уравнение Эйлера после упрощений имеет вид:
Его общее решение
Находим произвольные постоянные из граничных условий (3.22). Подставляем решение (3.25) в эти граничные условия:
Мы видим, что из полученной системы уравнений можно найти только а C2 может быть произвольной. Поэтому данная вариационная задача имеет бесчисленное множество решений вида
На любой из этих функций функционал принимает постоянное значение (какое − мы сейчас посчитаем). Проверка по достаточному условию Лежандра даёт:
поэтому на экстремалях (3.27) достигается сильный минимум.
Посчитаем значение функционала (2.21) на функциях вида (2.27) и нарисуем несколько экстремалей с помощью MATLAB.
На каждой из наших функций функционал равен нулю.
2.2. Частные случаи уравнений Эйлера
Иногда решение уравнения Эйлера существенно упрощается. Рассмотрим соответствующие частные случаи.
2.2.1. Подынтегральная функция F не зависит явно от y‘
Материал этого подраздела изложен в книге.
2.2.2. Подынтегральная функция F линейно зависит от y‘
Материал этого подраздела изложен в книге.
2.2.3. Подынтегральная функция F не зависит явно от y
Материал этого подраздела изложен в книге.
2.2.4. Подынтегральная функция F зависит только от y‘
Материал этого подраздела изложен в книге.
2.2.5. Подынтегральная функция F не зависит явно от x
Материал этого подраздела изложен в книге.
2.3. Вопросы для самопроверки
- Какую вариационную задачу мы решаем?
- Как выводится дифференциальное уравнение Эйлера?
- Где используется в выводе дифференциального уравнения Эйлера основная лемма вариационного исчисления?
- Почему обращается в нуль внеинтегральное слагаемое в формуле (2.8) при интегрировании по частям?
- Чем отличается частная производная от полной?
- Какие Вы знаете методы решения дифференциальных уравнений порядка?
- Всегда ли решение вариационной задачи будет единственным? От чего это зависит?
- Какие частные случаи уравнения Эйлера Вы знаете?
- В каких случаях уравнение Эйлера перестаёт быть дифференциальным и становится конечным?
- В каких случаях вариационная задача теряет смысл?
- Как записывается интеграл уравнения Эйлера, если подынтегральная функция F не зависит явно от y?
- Каким будет решение уравнения Эйлера, если подынтегральная функция F зависит только от y‘?
- Как решается уравнение Эйлера, если подынтегральная функция F не зависит явно от y‘?
- Как решается задача о брахистохроне?
2.4. Примеры выполнения заданий
2.4.1. Задание 1
Найти экстремаль функционала
Исследовать полученную экстремаль на достаточные условия экстремума. Вычислить значение функционала на найденной экстремали и, для сравнения, на прямой, соединяющей точки и Построить график решения.
В этом примере подынтегральная функция является функцией общего вида, поэтому составим уравнение Эйлера в виде (2.9) и решим его. Затем построим график решения. Попутно исследуем на выполнение достаточных условий экстремума и вычислим значение функционала на экстремали и отрезке прямой M1M2. Применим для решения задачи MATLAB.
Очистим память. Напечатаем заголовок решаемой задачи. Если хотите, задайте другую строку для вывода (например, свою фамилию). Опишем символические переменные [58]. Для решения уравнения Эйлера используем принятые в MATLAB обозначения производных: Dy для y‘ и D2y для y”. Аргумент обозначим x , а функцию − y .
Вводим подынтегральную функцию и граничные условия. Печатаем их. Здесь вы должны поставить свои исходные данные: подынтегральную функцию F и граничные условия x1, y1, x2, y2.
Начинаем вывод дифференциального уравнения Эйлера (2.9). Найдём частные производные Fy и Fy’. Напечатаем их.
В уравнение Эйлера (2.9) входит полная производная Вычислим её по обычной формуле дифференцирования сложной функции:
Напечатаем её. Напечатаем также величину необходимую для проверки достаточных условий экстремума по признаку Лежандра.
Составим левую часть дифференциального уравнения Эйлера (2.9) и упростим её. Преобразуем символическую переменную Euler в строку.
Мы составили уравнение Эйлера, теперь решим его. Команда dsolve позволяет находить как общее решение дифференциального уравнения, так и частное его решение, удовлетворяющее заданным начальным или граничным условиям. В следующих главах при решении других заданий нам нужно будет иметь общее решение уравнения Эйлера. Найдём его.
Сформируем теперь уравнения для граничных условий. Подставим в найденное аналитическое решение Sol граничные точки x1 и x2 , и приравняем их соответственно y1 и y2 .
Решаем полученную систему конечных уравнений − находим значения произвольных постоянных C1 и C2 . Присваиваем найденные решения символическим константам, полученным при решении дифференциального уравнения. Теперь вычисляем аналитическое решение Sol21 . Такое вычисление сводится к тому, что в него будут подставлены найденные значения констант C1 и C2 . Печатаем найденное уравнение экстремали.
Вычислим значения функционала (2.86) на найденной экстремали и на прямой, соединяющей точки M1 и M2. Подставим в подынтегральную функцию F аналитические выражения для этих линий и их производных, а затем проинтегрируем. Напечатаем результаты.
В данном примере условие Лежандра говорит о сильном минимуме, что подтверждается полученным результатом: значение функционала на экстремали меньше, чем на другой допустимой функции. А как в вашем варианте: какой экстремум достигается? И подтверждается ли этот результат сравнением величин Jextr и Jlin ? Если нет, то не забудьте, что найденный экстремум − только локальный, а не глобальный! Попробуйте вычислить значение функционала не на прямой M1M2, а на какой-нибудь другой допустимой кривой, достаточно близкой к экстремали. Например, можно наложить на экстремаль несколько полуволн синусоиды, смещённой и деформированной вдоль оси Ox так, что
И, наконец, строим график. Задаём массив аргументов для рисования графика функции и вычисляем значения функции. Рисуем график, подписываем заголовок и координатные оси установленным шрифтом.
2.4.2. Задание 2
Найти экстремаль функционала
Исследовать на выполнение достаточных условий экстремума. Построить график решения.
В этом примере подынтегральная функция не зависит явно от y. Первый интеграл уравнения Эйлера имеет вид (2.43). Составим программу для решения этой вариационной задачи. Вначале введём исходные данные. У нас будет первый интеграл уравнения Эйлера, поэтому ни сама функция y, ни её вторая производная y” нам не нужны, и мы их не описываем. Поставьте свою подынтегральную функцию и граничные условия.
Строим первый интеграл и решаем полученное дифференциальное уравнение. Названия констант C1 и C2 используются в команде dsolve , поэтому при составлении интеграла уравнения Эйлера обозначим константу C . Все использованные здесь функции и операторы MATLAB были описаны ранее, в примере 1.
В переменной Sol получено общее решение, произвольные постоянные обозначены C и C1 . Найдём их. Для этого подставим в Sol граничные точки. Приравняем полученные выражения соответственно y1 и y2 . Тем самым мы сформируем систему уравнений.
Решим полученную систему − найдём произвольные постоянные C и C1 . Подставим их в решение Sol . Ограничим решение 14 знаками. Напечатаем уравнение найденной экстремали.
Дальнейшие действия не отличаются от описанных в примере 1. Рисуем график и и вычисляем Fy’y’, которая нужна для проверки достаточных условий экстремума по признаку Лежандра.
Проанализируйте достаточное условие Лежандра. Достигается ли экстремум на вашей экстремали? Если да, то какой?
2.4.3. Задание 3
Решить задачу о брахистохроне, соединяющей точки и
Мы уже решили эту задачу аналитически. Нам осталось найти значение константы C1 и параметра в конечной точке t2 из решения системы уравнений (2.84). Составим программу для решения этого примера. Вначале введём исходные данные задачи. Подставьте свою правую точку.
Составляем систему уравнений (2.84). Левую часть каждого уравнения мы задаём сразу в виде строки. В правой части переводим числа x2 и y2 в их строковые представления с помощью функции num2str . Ранее мы использовали конструкцию char(sym(y2)) . Оба варианта работают правильно − вы можете это проверить. Решаем полученную систему уравнений аналитически. Печатаем решения.
Рисуем график полученной брахистохроны. Выбираем начало координат в левом верхнем углу с помощью команды axis . Задаём границы по оси Ox, чтобы график занимал всё место на рисунке. Выравниваем масштабы по осям координат, чтобы брахистохрона выглядела неискажённой. Надписываем заголовок и метки осей.
2.5. Задание
Для своего варианта функционалов 1, 2, 3 найти экстремали, построить их графики и исследовать на выполнение достаточных условий экстремума.
Дифференциальное уравнение Эйлера и методы его решения
Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.
Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.
Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;
;
;
.
Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.
Решение однородного уравнения Эйлера
Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.
Рассмотрим действительные корни. Пусть ki – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.
Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть ki – кратный корень кратности m . Выразим комплексный корень ki через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.
После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .
Примеры
Решение неоднородного уравнения Эйлера
Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.
Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).
Пример
Неоднородное уравнение Эйлера со специальной неоднородной частью
Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.
Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.
Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020
Дифференциальное уравнение Эйлера
Напомним, что необходимым условием существования у дифференцируемой функции экстремума в некоторой точке является равенство нулю производной в этой точке: , или, что то же самое, равенство нулю дифференциала функции .
Нашей ближайшей целью будет найти аналог этого условия в вариационном исчислении и выяснить, какому необходимому требованию должна удовлетворять функция, дающая экстремум функционалу.
Мы покажем, что такая функция должна удовлетворять некоторому дифференциальному уравнению. Форма уравнения будет зависеть от вида рассматриваемого функционала. Изложение мы начнем с так называемого простейшего интеграла вариационного исчисления, под которым подразумевают функционал, имеющий следующее интегральное представление:
Функция , стоящая под знаком интеграла, зависит от трех аргументов . Будем считать ее определенной и дважды непрерывно дифференцируемой по аргументу для всех значений, по аргументам же и — в некоторой области плоскости . Ниже предполагается, что мы всегда будем находиться внутри этой области.
Под понимается некоторая функция от
непрерывно дифференцируемая на отрезке , и есть производная от нее.
Геометрически функцию можно изобразить в плоскости некоторой линией , лежащей над отрезком (рис. 3).
Интеграл (9) является обобщением интегралов (3) и (6), с которыми мы встретились в задачах о линии наискорейшего ската и поверхности вращения наименьшей площади. Значение его зависит от выбора функции или от линии , и задача о его минимуме имеет следующий смысл.
Дано некоторое множество функций (10) (линий ). Среди них нужно найти ту функцию (линию ), для которой интеграл имеет наименьшее значение.
Мы должны прежде всего точно определить множество функций, для которых мы будем рассматривать значение интеграла (9). Функции этого множества в вариационном исчислении обычно называют допустимыми к сравнению. Рассмотрим задачу с закрепленными граничными значениями. Множество допустимых функций определяется здесь двумя следующими требованиями:
1) функция непрерывно дифференцируема на отрезке ;
2) на концах отрезка функция принимает заданные наперед значения
В остальном функция может быть совершенно произвольной. Если говорить языком геометрии, мы рассматриваем всевозможные гладкие линии, лежащие над промежутком , которые проходят через две точки и и могут быть заданы уравнением (10). Функцию, доставляющую минимум интегралу, будем считать существующей и назовем ее .
Следующие простые и остроумные соображения, часто применяемые в вариационном исчислении, дают возможность весьма просто выяснить необходимое условие, которому должна удовлетворять . По сути дела они позволяют задачу о минимуме интеграла (9) привести к задаче о минимуме функции.
Рассмотрим семейство функций, зависящее от численного параметра
Чтобы функция при любом была допустимой функцией, мы должны считать непрерывно дифференцируемой и обращающейся в нуль на концах отрезка
Интеграл (9), вычисленный для , будет некоторой функцией параметра
Разность называют вариацией (изменением) функции и обозначают , а разность — полной вариацией интеграла (9). Отсюда и произошло название вариационного исчисления.
Так как функция дает минимальное значение интегралу, то функция должна иметь минимум при , и производная от нее в этой точке обязана обращаться в нуль
Последнее равенство должно выполняться при всякой непрерывно дифференцируемой функции , обращающейся в нуль на концах отрезка . Для получения вытекающего отсюда следствия удобнее второй член в условии (14) преобразовать интегрированием по частям
и придать условию (14) другую форму
Может быть доказана следующая простая лемма.
Пусть выполняются условия:
1) функция непрерывна на отрезке ;
2) функция непрерывно дифференцируема на отрезке и на концах отрезка обращается в нуль.
Если при любой такой функции интеграл равен нулю, то отсюда следует, что .
Действительно, допустим, что в некоторой точке с функция отлична от нуля, и покажем, что тогда заведомо существует такая функция , для которой , вопреки условию леммы.
Так как и непрерывна, наверное существует около точки такой промежуток , в котором будет всюду отличной от нуля и, стало быть, сохранять знак.
Всегда можно построить функцию , непрерывно дифференцируемую на , положительную на и равную нулю всюду вне (рис. 4).
Такой будет, например, , определенная равенствами
Но для такой функции
Последний же интеграл не может быть равен нулю, так как произведение внутри промежутка интегрирования отлично от нуля и сохраняет знак.
Ввиду того, что равенство (15) должно выполняться для всякой , непрерывно дифференцируемой и обращающейся в нуль на концах отрезка , мы можем, согласно лемме, утверждать, что это может быть только в том случае, когда
или после вычисления производной по переменной
Равенство это является дифференциальным уравнением 2-го порядка относительно функции . Оно называется уравнением Эйлера .
Мы можем сделать следующее заключение.
Если функция доставляет интегралу минимум, то она должна удовлетворять дифференциальному уравнению Эйлера (17). Последнее в вариационном исчислении имеет значение, вполне сходное со значением необходимого условия в теории экстремумов функций. Оно позволяет сразу отбросить все допустимые функции, которые этому условию не удовлетворяют, так как на них интеграл заведомо не может достигать минимума. Этим очень сильно сужается круг допустимых функций, подлежащих изучению. Свое внимание мы можем сосредоточить только на решениях уравнения (17).
Сами решения уравнения (17) обладают тем свойством, что производная
для них обращается в нуль при любых , и они аналогичны по своему значению стационарным точкам функции. Поэтому часто говорят, что на решениях (17) интеграл имеет стационарное значение.
В нашей задаче с закрепленными граничными значениями нужно найти далеко не все решения эйлерова уравнения, а только те из них, которые принимают предписанные значения в точках .
Обратим внимание на то, что уравнение Эйлера (17) имеет 2-й порядок. Общее его решение будет содержать две произвольные постоянные
Их нужно определить так, чтобы интегральная кривая проходила через точки и , что доставляет два уравнения для нахождения постоянных и
Во многих случаях эта система имеет только одно решение, и тогда будет существовать только одна интегральная линия, проходящая через точки и .
Разыскание функций, подозрительных на минимум интеграла, мы привели к решению следующей граничной задачи дифференциальных уравнений: на отрезке нужно найти те решения уравнения (17), которые на концах этого отрезка принимают заданные значения .
Часто эту последнюю задачу удается решить при помощи методов, известных в теории дифференциальных уравнений.
Еще раз указываем на то, что каждое решение такой граничной задачи может только подозреваться на минимум и в дальнейшем еще надлежит проверить, будет ли оно или не будет доставлять минимальное значение интегралу. Но в частных случаях, особенно часто встречающихся в приложениях, уравнение Эйлера вполне решает задачу о нахождении минимума интеграла. Пусть нам заранее будет известно, что функция, доставляющая минимум интегралу, существует, и мы допустим, кроме того, что уравнение Эйлера (17) имеет только одно решение, удовлетворяющее граничным условиям (11), и, стало быть, только одна допустимая линия может быть заподозрена на минимум. При этих условиях можно быть уверенным в том, что найденное решение уравнения (17) действительно дает минимум интегралу.
Пример . Ранее было установлено, что [url]задача о линии наискорейшего ската[/url] может быть приведена к нахождению минимума интеграла
на множестве функций, удовлетворяющих граничным условиям .
[spoiler title=”источники:”]
http://1cov-edu.ru/differentsialnye-uravneniya/lineinie_postoyannie_koeffitsienti/eilera/
http://mathhelpplanet.com/static.php?p=differentsialnoe-uravnenie-eilera
[/spoiler]
В математике (дифференциальных уравнениях) уравнение Коши — Эйлера (Эйлера — Коши) является частным случаем линейного дифференциального уравнения, приводимым к линейному дифференциальному уравнению с постоянными коэффициентами, которое имеет простой алгоритм решения.
Уравнение порядка n[править | править код]
Общий вид уравнения :
.
Его частный случай :
.
Подстановка[править | править код]
,
.
что, аналогично, приводит к
Эта цепь вычислений может быть продолжена до любого порядка n
Пример[править | править код]
Дано неоднородное уравнение
.
Определив подстановку 

приходим к уравнению
.
После приведения имеем линейное неоднородное уравнение с постоянными коэффициентами
,
решение которого имеет вид
или в терминах
Уравнение второго порядка[править | править код]
Общий вид уравнения :
.
Его частный случай :
.
Подстановкой

или, соответственно,
то есть
приводится к виду
линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
.
.
Пример[править | править код]
Дано неоднородное уравнение
.
Определив подстановку 

приходим к уравнению
.
После приведения имеем линейное неоднородное уравнение с постоянными коэффициентами
,
решение которого имеет вид
или в терминах
Ещё один способ решения однородного уравнения второго порядка[править | править код]
Рассмотрим однородное уравнения второго порядка вида:
.
Его решениями являются функции вида:

где 
,
которое совпадает с характеристическим уравнением однородного уравнения с постоянными коэффициентами,
полученного из исходного уравнения путём описанной выше замены переменной. Если эти корни будут комплексными, то нужно воспользоваться формулой Эйлера и взять вещественную и мнимую части решения. Если же корни совпадут, то линейно независимыми решениями будут


Пример[править | править код]
Дано однородное уравнение
.
Характеристическое уравнение которого имеет вид
,
с решениями 

Тогда общее решение однородного уравнения