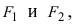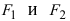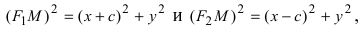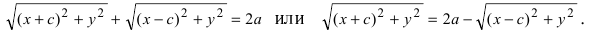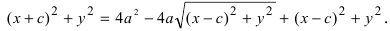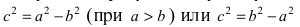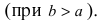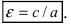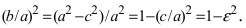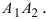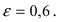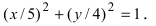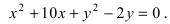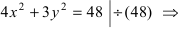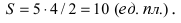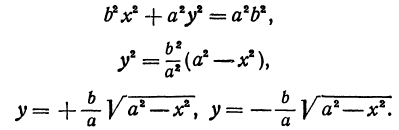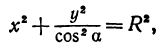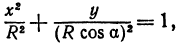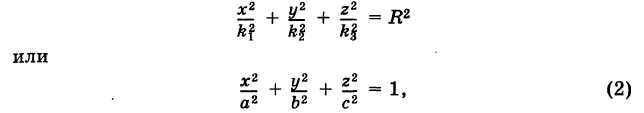фокусы которого лежат на оси абсцисс симметрично
относительно начала координат, зная, кроме того,
что:
и 2;
равна 10, а расстояние между фокусами 2c=8;
24, а расстояние между фокусами 2c=10;
его фокусами 2c=6 и эксцентриситет e=3/5.
равна 20, а эксцентриситет e=3/5.
10, а эксцентриситет e=12/13;
его директрисами равно 5 и расстояние между
фокусами 2c=4;
равна 8, а расстояние между директрисами равно 16;
6, а расстояние между директрисами равно 13;
его директрисами равно 32 и e=1/2.
уравнение эллипса, фокусы которого лежат на оси
ординат симметрично начала координат, зная,
кроме того, что:
соответственно 7 и 2;
равна 10, а расстояние между фокусами 2c=8;
его фокусами 2c=24 и эксцентриситет e=12/13.
16, а эксцентриситет e=3/5.
его фокусами 2c=6 и расстояние между директрисами
равно 50/3;
его директрисами равно 32/3 и эксцентриситет e=3/4.
каждого из следующих эллипсов:
эксцентриситет, уравнения директрис.
четырехугольника, две вершины которого лежат в
фокусах эллипса
совпадают с концами его малой оси.
эксцентриситет, уравнения директрис.
четырехугольника, две вершины которого лежат в
фокусах эллипса
концами его малой оси.
расстояние от фокуса F(c; 0) эллипса
односторонней с этим фокусом директрисы.
циркулем, построить фокусы эллипса
что изображены оси координат и задана масштабная
единица).
–3.
из точек A1(-2; 3), A2(2; -2), A3(2;
-4), A4(-1; 3), A5(-4; -3), A6(3; -1), A7(3;
-2), A8(2; 1), A9(0; 15), A10(0; -16) лежат на эллипсе
внутри и какие вне его.
линии опеределяются следующими уравнениями.
Изобразить эти линии на чертеже.
эллипса e=2/3, фокальный радиус точки М эллипса
равен 10. Вычислить расстояние от точки М до
односторонней с этим фокусом директрисы.
эллипса e=2/5, расстояние от точки эллипса до
директрисы равно 20. Вычислить расстояние от
точки М до фокуса, односторонней с этой
директрисой.
уравнения прямых, на которых лежат фокальные
радиусы точки М1.
459
точка M1(-4; 2,4) лежит
на эллипсе
М1.
эллипса e=1/3, центр его совпадает с началом
координат, один из фокусов (-2; 0). Вычислить
расстояние от точки М1 эллипса с абсциссой, равной 2, до
директрисы, односторонней с данным фокусом.
эллипса e=1/2, центр его совпадает с началом
координат, одна из директрис дана уравнением x=16.
Вычислить расстояние от точки M1
эллипса с абсциссой, равной –4, до
фокуса, одностороннего с данной директрисой.
эллипса
правого фокуса равно 14.
эллипса
левого фокуса равно 2,5.
большой оси. Определить расстояния от точек
пересечения этого перпендикуляра с эллипсом до
фокусов.
уравнения эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если даны:
и его малая полуось b=3;
-2) эллипса и его большая полуось
a=4;
М2(
и его эксцентриситет e=2/3;
-5/3) эллипса и его эксцентриситет
e=2/3;
12) эллипса и расстояние r1=20
от нее до левого фокуса.
и расстояние между его директрисами, равное 10.
эксцентриситет e эллипса, если:
из фокусов под углом 600;
фокусами виден и вершин малой оси под прямым
углом;
директрисами в три раза больше расстояния между
фокусами;
перпендикуляра, опущенного из центра эллипса на
его директрису, делится вершиной эллипса
пополам.
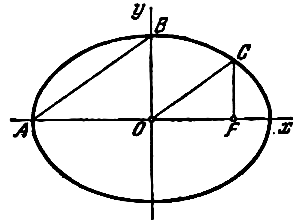
эллипса проведен перпендикуляр к его большой оси
(см. рис.). Определить, при каком значении
эксцентриситета эллипса отрезки
параллельны.
уравнение эллипса с полуосями a, b и центром C(x0, y0), если
известно, что оси симметрии эллипса параллельны
осям координат.
абсцисс в точке А(3; 0) и оси ординат в точке В(0; -4).
Составить уравнение этого эллипса, зная, что его
оси симметрии параллельны координатным осям.
является центром эллипса, касающегося обеих
координатных осей. Составить уравнение этого
эллипса, зная, что его оси симметрии параллельны
координатным осям.
каждое из следующих уравнений определяет эллипс,
и найти координаты его центра С, полуоси,
эксцентриситет и уравнения директрис:
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
уравнение эллипса, зная, что:
равна 26 и фокусы суть F1(-10; 0), F2(14;0);
473.2
2 и фокусы суть F1(-1; -1), F2(1;
1);
473.3
эксцентриситет e=
473.4
расстояние между директрисами равно
474
эксцентриситет
фокус F (-4; 1) и уравнение соответствующей
директрисы
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(-4; 1) и уравнение
соответствующей директрисы
на эллипсе, фокус которого F(-1; -4), а
соответствующая директриса дана уравнением
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(3; 0) и уравнение
соответствующей директрисы
-1) лежит на эллипсе, фокус
которого F(1; 0), а соответствующая директриса дана
уравнением
-1) является концом малой оси
эллипса, фокусы которого лежат на прямой
уравнение этого эллипса, зная его эксцентриситет
e=
пересечения прямой
пересечения прямой
пересечения прямой
расположена прямая относительно эллипса:
пересекает ли, касается или проходит вне его,
если прямая и эллипс заданы следующими
уравнениями:
каких начениях m прямая
эллипса.
при котором прямая
уравнение касательной к эллипсу
точке M1(x1; y1).
касательные к эллипсу
в концах одного и того же диаметра, параллельны.
(Диаметром эллипса называется его хорда,
проходящая через его центр).
уравнения касательных к эллипсу
прямой
уравнения касательных к эллипсу
к прямой
прямой
ближайшую к прямой
этой прямой.
проведены касательные к эллипсу
их уравнения.
проведены касательные к эллипсу
уравнение хорды, соединяющей точки касания.
проведены касательные к эллипсу
расстояние d от точки Р до хорды эллипса,
соединяющей точки касания.
через точку А(4; -1) и касается прямой
уравнение этого эллипса при условии, что его оси
совпадают с осями координат.
уравнение эллипса, касающегося двух прямых
условии, что его ося совпадают с осями координат.
произведение расстояний от центра эллипса до
точки пересечения любой его касательной с
фокальной осью и до основания перпендикуляра,
опущенного из точки касания на фокульную ось,
если величина постоянная, равная квадрату
большой полуоси эллипса.
произвдение расстояний от фокусов до любой
касательной к эллипсу равно квадрату малой
полуоси.
эллипса, фокусы которого находятся в точках F1(-3;
0), F2(3; 0). Составить
уравнение этого эллипса.
уравнение эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если известны уравнение касательной к
эллипсу
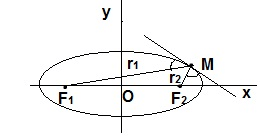
прямая, касающаяся эллипса в некоторой точке М,
составляет равные углы с фокальными радиусами F1M, F2M и проходит
вне угла F1MF2.
эллипса
Ox направлен луч света. Известно, что
до эллипса, луч на него отразился. Составить
уравнение прямой, на которой лежит отраженный
луч.
пересечения эллипсов
эллипсы
в четырех точках, лежающих на окружности с
центром в начале координат, определить радиус R
этой окружности.
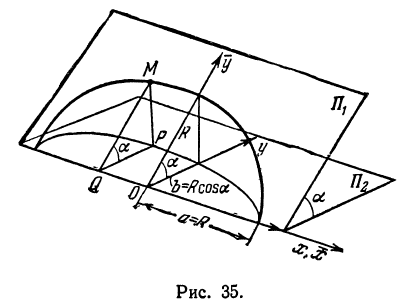
полуоси эллипса, полученного проектированием на
плоскость
плоскости
полуось которого равна 6, является проекцией
окружности радиуса R=12. Опредилть угол
эллипс и окружность.
круглого цилиндра является окружность радиуса
R=8. Определить полуоси эллипса, полученного в
сечении этого цилиндра плоскостью, наклоненной к
его оси под уголом
круглого цилиндра является окружность радиуса R=
цилиндра нужно его пересечь плоскостью, чтобы в
сечении получить эллипс с большой полуосью a=2.
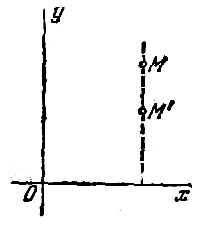
сжатием (или равномерным растяжением) плоскости
к оси абсцисс называется такое преобразование
точек плоскости, при котором произвольная точка
M(x; y) перемещается в точку M’(x’; y’) (рис.1 ) так, что
x’=x, y’=qy, где q>0 – постоянная, называемая
коэффициентом равномерного сжатия. Аналогично
рпи помощи уравнения x’=qx, y’=y определяется
равномерное сжатия плоскости к оси Oy (рис. 2).
Определить, в какую линию преобразуется
окружность
равномерного сжатия плоскости к оси абсцисс q=4/5.
равномерного сжатия плоскости к оси Oy равен 3/4.
Определить уравнение линии, в которую при таком
сжатии преобразуется эллипс
линии, в которую преобразуется эллипс
равномерных сжатиях плоскости к координатным
осям, если коэффициенты равномерного сжатия
плоскости к осям Ox и Oy равны соответственно 4/3 и
6/7.
коэффициент q равномерного сжатия плоскости к
оси Ox, при котором эллипс
в эллипс
коэффициент q равномерного сжатия плоскости к
оси Oy, при котором эллипс
в эллипс
коэффициенты q1, q2 двух последовательных равномерных
сжатий плоскости к осям Ox и Oy, при которых
эллипс
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 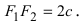
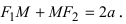
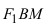
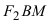
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 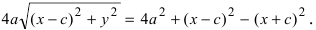
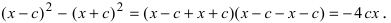
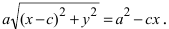
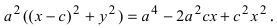
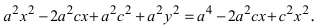
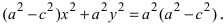
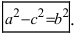
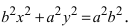
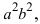
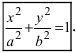
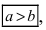
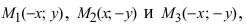
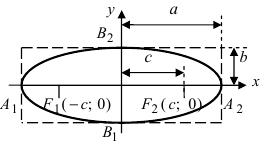
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 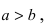
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 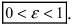
Если 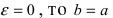
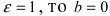
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 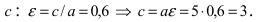
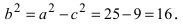
Пример:
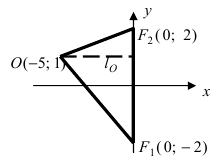
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 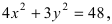
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
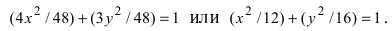
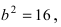
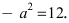
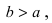
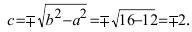
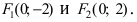
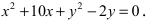
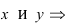
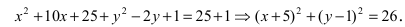
Построим в декартовой системе координат треугольник 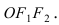
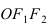
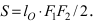
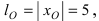
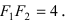
Эллипс в высшей математике
Рассмотрим уравнение
где 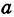
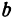
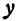
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
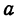

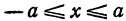
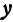
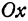
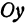
При 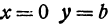
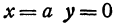
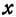

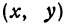
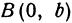
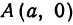
Полученная линия называется эллипсом. Число 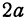
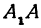
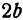
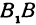
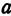
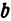
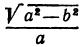
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 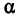
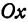
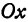
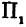
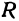
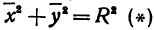
Пусть точка 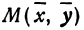
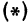
Обозначим проекцию точки 
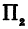
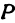
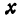
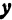


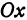
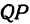
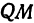
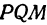
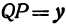
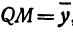
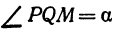
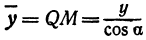


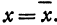
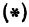
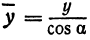
или
а это есть уравнение эллипса с полуосями 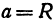
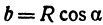
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 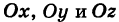
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 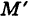
(рис. 206). Отсюда
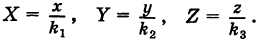
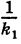
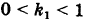
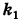
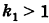
Подставляя эти формулы в уравнение (1), будем иметь
где 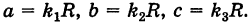
Величины 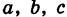
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 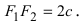
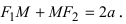
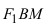
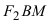
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 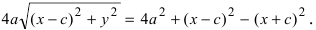
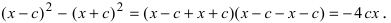
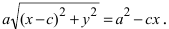
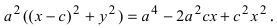
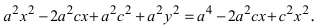
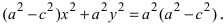
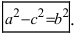
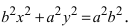
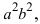
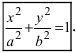
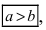
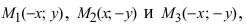
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 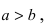
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 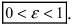
Если 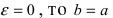
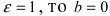
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 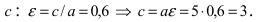
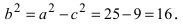
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 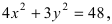
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
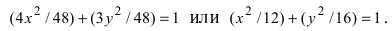
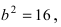
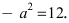
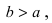
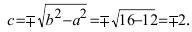
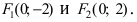
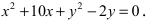
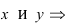
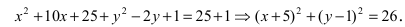
Построим в декартовой системе координат треугольник 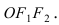
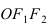
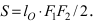
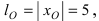
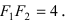
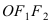
Эллипс в высшей математике
где 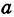
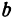
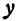
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
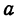

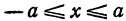
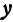
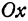
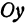
При 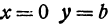
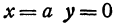
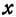

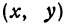
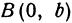
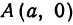
Полученная линия называется эллипсом. Число 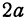
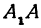
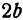
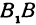
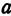
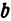
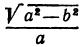
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 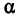
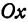
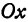
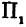
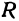
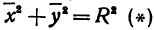
Пусть точка 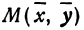
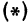
Обозначим проекцию точки 
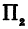
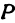
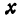
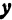


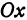
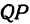
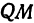
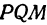
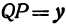
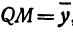
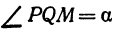
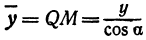


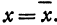
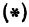
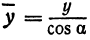
а это есть уравнение эллипса с полуосями 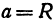
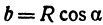
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 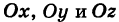
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 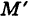
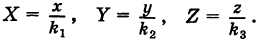
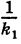
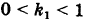
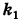
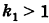
Подставляя эти формулы в уравнение (1), будем иметь
где 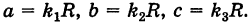
Величины 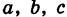
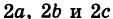
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Кривые второго порядка. Эллипс: формулы и задачи
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как 

Каноническое уравнение эллипса имеет вид:

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка 

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид 
Пример 1. Проверить, является ли линия, заданная общим уравнением 
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

Точки 


называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет 
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением 
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет 
Продолжаем решать задачи на эллипс вместе
Если 



Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

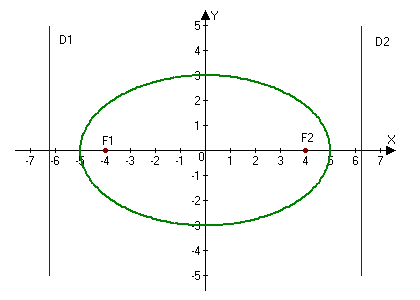
называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса

где 



Пример 7. Дан эллипс 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. 

Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки 

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка 

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

так как из исходного уравнения эллипса 
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Эллипс.
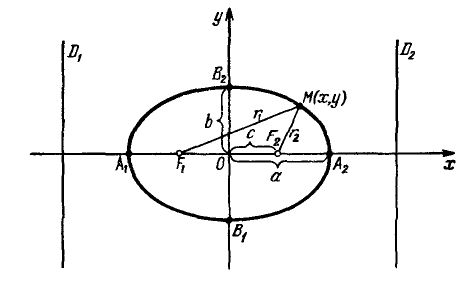
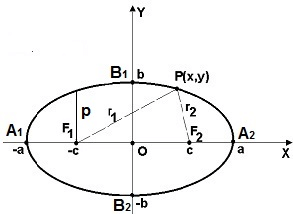
Эллипс с каноническим уравнением $frac+frac=1, ageq b>0,$ и меет форму изображенную на рисунке.
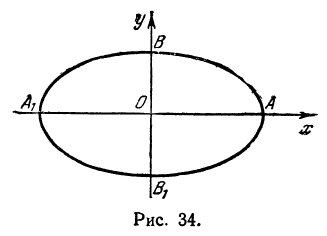
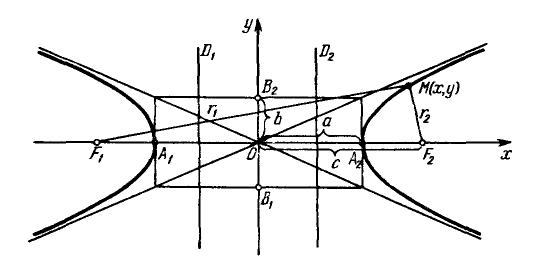
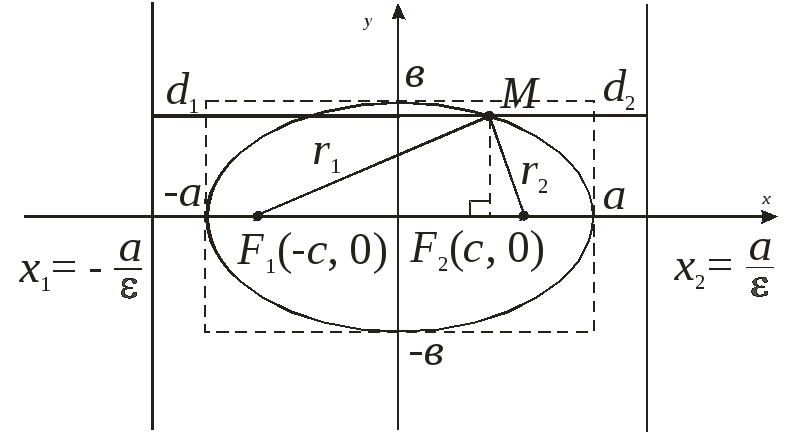
Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ — главными осями а центр симметрии $O -$ центром эллипса.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами эллипса векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $frac+frac=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.
Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.
Теорема. ( Директориальное свойство эллипса)
Эллипс является множеством точек, отноше ние расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$
Примеры.
2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.
Приведем уравнение эллипса к каноническому виду:
а) Находим полуоси $a=5,$ $b=3.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$
$c=sqrt<5^2-3^2>=sqrt<16>=4Rightarrow F_1(-4, 0),qquad F_2(4, 0).$
г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),qquad F_2(4, 0);$ в) $e=frac<4><5>;$ г) $D_1: x=-frac<25><4>$ и $D_2: x=frac<25><4>.$
2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.
Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:
Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=sqrt 5.$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<3><2/3>=-frac<9> <2>$ и $D_2: x=frac<3><2/3>=frac<9><2>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=sqrt 5;$ $ e=frac<2><3>.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$
2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.
Решение.
Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$
Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, sqrt 3)$ в каноническое уравнение эллипса $frac+frac=1:$
Таким образом, уравнение эллипса $frac<16>+frac<4>=1.$
Далее найдем координаты фокусов:
$c=sqrt=sqrt<16-4>=2sqrt 3Rightarrow F_1(-2sqrt 3, 0),,,, F_2(2sqrt 3, 0).$
Отсюда находим $overline =(2+2sqrt 3, sqrt 3),$ $overline=(2-2sqrt 3, sqrt 3).$
Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Таким образом, расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_1: sqrt 3 x+8=0$
расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_2: sqrt 3 x-8=0$
Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) — $ ее вершинами. Оси симметрии $Ox$ и $Oy$ — действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами гиперболы, векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.
Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.
Теорема. (Директориальное свойство гиперболы).
Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей дирек трисы постоянно и равно $e.$
Примеры.
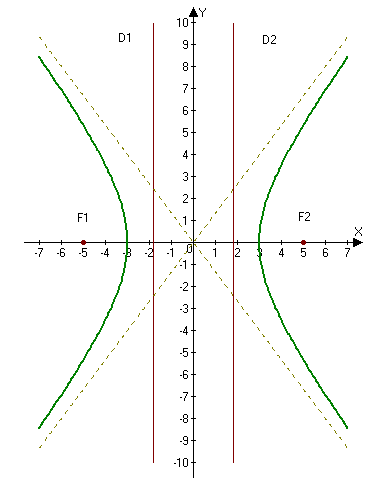
2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.
Приведем уравнение гиперболы к каноническому виду:
а) Находим полуоси $a=3,$ $b=4.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$
$c=sqrt<3^2+4^2>=sqrt<25>=5Rightarrow F_1(-5, 0),qquad F_2(5, 0).$
г) Асимптоты гиперболы находим по формулам $y=pmfracx:$
д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),qquad F_2(5, 0);$ в) $e=frac<5><3>;$ г) $y=pmfrac<4><3>x;$ д ) $D_1: x=-frac<9><5>$ и $D_2: x=frac<9><5>.$
2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.
Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:
Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$
Асимптоты гиперболы c центром в начале координат, находим по формулам $y=pmfracx,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=pmfrac(x-x_0),$
$$y+3=frac<4><3>(x-2)Rightarrow 3y+9=4x-8Rightarrow 4x-3y-17=0.$$
$$y+3=-frac<4><3>(x-2)Rightarrow 3y+9=-4x+8Rightarrow 4x+3y+1=0.$$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<3><5/3>=-frac<9> <5>$ и $D_2: x=frac<3><5/3>=frac<9><5>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=frac<5><3>,$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$
2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $frac<16>-frac<9>=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.
Решение.
Проверим, что заданная точка лежит на гиперболе:
Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $frac<16>-frac<9>=1.$
Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:
$c=sqrtRightarrow c=sqrt<16+9>=sqrt <25>=5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$
Фокальные радиусы точки, можно найти по формулам $r_1=|overline|$ и $r_2=|overline|.$
Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<4><5/4>Rightarrow x=-frac<16><5>Rightarrow 5x+16=0;$
$D_2: x=frac<4><5/4>Rightarrow x=frac<16><5>Rightarrow 5x-16=0;$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: sqrt 5x+16=0$
расстояние от точки $M(5, 9/4)$ до прямой $D_2: sqrt 5x-16=0$
Ответ: $r_1=9/4,$ $r_2=frac<41><4>;$ $d_1=frac<41><5>;$ $d_2=frac<9><5>.$
2.273. Найти точки гиперболы $frac<9>-frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$
Решение.
Из уравнения гиперболы находим полуоси: $a=3, , b=4.$ Следовательно, $c=sqrtRightarrow c=sqrt<9+16>=sqrt <25>=5.$
Отсюда находим $F_1=(-5, 0).$
Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$
Чтобы н айти точки гиперболы $frac<9>-frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений
Решим уравнение $5x^2+18x-72=0:$
Находим соответствующие координаты $y:$ $y_1=pmsqrt<24-2,4^2-10cdot 2,4>=sqrt<-5,76>$ — нет корней .
Ответ: $(-6, pm4sqrt 3).$
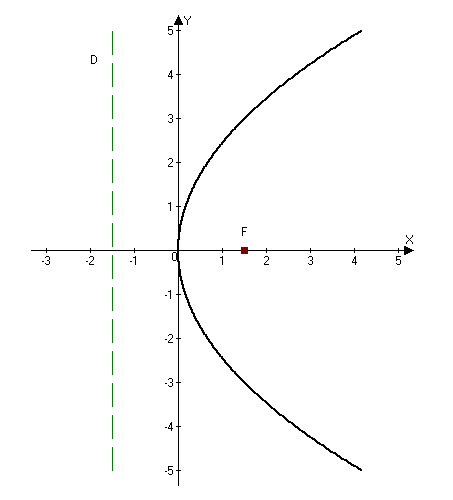
Парабола.
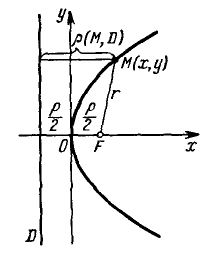
Парабола с каноническим уравнением $y^2=2px, p>0,$ и меет форму изображенную на рисунке.
Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ — осью параболы.
Точка $Fleft(frac
<2>, 0right)$ называется фокусом параболы, вектор $overline -$ фокальным радиус-векторам, а число $r=|overline| -$ фокальным радиусом точки $M,$ принадлежащей параболе.
Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.
Примеры.
2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.
Решение.
Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $
$$y^2=6xRightarrow y^2=2cdot 3xRightarrow p=2.$$
Ответ: $p=3.$
2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$
Решение.
Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:
Ответ: $y^2=-x.$
2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$
Решение.
Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$
Приведем заданное уравнние к такому виду:
Таким образом, $y^2=4(x^2-2)$ — парабола с центром в точке $(0, 2).$ Параметр $p=2.$
Ответ: $C(0, 2),$ $p=2.$
2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$
Решение.
Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12xRightarrow 36=12xRightarrow x=3.$$
Таким образом, точка $M$ имеет координаты $(3, 6).$
Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2cdot 6xRightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$
Далее находим фокальный параметр точки:
Ответ: $6.$
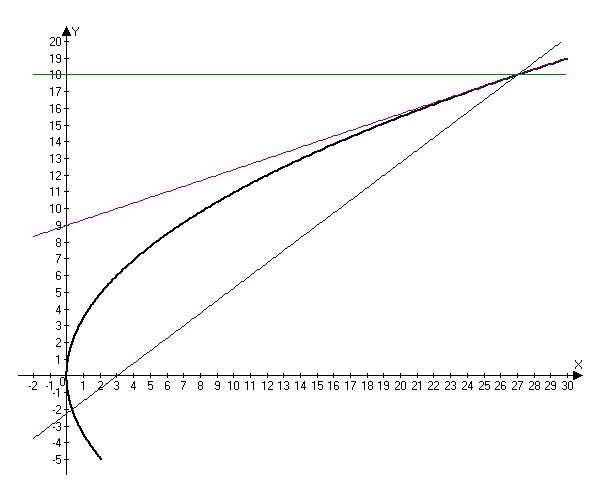
2.298. Из фокуса параболы $y^2=12x$ под острым углом $alpha$ к оси $Ox$ направлен луч света, причем $tgalpha=frac<3><4>.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.
Решение.
Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2cdot 6xRightarrow p=6.$
Координаты фокуса $F(p/2, 0)Rightarrow F(3,0).$
Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $alpha: tgalpha=frac<3><4>$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tgalpha=frac<3><4>.$
Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$
$0=frac<3><4>cdot 3+bRightarrow b=-frac<9><4>.$ Таким образом, уравнение луча, направленного из фокуса $y=frac<3><4>x-frac<9><4>.$
Далее, найдем точку пересечения найденной прямой с параболой:
Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=frac<18^2><12>=frac<324><12>=27.$
Таким образом, луч пересекает параболу в точке $(27, 18).$
Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$
Подставляем все найденные значения в уравнение касательной:
$y-18=frac<1><3>(x-27)Rightarrow 3y-54=x-27Rightarrow x-3y+27=0.$
Далее, найдем угол $beta$ между лучем $y=frac<3><4>x-frac<9><4>$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=frac<1+k_1cdot k_2>$
$$L_2: x-3y+27=0Rightarrow y=frac<1><3>x+9Rightarrow k_2=frac<1><3>.$$
Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $pi-2beta,$ а угол между отраженным лучем и осью $Ox$ $pi-(pi-2beta)-alpha=2beta-alpha.$
Зная $tgbeta=frac<1><3>$ и $tgalpha=k_1=frac<3><4>$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2beta-alpha):$
$$tg(2beta-alpha)=frac<1+tg2beta tgalpha>=frac<frac<3><4>-frac<3><4>><1+frac<3><4>frac<3><4>>=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$
источники:
http://function-x.ru/curves_ellipse.html
http://mathportal.net/index.php/component/content/article/87-visshaya-matematika/analiticheskaya-geometriya/154-ellips-giperbola-parabola-direktorialnoe-svojstvo-ellipsa-i-giperboly-polyarnyj-parametr
Что мы знаем со школы про эллипс? К сожалению, исходя из своей практики работы с учениками, многие вплоть до 11 класса не сталкиваются с такой замечательной плоской фигурой, впрочем как и с её частным случаем – окружностью. Некоторые знают только примерный вид уравнения…
Кстати, какое оно? Каноническим уравнением эллипса считается следующее уравнение:
Почему оно именно такое? Что ж, это можно вывести из определения. Поэтому давайте его напишем.
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.
Давайте сделаем рисунок и попробуем вывести каноническое уравнение из определения эллипса.
Обозначим фокусы через F₁ и F₂, расстояние между ними через 2c, а сумму расстояний от произвольной точки эллипса M(x; y) до фокусов – через 2a. По определению 2а > 2c, т.е. а > c.
Для вывода уравнения эллипса выберем систему координат OXY так, чтобы фокусы F₁ и F₂ лежали а оси OX, а начало координат совпадало с серединой отрезка F₁F₂. Тогда фокусы будут иметь следующие координаты: F₁(-c; 0) и F₂(+c; 0).
Тогда, согласно определению эллипса, MF₁ + MF₂ = 2a, то есть:
Мы вывели каноническое уравнение эллипса и доказали, что оно эквивалентно начальному уравнению из определения.
Эллипс – кривая второго порядка.
Исследование формы эллипса по его уравнению
Установим форму эллипса, используя его каноническое уравнение.
1. Каноническое уравнение содержит x и y только в четных степенях, поэтому если точка (x; y) принадлежит эллипсу, то ему также принадлежат точки (x; -y), (-x; y), (-x; -y). Отсюда следует, что эллипс симметричен относительно осей координат Ox и Oy, а также точки O(0; 0), которая является центром эллипса.
2. Точки пересечения эллипса с осями координат. Положив y = 0, находим две точки A₁(a; 0) и A₂(-a;0), в которых ось Ox пересекает эллипс. Положив в уравнении x = 0, находим точки пересечения эллипса с осью Oy: B₁(0; b) и B₂(0; -b). Все эти 4 точки называются вершинами эллипса.
Отрезки A₁A₂ и B₁B₂, а также их длины 2a и 2b называются соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.
3. Также из канонического уравнения следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства
Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми x = ±a и y = ±b.
4. В каноническом уравнении сумма неотрицательных слагаемых (x/a)² и (y/b)² равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т.е. если |x| возрастает, то |y| уменьшается и наоборот.
Дополнительные сведения об эллипсе
Форма эллипса зависит от отношения b/a. При a = b = R эллипс превращается в окружность, уравнение эллипса принимает вид x² + y² = R². Однако, в качестве характеристики формы эллипса чаще используется отношение c/a.
Отношение c/a половины расстояния между фокусами к большей полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой «эпсилон» ε:
Из последней строки видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным, то есть больше походить на окружность, быть ближе к ней по форме. Если положить ε = 0, то эллипс превращается в окружность.
Пусть M(x; y) – произвольная точка эллипса с фокусами F₁ и F₂. Длины отрезков F₁M = r₁ и F₂M = r₂ называются фокальными радиусами точки M.
Очевидно, что r₁ + r₂ = 2a.
Тогда имеют место быть формулы: r₁ = a + εx и r₂ = a + εx
Выведем эти формулы
Прямые x = ±a/ε называются директрисами эллипса. Значение директрисы эллипса выявляется следующим утверждением.
Теорема
Если r – расстояние от произвольной точки эллипса до какого-нибудь фокуса, d – расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение r/d есть величина постоянная, равная эксцентриситету эллипса: r/d = ε.
Из равенства a² – c² = b² следует, что a > b. Если же a < b, то каноническое уравнение (x/a)² + (y/b)² = 1 определяет эллипс, большая ось которого 2b лежит на оси OY, а малая ось 2a – лежит на оси Ox. Фокусы такого эллипса находятся в точках F₁(0; +c) и F₂(0; -c), где c = √(b² – a²).
Площадь фигуры, ограниченной эллипсом
Допустим, что перед нами стоит следующая задача:
Вычислить площадь фигуры, ограниченной эллипсом.
Решение:
Зададим эллипс параметрическими уравнениями:
x = a⋅cos(t) и y = b ⋅ sin(t). Кстати, выразив косинус и синус из каждого, а потом возведя в квадрат оба уравнения, сложив их, можно прийти к каноническому уравнению эллипса.
В силу симметричности эллипса относительно начала координат, нам достаточно найти площадь 1/4 части эллипса, а затем умножить результат на 4. Сделаем подходящий рисунок.
Здесь x изменяется от 0 до a, следовательно параметр t изменяется от π/2 до 0. Площадь четверти эллипса будем искать с помощью интегрирования функции, задающей эллипс в первой четверти координат.
Длина дуги эллипса (периметр эллипса)
Ознакомиться с эллиптическими интегралами
Стоит заметить, что для окружности всё получается гораздо проще, и мы легко выводим формулу, знакомую нам со школы C = 2πR.
Приближённые формулы для периметра
Точные формулы для периметра
Джеймс Айвори и Фридрих Бессель независимо друг от друга получили формулу для периметра эллипса:
Площадь сегмента эллипса
Площадь сегмента между дугой, выпуклой влево, и вертикальной хордой , проходящей через точки (x; y) и (x; -y) можно определить по формуле:
Если эллипс задан уравнением Ax² + Bxy + Cy² = 1, то площадь можно определить по формуле
Физический смысл фокусов
1. Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
2. Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
3. Если F₁ и F₂ — фокусы эллипса, то для любой точки M, принадлежащей эллипсу, угол между касательной в этой точке и прямой F₁M равен углу между касательно и прямой F₂M.
4. Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
5. Эволютой эллипса является астроида , вытянутая вдоль вертикальной оси. Эволюта плоской кривой — геометрическое место точек , являющихся центрами кривизны кривой. По отношению к своей эволюте любая кривая является эвольвентой .
6. Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипсы и только они имеет максимальную аффинную длину .
Аффинная длина — параметр плоской кривой , который сохраняется при эквиаффинных преобразованиях (то есть аффинных преобразованиях , сохраняющих площадь ).
7. Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном выше эллипсографе.
Построение эллипса с помощью иголок, нитки и карандаша.
Эллипсы в астрономии. Все планеты и другие небесные тела Солнечной системы движутся вокруг Солнца по эллиптическим орбитам, в одном из фокусов – Солнце. Этот закон был открыт ещё Кеплером. Ближайшую точку к Солнцу Земля проходит 4 января, таким образом, для северного полушария зима чуть теплее, чем для южного. К тому же, из-за такой формы орбиты, зима для северного полушария чуть короче, то есть период между осенним и весенним равноденствием не ровно 1/2 года, а меньше. Действительно, на южном полюсе температуры бывают ниже, чем на северном полюсе.
Физическое свойство фокусировки. Лучи, испущенные из одного фокуса, после отражения соберутся во втором фокусе. Название «фокус» как раз и связано со словом «фокусировка» лучей. Если на орбите Земли расположить зеркала, так чтобы они были повёрнуты ровно по касательной к орбите, то все лучи соберутся во 2 фокусе, то есть из той точки будет видно, что вся орбита светится.
Последнее свойство используется в физике для построение оптических резонаторов в лазерной технике. Лампа накачки размещается вдоль одной из фокальных осей зеркально отражающего эллиптического цилиндра, а лазерный стержень располагается вдоль другой фокальной оси. На второй фокальной оси помещают активную среду. А свойства эллиптической поверхности помогают быть уверенными в том, что вся энергия лампы накачки соберется в области активной среды.
Почитать подробнее здесь
Поместим в одном из фокусов зеркального эллипса лампочку
и проследим за выпущенными из неё лучами света. Отразившись от эллипса, они соберутся в другом фокусе. Причём окажутся там одновременно:
Зрительно напомним геометрическое определение эллипса: эллипс есть множество точек M плоскости, сумма расстояний от которых до данных точек A и B постоянна:
Решим вспомогательную задачу. Даны две точки по одну сторону от прямой. Мы хотим пройти из A в B, набрав по пути воды из реки l.
Мы хотим пройти из A в B, набрав по пути воды из реки l. В какой точке M надо набирать воду, чтобы общий путь имел минимальную длину?
Рассмотрим точку B’, симметричную точке B. Тогда XB = XB’. Длина AX+XB = AX+XB’ минимальна, когда ломаная AXB’ превращается в прямую.
Мы хотим пройти из A в B, набрав по пути воды из реки l. В какой точке набирать воду? Ответ: в точке пересечения l с AB’ (где B’ симметрична B относительно l). Заодно мы доказали равенство углов. Мы хотим пройти из A в B, набрав по пути воды из реки l. Где набирать воду?
Ответ 1: в точке пересечения l с AB’.
Ответ 2: там, где «угол падения равен углу отражения».
Принцип Ферма: свет выбирает кратчайший путь между двумя точками.
Вернемся к доказательству оптического свойства эллипса. На эллипсе сумма AM+MB постоянна. А для точек вне эллипса эта сумма больше, AX+XB > AM+MB.
В частности, если провести в точке M касательную к эллипсу, то для любой другой точки X на этой касательной AX+XB > AM+MB. Значит, по предыдущей задаче «угол падения равен углу отражения».
…по предыдущей задаче «угол падения равен углу отражения». Оптическое свойство эллипса доказано.
Многофокусные эллипсы
N-эллипс — обобщение эллипса , имеющее более двух фокусов. N-эллипсы называют также мультифокальными эллипсами , полиэллипсами, k -эллипсами, эллипсами Чирнхауса . Впервые такие фигуры исследовал Джеймс Максвелл в 1846 году.
Пусть на плоскости задано n точек (ui , vi ) (фокусы ), тогда n -эллипс является геометрическим местом точек плоскости, для которых сумма расстояний до n фокусов является постоянной величиной d . В виде формулы данное утверждение записывается как
1-эллипс представляет собой окружность , 2-эллипс — обычный эллипс. Обе данные кривые являются алгебраическими кривыми степени 2.
Для любого числа n фокусов n -эллипс представляет собой замкнутую выпуклую кривую. Кривая является гладкой вне окрестностей фокуса.
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Эллипсом называют плоскую кривую, состоящую из точек, сумма расстояний которых от двух определённых точек плоскости является неизменной, строго заданной величиной, равной суммарной длине двух больших его полуосей (2a). Эти две точки называются фокусами эллипса.
F1 и F2 – фокусы эллипса;
а – большая полуось;
b – малая полуось
с – фокусное расстояние
Теорема
Фокусное расстояние эллипса и его полуоси связаны между собой соотношением [boldsymbol{a^{2}=b^{2}+c^{2}}]
Доказательство:
Когда точка M на линии эллипса находится на его пересечении с вертикальной осью, из теоремы Пифагора выходит, что
r1 + r2 = 2*√(b2 + c2)
Когда точка M пересекает горизонтальную ось
r1 + r2 = а – c + а + c
По определению эллипса r1 + r 2 = const
Это позволяет после приравнивания получить
a² = b² + c²
r1 + r2 = 2а
Что и требовалось доказать.
Уравнение эллипса
Каноническим уравнением эллипса называют уравнение [boldsymbol{1=left(x^{2} / a^{2}right)+left(y^{2} / b^{2}right)}]
Доказательство уравнения:
Введём прямоугольную декартову систему координат.
Сначала докажем, что координаты любой из точек на эллипсе удовлетворяют приведённому каноническому уравнению. Затем покажем, что любое из решений уравнения является координатами точки, лежащей на линии эллипса. Из этого будет следовать удовлетворение каноническому уравнению только тех точек, которые лежат на поверхности эллипса. Опираясь на этот факт и на определение эллипса можно будет однозначно сделать вывод, что написанное нами уравнением является каноническим уравнением или, как ещё говорят, основной формулой эллипса.
- Пусть М(х, у) будет точкой эллипса, т.е. сумму её фокальных радиусов примем равной 2а, т. е. r1 + r2 = 2a.
С помощью формулы расстояния, разделяющего две точки на координатной плоскости, можно легко найти фокальные радиусы точки M.r1 = √[(x + c)2 + y2]
r2 = √[(x — c)2 + y2]Из этих уравнений получаем √[(x + c)2 + y2] + √[(x — c)2 + y2] = 2a
Если один из корней перенести в правую часть и возвести всё в квадрат, то придём к выражению
(x + c)2 + y2 = 4a2 – 4a√[(x — c)2 + y2] + (x – c)2 + y2После сокращения приходим к 2xc = 4a2 – 4a√[(x-c)2 + y2] – 2xc
После приведения подобных членов, сокращения на 4 и уединения радикала будем иметь
a√[(x-c)2 + y2] = a2 – xcВозведём это выражение в квадрат
a2(x-c)2 + a2 y2 = a4 – 2a2xc + x2c2Если раскрыть скобки и сократить на -2a2 xc, то a2x2 + a2c2 + a2y2 = a4 + x2c2
Отсюда легко получить (a2 – c2)x2 + a2y2 = a2(a2 – c2)
Из этого следует, что b2x2 +a2y2 = a2b2 - Пусть некоторые числа (x, y) полностью удовлетворяют каноническому уравнению
1 = (x2/a2) + (y2/b2)
Пусть нам дана точка M(x,y) на координатной плоскости 0xy
Из канонического уравнения следует, что Y2 = b2(1- x2/a2)
Если это равенство подставить в выражение для фокальных радиусов, которые имеет точка M, то можно получить
r1 = √[(x + c)2 +y2] = √[x2 +2xc + c2 +b2 – b2x2/a2] = √[x2(1 – b2/a2) + 2xc +c2 +b2] =
= √[x2(a2 – b2)/a2 + 2xc + (c2 + b2)] = √[x2 (c2/a2) + 2xc +a2] = √[x(c/a) +a]2 = |a +xε|
т. е. r1 = |a +xε|
Отношение 2с/2a = c/a = ε называется эксцентриситетом эллипса. Оно у него всегда меньше 1.
То же самое просчитываем для r2.
Т. к. x2/a2 больше или равно 1 или x больше или равно большой полуоси (a), то можно сделать вывод о справедливости неравенства a≥|x|> |x|* ε = |xε|
Отсюда явно следует, что a+-|xε|>0 или a+-xε > 0 и r1 = a + xε, r2 = a — xε
Из полученных равенств выходит, что r1 + r2 = 2a, это значит, что точка M однозначно является точкой эллипса. Это нам и нужно было доказать.
Свойства эллипса
- У эллипса имеются две взаимно перпендикулярные оси симметрии.
Доказательство:
Переменные x и y в уравнение эллипса входят лишь во второй степени. Это означает, что если точка M с координатами (x,y) ему принадлежит, то и точки М1 (-x, y) и M2 (x, -y) тоже принадлежат ему. Легко проверить, что указанные координаты удовлетворяют каноническому уравнению эллипса. M1 симметрична по отношению к оси X, а M2 по отношению к оси Y. Получается, что у эллипса есть две взаимно перпендикулярные точки симметрии. - У эллипса есть центр симметрии.
Доказательство:
Если координаты точки М(x,y) будут удовлетворять уравнению эллипса, то и точка
N (–x; –y) ему тоже будет удовлетворять. M и N симметричны по отношению к началу координат. Это как раз и означает, что у эллипса имеется центр симметрии. - Эллипс пересекает каждую из осей в двух точках.
Доказательство:
Возьмём произвольную точку эллипса M(x,y). Расстояние этой точки до фокусов будетr1 = √[(x + c)2 + y2]
r2 = √[(x — c)2 + y2]Теперь давайте рассмотрим выражение
(x+-c)2 + y2 = x2 +- 2xc + c2+ y2 =
= x2 +- 2xc + a2 – b2 +y2 = x2 +- 2xc+ a2 — b2 + b2(1-x2/a2) =
= (a2 – b2)*x2/a2 +-2xc +a2 = c2*x2/a2+-2xa(c/a) + a2 = (a +c*x/a)2Эксцентриситет эллипса, как сказано ранее, меньше 1. Т. к. |x|≤ a, то a – εx > 0. Поэтому
F1M = a + εx и F2M = a – εx. Напомним, что ε – это эксцентриситет эллипса.
А теперь несколько свойств эллипса без доказательств.
- Эллипс можно получить, сжав окружность.
- Если через эллипс проходят две прямые, то отрезок, концами которого являются середины отрезков созданных при пересечении прямых, обязательно пересекает середину, центр эллипса.
- Угол, созданный касательной к эллипсу и его радиусом, проходящем через фокусы указанной геометрической фигуры, в любых случаях пересекает середину эллипса.
- Уравнение касательной к эллипсу в точке М, имеющей координаты xM и yM
1 = (x*xM)/a2 + (y*yM)/b2 - Эволюта эллипса представляет собой астероиду, растянутую вдоль его малой оси.
- Угол между касательной к эллипсу и одним его фокальным радиусом (r1) имеет ту же величину, что и угол, разделяющий касательную и другой фокальный радиус (r2) фигуры.
Как построить эллипс
Расскажем, как построить эллипс по его большой и малой полуосям и с помощью циркуля.
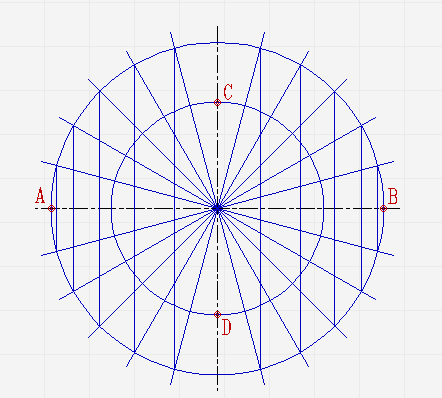
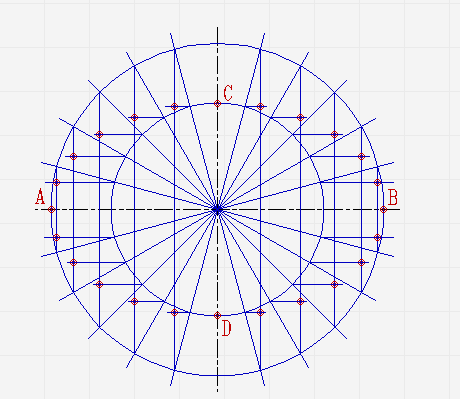
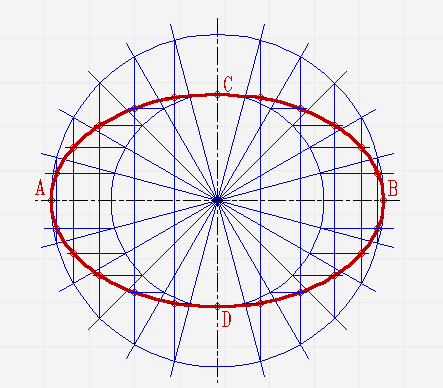
Построение эллипса по его большой и малой осям
Считается самым простым, не требующим серьёзных навыков.
Проведите две перпендикулярные оси;
От места пересечения осей на вертикальной отложите верх и вниз отрезки. Они будут составлять малую ось эллипса. На горизонтальной отложите отрезки вправо и влево. Из них будет состоять большая ось;
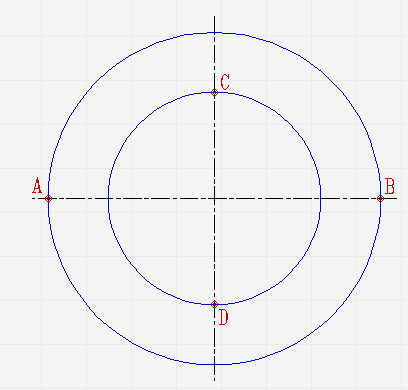
Проведите две концентрические окружности. Одну диаметром AB, диаметром CD;
Проведите ещё диаметры в различных направлениях;
В местах, где лучи соприкасаются с окружностями, проведите линии параллельные малой и большой осям эллипса, пока они не пересекутся в точках, которые принадлежат эллипсу;
Соедините полученные точки плавной линией.
Нет времени решать самому?
Наши эксперты помогут!
Как построить эллипс с помощью циркуля
Во многом здесь всё аналогично предыдущему способу, поэтому перегружать текст иллюстрациями не будем.
Порядок действий следующий:
- Проведите две перпендикулярные линии. Они будут осями эллипса, а точка их пересечения центром геометрической фигуры;
- Определитесь с величиной большой и малой полуосей, если их значения не заданы в условии задачи;
- Установите раствор циркуля на длину большой полуоси (a). Поместите циркуль в точку O и отметьте на одной из линий две точки, P1 и P2. Установите раствор циркуля на длину малой полуоси. Опять поместите его в точку O и отметьте на другой из линий ещё две точки, обозначьте их как Q1 и Q2. Отрезки P1P2 и Q1Q2 будут большой и малой полуосями будущего эллипса;
- Установите раствор циркуля на величину a. Поместите циркуль в точке Q1 или Q2. После этого обозначьте циркулем на отрезке P1P2 точки F1 и F2. Это будут фокусы фигуры.
- Отметьте на P1P2 любую точку и обозначьте её T. Поставьте в этой точке циркуль и измерьте этим инструментом расстояние до P1. Затем начертите окружность данного радиуса из фокуса F1. После этого нужно сделать ещё одну окружность с радиусом величиной с расстояние от T до P2, но уже с центром из F2;
- Отметьте точки, в которых пересекаются обе окружности. Повторяйте процедуру, описанную в предыдущем пункте с новыми точками, отмечаемыми на отрезке P1P2;
- Соедините точки пересечения окружностей сплошной линией, когда построите их достаточное количество. Так у вас получится построить фигуру эллипс с помощью циркуля.
Примеры решения задач
Задача 1
Эллипс задан уравнением 16x2 + 25y2 = 400. Требуется найти большую и малую полуоси эллипса, координаты его фокусов и эксцентриситет.
Решение:
Разделим полученное уравнение на 400. Этим мы приведём его к виду
(x2/25) + (y2/16) =1. Большая полуось равна 5, корню квадратному из 25, а малая 4, корню квадратному из 16.
Из соотношения a² = b² + c² находим фокусное расстояние. Оно равно
c=+-√(a2 – b2) = +-√(25-16) = +-3, а значит координаты фокусов будут
F1(-3,0) и F2 (3,0). Эксцентриситет ε = с/a = 3/5.
Ответ: a = 5, b = 4, ε = 3/5.
Задача 2
Выяснить, является ли эллипсом линия, заданная как
9x2 + 25y2 – 225 = 0
Преобразуем данное нам уравнение к каноническому виду. Для этого:
Перенесём 225 в правую сторону
9x2 + 25y2 = 225
Поделим обе части этого уравнения на 225
(9x2/225) + (25y2/225) = 1
Сократим дроби и получим
(x2/25) + (y2/9) = 1
Как видим, нам удалось получить каноническое уравнение эллипса в чистом виде, т. е. исходное уравнение представляет собой эллипс, что и требовалось выяснить.
Ответ: 9x2 + 25y2 – 225 = 0 является уравнением эллипса.
Задача 3
Составить каноническое уравнение эллипса если расстояние между фокусами равно 8, а большая ось 10.
Решение:
Если большая ось равняется 10, значит полуось будет 5.
Если фокусное расстояние равно 8, то число c из координат фокусов будет 4.
Далее нужно подставить и вычислить
4 = √(25-b2)
Возведём это уравнение в квадрат
16 = 25 – b2
Перенесём b2 влево, а 16 вправо
b2 = 25 – 16 =9
В результате этих не сложных преобразований и вычислений получим каноническое уравнение
(x2/25) + (y2/9) = 1
Ответ: (x2/25) + (y2/9) = 1.
Задача 4
Получить каноническое уравнение эллипса, если его эксцентриситет равен 12/13, а большая полуось равна 26.
Решение:
Из уравнения эксцентриситета ε = с/a находим, что a = 13, а величина с = 12. Далее нужно вычислить квадрат длины меньшей полуоси
c = √(169 – b2)
Возведём обе части уравнения в квадрат
c2 = 169 – b2
Отсюда
b2 = 169 – 144 = 25
Далее остаётся лишь составить каноническое уравнение
(x2/169) + (y2/25) = 1
Ответ: (x2/169) + (y2/25) = 1
Задача 5
Найти фокусы у эллипса, который задан уравнением (x2/25) + (y2/16) = 1
Решение:
Нам нужно найти число с, которое определяет первые координаты фокусов
c = √(25-16) =3
Фокусы заданного эллипса будут равны
F1(-3,0) и F2(3,0).
Ответ: F1(-3,0) и F2(3,0).