A conic section can be defined as the set of points that describe the intersection of a right circular cone with a plane. The angle of intersection between the plane and the cone determines the shape of the conic section. When this angle is acute, that is, between 45° and 90°.
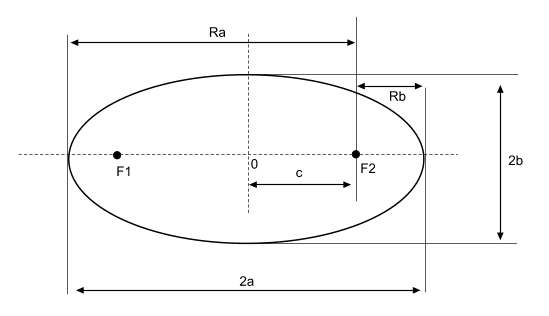
Alternatively, an ellipse can also be defined as such: a closed curve formed by a set of points whose sum of the distance from two fixed points is constant.
The standard equation of the ellipse whose center is (h, k) is,
Question: Determine the equation of the standard form of the ellipse given: The coordinates of two points P (p, q) and M (m, n), and the coordinates of the center, O (h, k).
Solution:
It is known that the standard equation of the ellipse is,
We have been provided the value of (h, k) in the question. Both P(p, q) and M(m, n) will satisfy the equation.
So, now we have two equations:
Equation 1:
Equation 2:
We can equate both the LHS of the equations (since the RHS is equal). Then, we get:
We can simplify this as:
Using the formula a2 – b2 = (a – b)×(a + b), we can simplify the equation further:
From this, we can get the relation between a and b as:
Now, we can plug this value in Equation 1 or Equation 2 to solve it finally.
Let us plug it into equation 1:
Finally, we can deduce that b is:
And hence, a is:
Given two points P (p, q) and M (m, n) of an ellipse with center (h, k), the equation of the ellipse in standard form is:
where,
and
Sample Problems
Problem 1: Given that the center of an ellipse is (5, 2) and the points A (3, 4) and B (5, 6) pass through the ellipse, form the standard equation of the ellipse.
Solution:
Given that center of the ellipse is (h, k) = (5, 2) and (p, q) = (3, 4) and (m, n) = (5, 6) are two points on the ellipse.
We can use the values of a and b from the above formula to create the standard equation as:
We know that,
Substituting the values of p, q, h, k, m and n we get:
Solving, we get a ≈ 2.31.
Similarly, substituting the values of p, q, h, k, m and n in the formula for b, we get:
Solving, we get b = 4.
Therefore, the equation of the ellipse is:
Problem 2: A hypothetical ellipse has its center at (5, 8). The points A (9, 2) and B (7, 6) pass through the ellipse. Is it possible for such an ellipse to exist in the real plane? Explain your answer.
Solution:
Our hypothesis is that the ellipse exists.
Given that center of the ellipse is (h, k) = (5, 8) and (p, q) = (9, 2) and (m, n) = (7, 6) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation
We know that,
Substituting the values of p, q, h, k, m and n we get:
We cannot solve this and get a real value of a.
Therefore, our hypothesis is False. An ellipse with the given conditions cannot exist.
Problem 3: Given that the center of an ellipse is (1, 4) and the points A (2, 9) and B (12, 5) pass through the ellipse, form the standard equation of the ellipse.
Solution:
Given that center of the ellipse is (h, k) = (1, 4) and (p, q) = (2, 9) and (m, n) = (12, 5) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation:
We know that,
Substituting the values of p, q, h, k, m and n we get:
Solving, we get a ≈ 11.22.
Similarly, substituting the values of p, q, h, k, m and n in the formula for b, we get:
Solving, we get b ≈ 5.02.
Therefore, the equation of the ellipse is:
Problem 4: A hypothetical ellipse has its center at (1, 3). The points A (8, 2) and B (7, 5) pass through the ellipse. Is it possible for such an ellipse to exist in the real plane? Explain your answer.
Solution:
Our hypothesis is that the ellipse exists.
Given that center of the ellipse is (h, k) = (1, 3) and (p, q) = (8, 2) and (m, n) = (7, 5) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation:
We know that,
Substituting the values of p, q, h, k, m and n we get:
Solving this, we get a ≈ 7.3.
Similarly, substituting the values of p, q, h, k, m, and n in the formula for b, we get:
Solving this, we get b ≈ 3.51.
As the values of a and b are real, our hypothesis is True. An ellipse that satisfies the given conditions can exist.
Problem 5: The center of an ellipse is at the Origin. The point (1, 5) lies on the ellipse. Does the point (11, 2) also lie on the ellipse?
Solution:
Our hypothesis is that an ellipse with a center at Origin (0, 0) passing through the points (11, 2) and (1, 5) exists.
Now, we can use the values of a and b from the above formula to create the standard equation
We know that,
Substituting the values of p, q, h, k, m and n we get:
Solving this, we get a ≈ 11.99.
Similarly, substituting the values of p, q, h, k, m and n in the formula for b, we get:
Solving this, we get b ≈ 5.02.
As the values of a and b are real, our hypothesis is True. The point (11, 2) does lie on the ellipse.
Каноническое уравнение эллипса по двум точкам
| Две точки с координатами |
|
Первая координата |
|
Вторая координата |
| Каноническое уравнение эллипса |
| Большая полуось эллипса |
| Малая полуось эллипса |
| Эксцентриситет эллипса |
| Фокусное/фокальное расстояние |
| Коэффициент сжатия |
| Координаты первого фокуса F1(x1:y1) |
| Координаты второго фокуса F2(x2:y2) |
| Фокальный параметр |
| Перифокусное расстояние |
| Апофокусное расстояние |
Уравнение эллипса в каноническом виде имеет вот такой вид.
Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.
Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.
Кроме этого, на этой странице мы получим следующую информацию.
Фокальный параметр – половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса
Значение полуосей – большая полуось 

Эксцентриситет – коэффициент, показывающий насколько его фигура отличается от окружности
Фокальное расстояние
Коэффициент сжатия – отношение длин малой и большой полуосей
Перифокусное расстояние
Апофокусное расстояние
Примеры задач
Cоставить каноническое уравнение эллипса по двум точкам
Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt
и получаем результат
| Каноническое уравнение эллипса |
 |
| Большая полуось эллипса |
|
8.48528137423857 |
| Малая полуось эллипса |
|
5.656854249492381 |
| Эксцентриситет эллипса |
|
0.8958064164776166 |
| Фокусное/фокальное расстояние |
|
32.2490309931942 |
| Коэффициент сжатия |
|
0.4444444444444444 |
| Координаты первого фокуса F1(x1:y1) |
|
-16.1245154965971 : 0 |
| Координаты второго фокуса F2(x2:y2) |
|
16.1245154965971 : 0 |
| Фокальный параметр |
|
3.5555555555555554 |
| Перифокусное расстояние |
|
1.875484503402901 |
| Апофокусное расстояние |
|
34.1245154965971 |
И еще один пример
Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса.
Если мы введем данные в калькулятор получим
 |
| Большая полуось эллипса |
|
5.877538136328849 |
| Малая полуось эллипса |
|
NaN |
Как видно, одна из осей не может быть определена, так как нам придется брать корень квадратный из отрицательного числа, а следовательно одна из осей будет комплексным числом, что быть не может.
Таким образом по этим двум точкам, нельзя построить эллипс.
А что же можно построить? Перейдя по ссылке данной в начале статьи, мы можем увидеть что это каноническое уравнение гиперболы.
Более подробно, про гиперболу есть отдельный калькулятор Каноническое уравнение гиперболы по двум точкам
Удачных расчетов!
Кривые второго
порядка.
Линии,
определяемые алгебраическими уравнениями
второй степени относительно переменных
x
и y
,т.е. уравнениями вида
Ax2+2By2+Cy2+2Dx+2Ey+F=0
(A2+B2+C2
0)
(3.1)
Называются
кривыми второго порядка.
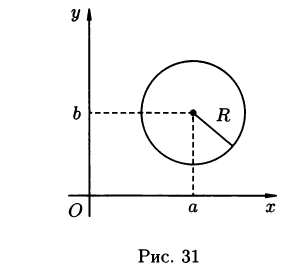
Окружность
Окружностью
называется множество всех точек
плоскости, удалённых от заданной точки
А этой же плоскости на одно и тоже
расстояние R>0.
Точка
А называется центром , а R–
радиусом окружности.
В прямоугольной
системе координат уравнение окружности
имеет вид
(x–a)2+(y–b)2=R2
(3.2)
Где
(a;b)-
координаты её центра, (рис. 31). Уравнение
(3.2) называется каноническим уравнением
окружности. В частности, если a=0;
b=0
(т.е. центр окружности совпадает с началом
координат ), то уравнение (3.2) имеет вид
x2+y2=R2.
(3.3)
Общее
уравнение второй степени (3.1) определяет
окружность , если A=C0
и B=0.
4.3.1.
Найти координаты центра и радиус
окружности :
x2+y2-4x+8y-16=0;
выделяя полные
квадраты в левой части данного уравнения
, приведём его к виду (3.2):
x2-4x+4-4+y2+8y+16-16-16=0,
т.е.
(x-2)2+(y+4)2=62.
Центр окружности находится в точке
(2;-4), а радиус равен 6.
4.3.3.
Написать уравнения касательных к
окружности точк4.3.3. Написать уравнения
касательных к окружности точки
x2+y2-6x+4y-12=0,
проведённых из точки М(0;3).
Уравнения
касательных будем искать в виде уравнения
прямых с угловыми коэффициентами :
y=kx+3.
Уравнение окружности приведём к
каноническому виду (3.2) : (x-3)2+(y+2)2=25.
Для нахождения общих точек прямой и
окружности решим систему уравнений
![]()
Имеем
(x-3)2+(kx+3+2)2=25,
т. е. x2-6x+9+k2x2+10kx+25=25,
поэтому (k2+1)x2+(10k-6)x+9=0.
Так как прямая касается окружности , то
это уравнение имеет единственное решение
.Следовательно , его дискриминант равен
нулю ,т.е. (5k-3)2-9(k2+1)=0,
или 16k2-30k=0,
откуда k1=0
, k2=![]() .
.
Значит , y=3
и y=
![]() x+3-искомые
x+3-искомые
уравнения.
4.3.7.
Написать уравнение окружности ,проходящей
через точки: (-1;3), (0;2), (-1;1) .
Уравнение
окружности ищем в виде (3.2) :
(x–a)2+(y–b)2=R2.
Подставляя
в это уравнение координаты точек ,
получим три уравнения для определения
a,b
и d,:
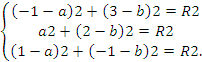
Из
первых двух уравнений получаем
(-1-a)2+(3-b)2=a2+(2-b)2,
т.е. 1+2a+a2+9-6b+b2=a2+4b+b2,
поэтому a–b=-3;
из второго и третий уравнений системы
получаем a2+(2-b)2=(1-a)2+(-1-b)2,
отсюда a-3b=-1.
Решая систему уравнений
Находим
a=-4,
b=-1.
Подставляя эти значения a
и b
во второе уравнение первоначальной
системы , находим : 16+9=R2
, т.е. К2=25.
Искомое уравнение есть (x+4)2+(y+1)2=25.
Заметим,
что уравнение окружности можно искать
в виде x2+y2+2Dx+2ey+F=0.
Так как данные три точки принадлежат
окружности , то подставив их координаты
в записанное уравнение, получим систему
трёх уравнений:
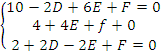
Решив
систему найдём , D=4,
E=1,F=-8
и искомое уравнение окружности
x2+y2+8x+2y-8=0
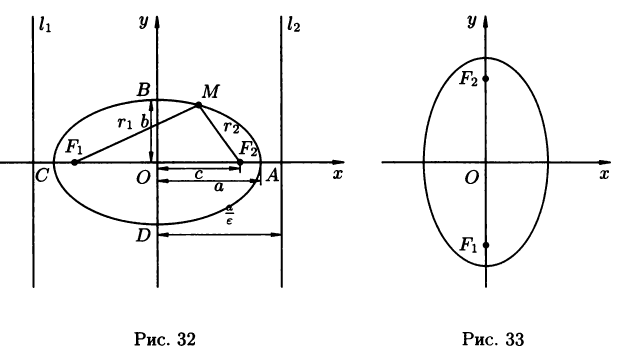
Эллипс
Эллипсом называется
множество всех точек плоскости , сумма
расстояний от каждой из которых до двух
данных точек этой же плоскости ,
называемых фокусами , есть величина
постоянная, большая, чем расстояние
между фокусами.
Каноническое
уравнение эллипса:
![]()
+![]() =
=
1, (3.4)
Где
a
– большая полуось, b
– малая полуось эллипса. Координаты
фокусов : F1(-c;0),
F2(c;0),
где c
– половина расстояния между фокусами
(рис. 32). Числа a,
b
и c
связаны соотношением
c2=a2
–
b2
(3.5)
Точки
A,
B,
C
и D
– называются вершинами эллипса, точка
О – центром эллипса, расстояние r1
и
r2
от произвольной точки М эллипса до его
фокусов называются фокальными радиусами
этой точки.
Эксцентриситетом
![]()
эллипса называется отношение фокусного
расстояния 2с ( расстояние между фокусами
) к большой оси 2а:
![]()
=![]()
(![]() <
<
1, т. к. c
< a).
(3.6)
Фокальные радиусы
определяются формулами:
r1=a+![]() x,
x,
r2=a
–![]() x
x
(r1+r2=2a).
(3.7)
Директрисами
эллипса называются прямые l1
и l2
параллельные малой оси эллипса и
отстоящие от не на расстоянии , равном
![]() ;
;
уравнения директрис:
x=
![]()
и x=-
![]()
(3.8)
Замечания.
1) Если a=b
, то уравнение (3.4) определяет окружность
x2+y2=a2
;
2)
если фокусы эллипса лежат на оси Oy
, то эллипс имеет вид , изображенный на
рисунке 33: В этом случае :
b>a,
c2=b2–a2,
(3.9)
![]()
=![]()
, (3.10)
Уравнения
директрис y=![]() ;
;
3)
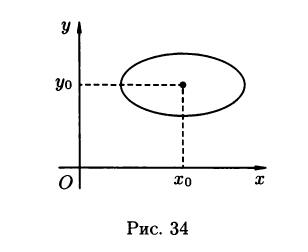
уравнение эллипса с осями, параллельными
координатным, имеет вид
![]()
+ ![]() =1,
=1,
(3.11)
Где
(x0;y0)
– координаты центра эллипса (рис. 34) ;
4) уравнения
![]()
t![]()
Являются
параметрическими уравнениями эллипса.
4.3.27
Показать , что уравнение 4x2+3y2-8x+12y-32=0
определяет эллипс, найти его оси,
координаты центра и эксцентриситет.
Преобразуем
данное уравнение кривой. Так как
4x2+3y2-8x+12-32=4(x2-2x)+3(y2+4y)-32=4(x2-2x+1-1)+3(y2+4y+4-4)-32=
4(x-1)2-4+3(y+2)2-12-32,
То
уравнение можно переписать в виде
4(x-1)2+3(y+2)2=48,
т. е.
![]()
+ ![]() =1.
=1.
Получили уравнение вида (3.11); его центр
симметрии имеет координаты (1;-2). Из
уравнения находим : a2=12,
a=2![]()
и b2=16,
b=4
(b>0).
Поэтому c=![]() =
=![]() =2.
=2.
Эксцентриситет эллипса ![]()
= ![]() .
.
4.3.28.
Дано уравнение эллипса 24x2+49y2=1176.
Найти :
1) длины его
полуосей;
2)координаты
фокусов;
3) эксцентриситет
эллипса;
4) уравнения
директрис и расстояние между ними;
5)
точки эллипса, расстояние от которых
до левого фокуса F1=12.
Запишем уравнение
эллипса в виде (3.4), разделив обе части
на 1176:
![]()
+ ![]() =1
=1
-
Отсюда
a2=49,
b2=24,
т.
е.
a=7, b=2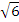 .
. -
Используя
соотношение (3.5) , находим c2
=72-(2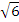 )2=25,
)2=25,
c=5.
Следовательно , F1(-5;0)
и F2(5;0). -
По
формуле (3.6) находим :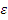
= .
. -
Уравнения
директрис (3.8) имеет вид x=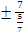
т. е. x=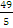
и x=-
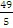 ;
;
расстояние между ними d=
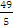
-(-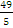 )
)
=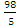 =19.6.
=19.6. -
По
формуле r1=a+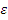 x
x
находим абсциссу точек , расстояние от
которых до точки F1
равно
12: 12=7+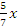 ,
,
т. е. x=7.
Подставляя
значения x
в уравнение эллипса, найдём ординаты
этих точек :24![]() 49+49y2=1176,
49+49y2=1176,
49y2
= 0, y=0.
Условию задачи удовлетворяет точка
А(7;0).
4.3.31.
Составить уравнение эллипса , проходящего
через точки
М1(2;-4![]()
и М2(-1;2![]()
Уравнение эллипса
ищем в виде (3.4)
![]()
+ ![]()
=1
Так
как эллипс проходит через точки М1
и М2
, то их координаты удовлетворяют
уравнению эллипса : ![]()
+ ![]()
=1 и ![]()
+ ![]()
=1. Умножая второе равенство на (-4) и
складывая с первым , находим – ![]() =-3,
=-3,
т. е. b2=64.
Подставляя найденное значение b2
в первое уравнение, получаем ![]()
+ ![]()
=1, откуда a2=16.
Таким образом, искомое уравнение эллипса
есть ![]()
+ ![]()
=1.
Составить
уравнение эллипса, фокусы которого
лежат на оси Oy,
а малая ось равна 2![]() .
.
Каждый из фокусов равноудалён от центра
эллипса и от ближайшего конца фокальной
оси. Уравнение эллипса имеет вид ![]()
+ ![]() =1,
=1,
b>a.
По условию задачи 2a=2![]() ,
,
т. е. a=![]() ,
,
и с=![]() .
.
Так как c2=b2–a2
(3.9), то получаем: ![]()
=b2-3
, т.е. b2=4.
Таким образом, уравнение эллипса есть
![]()
+ ![]()
=1.
Гипербола
Гиперболой
называется множество всех точек
плоскости, модуль разности расстояний
от каждой из которых до двух заданных
точек этой же плоскости , называемых
фокусами, есть величина постоянная,
меньшая, чем расстояние между фокусами.
Каноническое
уравнение гиперболы:
![]()
+ ![]()
=1, (3.12)
Где а
– действительная, b
– мнимая полуось гиперболы. Числа 2a
и 2b
называются соответственно действительной
и мнимой осями гиперболы. Координаты
фокусов : F1(-c;0),
F2(c;0),
c–
половина расстояния между фокусами
(рис.35). Числа a,
b
и c,
связаны соотношением
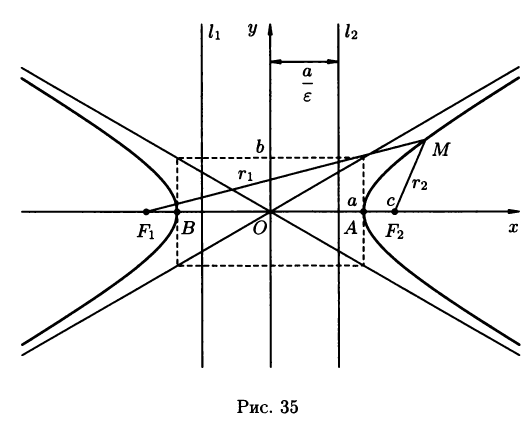
с2=a2+b2
(3.13)
Точки
А и В называются вершинами2гиперболы,
точка О – центром гиперболы, расстояния
r1
и r2
от произвольной точки М гиперболы до
её фокусов называются фокальными
радиусами этой точки .
Число
![]() =
=
![]()
(![]() >1,
>1,
т. к. с >a).
(3.14)
Называется
эксцентриситетом гиперболы.
Фокальные радиусы
определяются формулами: для точек правой
ветви гиперболы:
r1=a+![]() x,
x,
r2=-a+![]() x;
x;
(3.15)
для точек левой
ветви:
r1=-a–![]() x,
x,
r2=a–![]() x.
x.
(3.16)
Прямоугольник,
центр которого совпадает с точкой О, а
стороны равны и параллельны осям
гиперболы называется основным
прямоугольником гиперболы. Диагонали
основного прямоугольника гиперболы
лежат на двух прямых, называемых
асимптотами гиперболы; они определяются
уравнениями
y=
![]() x.
x.
(3.17)
Две
прямые l1
и l2
параллельные мнимой оси гиперболы и
отстоящие от неё на расстоянии, равном
![]()
, называются директрисами гиперболы.
Их уравнения
x=![]()
и x=![]()
(3.18)
Замечания.
1) Если a=b,
то гипербола (3.12) называется равносторонней
(равнобочной). Её уравнение принимает
вид
x2–y2=a2
(3.19)
2) если
фокусы гиперболы лежат на оси Oy,
то уравнение гиперболы имеет вид
![]()
– ![]() =1.
=1.
(3.20)
Эксцентриситет
этой гиперболы равен ![]() =
=![]() ,
,
асимптоты определяются уравнениями
y=![]()
![]() x,
x,
а уравнение директрис y=![]()
![]() .
.
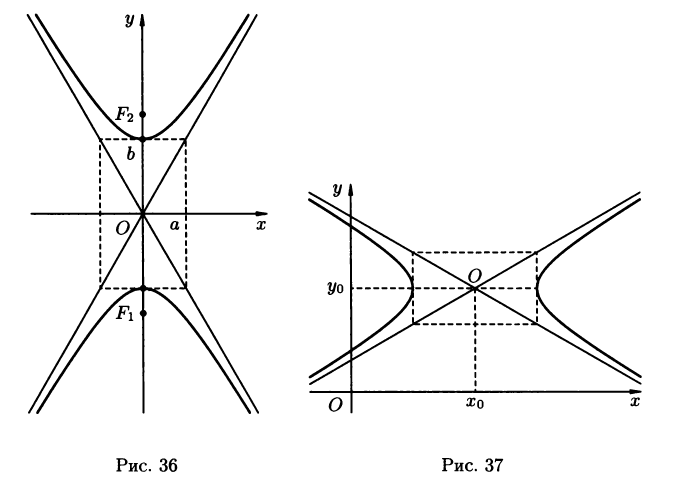
Гипербола называется сопряжённой
гиперболе(3.12) ; она имеет вид , изображенный
на рисунке 36.
3) уравнение
гиперболы с осями, параллельными
координатным, имеет вид
![]()
– ![]() =1
=1
(3.21)
Где
(x0;
y0)-
координаты центра гиперболы (рис. 37.)
4.3.60.
Дано уравнение гиперболы 5x2-4y2=20.
Найти :
1) длины его
полуосей;
2) координаты
фокусов;
3) эксцентриситет
гиперболы;
4) уравнение
асимптот и директрис;
5) фокальные
радиусы точки М(3;2.5).
Решение: разделив
обе части уравнения на 20, приведём
уравнение гиперболы к каноническому
виду (3.12):
![]()
– ![]() =1.
=1.
Отсюда:
-
a2=4,
b2=5,
т.
е. a=2,
b=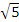 ;
; -
Используя
соотношение (3.13) , находим с2=4+5,
т. е. c=3.
Отсюда находим фокусы гиперболы:F1(-3;0)
и F2(3;0); -
По
формуле (3.14) находим
= ;
; -
Уравнения
асимптот и директрис найдём по формулам
(3.17) и (3.18) : y=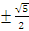 x
x
и x=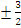 ;
; -
Точка
М лежит на правой ветви гиперболы
(x=3>0),
воспользуемся формулами (3.15) : r1=2
+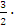 3=6.5,
3=6.5,
r2=-
2 +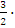 3=2.5.
3=2.5.
4.3.67.
Найти угол между асимптотами гиперболы,
если её эксцентриситет равен 2.
Уравнения
асимптот гиперболы имеют вид y=
=![]() x.
x.
Найдём отношение ![]()
, воспользовавшись формулами (3.13) и
(3.14) и условием ![]() =
=
![]()
= ![]()
= ![]()
. Отсюда ![]() 2=
2=
![]() 2-1,
2-1,
т. е. ![]() =
=
![]() .
.
Имеем: ![]() =
=![]()
= ![]() .
.
Стало
быть, уравнения асимптот гиперболы есть
y
= ![]() x
x
и y
= –![]() x.
x.
Угол ![]()
между асимптотами найдём по формуле
tg
![]()
= ![]()
= ![]()
= ![]() ,
,
![]()
= 600.
Парабола
Параболой
называется множество всех точек
плоскости, каждая из которых равноудалена
от заданной точки этой же плоскости ,
называемой фокусом , и заданной прямой
, называемой директрисой .
Каноническое
уравнение параболы имеет вид
y2
= 2px,
(3.22)
где
число p>0
, равное расстояние от фокуса F
до директрисы l,
называется параметром параболы.
Координаты фокуса F(![]() ;
;
0). Точка О(0;0) называется вершиной
параболы, длина r
отрезка FM
–фокальный радиус точки М, ось Ox
– ось симметрии параболы.
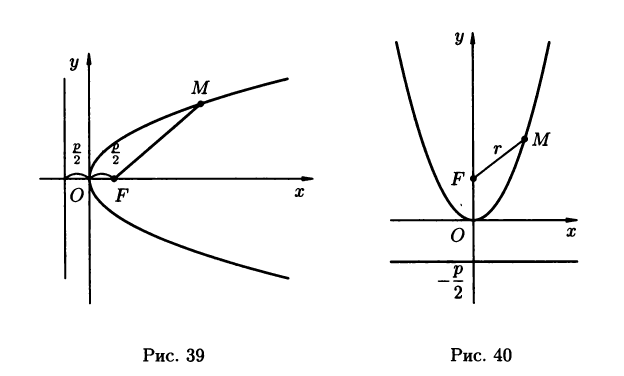
Уравнение
директрисы l
параболы имеет вид
x=
– ![]() ;
;
(3.23)
фокальный радиус
вычисляется по формуле
r=
x+
![]() .
.
(3.24)
В прямоугольной
системе координат парабола, заданная
каноническим уравнением (3.22), расположена
так, как указано на рисунке 39.
Замечания.
1) Парабола, симметричная относительно
оси Oy
и проходящая через начало координат
(рис. 40), имеет уравнение
x2
= 2py.
(3.25)
Фокусом параболы
(3.25) является точка
F(0
; ![]() ).
).
(3.26)
Уравнение
директрисы этой параболы
y
= – ![]()
(3.27)
Фокальный радиус
точки М параболы
r
= y
+ ![]()
. (3.28)
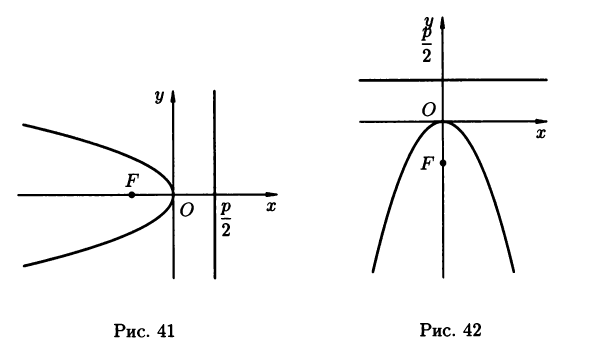
2) На
рисунках 41 и 42 изображены графики парабол
y2
= -2px
и x2
=
-2py
Соответственно.
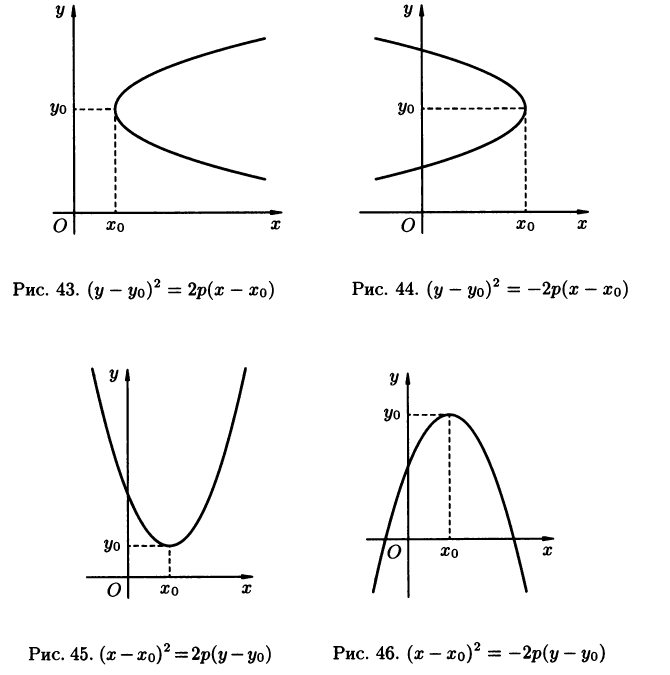
3) На рисунках
43-46 приведены уравнения и графики парабол
с осями симметрии, параллельными
координатным осям.
Дана
парабола x2
= 4y.
Найти координаты её фокуса, уравнение
директрисы, длину фокального радиуса
точки М(4;4).
Парабола
задана каноническим уравнением (3.25).
Следовательно , 2p=4,
p=2.
Используя формулы (3.26) ,(3.27) , (3.28) находим
, что фокус имеет координаты (0;1) , т. е.
F(0;1);
уравнение директрисы есть y=-1;
фокальный радиус точки М(4;4) равен r
= 4+1=5.
4.3.106.
Найти вершину, фокус и директрису
параболы y
= -2x2+8x-5,
построить эскиз графика.
Преобразуем
уравнение y
= -2x2+8x-5
, выделив полный квадрат:
y
= -2(x2+4x
– ![]() )
)
= -2(x2–
4x
+ 4 – 4 + ![]() )=
)=
– 2((x-2)2
–
![]() )
)
= -2(x-2)2
+ 3, т. е. y=-2(x-2)2
+ 3, или (x-2)2=
– ![]() (y-3).
(y-3).
Уравнение параболы имеет вид, как на
рис.46. Вершина параболы имеет координаты
(2;3); 2p
= ![]()
, p
= ![]() .
.
Прямая x
= 2 является осью симметрии параболы.
Координаты фокуса x=2,
y=3
– ![]()
= 2![]() ,
,
т. е. F(2;
2![]() )
)
. Уравнение директрисы y
= 3 + ![]()
= 3 + ![]() ,
,
т. е. y
= 3![]() .
.
График изображён на рис. 47.
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек 
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы 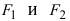
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 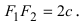 Согласно определению эллипса имеем
Согласно определению эллипса имеем 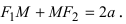 Из треугольников
Из треугольников 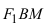 и
и 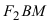 по теореме Пифагора найдем
по теореме Пифагора найдем
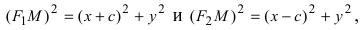
соответственно. Следовательно, согласно определению имеем
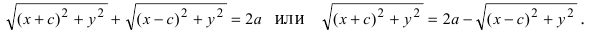
Возведем обе части равенства в квадрат, получим
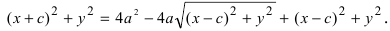
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 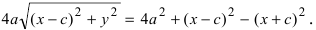 Раскроем разность квадратов
Раскроем разность квадратов 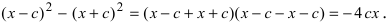 Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение
Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение 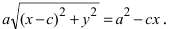 Вновь возведем обе части равенства в квадрат
Вновь возведем обе части равенства в квадрат 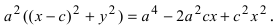 Раскрывая все скобки в правой части уравнения, получим
Раскрывая все скобки в правой части уравнения, получим 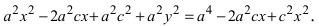 Соберем не- известные в левой части, а все известные величины перенесем в правую часть уравнения, получим
Соберем не- известные в левой части, а все известные величины перенесем в правую часть уравнения, получим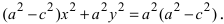 Введем обозначение для разности, стоящей в скобках
Введем обозначение для разности, стоящей в скобках 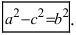 Уравнение принимает вид
Уравнение принимает вид 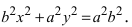 Разделив все члены уравнения на
Разделив все члены уравнения на 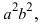 получаем каноническое уравнение эллипса:
получаем каноническое уравнение эллипса: 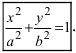 Если
Если 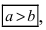 то эллипс вытянут вдоль оси Ох, для противоположного неравенства – вдоль оси Оу (при этом фокусы тоже расположены на этой оси). Проанализируем полученное уравнение. Если точка М(х; у) принадлежит эллипсу, то ему принадлежат и точки
то эллипс вытянут вдоль оси Ох, для противоположного неравенства – вдоль оси Оу (при этом фокусы тоже расположены на этой оси). Проанализируем полученное уравнение. Если точка М(х; у) принадлежит эллипсу, то ему принадлежат и точки  следовательно, эллипс симметричен относительно координатных осей, которые в данном случае будут называться осями симметрии эллипса. Найдем координаты точек пересечения эллипса с декартовыми осями:
следовательно, эллипс симметричен относительно координатных осей, которые в данном случае будут называться осями симметрии эллипса. Найдем координаты точек пересечения эллипса с декартовыми осями:
Определение: Найденные точки называются вершинами эллипса.
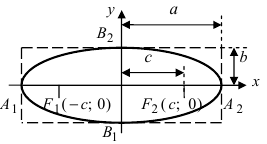
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 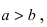 то параметр а называется большой, а параметр b – малой полуосями эллипса.
то параметр а называется большой, а параметр b – малой полуосями эллипса.
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса 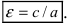
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 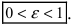 Кроме того, эта характеристика описывает форму эллипса. Для демонстрации этого факта рассмотрим квадрат отношения малой полуоси эллипса к большой полуоси
Кроме того, эта характеристика описывает форму эллипса. Для демонстрации этого факта рассмотрим квадрат отношения малой полуоси эллипса к большой полуоси 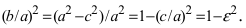
Если 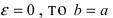 и эллипс вырождается в окружность. Если
и эллипс вырождается в окружность. Если 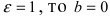 и эллипс вырождается в отрезок
и эллипс вырождается в отрезок 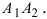
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет 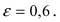
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 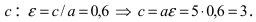 Зная параметр с, можно вычислить малую полуось эллипса
Зная параметр с, можно вычислить малую полуось эллипса 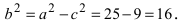 Следовательно, каноническое уравнение заданного эллипса имеет вид:
Следовательно, каноническое уравнение заданного эллипса имеет вид: 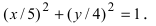
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 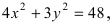 а третья вершина – в центре окружности
а третья вершина – в центре окружности
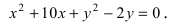
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс: 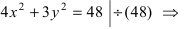
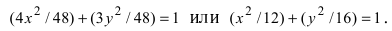 Следовательно, большая полуось эллипса
Следовательно, большая полуось эллипса 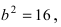 а малая полуось
а малая полуось 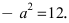 Так как
Так как 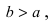 то эллипс вытянут вдоль оси ординат Оу. Определим расположение фокусов данного эллипса
то эллипс вытянут вдоль оси ординат Оу. Определим расположение фокусов данного эллипса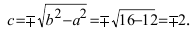 Итак,
Итак,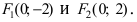 Окружность:
Окружность: 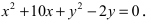 Выделим полные квадраты по переменным
Выделим полные квадраты по переменным 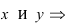
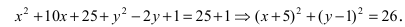 Следовательно, центр окружности находится в точке О(-5; 1).
Следовательно, центр окружности находится в точке О(-5; 1).
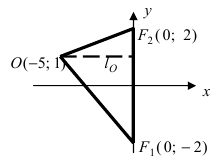
Построим в декартовой системе координат треугольник  Согласно школьной формуле площадь треугольника
Согласно школьной формуле площадь треугольника 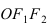 равна
равна 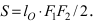 Высота
Высота 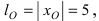 а основание
а основание 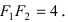 Следовательно, площадь треугольника
Следовательно, площадь треугольника 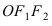 равна:
равна:
Эллипс в высшей математике
Рассмотрим уравнение

где 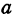 и
и 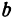 —заданные положительные числа. Решая его относительно
—заданные положительные числа. Решая его относительно 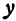 , получим:
, получим:
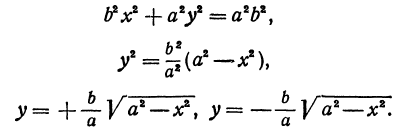
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 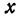 по абсолютной величине меньше
по абсолютной величине меньше 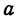 , подкоренное выражение положительно, корень имеет два значения. Каждому значению
, подкоренное выражение положительно, корень имеет два значения. Каждому значению 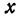 , удовлетворяющему неравенству
, удовлетворяющему неравенству 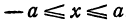 соответствуют два значения
соответствуют два значения 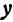 , равных по абсолютной величине. Значит, геометрическое место точек, определяемое уравнением (2), симметрично относительно оси
, равных по абсолютной величине. Значит, геометрическое место точек, определяемое уравнением (2), симметрично относительно оси 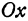 . Так же можно убедиться в том, что оно симметрично и относительно оси
. Так же можно убедиться в том, что оно симметрично и относительно оси 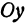 . Поэтому ограничимся рассмотрением только первой четверти.
. Поэтому ограничимся рассмотрением только первой четверти.
При 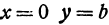 , при
, при 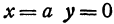 . Кроме того, заметим, что если
. Кроме того, заметим, что если 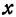 увеличивается, то разность
увеличивается, то разность уменьшается; стало быть, точка
уменьшается; стало быть, точка 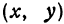 будет перемещаться от точки
будет перемещаться от точки 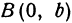 вправо вниз и попадет в точку
вправо вниз и попадет в точку 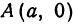 . Из соображений симметрии изучаемое геометрическое место точек будет иметь вид, изображенный на рис. 34.
. Из соображений симметрии изучаемое геометрическое место точек будет иметь вид, изображенный на рис. 34.
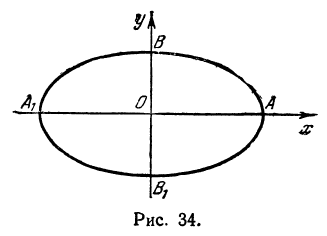
Полученная линия называется эллипсом. Число 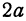 является длиной отрезка
является длиной отрезка 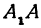 , число
, число 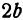 —длиной отрезка
—длиной отрезка 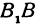 . Числа
. Числа 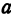 и
и 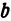 называются полуосями эллипса. Число
называются полуосями эллипса. Число 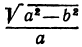 эксцентриситетом.
эксцентриситетом.
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 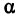 (рис. 35). В каждой из этих плоскостей возьмем систему координат, причем за ось
(рис. 35). В каждой из этих плоскостей возьмем систему координат, причем за ось 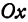 примем прямую пересечения плоскостей, стало быть, ось
примем прямую пересечения плоскостей, стало быть, ось 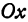 будет общей для обеих систем. Оси ординат различны, начало координат общее для обеих систем. В плоскости
будет общей для обеих систем. Оси ординат различны, начало координат общее для обеих систем. В плоскости  возьмем окружность радиуса
возьмем окружность радиуса  с центром в начале координат, ее уравнение
с центром в начале координат, ее уравнение 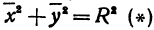 .
.
Пусть точка 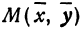 лежит на этой окружности, тогда ее координаты удовлетворяют уравнению
лежит на этой окружности, тогда ее координаты удовлетворяют уравнению 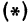 .
.
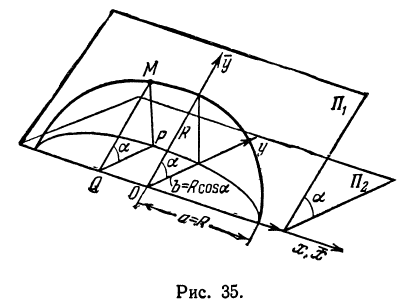
Обозначим проекцию точки  на плоскость
на плоскость  буквой
буквой 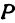 , а координаты ее—через
, а координаты ее—через 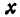 и
и 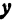 . Опустим перпендикуляры из
. Опустим перпендикуляры из  и
и  на ось
на ось  , это будут отрезки
, это будут отрезки  и
и  . Треугольник
. Треугольник 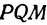 прямоугольный, в нем
прямоугольный, в нем 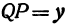 ,
, 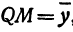 ,
,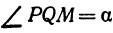 , следовательно,
, следовательно, 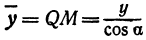 . Абсциссы точек
. Абсциссы точек  и
и  равны, т. е.
равны, т. е. 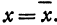 . Подставим в уравнение
. Подставим в уравнение 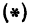 значение
значение 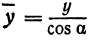 , тогда cos
, тогда cos
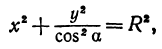
или
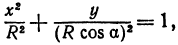
а это есть уравнение эллипса с полуосями 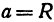 и
и 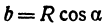 .
.
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:

где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 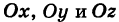 с коэффициентами деформации, равными
с коэффициентами деформации, равными 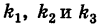
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 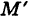 (х, у, z) с текущими координатами х, у, г, причем
(х, у, z) с текущими координатами х, у, г, причем
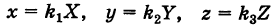
(рис. 206). Отсюда
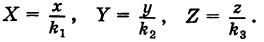 Иными словами, линейные размеры сферы в направлении оси Ох уменьшаются в
Иными словами, линейные размеры сферы в направлении оси Ох уменьшаются в 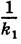 раз, если
раз, если 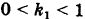 , и увеличиваются в
, и увеличиваются в 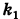 раз, если
раз, если 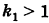 и т. д.
и т. д.
Подставляя эти формулы в уравнение (1), будем иметь
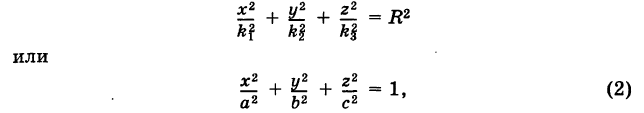
где 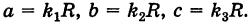 Уравнение (2) связывает текущие координаты точки М’ эллипсоида и, следовательно, является уравнением трехосного эллипсоида.
Уравнение (2) связывает текущие координаты точки М’ эллипсоида и, следовательно, является уравнением трехосного эллипсоида.
Величины 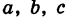 называются полуосями эллипсоида; удвоенные величины
называются полуосями эллипсоида; удвоенные величины 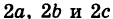 называются осями эллипсоида и, очевидно, представляют линейные размеры его в направлениях деформации (в данном случае в направлениях осей координат).
называются осями эллипсоида и, очевидно, представляют линейные размеры его в направлениях деформации (в данном случае в направлениях осей координат).
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
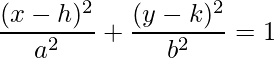


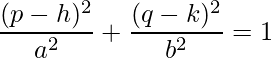
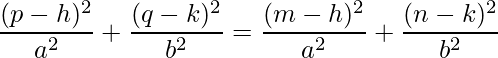
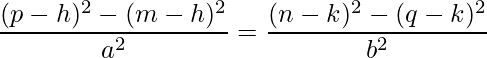
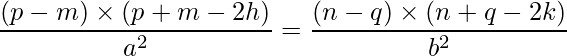
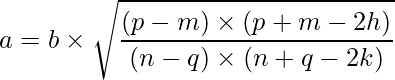
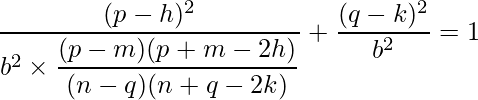
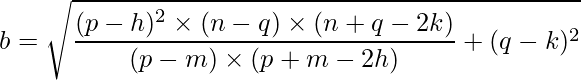
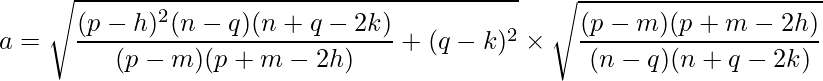
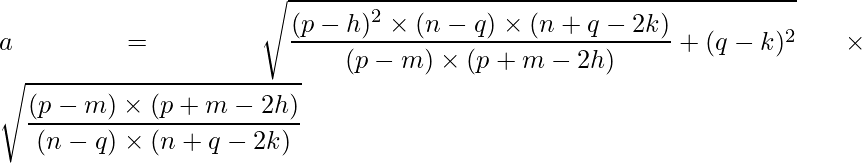
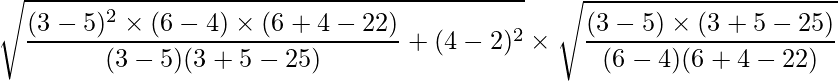
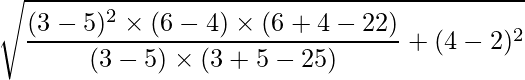
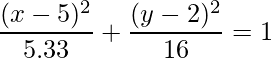
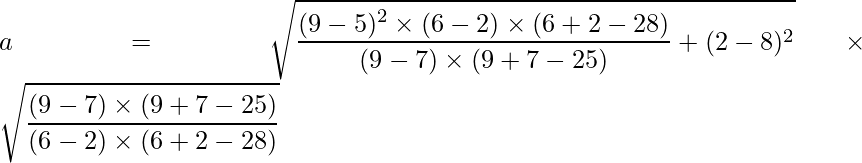
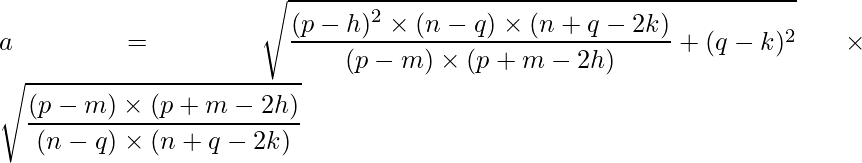
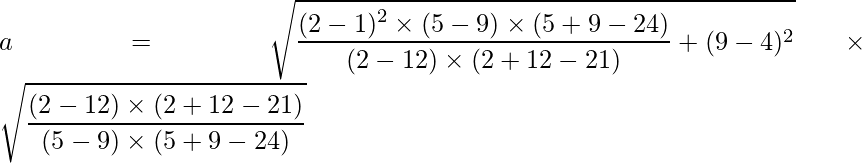
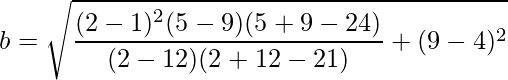
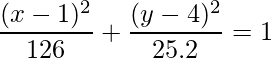
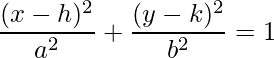
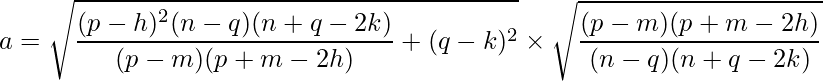
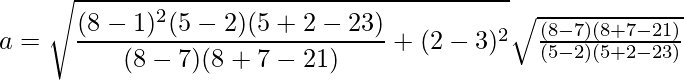

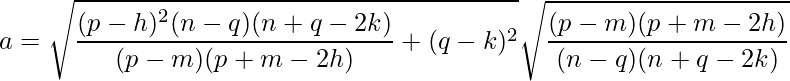
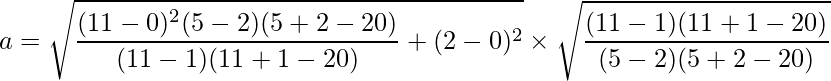
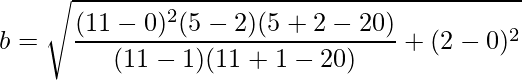




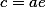


;M_2(3sqrt{1.5}:sqrt{2}))

