Как составить уравнение гармонических колебаний материальной точки

Как составить уравнение гармонических колебаний материальной точки

§
6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные
формулы

• Уравнение
гармонических колебаний

где х
— смещение
колеблющейся точки от положения
равновесия;
t
— время; А,
ω,
φ—
соответственно амплитуда, угловая
частота,
начальная фаза колебаний;
—
фаза колебаний в момент t.

• Угловая частота
колебаний


, или
,

где ν
и
Т — частота и период колебаний.

• Скорость точки,
совершающей гармонические колебания,

• Ускорение при
гармоническом колебании

• Амплитуда
А
результирующего
колебания, полученного при сложении
двух колебаний с одинаковыми частотами,
происходящих по одной прямой, определяется
по формуле

где
a1
и
А2—
амплитуды
составляющих колебаний; φ1
и
φ2—
их
начальные фазы.

•
Начальная фаза φ
результирующего колебания может быть
найдена
из формулы

•
Частота биений,
возникающих при сложении двух колебаний,
происходящих
по одной прямой с различными, но близкими
по зна­чению
частотами ν1
и
ν2,

•
Уравнение траектории
точки, участвующей в двух взаимно
перпендикулярных
колебаниях с амплитудами A1
и A2
и начальны­ми
фазами φ1
и φ2,

Если
начальные фазы φ1
и
φ2
составляющих колебаний одинако­вы,
то уравнение траектории принимает вид

т. е. точка движется
по прямой.

В том
случае, если разность фаз
,
уравнение
принимает вид

т. е. точка движется
по эллипсу.

• Дифференциальное
уравнение гармонических колебаний
ма­териальной точки


, или
,
где
m
—
масса точки; k
—
коэффициент
квазиупругой силы (k=тω2).

•
Полная энергия
материальной точки, совершающей
гармони­ческие
колебания,

• Период
колебаний тела, подвешенного на пружине
(пружин­ный
маятник),

где
m
—
масса тела; k
—
жесткость
пружины.
Формула справедлива для упругих
колебаний в пределах, в ко­торых
выполняется закон Гука (при малой массе
пружины в срав­нении
с массой тела).

Период колебаний
математического маятника

где
l
— длина маятника; g
—
ускорение
свободного падения. Период
колебаний физического маятника

где J
— момент инерции колеблющегося тела
относительно оси

колебаний;
а
— расстояние центра масс маятника от
оси колебаний;


— приведенная
длина физического маятника.

Приведенные
формулы являются точными для случая
бесконеч­но малых амплитуд. При
конечных амплитудах эти формулы дают
лишь приближенные результаты. При
амплитудах не более
ошибка в значении периода не превышает
1 %.

Период
крутильных колебаний тела, подвешенного
на упругой нити,

где J
—
момент
инерции тела относительно оси, совпадающей
с упругой нитью; k
—
жесткость
упругой нити, равная отношению упругого
момента, возникающего при закручивании
нити, к углу, на который нить закручивается.

• Дифференциальное
уравнение затухающих колебаний

, или
,

где r
— коэффициент сопротивления; δ
— коэффициент
затухания:

; ω0—
собственная угловая частота колебаний
*

• Уравнение
затухающих колебаний

где A
(t) —
амплитуда
затухающих колебаний в момент t;
ω
— их угловая частота.

• Угловая частота
затухающих колебаний

О Зависимость
амплитуды затухающих колебаний от
времени


I

где
А0
— амплитуда
колебаний в момент t=0.

• Логарифмический
декремент колебаний

где
A
(t) и
A
(t+T) —
амплитуды
двух последовательных колеба­ний,
отстоящих по времени друг от друга на
период.

• Дифференциальное
уравнение вынужденных колебаний


, или


,

где

—
внешняя периодическая сила, действующая
на
колеблющуюся
материальную точку и вызывающая
вынужденные
колебания;
F0
—
ее
амплитудное значение;

•
Амплитуда вынужденных
колебаний

•
Резонансная частота
и резонансная амплитуда

и

Примеры решения
задач

Пример
1. Точка
совершает колебания по закону
x(t)= ,
где
А=2
см.
Определить начальную фазу φ,
если

x(0)= см
и х,(0)<0.
Построить векторную диаграмму для
мо-­
мента t=0.

Решение.
Воспользуемся уравнением движения и
выразим смещение в момент t=0
через начальную фазу:

Отсюда
найдем начальную фазу:

*
В приведенных ранее формулах
гармонических колебаний та же
величина
обозначалась просто ω
(без индекса 0).

Подставим
в это выражение заданные значения x(0)
и А:
φ=
= .
Значению аргумента

удовлетворяют
два
значения угла:

Для
того чтобы решить, какое из этих значений
угла φ
удовлет-­
воряет
еще и условию
,
найдем сначала
:

Подставив
в это выражение значение t=0
и поочередно значения
начальных
фаз
и
,
найдем

Так
как всегда A>0
и ω>0,
то условию удовлетворяет
толь­
ко
первое значение начальной фазы.
Таким
образом, искомая начальная
фаза

По
найденному значению φ
постро-­
им
векторную диаграмму (рис. 6.1).
Пример
2. Материальная
точка
массой т=5
г совершает гармоничес-­
кие колебания
с частотой ν
=0,5 Гц.
Амплитуда
колебаний A=3
см. Оп-­
ределить: 1) скорость υ
точки
в мо-­
мент времени, когда смещение
х=
=
1,5 см; 2) максимальную силу
Fmax,
действующую
на точку; 3)
Рис.
6.1 полную
энергию Е
колеблющейся
точ­
ки.

Решение.
1. Уравнение гармонического колебания
имеет вид

(1)

а
формулу скорости получим, взяв первую
производную по времени от смещения:

(2)

Чтобы
выразить скорость через смещение, надо
исключить из формул (1) и (2) время. Для
этого возведем оба уравнения в квад­рат,
разделим первое на А2,
второе
на A2
ω
2
и сложим:


, или

Решив
последнее уравнение относительно υ,
найдем

Выполнив вычисления
по этой формуле, получим


см/с.

Знак
плюс соответствует случаю, когда
направление скорости совпадает
с положительным направлением оси х,
знак
минус — ког­да
направление скорости совпадает с
отрицательным направлением оси
х.

Смещение при
гармоническом колебании кроме уравнения
(1) может быть определено также уравнением

Повторив
с этим уравнением такое же решение,
получим тот же ответ.

2.
Силу действующую на точку, найдем по
второму закону Нью­тона:

(3)

где а
— ускорение
точки, которое получим, взяв производную
по времени
от скорости:


, или

Подставив выражение
ускорения в формулу (3), получим

Отсюда максимальное
значение силы

Подставив
в это уравнение значения величин π,
ν,
т
и
A,
найдем

3.
Полная энергия колеблющейся точки есть
сумма кинетической и
потенциальной энергий, вычисленных для
любого момента вре­мени.

Проще
всего вычислить полную энергию в момент,
когда кинети­ческая
энергия достигает максимального
значения. В этот момент потенциальная
энергия равна нулю. Поэтому полная
энергия E
колеблющейся точки равна максимальной
кинетической энергии

Tmax:

(4)

Максимальную
скорость определим из формулы (2),
положив

:
.
Подставив выражение скорости в фор­-
мулу
(4), найдем

Подставив
значения величин в эту формулу и произведя
вычис­ления, получим

или

мкДж.

Пример
3.
На концах тонкого стержня длиной l
=
1 м и массой m3=400
г
укреплены шарики малых размеров массами
m1=200
г
и
m2=300г.
Стержень
колеблется около горизонтальной оси,
перпен-

дикулярной
стержню и проходящей через его середину
(точка О на рис. 6.2). Определить период Т
колебаний,
совершаемых стержнем.

Решение.
Период колебаний физического маятника,
каким является стержень с шариками,
определяется соотношением


(1)

где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; lС
— расстояние
от центра масс ма­ятника
до оси.

Момент
инерции данного маятника равен сумме
моментов
инерции шариков J1
и
J2
и
стержня J3:


(2)

Принимая
шарики за материальные точки, вы­разим
моменты их инерции:

Так
как ось проходит через середину стержня,
то
его
момент инерции относительно этой оси
J3=
= .
Подставив
полученные выражения
J1
,
J2
и

J3
в формулу (2), найдем общий момент инерции
фи-­
зического маятника:

Произведя
вычисления по этой формуле, найдем

Рис.
6.2 Масса маятника состоит из масс шариков
и массы
стержня:

Расстояние
lС
центра
масс маятника от оси колебаний найдем,
исходя
из следующих соображений. Если ось х
направить
вдоль стержня
и начало координат совместить с точкой
О,
то
искомое рас­стояние
l
равно координате центра масс маятника,
т. е.


, или

Подставив
значения величин m1,
m2,
m,
l
и произведя вычисле­ния,
найдем


см.

Произведя
расчеты по формуле (1), получим период
колебаний физического
маятника:

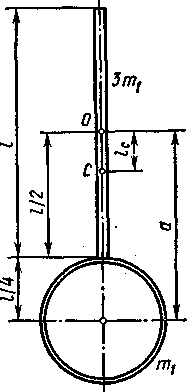
Пример
4. Физический
маятник представляет собой стержень
длиной
l=
1 м и массой 3т1
с прикрепленным
к одному из его концов
обручем
диаметром
и
массой т1.
Горизонтальная
ось Oz

маятника
проходит через середину стержня
перпендикулярно ему (рис. 6.3). Определить
период Т
колебаний
такого маятника.

Решение.
Период
колебаний физического маятника
опреде­ляется
по формуле


(1)

где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; lC
— расстояние
от центра масс
маятника до оси колебаний.

Момент
инерции маятника равен сумме мо­ментов
инерции стержня J1
и
обруча J2:


(2).

Момент
инерции стержня относительно
оси,
перпендикулярной
стержню и проходящей
через
его центр масс, определяется по форму-­
ле
.
В данном случае т=3т1
и

Момент
инерции обруча найдем, восполь-­
зовавшись
теоремой Штейнера
,
где
J
—
момент
инерции относительно про-­
извольной
оси;
J0
—
момент
инерции отно-­
сительно
оси, проходящей через центр масс
параллельно
заданной оси; а
— расстояние
между
указанными осями. Применив эту фор-­
мулу
к обручу, получим

Рис. 6.3

Подставив
выражения J1
и
J2
в форму­лу
(2), найдем момент инерции маятника
относительно оси вра­щения:

Расстояние
lС
от
оси маятника до его центра масс равно

Подставив
в формулу (1) выражения J,
lс
и массы маятника

, найдем период его колебаний:

После
вычисления по этой формуле получим
T=2,17
с.

Пример
5. Складываются
два колебания одинакового направле-­
ния,
выражаемых уравнениями
;
х2=
=,
где А1=1
см,
A2=2
см,

с,

с, ω
=
=.
1. Определить начальные фазы φ1
и φ
2
составляющих коле-

баний.
2. Найти амплитуду А
и
начальную фазу φ
результирующего колебания.
Написать уравнение результирующего
колебания.

Решение.
1. Уравнение гармонического колебания
имеет вид


(1)

Преобразуем
уравнения, заданные в условии задачи,
к такому же
виду:


(2)

Из
сравнения выражений (2) с равенством (1)
находим начальные фазы
первого и второго колебаний:


рад и

рад.

2.
Для определения амплитуды А
результирую­щего
колебания удобно воспользоваться
векторной диаграммой,
представленной на рис.
6.4.
Согласно теореме косинусов, получим


(3)

где

— разность фаз составляющих колебаний.
Так
как
,
то, подставляя найденные
значения
φ2
и φ1
получим

рад.

Рис. 6.4

Подставим
значения А1
,
А2
и

в формулу (3)
и
произведем вычисления:

A=2,65
см.

Тангенс
начальной фазы φ
результирующего колебания опреде-­
лим
непосредственно из рис. 6.4:

, отку-­
да
начальная фаза

Подставим
значения А1,
А2,
φ
1,
φ
2
и произведем вычисления:


= рад.

Так
как угловые частоты складываемых
колебаний одинаковы,
то
результирующее колебание будет иметь
ту же частоту ω.
Это
позволяет
написать уравнение результирующего
колебания в виде

, где A=2,65
см,
,

рад.

Пример
6. Материальная
точка участвует одновременно в двух
взаимно перпендикулярных гармонических
колебаниях, уравне­ния
которых


(1).


(2)

где
a1=1
см,
A2=2
см,
.
Найти уравнение траектории точ-­
ки.
Построить траекторию с соблюдением
масштаба и указать
направление
движения точки.

Решение.
Чтобы
найти уравнение траектории точки,
ис­ключим
время t
из
заданных уравнений (1) и (2). Для этого
восполь-

зуемся
формулой
.
В данном случае

, поэтому

Так
как согласно формуле (1)
,
то уравнение траекто-­
рии


(3)

Полученное
выражение представляет собой уравнение
параболы, ось которой совпадает с осью
Ох.
Из
уравнений (1) и (2) следует, что смещение
точки по осям координат ограничено и
заключено в пределах от —1 до +1 см по
оси Ох
и
от —2 до +2 см по оси Оу.

Для
построения траектории найдем по уравнению
(3) значения у,
соответствующие
ряду значений х,
удовлетворяющих
условию

см, и составим таблицу:

X
,
СМ

-1

—0,75

—0,5

0

+0,5

+ 1

у,
см

0

±0,707

±1

±1,41

±1,73

±2

Начертив
координатные оси и выбрав масштаб,
нанесем на пло­скость
хОу
найденные
точки. Соединив их плавной кривой,
получим траекторию точки, совершающей
колеба­ния
в соответствии с уравнениями движе­ния
(1) и (2) (рис. 6.5).

Рис. 6.5

Для
того чтобы указать направление движения
точки, проследим за тем, как из­меняется
ее положение с течением времени. В
начальный момент t=0
координаты точ­ки
равны x(0)=1
см и y(0)=2
см. В по­следующий
момент времени, например при t1=l
с,
координаты точек изменятся и ста­нут
равными х
(1)=
—1
см, y(t)=0.
Зная
положения
точек в начальный и последую­щий
(близкий) моменты времени, можно указать
направление движения точки по траектории.
На рис. 6.5 это направление движения
указано стрелкой (от точки А
к
началу
координат). После того как в мо­мент
t2
= 2 с колеблющаяся точка достиг­нет
точки D,
она
будет двигаться в обратном направлении.

Задачи

Кинематика
гармонических колебаний

6.1.
Уравнение колебаний точки имеет вид
,
где
ω=π
с-1,
τ=0,2
с. Определить период Т
и
начальную фазу φ
колебаний.

6.2.
Определить
период Т,
частоту
v
и
начальную фазу φ
коле­баний,
заданных уравнением
,
где ω=2,5π
с-1,
τ=0,4
с.

6.3.
Точка
совершает колебания по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и

;
2)
х(0)
=см
и
;
3) х(0)=2см
и
;
4)
х(0)=
и
.
Построить векторную диаграмму
для
момента
t=0.

6.4.
Точка
совершает колебания .по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и

; 2) x(0)=
см и
;
3) х(0)=
см и
;
4)
x(0)=см
и
.
Построить векторную диаграмму для
момента
t=0.

Источник

Колебательное движение – движение (изменение состояния), обладающее той или иной степенью повторяемости во времени.

Т.е. колебанием можно назвать любой вид движения, при котором через одинаковые промежутки времени повторяются кинематические характеристики движения (координата, скорость, ускорение).

Гармоническими колебаниями называются колебания, кинематические характеристики в которых меняются по закону синуса или косинуса.

Колебательное движение

Рис. 1. Колебательное движение. Вывод через окружность. Начальные условия

Для визуализации, представим вращательное движение в виде колебательного движения вдоль двух взаимно перпендикулярных осей.

Пусть тело, вращающееся по окружности радиуса A, в начале движения находилось в точке C. Пусть в начале движения радиус-вектор, описывающий выбранную точку, наклонён под углом displaystyle {{varphi }_{0}} к оси OX. Определим начальные координаты тела (исходя из проекций радиуса на оси):

displaystyle {{x}_{0}}=Acos {{varphi }_{0}} (1)

displaystyle {{y}_{0}}=Asin {{varphi }_{0}} (2)

Колебательное движение - 2

Рис. 2. Колебательное движение. Вывод через окружность

Пусть через время displaystyle omega тело, вращаясь с угловой скоростью displaystyle varphi ,  переместилось в точку D. При этом угол поворота радиус-вектора, относительно начального положения составил displaystyle varphi (рис. 2).

Определим текущие координаты тела тем же методом:

displaystyle x=Acos (varphi +{{varphi }_{0}}) (3)

displaystyle y=Asin (varphi +{{varphi }_{0}}) (4)

Учитывая, что при равномерном движении по окружности displaystyle varphi =omega t, получим:

displaystyle x=Acos (omega t+{{varphi }_{0}}) (5)

displaystyle y=Asin (omega t+{{varphi }_{0}}) (6)

Уравнения (5) и (6) являются законом движения материальной точки при гармонических колебаниях. Причём, одним и тем же законом, так как с тригонометрической точки зрения  displaystyle sin ({{90}^{{}^circ }}-alpha )=cos alpha , тогда из (5):

displaystyle Asin (omega t+{{varphi }^{/}}_{0}) = displaystyle Asin (omega t+{{varphi }^{/}}_{0}) (7)

  • где displaystyle {{varphi }^{/}}_{0}={{varphi }_{0}}-{{90}^{{}^circ }} — новый параметр, характеризующий некое другое начальное положение тела.

Таким образом, уравнения (5) и (6), по сути, являются одинаковыми уравнениями только при разных начальных условиях.

Разберём уравнение (5). Каждый из введённых параметров, имея аналог во вращательном движении, описывается по-другому в колебательном движении:

displaystyle x=Acos (omega t+{{varphi }_{0}})

Зная общий вид колебательного движения, можем найти зависимости скорости и ускорения от времени. Для уравнения (5):

displaystyle x=Acos (omega t+{{varphi }_{0}})

displaystyle {{upsilon }_{x}}=-Aomega sin (omega t+{{varphi }_{0}}) (7)

displaystyle {{a}_{x}}=-A{{omega }^{2}}cos (omega t+{{varphi }_{0}}) (8)

Аналогичным образом можно провести рассмотрение уравнения (6).

Проанализируем (5) и (8), исходя из внешнего вида правой части обоих уравнений, можем вывести:

displaystyle {{a}_{x}}=-{{omega }^{2}}x (9)

Уравнение (9) называется основным уравнением гармонических колебаний.

Среди параметров колебаний также присутствуют параметры, знакомые нам по вращательному движению:

displaystyle omega =frac{2pi }{T} (10)

displaystyle T=frac{1}{nu } (11)

Вывод: для школьных задач почти все колебания являются гармоническими и описываются соотношениями (5), (6). Соответствующие скорость и ускорение частицы рассчитываются исходя из конкретного колебания. Параметры колебания также рассчитываются формульно.

Источник

I. Механика

Тестирование онлайн

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.


Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия – достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Как получить зависимости v(t) и a(t)

Источник

Уравнение гармонических колебаний

  1. Гармонические колебания как простейший периодический процесс
  2. Перемещение, скорость и ускорение при гармоническом движении
  3. Примеры

п.1. Гармонические колебания как простейший периодический процесс

Процессы, в которых состояние системы полностью повторяется через определенные промежутки времени, называются периодическими.

Например:
1) Вращение Луны вокруг Земли, Земли и других планет вокруг Солнца, Солнечной системы в целом вокруг центра Галактики;
2) Колебания атомов в молекуле, колебания электромагнитного поля;
3) Сокращения сердечной мышцы, колебания маятника часов, движение поршня в двигателе внутреннего сгорания, смена дня и ночи, приливы и отливы.

Минимальное время T, в течение которого система возвращается в исходное состояние, называется периодом.

Например:
1) Период вращения минутной стрелки часов T=1 час
Период вращения Земли вокруг своей оси T=1 сут=24 ч
Период вращения Земли вокруг Солнца T=1 год=365 сут
2) Период колебаний атомов в двухатомных молекулах T=10-14 с
Период вращения Солнца вокруг центра Галактики T=240 млн.лет.≈7,6·1015 с

Если состояние системы характеризуется некоторой функцией от времени (s=x(t)), то для периодического процесса выполняется равенство: (x(t+T)=x(t)).
Простейшими периодическими функциями являются тригонометрические функции (sin⁡t) и (cos⁡t) с периодом (T=2pi).

Простейшим периодическим процессом являются гармонические колебания, для которых состояние системы изменяется со временем по закону синуса или косинуса: $$ x(t)=Asin⁡(omega t+varphi_0) text{или} x(t)=A cos⁡(omega t+varphi_0) $$ где:
(x(t)) – отклонение характеристики системы от среднего за период значения;
(A) – амплитуда колебаний, максимальное отклонение от среднего за период значения;
(omega) – циклическая частота, изменение фазы колебаний за 1 с, рад/с;
(varphi_0) – начальная фаза колебаний, значение фазы при t=0, рад;
((omega t+varphi_0) )– полная фаза колебаний (просто «фаза»), рад;

Множитель (omega) перед аргументом (t) тригонометрической функции сокращает её период в (omega) раз (см. §8 данного справочника). Поэтому:

Период гармонических колебаний равен: $$ T=frac{2pi}{omega} $$

Число колебаний в единицу времени называют частотой. Частота является величиной, обратной периоду: $$ nu=frac1T $$ Связь циклической частоты и частоты: (omega=2pinu)

Например:
Запишем закон колебаний математического маятника – шарика на нити, если в начальный момент времени он был отклонен на 5 см, а затем отпущен. При подсчете за 10 с он совершил 20 колебаний.
Отклонение в начальный момент соответствует амплитудному значению A=5 см при (t_0=0), значит, будем описывать колебания по закону косинуса с начальной фазой (varphi_0=0). По условию за t=10 с зафиксировано N=20 колебаний, откуда частота: begin{gather*} nu=frac Nt, omega=2pinu=2pifrac Nt\ omega=2picdotfrac{20}{10}=4pi text{(рад/с)} end{gather*} Получаем закон колебаний: (x(t)=5cos(4pi t))

п.2. Перемещение, скорость и ускорение при гармоническом движении

Пусть (x(t)) – координата тела, участвующего в периодическом движении по закону: $$ x(t)=Acos⁡omega t $$ Найдем скорость как первую производную от координаты: $$ v(t)=x'(t)=-Aomega sinomega t=Aomega cos⁡left(omega t+fracpi 2right) $$ Мы видим, что колебания скорости происходят с той же частотой, что и колебания координаты, но опережают их по фазе на (fracpi 2). Амплитудное значение скорости: $$ v_m=Aomega $$ Найдем ускорение как первую производную от скорости (и соответственно, вторую производную от координаты): $$ a(t)=v'(t)=x”(t)=-Aomega^2 cosomega t=Aomega^2 cos⁡(omega t+pi) $$ Колебания ускорения также происходят с той же частотой, опережая колебания скорости на (fracpi 2) и колебания координаты на (pi). Амплитудное значение ускорения: $$ a_m=Aomega^2 $$ Например:
При A=2 и (omega=frac12) получаем такие синусоиды:
Перемещение, скорость и ускорение при гармоническом движении
Из уравнения для ускорения получаем: $$ x”(t)=-Aomega^2cosomega t=-omega^2(Acosomega t)=-omega^2 x(t) $$ Откуда следует:

Уравнение гармонических колебаний: $$ x”(t)+omega^2x(t)=0 $$

Решением этого уравнения в общем виде будут: $$ x(t)=Asin⁡(omega t+varphi_0) text{или} x(t)=A cos⁡(omega t+varphi_0) $$ Для каждой из систем физический смысл (x(t)) и (omega) будет разным.

п.3. Примеры

Пример 1. Получите уравнение гармонических колебаний для горизонтального пружинного маятника с массой m и жесткостью пружины k. Чему равна циклическая частота этих колебаний?

Пример 1 Горизонтальный пружинный маятник – это грузик массой m, прикрепленный к пружине жесткостью k. Грузик может перемещаться в горизонтальном направлении без трения.

По вертикали на грузик действую сила тяжести и реакция опоры, равнодействующая которых равна нулю.
По горизонтали на грузик действует только сила упругости: (F=-kcdot x(t))
Самое время вспомнить о втором законе Ньютона. Сила, действующая на грузик, приводит его в движение с ускорением a: begin{gather*} F=ma=mcdot x”(t)\ mcdot x”(t)=-kcdot x(t) end{gather*} Уравнение движения грузика: $$ x”(t)+frac km x(t)=0 $$ что является уравнением гармонических колебаний с частотой: (omega=sqrt{frac km})
Общее решение уравнения: (x(t)=Acosleft(sqrt{frac km}+varphi_0right))
Амплитудные значения скорости и ускорения: $$ v_m=Asqrt{frac km}, a_m=Afrac km $$ Ответ: (omega=sqrt{frac km})

Пример 2. Получите уравнение гармонических колебаний для малых углов отклонений математического маятника на нити длиной l при ускорении свободного падения g. Чему равна циклическая частота этих колебаний?

Пример 2 Математический маятник – это шарик, который можно считать материальной точкой, на длинной невесомой нерастяжимой нити длиной l в поле тяготения с ускорением свободного падения g.

В положении равновесия на шарик действуют и уравновешивают друг друга две силы: сила тяжести mg и сила натяжения нити FH.
В положении максимального отклонения под углом α к вертикали равнодействующая уже не равна 0, и, как только мы отпустим шарик, он начинает перемещаться вниз. Уравнение движения: begin{gather*} moverrightarrow{a}=-overrightarrow{F_H}-moverrightarrow{g} end{gather*} (overrightarrow{F_H}perpoverrightarrow{F}) т.к. равнодействующая (overrightarrow{F}=moverrightarrow{a}) направлена по касательной. В проекции на направление (overrightarrow{F}) сила натяжения (overrightarrow{F_H}) даст 0, а сила тяжести (mgsin⁡alpha). Получаем: begin{gather*} ma=0-mgsinalpha=-mgsinalpha\ a=-gsinalpha end{gather*} Для смещения x по дуге окружности радиусом угол (alpha=frac xl). Для небольших углов (до 20°) (sinfrac xlapproxfrac xl) (см. приближения функций при малых x в §52 данного справочника). Поэтому: $$ a=-gsinfrac xlapprox-frac gl x $$ И мы получаем уравнение гармонических колебаний: (x”(t)+frac gl x=0, omega=sqrt{frac gl})
Общее решение уравнения: (x(t)=Acosleft(frac gl t+varphi_0right))
Амплитудные значения скорости и ускорения: (v_m=Asqrt{frac gl}, a_m=Afrac gl)
Ответ: (omega=sqrt{frac gl})

Пример 3. Получите уравнение гармонических колебаний для L-контура.
Чему равна циклическая частота этих колебаний?

Пример 3 LC-контур – это электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C.
Модель является идеальной, т.к. предполагает, что в цепи полностью отсутствует активное сопротивление R, и колебания не затухают со временем.

Напряжение на конденсаторе (U_C(t)=frac{Q(t)}{C}). Ток, протекающий через катушку, создает ЭДС (varepsilon_L(t)=-Lfrac{triangle I}{triangle t}). При переходе к пределу (triangle trightarrow 0) получаем производную (varepsilon_L(t)=-LI'(t)). По второму закону Кирхгофа для замкнутого контура: begin{gather*} U_c(t)=varepsilon_L(t)Rightarrow frac{Q(t)}{C}=-LI'(t)Rightarrow frac{Q(t)}{C}+LI'(t)=0 end{gather*} Вспомним, что (Q'(t)=I(t)) – ток равен производной от заряда по времени.
Тогда первая производная от тока равна второй производной от заряда (I'(t)=Q”(t)).
begin{gather*} frac{Q(t)}{C}+LQ”(t)=0 end{gather*} Получаем уравнение гармонических колебаний: $$ Q”(t)=frac{1}{LC}Q(t)=0, omega=frac{1}{sqrt{LC}} $$ Общее решение уравнения: (Q(t)=Q_m cosleft(frac{1}{sqrt{LC}}t+varphi_0right))
Напряжение на конденсаторе: $$ U_C(t)=frac{Q(t)}{C}=frac{Q_m}{C}cosleft(frac{1}{sqrt{Lc}}t+varphi_0right) $$ Амплитудное значение напряжения: (U_m=frac{Q_m}{C})
Ток как скорость изменения заряда: $$ I(t)=Q'(t)=-frac{Q_m}{sqrt{LC}}sinleft(frac{1}{sqrt{LC}}t+varphi_0right)=frac{Q_m}{sqrt{LC}}cosleft(frac{1}{sqrt{LC}}t+varphi_0+fracpi 2right) $$ Амплитудное значение тока: (I_m=frac{Q_m}{sqrt{LC}})
Ток опережает колебания заряда и напряжения на (fracpi 2)

Ответ: (omega=frac{1}{sqrt{LC}})

Источник

1.1. Уравнение гармонических колебаний

В этом разделе мы покажем, что уравнения колебательного движения многих систем, в сущности, одинаковы, так что различные физические процессы могут быть описаны одними и теми же математическими формулами.

Пружинный маятник — это система, состоящая из шарика массой m, подвешенного на пружине длиной .

Рис. 1.2. К выводу уравнения движения для пружинного маятника

В положении равновесия (рис. 1.2) сила тяжести уравновешивается упругой силой :

где – статическое удлинение пружины. Направим ось x вниз и выберем начало отсчета так, что координата x = 0 соответствует положению неподвижного шарика в положении равновесия.

Если теперь оттянуть шарик от положения равновесия на расстояние x, то полное удлинение пружины станет равным . По закону Гука проекция результирующей силы на ось ОХ будет тогда равна

Знак минус означает, что сила стремится уменьшить отклонение от положения равновесия. Полученное выражение соответствует упругой силе слабо деформированной пружины.

Запишем теперь уравнение второго закона Ньютона:

Его можно также представить в виде:

Математический маятник

Математический маятник — это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.

Будем характеризовать отклонение маятника от положения равновесия углом , который образует нить с вертикалью (рис. 1.3).

Рис. 1.3. К выводу уравнения движения математического маятника

При отклонении маятника от положения равновесия на материальную точку массой m действуют сила тяжести и сила натяжения нити . Соответственно, уравнение движения этой материальной точки имеет вид

.

Проецируя его на направления нормали и касательной к траектории (окружности радиуса ), получаем

Модуль скорости равен , учитывая, что при движении точки к положению равновесия угол убывает, а скорость точки растет, напишем

.

Тогда второе из написанных выше уравнений движения приобретает вид

При малых отклонениях маятника от вертикали, когда ,

Физический маятник

Физический маятник — это протяженное колеблющееся тело, закрепленное на оси. Его размеры таковы, что его невозможно рассматривать как материальную точку.

Пример физического маятника приведен на рис. 1.4.

Рис. 1.4. К выводу уравнения движения физического маятника

При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

где m – масса маятника, а l – расстояние 0C между точкой подвеса 0 и центром масс C маятника.

Рассматривая как вектор, связанный с направлением поворота правилом правого винта, противоположность знаков и можно объяснить тем, что векторы и направлены в противоположные стороны. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, как I, для маятника можно записать основное уравнение динамики вращательного движения:

Ограничимся рассмотрением малых отклонений от положения равновесия:

В этом случае уравнение колебаний принимает вид:

В случае, когда физический маятник можно представить как материальную точку, колеблющуюся на нити длиной l, момент инерции равен

и мы приходим к уравнению (1.6) движения математического маятника.

Колебания поршня в сосуде с идеальным газом

Рассмотрим цилиндр с площадью поперечного сечения , в который вставлен поршень массы (рис. 1.5). Под поршнем в цилиндре идеальный газ с показателем адиабаты , над поршнем воздух с постоянным (атмосферным) давлением . Поршень может двигаться в цилиндре вверх и вниз без трения. Будем считать, что в равновесии объем идеального газа под поршнем равен и изменения объема газа, обусловленные движением поршня, происходят адиабатно, то есть без теплообмена со стенками цилиндра и поршнем.

Рис. 1.5. Колебания поршня, закрывающего сосуд с идеальным газом

В состоянии равновесия давление в газе под поршнем складывается из атмосферного давления и давления , оказываемого поршнем. Обозначим это результирующее давление :

Переместим поршень на расстояние x вверх. Объем сосуда увеличится и станет равным

Соответственно уменьшится давление. В силу предположения об отсутствии теплообмена, новое давление в газе можно найти из уравнения адиабаты Пуассона

Здесь — показатель адиабаты, зависящий от числа степеней свободы молекул газа.

При малых колебаниях, когда изменение объема газа много меньше его «равновесной» величины , то есть когда

выражение (1.11) можно разложить в ряд Тейлора:

На поршень действуют три силы: сила атмосферного давления , сила давления газа под поршнем и сила тяжести . Знаки сил соответствуют выбору положительного направления оси x вверх. Используя (1.10) и (1.12), находим для равнодействующей этих сил:

Используя (1.13), уравнение движения поршня

Гармонические колебания

Колебательное движение – движение (изменение состояния), обладающее той или иной степенью повторяемости во времени.

Т.е. колебанием можно назвать любой вид движения, при котором через одинаковые промежутки времени повторяются кинематические характеристики движения (координата, скорость, ускорение).

Гармоническими колебаниями называются колебания, кинематические характеристики в которых меняются по закону синуса или косинуса.

Рис. 1. Колебательное движение. Вывод через окружность. Начальные условия

Для визуализации, представим вращательное движение в виде колебательного движения вдоль двух взаимно перпендикулярных осей.

Пусть тело, вращающееся по окружности радиуса A, в начале движения находилось в точке C. Пусть в начале движения радиус-вектор, описывающий выбранную точку, наклонён под углом к оси OX. Определим начальные координаты тела (исходя из проекций радиуса на оси):

Рис. 2. Колебательное движение. Вывод через окружность

Пусть через время тело, вращаясь с угловой скоростью , переместилось в точку D. При этом угол поворота радиус-вектора, относительно начального положения составил (рис. 2).

Определим текущие координаты тела тем же методом:

Учитывая, что при равномерном движении по окружности , получим:

Уравнения (5) и (6) являются законом движения материальной точки при гармонических колебаниях. Причём, одним и тем же законом, так как с тригонометрической точки зрения , тогда из (5):

  • где — новый параметр, характеризующий некое другое начальное положение тела.

Таким образом, уравнения (5) и (6), по сути, являются одинаковыми уравнениями только при разных начальных условиях.

Разберём уравнение (5). Каждый из введённых параметров, имея аналог во вращательном движении, описывается по-другому в колебательном движении:

  • где
    • — текущая координата тела,
    • — амплитуда колебаний (максимальное отклонение тела от положения равновесия)
    • — циклическая частота колебания
    • — время движения
    • — начальная фаза колебания
    • — текущая фаза колебания (всё, что стоит под тригонометрической функцией).

Зная общий вид колебательного движения, можем найти зависимости скорости и ускорения от времени. Для уравнения (5):

Аналогичным образом можно провести рассмотрение уравнения (6).

Проанализируем (5) и (8), исходя из внешнего вида правой части обоих уравнений, можем вывести:

Уравнение (9) называется основным уравнением гармонических колебаний.

Среди параметров колебаний также присутствуют параметры, знакомые нам по вращательному движению:

  • где
    • — циклическая частота колебаний
    • — период колебаний
    • — частота колебания.

Вывод: для школьных задач почти все колебания являются гармоническими и описываются соотношениями (5), (6). Соответствующие скорость и ускорение частицы рассчитываются исходя из конкретного колебания. Параметры колебания также рассчитываются формульно.

I. Механика

Тестирование онлайн

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия – достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Как получить зависимости v(t) и a(t)

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) – это первая производная x(t). А зависимость a(t) – это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

[spoiler title=”источники:”]

http://www.abitur.by/fizika/teoreticheskie-osnovy-fiziki/garmonicheskie-kolebaniya/

http://fizmat.by/kursy/kolebanija_volny/garmonicheskoe

[/spoiler]

Источник

Добавить комментарий