Дифференциальное уравнение первого порядка
(1)
определяет в каждой точке , где существует функция
, значение
, т.е. угловой коэффициент касательной к интегральной кривой в этой точке.
Если в каждой точке области задано значение некоторой величины, то говорят, что в области
задано поле этой величины. Таким образом, дифференциальное уравнение (1) определяет поле направлений.
Тройка чисел определяет направление прямой, проходящей через точку
. Совокупность отрезков этих прямых дает геометрическую картину поля направлений.
Задача интегрирования дифференциального уравнения (1) может быть теперь истолкована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке.
Задача построения интегральной кривой часто решается введением изоклин. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и тоже направление. Семейство изоклин дифференциального уравнения (1) определяется уравнением
(2)
где — параметр. Придавая параметру
близкие числовые значения, получаем достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального yравнения (1).
Замечание 1. Нулевая изоклина дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых.
Для большей точности построения интегральных кривых находят также геометрическое место точек перегиба. Для этого находят в силу уравнения (1):
(3)
и приравнивают ее нулю. Линия, определяемая уравнением
(4)
и есть возможное геометрическое место точек перегиба.
Пример 1. С помощью изоклин построить приближенно интегральные кривые дифференциального уравнения .
Решение. Для получения уравнения изоклин положим , тогда
или
.
Изоклинами являются параллельные прямые. При получим изоклину
. Эта прямая делит плоскость
на две части, в каждой из которых производная
имеет один и тот же знак (рис. 6).
Интегральные кривые, пересекая прямую , переходят из области убывания функции
в область возрастания, и наоборот, а значит на этой прямой находятся точки экстремума интегральных кривых, именно точки минимума.
Возьмем еще две изоклины: и
.
Касательные, проведенные к интегральным кривым в точках пересечения с изоклинами и
, образуют с осью
углы в
и
соответственно. Найдем далее вторую производную
.
Прямая , на которой
, является изоклиной, получаемой при
, и в то же время интегральной линией, в чем можно убедиться подстановкой в уравнение. Так как правая часть данного уравнения
удовлетворяет условиям теоремы существования и единственности во всей плоскости
, то остальные интегральные кривые не пересекают эту изоклину. Изоклина
, на которой находятся точки минимума интегральных кривых, расположена над изоклиной
, а поэтому интегральные кривые, проходящие ниже изоклины
, не имеют точек экстремума.
Прямая делит плоскость
на две части, в одной из которых (расположенной над прямой)
, а значит интегральные кривые обращены вогнутостью вверх, а в другой
и, значит, интегральные кривые обращены вогнутостью вниз. Интегральные кривые не пересекают прямой
, значит, она не является геометрическим местом точек перегиба. Интегральные кривые данного уравнения не имеют точек перегиба.
Проведенное исследование позволяет нам приближенно построить семейство интегральных кривых уравнения (рис.6).
Пример 2. Методом изоклин построить приближенно интегральные кривые дифференциального уравнения .
Решение. Полагая , где
, получаем уравнение изоклин
, причем
. При
получим
, откуда
(5)
Интегральные кривые в точках пересечения с этими изоклинами имеют горизонтальные касательные.
Определим, имеют ли интегральные кривые на изоклинах экстремум. Для этого найдем вторую производную:
При имеем
Если четное, то
, и, значит, в точках пересечения с изоклинами
, интегральные кривые имеют минимум; если же
нечетное, то
и интегральные кривые в точках пересечения с изоклинами имеют максимум. Находим изоклины:
(6)
(7)
Изоклинами являются параллельные прямыми с угловым коэффициентом, равным –1 , т. е. изоклины пересекают ось под углом
. Легко убедиться в том, что изоклины
, являются интегральными кривыми данного дифференциального уравнения (для этого достаточно подставить функции
в уравнение
).
Во всех точках плоскости правая часть данного уравнения, т.е. функция
, удовлетворяет всем условиям теоремы существования и единственности, а поэтому интегральные кривые не пересекаются, и, следовательно, не пересекают изоклины
. Производная
обращается в ноль при
, т.е. на изоклинах (6), и при
, т. е. на изоклинах (6) и (7). При переходе (слева направо) через изоклины (7)
меняет знак с плюса на минус. Например, если рассмотреть полосу, заключенную между изоклинами
и
, то на изоклине
производная
, причем под изоклиной
. Значит, интегральные кривые обращены вогнутостью вверх, а над изоклиной
, значит, интегральные кривые обращены вогнутостью вниз. Таким образом, изоклины (7) являются геометрическим местом точек перегиба интегральных кривых. Полученные данные позволяют приближенно построить семейство интегральных кривых данного уравнения. Для более точного построения следует нанести еще несколько изоклин (рис. 7).
Пример 3. Методом изоклин построить интегральные кривые уравнения .
Решение. Положим . Тогда уравнение изоклин будет
, или
.
Изоклинами являются параболы с вертикальной осью симметрии . Среди изоклин нет интегральных кривых. В самом деле, подставляя в данное уравнение
и
, будем иметь
, или
. Но это равенство ни при каком значении
не может выполняться тождественно относительно
.
Пусть , тогда в точках пересечения с изоклиной
интегральные кривые будут иметь горизонтальные касательные. Изоклина
разбивает плоскость
на две части: в одной из них
(решения
убывают), а в другой
(решения
возрастают). И так как эта изоклина не является интегральной кривой, то на ней находятся точки экстремума интегральных кривых, именно на той части параболы
, где
— точки минимума, а на другой части этой параболы, где
— точки максимума. Интегральная кривая, проходящая через точку
, т.е. через вершину параболы
, в этой точке не имеет экстремума. В точках изоклин
и
касательные к интегральным кривым имеют угловые коэффициенты, соответственно равные 1 и –1.
Для исследования направления вогнутости интегральных кривых найдем вторую производную:
Она обращается в ноль только в точках, лежащих на параболе . В точках плоскости
, координаты которых удовлетворяют условию
, интегральные кривые вогнуты вниз
, а в точках, где
, они вогнуты вверх
. Точки пересечения интегральных кривых с параболой
являются точками перегиба этих кривых. Итак, парабола
есть геометрическое место точек перегиба интегральных кривых.
Правая часть исходного уравнения во всех точках плоскости
удовлетворяет условиям теоремы существования и единственности, поэтому через каждую точку плоскости проходит единственная интегральная кривая уравнения.
Используя полученные сведения, строим приближенно семейство интегральных кривых данного уравнения (рис. 8).
Замечание 2. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.
Рассмотрим уравнение . Семейство изоклин определяется уравнением
. Это семейство прямых, проходящих через начало координат, так что в начале координат пересекаются изоклины, отвечающие различным наклонам касательных к интегральным кривым. Нетрудно убедиться, что общее решение данного уравнения имеет вид
и точка
является особой точкой дифференциального уравнения. Здесь изоклины являются интегральными кривыми уравнения (рис. 9).
Пример 4. Методом изоклин построить интегральные кривые уравнения .
Решение. Полагая , получаем уравнение семейства изоклин
. Таким образом, изоклинами являются прямые, проходящие через начало координат
.
При получим изоклину
, при
— изоклину
, при
— изоклину
.
Рассматривая обратное уравнение найдем изоклину
, во всех точках которой интегральные кривые имеют вертикальные касательные.
В точке пересекаются все изоклины данного уравнения (особая точка уравнения). С помощью полученных изоклин строим интегральные кривые (рис. 10).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Рассмотрим более подробно применение
геометрического подхода к построению
решений дифференциальных уравнений
первого порядка.
Уравнение
y’ = f(x, y)
(3.1)
определяет
в каждой точке (x, y),
где существует функция f(x,
y), значение y’,
т. е. угловой коэффициент касательной
к интегральной кривой в этой точке.
Если в каждой точке области D
задано значение некоторой величины, то
говорят, что в области D
задано поле этой величины.
Таким образом, дифференциальное уравнение
(3.1) определяет поле направлений.
Тройка чисел (x, y,
y’) определяет направление
прямой, проходящей через точку (x,
y). Совокупность отрезков
этих прямых дает геометрическую картину
поля направлений.
Задача интегрирования дифференциального
уравнения (3.1) может быть теперь истолковано
так: найти такую прямую, чтобы касательная
к ней в каждой точке имела направление,
совпадающее с направлением поля в этой
точке.
Задача построения интегральной кривой
часто решается с помощью метода изоклин.
Изоклиной называется геометрическое
место точек, в которых касательные к
искомым интегральным прямым имеют одно
и тоже направление. Семейство изоклин
дифференциального уравнения (3.1)
определяется уравнением
f(x, y) = k,
(3.2)
где k
– параметр. Строя достаточно густую
сеть изоклин, т.е. давая k
близкие числовые значения, мы можем
достаточно точно построить интегральную
кривую дифференциального уравнения
(3.1).
З а м е ч а н
и е 1. Нулевая изоклина f(x,
y) = 0 дает уравнение линий,
на которых могут располагаться точки
максимума и минимума интегральных
кривых. Для большей точности построения
интегральных кривых находят также
геометрическое место точек перегиба.
Для этого находят y’’ в
силу уравнения (3.1)
и приравнивают
ее нулю. Линия, определяемая уравнением
и есть геометрическое
место точек перегиба, если они существуют.
З а м е ч а н и е 2. Точки пересечения двух
или нескольких изоклин являются особыми
точками дифференциального уравнения
(3.1), так как. в них направление интегральных
кривых становится неопределенным.
Например, рассмотрим уравнения
.
семейство изоклин определяется уравнением
.
Это семейство прямых, проходящих через
начало координат, т. е. В начале координат,
пересекаются изоклины, отвечающие
различным наклонам касательных к
интегральным кривым. Не трудно убедится,
что общее решение данного уравнения
имеет вид
y
= Cx и точка (0, 0) является
особой точкой дифференциального
уравнения. Здесь изоклины являются
интегральными кривыми уравнения (рис.
2).
Пример 1. С помощью изоклин построить
приближенно интегральные кривые
дифференциального уравнения y’
= 2x – y.
Р е ш е н и е. Для получения уравнения
изоклин положим y’ =k
(k = const).
Имеем
2x – y = k
или y = 2x
– k.
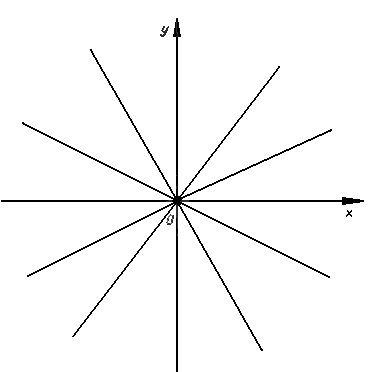
рис. 2
Изоклинами являются параллельные
прямые. При k=0 получим
изоклину y = 2x.
Эта прямая делит плоскость XOY
на две части, в каждой из которых
производная y’ имеет один
и тот же знак (рис. 3).
Интегральные кривые, пересекая прямую
y = 2x, переходят
из области убывания функции y(х)
в область
возрастания,
и наоборот, а значит, на этой прямой
находятся точки экстремума интегральных
кривых, именно точки минимума.
Возьмем еще две изоклины:
k = -1, y = 2x
+1 и k = 1, y
= 2x – 1.
Касательные, проведенные к интегральным
кривым в точках пересечения с изоклинами
k = -1 и k = 1,
образуют с осью OX углы в
135о и 45о соответственно.
Найдем далее вторую производную
y’ = 2 – y’
= 2 – 2x +y.
Прямая y = 2x
–2, на которой y’’ = 0,
является изоклиной, получаемой при k
=2, и в тоже время интегральной линией,
в чем можно убедиться подстановкой в
уравнение. Так как правая часть данного
уравнения f(x,
y) = 2x – y
удовлетворяет условиям теоремы
существования и единственности во всей
плоскости XOY, то остальные
интегральные кривые не пересекают эту
изоклину. Изоклина y = 2x,
на которой находятся точки минимума
интегральных кривых, расположена над
изоклиной y = 2x
– 2, а по этому интегральные кривые,
проходящие ниже изоклины y = 2x
– 2, не имеют точек экстремума.
Прямая y = 2x
– 2 делит плоскость XOY
на две части, в одной из которых (
расположенной над прямой ) y>0,
а значит, интегральные кривые обращены
вогнутостью вверх, а в другой y”
<0 и значит, интегральные кривые обращены
вогнутостью вниз. Так как. интегральные
кривые не пересекают прямой y
= 2x – 2, то она не является
геометрическим местом точек перегиба.
Следовательно, интегральные кривые
данного уравнения не имеют точек
перегиба.
Проведенное исследование позволяет
нам приближенно построить семейство
интегральных кривых уравнения (рис. 3).
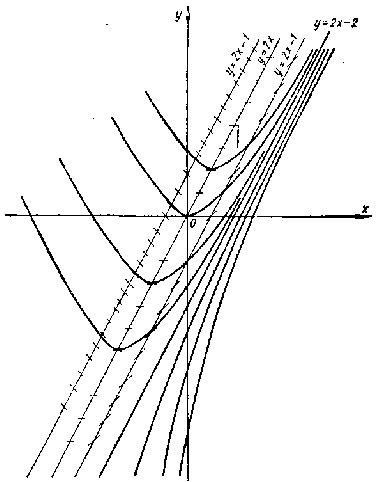
Рис.3
Рассмотрим простейшие и наиболее
распространенные в приложениях случаи,
когда уравнение (3.1)
интегрируемо в квадратурах.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Изоклиной дифференциального уравнения (y’=f(x,y)) является геометрическое место точек плоскости ((x,y)), в которых касательные к интегральным кривым имеют одинаковый наклон, то есть выполняется соотношение (y’=k), где (k) – постоянная.
Очевидно, уравнение изоклины соответствующей определенному значению (k):
[f(x,y)=k.]
На практике, изоклины используются для приближенного построения семейства интегральных кривых дифференциальных уравнений. Что позволяет даже для не интегрируемых явно дифференциальных уравнений выявить характер интегральных кривых.
Обычно при построении интегральных кривых достаточно построить несколько изоклин для (k=0,pm 1, pm2), но в некоторых случаях придется строить дополнительные изоклины и подбирать необходимое значение (k).
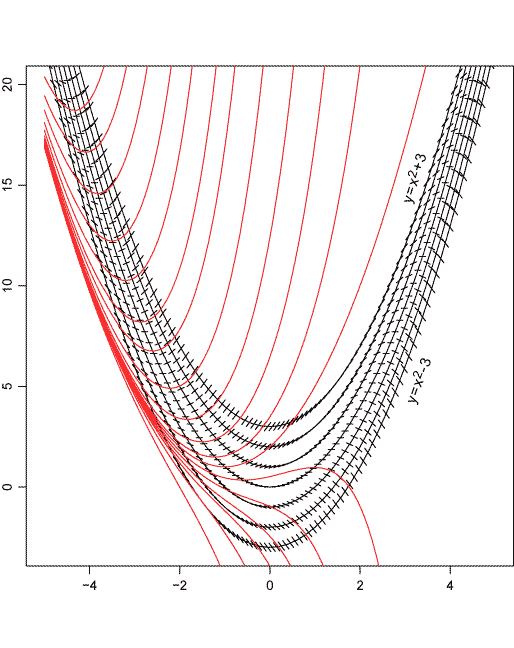
Пример. C помощью изоклин начертить (приближенно) решения уравнения (y’=y-x^2).
Для получения уравнения изоклин положим (y′=const=k).
Тогда (y-x^2=k) или (y=x^2+k). Изоклинами являются параболы.Составим таблицу:
(k) -3 -2 -1 0 1 2 3 Уравнение изоклины (y=x^2-3) (y=x^2-2) (y=x^2-1) (y=x^2) (y=x^2+1) (y=x^2+2) (y=x^2+3) Угол наклона (градусы) -71.57 -63.43 -45.00 0.00 45.00 63.43 71.57 Построим семейство парабол для значений (k) равных (-3, -2,-1, 0,1,2,3), отметим на параболах направления задаваемые параметром (k) и построим интегральные кривые:
- Авторы
- Файлы
- Литература
Веретеников А.С.
1
Потапов Д.Н.
1
1 Самарская государственная сельскохозяйственная академия
1. Пискунов Н.С. Дифференциальное и интегральное исчисления: учебник в 2-х томах. Том 2. – М.: Наука – Главная редакция физико-математической литературы, 1985. – 560 с.
2. Пушкарь Е.А. Дифференциальные уравнения в задачах и примерах: учебно-методическое пособие. – М.: МГИУ, 2007. – 158 с.
Дифференциальное уравнение первого порядка ý = f(x, y) имеет общее решение 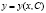
Если переменные х и у правой части дифференциального уравнения рассматривать как координаты точки М(х, у) плоскости хОу, то производная 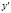

Изображая направление в каждой точке области существования функции 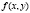
Изоклинами дифференциального уравнения ý = f(x, y) называются геометрические места точек плоскости хОу, в которых интегральные кривые уравнения имеют одно и то же направление. Уравнение 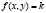
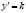
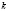
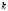
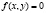
Метод изоклин состоит в следующем:
1. Строится достаточно густая сетка изоклин для различных значений k и на каждой изоклине изображаются небольшие отрезки с наклоном k.
2. Начиная из точки (x0, y0), поводится линия, которая, будет пересекать каждую изоклину под углом, заданным полем направлений. Полученная таким образом кривая и будет приближенным изображением (эскизом) интегральной кривой уравнения, проходящей через точку (x0, y0).
Пусть дано уравнение 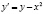
Сначала строятся графики изоклин. Уравнение семейства изоклин данного уравнения 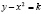
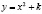
При k=0 получается изоклина 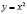
При k=1 получается изоклина 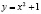
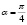
При k=-1 получается изоклина 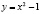
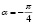
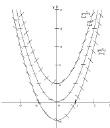
Рис. 1. Поле направлений уравнения 
Задается определенная точка (x0, y0) и поводится линия, которая, будет пересекать каждую изоклину под углом, заданным полем направлений. На рис. 2 показаны интегральные кривые, касающиеся поля направлений.
Метод изоклин как метод приближенного решения задачи Коши устарел. В его в основе лежит алгоритм изображения фрагмента поля направления, а современные компьютеры могут мгновенно и как угодно подробно нарисовать поле направлений, и достаточно точно изобразить интегральную кривую.
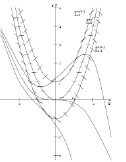
Рис. 2. Интегральные кривые уравнения 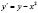
Однако, метод изоклин эффективно работает как инструмент исследования поведения решений. Он позволяет изобразить области характерного поведения интегральных кривых и как средство эскизного представления интегральных кривых сохраняет свое значение и в нынешнюю эпоху бурного развития вычислительных машин и вычислительных методов.
Библиографическая ссылка
Веретеников А.С., Потапов Д.Н. ИСПОЛЬЗОВАНИЕ МЕТОДА ИЗОКЛИН ПРИ РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА // Международный студенческий научный вестник. – 2015. – № 3-4.
;
URL: https://eduherald.ru/ru/article/view?id=14105 (дата обращения: 19.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Метод изоклин – это метод графического решения дифференциального уравнения. Семейство изоклин дифференциального уравнения (1) определяется уравнением
, где
– параметр.
Метод изоклин заключается в построении семейства изоклин с нанесенными на них отрезками касательных.
Множество отрезков касательных образует поле направлений касательных интегральных кривых. Главное соединение касательных дает семейство интегральных кривых.
Рассмотрим примеры.
Пример 1. Решить методом изоклин уравнение
.
Решение. Данное уравнение определено во всей плоскости , исключая точки прямых
и
. В области определения его можно записать в виде:
Поэтому в I и II квадрантах координатной плоскости интегральные кривые – это графики функций , а во II и IV квадрантах – графики функций
(см. рис.2).
Пример 2. Решить методом изоклин уравнение:
.
Решение. Уравнение изоклины . В данном случае уравнение изоклины совпадает с уравнением нормали
.
Запишем несколько уравнений изоклин для фиксированных угловых коэффициентов касательных, если
На рис.3 поле направлений касательных дает семейство интегральных кривых в виде окружностей.
Дифференциальное уравнение вида
,
В котором коэффициенты при дифференциалах распадаются на множители, зависящие только от и только от
, называется уравнением с разделяющимися переменными.
Путем деления на произведение оно приводится к уравнению с разделенными переменными:
.
Общий интеграл этого уравнения имеет вид:
.
Пример 1. Решить уравнение
.
Решение. Представим данное уравнение в виде
.
Разделив обе части этого уравнения на произведение , получим уравнение с разделенными переменными
.
Интегрируя это уравнение, последовательно находим
.
Используя метод подстановки, вычислим интегралы
.
Решением данного дифференциального уравнения является функция:
.
Пример 2. Найти частное решение уравнения
,
Удовлетворяющее начальному условию .
Решение. Найти частные решения данного дифференциального уравнения – это значит решить задачу Коши.
А) Найдем общее решение данного уравнения. Запишем его иначе
.
Данное уравнение является уравнением с разделяющимися переменными. Разделим обе части этого уравнения на , получим:
.
Интегрируем:

Таким образом общий интеграл имеет вид :
Б) Найдем частное решение, для этого определим значение постоянной При данных начальных условиях
; будем иметь
Следовательно .
Подставив найденное значение в общее решение, получим частное решение данного дифференциального уравнения

Откуда

Из начального условия следует, что (т. к.
), поэтому перед корнем берем знак плюс. Итак, искомое частное решение:

| < Предыдущая | Следующая > |
|---|