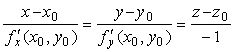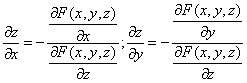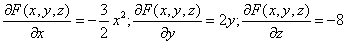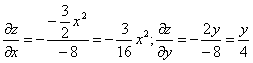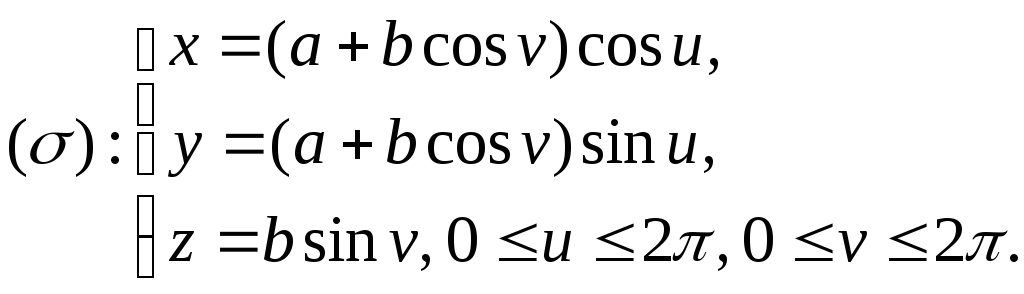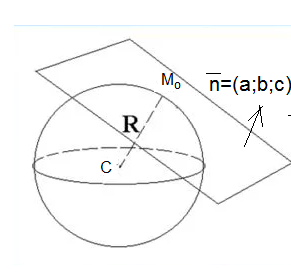
Как составить уравнение касательной плоскости к сфере

Условие

Решение

Написать комментарий

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z – z₀ = f’_x(x₀,y₀,z₀)(x – x₀) + f’_y(x₀,y₀,z₀)(y – y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z – 5 = 0(x – 0) + 5(y – 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z – 1 = -3 /₁₆(x – 1) + 0(y – 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z – z₀ = f’_x(x₀,y₀,z₀)(x – x₀) + f’_y(x₀,y₀,z₀)(y – y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z – 25 = 26(x – 1) + 36(y – 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Касательная плоскость и нормаль к поверхности.

Пусть поверхность задана в неявном виде: $F(x,y,z)=0$ и пусть точка $M_0(x_0,y_0,z_0)$ принадлежит данной поверхности. Тогда уравнение касательной плоскости к этой поверхности в точке $M_0$ таково:

Уравнение нормали имеет вид:

Если же уравнение поверхности задано в явном виде $z=f(x,y)$, то уравнение касательной плоскости имеет вид:

Уравнение нормали в случае явного задания поверхности таково:

Примечание (желательное для более полного понимания текста): показатьскрыть

Формулы (3) и (4) легко получить из формул (1) и (2). Если $z=f(x,y)$, то перенося $z$ в правую часть равенства получим: $f(x,y)-z=0$. Обозначая $F(x,y,z)=f(x,y)-z$, получим: $F_^<‘>=left(f(x,y)-zright)_^<‘>=f_^<‘>(x,y)-0=f_^<‘>(x,y)$. Аналогично и $F_^<‘>=left(f(x,y)-zright)_^<‘>=f_^<‘>(x,y)-0=f_^<‘>(x,y)$. Что же касается последней производной (т.е. производной по переменной $z$), то тут нужно учесть, что выражение $f(x,y)$ не содержит $z$, поэтому: $F_^<‘>=left(f(x,y)-zright)_^<‘>=0-1=-1$. Подставляя в формулы (1) и (2) вместо $F_^<‘>$, $F_^<‘>$, $F_^<‘>$ соответственно $f_^<‘>$, $f_^<‘>$ и $-1$ и получим формулы (3) и (4).

Найти уравнение касательной плоскости и нормали к поверхности $z=3x^2y^4-6xy^3+5x-4y+10$ в точке $M_0(-2;1;20)$.

Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$, $y_0$, $z_0$ (координаты точки $M_0$) в нашем случае таковы: $x_0=-2$, $y_0=1$, $z_0=20$. Но перед тем, как переходить к решению, осуществим небольшую проверку. Убедимся, что точка $M_0$ действительно лежит на заданной поверхности. Эта проверка не является обязательной, но желательна, ибо ошибка в условиях подобных задач – дело вовсе не редкое. Подставим $x=x_0$, $y=y_0$ в уравнение нашей поверхности и убедимся, что $z_0$ действительно равно 20:

$$ z_0=3x_<0>^<2>y_<0>^<4>-6x_0y_<0>^<3>+5x_0-4y_0+10=3cdot (-2)^2cdot 1^4-6cdot (-2)cdot 1^3-4cdot 1+10=12+12-4=20. $$

Проверка пройдена, точка $M_0$ действительно лежит на заданной поверхности. Теперь найдём частные производные, т.е. $z_^<‘>$ и $z_^<‘>$:

Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ в выражения частных производных:

Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_^ <‘>left(x_0, y_0right)=-13$, $z_^ <‘>left(x_0, y_0right)=80$ в формулу (3) получим уравнение касательной плоскости:

Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_^ <‘>left(x_0, y_0right)=-13$, $z_^ <‘>left(x_0, y_0right)=80$ в формулу (4) получим уравнение нормали:

Ответ: Касательная плоскость: $-13x+80y-z-86=0$; нормаль: $frac<-13>=frac<80>=frac<-1>$.

Найти уравнение касательной плоскости и нормали к поверхности $z=5sqrt-2xy-39$ в точке $M_0(3;-4;z_0)$.

Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=3$, $y_0=-4$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:

Теперь, как и в предыдущем примере, перейдём к нахождению частных производных $z_^<‘>$ и $z_^<‘>$. После того, как мы найдём эти производные в общем виде, укажем их значения при $x=x_0$ и $y=y_0$:

Подставляя $x_0=3$, $y_0=-4$, $z_0=10$, $z_^ <‘>left(x_0, y_0right)=11$, $z_^ <‘>left(x_0, y_0right)=-10$ в формулы (3) и (4) получим уравнения касательной плоскости и нормали:

Ответ: Касательная плоскость: $11x-10y-z-63=0$; нормаль: $frac<11>=frac<-10>=frac<-1>$.

Найти уравнение касательной плоскости и нормали к поверхности $3xy^2z+5xy+z^2=10xz-2y+1$ в точке $M_0(1;-2;3)$.

Перенесём все слагаемые в левую часть равенства и обозначим полученное в левой части выражение как $F(x,y,z)$:

Используем формулы (1) и (2). Значения $x_0$, $y_0$ и $z_0$ как и ранее обозначают координаты точки $M_0$, т.е. $x_0=1$, $y_0=-2$, $z_0=3$.

Проверим, действительно ли точка $M_0$ лежит на данной поверхности. Для этого подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражение $3xy^2z+5xy+z^2-10xz+2y-1$ и выясним, равен ли нулю полученный результат:

Итак, точка $M_0$ действительно лежит на данной поверхности. Естественно, что данная проверка не является обязательной, но она крайне желательна. Перейдём к дальнейшему решению. Нам нужно найти $F_^<‘>$, $F_^<‘>$ и $F_^<‘>$:

Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражения частных производных:

Подставляя $x_0=1$, $y_0=-2$, $z_0=3$, $F_^ <‘>left(M_0right)=-4$, $F_^ <‘>left(M_0right)=-29$ и $F_^ <‘>left(M_0right)=8$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:

Ответ: Касательная плоскость: $-4x-29y+8z-78=0$; нормаль: $frac<-4>=frac<-29>=frac<8>$.

Найти уравнение касательной плоскости и нормали к поверхности $z^3+4xyz=-3x^2+5y+7$ в точке $M_0(0;-3;z_0)$.

Поверхность задана в неявном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (1) и (2). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=0$, $y_0=-3$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:

Перенесём все слагаемые в левую часть равенства:

Обозначим $F(x,y,z)=z^3+4xyz+3x^2-5y-7$ и применим формулы (1) и (2). Найдём частные производные первого порядка $F_^<‘>$, $F_^<‘>$ и $F_^<‘>$. После того, как мы найдём эти производные в общем виде, укажем их значения в точке $M_0$:

Подставляя $x_0=0$, $y_0=-3$, $z_0=-2$, $F_^ <‘>left(M_0right)=-24$, $F_^ <‘>left(M_0right)=-5$ и $F_^ <‘>left(M_0right)=12$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:

Ответ: Касательная плоскость: $-24x-5y+12z+9=0$; нормаль: $frac<-24>=frac<-5>=frac<12>$.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Поверхности. Касательная плоскость и нормаль

Краткие теоретические сведения

Способы задания поверхностей

Рассматриваем вектор–функцию двух скалярных аргументов: $$vec=vec(u,v).$$ Годографом такой функции является поверхность.

Запишем четыре способа задания поверхности: 1. Векторное уравнение: $$vec=vec(u,v).$$ 2. Параметрическое уравнение: $$x=x(u,v),,, y=y(u,v),,, z=z(u,v).$$ 3. Неявное уравнение: $$varPhi(x,y,z)=0.$$ 4. Явное уравнение: $$z=z(x,y).$$

Поверхность называется регулярной ($k$ раз дифференцируемой), если у каждой точки этой поверхности есть окрестность, допускающая регулярную параметризацию (то есть функции $x(u,v), y(u,v),z=z(u,v)$ $k$ раз непрерывно дифференцируемы). При $k=1$ поверхность называется гладкой.

Регулярная поверхность в окрестности каждой своей точки допускает бесчисленное множество параметризаций.

Кривая, лежащая на поверхности $vec=vec(u,v)$, задается уравнениями $$ u=u(t),,, v=v(t).$$ Линии $u=mbox$, $v=mbox$ являются координатными линиями данной параметризации поверхности.

Решение задач

Задача 1 (Феденко №544)

Дана поверхность begin x=u+v, ,, y=u-v,,, z=uv. end Проверить, принадлежат ли ей точки $A(4,2,3)$ и $B(1,4,-2)$.

Ответ. Точка $A$ принадлежит, так как ее координаты удовлетворяют системе уравнений, задающих поверхность. Точка $B$ не принадлежит поверхности.

Задача 2 (Феденко № 546)

Найдите неявное уравнение поверхности, заданной параметрическими уравнениями: begin begin x & = x_0 + a,mbox,u,mbox,v, \ y & = y_0 + b,mbox,u,mbox,v, \ z & = z_0 + c,mbox,u. end end

Ответ. Эллипсоид с полуосями $a$, $b$, $c$ и центром в точке $(x_0, y_0, z_0)$: begin frac<(x-x_0)^2>+frac<(y-y_0)^2>+frac<(z-z_0)^2>=1. end

Задача 3 (Феденко №528)

В плоскости $xOz$ задана кривая $x=f(u)$, $z=g(u)$, не пересекающая ось $Oz$. Найдите параметризацию поверхности, полученной при вращении этой кривой вокруг оси $Oz$.

Решение задачи 3

Произвольная точка $M$, принадлежащая кривой и имеющая координаты $x_0=f(u_0)$, $y_0=0$, $z_0=g(u_0)$, движется по окружности с центром на оси $Oz$ и радиусом $R=f(u_0)$ в плоскости, параллельной плоскости $xOy$: $z=g(u_0)$. Поэтому изменение ее координат можно записать следующими уравнениями: begin left< begin x_0 & = & f(u_0),mbox,v, \ y_0 & = & f(u_0),mbox,v, \ z_0 & = & g(u_0). \ end right. end

Поскольку точка $M$ произвольная, уравнение искомой поверхности: begin left< begin x & = & f(u),mbox,v, \ y & = & f(u),mbox,v, \ z & = & g(u). \ end right. end

Касательная плоскость. Нормаль

Краткие теоретические сведения

Пусть $vec=vec(u,v)in C^1$ — поверхность, проходящая через точку $P(u_0, v_0)$. Пусть $u=u(t)$, $v=v(t)$ — уравнения гладкой кривой, проходящей через точку $P(u_0, v_0)$ и лежащей на заданной поверхности.

Пусть точка $P$ не является особой, то есть ранг матрицы begin left( begin x_u & y_u & z_u \ x_v & y_v & z_v \ end right) end в точке $P$ равен $2$ (для особой точки ранг меньше $2$). Если поверхность задана неявно $varPhi(x,y,z)=0$, то в не особой точке $P$ выполняется условие: $varPhi_x^2+varPhi_y^2+varPhi_z^2neq0.$

Касательная к кривой $u=u(t)$, $v=v(t)$ на поверхности $vec=vec(u,v)$ определяется вектором: begin displaystylefrac>

=vec_udisplaystylefrac

+vec_vdisplaystylefrac

, end где $vec_u=displaystylefrac>$, $vec_v=displaystylefrac>$. Для разных кривых, проходящих через точку $P(u_0, v_0)$, значения $displaystylefrac

$, $displaystylefrac

$ будут разными, а $vec_u$, $vec_v$ теми же. Следовательно, все векторы $displaystylefrac>

$ лежат в одной плоскости, определяемой векторами $vec_u$, $vec_v$. Эта плоскость называется касательной плоскостью к поверхности в точке $P$. Запишем уравнение касательной плоскости.

Обозначения:
– $vec=$ — радиус-вектор произвольной точки касательной плоскости.
– $vec=$ — радиус вектор точки $P(u_0, v_0)$.
– Частные производные $x_u$, $y_u$, $z_u$, $x_v$, $y_v$, $z_v$ вычисляются в точке $P(u_0, v_0)$.

Уравнение касательной плоскости:

1. Если поверхность задана векторно, то уравнение касательной плоскости можно записать через смешанное произведение трех линейно зависимых векторов: $$ left(vec-vec, , vec_u, , vec_v right)=0. $$ 2. Если поверхность задана параметрически, запишем определитель: begin left| begin X-x & Y-y & Z-z \ x_u & y_u & z_u\ x_v & y_v & z_v\ end right|=0 end 3. Если поверхность задана неявным уравнением: begin varPhi_x(X-x)+varPhi_y(Y-y)+varPhi_z(Z-z)=0. end 4. В случая явного задания поверхности, уравнение касательной плоскости примет вид: begin (Z-z)=z_x(X-x)+z_y(Y-y). end

Нормалью поверхности в точке $P$ называется прямая, проходящая через $P$ перпендикулярно касательной плоскости в этой точке.

Уравнение нормали:

1.$$ vec=vec + lambdavec, ,, vec=vec_utimesvec_v. $$ 2. begin displaystylefrac< left| begin y_u & z_u\ y_v & z_v\ end right|>= displaystylefrac< left| begin z_u & x_u\ z_v & x_v\ end right|>= displaystylefrac< left| begin x_u & y_u\ x_v & y_v\ end right|>. end 3. begin displaystylefrac<varPhi_x>=displaystylefrac<varPhi_y>=displaystylefrac<varPhi_z>. end 4. begin displaystylefrac=displaystylefrac=displaystylefrac<-1>. end

Решение задач

Задача 1 (Феденко №574)

Дана поверхность begin x=u,mbox,v,,, y=u,mbox,v,,, z=u. end Написать:
а) уравнение касательной плоскости к поверхности;
б] уравнение нормали к поверхности;
в) касательной к линии $u=2$
в точке $Mleft(u=2, v=displaystylefrac<pi><4>right)$ поверхности.

Задача 2

Через точки $A(0,1,0)$ и $B(1,0,0)$ провести плоскость, касательную к поверхности $vec=$.

Ответ. $z=0, -2X-2Y+Z+2=0$.

Задача 3

Построить касательную плоскость к поверхности $y=x^2+z^2$, перпендикулярную вектору $vec<2,1,-1>$.

Задача 4

Через точку $M(1,2,1)$ провести плоскость, касательную к поверхности $x^2+y^2-z^2=0$.

Ответ. $X-Z=0$, $3X-4Y+5Z=0$.

Задача 5 (Феденко №594)

Докажите, что поверхности begin z=mbox(xy), ,, x^2-y^2=a end ортогональны в точках их пересечения.

Решение задачи 5

Запишем направляющие векторы нормалей к поверхностям, проведенным в точках их пересечения: begin begin vec_1&=left<frac<mbox^2(x_0y_0)>,frac<mbox^2(x_0y_0)>,-1right>,\ vec_2&=left<2x_0,-2y_0,0right>. end end Скалярные произведения векторов $n_1$ и $n_2$ равны нулю, следовательно векторы ортогональны. begin n_1cdot n_2=0. end

[spoiler title=”источники:”]

http://math1.ru/education/funct_sev_var/tannorm.html

http://vmath.ru/vf5/diffgeom/seminar5

[/spoiler]

1084 Составить уравнение сферы в
каждом из следующих случаев: 1084.1 сфера имеет центр
С(0; 0; 0) и радиус r=9; 1084.2 сфера имеет центр
С(5; -3; 7) и радиус r=2; 1084.3 сфера проходит
через начало координат и имеет центр С(4; -4; -2); 1084.4 сфера проходит
через точку А(2; -1; -3) и имеет центр С(3; -2; 1); 1084.5 точки А(2; -3; 5) и В(4; 1;
-3) являются концами одного из диаметров сферы; 1084.6 центром сферы
является начало координат и плоскость является касательной к сфере; 1084.7 сфера имеет центр
С(3; -5; -2) и плоскость является
касательной к сфере; 1084.8 сфера проходит
через точки М₁(3; 1; -3), М₂(-2; 4; 1), М₃(-5;
0; 0), а ее центр лежит на плоскости ; 1084.9 сфера проходит
через точки М₁(1; -2; -1), М₂(-5; 10; -1), М₃(4;
1; 11), М₄(-8; -2; 2).
1085 Составить
уравнение сфера радиуса r=3, касающейся плоскости в точке М₁(1; 1; -3).
1086 Вычислить радиус R
сферы, которая касается плоскостей , .
1087 Сфера, центр
которой лежит на прямой , , касается
плоскостей , . Составить
уравнение этой сферы.
1088 Составить
уравнение сферы, касающейся двух параллельных
плоскостей , , причем одной из них в точке М₁(5;
-1; -1).
1089 Составить
уравнение сферы с центром С(2; 3; -1), которая
отсекает от прямой , хорду, имеющую длину, равную 16.
1090 Определить
координаты центра С и радиус r сферы, заданной
одним из следующих уравнений: 1090.1 ; 1090.2 ; 1090.3 ; 1090.4 ; 1090.5 .
1091 Составить
параметрические уравнение диаметра сферы , перпендикулярного к плоскости .
1092 Составить
канонические уравнения диаметра сферы , параллельного прямой , , .
1093 Установить, как
расположена точка А(2; -1; 3) относительно каждой из
следующих сфер – внутри, вне или на поверхности: 1093.1 ; 1093.2 ; 1093.3 ; 1093.4 ; 1093.5 .
1094 Вычислить
кратчайшее расстояние от точки А до данной сферы
в следующих случаях: 1094.1 А(-2; 6; -3), ; 1094.2 А(9; -4; -3), ; 1094.3 А(1; -1; 3), .
1095 Определить, как
расположена плоскость относительной сферы –
пересекает ли, касается или проходит вне ее;
плоскость и сфера заданы следующими уравнениями: 1095.1 , ; 1095.2 , ; 1095.3 , .
1096 Определить, как
расположена прямая относительно сферы –
пересекает ли, касается или проходит вне ее;
прямая и сфера заданы следующими уравнениями: 1096.1 , , , ; 1096.2 , ; 1096.3 , , .
1097 На сфере найти точку М₁, ближайшую к плоскости , и
вычислить расстояние d от точки М₁ до этой плоскости.
1098 Определить центр С
и радиус R окружности , .
1099 Точки А(3; -2; 5), В(-1; 6;
-3) являются концами диаметра окружности,
проходящей через точку С(1; -4; 1). Составить
уравнения этой окружности.
1100 Точка С(1; -1; -2)
является центром окружности, отсекающей от
прямой , хорду, длина которой равна 8.
Составить уравнения этой окружности.
1101 Составить
уравнения окружности, проходящей через точки М₁(3; -1; -2), М₂(1; 1;
-2), М₃(-1; 3; 0).
1102 Даны сферы , , которые
пересекаются по окружности, лежащей в некоторой
плоскости . Доказать, что любая сфера,
проходящая через окружность пересечения данных
сфер, а также плоскость могут быть
представлены уравнением вида при
надлежащем выборе чисел и .
1103 Составить
уравнение плоскости, проходящей через линию
пересечения сфер , .
1104 Составить
уравнение сферы, проходящей через начало
координат и окружность , .
1105 Составить
уравнение сферы, проходящей через окружность , и
точку А(2; -1; 1).
1106 Составить
уравнение сферы, проходящей через окружности , и , .
1107 Составить
уравнение касательной плоскости к сфере в точке М₁(6; -3; -2).
1108 Доказать, что
плоскость касается сферы . Вычислить
координаты точки касания.
1109 При каких значения
а плоскость касается сферы .
1110 Составить
уравнение касательной плоскости к сфере в точке М₁(-1; 3; 0).
1111 Точка М₁(x₁;
y₁; z₁) лежит на сфере . Составить
уравнение касательной плоскости к этой сфере в
точке М₁.
1112 Вывести условие,
при котором плоскость касается
сферы .
1113 Точка М₁(x₁;
y₁; z₁) лежит на сфере . Составить
уравнение касательной плоскости к этой сфере в
точке М₁.
1114 Через точки
пересечения прямой , , и
сферы проведены касательные плоскости к
этой сфере. Составить их уравнения.
1115 Составить
уравнения плоскостей, касательных к сфере и параллельных плоскости .
1116 Составить
уравнения плоскостей, касательных к сфере и параллельных плоскости .
1117 Составить
уравнения плоскостей, касательных к сфере и параллельных прямым , .
1118 Доказать, что через
прямую , можно провести две плоскости,
касательные к сфере , и составить их уравнения.
1119 Доказать, что через
прямую нельзя провести
плоскость, касательную к сфере .
1120 Доказать, что через
прямую ,
, можно провести
только одну плоскость, касательную к сфере , и
составить ее уравнение.

План урока:

Понятие сферы и шара

Уравнение сферы

Пересечение сферы плоскостью

Касательная плоскость к сфере

Пересечение двух сфер

Площадь сферы

Вписанные и описанные сферы

Понятие сферы и шара

Люди постоянно сталкиваются с предметами, имеющими форму шара. В большинстве спортивных игр (баскетболе, большом и настольном теннисе, футболе) используются мячи, которые по форме как раз являются шарами. Такую же форму имеют многие фрукты – яблоки, апельсины, мандарины. Более того, известно, что Земля, другие планеты и звезды, большинство крупных спутников также представляют собой шары.

Важно отличать шар от сферы. Сферой называют только поверхность шара. Сам же шар является объемной фигурой, к нему относят всю часть пространства, ограниченную сферой.

Дадим строгие определения сферы и шара:

Отрезок, соединяющий точку на сфере с ее центром, именуется радиусом сферы. Он же называется и радиусом шара, заключенного внутри этой сферы.

Проходящий через центр сферы отрезок, чьи концы принадлежат сфере, именуется диаметром сферы. Сама сфера считается частью шара, также как и окружность считается частью круга.Показывают шар или сферу на рисунке так:

Из определения сферы явно вытекает тот факт, что все ее радиусы одинаковы. Это в свою очередь означает, что центр сферы – это середина диаметра, и диаметр вдвое длиннее радиуса.

Заметим, что сфера является телом вращения. Она получается при повороте полуокружности вокруг ее диаметра:

Уравнение сферы

В планиметрии мы уже изучали уравнения линии. Так назывались ур-ния с двумя переменными, каждое решение которых соответствовало точке на координатной плос-ти, принадлежавшей заданной линии. Если же точка не принадлежала линии, то ее координаты решением соответствующего ур-ния не являлись. В частности, нам удалось получить уравнения прямой и окружности.

Аналогично в стереометрии вводится понятие уравнения поверхности. Так как в пространстве используются уже три координаты (х, у и z), то ур-ния поверхности содержат три переменных. Координаты всякой точки, принадлежащей поверхности, будут являться решениями ур-ния этой поверхности. И наоборот, координаты точки, не принадлежащей поверхности, будут обращать ур-ние поверхности в неверное равенство.

Выведем ур-ние сферы. Пусть ее центр располагается в точке С с координатами (х₀, у₀, z₀), а радиус обозначен как R. Возьмем произвольную точку А на сфере. По определению сферы расстояние между А и С должно составлять R:

Мы уже знаем формулу для расчета расстояния между А и С:

Точки, координаты которых удовлетворяют этому неравенству, находятся от центра сферы на расстоянии меньше ее радиуса. Это значит, что они находятся внутри сферы, то есть принадлежат шару, чьей поверхностью является рассматриваемая сфера. Если же координаты точки удовлетворяют неравенству

то можно утверждать, что точка находится вне пределов сферы, то есть она не принадлежит ни сфере, ни шару.

Задание. Напишите уравнение сферы, центр которой располагается в точке (2; – 4; 7) и чей радиус равен 3.

Решение. Здесь мы просто подставляем координаты центра сферы и ее радиус в ур-ние сферы:

Задание. Есть сфера с радиусом 9, чей центр располагается в точке О(2; 3; 4). Определите, какие из следующих точек будут принадлежать этой сфере: А(1; 7; – 4), В(0; 6; 10), С(– 2; – 1; 11), D(5; 6; 8).

Решение. Сначала составляем уравнение сферы, описанной в условии:

Равенство неверное, значит, В не располагается на сфере (более того, раз 49 < 81, то можно утверждать, что точка располагается внутри сферы). Далее проверяем точку С(– 2; – 1; 11):

Задание. Докажите, что ур-ние

является ур-нием сферы, после чего определите радиус этой сферы.

Решение. Здесь необходимо выполнить некоторые преобразования ур-ния, чтобы оно стало похожим на ур-ние сферы. Для этого используем формулы квадратов суммы и разности:

Пересечение сферы плоскостью

Рассмотрим ситуацию, когда секущая плоскость α пересекает сферу. Нас в первую очередь интересует форма получающегося сечения. Опустим из точки О, центра сферы, перпендикуляр ОН на секущую плос-ть (пока мы рассматриваем случай, когда секущая плос-ть проходит не через О):

Буквами А и В обозначим любые две точки сечения, которые принадлежат одновременно и сфере, и плос-ти α. Теперь сравним ∆ОНА и ∆ОНВ. Они прямоугольные, ведь ОН – перпендикуляр к α. При этом у них есть общий катет ОН и одинаковые гипотенузы ОА и ОВ (это радиусы одной сферы).Тогда эти ∆ОНА и ∆ОНВ одинаковы, и поэтому

AH = BH

Мы выбрали точки А и В произвольно, и они оказались равноудаленными от Н. Значит, А и В находятся на одной окруж-ти с центром Н. Легко показать и обратное – любая точка этой окруж-ти будет лежать и на сфере (попробуйте сделать этот сами). Значит, сечение имеет форму окруж-ти, причем ее центр – это основание перпендикуляра, проведенного из О на α.

Обозначим длину перпендикуляра ОН буквой h, радиус сферы буквой R и радиус сечения буквой r. Тогда, используя теорему Пифагора, мы можем составить формулу для расчета радиуса r сечения:

Видно, что чем длиннее перпендикуляр h(он представляет собой расстояние от О до α), тем меньше радиус сечения. Тогда ясно, что наибольший радиус будет у того сечения, которое проходит через центр О. Действительно, если сечение проходит через О, то все его точки по определению сферы будут удалены на расстояние R от О. Но уже по другому определению такое множество точек – окруж-ть с центром в О и радиусом R. Плос-ть, проходящая через центр сферы, именуется диаметральной плоскостью, а само сечение именуют большой окружностью сферы. Радиус большой окруж-ти совпадает с радиусом самой сферы.

Задание. Сфера с радиусом 41 пересечена плос-тью, которая находится на расстоянии 9 от центра этой сферы. Найдите площадь сечения.

Решение. Опустим из центра сферы О перпендикуляр ОН на секущую плос-ть, тогда по условию ОН = 9. Пусть А – точка на сечении, тогда ОА = 41. ∆ОНА – прямоугольный, поэтому мы можем найти радиус АН:

Теперь площадь сечения можно рассчитать по известной формуле площади круга:

Ответ: 1600π.

Задание. Докажите, что если через три точки сферы провести окруж-ть, то все точки этой окруж-ти будут также принадлежать сфере.

Решение. Пусть на сфере есть точки А, В, С. Проведем через них окруж-ть L. Надо доказать, что произвольная точка D, принадлежащая этой окруж-ти, также будет находиться на сфере.

Через точки А, В и С можно провести единственную плос-ть АВС. Она будет секущей для сферы, ведь она имеет с ней как минимум три общих точки – А, В и С. Формой этого сечения будет некоторая окруж-ть L₁. L₁ обязательно будет проходить через А, В и С. Но через любые три точки можно провести не более одной окружности, поэтому L и L₁ совпадают. Значит, D, принадлежащая по условию L, будет также принадлежать и L₁. Но L₁– это сечение, все его точки, в том числе и D, принадлежат сфере, ч. т. д.

Есть смысл запомнить доказанное утверждение:

Задание. На сфере радиусом 13 отмечены точки А, В и С так, что АВ = 6, ВС = 8 и АС = 10. Каково расстояние между центром сферы и плос-тью АВС?

Решение. Сначала заметим, что ∆АВС является прямоугольным, ведь его стороны удовлетворяют теореме Пифагора:

Напомним одного из свойств прямоугольного треугольника – центр окруж-ти, описанной около него, совпадает с серединой его гипотенузы. То есть если через точки А, В и С провести окруж-ть, то ее центр Н будет серединой АВ, и поэтому

Теперь заметим, что эта описанная окруж-ть должна быть сечением сферы. Это значит, что ОН – перпендикуляр к плос-ти АВС, ведь центр сечения должен лежать на перпендикуляре к плос-ти, проведенном из О. Тогда ∆ОНС – прямоугольный, и ОН – искомое нами расстояние. ОС – радиус сферы. Рассчитаем по теореме Пифагора ОН:

Касательная плоскость к сфере

Плос-ть, имеющая со сферой строго одну общую точку, именуется касательной плоскостью к сфере.

Действительно, если плос-ть касается окруж-ти, то точка касания А должна располагаться на расстоянии R от центра сферы О, где R– радиус сферы. Все остальные точки касательной плос-ти находятся вне пределов сферы, то есть должны находиться от О на расстоянии, превышающем R. Это значит, что отрезок ОА должен быть кратчайшим отрезком, соединяющим О и касательную плос-ть. Но мы знаем, что кратчайший отрезок между плос-тью и точкой – это как раз перпендикуляр, опущенный из точки на плос-ть.

Справедливо и обратное утверждение:

Доказательство. Если радиус ОА – перпендикуляр к плос-ти α, то он является кратчайшим расстоянием между плос-тью и центром О. Тогда все остальные точки плос-ти располагаются на большем расстоянии от О, чем точка А. Это значит, что они не располагаются на сфере. Значит, у сферы и плос-ти α одна общая точка А, а потому α по определению – касательная плос-ть.

По аналогии с касательной плос-тью существует понятие касательной прямой к сфере.

Касательная к сфере обладает почти теми же свойствами, что и касательная к окруж-ти.

Доказательство. Пусть m– касательная прямая к сфере с центром О. обозначим точку касания как А. Далее через прямую m и центр О проведем плос-ть α. Нам надо показать, что ОА⊥m:

Плос-ть α будет диаметральной плос-тью. Сечение будет иметь форму окруж-ти с центром О и радиусом ОА. Прямая m будет касательной к этой окруж-ти, ведь она имеет с ней общую точку А, а второй общей точки m и окруж-ть иметь не могут, ведь такая бы точка была бы также общей для m и сферы, а m по определению имеет лишь одну общую точку со сферой. Напомним, что касательная к окруж-ти перпендикулярна радиусу, то есть m⊥ОА, ч. т. д.

Будет верным и обратное утверждение:

Для доказательства используем ту же картинку. Известно, что m⊥ОА, надо показать, что m– касательная к сфере. Проведем через пересекающиеся прямые m и ОА плос-ть α. Она снова окажется диаметральной плоскостью, и снова сечением будут окруж-ть с радиусом ОА. По признаку касательной, который мы изучали в планиметрии, m– касательная к этой окруж-ти, ведь m⊥ОА. То есть в плос-ти α есть лишь одна общая точка m и сферы. В других плос-тях у них не может быть общих точек, так как m полностью принадлежит α. В итоге у m и сферы только одна общая точка, а потому m– касательная к сфере, ч. т. д.

Рассмотрим ещё одно утверждение:

Сначала разберемся с понятием отрезков касательных. Пусть из точки А, лежащей вне сферы, к ней проведены две касательные, а точки касания обозначены буквами В и С. Тогда АВ и АС как раз и будут отрезками касательных:

Докажем, что эти отрезки одинаковы. Для этого к точкам касания проведем радиусы ОВ и ОС. Теперь сравним ∆АВО и ∆АСО. Они прямоугольные, ведь ОВ⊥АВ по свойству касательной, и ОС⊥АС. Гипотенуза АО у этих треугольников общая, а катеты ОВ и ОС – это одинаковые радиусы. Получается, что ∆АВО и ∆АСО равны, а потому отрезки АВ и АС одинаковы.

Задание. Дан шар радиусом 10 см, к которому проведена касательная плос-ть α. Через точку касания проведена секущая плос-ть β, образующая с α угол в 30°. Вычислите площадь сечения шара плос-тью β.

Решение. Обозначим точку касания как А. Опустим из центра сферы о перпендикуляр ОН на плос-ть β. Тогда отрезок АН будет радиусом сечения. Так как угол между плос-тями α и β составляет 30° (на рисунке он показан как ∠НАС), то

Ответ: 25π см².

Задание. Некоторое тело представляет собой шар, внутри которого есть полость, также имеющая форму шара, причем центры этих шаров совпадают. Докажите, что площадь сечения этого тела, проходящего через центр шаров, совпадает с площадью сечения, являющегося касательной к внутреннему шару.

Решение. Обозначим радиус большей сферы как R, а радиус меньшей (внутренней сферы) как r. Площадь центрального сечения в виде кольца (показано синим цветом) представляет собой разницу между площадью большого круга с радиусом R и малого с радиусом r:

Задание. Сфера радиусом 5 см касается каждой стороны треугольника со сторонами 13, 14 и 15 см. Каково расстояние между центром этой сферы и плос-тью треугольника?

Решение. Обозначим вершины треугольника точками А, В и С. Пусть

AB = 13

AC = 14

BC = 15

Заметим, что плос-ть АВС – секущая, а само сечение имеет форму окруж-ти. Эта окруж-ть будет касаться сторон ∆АВС, то есть она является вписанной окруж-тью. Как вычислить ее радиус НK?

Напомним одну из формул для расчета площади треугольника:

Площадь ∆АВС можно найти по формуле Герона. Предварительно найдем полупериметр ∆АВС:

Пересечение двух сфер

Пусть есть две пересекающиеся сферы с центрами в точках О₁ и О₂ с радиусами R₁ и R₂ соответственно. Какую форму будет иметь линия L, по которой они пересекаются?

Эта линия является множеством точек, которые принадлежат как первой, так и второй сфере. Обозначим две произвольные точки этой линии буквами А и В:

Проведем радиусы О₁А, О₁В, О₂А и О₂В. Теперь сравним ∆АО₁О₂ и ∆ВО₁О₂. Сторона О₁О₂ у них общая, а другие стороны попарно равны как радиусы сфер:

Получается, что ∆АО₁О₂ и ∆ВО₁О₂ равны. Теперь из точек А и В опустим высоты на прямую О₁О₂. Из равенства ∆АО₁О₂ и ∆ВО₁О₂ вытекает два факта:

• эти высоты упадут в одну точку Н;
• эти высоты будут одинаковы, то есть АН = НВ.

Другими словами, А и В равноудалены от Н. Получается, что точки А и В находятся на окруж-ти, центр которой – точка Н. Заметим, что О₁О₂ – перпендикуляр к плоскости окружности, ведь О₁О₂⊥АН и О₁О₂⊥ВН.

Точки А и В были выбраны произвольно, поэтому можно утверждать, что любые точки линии L будут находиться на одной окруж-ти. Докажем и обратное утверждение – любая точка, лежащая на этой окруж-ти, будет принадлежать линии L. Возьмем на окруж-ти какую-нибудь точку С и построим радиус НС:

Теперь сравним ∆О₁НС и ∆О₁НА. Они прямоугольные, ведь О₁Н – перпендикуляр к плос-ти окружности. Катет О₁Н у них общий, а катеты АН и НС одинаковы как радиусы окруж-ти. Значит, ∆О₁НС и ∆О₁НА равны, и потому

Это равенство означает, что С принадлежит сфере с центром в О₁. Аналогично рассмотрев ∆О₂НС и ∆О₂НА, можно показать, что С также принадлежит и второй сфере. Тогда С принадлежит пересечению этих сфер.

Итак, всякая точка линии L лежит на окруж-ти с центром Н, и наоборот, каждая точка этой окруж-ти лежит на линии L. Это означает, что L как раз и является этой окружностью.

Отметим ещё один факт: по неравенству треугольника отрезок О₁О₂ должен быть меньше суммы отрезков О₁А и О₂А, то есть суммы радиусов сфер.

Задание. Сферы имеют радиусы 25 см и 29 см, а расстояние между их центрами составляет 36 см. Вычислите радиус окруж-ти, по которой они пересекаются.

Решение. Пусть А – одна их точек сечения. Искомый радиус обозначим как АН. В итоге получим такую картинку:

Площадь сферы

Сферическая поверхность, как и всякая другая ограниченная поверхность, имеет какую-то площадь. Напомним, что для вычисления площадей цилиндрической и конической поверхности мы строили их плоские развертки и находили площади уже этих разверток, используя формулы из планиметрии. Оказывается, что для сферы построить такую развертку невозможно. Мы не будем доказывать строго этот факт, но он известен из географии – любая карта Земли, которая как раз и должна быть разверткой сферической поверхности нашей планеты, является неточной и сильно искажает форму и размеры континентов. Если бы существовал способ построить точную развертку, то и географические карты не имели бы таких искажений.

Однако вычислить площадь сферы всё же можно по известной формуле:

Сейчас мы не будем доказывать эту формулу. Отметим лишь, что для ее получения необходимо использовать интегралы.

Задание. Какова площадь сферы с радиусом 5 см?

Решение. Просто используем формулу:

Ответ: 100π см².

Вписанные и описанные сферы

Если каждая точка многогранника лежит на поверхности сферы, то говорят, что многогранник вписан в сферу. Тогда сферу именуют описанной, а многогранник – вписанным.

Если же сфера касается каждой грани многогранника, то уже наоборот, сфера вписана в многогранник. Тогда уже сфера будет вписанной фигурой, а многогранник – описанной.

Заметим, что не в каждый многогранник может быть вписанным или описанным. Например, в куб вписать сферу можно, а в прямоугольный параллелепипед, измерения которого отличаются, уже вписать сферу не получится.

Надо отметить, что в сферу можно вписать не только в многогранник, но и другие геометрические фигуры, в частности конус и цилиндр. Здесь нужно уточнить (без доказательства), что если касание плос-ти и сферы происходит только в одной точке, то цилиндрическая и коническая поверхности касаются сферы уже по окруж-ти.

Задание. Правильная пирамида вписана в сферу. Докажите, высота этой пирамиды проходит через центр сферы.

Решение. Опустим из центра сферы О перпендикуляр ОН на основание пирамиды. Далее возьмем произвольную вершину Х основания пирамиды, и соединим ее с Н отрезком ХН. По теореме Пифагора можно вычислить длину ХН (радиус сферы ОХ обозначим, буквой R):

Получилось, что расстояние ХН не зависит от самой точки Х. То есть все вершины основания равноудалены от точки, то есть Н – центр описанной около основания окруж-ти. Это означает, что перпендикуляр ОН одновременно является высотой правильной пирамиды, ч. т. д.

Задание. Вычислите радиус описанной сферы, в которую вписан правильный тетраэдр со стороной а.

Решение. Правильный тетраэдр можно считать правильной треугольной пирамидой, поэтому (согласно предыдущей задаче) из центра сферы О можно опустить перпендикуляр на основание АВС, который упадет в точку Н – центр основания. Так как тетраэдр правильный, то ∆АВС – равносторонний, то есть Н – эта точка пересечения и медиан, и высот. Опустим из А высоту АК, она пройдет через Н. Так как АК – ещё и медиана, то

Далее найдем длину АН. Вспомним, что АН – медиана, а точка пересечения медиан Н делит их в отношении 2:1. Это значит, что

Буквой R здесь обозначен радиус описанной сферы. Осталось применить теорему Пифагора к ∆АНD:

Задание. Докажите что вокруг любого тетраэдра можно описать сферу.

Решение. Обозначим вершины произвольного тетраэдра буквами А, В, С и D. Далее на грани АВС отметим точку К – центр окруж-ти, описанной около ∆АВС. Аналогично на грани АВD отметим Н – центр окруж-ти, описанной около ∆АВD:

Напомним, что центры описанных окружностей располагаются в той точке, где пересекаются серединные перпендикуляры. Это значит, что если мы из К и Н опустим перпендикуляры на ребро АВ, то эти перпендикуляры будут серединными, то есть они попадут в одну точку М, являющуюся серединой ребра АВ.

Мы получили плос-ть НМК. Заметим, что НМК⊥АВ по признаку перпендикулярности прямой и плоскости, так как АВ⊥МН и АВ⊥МК. Но тогда АВС⊥МНК уже по признаку перпендикулярности плоскостей, ведь АВС проходит через АВ, являющийся перпендикуляром к НМК. По той же причине и АВD⊥НМК.

Далее проведем через К перпендикуляр m к АВС. Он должен будет принадлежать НМК, ведь НМК⊥АВD. Аналогично и через Н проведем перпендикуляр n к АВD, который также будет принадлежать НМК.

В плос-ти НМК есть две прямые, mи n. Они либо параллельны, либо пересекаются. Но перпендикуляры к двум плос-тям могут быть параллельны только в случае, если сами эти плос-ти параллельны (или совпадают). Но АВС и АВD непараллельны и не совпадают, поэтому m и n непаралелльны, то есть они пересекаются в какой-то точке О.

Покажем, что точка О равноудалена от всех вершин тетраэдра. Сравним ∆АОК и ∆СОК. Они прямоугольные, ведь ОК – перпендикуляр к АВС. ОК – общий катет, а катеты АК и СК одинаковы как радиусы описанной окруж-ти. Значит, ∆АОК и ∆СОК равны, ОА = ОС. Аналогично рассмотрев ∆АОК и ∆ВОК, приходим к выводу, что ОА = ОВ. Далее рассматриваем ∆ОНD и ∆ОНА и получаем, что ОА = ОD. Эти три равенства все вместе означают, что О равноудалена от точек А, В, С и D. А это значит, что на сфере с центром О и радиусом ОА будут лежать все вершины тетраэдра, то есть такая сфера окажется описанной, ч. т. д.

Примечание. Несложно доказать, что описанная сфера будет единственной. Действительно, если бы около тетраэдра можно было описать две различных сферы, то они пересекались бы в точках А, В, С и D. Сферы пересекаются по окруж-ти, то есть А, В, С и D должны лежать на одной окруж-ти, но это невозможно, ведь они не располагаются в одной плос-ти. Значит, двух описанных сфер существовать не может.

Доказанное в задаче утверждение можно сформулировать несколько иначе:

Сегодня мы изучили сферу – одну из важнейших геометрических фигур. Именно сферическую форму имеют звезды и планеты. Жидкость, оказавшаяся в невесомости, также принимает форму шара. Важно запомнить, что сечение сферы имеет форму окруж-ти, и касательные к сфере обладают почти такими ми же свойствами, как и касательные к окруж-ти в планиметрии.

– 181–

Тема поверхностные интегралы

§1. Параметрическое задание поверхности

Линию на плоскости
можно задавать явно (– парабола), неявно (– лемниската
Бернулли)
и параметрически
– эллипс). Для поверхностей в пространстве
мы знакомы с явным заданием– параболоид вращения) и неявным заданием– коническая поверхность). Осталось
познакомиться ещё с одним способом –
параметрическим.

Сразу заметим,
что система трёх однопараметрических
уравнений

задаёт в пространстве
некоторую линию
Для такого задания линии удобно
использовать векторную форму записи,
а именно: линиясостоит из тех точекрадиус-векторы которых имеют вид

(Подробнее об этом
смотри «Математический анализ, ч.1»,
тема «Функции нескольких переменных»).

Для параметрического
задания поверхности необходимы два
параметра. Пусть на плоскости с декартовой
прямоугольной системой координат в некоторой области
заданы три функции
Другими словами,
каждой точке
поставлена в соответствие тройка чисел
,
которые
естественно понимать как координаты
точки пространства
Множество всех таких точек, и есть
некоторая поверхность:

(1)

Здесь также удобна
векторная форма записи: поверхность состоит из точек
радиус-векторы которых задаются
вектор-функцией двух переменных

.

Замечание
1. Исключая
из параметрических уравнений оба
параметра, можно получить неявное
уравнение поверхности и тем самым
идентифицировать поверхность.

Пример 1.
Уравнения

(2)

определяют сферу
.

Пример
2. Уравнения

определяют
коническую поверхность

Пример
3. Пусть в
плоскости
дана окружностьс центром в точке,
причёмПри вращении этой окружности вокруг
осиполучается поверхность, называемая
тором.

Выведем параметрические
уравнения тора. Пусть
– текущая точка тора. В качестве
параметров возьмём два угла:– угол междуи плоскостью,– угол междуи осью,
где

Обозначим

Тогда

а

кроме
того

Окончательно имеем
для тора:

Пример 4.
Уравнения

определяют т.н.
геликоид (прямой), т.е. поверхность,
описываемую прямой
,
которая вращается вокруг осии одновременно перемещается вдоль этой
оси, причем,
скорости вращения и перемещения
постоянные, в начальный моментсовпадает с

Замечание
2. Явное
задание поверхности
является частным случаем параметрического:

В параметрических
уравнениях (1) зафиксируем значение
одного из параметров: пусть, например,
Получим систему однопараметрических
уравнений

определяющую
некоторую линию
,
которая называется координатной линией.
Меняя значение,
получим целое семейство таких линий.
Аналогично можно получить ещё одно
семейство координатных линий:

Через каждую точку

(за исключением некоторых точек, таких,
как полюса сферы или вершина конуса)
проходит по одной линии каждого семейства
координатных линий. Соответствующие
значения параметров называются
криволинейными координатами точки
поверхности.

Для сферы (2)
координатные линии – это параллели ()
и меридианы ().

§2. Касательная плоскость к поверхности, заданной параметрически

Напомним, что
направляющий вектор касательной к линии

имеет вид .
Здесь
– значение параметра, которое соответствует
точке касания.

Далее, касательная
линия к поверхности – это касательная
к линии, лежащей на поверхности, а
касательная плоскость – это плоскость,
в которой лежат все касательные прямые
(Подробно обо всём этом смотри
«Математический анализ, ч.1», тема
«Функции нескольких переменных», §8 и
§9).

Что касается
нормального вектора касательной
плоскости к поверхности

можно рассуждать
таким образом. Через точку
проходят две координатные линии:
и .
Их векторные уравнения:

Направляющие
векторы касательных к этим линиям
и
соответственно. Векторное произведение
этих векторов

можно взять в
качестве нормального вектора касательной
плоскости. Зная точку касания ,
криволинейные координаты которой ,
и нормальный вектор ,
нетрудно написать уравнение касательной
плоскости

Можно написать
готовую формулу касательной плоскости
(без вычисления вектора ),
если воспользоваться общим приёмом.
Берём текущую точку касательной плоскости
и
рассматриваем три вектора: ,

и .
Они компланарны и, следовательно, их
смешанное произведение равно нулю.
Отсюда получаем уравнение касательной
плоскости

Здесь производные
функций
вычисляются при значениях параметров

и ,
которые соответствуют точке касания
.

Пример.
Составить уравнения касательной
плоскости к винтовой поверхности

в токе ,
криволинейные координаты которой .

Решение.
Находим частные производные функций
и подставляем в соответствующую формулу:

.

Разлагаем
определитель по 1^й
строке:

.

Оставим в левой
части уравнения только члены, содержащие
текущие координаты
и разделим обе части уравнения на :

Соседние файлы в папке Лекции по мат.анализу

• #
• #
• #
• #
• #
• #
• #
• #