Как составить уравнение кинематического баланса станка

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Кинематическая настройка станков

Кинематическую настройку станка производят для обеспечения необходимых перемещений конечных звеньев кинематической цепи и для получения заданных формы и размеров детали, которая в основном сводится к определению параметров органа настройки. Расчетные перемещения звеньев определяют исходя из формы поверхности, которая должна быть образована на заготовке, и вида режущего инструмента.

Затем по кинематической цепи составляют уравнение кинематического баланса, связывающее начальное и конечное перемещения, и находят зависимость параметра органа настройки от расчетных перемещений и постоянных цепи.

Кинематическая цепь

Кинематическая цепь составляется из движущихся сопряженных между собой и передающих друг другу движения деталей. Если началом кинематической цепи является электродвигатель (рис. 3,б), то можно найти связь между начальным и конечным звеньями:

где n, n_шп – частота вращения начального и конечного звеньев; n_p, i_p – КПД и передаточное отношение ременной передачи.

Для удобства вычислений рекомендуется в уравнении кинематического баланса (4.1) выделить постоянные величины структурной формулы и подсчитать их как коэффициент данной кинематической цепи, например:

Это выражение справедливо и для станков, в цепи главного движения которых в качестве органа настройки используется коробка скоростей. Тогда в выражении (4.2) i_v будет передаточным отношением коробки скоростей.

Уравнение кинематического баланса

Уравнение кинематического баланса для цепи главного вращательного движения имеет вид (об/с)

n_c i = n_k, (4.3), где n_c и n_k– частота вращения соответственно начального и конечного звена, об/с; i- передаточное отношение кинематической цепи.

Уравнение кинематического баланса для цепи, у которой начальное звено имеет вращательное движение, а конечное – прямолинейное, будет (мм/с)

n_c i H = S_c, где Н – ход кинематической пары, преобразующей вращательное движение в прямолинейное, мм/об; s_c – линейное перемещение конечного звена, мм/с.

Величина хода

Величина хода равна перемещению прямолинейно движущегося звена за один оборот вращающегося звена. Для винтовой пары (винт – гайка)

H = k t_в (4.4), где t_в – шаг ходового винта, мм; k – число заходов.

Для реечной передачи.

H = π m z, где m – модуль зацепления, мм; z – число зубьев реечного колеса.

На этом основании уравнение кинематического баланса для секундной подачи (мм/с):

для цепи с винтовой парой

для реечной передачи

Уравнение кинематического баланса для оборотной подачи (мм/об)

где s – линейное перемещение конечного звена, мм/об.

Из уравнений (4.5)-(4.7) определяют передаточное отношение органа настройки. Например, из уравнения (4.2) находят

Это выражение является формулой настройки сменных колес гитары скоростей цепи (см. рис. 3,б).

Выводы

Анализ структурных схем металлорежущих станков позволяет сделать следующие выводы. Кинематическая структура станков зависит от геометрической формы, размеров обрабатываемой поверхности и метода обработки. Чем меньше необходимое число исполнительных формообразующих движений, тем меньше кинематических цепей в структуре станка, тем проще его кинематика и конструкция. Существенное значение имеют и другие факторы, например точность и шероховатость поверхности, динамика резания, условия обслуживания станка, а также экономические факторы.

Похожие материалы

ОБЩАЯ МЕТОДИКА НАЛАДКИ МЕТАЛЛООБРАБАТЫВАЮЩИХ СТАНКОВ

Уравнение кинематического баланса. Для большинства метал­лообрабатывающих станков независимо от их сложности методика наладки одинакова. Она заключается в сообщении исполнительным органам станка согласованных друг с другом движений для изготовле­ния деталей.

Процесс наладки станка требует расчета передаточных отношений органа, наладки скоростей для получения заданной частоты вращения шпинделя и передаточных отношений органов наладки цепей для осуществления необходимых подач (подачи).

Для этих целей намечают расчетные кинематические цепи, состав­ляют расчетные перемещения конечных звеньев этих цепей и уравне­ния кинематического баланса, из которых выводят формулы наладки цепей.

Уравнением кинематического баланса называют уравнение, связы­вающее расчетные перемещения конечных звеньев кинематической цепи. Это уравнение служит основой для определения передаточных отношений органа наладки. Конечные звенья могут иметь как враща­тельное, так и прямолинейное движение. Если оба конечных звена вращаются, то расчетные перемещения этих звеньев условно записы­вают следующим образом: лнмин-1 -» лкмин-1. Стрелка в этой записи заменяет слово «соответствует». По этим расчетным перемещениям составляют уравнения кинематического баланса данных кинематиче­ских цепей: пн • /пост • /х = Якмин’1, где пк — частота вращения в минуту конечного звена органа наладки; пн — частота вращения в минуту начального звена органа наладки; /пост — постоянное передаточное отношение органа наладки; /х — искомое передаточное отношение органа наладки.

Решая уравнения кинематического баланса относительно /х, полу­чим формулы наладки рассматриваемых кинематических цепей.

Если одно из конечных звеньев в кинематической цепи имеет вращательное движение, а другое — прямолинейное, то при подаче, выраженной в миллиметрах на один оборот начального звена, расчет­ные перемещения можно записать: 1 оборот начального звена -» Suu продольного перемещения конечного звена. Уравнение кинематиче­ского баланса будет иметь вид: 1 оборот начального звена іпосг • /х • 1 = =5, где S — перемещение кинематической пары, преобразующей вра­щательное движение в прямолинейное (например, перемещение гайки за один оборот винта), мм; 1 = Z • Рь (здесь Z— число заходов винта; Рв — шаг винта, мм).

При наладке станков в общем случае необходимо:

1. По технологическому процессу изготовления детали установить характер движений в станке и их взаимосвязь;

2. Определить все кинематические цепи, по которым будет осуще­ствляться необходимое для этого движение;

3. Составить соответствующие уравнения кинематических цепей, связывающих попарно рабочие органы станка;

4. По полученным передаточным отношениям вычислить и подо­брать сменные зубчатые колеса и т. п.

При составлении уравнения кинематической цепи безразлично, в каком порядке рассматривается данная кинематическая цепь — от первого элемента ее (считая в направлении передачи движения) к последнему звену или наоборот, от последнего звена к первому.

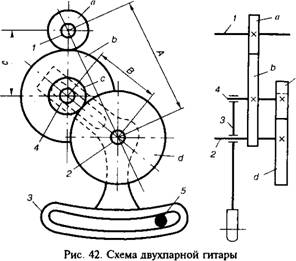
У некоторых металлообрабатывающих станков для наладки кине­матических цепей применяют устройства, называемые «гитары». В ос­новном металлорежущих станках встречаются двухпарные гитары, лишь в редких случаях, когда необходимы особенно малые передаточ­ные отношения или требуется особенно высокая точность подбора этих отношений, используют трехпарную гитару.

На рис. 42 показана схема двухпарной гитары. Расстояние А между ведущим 1 (колеса а) и ведомым 2 (колеса Ь) валами неизменно. На ведомом валу свободно посажен «приклон» 3 гитары. В приклоне имеются радиальный и дуговой пазы. В радиальном пазу закреплена ось 4 колес «Ь» и «с». Перемещая ось вдоль паза, можно менять расстояние В между колесами «с» и «d». Дуговой паз в приклоне позволяет изменять расстояние между колесами «а» и «Ъ» при повороте приклона на валу 2. В требуемом положении приклон закрепляют болтом 5. Чтобы подобранные зубчатые колеса могли переместиться на гитаре и не упирались во втулки валиков зубчатых колес, необходимо соблюдать следующие условия зацепляемости: а = Ъ> с + 15. 20 мм; с+*/>/>+ 15. 22 мм. Необходимо также, чтобы 0,2

Технологическое оборудование машиностроительных произ­водств

КИПиА позволяют следить за тем, что оборудование работает исправно

Контрольно-измерительные приборы необходимы, чтобы измерять ту или иную физическую величину.

СТАНКИ СВЕРЛ ИЛ ЬНО-РАСТОЧНОЙ ГРУППЫ С ЧПУ

Производим и продаем электроприводы ЭТУ, ЭПУ для двигателей постоянного тока, тел./email +38 050 4571330 / rashid@msd.com.ua Назначение, классификация и конструктивные особенности свер­лильных и расточных станков с ЧПУ. Эти станки предназначены …

Повышение эффективности производства

Производим и продаем электроприводы ЭТУ, ЭПУ для двигателей постоянного тока, тел./email +38 050 4571330 / rashid@msd.com.ua Развитие производства во многом определяется техническим про­грессом машиностроения. Увеличение выпуска продукции машино­строения осуществляется за …

Продажа шагающий экскаватор 20/90

Цена договорная
Используются в горнодобывающей промышленности при добыче полезных ископаемых (уголь, сланцы, руды черных и
цветных металлов, золото, сырье для химической промышленности, огнеупоров и др.) открытым способом. Их назначение – вскрышные работы с укладкой породы в выработанное пространство или на борт карьера. Экскаваторы способны
перемещать горную массу на большие расстояния. При разработке пород повышенной прочности требуется частичное или
сплошное рыхление взрыванием.
Вместимость ковша, м3 20
Длина стрелы, м 90
Угол наклона стрелы, град 32
Концевая нагрузка (max.) тс 63
Продолжительность рабочего цикла (грунт первой категории), с 60
Высота выгрузки, м 38,5
Глубина копания, м 42,5
Радиус выгрузки, м 83
Просвет под задней частью платформы, м 1,61
Диаметр опорной базы, м 14,5
Удельное давление на грунт при работе и передвижении, МПа 0,105/0,24
Размеры башмака (длина и ширина), м 13 х 2,5
Рабочая масса, т 1690
Мощность механизма подъема, кВт 2х1120
Мощность механизма поворота, кВт 4х250
Мощность механизма тяги, кВт 2х1120
Мощность механизма хода, кВт 2х400
Мощность сетевого двигателя, кВ 2х1600
Напряжение питающей сети, кВ 6
Более детальную информацию можете получить по телефону (063)0416788

Кинематическая настройка станков

Кинематическую настройку станка производят для обеспечения необходимых перемещений конечных звеньев кинематической цепи и для получения заданных формы и размеров детали, которая в основном сводится к определению параметров органа настройки. Расчетные перемещения звеньев определяют исходя из формы поверхности, которая должна быть образована на заготовке, и вида режущего инструмента.

Затем по кинематической цепи составляют уравнение кинематического баланса, связывающее начальное и конечное перемещения, и находят зависимость параметра органа настройки от расчетных перемещений и постоянных цепи.

Кинематическая цепь

Кинематическая цепь составляется из движущихся сопряженных между собой и передающих друг другу движения деталей. Если началом кинематической цепи является электродвигатель (рис. 3,б), то можно найти связь между начальным и конечным звеньями:

где n, n_шп – частота вращения начального и конечного звеньев; n_p, i_p – КПД и передаточное отношение ременной передачи.

Для удобства вычислений рекомендуется в уравнении кинематического баланса (4.1) выделить постоянные величины структурной формулы и подсчитать их как коэффициент данной кинематической цепи, например:

Это выражение справедливо и для станков, в цепи главного движения которых в качестве органа настройки используется коробка скоростей. Тогда в выражении (4.2) i_v будет передаточным отношением коробки скоростей.

Уравнение кинематического баланса

Уравнение кинематического баланса для цепи главного вращательного движения имеет вид (об/с)

n_c i = n_k, (4.3) , где n_c и n_k– частота вращения соответственно начального и конечного звена, об/с; i- передаточное отношение кинематической цепи.

Уравнение кинематического баланса для цепи, у которой начальное звено имеет вращательное движение, а конечное – прямолинейное, будет (мм/с)

n_c i H = S_c, где Н – ход кинематической пары, преобразующей вращательное движение в прямолинейное, мм/об; s_c – линейное перемещение конечного звена, мм/с.

Величина хода

Величина хода равна перемещению прямолинейно движущегося звена за один оборот вращающегося звена. Для винтовой пары (винт – гайка)

H = k t_в (4.4), где t_в – шаг ходового винта, мм; k – число заходов.

Для реечной передачи.

H = π m z, где m – модуль зацепления, мм; z – число зубьев реечного колеса.

На этом основании уравнение кинематического баланса для секундной подачи (мм/с):

для цепи с винтовой парой

для реечной передачи

Уравнение кинематического баланса для оборотной подачи (мм/об)

где s – линейное перемещение конечного звена, мм/об.

Из уравнений (4.5)-(4.7) определяют передаточное отношение органа настройки. Например, из уравнения (4.2) находят

Это выражение является формулой настройки сменных колес гитары скоростей цепи (см. рис. 3,б).

Выводы

Анализ структурных схем металлорежущих станков позволяет сделать следующие выводы. Кинематическая структура станков зависит от геометрической формы, размеров обрабатываемой поверхности и метода обработки. Чем меньше необходимое число исполнительных формообразующих движений, тем меньше кинематических цепей в структуре станка, тем проще его кинематика и конструкция. Существенное значение имеют и другие факторы, например точность и шероховатость поверхности, динамика резания, условия обслуживания станка, а также экономические факторы.

§ 2. МЕТОДИКА КИНЕМАТИЧЕСКОЙ НАЛАДКИ МЕТАЛЛОРЕЖУЩИХ СТАНКОВ.

Кинематическая наладка станка заключается в согласовании движений исполнительных органов. Методика наладки одинакова для большинства станков и не зависит от их сложности. Для примера рассмотрим наладку токарно-винторезного станка на нарезание резьбы (рис. 1). Чтобы нарезать резьбу на заготовке 1, необходимо сообщить суппорту 3 с резцом 2 продольную подачу вдоль оси заготовки, согласованную с частотой вращения шпинделя 5. Следовательно, нужно рассчитать две кинематические цепи: скоростную (цепь главного движения) и нарезания резьбы. В обоих случаях следует составить уравнения кинематического баланса, связывающие расчетные перемещения конечных элементов кинематической цепи.

Рассмотрим кинематическую цепь главного движения. Шпиндель 5 с заготовкой 1 получает вращение от электродвигателя через ременную передачу и три пары зубчатых колес. Частоту вращения (мин -1 ) шпинделя рассчитывают по формуле n шп =1000v/(πd),

где v – скорость резания, м/мин (выбирается по справочнику режимов резания); d – диаметр заготовки, мм.

Составим уравнение кинематической цепи от электродвигателя к шпинделю при условии, что шпиндель должен вращаться с частотой

где n – частота вращения вала электродвигателя, мин -1 ; 0,985 – коэффициент, учитывающий скольжение ремня.

Это уравнение можно представить и в общем виде:

n шп =ni пост i см , откуда i см = n шп /ni пост ,

где i пост – постоянное передаточное отношение, характеризующее цепь; i см – сменное передаточное отношение механизма наладки.

Рис. 1. Кинематическая схема токарно-винторезного станка

В рассматриваемой кинематической цепи известны все величины, за исключением сменных колес a-b, являющихся механизмом наладки. Подставив численные значения, получим

Так как n шп = 1000v/(πd), определим значение i см =a/b; определим колеса a и b и тем самым произведем наладку цепи главного движения. Затем приступим к наладке кинематической цепи движения подачи (или цепи нарезания резьбы). Резец 2, укрепленный на суппорте 3, получает перемещение от ходового винта 4, который приводится во вращение от шпинделя 5 через пару цилиндрических колес, две пары конических колес и сменные зубчатые колеса с-d, е-f (см. рис. 1).

Составим уравнение кинематического баланса исходя из условия, что за один оборот шпинделя резец переместится вдоль оси заготовки на величину шага Р р нарезаемой резьбы:

В общем виде это уравнение будет выглядеть следующим образом:

где Р р – шаг нарезаемой резьбы; Р х.в – шаг ходового винта.

В рассматриваемой цепи

Подобрав сменные колеса с-d, е-f, произведем наладку цепи движения подачи.

При кинематической наладке станков необходимо:

1) выяснить характер движения рабочих органов и их согласованность;

2) выявить все кинематические цепи станка;

3) составить уравнения кинематических цепей, связывающих попарно рабочие органы станка;

4) определить передаточные отношения механизма наладки и подобрать в соответствии с ними сменные зубчатые колеса или другие элементы наладки.

[spoiler title=”источники:”]

http://www.metalcutting.ru/content/kinematicheskaya-nastroyka-stankov

http://delta-grup.ru/bibliot/35/6.htm

[/spoiler]

Z = P_а * P_б * P_в = 3*2*2=12

6.3.
Числа зубьев шестерен

Подсчитываются числа зубьев
каждой шестерни. Правильность подсчетов контролируется проверкой сумм зубьев
каждой передачи. Сумма зубьев каждой передачи одной и той же группы в изучаемых
приводах с некоррегированными колесами одинакова.

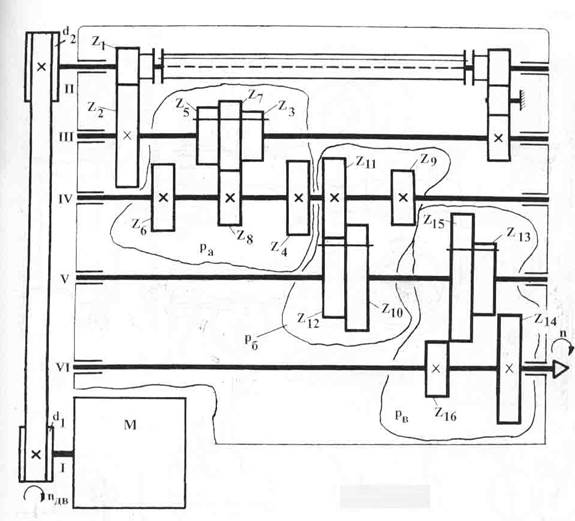
Рис. 1
Кинематическая схема узла:

P_a=3; P_б=2; P_в=2; P_a*P_б*P_в = 3*2*2=12

6.4.
Уравнение кинематического баланса привода

Уравнение кинематического баланса
привода составляются в трех видах, различающихся формой записи передаточных
отношений, входящих в уравнение. Передаточные отношения записываются как i с индексом группы и передачи в
данной группе; как отношения обозначений зубчатых колес; как отношения
конкретных чисел зубьев колес.

Пример записи уравнений для
привода, изображенного на рис. 1:

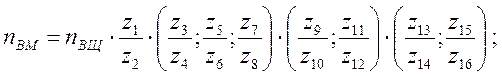
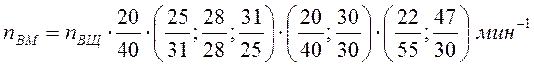
В уравнениях n_ВМ и n_ВЩ – частоты вращения первого и
последнего валов привода.
6.5. Расчет передаточных отношений зубчатых передач

Рассчитываются передаточные
отношения всех передач, одиночных и групповых, причем передаточные отношения
следует записывать в виде   или .

Примеры расчета и записи:

;     ;  ;    ;

            
;          ;     ;

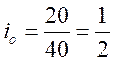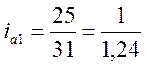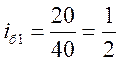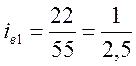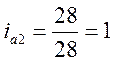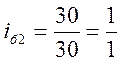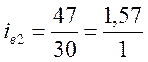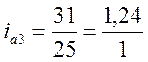
6.6. Установление зависимостей
между последовательными передаточными отношениями передач в группах

Устанавливается относительная
связь между передаточными отношениями всех передач по каждой группе в
отдельности. С этой целью следует разделить второе передаточное отношение
группы на первое, третье на второе и т.д. Частные от деления в конкретной
группе (обозначим их φ с индексом соответствующей группы) должны быть,
во-первых, больше 1, во-вторых, близки по величине между собой, т.е.

в группе P_а          φ = φ_а1 ≈
φ_а2 ≈ …= φ_а.

в группе P_б          φ = φ_б1 ≈
φ_б2 ≈ …= φ_б            и т.д.

При этом φ_а ≠
φ_б ≠…, а меньшее из них (обозначим его φ_мин)
близко по величине к какому-либо стандартному значению знаменателя ряда приведенных
ниже:

φ

1,06

1,12

1,26

1,41

1,58

1,78

2,0

φ_мин следует принять равным
ближайшему стандартному значению.

Пример расчета зависимостей между
соседними передаточными отношениями групп передач а, б, в (рис.1):

      

      

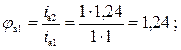
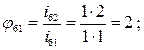
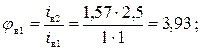
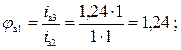
Принимаем φ_мин
=1,26.

6.7. Выявление основной и
множительной групп в приводе

6.7.1. 
Если
привод построен по закону геометрического ряда, т.е. обеспечивает на выходном
валу геометрический ряд частот вращения со знаменателем φ, то
передаточные отношения в каждой группе образуют геометрический ряд со
знаменателем φ^x:

Показатель степени при φ,
называемый характеристикой группы равен: 

x_o = 1 для основной группы, имеющей
P_o передаточных отношений; x₁=P_o для первой множительной группы,
имеющей P₁ передаточных отношений,  x₂=P_o * P₁ для второй множительной группы,
имеющей P₂ передаточных отношений и т.д.

Итак, знаменатель основной группы
φ_o=  φ,

Знаменатель первой множительной
группы φ₁= 
φ_o^Po ,

Знаменатель второй множительной
группы φ₁=  φ_o^{Po* P1}  и т.д.

Вполне очевидно, что φ_o= φ_min и φ_o< φ₁ < φ₂
<… .

Пример проведения кинематического
анализа (для рассматриваемого случая: φ_o= φ_min=1,26; x_o = x_a=1 и группа является основной. P_a=P_o=3 .

В первой множительной группе x₁=P_o =3, тогда φ₁= φ_o ^Po =1,26³=2, что равно φ_б.

Таким образом, группа б является
первой множительной; P_б=P₁=2 и x_б=3.

Во второй множительной группе x₂=P_o*P₁=3*2=6, тогда φ₂= φ_o ^PoP1 =1,26⁶=4, что
примерно равно φ_в =3,93. Таким образом, группа в является
второй множительной: P_в=P₂=2; x_в=6.

Практическое занятие №12 Расчет числа оборотов шпинделя по кинематической схеме токарного станка

Цель: Научиться производить расчет числа оборотов шпинделя по кинематической схеме токарного станка

Краткие теоретические сведения

Уравнение кинематического баланса – это математическое выражение связи движений ведущего и ведомого элементов (начального и конечного звеньев) кинематической цепи станка. В него входят составляющие, характеризующие все элементы цепи от начального до конечного звена.

Начальные звенья кинематической цепи в большинстве случаев имеют вращательное движение, конечные звенья получают как вращательное, так и прямолинейное движение.

Если начальное и конечное звенья оба вращаются, то уравнение кинематического баланса может быть представлено в следующем виде:

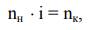
где n_к – частота вращения конечного звена (шпинделя), об/мин;

n_н – частота вращения начального звена (вала электродвигателя), об/мин;

i – передаточное отношение кинематической цепи.

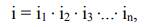
где i₁, i₂, i₃, …, i_n – передаточные отношения отдельных кинематических пар цепи.

Определение передаточных отношений для разного вида передач

Ременная передача (рис. 1) состоит из двух шкивов, один из которых ведущий (D₁, n₁), а второй ведомый (D₂, n₂).

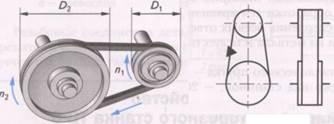
Рисунок 1 – Ременная передача

Отношение диаметра ведущего шкива D₁ к диаметру ведомого шкива D₂ или отношение частот вращения ведомого и ведущего шкивов называется передаточным отношением и обозначается i.

,

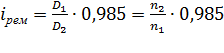где 0,985 – коэффициент, учитывающий проскальзывание ремня

Зубчатая передача (рисунок 2) – это меха­низм, служащий для передачи вращательного движения с одного вала на другой и изменения частоты вращения посредством зубчатых колес.

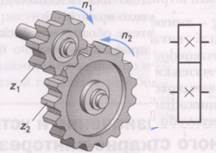
Рисунок 2 – Зубчатая передача

Передаточное отношение будет равно отношению чисел зубьев ведущего колеса к числу зубьев ведомого колеса.

,

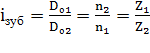Для того, чтобы зубчатые колеса вошли в зацепление расстояние между зубьями должно быть одинаково, это расстояние называется шаг зацепления.

Задание:

1. Написать определение уравнения кинематического баланса и формулу его определения, если начальное и конечное звенья имеют вращательные движения.

2. Записать формулы для определения передаточных отношений ременной и зубчатой передач

3. Составить уравнение кинематического баланса по кинематической схеме токарного станка для своего варианта (рисунок 3).

4. Определить сколько скоростей имеет шпиндель.

5. Рассчитать число оборотов шпинделя по кинематической схеме токарного станка. Выбрать максимальную и минимальную скорости.

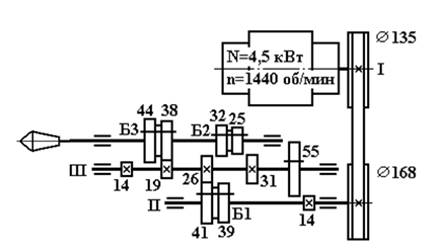
Вариант 1

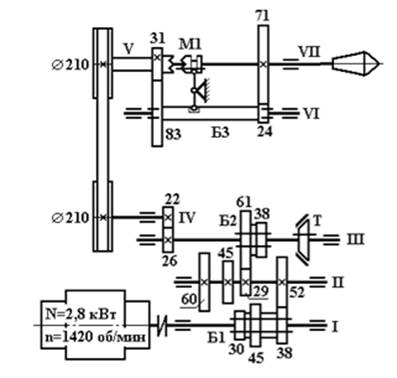
Вариант 2

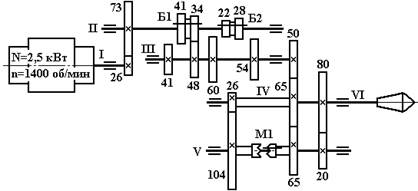
Вариант 3

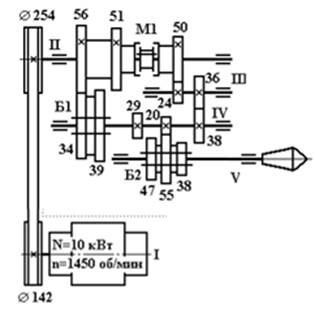
                                                                       Вариант 4

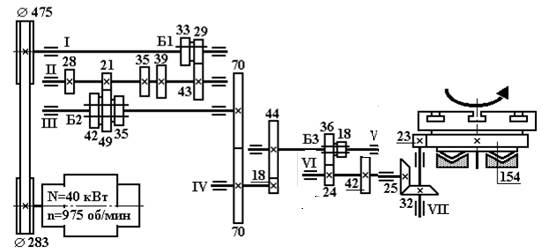
Вариант 5

Рисунок 1 – Исходные данные