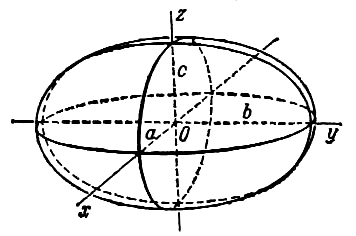
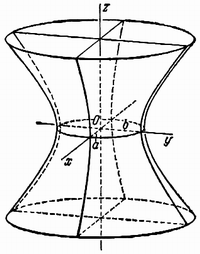
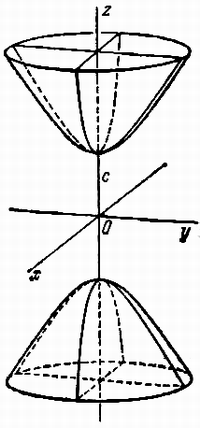
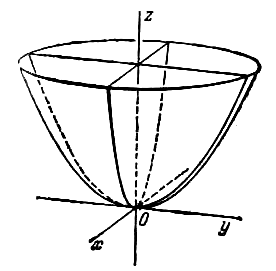
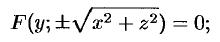Как составить уравнение конуса - Сайт, где вы сможете решить свои вопросы

Эллипсоидом
называется поверхность, которая в некоторой
системе декартовых прямоугольных координат
определяется уравнением

(1).

Уравнение (1) называется каноническим
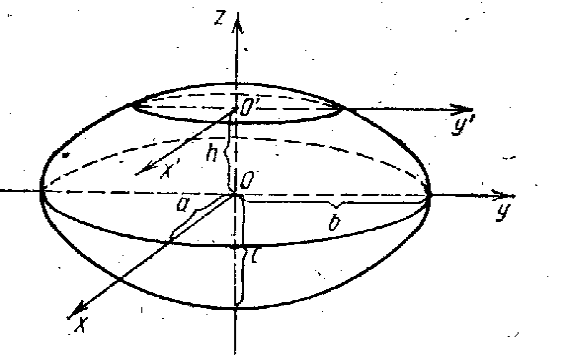
уравнением эллипсоида. Величины a,
b, c суть полуоси эллипсоида (рис. 1). Если все
они различны, эллипсоид называется трехосным; в
случае, когда какие-нибудь две из них одинаковы,
эллипсоид называется вытянутым, при a=b>c – сжатым. В случае, когда a=b=c, эллипсоид представляет
собой сферу.

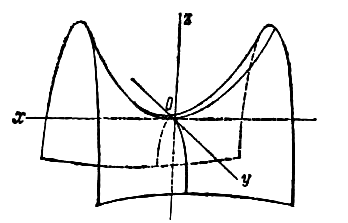
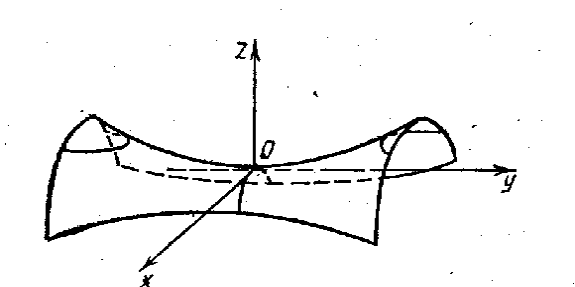
Гиперболоидами называются
поверхности, которые в некоторой системе
декартовых прямоугольных координат
определяются уравнениями

, (2)

. (3)

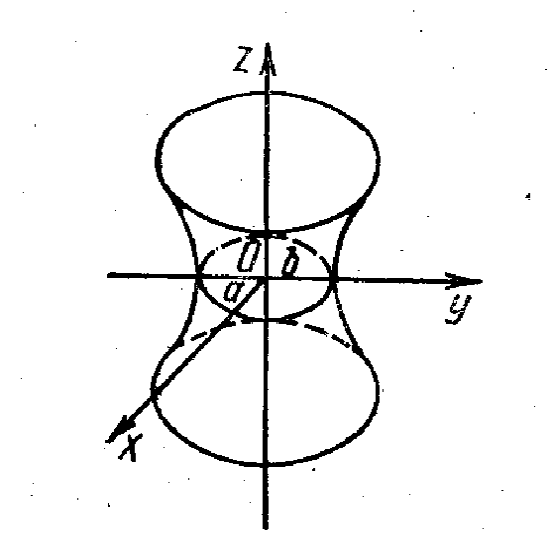
Гиперболоид, определяемый уравнением
(2), называется однополостным (рис. 2); гиперболоид,
определяемый уравнением (3), – двуполостным (рис. 3);
уравнения (2) и (3) называются каноническими
уравнениями соответствующих гиперболоидов.
Величины a, b, c называются
полуосями гиперболоида. В случае однополостного
гиперболоида, заданного уравнением (2), только
первые из них (а и b) показаны
на рис. 2. В случае двуполостного гиперболоида,
заданного уравнением (3), одна из них (именно, с)
показана на рис. 3. Гиперболоиды, определяемые
уравнениями (2) и (3), при a=b
являются поверхностями вращения.

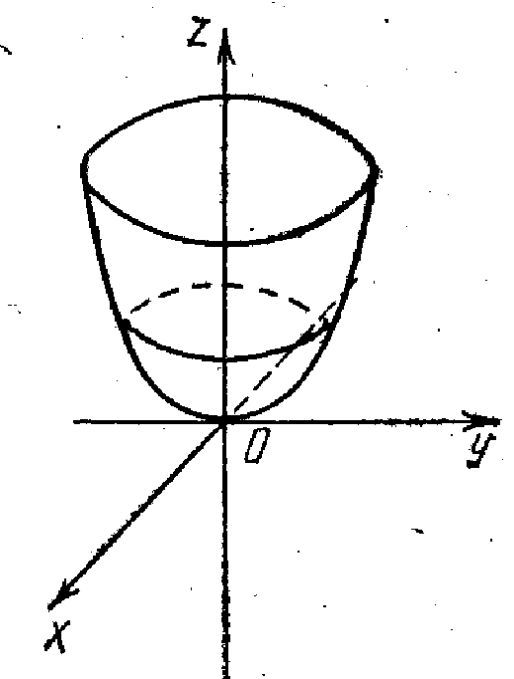
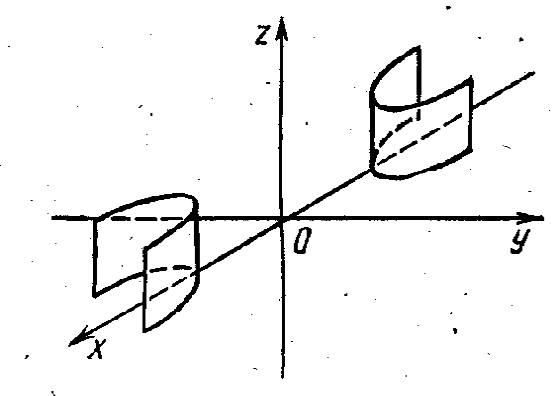
Параболоидами называются поверхности,
которые в некоторой системе декартовых
прямоугольных координат определяются
уравнениями

, (4)

, (5)

где p и q – положительные числа,
называемые параметрами параболоида. Параболоид,
определяемый уравнением (4), называется
эллиптическим (рис. 4); параболоид, определяемый
уравнением (5), – гиперболическим (рис. 5). Уравнения
(4) и (5) называют каноническими уравнениями
соответствующих параболоидов. В случае, когда p=q, параболоид, определяемый
уравнением (4), является поверхностью вращения
(вокруг Oz).

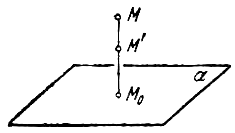
Рассмотрим теперь преобразование
пространства, которое называется равномерным
сжатием (или равномерным растяжением).

Выберем какую-нибудь плоскость;
обозначим ее буквой
. Зададим, кроме
того, некоторое положительное число q. Пусть М – произвольная точка
пространства, не лежащая на плоскости
,
– основание
перпендикуляра, опущенного на плоскость

из точки М. Переместим точку М по прямой
в
новое положение
так, чтобы имело
место равенство

и чтобы после перемещения точка
осталась с той же стороны от плоскости
,
где она была первоначально (рис. 6). Точно так же мы
поступим со всеми точками пространства, не
лежащими на плоскости
; точки, которые
расположены на плоскости
, оставим на своих
местах. Таким образом, все точки пространства, за
исключением тех, что лежат на плоскости
,
переместятся; при этом расстояние от каждой
точки до плоскости
изменится в
некоторое определенное число раз, общее для всех
точек. Описываемое сейчас перемещение точек
пространства называется его равномерным сжатием
к плоскости
; число q
носит название коэффициента сжатия.

Пусть дана некоторая поверхность F; при равномерном сжатии
пространства точки, которые ее составляют,
переместятся и в новых положениях сотавят
поверхность F’. Будем
говорить, что поверхность F’
получено из F в результате
равномерного сжатия пространства. Оказывается,
что многие поверхности второго порядка (все,
кроме гиперболического параболоида) можно
получить в результате равномерного сжатия из
поверхностей вращения).

ПРИМЕР. Доказать, что произвольный
трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных
равномерных сжатий пространства к координатным
плоскостям: к плоскости Oxy с
коэффициентом сжатия
и к плоскости Oxz с коэффициентом сжатия
.

ДОКАЗАТЕЛЬСТВО. Пусть производится
равномерное сжатие пространства к плоскости Oxy с коэффициентом
и
пусть
– точка, в которую переходит при этом
точка
. Выразим координаты x’,
y’, z’ точки М’ через координаты x, y, z точки М. Так как прямая MM’ перпендикулярна к плоскости Oxy, то x’=x, y’=y.
С другой стороны, так как расстояние от точки М’
до плоскости Oxy равно
расстоянию от точки М до этой плоскости,
умноженному на число
, то
.

Таким образом, мы получаем искомые
выражения:

,
,
(6)

или

,
,
(7)

Предположим, что M(x; y; z)
– произвольная точка сферы

Заменим здесь x, y, z
их выражениями (7); получим

откуда

Следовательно, точка M’(x’;
y’; z’) лежит на эллипсоиде вращения.
Аналогично, мы должны осуществить сжатие
пространства к плоскости Oxz
по формулам

,
,
;

тогда получим трехосный эллипсоид и
именно тот, уравнение которого дано в условии
задачи.

Отметим еще, что однополостный
гиперболоид и гиперболический параболоид суть
линейчатые поверхности, то есть они состоят из
прямых; эти прямые называются прямолинейными
образующими указанных поверхностей.

Однополостный гиперболоид

имеет две системы прямолинейных
образующих, которые определяются уравнениями:

,
;

,
,

где
и
– некоторые
числа, не равные одновременно нулю.
Гиперболический параболоид

также имеет две системы прямолинейных
образующих, которые определяются уравнениями

,
;

,
.

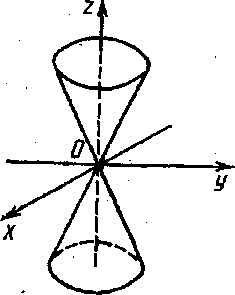
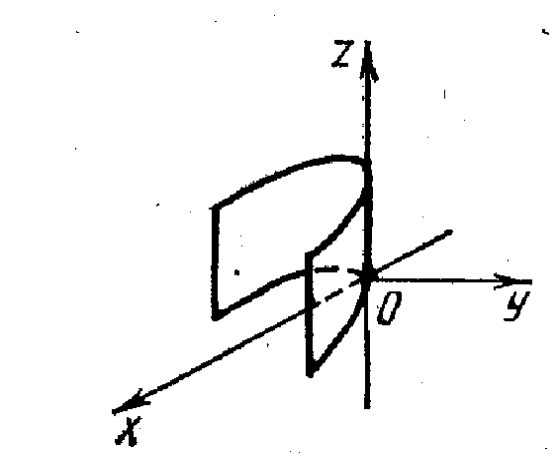
Конической поверхностью, или конусом,
называется поверхность, которая описывается
движущейся прямой (образующей) при условии, что
эта прямая проходит через постоянную точку S и пересекает некоторую
определенную линию L. Точка S называется вершиной конуса;
линия L – направляющей.

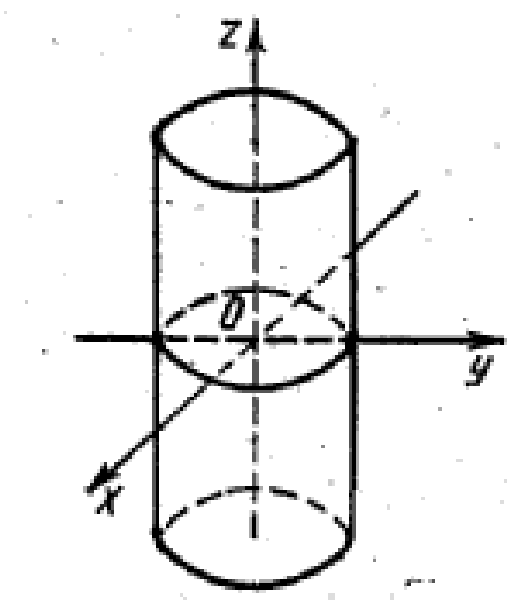
Цилиндрической поверхностью, или
цилиндром, называется поверхность, которая
описывается движущейся прямой (образующей) при
услвоии, что эта прямая имеет постоянное
направление и пересекает некоторую определенную
линию L (направляющую).

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 ноября 2022 года; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. Конус (значения).

Ко́нус (через нем. Konus и лат. cōnus, от др.-греч. κώνος^[1] — «сосновая шишка»^[2]) — поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса)^[3].

Если направляющая конуса — замкнутая кривая, то коническая поверхность служит границей пространственного тела, которое также называют «конусом» (см. рисунок), а внутренность этой кривой называют «основанием конуса», если основание конуса представляет собой многоугольник, такой конус является пирамидой.

Иногда вместо лучей рассматривают прямые, тогда получается двойной конус, состоящий из двух симметричных относительно вершины частей.

Конус и связанные с ним конические сечения играют большую роль в математике, астрономии и других науках.

Связанные определения[править | править код]

Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
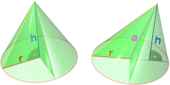
Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
Конусность — соотношение высоты и диаметра основания конуса.

Типы конусов[править | править код]

Прямой круговой конус
Прямой и косой круговые конусы с равным основанием и высотой: их объём одинаков
Усечённый прямой круговой конус

Прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
Косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
Круговой конус — конус, основание которого является кругом.
Конус вращения, или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.
Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
Равносторонний конус — конус вращения, образующая которого равна диаметру основания ^[4].

Свойства[править | править код]

Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.

где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
Телесный угол при вершине прямого кругового конуса равен

где α — угол раствора конуса.

Площадь боковой поверхности прямого кругового конуса равна

а в общем случае

${displaystyle S={frac {tl}{2}},}$

где R — радиус основания, ${displaystyle t={sqrt {R^{2}+H^{2}}}}$

— длина образующей,

— длина границы основания.

Полная площадь поверхности (то есть сумма площадей боковой поверхности и основания) равна

для прямого кругового конуса и

${displaystyle S={frac {tl}{2}}+S_{text{ос}},}$

для произвольного, где ${displaystyle S_{text{ос}}}$

— площадь основания.

Объём кругового (не обязательно прямого) конуса равен

$V={1 over 3}pi R^{2}H.$

Для усечённого кругового конуса (не обязательно прямого) объём равен:

${displaystyle V={1 over 3}pi H(R^{2}+Rr+r^{2}),}$

где

— радиусы соответственно нижнего и верхнего оснований,

— высота от плоскости нижнего основания,до верхнего основания.

Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:

${displaystyle V={1 over 3}(H_{2}S_{2}-H_{1}S_{1}),}$

где $S_{1}$

и $S_{2}$

— площади соответственно верхнего (ближнего к вершине) и нижнего оснований, H_1

— расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).

Уравнение прямого кругового конуса[править | править код]

Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:

В сферической системе координат с координатами (r, φ, θ):

В цилиндрической системе координат с координатами (r, φ, z):

или

В декартовой системе координат с координатами (x, y, z):

$z=pm {sqrt {x^{2}+y^{2}}}cdot operatorname {ctg}Theta .$

Это уравнение в каноническом виде записывается как

${frac {x^{2}}{a^{2}}}+{frac {y^{2}}{a^{2}}}-{frac {z^{2}}{c^{2}}}=0,$

где константы a, с определяются пропорцией

Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид

${frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}-{frac {z^{2}}{c^{2}}}=0,$

причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением

где функция

является однородной, то есть удовлетворяющей условию $f(alpha x,alpha y,alpha z)=alpha ^{n}f(x,y,z)$

для любого действительного числа α.

Развёртка[править | править код]

Развёртка прямого кругового конуса

Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.

В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора varphi в развёртке боковой поверхности конуса определяется по формуле:

φ = 360°·(r/l).

Вариации и обобщения[править | править код]

См. также[править | править код]

Коническая поверхность
Коническое сечение
Конус (топология)
Световой конус

Примечания[править | править код]

↑ Этимологический словарь русского языка Макса Фасмера
↑ «I κῶνος»
↑ Математический энциклопедический словарь, 1988, с. 288.
↑ Математический справочник. Дата обращения: 22 мая 2020. Архивировано 2 декабря 2020 года.

Литература[править | править код]

Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд. — М.: Наука, 1970. — 720 с.
Конус // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 288. — 847 с.

Источник

Конусы: определение, сечения, построение

Конусом называется поверхность, определяемая в некоторой прямоугольной системе координат Oxyz каноническим уравнением

$frac{x^2}{a^2}+frac{y^2}{b^2}-frac{z^2}{c^2}=0,$

(4.50)

где a,b,c — положительные параметры, характеризующие конус, причем ageqslant b .

Начало координат называется центром конуса (рис.4.44,а).

Конус является конической фигурой, поскольку вместе с любой своей точкой M(x,y,z) уравнению (4.50) удовлетворяют также все точки (tx,,ty,,tz) при tgeqslant0 луча . Точка является вершиной конуса (4.50), а любой луч , принадлежащий конусу, является его образующей.

Плоские сечения конуса

Сечения конуса координатными плоскостями Oxz,,Oyz представляют собой пары пересекающихся прямых, удовлетворяющих в этих плоскостях уравнениям $frac{x^2}{a^2}-frac{z^2}{c^2}=0$ (при y=0 ) или $frac{y^2}{b^2}-frac{z^2}{c^2}=0$ (при x=0 ) соответственно.

Рассмотрим теперь сечение конуса плоскостями, параллельными плоскости Oxy . Подставляя z=h , где — произвольная постоянная (параметр), в уравнение (4.50), получаем

$frac{x^2}{a^2}+frac{y^2}{b^2}-frac{z^2}{c^2}=0 quad Leftrightarrow quad frac{x^2}{a^2}+frac{y^2}{b^2}=frac{z^2}{c^2},.$

При h=0 этому уравнению удовлетворяет одна вещественная точка — начало координат. При любом отличном от нуля значении параметра уравнение определяет эллипс $frac{x^2}{(a')^2}+frac{y^2}{(b')^2}=1$ с полуосями $a'=frac{a}{c}|h|,$ $b'=frac{b}{c}|h|$ . Следовательно, сечение конуса плоскостью z=h представляет с собой эллипс, центр которого лежит на оси аппликат, а вершины принадлежат координатным плоскостям Oxz и Oyz .

Таким образом, конус можно представить как поверхность, образованную эллипсами, центры которых лежат на оси аппликат, а вершины принадлежат координатным плоскостям Oxz и Oyz (см. рис.4.44,а).

Конус и плоские сечения, Асимптотический конус

Круговой конус

При a=b все сечения конуса плоскостями z=hne0 становятся окружностями. Такой конус является фигурой вращения и называется прямым круговым конусом. Он может быть получен в результате вращения, например, прямой $z=frac{c}{b}y$ (образующей) вокруг оси аппликат (рис.4.44,б).

Замечания 4.10.

1. Конус является линейчатой поверхностью, поскольку может быть получен при помощи перемещения прямой.

2. Конус, образованный асимптотами гипербол, получающихся при пересечении гиперболоида плоскостями, проходящими через ось , называется асимптотическим конусом этого гиперболоида. На рис.4.44,в изображен асимптотический конус для однополостного и двуполостного гиперболоидов.

3. Конус (4.50) может быть получен из прямого кругового конуса x^2+y^2-z^2=0 (у которого a=b=c=1 ) в результате двух сжатий (растяжений) к координатным плоскостям Oxz и Oyz .

4. Начало канонической системы координат является центром симметрии конуса, координатные оси — осями симметрии конуса, координатные плоскости — плоскостями симметрии конуса.

В самом деле, если точка M(x,y,z) принадлежит конусу, то точки с координатами (pm x,pm y,pm z) при любом выборе знаков также принадлежат конусу, поскольку их координаты удовлетворяют уравнению (4.50).

5. Рассмотрим сечение прямого кругового конуса x^2+y^2-z^2=0 плоскостями, не проходящими через его вершину, например, плоскостями z=ky+1 , где — произвольная постоянная (параметр) — угловой коэффициент прямой z=ky+1 в плоскости Oyz . Заметим, что образующие рассматриваемого конуса в плоскости Oyz описываются уравнением z=ky с угловым коэффициентом k=pm1 . Подставляя z=ky+1 в уравнение конуса, получаем

x^2+y^2-(ky+1)^2=0 quad Leftrightarrow quad x^2+(1-k^2)cdot y^2-2cdot kcdot y-1=0.

Это уравнение проекции на координатную плоскость Oxy линии пересечения плоскости с конусом. Вычисляем инварианты

$delta= begin{vmatrix}1&0\0&1-k^2end{vmatrix}=1-k^2; quad Delta= begin{vmatrix}1&0&0\0&1-k^2&-k\0&-k&-1end{vmatrix}=-1; quad tau=2-k^2.$

При |k|<1 имеем delta>0,~Deltane0,~taucdotDelta=k^2-2<0 . По таблице 3.2 определяем, что рассматриваемое сечение, которое пересекает все образующие прямого кругового конуса, является эллипсом. При |k|>1 имеем delta<0,~Deltane0 . По таблице 3.2 определяем, что рассматриваемое сечение, которое параллельно двум образующим кругового конуса, является гиперболой. При k=pm1 имеем delta=0,~Deltane0 . По таблице 3.2 определяем, что рассматриваемое сечение, которое параллельно одной образующей кругового конуса, является параболой. Поскольку при аффинных преобразованиях тип линий не изменяется, такой же вывод можно сделать для произвольного конуса (4.50):

– сечение конуса плоскостью, пересекающей все его образующие, является эллипсом (рис.4.45,а);

– сечение конуса плоскостью, параллельной двум его образующим, является гиперболой (рис.4.45,б);

– сечение конуса плоскостью, параллельной одной его образующей, является параболой (рис.4.45,в).

6. Конические сечения могут быть взяты в качестве эквивалентных определений эллипса, гиперболы, параболы.

Конические сечения

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Поверхности вращения. Конические поверхности

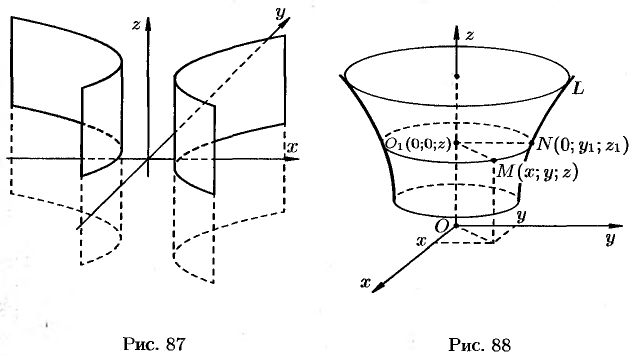
Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая кривая 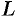лежит в плоскости . Уравнения этой кривой запишутся в виде

Найдем уравнение поверхности, образованной вращением кривой вокруг оси .

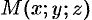
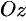
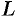
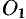
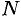
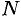
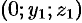
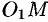
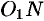
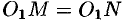
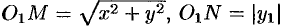
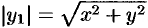
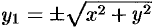
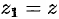
Возьмем на поверхности произвольную точку (см. рис. 88). Проведем через точку плоскость, перпендикулярную оси , и обозначим точки пересечения ее с осью и кривой соответственно через и . Обозначим координаты точки через . Отрезки и являются радиусами одной и той же окружности. Поэтому . Но . Следовательно, или . Кроме того, очевидно, .

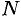
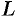
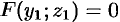
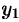
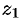
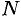
Так как точка лежит на кривой , то ее координаты удовлетворяют уравнению (12.22). Стало быть, . Исключая вспомогательные координаты и точки , приходим к уравнению

Уравнение (12.23) — искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точки этой поверхности и не удовлетворяют координаты точек, не лежащих на поверхности вращения.

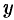
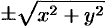
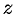
Как видно, уравнение (12.23) получается из (12.22) простой заменой на , координата сохраняется.

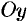
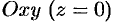
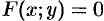
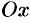
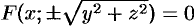
Понятно, что если кривая (12.22) вращается вокруг оси , то уравнение поверхности вращения имеет вид

если кривая лежит в плоскости и ее уравнение , то уравнение поверхности вращения, образованной вращением кривой вокруг оси , есть .

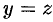
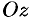
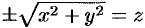
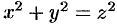
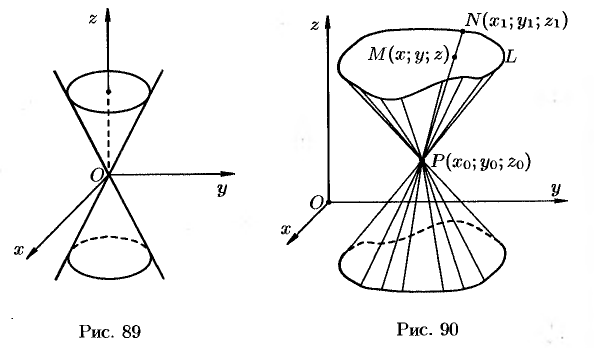
Так, например, вращая прямую вокруг оси (см. рис. 89), получим поверхность вращения (ее уравнение или ). Она называется конусом второго порядка.

Поверхность, образованная прямыми линиями, проходящими через данную точку и пересекающими данную плоскую линию (не проходящую через ), называется конической поверхностью или конусом. При этом линия называется направляющей конуса, точка — ее вершиной, а прямая, описывающая поверхность, называется образующей.

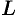
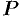
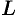
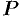
Пусть направляющая 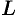задана уравнениями

а точка 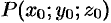— вершина конуса. Найдем уравнение конуса.

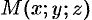
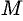
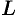
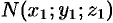
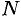
Возьмем на поверхности конуса произвольную точку (см. рис. 90). Образующая, проходящая через точки и , пересечет направляющую в некоторой точке . Координаты точки удовлетворяют уравнениям (12.24) направляющей:

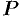
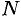
Канонические уравнения образующих, проходящих через точки и , имеют вид

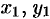
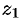
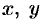
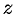
Исключая и из уравнений (12.25) и (12.26), получим уравнение конической поверхности, связывающее текущие координаты и .

Пример №12.3.

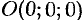
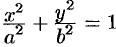
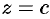
Составить уравнение конуса с вершиной в точке , если направляющей служит эллипс , лежащий в плоскости .

Решение:

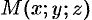
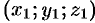
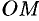
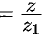
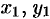
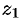
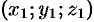
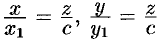
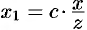
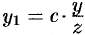
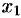
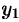
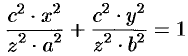
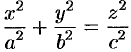
Пусть — любая точка конуса. Канонические уравнения образующих, проходящих через точки (0; 0; 0) и точку пересечения образующей с эллипсом будут . Исключим и из этих уравнений и уравнения

(точка лежит на эллипсе), . Имеем: . Отсюда и . Подставляя значения и в уравнение эллипса (12.27), получим

или .

Это и есть искомое уравнение конуса.

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Источник

В декартовой
системе координат общее уравнение
поверхности второго порядка имеет
вид

(28)

где
коэффициенты А, В, С … L

R
и А, В, С, D,
E,
F
не равны нулю одновремен-но.

Уравнение
(28)
называется
общим уравнением поверхности второго
порядка.

В некоторых случаях
это уравнение определяет так называемые
вырожденные поверхности (пустое
множество, точку, прямую, плоскость или
пару плоскостей). Уравнение невырожденной
поверхности преобразованием системы
координат можно привести к одному из
перечисленных ниже видов, называемых
каноническими.

1.
Эллипсоид. Каноническое уравнение
эллипсоида имеет вид

(29)

Числа
a,
b,
c
называются полуосями эллипсоида. Если

– эллипсоид называют трехосным, если
две полуоси равны, эллипсоид называют
эллипсои-дом вращения, так как этот
эллипсоид может быть получен вращением
эллипса
вокруг одной из его осей. Если a
= b
= c,
уравнение (29) определяет сферу.

Рис.
22

Гиперболоиды.
Каноническое
уравнение гиперболоида имеет вид

Однополостный
гиперболоид
(рис.23) определяется уравнением

Рис.
23
Рис. 24

Двуполостный
гиперболоид
(рис. 24) определяется уравнением

.
Поверхности, которые задаются уравнениями

также
являются однополостными гиперболоидами,
только иначе расположены относительно
системы координат.

3. Конус второго порядка (рис. 25). Каноническое уравнение конуса имеет вид

Поверхности, заданные уравнениями

,
также определяют конические поверхности,
только иначе расположены относительно
системы координат.

Рис.
25

4.
Параболоиды. Каноническое
уравнение параболоида имеет вид

Эллиптический
параболоид (рис. 26) определяется уравнением

,
а гиперболический (рис. 27) – уравнением

Рис.
26 Рис. 27

Поверхности, заданные в декартовой системе координат уравнением

или

также
определяют эллиптический и
гиперболический параболоиды, иначе
расположенные относительно системы
координат.

5.
Цилиндры второго порядка. Уравнения
эллиптического (рис. 28), гиперболического
(рис. 29) и параболического (рис. 30) цилиндров
имеют вид

соответственно.

Рис. 28
Рис. 29
Рис. 30

Поверхности,
которые задаются уравнениями

или

, а также
,
являются иначе располо-женными
относительно системы координат
цилиндрами.

Общие
методы приведения уравнения поверхности
второго порядка используют теорию
квадратичных форм и здесь на рассматриваются.
Рассмотрим только слу-чай, когда
коэффициенты D,
E
и F
( при xy,
yz,
xz
соответственно) равны нулю. В этом
случае уравнения (28) с помощью параллельного
переноса осей координат легко приводятся
к каноническому виду.

Пример
1. Установить,
какая поверхность задана уравнением

4х²
+ у²
– z²
– 24х + 4у + 2z
+ 35 = 0.

Решение.
4(x²
– 6х)+ (у²
+ 4у) – (z²
+ 2z)=
-35.

Выражения в скобках
дополняем до полных квадратов

Переносим
параллельно систему координат, приняв
за новый центр точку

О(3,–2,–1):
x
= x’
+ 3; y’
= y
– 2; z
= z’–
l.

В
новой системе координат данное уравнение
имеет вид

Это однополостный
гиперболоид.

Пример
2.
Составить каноническое уравнение
эллипсоида, если оси совпадают с осями
координат, который проходит через точку
М(2; 0; 1) и пересекает

плоскость
XOY
по эллипсу
.

Решение.
Так
как оси эллипсоида совпадают с осями
координат, его уравнение будет иметь
вид
.
Из условия пересечения эллипсоидом
плоскости ХОY
по эллипсу
,
следует система
,
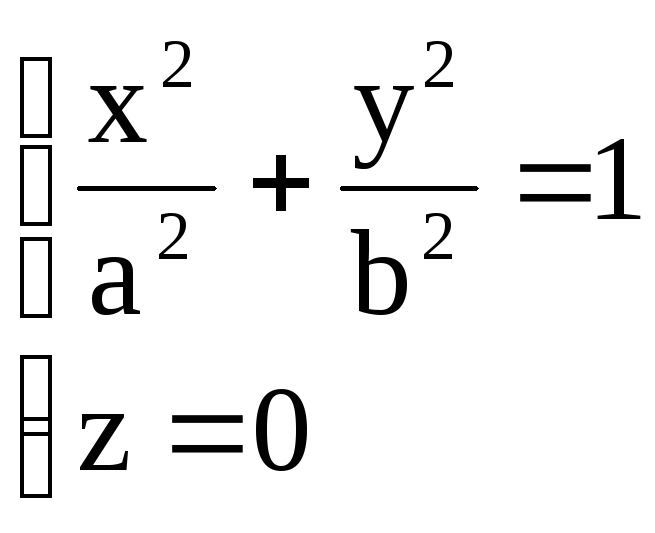
откуда а²
= 8; b²
= 1. Далее следует, что
,
так как эллипсоид по условию проходит
через точку М(2; 0; 1).