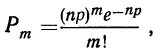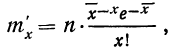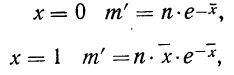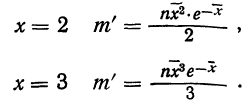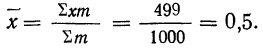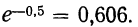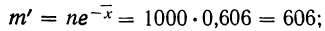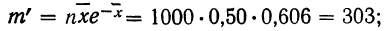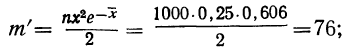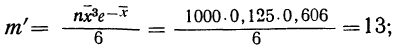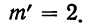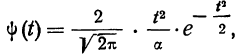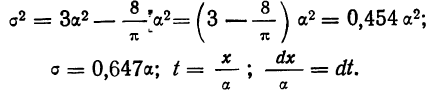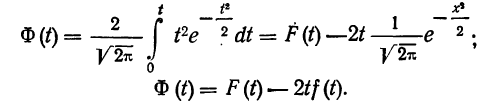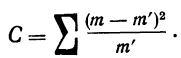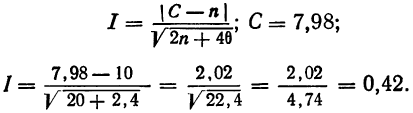В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
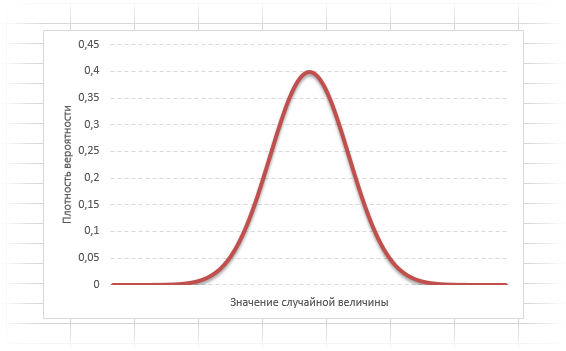
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
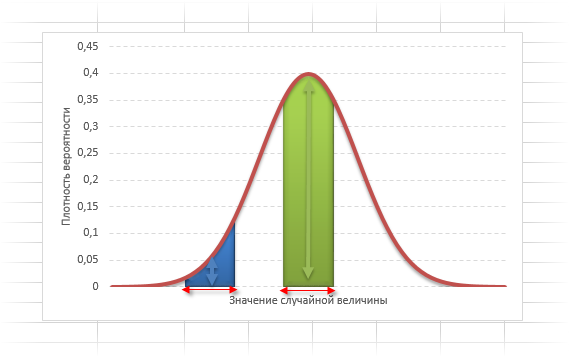
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
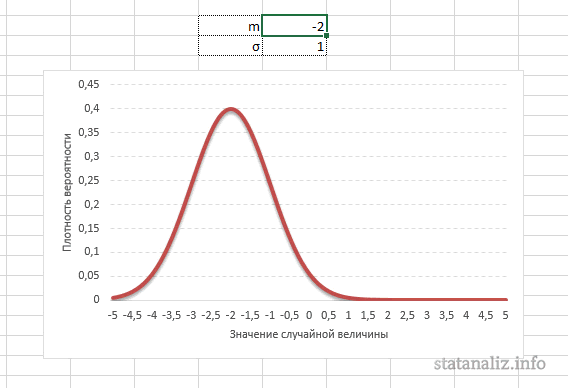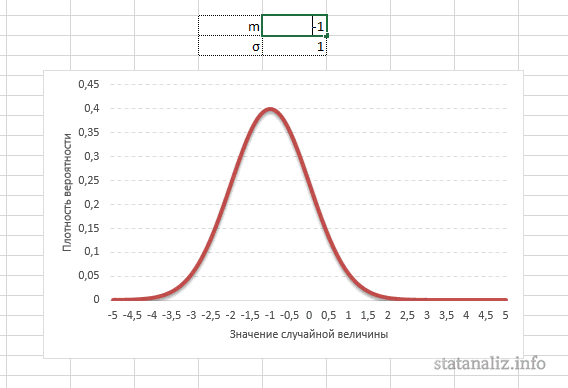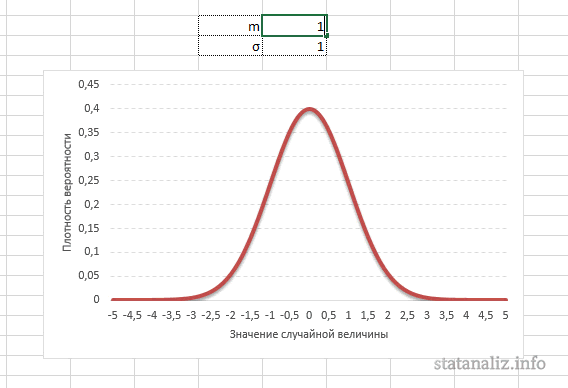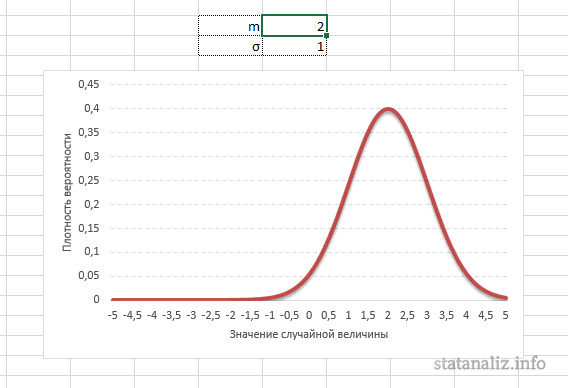
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
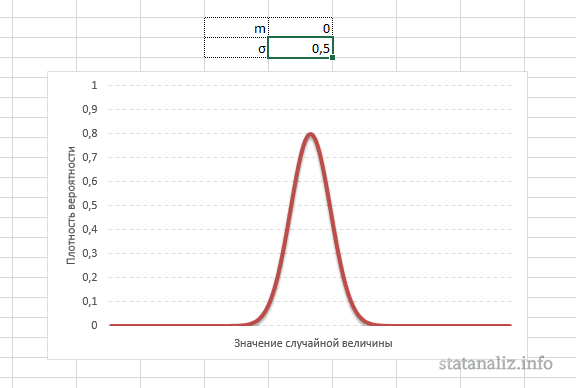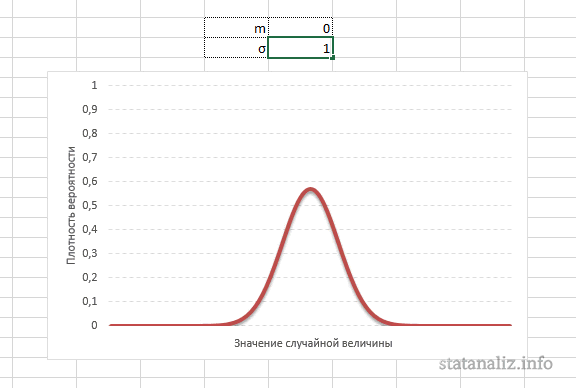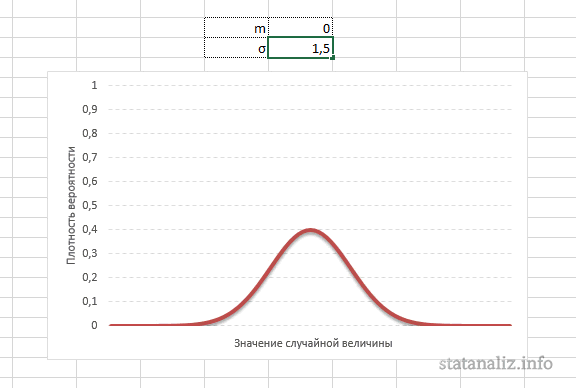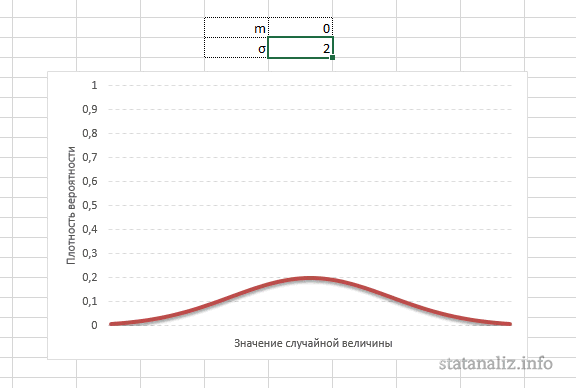
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X < b) = Ф(b) – Ф(a)
Стандартное нормальное распределение
Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).
Любое нормальное распределение легко превращается в стандартное путем нормирования:
где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.
Для выборочных данных берутся оценки:
Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.
В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:
Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:
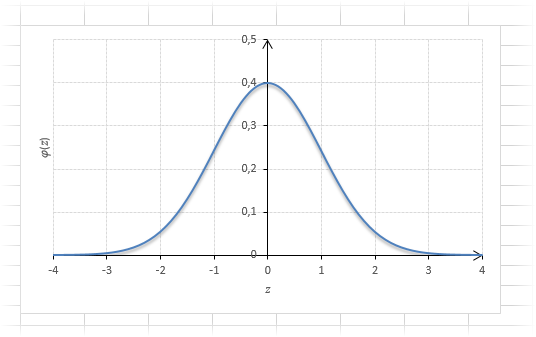
График плотности:
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e0=1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
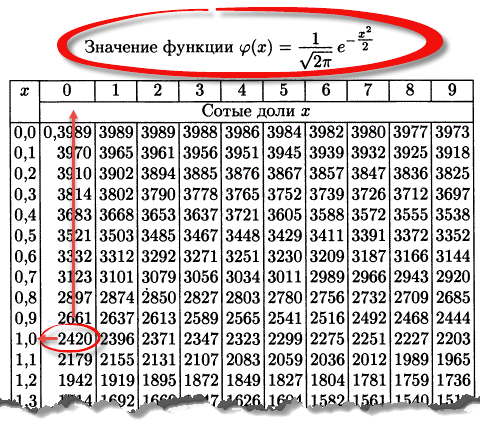
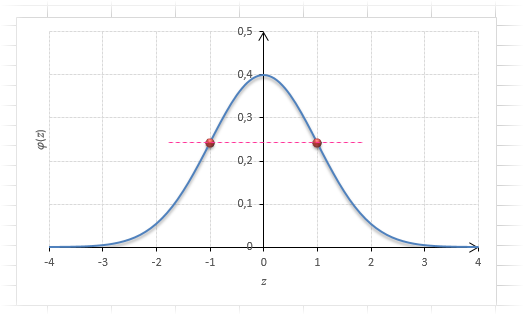
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
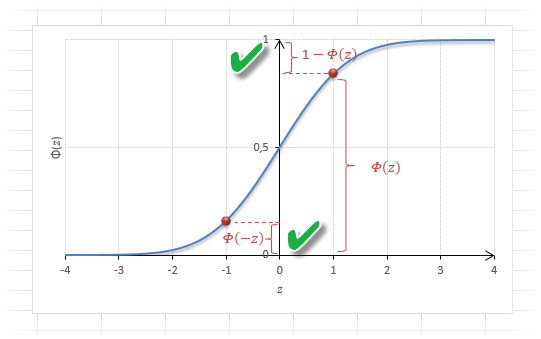
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
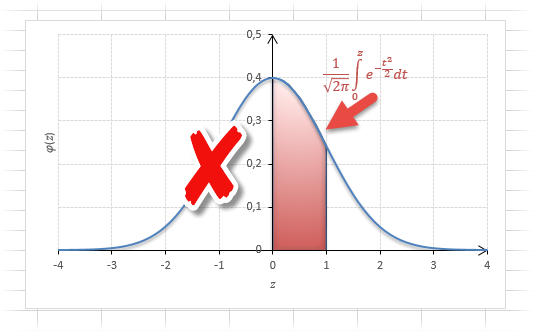
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
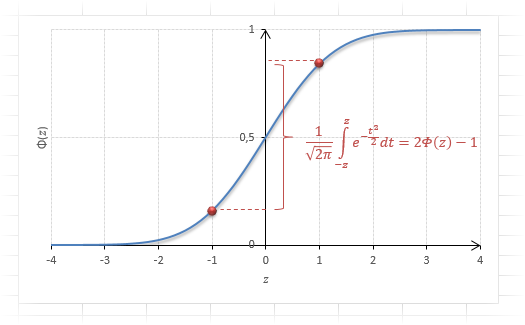
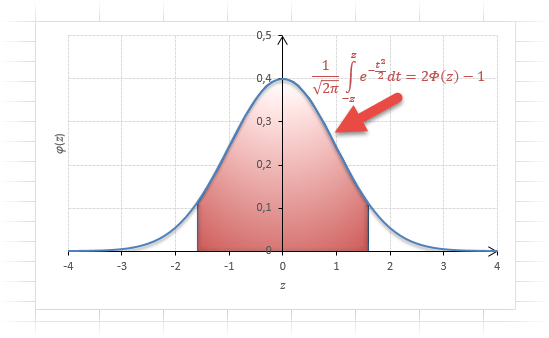
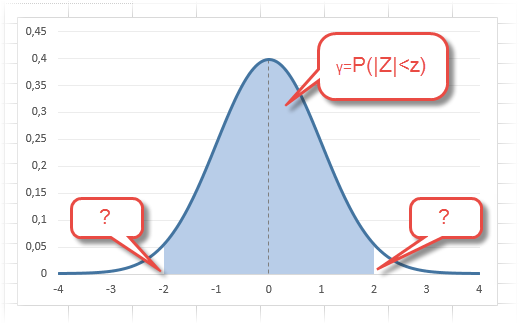
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Рисунок ниже.
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
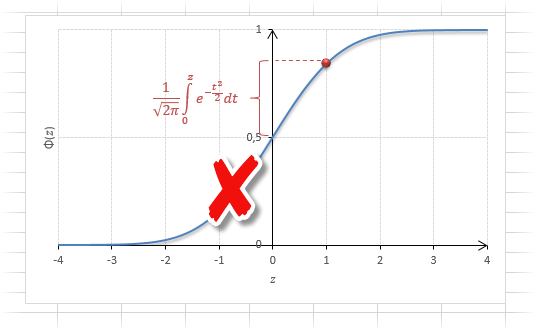
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
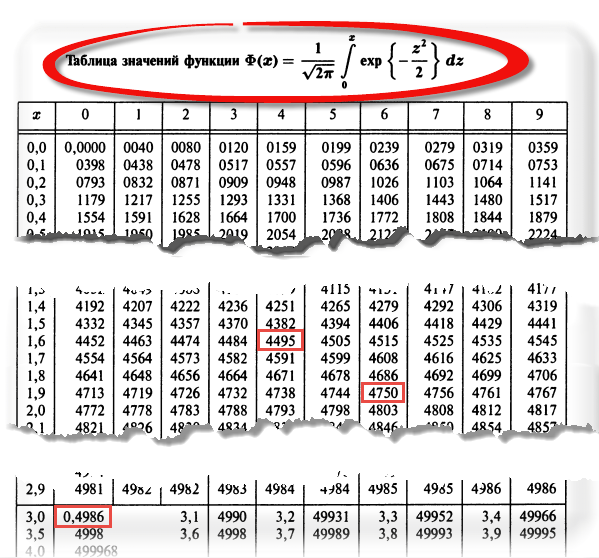
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
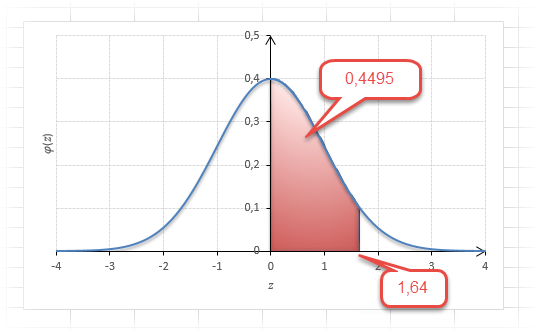
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
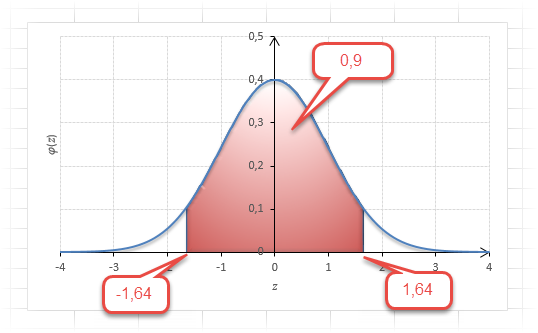
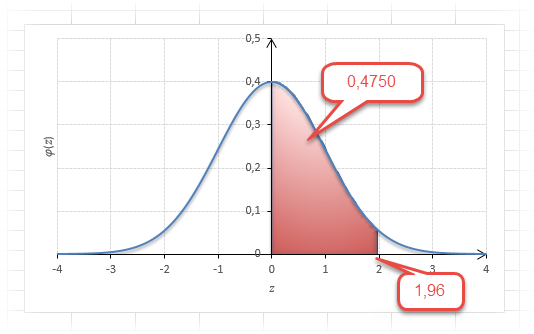
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
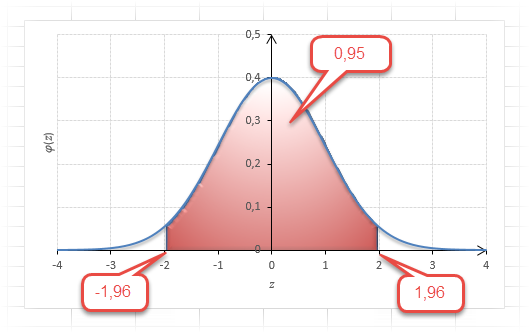
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
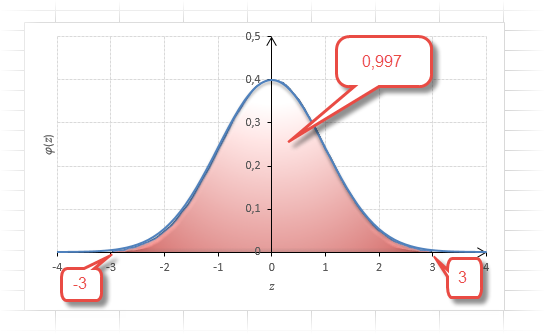
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).
=НОРМ.СТ.РАСП(z;интегральная)
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).
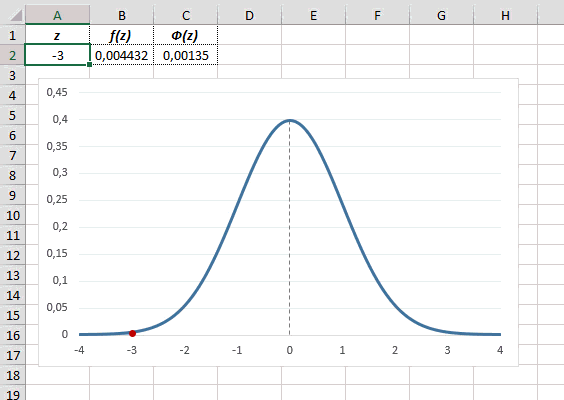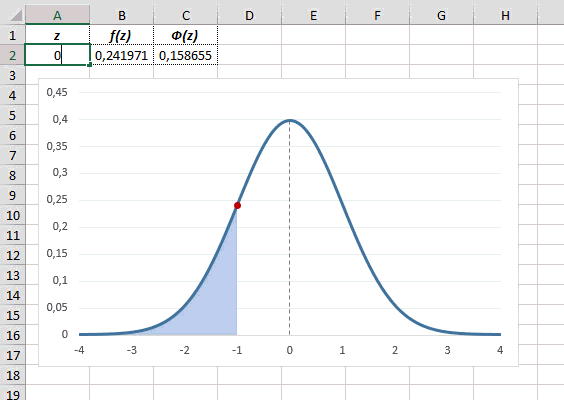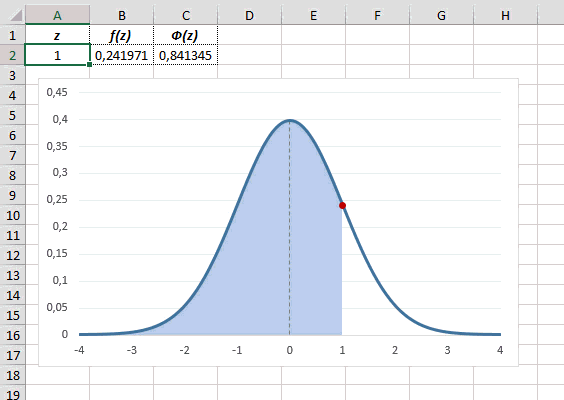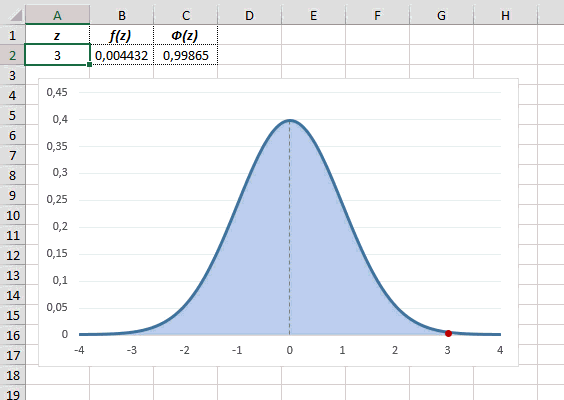
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).
Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.
Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.
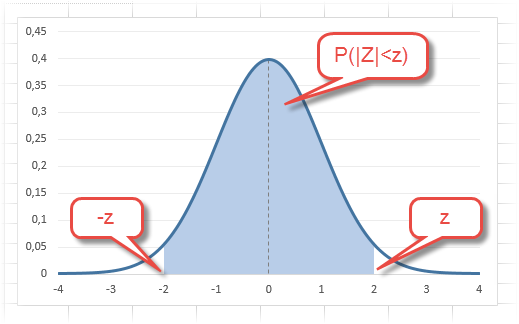
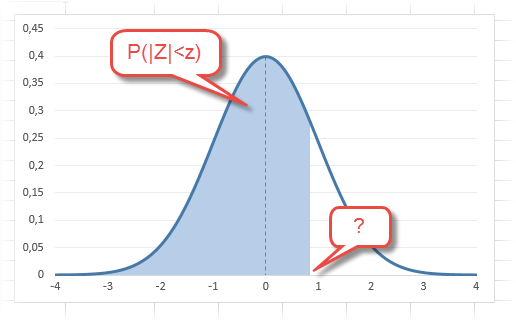
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).
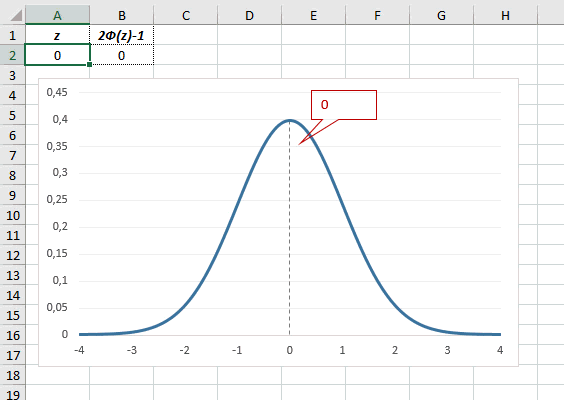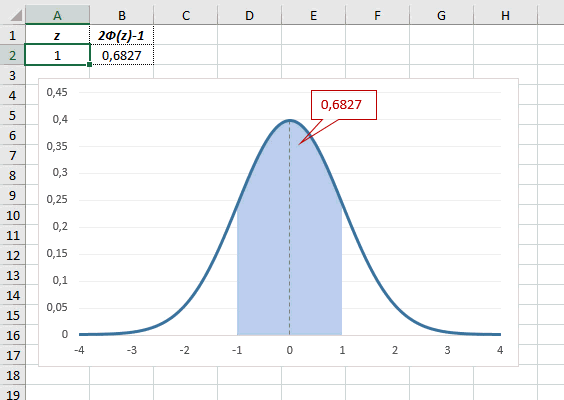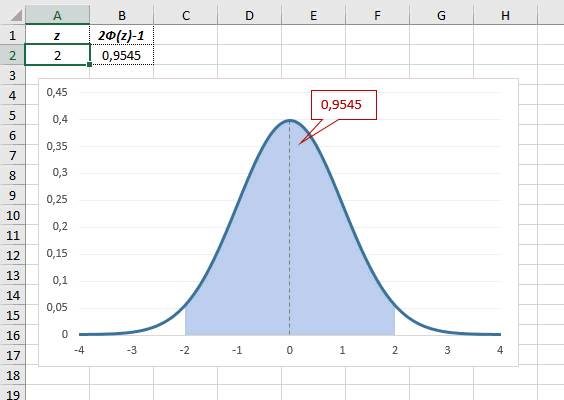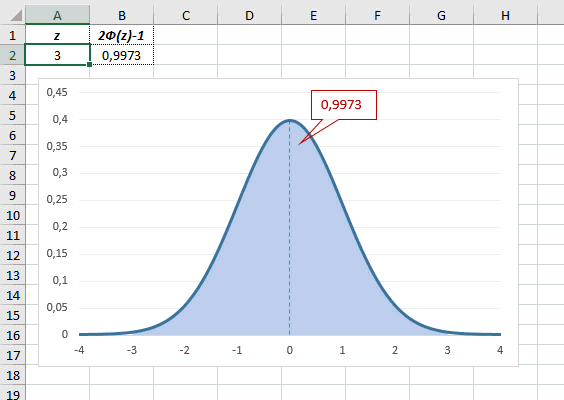
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.
На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.
Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.
Функция НОРМ.СТ.ОБР
НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:
=НОРМ.СТ.ОБР(вероятность)
вероятность – это вероятность.
Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.
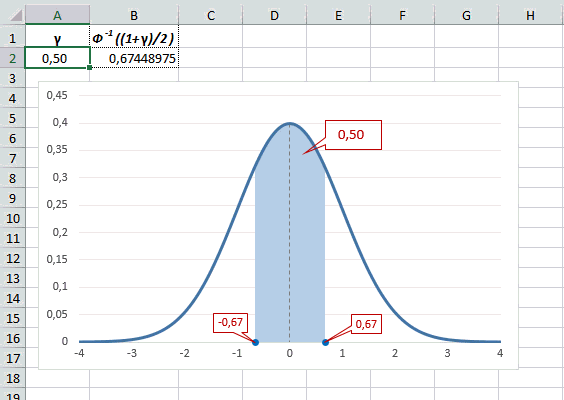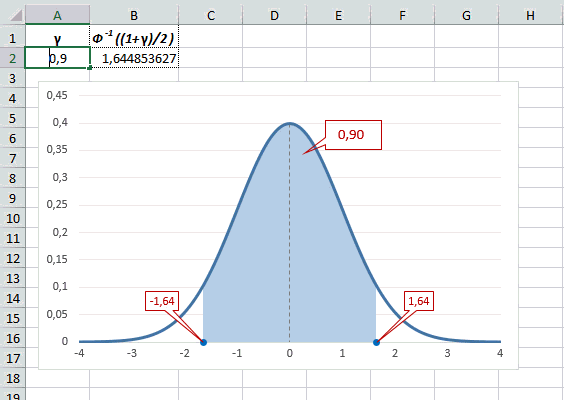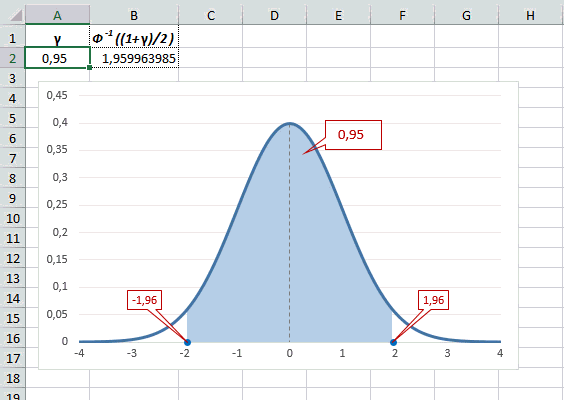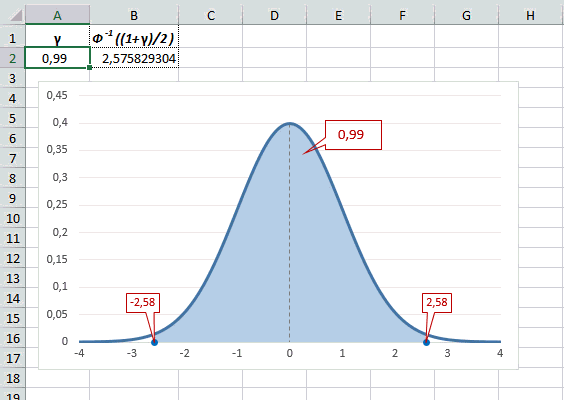
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.
Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.
В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.
Рассмотрим еще пару полезных формул с примерами.
Функция НОРМ.РАСП
Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.
=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения
среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения
стандартное_откл – среднеквадратичное отклонение – второй параметр модели
интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).
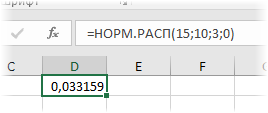
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:
Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.
Функция НОРМ.ОБР
Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.
=НОРМ.ОБР(вероятность;среднее;стандартное_откл)
вероятность – вероятность
среднее – матожидание
стандартное_откл – среднеквадратичное отклонение
Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.
Пример показан в ролике в конце статьи.
Моделирование нормального распределения
Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.
Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.
=НОРМ.ОБР(СЛЧИС();10;3)
Протянем ее на необходимое количество ячеек и нормальная выборка готова.
Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.
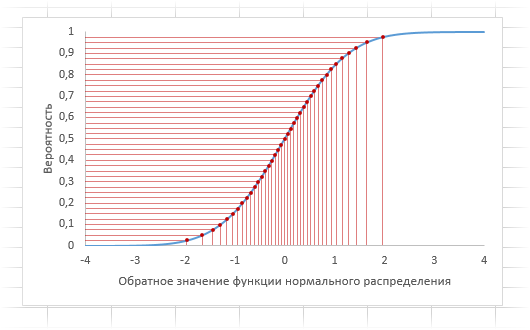
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.
На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.
Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.
Скачать файл с примером.
Поделиться в социальных сетях:
Как
уже указывалось, функции f(x),
F(x),
P(x)
и (x)
полностью
характеризуют распределение случайной
величины. Обычно эти функции задаются
аналитическими выражениями (формулами).
Существует несколько таких основных
типов формул и соответствующих им типов
распределений. В рамках одного типа
распределения могут отличаться друг
от друга параметрами. Для задания
распределения случайной величины
необходимо указать как тип, так и
параметры распределения. Если у двух
случайных величин совпадают и тип
распределения, и параметры, то говорят,
что они одинаково распределены. Рассмотрим
основные распределения, встречающиеся
в теории надежности.
1.9.1. Закон нормального распределения (закон Гаусса)
Этот закон является
одним из наиболее распространенных
законов распределения погрешностей.
Уравнение кривой нормального распределения
имеет следующий вид:
.
(1.25)
Функция распределения
имеет вид:
.
(1.26)
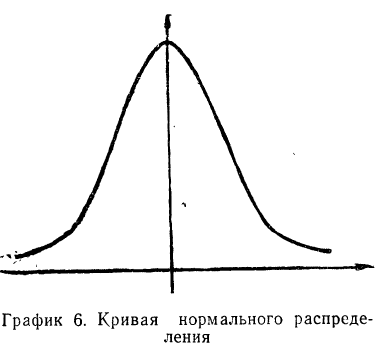
График плотности
нормального распределения называется
нормальной кривой или кривой Гаусса
(рис.1.14). Отметим смысл характеристик
этой кривой:
-
–центр группирования,
характеризует распределение размеров; -
–характеризует кучность
распределения размеров (погрешностей)
около
;
чем меньше s,
тем кучнее распределяются размеры
около
.
Кривая Гаусса имеет следующие особенности.
-
Кривая симметрична
относительно
.
-
При
,
кривая имеет максимум, равный:.
-
На расстоянии ±
σ от вершины кривая имеет две точки
перегиба А и Б, координаты которых
равны:
.
-
На расстоянии ±
3 σ от вершины кривой ее ветви так близки
к оси абсцисс, что в пределах ± 3σ 99,73 %
всей площади ограничивается кривой.
Практически принято считать, что на
расстоянии ± 3 σ от вершины кривой ее
ветви пересекаются с осью абсцисс и в
этих пределах заключена вся площадь
кривой, т.е. 100,0 %. Погрешность в этом
случае составляет 0,27 %, что допустимо
при решении многих задач производства. -
σ – это мера рассеяния,
мера точности. При различных значениях
средних квадратических отклонений
кривые Гаусса представлены на рис.
1.15. На основании п.4 справедливо
утверждение, что поле рассеяния равно
ω ≈ 6 σ.
(1.27)
При определении
s
по данным непосредственных измерений
заготовок и расчетов по формуле (1.10)
погрешность определения среднего
квадратического, обозначаемого в этом
случае буквой S,
зависит от общего количества N
измеренных заготовок и в отдельных
случаях весьма значительно. Учитывая
это обстоятельство, для предотвращения
возможного появления брака
целесообразно при использовании формулы
(1.27) принять соотношение
σ = k×S,
где
k
коэффициент, учитывающий погрешность
определения среднего квадратического;
S
– среднее квадратическое, определяемое
по формуле (1.10). Максимальная погрешность
(D
S)
определения S
выбирается по табл. 1.5.
Таблица 1.5
Значения максимальной
погрешности
S
определения S
|
N, |
|
kσ |
N, |
S, |
kσ |
|
25 |
42,4 |
1,40 |
200 |
15,0 |
1,15 |
|
50 |
30,0 |
1,30 |
300 |
12,2 |
1,12 |
|
75 |
25,0 |
1,25 |
400 |
10,6 |
1,11 |
|
100 |
21,2 |
1,20 |
500 |
10,0 |
1,10 |
В
тех случаях, когда поле рассеяния
параметров (размеров) превосходит поле
допуска (ω > δ), условие обработки без
брака не выполняется и брак является
возможным.
Вероятный процент
брака вычисляется следующим образом.
При рассеянии размеров, соответствующих
закону нормального распределения
Гаусса, оценка точности принимается с
погрешностью не более 0,27 %, что все детали
партии имеют действительные размеры в
пределах поля рассеяния
6 σ = xmax
– xmin,
где xmax,
xmin
– максимальное и
минимальное значения параметра (размера).
При этом площадь, ограниченная кривой
нормального распределения и осью
абсцисс, равна единице и определяет
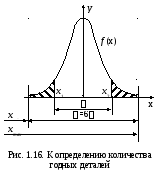
100% заготовок партии. Площадь заштрихованных
участков (рис. 1.16) представляет собой
количество деталей, выходящих по своим
размерам за пределы допуска.
Для определения
количества годных деталей необходимо
найти площадь, ограниченную кривой и
осью абсцисс на длине, равной допуску
δ. При симметричном расположении поля
рассеяния относительно поля допуска
следует найти значение интервала,
определяющего половину площади,
ограниченной кривой Гаусса и абсциссой
х1
(х2).
Функция распределения
для нормального закона имеет вид:
.
(1.28)
Для случая, когда
распределение называют стандартным и
функция распределения (1.28) имеет вид
(см. рис. 1.17.):
.
(1.29)
Таким образом,
если случайная величина Х
следует закону нормального
распределения, то вероятность появления
случайной погрешности определяется
площадью, ограниченной кривой f(x)
и ее частью и осью абсцисс:

(1.30)
Подынтегральное
значение есть элемент вероятности,
равный площади прямоугольника с
основанием dx
и абсциссами x1
и x2,
называемыми квантилями.
Произведем замену
переменной: t
= x
/ s
, dx
= s×dt

(1.31)
Представим правую
часть в виде суммы двух интегралов:

Интеграл вида
(1.32)
носит
название нормальной функции Лапласа.
Значения этого интеграла сведены в
табл. (П.3). Таким образом, указанная
вероятность (1.30) сводится к разности
нормальных функций Лапласа
Р { x1
< x
< x2
} = Ф (t2)
– Ф (t1)
. (1.33)
Расчет количества
годных деталей сводится к установлению
величины t
и определению Ф(t)
по таблице с последующим пересчетом
полученных величин в проценты или в
число штук изделий.
В
общем случае, когда
,
имеем следующую вероятность появления
случайных погрешностей:

(1.34)
Отметим
свойства функции Лапласа: Ф(0) = 0; Ф(–х)
= –Ф(х)
(функция
нечетная); Ф()=1/2.
Из рис. 1.17 видно, что кривыеF(х)
и Ф(x) эквидистантны.
Если
в равенстве (1.34) положить х1
= –,
то
,
(1.35)
так
как Ф(–}=
–Ф()=
–1/2. Положив в соотношении (1.34)х2
=,находим:
.
(1.36)
Пример
1.3.
При измерении
сопротивлений делителя напряжения
установлено, что
среднее
значение этого сопротивления
= 5,5 кОм, а среднее квадратическое
отклонение
=
1,5 кОм.
Принимая нормальный закон распределения,
найти вероятность появления сопротивлений
свыше 10 кОм.
Решение.
По равенству (1.36) и из таблиц (П3) находим:
Р(R>10)
= 1/2
– Ф[(10
–
5,5)/1,5] = 0,5
– 0,4986 = 0,0014.
Пример 1.4.
Определить количество бракованных и
годных деталей, если допуск на обработку
δ = 0,10 мм. Среднее квадратическое
отклонение S
= 0,02 (получено по результатам замеров
75 штук). Общее количество обработанных
деталей – 300 шт.
Решение.
1. Определяем расчетное значение σ = k×S
= 1,25×0,02
= 0,025 мм.
2. Поле фактического
рассеяния ω = 6×σ
= 6×0,025
= 0,15 мм превосходит поле допуска δ = 0,1
мм; следовательно, условие обработки
без брака не выполнено и появление брака
возможно.
3. x
= δ/2
= 0,1/2 = 0,05; t
= x/σ
= 0,05/0,025 = 2,0. Ф(t)
= 0,4772, что соответствует 47,72% годных
деталей для половины партии. Для всей
партии количество годных деталей –
95,44 % или 286 шт., а бракованных 4,56% или 14
шт.
Метод оценки
точности на основе кривых распределения
универсален и позволяет объективно
оценить точность механической обработки,
сборочных, контрольных и других операций.
Недостаток метода – невозможность
выявить изменение изучаемого параметра
во времени, т.е. последовательности
обработки заготовок, что не позволяет
осуществить регулирование хода
технологического процесса. Кроме того,
переменные систематические погрешности
нельзя отделить от случайных; это
затрудняет выявление и устранение
причин погрешностей. От этих недостатков
свободен метод статистического
регулирования технологического процесса.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нормальное распределение (Гаусса) в Excel
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии ( σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X 0 =1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
Нормальное распределение в Excel
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ( z ) или вероятности Φ(z) по нормированным данным (z).
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ( z ) , если 1 – значение функции Ф(z), т.е. вероятность P(Z
Уравнение кривой нормального распределения
Необходимо отметить, что форма кривой нормального распределения полностью определяется величиной s.
у – плотность вероятности
Чем меньше величина s, тем более остроконечную форму имеет кривая нормального распределения. s1
Тогда вероятностный процент брака в сторону уменьшения значения контролируемого параметра определится как Pz1=0,5(1-Ф(z1)) 100%.
Аналогично определяется относительное отклонение в сторону увеличения параметра
По расположению кривой относительно допуска и т.д. можно определить категорию брака: исправимый или неисправимый.
вал мм
Псл=6σ=6 . 0,03 мм → работа без брака невозможна
б) определить процент брака при настройке без ошибки (ΔС=0)
в) определить средний диаметр, на который нужно настроить станок, чтобы исключить появление неисправимого брака, определить процент исправимого брака
необходимо иметь отклонение в сторону уменьшения диаметра вала!
мм – условие работы без брака
мм
мм
F(z2)=0,4772 – половинное значение
нормальное распределение с σ=0,025 мм
вершина кривой распределения смещена на ΔС=0,03 мм
Определить процент годных деталей
Для оценки точности технологических процессов применяются не только кривые нормального распределения.
Если при выполнении какой-либо операции имеет место ярко выраженная систематическая переменная погрешность (размерный износ инструмента), то её оценивают с помощью кривой равной вероятности
Если же при выполнении операции имеет место совместное действие, скажем, размерного износа и увеличение силы резания в процессе затупления инструмента, распределение происходит по закону Симпсона или треугольника
Оценка точности с помощью кривых распределения является универсальным методом, то есть он применяется для оценки различных процессов. Использование данного метода позволяет дать оценку точности физического процесса и ее соответствие заданным допускам, сравнить процессы по точности, выявить стабильность и влияние факторов.
Недостатком метода является его направленность в прошлое, то есть точность оценивается уже после изготовления партии деталей. Не учитывается последовательность обработки детали, влияние и постоянных, и переменных погрешностей выявляется как рассеивание размеров. Метод исключает возможность оперативного вмешательства в ТП с целью повышения точности, а также не выявляет физической сущности факторов, влияющих на точность.
С точки зрения увеличения точности процесса он недостаточно пригоден.
В крупносерийном и массовом производстве для оценки точности применяют точечные и точностные диаграммы.
На точечной диаграмме отмечается контролируемый параметр деталей после выполнения конкретной операции. Для сокращения длины диаграммы иногда контролируют и проставляют размеры для группы деталей. В некоторых случаях отмечается средний параметр группы деталей.
Псл – случайная сумманрная погрешность параметра
m – количество элементов в выборке
Точечные диаграммы достаточно просто преобразуются в точностные. На точностных диаграммах проставляется среднее значение параметра группы деталей, среднеквадратическое отклонение (в плюс и в минус), а также максимальное и минимальное значение контролируемого параметра в данной группе деталей. По поведению средней величины и изменению величины поля рассеивания судят об устойчивости и стабильности ТП. Считается, что ТП стабильный и устойчивый, если амплитуда колебания W и хср не превышает (0,4-0,5)Т допуска на данный параметр, то есть ТП может быть устойчивым и стабильным, неустойчивым и стабильным и т.д.
Смещение центра группирования погрешностей говорит о нестабильности процесса.
– уравнение, описывающее систематическую погрешность.
В более общем случае наряду со смещением центра группирования погрешности происходит изменение распределения.
σ – характеристика кривой
Считается,что техпроцесс стабилен и устойчив, если амплитуда колебаний средних значений и поля рассеивания не превышают (0,4…0,5)Т.
Управление эффективностью: кривая нормального распределения
Сегодня многие консультанты и специалисты в сфере HRM говорят об управлении эффективностью, дают различные советы и делают выводы «космического масштаба» о том, как ее повысить. Но какова суть эффективности, ее природа? Каким правилам и законам она подчиняется?
Чем более глубокими теоретическими знаниями мы обладаем, тем более совершенна наша практическая деятельность. Действительно, управлять эффективностью можно только в том случае, если мы глубоко понимаем природу этого феномена.
Эффективность — это результативность процесса, операции, проекта. Она определяется как отношение полученного результата (достигнутого эффекта) к затратам — расходам на его получение. Для оценки этого параметра деятельности используется специальный математический аппарат (коэффициенты, формулы, методы расчета и т. д.). Использование метрик эффективности позволяет эйчарам разработать определенный алгоритм собственной работы.
Эффективность деятельности компании в целом зависит от эффективности работы каждого ее сотрудника. В крупном коллективе работают разные люди — естественно, они демонстрируют различную результативность. Количество людей с высокой/ средней/ низкой результативностью труда — математики используют термин «распределение» — подчиняется закономерности, которую называют кривой нормального распределения.
На рисунке 1 изображена кривая нормального распределения — гауссиана. Вся живая и неживая природа подчиняется этому закону. Например, в каждом классе любой школы (и во всех школах мира) подавляющее большинство составляют «середнячки», часть учеников учится немного лучше и немного хуже, и несколько процентов детей — очень способны (еще реже — одарены, талантливы) и столько же — плохо обучаемы и не имеют никакой мотивации к учебе.
Рис. 1. Кривая нормального распределения Гаусса
Но констатации факта, что наиболее эффективных сотрудников (в любом коллективе!) примерно столько же, сколько низкопроизводительных, а большая часть работников — «середнячки», недостаточно для того, чтобы управлять результативностью.
Следствия закона нормального распределения могут показаться парадоксальными: в любом коллективе будут лучшие и худшие. Всегда! Иначе теряет смысл само определение «лучший»… Это не значит, что если уволить лодырей, то «разленятся» другие сотрудники, скорее — повысятся критерии оценки эффективности для этого коллектива. Любая система стремится к равновесию, и смысл управления в том, чтобы устанавливать это равновесие на все более высоком «базовом» уровне…
Если мы посмотрим на результаты оценки сотрудников реальной компании (по критерию эффективности в достижении поставленных целей), то увидим, что они «выстраиваются» в гауссиану (рис. 2): в группу III входят 5% самых результативных сотрудников, в группу I — 5% самых неэффективных, а остальные (группа II) демонстрируют средние показатели.
Рис. 2. Распределение сотрудников компании по показателю «эффективность» описывается кривой нормального распределения
Далее рассмотрим графики на рисунке 3. Отсутствие «передовиков производства» (вариант на рис. 3а), «отстающих» (рис. 3б) или и тех и других одновременно (рис. 3в) — утопия. Если статистика противоречит закону Гаусса, значит, у компании есть серьезные проблемы с организацией труда, а также неудачно выстроена система оценки результативности деятельности. Скорее всего, работа на конкретных рабочих местах плохо описана, неправильно пронормированна и неэффективно стимулируется (то есть нормы выработки, рабочие задания завышены или занижены, а система оплаты не мотивирует к тому, чтобы люди прикладывали больше усилий). Возможно также, что в этих компаниях неудачно выбрана система показателей для оценки результатов (например, оценивается качество продукции, а реально оплачиваются объемы ее изготовления) и/или есть серьезные управленческие ошибки с постановкой целей и определением приоритетности задач.
Рис 3. Графики распределения сотрудников компании по показателю «эффективность»
Особый практический интерес (исходя из собственного опыта) представляет ситуация «все хорошие» (рис. 3в). Когда дело доходит до периодической оценки сотрудников, многие линейные менеджеры подходят к подчиненным «уравнительно», мотивируя свои решения «благими намерениями»: чтобы не осложнять отношения в коллективе, не провоцировать конфликты. Дело не только в том, что они не хотят задуматься над тем, что каждый человек уникален по своему, и работать одинаково «хорошо» все не могут. Это проблема качества управления: справедливая оценка ставит перед сотрудниками реалистичные цели, она сама по себе мотивирует людей, а значит, работает на повышение общей эффективности подразделения и компании в целом.
Впервые с подобным подходом я столкнулся при внедрении периодической системы оценки деятельности сотрудников одного из предприятий тяжелой промышленности: начальник одного из цехов утверждал, что у него все работают хорошо, и он не может кого-либо выделить. О каком развитии, повышении эффективности может идти речь, если руководитель не может отличить плохую работу от хорошей, а хорошую от отличной? Он сам лишает своих подчиненных возможности развиваться (и, как следствие, препятствует повышению эффективности их труда).
Нередко затратив огромные средства на внедрение системы управления эффективностью, компании не получают ожидаемого результата… Вывод один: пока линейные менеджеры не будут правильно применять инструменты и методы управления сотрудниками, которые им предлагают коллеги из службы по управлению персоналом, явного сдвига в повышении эффективности деятельности организации не будет.
Вернемся к закону Гаусса. Что можно сделать для повышения эффективности компании? Как перевести сотрудников из разряда лодырей хотя бы в разряд «середнячков»? Я предлагаю вниманию коллег проверенные на практике рекомендации:
Работать нужно со всем персоналом, повышая результативность каждого. Успеха можно добиться только в масштабах всей компании. Если сосредотачивать внимание на «воспитании» самых неэффективных работников или отдавать предпочтение лишь самым успешным, то в результате можно повысить только их личную эффективность. Затраты ресурсов и усилий в данном направлении приведут к частичным изменениям (рис. 4).
Рис. 4. Работа только с одной категорией сотрудников приведет к частичным изменениям
- Цель внедрения системы управления эффективностью — увеличить «норму для середнячков». Если менеджеры будут уделять внимание всему коллективу, то в итоге сохранятся и передовики, и относительно «отстающие» (для данного подразделения на этом этапе развития), но показатели результативности, которых достигают средние работники, — повысятся.
Отражение этого прогресса мы видим на рисунке 5: кривая распределения показателей эффективности сотрудников сместилась вправо по оси Х. По-прежнему 5% работников показывают лучшие в своей группе результаты, 5% — худшие, а подавляющее большинство, как и раньше, демонстрирует средние показатели. Но теперь:
самые слабые сотрудники работают на уровне «середнячков»;
«средние» уже подтянулись до уровня лидеров предыдущего периода;
лидеры достигли суперэффективности.
Рис. 5. Результат: повышение эффективности всей компании
Так все — каждый сотрудник, подразделение и компания в целом — выходят на новый уровень развития.
«Сдвинуть гору» с места, конечно, очень и очень непросто. Этого можно добиться, систематически проводя грамотную управленческую работу со всем персоналом, а не только с лучшими (кадровым резервом) или худшими. Для каждой группы сотрудников следует разрабатывать программы повышения эффективности. Непременное условие — они должны охватывать весь коллектив, тогда закон Гаусса будет работать на компанию!
Хочу также акцентировать внимание читателей на том, что управление эффективностью компании — это не разовое событие или мероприятие, а процесс, ежедневный кропотливый труд линейных руководителей и эйчаров. Поэтому топ-менеджеры каждой компании, перед тем как стать на стезю управления эффективностью, должны ответить на вопрос: «Готовы ли мы инвестировать в эффективность? Готовы ли линейные менеджеры культивировать в своих подразделениях стремление к эффективности? Готовы ли рядовые сотрудники постоянно участвовать в гонке за повышение эффективности? Готов ли весь коллектив вступить в борьбу за результативность, буквально — с мировой энтропией*?» Если ответ положительный — дерзайте!
Рост эффективности каждого отдельного сотрудника повышает эффективность подразделения, компании в целом. Как только количество высокорезультативных работников достигает критической отметки, наблюдается своего рода «квантовый скачок» повышения эффективности всей компании. Переход на качественно новый уровень происходит в соответствии с законами диалектики, которые сформулировал великий немецкий философ Фридрих Гегель. Задача менеджеров — по возможности приблизить момент «перехода количества в качество».
Этот закон замечателен своей универсальностью: ему подчиняются не только процессы развития галактик и человеческих цивилизаций, но и профессиональный рост отдельного специалиста (например, эйчара). Здесь важно наблюдать за собственной результативностью. Анализируйте ее: ежедневные результаты скажут вам об эффективности больше, чем тысяча книг, лекций, разговоров, за которыми не следует действий.
_________
* Энтропия (от греч. поворот, превращение) — 1) в теории информации: величина, характеризующая степень неопределенности системы; 2) в теории систем: величина, обратная уровню организации системы.
[spoiler title=”источники:”]
http://zdamsam.ru/a50105.html
http://hr-portal.ru/article/upravlenie-effektivnostyu-krivaya-normalnogo-raspredeleniya
[/spoiler]
Содержание:
Законы распределения:
Распределение случайных переменных: Каждая из случайных переменных имеет ряд возможных значений, могущих возникнуть с определенной вероятностью.
Случайные переменные величины могут носить прерывный (дискретный) и непрерывный характер. Возможные значения прерывной случайной переменной отделены друг от друга конечными интервалами. Возможные значения непрерывной случайной переменной не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Примерами прерывных случайных переменных могут служить:
- число попаданий при п выстрелах, если известна вероятность попадания при 1 выстреле. Число попаданий может быть 0, 1, 2….. n;
- число появлений герба при n бросаниях монеты.
Примеры непрерывных случайных переменных:
- ошибка измерения;
- дальность полета снаряда.
Если перечислить все возможные значения случайной переменной и указать вероятности этих значений, то получится распределение случайной переменной. Распределение случайной переменной указывает на соотношение между отдельными значениями случайной величины и их вероятностями.
Распределение случайной переменной будет задано законом распределения, если точно указать, какой вероятностью обладает каждое значение случайной переменной.
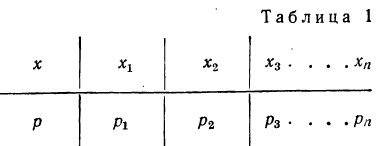
Закон распределения имеет чаще всего табличную -форму изложения. В этом случае перечисляются все возможные значения случайной переменной и соответствующие им вероятности:
Такая таблица называется также рядом распределения случайной переменной.
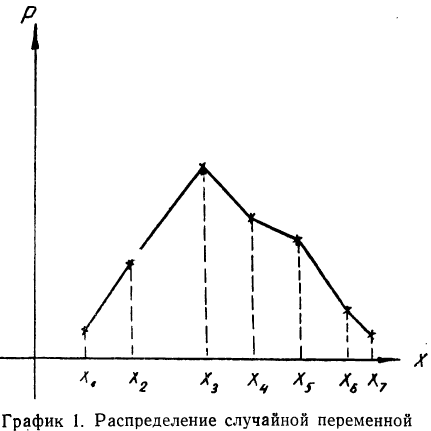
Для наглядности ряд распределения изображают графически, откладывая на прямоугольной системе координат по оси абсцисс возможные значения случайной переменной, а по оси ординат — их вероятности. В результате графического изображения получается многоугольник или полигон распределения (график 1). Многоугольник распределения является одной из форм закона распределения.
Функция распределения
Ряд распределения является исчерпывающей характеристикой прерывной случайной перемен-
Вероятность того, что Х<х, зависит от текущей переменной х и является функцией от х. Эта функция носит название функции распределения случайной переменной X.
F(x) = P(X
Функция распределения является одной из форм выражения закона распределения. Она является универсальной характеристикой случайной переменной и может существовать для прерывных и непрерывных случайных переменных.
Функция распределения F(x) называется также интегральной функцией распределения, или интегральным законом распределения.
Основные свойства функции распределения могут быть сформулированы так:
- F(x) всегда неотрицательная функция, т. е.
- Так как вероятность не может быть больше единицы, то
- Ввиду того что F(x) является неубывающей функцией, то при
- Предельное значение функции распределения при х=
равно нулю, а при х=
равно единице.
Если случайная переменная X дискретна и задана рядом распределения, то для нахождения F(x) для каждого х необходимо найти сумму вероятностей значений X, которые лежат до точки х.
Графическое изображение функции распределения представляет собой некоторую неубывающую кривую, значения которой начинаются с 0 и доходят до 1.
В случае дискретной случайной переменной величины вероятность F(x) увеличивается скачками всякий раз, когда х при своем изменении проходит через одно из возможных значений 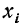
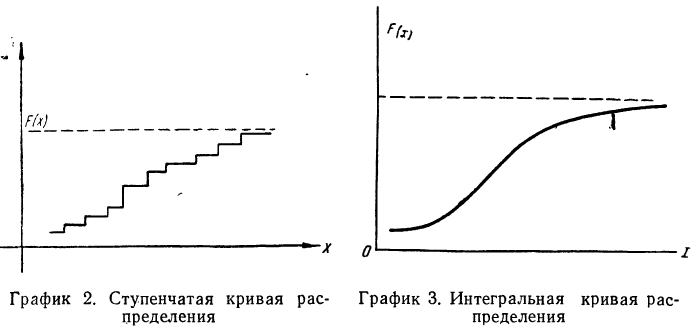
В случае непрерывной случайной переменной величины функция F(x) при графическом изображении дает плавную, монотонно возрастающую кривую следующего вида (см. график 3).
Обычно функция распределения непрерывной случайной переменной представляет собой функцию, непрерывную во всех точках. Эта функция является также дифференцируемой функцией. График функции распределения такой случайной переменной является плавной кривой и имеет касательную в любой ее точке.
Плотность распределения
Если для непрерывной случайной переменной X с функцией распределения F(x) вычислять вероятность попадания ее на участок от х до х+ 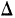
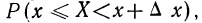
Если величину 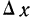
т. е. производной от функции распределения, которая характеризует плотность, с которой распределяются значения случайной переменной в данной точке. Эта функция называется плотностью распределения и часто обозначается f(x). Ее называют также дифференциальной функцией распределения, или дифференциальным законом распределения.
Таким образом, функция плотности распределения f(x) является производной интегральной функции распределения F(x).
Вероятность того, что случайная переменная X примет значение, лежащее в границах от а до 6, равна определенному интегралу в тех же пределах от плотности вероятности, или:
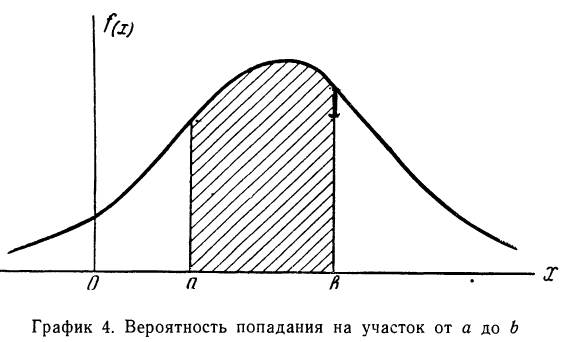
Кривая, изображающая плотность распределения случайной переменной, называется кривой распределения (дифференциальной).
Построим кривую некоторой заданной функции плотности вероятности и найдем участок, ограниченный абсциссами а и b. Площадь, ограниченная соответствующими ординатами кривой распределения самой кривой и осью абсцисс, и отобразит вероятность того, что случайная переменная будет находиться в данных пределах (см. график 4).
Плотность распределения является одной из форм закона распределения, но существует только для непрерывных случайных величин.
Основные свойства плотности распределения могут быть сформулированы так:
1. Плотность распределения есть функция, не могущая принимать отрицательных значений, т. е.
Отсюда в геометрическом изображении плотности распределения (в кривой распределения) не может быть точек, лежащих ниже оси абсцисс.
2.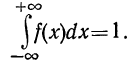
Среди законов распределения большое значение имеют биномиальное распределение, распределение Пуассона и нормальное распределение.
Биномиальное распределение
Если производится n независимых испытаний, в каждом из которых вероятность появления данного события А есть величина постоянная, равная р, и, следовательно, вероятность непоявления события А также постоянна и равна q=1—р, то число появлений события А во всех n испытаниях представляет собой случайную переменную. Вероятность того, что событие А появится в n испытаниях m раз, равна:
т. е. m+1, члену разложения бинома 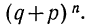
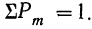
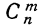
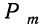
Ввиду того что вероятности 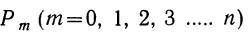
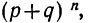
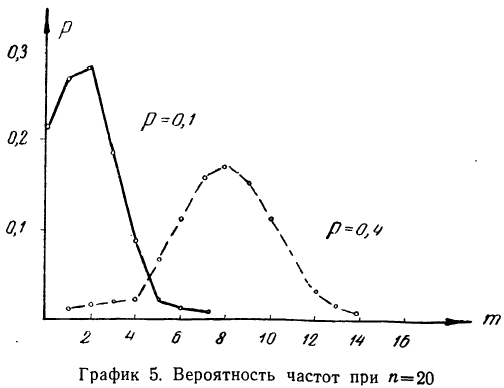
График биномиального распределения, на котором по оси абсцисс откладываются числа наступлений события, а по оси ординат — вероятности этих чисел, представляет собой ломаную линию. Форма графика зависит от значений р, q и n.
Если р и q одинаковы, то график распределения симметричен. Если же р и q неодинаковы, то график распределения будет скошенным.
Одна из частот на графике имеет максимальное значение. Это наиболее вероятная частота. Ее значение можно определить приближенно, аналитически как произведение nр.
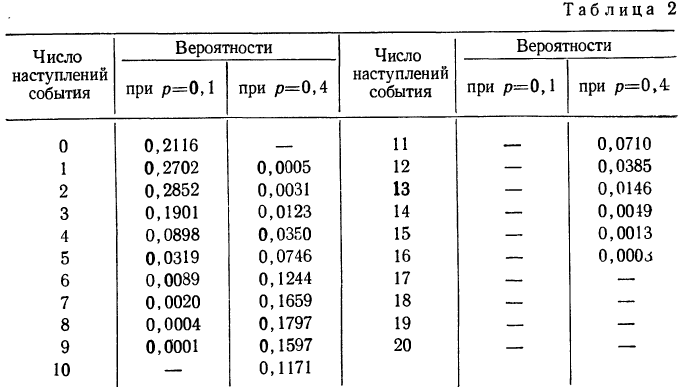
Найдем вероятности числа наступления события А при 20 испытаниях при p = 0,1 и р = 0,4 и построим график их распределений (см. график 5). Найдем вероятности частот при n = 20 для p = 0,1 и р=0,4.
График показывает, что приближение р к 0,5 вносит в распределение большую симметрию. Оказывается также, что при увеличении n распределение становится симметричным и для
Биномиальное распределение имеет широкое распространение в практической деятельности людей. Например, продолжительное наблюдение за качеством выпускаемой заводом продукции показало, что p-я часть ее является браком. Иначе говоря, мы выражаем через р вероятность для любого изделия оказаться бракованным. Биномиальное распределение показывает вероятность того, что в партии, содержащей n изделий, окажется m бракованных, где m = 0, 1, 2, 3 … n.
Предположим, имеется 100 изделий из партии изделий, в ко торой доля брака равна 0,05. Вероятность того, что из этих из делий окажется 10 бракованных, равна:
Закон биномиального распределения называется также схемой Бернулли. .
Нормальное распределение
Расчет вероятностей по формуле биномиального распределения при больших n очень громоздок. При этом значении m прерывны, и нет возможности аналитически отыскать их сумму в некоторых границах. Лаплас нашел закон распределения, являющийся предельным законом при неограниченном возрастании числа испытаний n и называемый законом нормального распределения.
Плотность вероятности нормального распределения выражается при этом формулой:
где t представляет собой нормированное отклонение частоты т от наиболее вероятной частоты nр, т. е. 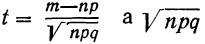
Максимальная ордината кривой соответствует точке m=nр, т. е. математическому ожиданию случайной переменной m; величина этой ординаты равна 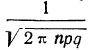
Для практического нахождения вероятностей используют таблицу значений f(t).
Эмпирические и теоретические распределения
В примерах распределений, приведенных в разделе I, мы пользовались данными, почерпнутыми из наблюдений.
Поэтому всякий наблюденный ряд распределения назовем эмпирическим, а график, изображающий распределение
частот этого ряда, — эмпирической кривой распределения. Эмпирические кривые распределения могут быть представлены полигоном и гистограммой. При этом изображение в виде полигона применяется для рядов с прерывными значениями признака, а гистограмма— для рядов с непрерывными значениями признака.
Наблюдая многочисленные ряды распределения, математики стремятся описать эти распределения путем анализа образования величины признака, пытаются построить теоретическое распределение, исходя из данных об эмпирическом распределении.
Мы уже видели на примере распределения случайной переменной, что распределение ее задается законом распределения. Закон распределения, заданный в виде функции распределения, позволяет математически описать ряды распределения некоторых совокупностей.
Теоретическим законом распределения многих совокупностей, наблюдаемых на практике, является нормальное распределение. Иначе говоря, многие эмпирические подчинены закону нормального распределения, функция плотности вероятности которого приведена в предыдущем параграфе.
Чтобы эту формулу применять для нахождения теоретических данных по некоторому эмпирическому ряду, необходимо вероятностные характеристики заменить данными эмпирического ряда. При этой замене величина стандартизованного отклонения t будет представлять собой 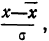
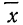
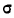
Следовательно, нормальное распределение ряда распределения зависит от величин средней арифметической и его среднего квадратического отклонения.
Свойства кривой нормального распределения
Дифференциальный закон нормального распределения, заданный функцией:
имеет ряд свойств. Полагая 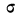
Рассмотрим ее свойства.
- Кривая нормального распределения имеет ветви, удаленные в бесконечность, причем кривая асимптотически приближается к оси Ot.
- Функция является четной: t(—t) = f(t). Следовательно, кривая нормального распределения симметрична относительно оси Оу.
- Функция имеет максимум при t = 0. Величина этого максимума равна
Следовательно, модального значения кривая
достигает при t = 0, а так как 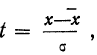
Наибольшую частоту кривая будет иметь при значении х, равном среднему арифметическому из отдельных вариантов. Средняя арифметическая является центром группирования частот ряда.
4. При t=±1 функция имеет точки перегиба. Это означает, что кривая имеет точки перегиба при отклонениях от центра
группирования 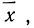
5. Сумма частостей, лежащих в пределах от а до b, равна определенному интегралу в тех же пределах от функции f(t), т. е.
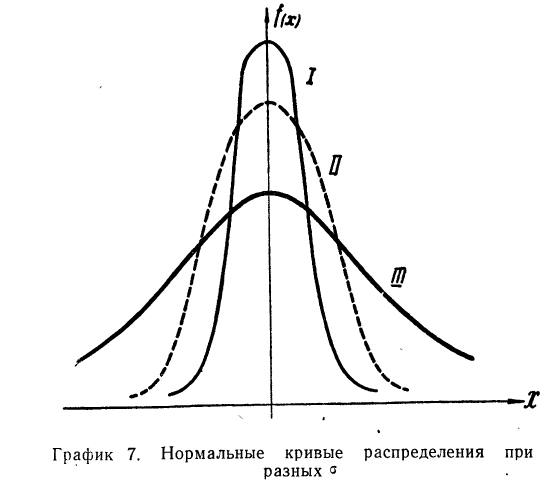
Если учесть действительную величину среднего квадратического отклонения, то окажется, что при больших величинах о значение f(t) мало, при малых, наоборот, велико. Отсюда изменяется и форма кривой распределения. При больших 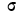
На графике 7 показаны 3 кривые нормального распределения (I, II, III) при 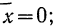
Зная общие свойства кривой нормального распределения, рассмотрим те условия, которые приводят к образованию кривых данного типа.
Формирование нормального распределения
Закон нормального распределения является наиболее распространенным законом не только потому, что он наиболее часто встречается, но и потому, что он является предельным законом распределения, к которому приближается ряд других законов распределения.
Нормальное распределение образуется в том случае, когда действует большое число независимых (или слабо зависимых), случайных причин. Подчиненность закону нормального распределения проявляется тем точнее, чем больше случайных величин действует вместе. Основное условие формирования нормального распределения состоит в том, чтобы все случайные величины, действующие вместе, играли в общей сумме примерно одинаковую роль. Если одна из случайных ошибок окажется по своему влиянию резко превалирующей над другими, то закон распределения будет обусловлен действием этой величины.
Если есть основания рассматривать изучаемую величину как сумму многих независимых слагаемых, то при соблюдении указанного выше условия ее распределение будет нормальным, независимо от характера распределения слагаемых.
Нормальное распределение встречается часто в биологических явлениях, отклонениях размеров изделий от их среднего размера, погрешностях измерения и т. д.
Если взять распределение людей по номеру носимой ими обуви, то это распределение будет нормальным. Но это правило применимо только в том случае, когда численность совокупности велика и сама совокупность однородна.
Из того факта, что нормальное распределение встречается нередко в разных областях, не следует, что всякий признак распределяется нормально. Наряду с нормальным распределением существуют другие различные распределения.
Но все же умение выявить нормальное распределение в некоторой эмпирической совокупности является важным условием для ряда практических расчетов и действий. Зная, что эмпирическое распределение является нормальным, можно определить оптимальные размеры предприятий, размеры резервов и т. д.
Важным условием определения характера данной эмпирической кривой является построение на основе эмпирических данных теоретического нормального распределения.
Построение кривой нормального распределения
Первый способ. Для того чтобы построить кривую нормального распределения, пользуются следующей егo формулой:
где N — число проведенных испытаний, равное сумме частот эмпирического распределения
k — величина интервала дробления эмпирического ряда распределения;
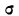
t—нормированное отклонение, т. е.
Величина 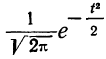
Для нахождения значений теоретических частот (см. пример 1) сначала необходимо найти среднюю арифметическую эмпирического ряда распределения, т. е. 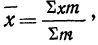
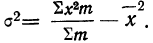
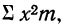
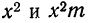
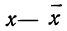
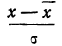
Найденная при умножении величина и составляет теоретическую частоту каждого варианта, записанного в строке (графа 9). Ввиду того что частоты могут быть только целыми числами, округляем их до целых и получим теоретические частоты, которые будем обозначать 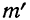
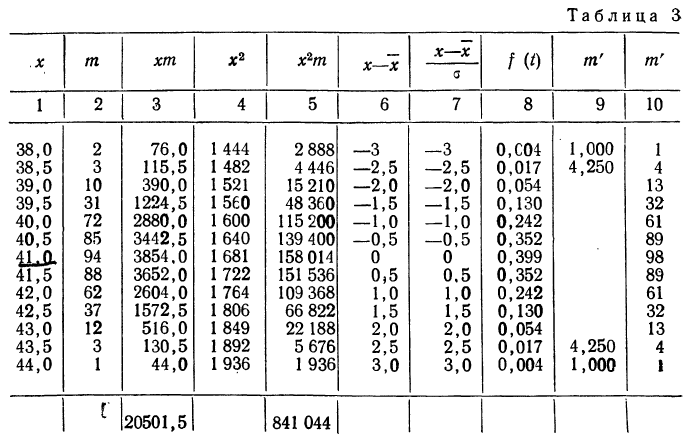
Пример 1.
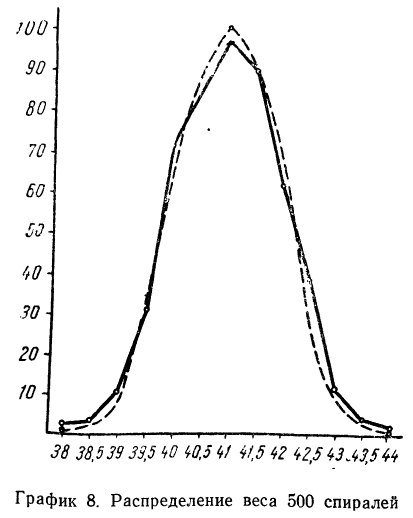
В таблице 3 приведено эмпирическое распределение веса 500 спиралей и расчет частот нормального распределения. (Вес спиралей х дан в миллиграммах.)
Из таблицы находим:
Строим график эмпирических и теоретических данных. На графике 8 сплошной линией дано изображение эмпирического распределения, а пунктирной — построенного на его основе теоретического распределения.
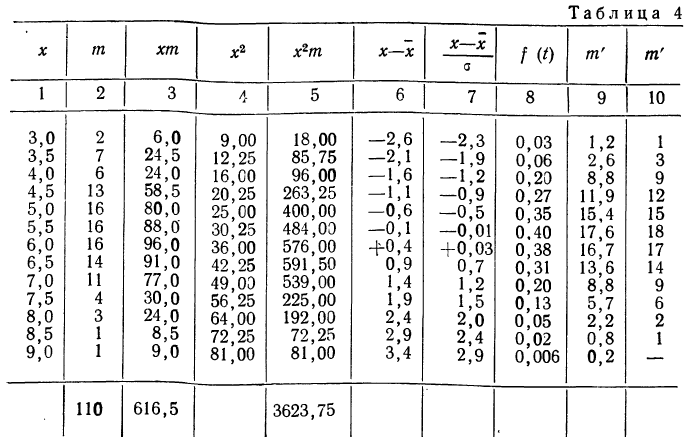
Пример 2.
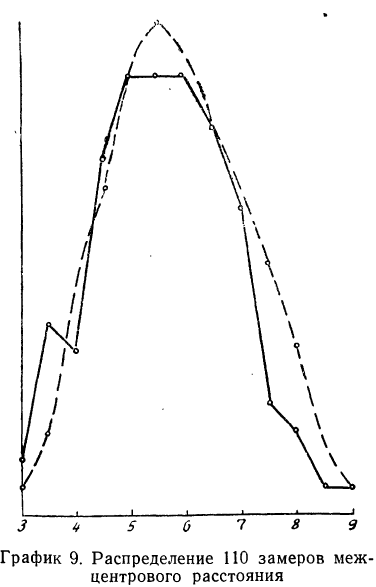
В таблице 4 дается эмпирическое распределение ПО замеров межцентрового расстояния при шевинговании зубцов динамомашины 110412 и расчет теоретических частот.
Исчислим:
Построим графики эмпирического и теоретического распределений (см. график 9).
Оба эмпирических распределения хорошо воспроизводятся теоретическим нормальным распределением.
Второй способ построения кривой нормального распределения основан на применении функции стандартизованного нормального распределения, в котором 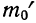
За начало отсчета признака при этом способе построения берется его средняя арифметическая. Ей соответствует наибольшая ордината.
Вычисление ординат производится по формуле:
где N — число наблюдений;
k — величина интервала эмпирического распределения.
Так как значение наибольшей ординаты получается при
t = 0, когда 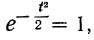
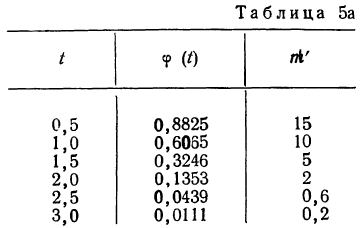
Придавая t последовательно значения 0,5; 1,0; 1,5; 2,0, т. е. сначала меньшие, а потом увеличивающиеся, находим в таблице стандартизованного нормального распределения для данных t соответствующие 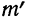
Например, при t = 0,5 величина стандартизованного нормального распределения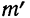
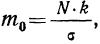
Пример 3.
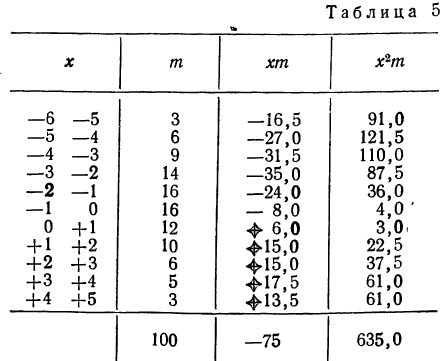
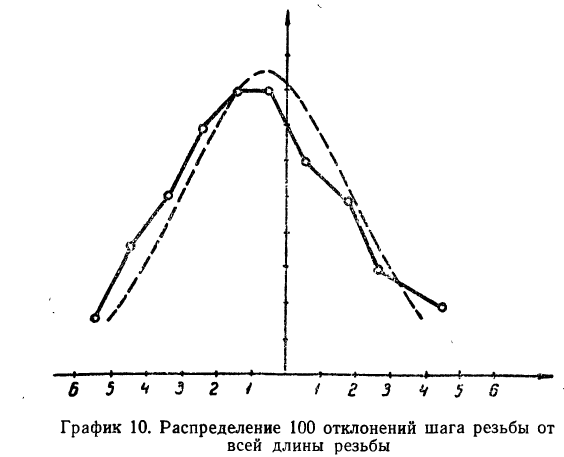
Взяты результаты измерения 100 отклонений шага резьбы х от всей длины резьбы. Получен следующий ряд распределения, для которого по общим правилам производится расчет средней и дисперсии.
Отсюда;
Рассчитаем наибольшую ординату:
так как величина 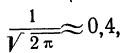
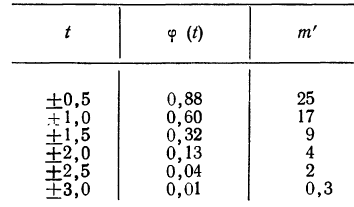
Взяв значение t = 0,5 по таблице стандартизованного нормального распределения, находим 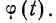
Для данного примера будем иметь:
Полученный результат наносим на график, а для сравнения наносим на график и результаты непосредственных измерений отклонений (см. график 10).
Как видно из графика, теоретическая кривая довольно близко воспроизводит полигон эмпирического распределения.
Пример 4.
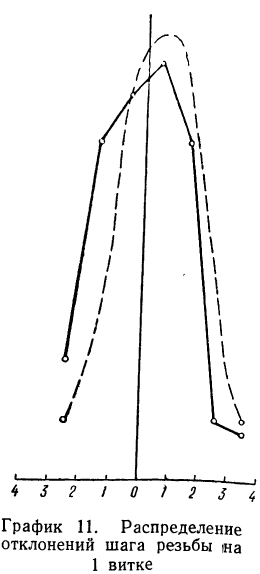
Даны результаты измерений отклонений шага резьбы (х) в микронах на 1 витке от среднего значения. Приводятся эти данные с соответствующими расчетами:
Теоретические частоты (ординаты) рассчитываются так же, как и в предыдущем примере. Сначала находится величина наибольшей частоты:
затем другие частоты:
Эмпирические и теоретические частоты наносим на график (см. график 11) и убеждаемся, что эмпирическое распределение довольно близко воспроизводится теоретическим распределением.
Третий способ построения кривой нормального распределения (или вычисления теоретических частот) по имеющимся эмпирическим данным основан на применении функции:
которая дает площадь нормальной кривой, заключенной между —t и +t.
Вообще говоря, можно находить площадь нормальной кривой, заключенную между любыми точками 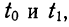
применяя функцию F(t). Искомая площадь будет представлять собой 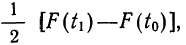
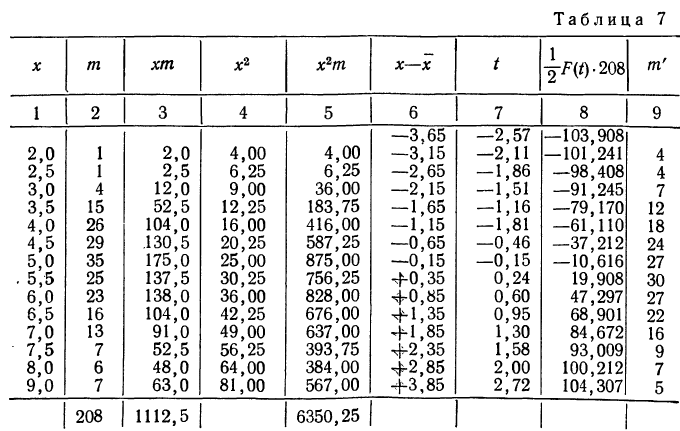
Пример 5.
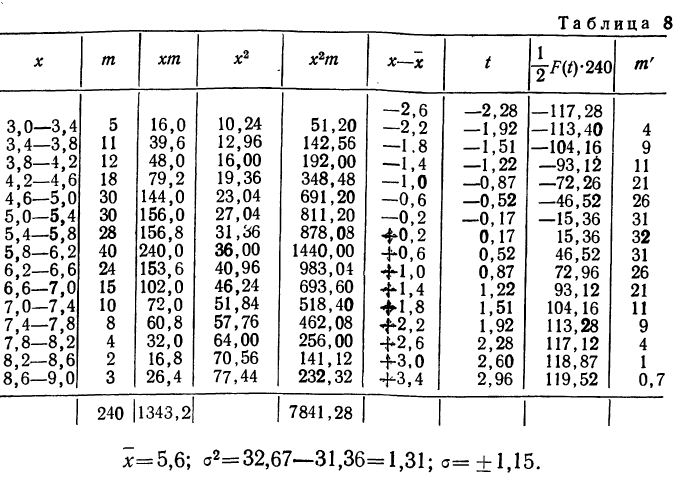
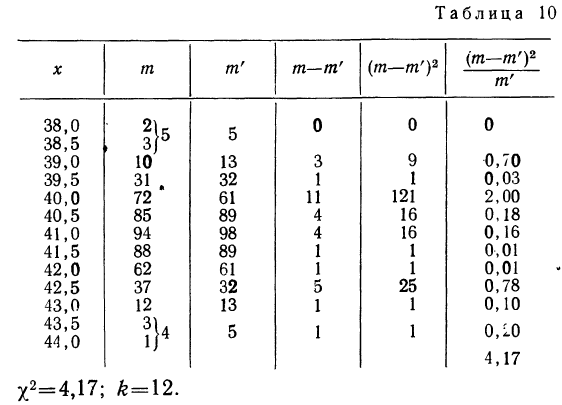
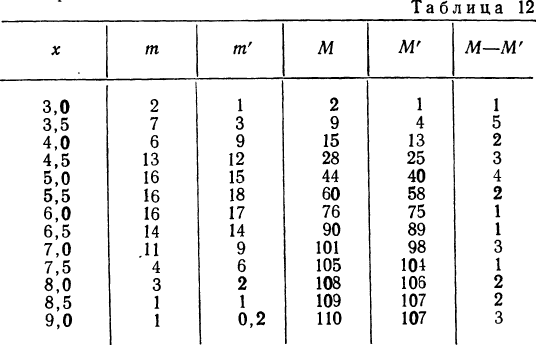
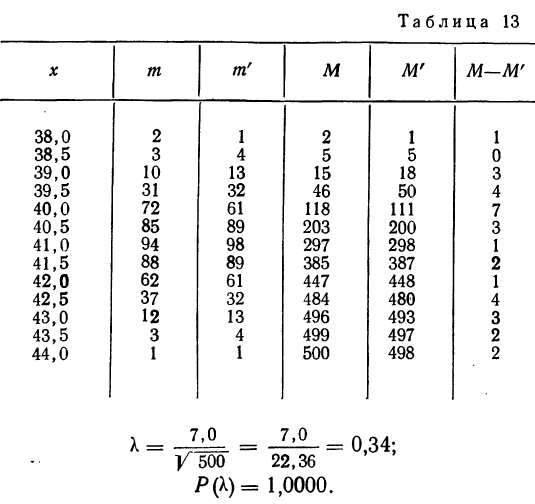
Получены результаты 208 измерений межцентровых расстояний при шевинговании зубцов шестерни динамо-машины (см. табл. 7). Вычислим нужные параметры и теоретические частоты и построим графики эмпирического и теоретического распределений.
Колонки 1, 2, 3, 4 и 5 необходимы для расчетов 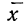
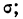
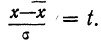
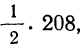
Чтобы получить теоретическую частоту для каждого интервала, достаточно из верхней строки (в 8-й колонке) вычесть число той же колонки, стоящее строкой ниже.
На графике 12 показано, что теоретическое распределение достаточно точно отражает эмпирически полученный материал, только наблюдается некоторое смещение теоретической кривой вправо, что, очевидно, вызвано большим удельным весом правого конца эмпирического распределения.
Пример 6.
Дается ряд распределения ударной вязкости в 240 испытаниях. Приведем этот ряд распределения и построим для него теоретическое распределение (см. график 13).
Критерии согласия
Определение близости эмпирических распределений к теоретическому нормальному распределению по графику может быть недостаточно точным, субъективным и по-разному оценивать расхождения между ними. Поэтому математики выработали ряд объективных оценок для того, чтобы определить, является ли данное эмпирическое распределение нормальным. Такие оценки называются критериями согласия. Критерии согласия были предложены разными учеными, занимавшимися этим вопросом. Рассмотрим критерии согласия Пирсона, Романовского, Колмогорова и Ястремского.
Критерий согласия Пирсона основан на определении величины 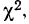
где m — эмпирические частоты;
m’ — теоретические частоты.
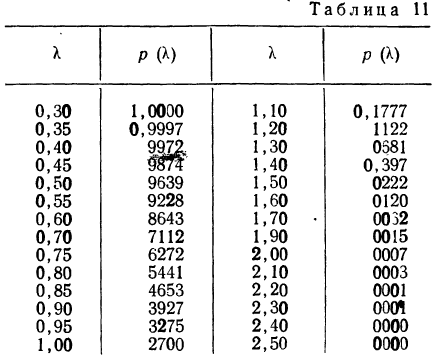
Для оценки того, насколько данное эмпирическое распределение воспроизводится нормальным распределением, исчисляют по распределению Пирсона вероятности достижения 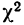
Значения 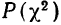
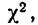
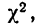
Пересечение данного столбца с соответствующей строкой дает искомую вероятность
При вероятностях, значительно отличающихся от нуля, расхождение между теоретическими и эмпирическими частотами можно считать случайным.
Проф. В. И. Романовский предложил более простой метод оценки близости эмпирического распределения к нормальному, используя величину
Он предложил вычислять отношение:
где k — число степеней свободы.
Если указанное отношение имеет абсолютное значение, меньшее трех, то предлагается расхождение между теоретическим и эмпирическим распределениями считать несущественным; если же это отношение больше трех, то расхождение существенно. Несущественность расхождения (когда величина отношения Романовского меньше трех) говорит о возможности принять за закон данного эмпирического распределения нормальное распределение.
По данным примера 2 рассчитаем величину
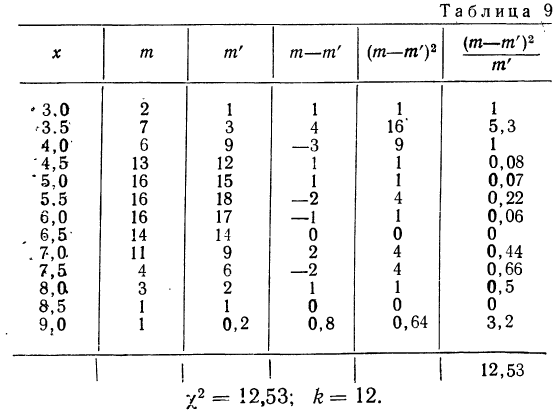
Пример 7.
Вычисление 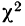
Из таблицы 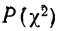
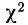
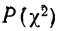
Находим отношение Романовского:
Это отношение значительно меньше трех, поэтому расхождение между теоретическими и эмпирическими частотами можно считать несущественными, и, таким образом, теоретическое распределение достаточно хорошо воспроизводит эмпирическое.
Пример 8.
Вычислим критерий 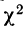
По таблице находим вероятность 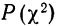
Отношение Романовского
также значительно меньше трех, поэтому теоретическое воспро* изведение эмпирического ряда достаточно удовлетворительное.
Критерий 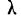
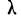
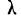
где D — максимальная граница разности: 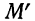
Приведем таблицу значений 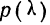
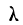
Если найденному значению 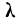
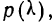
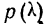
Рассмотрим применение этого критерия на двух примерах.
Пример 9.
В таблице вероятностей 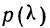
Эта большая вероятность указывает на то, что расхождение между наблюдением и теоретическим распределением вполне могло быть случайным.
Пример 10.
Величина вероятности 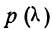
Критерий Б. С. Ястремского. В общем виде критерий Ястремского можно записать следующим неравенством:
где
— эмпирические частоты;
— теоретические частоты;
— число групп.
Для числа групп, меньших 20, 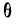
Значение I, меньшее 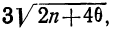
При значениях I, больших 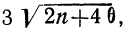
Пример 11.
Определим величину I и оценим эмпирическое распределение 500 спиралей (m) по сравнению с соответствующим нормальным (m’).
что говорит о нормальном распределении исследуемой совокупности.
Элементарные приемы определения «нормальности» распределения. Для определения элементарными способами близости данного опытного распределения к нормальному прибегают к числам Вестергарда и к сравнению средней арифметической, моды и медианы.
Числами Вестергарда являются: 0,3; 0,7; 1,1; 3. Для пользования ими определяют сначала основные характеристики — среднюю арифметическую 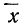
Для того чтобы данное эмпирическое распределение было подчинено закону нормального распределения, необходимо, чтобы распределение удовлетворяло следующим условиям:
- в промежутке от
была расположена
часть всей совокупности;
- в промежутке от
была расположена
часть всей совокупности;
- в промежутке от
было расположено
всей совокупности;
- в промежутках от —3 до +3 было расположено 0,998 всей совокупности.
Для приводимого распределения 500 спиралей по весу (пример 1) все эти условия соблюдаются, что говорит о подчинении данного распределения закону нормального распределения.
К элементарным приемам определения «нормальности» следует отнести применение графического метода, особенно удобное с помощью полулогарифмической сетки Турбина. На сетке накопленные эмпирические частоты при нормальном их распределении дают прямую линию. Всякое отклонение от прямой свидетельствует об отклонении эмпирического распределения от «нормального».
Распределение Пуассона
Вероятности частот событий, редко встречающихся при некотором числе испытаний, находят по формуле:
где m — частота данного события;
n — число испытаний;
р — вероятность события при одном испытании;
е= 2,71828.
Это выражение носит название закона распределения Пуассона.
Подставим вместо nр среднее число фактически наблюдавшихся случаев в эмпирическом материале. Теоретические ординаты кривой распределения по закону Пуассона m’ найдем по формуле:
где х — переменное значение числа раз;
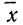
n — число наблюдений.
При
Пример 12.
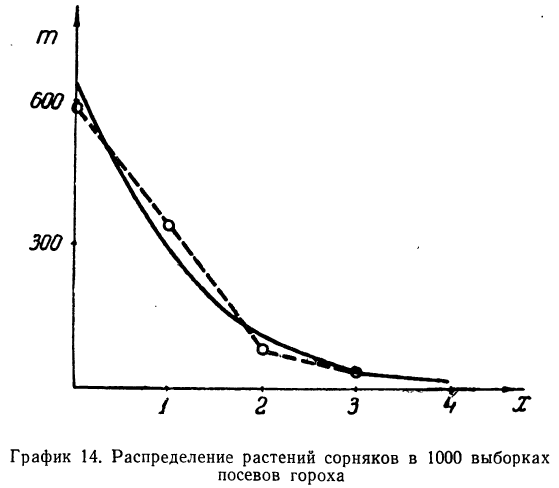
Наблюдалось следующее распределение растений сорняков в 1000 выборках посевов гороха. Результаты эксперимента записаны в следующей таблице:
Определим по закону Пуассона теоретические частоты разного числа растений сорняков. Для этого предварительно исчислим среднее число растений сорняков в одной выборке:
Из таблицы находим
Определим теоретическое число выборок, в которых число растений сорняков будет равно 0:
то же:
для числа растений сорняков, равного 1:
для числа растений сорняков, равного 2:
для числа растений сорняков, равного 3:
для числа растений сорняков более 3:
Графическое сопоставление обоих распределений говорит о соответствии между эмпирическим и теоретическим распределениями.
Распределение Максвелла
В технике часто встречается распределение по закону Максвелла. Это — распределение существенно положительных величин. Например, эмпирическое распределение эксцентриситетов биений теоретически воспроизводится распределением Максвелла.
Дифференциальный закон распределения Максвелла выражается следующей формулой:
где 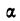
Интегральный закон распределения выразится тогда:
Пример 13.
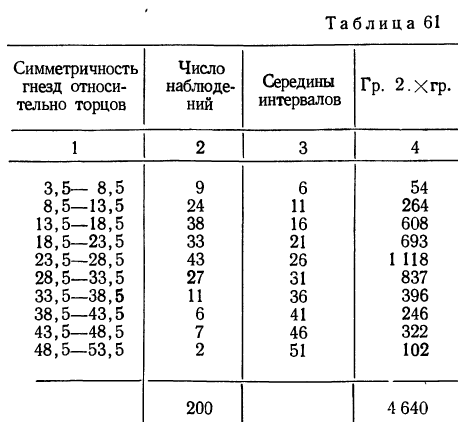
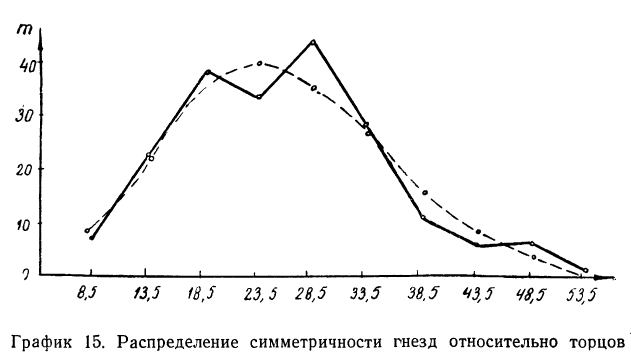
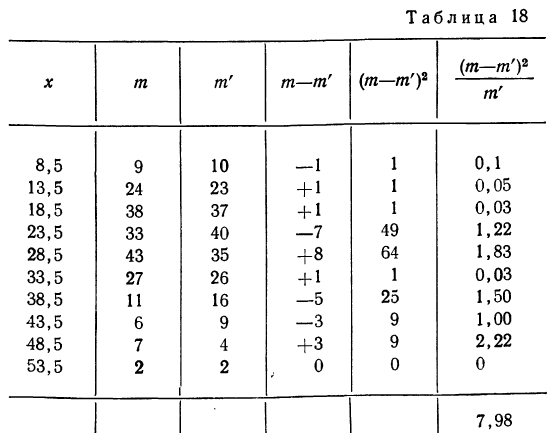
Заимствуем из книги А. М. Длина таблицу распределения симметричности гнезд относительно торцов в круглых плашках (в 0,01 мм) и проведем дополнительные расчеты.
Из этой таблицы легко определим среднюю симметричность:
и параметр рассеяния:
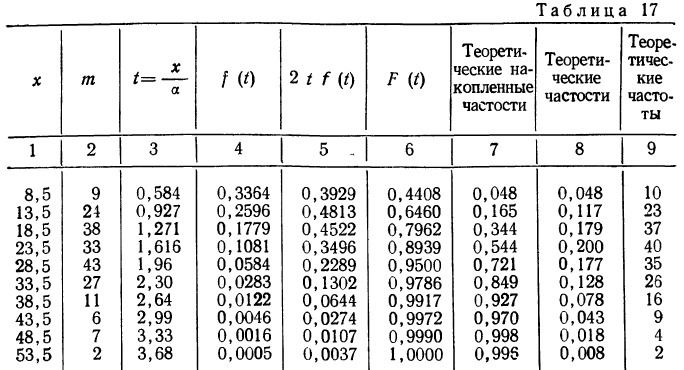
Формула интегрального распределения по закону Максвелла позволяет найти накопленные, а затем теоретические частости и частоты.
Изобразим на графике 15 данные эмпирического и теоретического рядов распределения.
Определим близость их по критерию согласия Ястремского. Для этого приведем в табл. 18 расчет величины С:
По критерию Ястремского находим
Величина I значительно меньше 3. Следовательно, данное эм лирическое распределение хорошо согласуется с законом распределения Максвелла.
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция – определение и вычисление
- Элементы теории ошибок
- Статистические оценки
- Теория статистической проверки гипотез
- Линейный регрессионный анализ
- Вариационный ряд
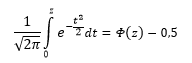
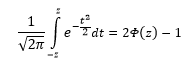
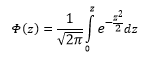








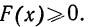
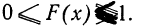
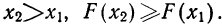
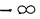 равно нулю, а при х=
равно нулю, а при х=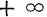 равно единице.
равно единице.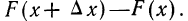
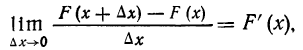
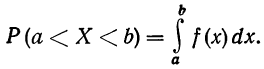
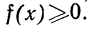
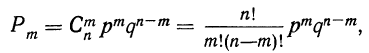
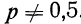
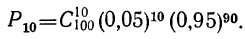
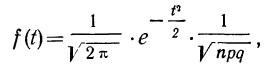
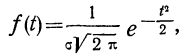
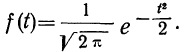
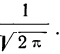
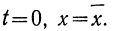
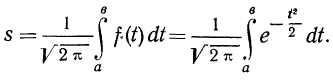
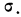
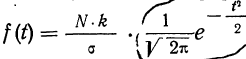
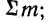
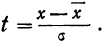
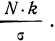
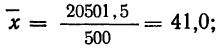
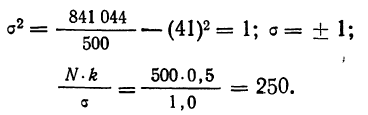
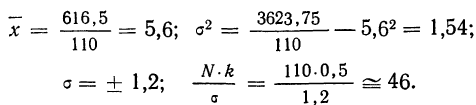
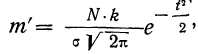
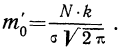
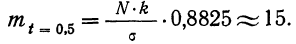
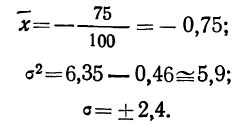
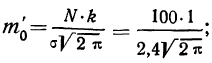
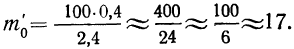

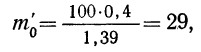
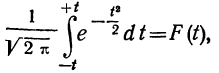
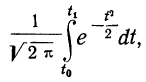
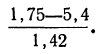
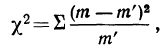
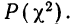
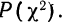
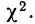
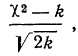
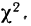
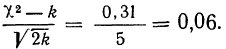
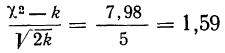
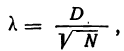
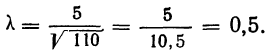
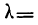
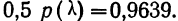
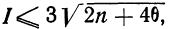
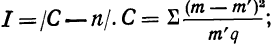
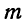 — эмпирические частоты;
— эмпирические частоты;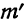 — теоретические частоты;
— теоретические частоты;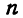 — число групп.
— число групп.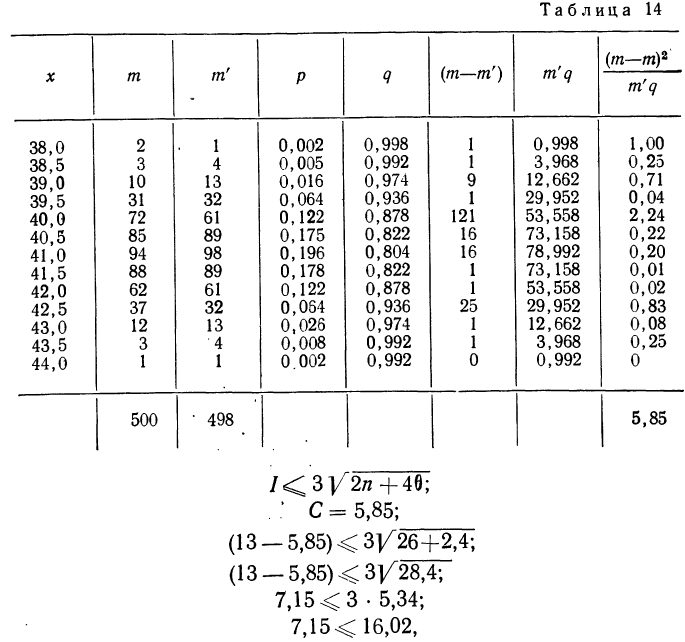
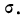
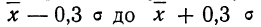 была расположена
была расположена 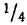 часть всей совокупности;
часть всей совокупности;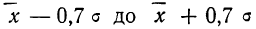 была расположена
была расположена 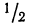 часть всей совокупности;
часть всей совокупности;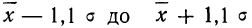 было расположено
было расположено 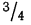 всей совокупности;
всей совокупности;