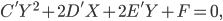Задача 57367 Составить уравнение линии, каждая точка.
Условие
Составить уравнение линии, каждая точка М которой удовлетворяет заданным условиям :отстоит от прямой x=2 на расстоянии ,в 2 раза большем , чем от точки А(4;-3).
Решение
Расстояние от точки М до точки А
Расстояние от точки М до прямой x=2
По условию, расстояние от точки М до прямой [b]х=2[/b] в два раза больше расстояния АМ
Составляем уравнение:
Возводим в квадрат
Упрощаем и получаем ответ
Эллипс со смещенным центром:
( cм рис.)
составить уравнение линии каждая точка которой отстоит от точки (2;1) в 3 раза больше, чем от прямой x=-5 кто знает?
0) Допустим, точка (x_0, y_0) — искомая точка кривой
1) Записываем расстояние от точки до прямой:
d_1 = |Ax_0 + By_0 + C|/sqrt(A^2 + B^2) = |x_0 + 5|
2) Записываем расстояние между двумя точками:
d_2 = sqrt[(x_0 – 2)^2 + (y_0 – 1)^2]
3) По условию d_2 = 3*d_1. Подставляем:
3*|x_0 + 5| = sqrt[(x_0 – 2)^2 + (y_0 – 1)^2]
4) Дальше возводим обе части в квадрат и раскрываем все скобочки. В итоге получим:
Множество точек на плоскости
Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как
то
После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 – 2x + 1 + y 2 – 4y + 4 = x 2 + 4x + 4 + y 2
или
– 6x – 4y + 1 = 0
Ответ: – 6x – 4y + 1 = 0.
Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /2.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /2. Так как:
то
или
Возведя левую и правую части в квадрат и упрощая, получим:
4(x – 1) 2 + 4(y + 2) 2 = |x – 1| 2
т.е.
4(x 2 – 2x + 1) + 4(y 2 + 4y + 4) = x 2 – 2x + 1
или
3x 2 + 4y 2 – 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 – 6x +16y +19 = 0.
Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.
Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.
[spoiler title=”источники:”]
http://sprashivalka.com/tqa/q/28000618
http://math.semestr.ru/line/points.php
[/spoiler]
Задача 57367 Составить уравнение линии, каждая точка.
Условие
Составить уравнение линии, каждая точка М которой удовлетворяет заданным условиям :отстоит от прямой x=2 на расстоянии ,в 2 раза большем , чем от точки А(4;-3).
Решение
Расстояние от точки М до точки А
Расстояние от точки М до прямой x=2
По условию, расстояние от точки М до прямой [b]х=2[/b] в два раза больше расстояния АМ
Составляем уравнение:
Возводим в квадрат
Упрощаем и получаем ответ
Эллипс со смещенным центром:
( cм рис.)
Уравнение линии — определение с примерами решения
Содержание:
Множества:
Под множеством X = <х, х х”, . >понимается собрание (совокупность) некоторых элементов х, х х’ . . Если х есть элемент множества X, то пишут х € X (читается: х принадлежит X); если у не является элементом множества X, то пишут у t X (читается: у не принадлежит множеству X).
Пример:
X — множество всех студентов в данной аудитории.
Пример:
Х = <1,2, 3, . >— множество натуральных чисел.
Удобно ввести понятие пустого множества
Пример:
Множество трехголовых людей пусто.
Множества X и X’ считаются равными, т. е. X = X’, если они состоят из одних и тех же элементов.
Определение: Множество У, состоящее из части элементов множества X или совпадающее с ним, называется подмножеством множества X; в этом случае пишут
Условились считать, что пустое множество есть подмножество любого множества.
Если множества изображать «логическими фигурами», то соотношению (1) соответствует рис. 10.
Если под символом V понимать «для любого», то соотношение (1) эквивалентно следующему:
где стрелка 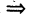
Пример:
Пусть X — множество всех студентов первого курса, У — множество студенток первого курса. Очевидно,
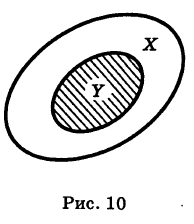
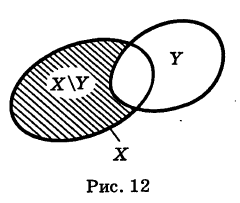
Определение: Под объединением (суммой) двух множеств X и Y понимается множество X U У (U — знак объединения), состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств, т. е. входящих или в X, или в У, или в X и в У одновременно (рис. 11).
Аналогично определяется объединение большего числа множеств. Так, под объединением X U У U Z трех множеств понимается множество всех элементов, принадлежащих хотя бы одному из множеств X, У, Z. Логически знак объединения множеств соответствует союзу «или» (соединительному).
Определение: Под пересечением (произведением) двух множеств X и У понимается множество 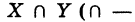
Таким образом, знак пересечения множеств логически соответствует союзу «и». Если множества X и У не имеют общих элементов, то их пересечение пусто:
Аналогично определяется пересечение большего числа множеств. Так, под пересечением 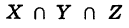
Например: <1, 2, 3> 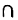
Определение: Для множеств X и У под их разностью ХУ понимается множество, содержащее все элементы множества X, не входящие в множество У (рис. 12).
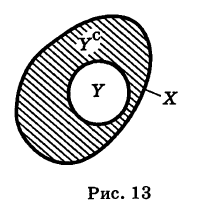
Если У X, то множество Ус = ХУ называется дополнением множества У до множества X (рис. 13).
Очевидно, 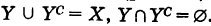
Например: <1, 2, 3> <2, 3, 4>= <1>.
Метод координат на плоскости
Раздел математики, занимающийся изучением свойств геометрических фигур с помощью алгебры, носит название аналитической геометрии, а использование для этой цели координат называется методом координат.
Выше мы применили метод координат для решения ряда важных, но частных задач. Теперь мы приступим к систематическому изложению того, как в аналитической геометрии решается общая задача, состоящая в исследовании методами математического анализа формы, расположения и свойств данной линии.
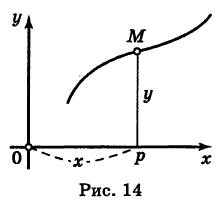
Пусть мы имеем некоторую линию на плоскости (рис. 14). Координаты х и у точки М, лежащей на этой линии, не могут быть вполне произвольными; они должны быть подчинены известным ограничениям, обусловленным геометрическими свойствами данной линии. Тот факт, что числа х и у являются координатами точки, лежащей на данной линии, аналитически записывается в виде некоторого уравнения. Это уравнение называется уравнением линии на плоскости.
Сущность метода координат на плоскости заключается в том, что всякой плоской линии сопоставляется ее уравнение1*, а затем свойства этой линии изучаются путем аналитического исследования соответствующего уравнения.
Линия как множество точек
Линия на плоскости обычно задается как множество точек, обладающих некоторыми геометрическими свойствами, исключительно им присущими.
Пример:
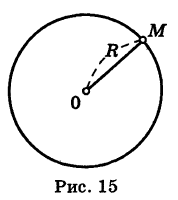
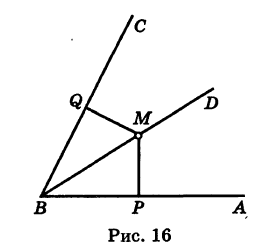
Окружность радиуса R (рис. 15) есть множество всех точек плоскости, удаленных на расстояние R от некоторой ее точки О (центр окружности).
Иными словами, на окружности расположены те и только те точки, расстояние которых от центра окружности равно ее радиусу.
Пример:
Биссектриса угла ABC (рис. 16) есть множество всех точек, лежащих внутри угла и равноудаленных от его сторон. Этим утверждается, что: 1) для каждой точки М, лежащей на биссектрисе BZ), длины перпендикуляров MP и MQ, опущенных соответственно на стороны ВА и ВС угла, равны между собой: MP = MQ, и 2) всякая точка, находящаяся внутри угла ABC и не лежащая на его биссектрисе, будет ближе к одной стороне угла, чем к другой.
Уравнение линии на плоскости
Сформулируем теперь точнее определение уравнения линии1* на плоскости.
Определение: Уравнением линии (уравнением кривой) на плоскости Оху называется уравнение, которому удовлетворяют координаты х и у каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Таким образом, для того чтобы установить, что данное уравнение является уравнением некоторой линии К, необходимо и достаточно: 1) доказать, что координаты .любой точки, лежащей на линии К у удовлетворяют этому уравнению, и 2) доказать, обратно, что если координаты некоторой точки удовлетворяют этому уравнению, то точка обязательно лежит на линии К.
Отсюда уже автоматически будет следовать, что: 1′) если координаты какой-нибудь точки не удовлетворяют данному уравнению, то точка эта не лежит на линии К, и 2′) если точка не лежит на линии К, то ее координаты не удовлетворяют данному уравнению.
Если точка М (*, у) передвигается по линии К, то ее координаты х и у, изменяясь, все время удовлетворяют уравнению этой кривой. Поэтому координаты точки М (х, у) называются текущими координатами точки линии К.
На плоскости Оху текущие координаты точки М данной кривой К обычно обозначаются через х и у, причем первая из них есть абсцисса точки М, а вторая — ее ордината. Однако, если это целесообразно, текущие координаты точки М можно обозначать.
Линию мы часто будем называть кривой независимо от того, прямолинейна она или не прямолинейна любыми буквами, например М (X, У) или М 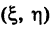
где точки N (х, у) и N (X, У) расположены на плоскости Оху, представляют собой уравнение одной и той же прямой на этой плоскости.
Основное понятие аналитической геометрии — уравнение линии — поясним на ряде примеров.
Пример:
Составить уравнение окружности данного радиуса R с центром в начале координат.
Решение:
Возьмем на окружности (рис. 17) произвольную точку М (х, у) и соединим ее с центром О. По определению окружности имеем ОМ = R,
т. е. 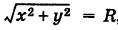
Уравнение (1) связывает между собой координаты х и у каждой точки данной окружности. Обратно, если координаты точки М (х, у) удовлетворяют уравнению (1), то, очевидно, ОМ = R и, следовательно, эта точка лежит на нашей окружности. Таким образом, уравнение (1) представляет собой уравнение окружности радиуса R с центром в начале координат.
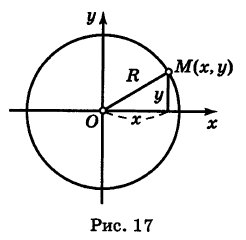
Пример:
Составить уравнения биссектрис координатных углов.
Решение:
Рассмотрим сначала биссектрису I и III координатных углов (рис. 18, а). Возьмем на ней произвольную точку М (х, у). Если точка М лежит в I квадранте, то абсцисса и ордината ее обе положительны и равны между собой (по свойству биссектрисы). Если же точка М (jc, у) лежит в III квадранте, то абсцисса и ордината будут обе отрицательны, а модули их равны, поэтому будут равны и координаты хм у этой точки. Следовательно, в обоих случаях имеем
Обратно, если координаты х и у какой-нибудь точки М (х, у) удовлетворяют уравнению (2), то эта точка, очевидно, лежит на биссектрисе
I и III координатных углов. Поэтому уравнение (2) представляет собой уравнение биссектрисы I и III координатных углов.
Рассмотрим теперь биссектрису II и IV координатных углов (рис. 18, б). Возьмем на ней произвольную точку N (х, у). В каком бы квадранте — II или IV — ни была расположена эта точка, координаты ее х и у равны по модулю и отличаются знаками.
Следовательно, в обоих случаях имеем
Обратно, если для какой-нибудь точки N (,х, у) выполнено уравнение (3), то эта точка, очевидно, лежит на биссектрисе II и IV координатных углов. Таким образом, уравнение (3) есть уравнение биссектрисы II и IV координатных углов.
Пример:
Составить уравнение прямой, параллельной оси ординат.
Решение:
Пусть прямая АВ || О у и пусть отрезок OA = а (рис. 19, а). Тогда для любой точки М (х, у) прямой АВ ее абсцисса х равна а:
Обратно, если абсцисса некоторой точки М (х, у) равна а, то эта точка лежит на прямой АВ.
Таким образом, уравнение (4) представляет собой уравнение прямой, параллельной оси Оу и отстоящей от нее на расстоянии, равном числовому значению а; при этом если прямая расположена справа от оси Оу, то а положительно; если же прямая расположена слева от оси Оу, то а отрицательно.
В частности, при а = 0 получаем уравнение оси ординат: х = 0.
Пример:
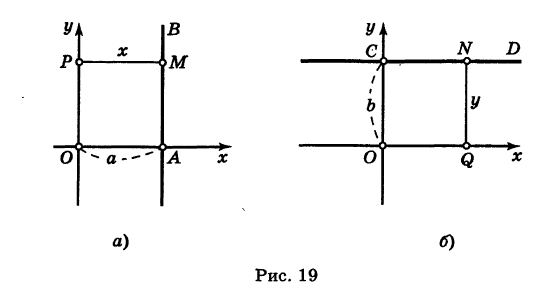
Составить уравнение прямой, параллельной оси абсцисс.
Решение:
Совершенно аналогично, если прямая CD || Ох и ОС = Ь (рис. 19, б), то ее уравнение будет
при этом если прямая CD расположена выше оси Оху то Ъ положительно, если же прямая CD расположена ниже оси Ох, то b отрицательно.
В частности, при b = 0 получаем уравнение оси абсцисс: у = 0.
Пример:
Найти линию, расстояние точек которой от точки В (12, 16) в два раза больше, чем от точки А (3, 4).
Решение:
Если М (х, у) — произвольная точка искомой линии, то согласно условию задачи имеем
Чтобы составить уравнение этой линии, надо выразить AM и ВМ через координаты х и у точки М. На основании формулы расстояния между двумя точками имеем
откуда, согласно соотношению (5),
Это и есть уравнение искомой линии.
Но в таком виде трудно судить, какую линию представляет это уравнение, поэтому упростим его. Возведя обе части в квадрат и раскрыв скобки, получим
или после несложных преобразований имеем равносильное уравнение
Сравнивая полученное уравнение с уравнением (1), мы видим, что искомая линия является окружностью радиуса 10 с центром в начале координат.
Построение линии по ее уравнению
Если переменные х и у связаны некоторым уравнением, то множество точек М (х, у), координаты которых удовлетворяют этому уравнению, представляет собой, вообще говоря, некоторую линию на плоскости (геометрический образ уравнения).
В частных случаях эта линия может вырождаться в одну или несколько точек. Возможны также случаи, когда уравнению не соответствует никакое множество точек.
соответствует единственная точка (1, 2), так как этому уравнению удовлетворяет единственная пара значений: х = 1 и у = 2.
не соответствует никакое множество точек, так как этому уравнению нельзя удовлетворить никакими действительными значениями x и у.
Зная уравнение линии, можно по точкам построить эту линию.
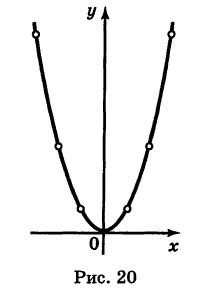
Пример:
Построить линию, выражаемую уравнением
(обычно говорят короче: построить линию у = х 2 ).
Решение:
Давая абсциссе х в уравнении (1) числовые значения и вычисляя соответствующие значения ординаты у, получим следующую таблицу:
Нанося соответствующие точки на плоскость, мы видим, что конфигурация этих точек определяет начертание некоторой линии; при этом чем гуще построена сеть точек, тем отчетливее выступает ее контур. Соединяя построенные точки линией, характер которой учитывает положение промежуточных точек1*, мы и получаем линию, определяемую данным уравнением (1) (рис. 20). Эта линия называется параболой.
Некоторые элементарные задачи с решением
Если известно уравнение линии, то легко могут быть решены простейшие задачи, связанные с расположением этой линии на плоскости.
Задача 1. Заданы уравнение линии К и координаты точки М (а, Ь). Определить, лежит точка М на линии К или нет.
Иными словами, требуется узнать, проходит линия К через точку М или не проходит.
На основании понятия уравнения линии получаем правило:
чтобы определить, лежит ли точка М на данной линии К, нужно в уравнение этой линии подставить координаты нашей точки. Если при этом уравнение удовлетворится (т. е. в результате подстановки получится тождество), то точка лежит на линии; в противном случае, если координаты точки не удовлетворяют уравнению линии, данная точка не лежит на линии.
Для того чтобы иметь возможность судить о положении промежуточных точек линии, мы должны предварительно изучить общие свойства уравнения этой линии (подробнее см. в гл. XI).
В частном случае линия проходит через начало координат тогда и только тогда, когда уравнение линии удовлетворяется при х = 0 и у — 0.
Пример:
Определить, лежат ли на ней точки М (-3, 4) и N (4, -2).
Решение:
Подставляя координаты точки М в уравнение (1), получаем тождество
Следовательно, точка М лежит на данной окружности.
Аналогично, подставляя координаты точки N в уравнение (1), будем иметь
Следовательно, точка N не лежит на данной окружности.
Задача 2. Найти точку пересечения двух линий, заданных своими уравнениями.
Точка пересечения одновременно находится как на первой линии, так и на второй. Следовательно, координаты этой точки удовлетворяют уравнениям обеих линий. Отсюда получаем правило:
чтобы найти координаты точки пересечения двух линий, достаточно совместно решить систему их уравнений.
Если эта система не имеет действительных решений, то линии не пересекаются.
Пример:
Найти точки пересечения параболы у = х2 и прямой у — 4.
Решение:
получаем две точки пересечения: А (-2, 4) и В (2, 4).
Задача 3. Найти точки пересечения данной линии с осями координат.
Эта задача является частным случаем задачи 2. Учитывая, что уравнение оси Ох есть у = 0, получаем правило: ‘
чтобы найти абсциссы точек пересечения данной линии с осью Ох, в уравнении этой линии нужно положить у = 0 и решить полученное уравнение относительно х.
Аналогично, так как уравнение оси Оу есть х — 0, то получаем правило:
чтобы найти ординаты точек пересечения данной линии с осью Оу, нужно в уравнении этой линии положить д: = 0 и решить полученное уравнение относительно у.
Пример:
Найти точки пересечения окружности 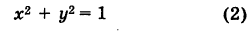
Решение:
Полагая у = 0 в уравнении (2), получаем х2= 1, т. е. х1 = -1 и х2 = 1. Отсюда находим две точки пересечения данной окружности с осью Ох (рис. 21): А (-1, 0) и В (1, 0).
Аналогично, полагая х = 0 в уравнении (2), получаем у2 = 1, т. е. ух = -1 и у2 = 1. Следовательно, имеются две точки пересечения данной окружности с осью Оу (рис. 21): С (0, -1) и D (0, 1).
Две основные задачи аналитической геометрии на плоскости
Резюмируя содержание этой главы, можно сказать, что всякой линии на плоскости соответствует некоторое уравнение между текущими координатами (х, у) точки этой линии. Наоборот, всякому уравнению между х и г/, где х и у — координаты точки на плоскости, соответствует, вообще говоря, некоторая линия, свойства которой вполне определяются данным уравнением.
Отсюда, естественно, возникают две основные задачи аналитической геометрии на плоскости.
Задача 1 .Дана линия, рассматриваемая как множество точек. Составить уравнение этой линии.
Задача 2. Дано уравнение некоторой линии. Изучить по этому уравнению ее геометрические свойства (форму и расположение).
Алгебраические линии
Определение: Линия называется линией (или кривой) n-го порядка(п = 1, 2. ), если она определяется уравнением п-й степени относительно текущих прямоугольных координат.
Такие линии называются алгебраическими. Например, линии
являются кривыми соответственно первого, второго и третьего порядков.
Общий вид кривых первого порядка есть
где коэффициенты А и Б не равны нулю одновременно, т. е. 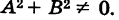
Общий вид кривых второго порядка следующий:
где коэффициенты А, Б и С не равны нулю одновременно, т. е.
Заметим, что не всякому уравнению второго порядка соответствует действительная кривая. Например, уравнению 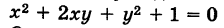
В следующих главах мы подробно изучим кривую первого порядка (прямую линию) и рассмотрим важнейшие представители кривых второго порядка (окружность, эллипс, гипербола, парабола).
Уравнение кривой n-го порядка может быть записано в следующем виде:
где хотя бы один из старших коэффициентов apqt т. е. таких, что p + q = п, отличен от нуля ( 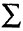
Отметим важное свойство: порядок кривой (1) не зависит от выбора прямоугольной системы координат.
Действительно, выбирая другую систему прямоугольных координат О’х’уна основании формул перехода имеем
где 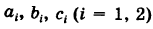
Отсюда уравнение кривой (1) в новых координатах О’х’у’ будет иметь вид
где п’ — порядок преобразованной кривой. Очевидно, что п’
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
1.3. Аналитическая геометрия. Аналитическая геометрия на плоскости
1.3.1. Аналитическая геометрия на плоскости
Если на плоскости произвольно взята декартова система координат, то всякое уравнение первой степени относительно текущих координат х и у
где А и B одновременно не равны нулю, определяет прямую в этой системе координат.
Верно и обратное утверждение: в декартовой системе координат всякая прямая может быть представлена уравнением первой степени вида (1.24).
Уравнение (1.24) называется общим уравнением прямой.
Углом наклона прямой к оси Ох называется наименьший угол j, на который нужно повернуть в положительном направлении ось абсцисс до ее совпадения с данной прямой. Направление любой прямой характеризуется ее угловым коэффициентом к, который определяется как тангенс угла наклона j этой прямой к оси Ох, т. е.
Исключение составляет только лишь прямая, перпендикулярная оси Ох, которая не имеет углового коэффициента.
Уравнение прямой, имеющей угловой коэффициент к и пересекающей ось Оу в точке, ордината которой равна b (начальная ордината), записывается в виде:
Частные случаи уравнения (1.24) приведены в следующей таблице.
Угловой коэффициент к прямой, заданной общим уравнением Ax + By + C= 0, находится как коэффициент при х в выражении у через х:
Угловой коэффициент к прямой, заданной двумя точками вычисляется по формуле
Уравнением прямой в отрезках называется уравнение вида:
где а и b — соответственно абсцисса и ордината точек пересечения прямой с осями Ох и Oy, т. е. длины отрезков, отсекаемых прямой на координатных осях, взятые с определенными знаками.
Уравнение прямой, проходящей через точку
щей угловой коэффициент к, записывается в виде:
Пучком прямых называется совокупность прямых плоскости, проходящих через одну и ту же точку А — центр пучка. Уравнение (1.28) можно рассматривать как уравнение пучка прямых, поскольку любая прямая пучка может быть получены из уравнения (1) при соответствующем значении углового коэффициента к. Исключение составляет лишь одна прямая пучка, которая параллельна оси Oy — ее уравнение х = xA.
Уравнение прямой, проходящей через две данные точки имеет вид:
Если точки A и B определяют прямую, параллельную оси 

писывается соответственно в виде:
Условия пересечения, параллельности или совпадения двух прямых, заданными своими общими уравнениями
приведены в следующей таблице.

Если известны угловые коэффициенты прямых, то ус
ловие параллельности этих прямых состоит в равенстве их угловых коэффициентов:
Условие перпендикулярности двух прямых, угловые коэффициенты которых соответственно равны
т. е. угловые коэффициенты этих прямых обратны по абсолютной величине и противоположны по знаку.
Под углом между двумя прямыми понимается один из двух смежных углов, образованных при их пересечении. Тангенс угла j между двумя прямыми, угловые коэффициенты которых соответственно равны к1 и к2, вычисляется по формуле
причем знак «плюс» соответствует острому углу
Уравнение окружности с центром в точке S^; b) и радиусом r имеем вид:
Это каноническое уравнение окружности (рис. 7).
Уравнение второй степени относительно текущих координат х и у является уравнением окружности тогда и только тогда, когда в этом уравнении коэффициенты при квадратах координат равны, а член с произведением координат отсутствует. Таким образом, это уравнение имеет вид:
В этом случае говорят, что окружность задана общим уравнением.
Для определения координат центра и радиуса окружности, заданной общим уравнением, надо с помощью тождественных преобразований уравнение (1.35) привести к виду (1.34).
Эллипс есть геометрическое место точек, сумма расстояний которых от двух фиксированных точек, называемых фокусами эллипса, есть величина постоянная (2а), большая, чем расстояние между фокусами (2с).
Простейшее уравнение эллипса получается, если расположить координатную систему следующим образом: за ось Оx принять прямую, проходящую через фокусы F1 и F2, а за ось Оу — перпен-
дикуляр к оси абсцисс в середине отрезка F1F2 (рис. 8). Тогда уравнение эллипса примет вид:
Точки А1 и А2, B1 и B2 пересечения эллипса с его осями симметрии (координатными осями) называются вершинами эллипса. Отрезки А1А2 = 2а и B1B2 = 2b называются осями эллипса, причем А1А2 — большой осью, а B1B2 — малой осью, так как а > b. Таким образом, параметры а и b, входящие в уравнение эллипса, равны его полуосям.
Эксцентриситетом эллипса называется отношение расстояния между фокусами к его большой оси, т. е.
Очевидно, что е а и уже большой осью будет отрезок B1B2 = 2b, а малой осью — отрезок А1А2 = 2а. Эксцентриситет такого эллипса вычисляется по формуле
Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых от двух данных точек, называемых фокусами, есть величина постоянная (2а), меньшая, чем расстояние между фокусами (2с).
Простейшее уравнение гиперболы получается, если расположить координатную систему следующим образом: за ось Ох принять прямую, проходящую через фокусы

Гипербола имеет две оси симметрии (координатные оси), с одной из которых (осью абсцисс) она пересекается в двух точках А1 и А2, называемых вершинами гиперболы. Отрезок.

Таким образом, параметры а и b, входящие в уравнение гиперболы, равны ее полуосям.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к ее действительной оси:
Ее асимптоты те же, что и у гиперболы (1.39).
Гиперболы (1.39) и (1.42) называются сопряженными. Гипербола называется равносторонней, если ее действительные и мнимые оси равны, т. е. а = b. Простейшее уравнение равносторонней гиперболы имеет вид:
Если мнимая ось гиперболы направлена по оси Ох и имеет длину 2а, а действительная ось длиной 2b направлена по оси Oy, то уравнение гиперболы (рис. 11) имеет вид:

Эксцентриситет такой гиперболы вычисляется по формуле

Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой параболы.
Величина р, равная расстоянию от фокуса до директрисы, называется параметром параболы; прямая, проходящая через фокус параболы перпендикулярно ее директрисе, называется осью, а точка пересечения параболы с ее осью — вершиной параболы.
Простейшее уравнение параболы получается, если координатная система расположена следующим образом: за одну из координатных осей берется ось параболы, а за другую — прямая, перпендикулярная оси параболы и проведенная посредине между фокусом и директрисой.
Тогда уравнение параболы примет вид:



определяет параболу, ось которой перпендикулярна оси абсцисс.
определяет параболу, ось которой перпендикулярна оси ординат.
Уравнения (1.48) и (1.49) приводятся к простейшему виду (1.44 — 1.47) путем тождественных преобразований с последующим параллельным переносом координатной системы.
Пример 1.16. Даны вершины А (2; 1), В (6; 3), C (4; 5) треугольника. Найти: 1) длину стороны АВ; 2) внутренний угол А в радианах с точностью до 0,01; 3) уравнение высоты, проведенной через вершину С; 4) уравнение медианы, проведенной через вершину С;
5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины С; 7) систему линейных неравенств, определяющую внутреннюю область треугольника. Сделать чертеж.
Делаем чертеж (рис. 16).
1. Длину стороны АВ находим как расстояние между двумя точками А и В.
2. Для определения внутреннего угла А найдем уравнение прямой AC:
отсюда 2х — у — 3 = 0 или у = 2х — 3 и угловой коэффициент прямой AC равен: kAC = 2; далее находим уравнение прямой АВ:
Находим угол А 
3. Уравнение высоты, проведенной через вершину C, ищем в виде у — yC = kCD (x — xC) и так как CD А прямой АВ, то
4. Для определения уравнения медианы CM находим координаты точки M, которая делит прямую АВ пополам
Уравнение прямой CM ищем в виде:
а это означает, что уравнение медианы имеет вид х = 4, т. е. прямая CM L Ох.
5. Точку пересечения высот треугольника найдем как точку К пересечения высот CD и BK.
Находим уравнение высоты ВК:
Решаем систему уравнений, описывающих прямые CD и BK:
Тогдат. е. координаты точ
ки К будут:
6. Для нахождения длины высоты CD запишем нормальное уравнение прямой АВ:

7. Находим систему линейных неравенств, определяющих внутреннюю область треугольника.
Найдем уравнение прямой BC:
Итак:
Берем любую точку, лежащую внутри треугольника, например, (4; 3) и подставляем ее координаты в левую часть уравнений прямых:
следовательно, система неравенств имеет вид:
Пример 1.17. Составить уравнение прямой I, проходящей через точку А (2; -4) и отстоящей от начала координат на расстоянии, равном 2 единицам.
Решение. Пусть уравнение искомой прямой имеет вид:
Для определения углового коэффициента к этой прямой воспользуемся тем, что она отстоит от начала координат на расстоянии, равном 2 единицам. Найдем это расстояние непосредственно. Уравнение перпендикуляра, опущенного из начала координат на прямую


С другой стороны, по условию OC = 2. Таким образом, получаем уравнение для нахождения углового коэффициента к искомой прямой I:
получим координаты точки C их пересечения:
Отсюда находим расстояние от начала координат до прямой I:

В заключение отметим, что отыскивая уравнение прямой I в виде у — yA = k(x — Xa), мы предполагали тем самым, что эта прямая не параллельна оси ординат. Но очевидно, что прямая х = 2 (параллельная оси Оу) также удовлетворяет условию задачи, так как она проходит через точку А (2; -4) и отстоит от начала координат на расстоянии, равном 2 единицам (рис. 17).
Пример 1.18. Составить уравнения прямых, параллельных прямой 3х + 4у — 1 = 0 (I) и отстоящих от нее на расстоянии равном 1.
Решение. Уравнение каждой из прямых будем искать в виде 
угловой коэффициент
нимает вид:
Для отыскания параметра b воспользуемся тем, что расстояние от любой точки прямой I, например, от точки А (3; -2) до прямой (*) согласно условию равно 1. Но это расстояние может быть вычислено и непосредственно. Запишем для этого
уравнение прямой h, проведенной из точки А перпендикулярно прямой I:
Решив, далее, совместно уравнения прямых h и I найдем координаты точки В их пересечения:

Тогда искомое расстояние равно длине отрезка АВ:
Приравнивая это выражение единице, получим уравнение относительно b:
Решения этого уравнения таковы:
Пример 1.19. Составить уравнение линии, расстояние каждой точки которой от точки F (8; 0) вдвое больше, чем от прямой х — 2 = 0. Сделать чертеж.
Пусть М(х; у) — текущая точка линии. По условию задачи MF = 2MN.
Возводя в квадрат и раскрывая скобки, получим
Это есть каноническое уравнение гиперболы (рис. 18).
Пример 1.20. Составить уравнение линии, каждая точка которой равноудалена от точки F (0; — 4) и от прямой у + 2 = 0. Сделать чертеж.
Если M(x; у) есть текущая точка линии, то по условию задачи MF = MN или
Подставляя координаты точек

источники:
http://www.evkova.org/uravnenie-linii
http://matica.org.ua/metodichki-i-knigi-po-matematike/a-s-shapkin-zadachi-po-vysshei-matematike-teorii-veroiatnostei-matematicheskoi-statistike-matematicheskomu-programmirovaniiu-s-resheniia/1-3-analiticheskaia-geometriia-analiticheskaia-geometriia-na-ploskosti
Аналитическая геометрия на плоскости
Первая задача аналитической геометрии – представление
геометрической фигуры уравнением или неравенством, системой уравнений
или неравенств на основе применения координат. Вторая задача
аналитической геометрии – исследовать, какие геометрические фигуры
представляются теми или иными уравнениями.
Пусть 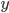
Уравнение 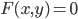
- координаты каждой точки линии удовлетворяют этому уравнению и
- координаты точки, не принадлежащей линии, не удовлетворяют
этому уравнению.
При этом уравнение может задавать точку, отрезок или пустое множество.
Уравнение называется алгебраическим степени 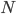
представляет собой многочлен степени 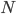
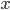
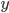
численными коэффициентами.
Упражнения
Циклоидой называется траектория, описываемая точкой
окружности радиуса r, катящейся без скольжения по данной прямой 
Приняв прямую за ось абсцисс, а начальное положение точки
за начало координат, напишите уравнение циклоиды и постройте ее.
Пусть 
катящейся окружности, а 
точки 
образует луч 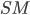
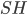
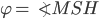
– основание перпендикуляра, опущенного из точки 

Получили следующее параметрическое задание циклоиды
Исключив 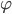
декартовых координатах. Циклоида – линия периодическая с периодом 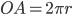
Параметрическое задание: 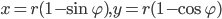
В декартовых координатах: 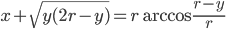
Эпициклоидой называется траектория, описываемая точкой 
Примем центр 
cистемы координат, а за параметр – угол 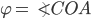

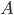
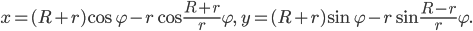
Кардиоидой называется кривая в частном случае, когда 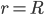
Гипоциклоидой называется траектория, описываемая точкой 
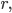
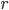
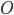
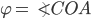

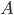
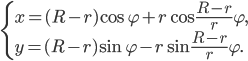
Астроидой называется кривая в частном случае, когда 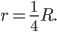
Дана прямая 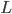
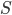
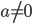
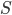
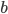
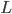
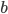
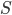
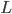
Пусть 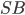
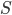
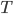
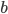
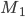
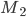
на расстоянии 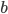
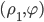
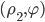
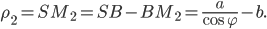
В обобщенной полярной системе кривая задается уравнением
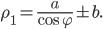
Конхоидой данной кривой называется кривая, получающаяся при
увеличении или уменьшении полярного радиуса каждой точки данной кривой
на постоянный отрезок.
Улиткой Паскаля называется конхоида окружности, если за полюс 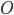
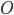
Если 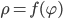
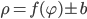
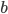
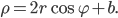
Если 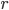
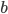
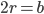
Овалом Кассини называется геометрическое место точек
плоскости, для которых произведение расстояний до двух фиксированных
точек этой плоскости постоянно. Пусть 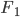
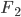
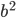
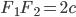
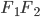
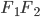
Для 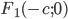
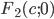
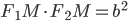
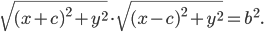
Отсюда
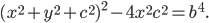
При 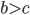
При 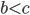
Лемнискатой Бернулли называется овал Кассини в частном случае, когда 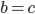
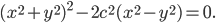
Четырехлепестковой розой называется геометрическое место
оснований перпендикуляров, опущенных из вершины прямого угла на отрезок
постоянной длины, который перемещается своими концами по сторонам
прямого угла. Приняв за полюс полярной системы координат вершину прямого
угла и направим полярную ось по одной из сторон прямого угла. Длина
отрезка 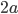
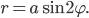
Луч 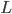
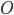
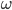

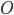
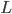
со скоростью 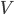

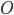
полюс. Напишите уравнение спирали Архимеда в полярной системе координат и постройте ее.
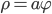
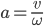
Пусть 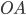
в конце диаметра. Через точку 
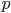
касательную 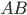
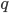
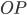
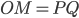
Геометрическое место точек 
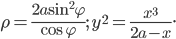
Даны диаметрально противоположные точки 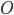

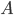
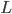

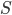

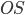
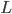

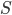

соответственно прямым 

кривую, называемую верзиерой. Выведите уравнение верзиеры в прямоугольной декартовой системе.
Следует из соотношения 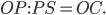
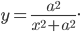
§12.1. Уравнения прямой на плоскости
Задача. Найдите уравнение прямой, проходящей через точку
перпендикулярно ненулевому вектору 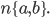
Точка 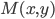

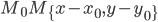
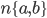
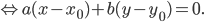
уравнение прямой, проходящей через данную точку
перпендикулярно ненулевому вектору 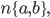
Здесь 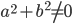
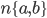
Основная теорема теории прямой на плоскости.
Геометрическое место точек плоскости, координаты которых в некоторой
прямоугольной декартовой системе координат удовлетворяют уравнению
есть прямая, параллельная вектору 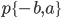
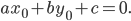
Доказательство.
Точка 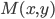

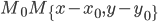
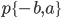
или в силу того, что 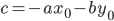
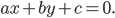
Уравнение
называется общим уравнением прямой на плоскости.
Частные случаи общего уравнения. При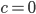
уравнение прямой, проходящей через начало координат.
Пусть 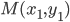
Из уравнения 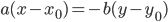
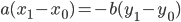
уравнение прямой, проходящей через точки две данные точки,
Если это точки 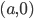
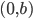
и получим уравнение прямой в отрезках
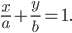
Ненулевой вектор, параллельный прямой, называется ее направляющим вектором.
Пусть некоторый направляющий вектор данной прямой имеет координаты 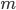
Тогда уравнение (3) можно переписать в виде канонического уравнения прямой
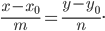
Приравняв отношения к параметру 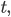
прямой на плоскости
Предположим, что в общем уравнении 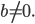
Введем обозначения 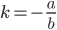
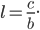
называется уравнением с угловым коэффициентом 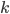
начальной ординатой
Если точка 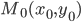
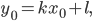
получим уравнение прямой через угловой коэффициент и точку
Если 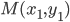
С другой стороны эта дробь равна тангенсу угла 
т. е. угловой коэффициент прямой равен тангенсу угла наклона этой прямой к оси абсцисс
Вернемся к самой первой задаче этого параграфа.
Задача. Найдите уравнение прямой, проходящей через точку
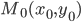
Пусть 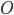

точка плоскости. Вектор 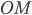
Точка 

векторы 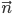
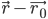
т. е 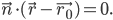
через 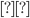
Упражнения
-
Докажите, что уравнение прямой, проходящей через две точки можно записать в виде
-
Докажите, что три точки лежат на одной прямой тогда и только тогда, когда
- Через каждую вершину треугольника
проведите прямую,
параллельную противоположной стороне, где(1; -2 ),
(0; 3),
(1; 1).
-
Покажите, что четырехугольник
является трапецией, где
(-2;2),
(-3;1),
и
Составьте уравнение средней линии и диагоналей трапеции. -
Даны уравнения двух смежных сторон параллелограмма
и
и
точка пересечения его диагоналей. Напишите уравнения двух других сторон
параллелограмма. - Через точку
проведите прямую, отсекающую равные отрезки на осях координат.
- Вершины треугольника находятся в точках
и
; 7).
- а) биссектрисы внутреннего угла
- б) медианы, проведенной из вершины
- в) высоты, опущенной из вершины
.
- Даны середины сторон треугольника
, где
(2; -1 ),
(-3; -3),
(-1; 0).
- Уравнение движения точки
имеет вид
Определите
- Найдите проекцию точки
(5, -2) на прямую
- Определите координаты точки, симметричной началу координат относительно
прямой - На прямой
найдите точку, сумма расстояний которой до
точек(-5;0) и
(-3;4) наименьшая.
Напишите уравнение
§ 12.2. Взаимное расположение прямых на плоскости
Прямые, определяемые уравнениями
параллельны тогда и только тогда, когда направляющие векторы
и 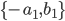
Условия, при которых два уравнения определяют одну и ту же прямую
Все коэффициенты одного уравнения получаются из другого умножением на
некоторое отличное от нуля число, т. е. уравнения эквивалентны. Ясно, что
если прямые совпадают, то имеет место пропорция (4).
Плоскость называется ориентированной, если на ней указано некоторое направление
вращения в качестве положительного. Углом 
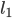
прямой 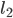
повернуть 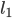
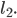
направлении, то 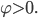
то 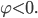
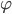
направляющими векторами
Отсюда условие перпендикулярности прямых:
Если уравнения записаны через угловой коэффициент,
то условия взаимного расположения прямых выглядят так:
условие параллельности 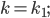
условие совпадения 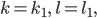
условие перпендикулярности
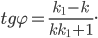
Если существует общая точка прямых, заданных уравнениями
то ее координаты удовлетворяют этим уравнениям и обратно, если координаты
некоторой точки удовлетворяют уравнениям одновременно, то эта точка есть
точка пересечения прямых. Следовательно, для нахождения координат общей точки
надо решить систему, составленную из этих двух уравнений. Если
то существует единственное решение системы.
Пучком пересекающихся прямых, определяемым прямыми (1) и (2),
называется совокупность всех прямых, проходящих через точку пересечения этих прямых,
если они пересекаются. Центром пучка называется точка пересечения прямых.
Пучком параллельных прямых называется совокупность всех прямых, имеющих
направления прямых (1) и (2), если они параллельны или совпадают.
ТЕОРЕМА. Уравнение пучка прямых, определяемого различными прямыми (1) и (2), имеет вид
где 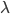
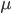
Доказательство. Ясно, что прямая
проходит через точку пересечения прямых (1) и (2). Пусть прямая
проходит через точку пересечения прямых (1) и (2). Система
имеет единственное решение и 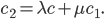
При решении задач удобнее это уравнение использовать в виде
в котором можно записать уравнение любой прямой, проходящей через точку пересечения
прямых (1) и (2), кроме второй из взятых прямых.
Задача. Даны уравнения двух пересекающихся прямых
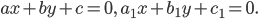
Найдите уравнения прямой, проходящей через данную точку 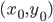
пересечения данных прямых.
Прямая пучка проходит через данную точку, если
Подставив полученное значение 
Упражнения
-
Выясните взаимное расположение прямых и в случае пересечения определите
координаты общей точки -
При каком значении параметра
прямые параллельны
и
- Докажите, что уравнение пучка с центром
можно записать так
- Докажите, что три прямые
- Даны уравнения сторон треугольника
- а) высот треугольника,
- б) прямых проходящих через вершины треугольника параллельно противоположным сторонам.
- Через точку пересечения прямых
и
проведите прямую:
- а) параллельную оси абсцисс;
- б) параллельную оси ординат;
- в) проходящую через начало координат.
- Определите общую прямую двух пучков
или
принадлежат одному пучку тогда и только тогда, когда
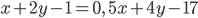
Составьте уравнения:
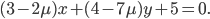
§12.3. Расстояние от точки до прямой
Уравнение 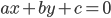
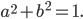
нормирующего множителя
где принято знак выбирать противоположным свободному члену,
т. е.
Пусть точка 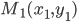
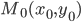
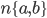
Для нормального уравнения длина вектора нормали равна 1.
Отклонением точки 
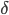
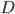
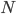
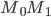
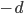
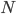
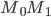
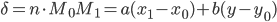
Так как 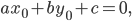
Для общего уравнения расстояние от точки 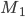
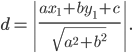
Нормальное уравнение часто записывают в виде
Здесь 

Геометрический смысл параметра 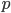
Вектор нормали направлен в сторону полуплоскости, в которой нет начала координат.
Геометрический смысл знака трехчлена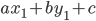
для того, чтобы точка 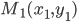
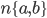
относительно прямой 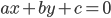
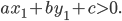
Задача. Даны точки 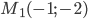
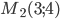
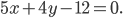
через внутреннюю точку отрезка 
Так как числа
и
имеют разные знаки, то точки принадлежат различным полуплоскостям относительно прямой.
прямая пересекает отрезок.
Упражнения
- Какие стороны треугольника с вершинами
пересекаются каждой из осей координат?
-
Докажите, что четырехугольник с вершинами
выпуклый.
-
Докажите, что четырехугольник с вершинами
невыпуклый.
-
Дан четырехугольник
-
Даны стороны треугольника
Составьте систему неравенств, определяющую внутреннюю область треугольника. -
Изобразите на чертеже область, определяемую системой неравенств
-
Найдите длины высот треугольника, стороны которого заданы уравнениями:
и
-
Напишите уравнение окружности с центром в точке
, касающейся прямой
-
Выведите формулу для вычисления расстояния между параллельными прямыми
и
Пользуясь полученной формулой, определите расстояние между прямыми
и
-
Составьте уравнения прямых, отстоящих от прямой
на расстоянии, равном 3.
- Составьте уравнение геометрического места точек, равноудаленных от двух параллельных прямых:
-
а)
-
б)
-
На прямой
найдите точки, равноудаленные от прямых
и
-
Составьте уравнение биссектрисы того угла между прямыми
и
в котором лежит начало координат.
-
Даны уравнения сторон треугольника:
и
Составьте уравнения вписанной и вневписанных окружностей.
-
Луч света направлен по прямой
Дойдя до прямой
луч отразился. Составьте уравнение прямой, на которой оказался отраженный луч.
-
Составьте уравнения сторон треугольника
зная уравнения двух биссектрис
и координаты вершины
§ 12.4. Полярные координаты
Возьмем на плоскости прямую. Выберем на ней точку 
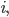
некоторое положительное направление обхода. Пусть 
отличная от 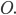
отрезка 
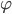
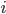
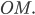
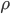
называются полярными координатами точки 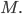
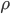
полярным радиусом,
а 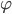

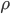
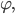
пишем 
полярной осью.
Точка 
полярную систему координат.
Заметим, что полярный угол имеет бесконечное много значений. Если 
то 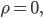
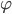
Пусть 
поворотом на 90

соотношениями
Иногда рассматривают обобщенные полярные координаты. В этом случае
считаем, что полярный радиус может принимать и отрицательные значения.
Например, точка с полярными координатами (3; 210
полярные координаты (-3; 30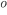
Найдем полярное уравнение прямой на плоскости. Пусть прямая задана
нормальным уравнением 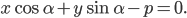
через полярные координаты, получим
или
Это и есть полярное уравнение прямой на плоскости.
Упражнения
-
В полярной системе координат даны точки
и
Вычислите расстояние между ними.
-
Вычислите площадь треугольника
если
– полюс и известны полярные
координаты вершин -
Треугольник задан полярными координатами вершин:
Докажите, что треугольник
равнобедренный. -
Треугольник задан полярными координатами вершин:
Докажите, что
треугольник прямоугольный. -
Как расположены точки на плоскости, полярные координаты которых
удовлетворяют одному из условий: а)б)
в)г)
д)е)
§ 12.5. Окружность
Окружностью называется геометрическое место точек плоскости,
равноудаленных от данной точки. Данная точка называется центром окружности.
Расстояние любой точки окружности до центра называется радиусом окружности.
Пусть 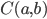
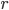
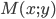
Возведя обе части равенства в квадрат, получим нормальное уравнение окружности
Если центр окружности совпадает с началом координат, то имеем
каноническое уравнение окружности
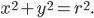
Пример. Найдите координаты центра и радиус окружности
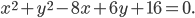
Выделив полные квадраты, преобразуем уравнение к виду
или
Упражнения
-
Если точка
лежит вне окружности
то
а если внутри окружности, то
Докажите это.
-
Найдите геометрическое место точек плоскости, отношение расстояний которых от
двух данных точеки
этой плоскости постоянно и равно
-
Найдите геометрическое место точек плоскости, сумма квадратов расстояний
которых от двух данных точеки
этой плоскости постоянна.
-
Найдите геометрическое место точек плоскости, сумма квадратов расстояний
которых от трех данных точеки
этой плоскости постоянна.
-
Найдите геометрическое место точек, касательные из которых, проведенные к
данной окружности, имеют постоянную длину. -
Определите геометрическое место точек плоскости, из которых данный отрезок
виден под прямым углом.
-
Дана окружность радиуса
и на ней точка
. Найдите геометрическое место
точек, делящих всевозможные хорды, проведенные черезв одном и том же
отношении. -
Найдите геометрическое место середин всех хорд окружности, имеющих данную
длину.
§ 12.6. Эллипс
Эллипсом называется геометрическое место точек плоскости, сумма
расстояний которых до двух фиксированных точек этой плоскости, постоянна.
Эти две фиксированные точки 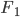
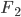
отрезка 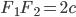
расстояний обозначим через 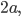

имеем 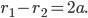
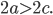
Эллипс можно построить с помощью нити длиной 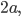
фокусах. Зацепив нить острием карандаша и двигая его так, чтобы нить все
время была в натянутом состоянии, мы острием карандаша вычертим эллипс.
Для изучения эллипса применим метод координат, который в данном
случае заключается в выборе системы координат, в которой уравнение эллипса
имеет наиболее простой вид и наиболее удобный для исследования. За ось абсцисс
примем прямую, проходящую через фокусы, а серединный перпендикуляр отрезка
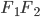
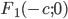
Точка 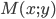
Получили уравнение эллипса. Преобразуем его.
Так как 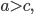
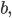
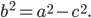
Разделив обе части уравнения на 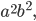
На самом деле уравнение (2) является следствием уравнения эллипса. Но мы покажем, что каждое
решение уравнения (2) является
решением уравнения (1). Пусть координаты точки 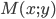
расстояние от этой точки до фокуса 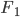
Аналогично вычисляется расстояние 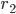
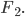
Так как 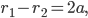
лежит на эллипсе. Тем самым доказана эквивалентность уравнений (1) и
(2) и мы имеем полное право уравнение (2) называть уравнением эллипса.
Формулы длин фокальных радиусов нам еще окажутся полезными:
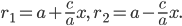
В каноническое уравнение эллипса переменные входят во второй степени.
Это означает, что оси координат являются осями симметрии эллипса, а начало
координат – центр симметрии эллипса. Для построения графика эллипса достаточно
построить его в первой четверти и затем отобразить полученную линию
относительно осей координат. В первой четверти уравнение эллипса имеет вид
При возрастании 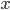
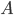
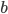
вверх. Отразив эту линию относительно осей координат, получим график эллипса. Точки
пересечения эллипса с его осями 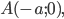
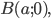
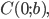
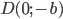
вершинами эллипса, центр симметрии эллипса 
отрезок 
большой осью эллипса, 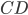
большой полуосью, число 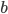
эллипс становится все более похож на окружность. Когда фокусы сольются с центром эллипса, то
эллипс обратится в окружность с уравнением
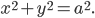
Основным прямоугольником эллипса называется прямоугольник, ограниченный прямыми, параллельными осям эллипса и отстоящими от них
соответственно на расстоянии 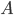
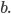
Рассмотрим окружность 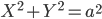
Получим
В результате сжатия окружности к ее оси симметрии она преобразуется в эллипс
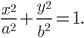
Всякий эллипс может быть получен как результат равномерного сжатия
некоторой окружности. Степень сжатия эллипса характеризуется
эксцентриситетом 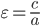
расстояния к длине большой оси). Эксцентриситет эллипса всегда меньше
единицы. Для эллипса, выродившегося в прямолинейный отрезок, эксцентриситет
равен 1. Для эллипса, превратившегося в окружность, когда его фокусы совпали,
эксцентриситет равен нулю. Директрисой эллипса называется прямая,
параллельная малой оси и отстоящая от нее на расстоянии 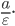
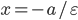
Фокус и директрису, лежащие в одной полуплоскости, называем
соответствующими.
ТЕОРЕМА. Отношение расстояния от любой точки эллипса до
фокуса к расстоянию от
этой точки до соответствующей директрисы равно эксцентриситету.
Доказательство. Воспользуемся формулой длины фокального радиуса: для левого
фокуса имеем 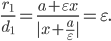
ТЕОРЕМА. Уравнение касательной к эллипсу
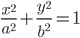
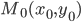
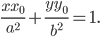
Доказательство. Продифференцировав обе части уравнения эллипса, получим
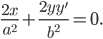
Отсюда, угловой коэффициент касательной в точке 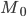
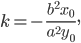
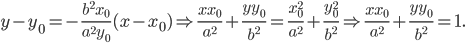
Задача. Отрезок постоянной длины скользит своими концами по двум
перпендикулярным прямым. Найдите линию, описываемую некоторой точкой
движущегося отрезка.
Примем данные перпендикулярные прямые в качестве осей
координат с началом координат в точке 
Точка 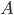
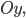
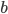
Пусть точка 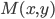
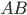
Если 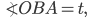
Исключим из этих уравнений параметр
т. е.
Таким образом, кривая, описываемая точкой 
называется параметрическим уравнением эллипса.
Задача. Луч света, выходя из одного фокуса, после отражения от эллипса
попадает в другой его фокус (оптическое свойство эллипса).
Сумма расстояний до фокусов эллипса точки касания
наименьшая среди остальных точек касательной, поскольку все они лежат
вне эллипса. Отразим фокус 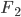

По закону: угол падения равен углу отражения, луч движется по маршруту
Задачи и упражнения
-
Докажите, что если точка находится вне эллипса, то сумма расстояний от
нее до фокусов больше, чем на эллипсе, если внутри, то меньше. - Докажите, что произведение расстояний от фокусов до любой касательной к эллипсу равно квадрату малой оси.
-
Докажите, что отрезок касательной к эллипсу в любой точке, заключенный
между касательными, проведенными в вершинах, лежащих на большой оси,
виден из фокусов под прямым углом. -
Докажите оптическое свойство эллипса: всякая касательная к эллипсу
образует равные углы с фокальными радиусами точки прикосновения. -
Составьте геометрическое место точек, из которых эллипс
виден под прямым углом.
-
Через фокус
эллипса
проведена хорда, касательная оси
Определите длину этой хорды.
-
Равномерным сжатием плоскости к прямой
называется преобразование точек плоскости,
при котором точкапереходит в точку
для которой
гдеи
– основание перпендикуляра, опущенного из
на прямую
Пусть прямаяпроходит через центр данной окружности. Докажите, что при равномерном
сжатии к этой прямой окружность преобразуется в эллипс.
§ 12.7. Гипербола
Гиперболой называется геометрическое место точек плоскости,
разность
расстояний которых до двух фиксированных точек этой плоскости, постоянна. Эти
две фиксированные точки 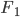
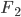
отрезка
называется фокусным расстоянием. Постоянную разность расстояний (из большего
расстояния вычитаем меньшее) обозначим через 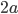
гиперболы имеем 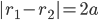
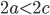
применим метод координат. За ось абсцисс примем прямую, проходящую через фокусы,
а серединный перпендикуляр отрезка 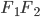
фокусов 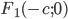
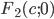
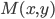
только тогда, когда
Получили уравнение гиперболы. Преобразуем его.
Так как 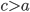
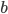
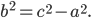
Каноническое уравнение гиперболы
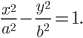
Уравнение (2) является следствием уравнения гиперболы. Покажем, что каждое
решение уравнения (2) является решением уравнения (1). Пусть координаты точки 
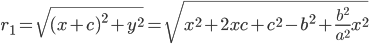
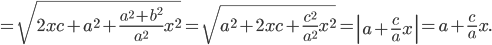
Аналогично вычисляется расстояние 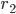
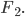
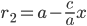
Так как
то точка 
мы имеем полное право уравнение (2) называть уравнением гиперболы. Формулы длин
фокальных радиусов нам еще окажутся полезными:
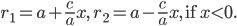
В каноническое уравнение гиперболы переменные входят во второй степени.
Это означает, что оси координат являются осями симметрии гиперболы, а начало
координат – центр симметрии гиперболы. Для построения графика достаточно
построить его в первой четверти и затем отобразить полученную линию
относительно осей координат. В первой
четверти уравнение гиперболы имеет вид
При возрастании 
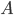
до 
координат, получим график гиперболы. Ось симметрии гиперболы, имеющую с ней
общие точки называем действительной осью гиперболы. Ось симметрии гиперболы,
не имеющую с ней общие точки называем мнимой осью гиперболы.
Точки пересечения
гиперболы с действительной осью 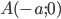
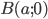
вершинами гиперболы, центр симметрии гиперболы 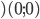
центром гиперболы. Гипербола
распадается на две ветви: “правую”, для точек которой абсцисса 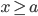
для точек которой 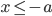
Отношение фокусного расстояния к расстоянию между вершинами называется
эксцентриситетом 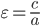
Директрисой гиперболы называется прямая, параллельная мнимой оси и
отстоящая
от нее на расстоянии 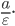
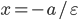
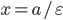
Называем соответствующими фокус и директрису, лежащие в одной полуплоскости.
ТЕОРЕМА. Отношение расстояния от любой точки гиперболы до
фокуса к расстоянию от этой точки до соответствующей директрисы равно
эксцентриситету.
Доказательство. Воспользуемся формулой длины фокального радиуса: для левого
фокуса при 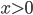
Аналогично вычисляем отношение в остальных случаях.
Продолжим изучение гиперболы в первой четверти. Положительная в первой
четверти разность между ординатами прямой и гиперболы
cтремится к нулю при бесконечном возрастании 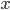
является асимптотой гиперболы. При бесконечном возрастании 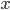
приближается к прямой, но не пересекает. В силу симметрии такая же картина
наблюдается в третьей четверти, а во второй и четвертой четвертях асимптотой
является прямая
Точка 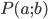
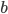
ордината асимптоты, восставленная из вершины гиперболы. Так как
то для нахождения фокуса гиперболы можно отложить на оси 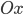
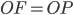
Основным прямоугольником гиперболы называется прямоугольник, ограниченный
прямыми, параллельными осям гиперболы и отстоящими от них соответственно на
расстоянии 
асимптоты.
Упражнения
-
Докажите, что уравнение касательной к гиперболе
в точке
гиперболы имеет вид -
Точка
называется внутренней точкой гиперболы, если любая секущая,
проходящая через эту точку и не параллельная асимптотам, пересекает гиперболу
в двух различных точках. Внешней точкой гиперболы называется точка,
не лежащая на гиперболе и не являющаяся внутренней. Докажите, что точка
внутренняя точка гиперболыв том и
только том случае, если
-
Найдите необходимое и достаточное условие касания прямой
с
гиперболой, если данная прямая не
параллельна асимптотам гиперболы. -
Найдите необходимое и достаточное условие касания прямой
с
гиперболой, если данная прямая не
параллельна асимптотам гиперболы. - Докажите, что касательные в вершинах гиперболы, параллельны ее мнимой оси.
-
Если угловой коэффициент прямой удовлетворяет неравенствам
, то прямая не может касаться
гиперболы
Докажите это. - Найдите геометрическое место точек плоскости, из которых гипербола видна под прямым углом.
- Докажите, что произведение расстояний от фокусов до любой касательной к гиперболе есть величина постоянная.
- Докажите, что отрезок асимптоты, заключенный между центром гиперболы и директрисой, равен действительной полуоси.
-
Докажите, что директрисы гиперболы проходят через основания
перпендикуляров, опущенных из соответствующих фокусов на асимптоты.
Выразите расстояние от фокусов до асимптот через полуоси гиперболы. - Докажите, что отрезок касательной к гиперболе, заключенный между асимптотами, делится в точке соприкосновения пополам.
-
Докажите оптическое свойство гиперболы: всякая касательная к гиперболе
составляет равные углы с фокальными радиусами точки касания.
§ 12.8. Парабола
Параболой называется геометрическое место точек плоскости,
равноудаленных от данной точки и данной прямой этой плоскости. Данная точка
Расстояние 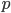
или параметром параболы.
Для изучения параболы применим метод координат. За ось абсцисс примем
прямую, проходящую через фокус перпендикулярно директрисе; за ось ординат –
прямую, параллельную директрисе и проходящую на равном расстоянии от фокуса и
директрисы. Координаты фокуса 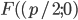
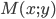
параболе тогда и только тогда, когда
Это – уравнение параболы. Преобразуем его.
Получили каноническое уравнение параболы
Каждому положительному значению х отвечают два значения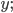
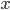
принимать только положительные значения и нуль. График симметричен
относительно оси 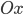
вершиной параболы.
Упражнения
-
Докажите, что уравнение касательной к параболе
в точке
параболы имеет вид
-
Найдите геометрическое место середин хорд параболы
, имеющих угловой
коэффициент.
-
Прямая
, не параллельная оси
касается параболы
тогда и только тогда, когда
. Докажите это.
-
Прямая
, не параллельная оси
, касается параболы
тогда и только тогда, когда
. Докажите это.
-
Точка
называется внутренней точкой параболы, если любая прямая,
проходящая через эту точку и не параллельная оси параболы, пересекает параболу
в двух различных точках. Внешней точкой параболы называется точка, не
лежащая на параболе и не являющаяся внутренней. Докажите, что точка
внутренняя точка параболыв том и только том случае, если
-
Найдите геометрическое место оснований перпендикуляров, опущенных из фокуса
параболы на ее касательные. -
Найдите геометрическое место точек плоскости, из которых парабола
видна под прямым углом.
-
Если из любой точки директрисы проведены к параболе две касательные, то прямая,
соединяющая точки касания, проходит через фокус параболы. Докажите это. -
Докажите оптическое свойство параболы: всякая касательная к параболе
составляет равные углы с фокальным радиусом точки и лучом, проходящим через
точку касания и сонаправленным с осью. -
Докажите, что произведение длин перпендикуляров, опущенных из концов любой
фокальной хорды на ось параболы имеет постоянную величину.
§ 12.9. Полярное уравнение линии второго порядка
Найдем уравнение эллипса, гиперболы и параболы в полярных координатах.
Начало полярной системы координат поместим в фокус (левый в случае эллипса,
правый в случае гиперболы). Полярная ось направлена по фокальной оси в сторону,
противоположную от соответствующей директрисы. Для произвольной точки
кривой обозначим через 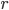

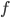
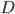
расстояние от 
для которых 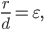
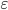
эллипса или гиперболы и 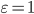
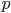
пересечения прямой, проведенной через 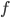
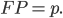
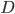
через 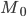

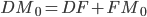
где 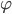
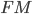
Это и есть уравнение эллипса, правой ветви гиперболы и параболы в
полярных координатах. Этими уравнениями постоянно пользуются в
астрономии и в механике.
§ 12.10. Общая теория линий второго порядка
Линией второго порядка называется линия, которая в некоторой декартовой
системе координат определяется уравнением второй степени. Запишем уравнение
второго порядка в самом общем виде
При условии, что 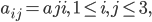
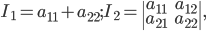
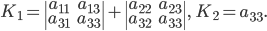
ПРИМЕР. Для эллипса 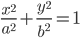
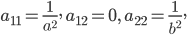
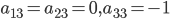
Тогда
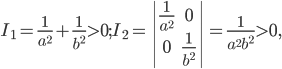
Можно доказать, что эти числа являются инвариантами относительно
преобразования параллельного переноса, т. е. при преобразовании поворота осей
координат
величины, составленные из соответствующих коэффициентов преобразованного
уравнения, сохранятся. Можно доказать также, что при параллельном переносе
осей координат
не изменяются величины 
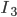
можно определить название линии второго порядка.
С помощью параллельного переноса системы координат можно освободиться от
слагаемых первой степени, а с помощью поворота осей можно освободиться
от слагаемого, содержащего произведение переменных. После подбора
подходящей системы координат уравнение второй степени примет наиболее
простой вид. Коэффициенты приведенных уравнений определяются при помощи
инвариантов.
Упражнения
-
Центром линии называется точка плоскости, по отношению к которой
точки линии симметричны парами. Линии второго порядка, обладающие центром,
называются центральными. Докажите, что точка
является центром линии (1) тогда и только тогда, когда
-
Определитель второго порядка
, составленный из коэффициентов при старших слагаемых уравнения (1),
называется дискриминантом уравнения (1). Докажите, что линия второго порядка
центральная тогда и только тогда, когда. Докажите, что координаты центра
находятся по формулам
-
Определитель
называется дискриминантом левой части уравнения (1); здесь
и
для
ю
При переносе начала координат в центр линии (1) с помощью преобразования
уравнение (1) приобрело вид
Докажите, что - Установите, что следующие линии являются центральными, и найдите координаты центра каждой линии:
-
Уравнение (2) подвергнем преобразованию поворота осей на угол
при условии, что
Докажите, что в новых координатах уравнение линии примет вид
где
и
-
Уравнение второй степени называется эллиптическим, если
,
гиперболическим, еслии параболическим, если
.
Докажите, что уравнение центральной линии может быть только эллиптическим или гиперболическим. - Докажите, что каждое эллиптическое уравнение является уравнением эллипса, либо вырожденного эллипса, либо мнимого эллипса.
- Докажите, что каждое гиперболическое уравнение определяет уравнение гиперболы либо вырожденной гиперболы.
-
Докажите, что если
, то линия либо не имеет центра, либо имеет бесконечно много центров.
-
Уравнение (1) подвергнем преобразованию поворота осей на угол
при условии, чтои
.
Докажите, что в новых координатах уравнение линии примет вид
где, либо вид
где
Условие
Составить уравнение линии, каждая точка М которой удовлетворяет заданным условиям :отстоит от прямой x=2 на расстоянии ,в 2 раза большем , чем от точки А(4;-3).
математика ВУЗ
1541
Решение
★
Пусть M(x;y)
Расстояние от точки М до точки А
АМ=sqrt((x-4)^2+(y-(-3))^2})=sqrt((x-4)^2+(y+3)^2);
Расстояние от точки М до прямой x=2
d=|x-2|
По условию, расстояние от точки М до прямой [b]х=2[/b] в два раза больше расстояния АМ
Составляем уравнение:
2*sqrt((x-4)^2+(y+3)^2)=|x-2|
Возводим в квадрат
4*((x-4)^2+(y+3)^2)=(x-2)^2
4(y+3)^2=(x-2)^2-4(x-4)^2
Упрощаем и получаем ответ
Эллипс со смещенным центром:
( cм рис.)
Написать комментарий
Составить уравнение линии, каждая точка М которой, удовлетворяет заданным условиям.
Катюня
Знаток
(269),
закрыт
13 лет назад
Отстоит от прямой у = -2 на расстоянии, в три раза большем, чем от точки А (5,0)
Елена Гужвенко
Гений
(53581)
13 лет назад
Пусть М (х, у) , тогда расстояние до прямой у+2=0 равно (0х+1у+2)/корень из (0^2+1^2).
Расстояние АМ=корень из ((х-5)^2+y^2)
Cогласно условию, получаем:
((у+2)/3)^2 = (x-5)^2 +y^2 – уравнение требуемой линии.
При желании раскройте сами скобки, упростите, приведите к каноническому виду.
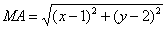
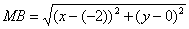
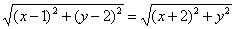
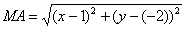
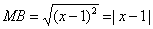
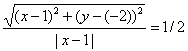
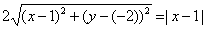

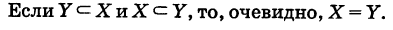
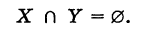
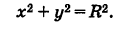


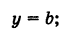

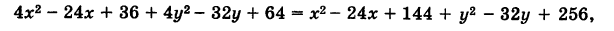
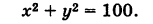
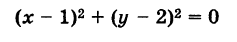
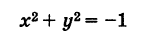



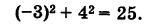
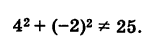
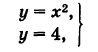
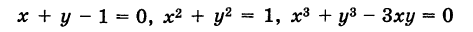
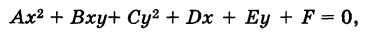
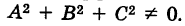
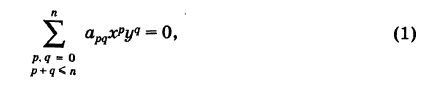
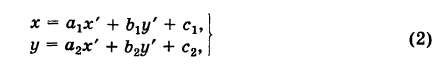
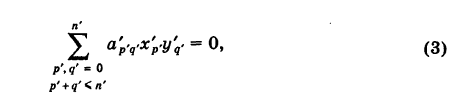





















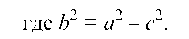









































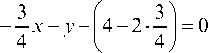


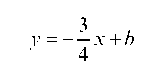









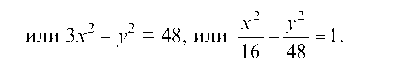




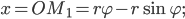
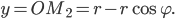
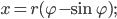
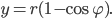
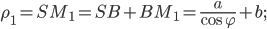
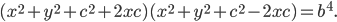
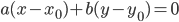
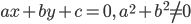
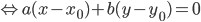
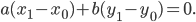
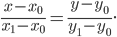
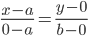
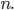
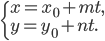
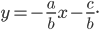
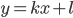
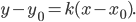
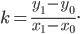
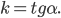
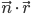
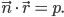
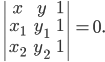
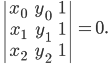
 проведите прямую,
проведите прямую, является трапецией, где
является трапецией, где
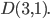
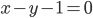 и
и 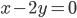 и
и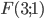 . Напишите уравнения двух других сторон
. Напишите уравнения двух других сторон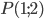 проведите прямую, отсекающую равные отрезки на осях координат.
проведите прямую, отсекающую равные отрезки на осях координат.
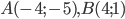 и
и ; 7).
; 7).
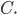 .
.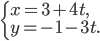
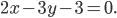
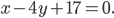
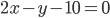 найдите точку, сумма расстояний которой до
найдите точку, сумма расстояний которой до (-3;4) наименьшая.
(-3;4) наименьшая.
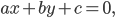
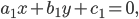
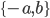
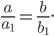
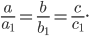
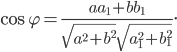
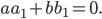
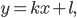
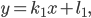
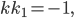
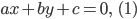
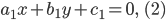
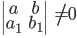
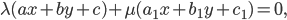
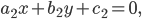
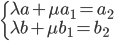
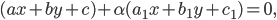
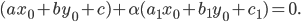
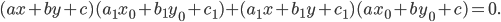
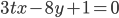 и
и 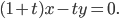
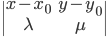
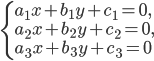
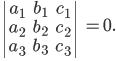
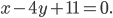
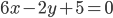 и
и 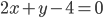 проведите прямую:
проведите прямую: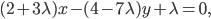
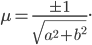
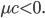
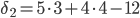
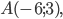
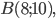
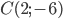 пересекаются каждой из осей координат?
пересекаются каждой из осей координат?
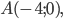
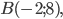
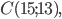
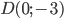 выпуклый.
выпуклый.
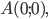
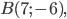
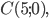
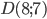 невыпуклый.
невыпуклый.
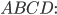
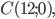
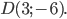
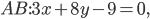
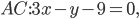
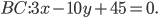
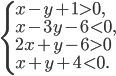
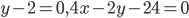 и
и 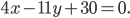
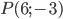 , касающейся прямой
, касающейся прямой 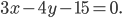
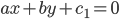 и
и 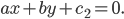 Пользуясь полученной формулой, определите расстояние между прямыми
Пользуясь полученной формулой, определите расстояние между прямыми 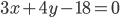 и
и 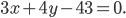
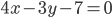 на расстоянии, равном 3.
на расстоянии, равном 3.
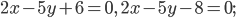
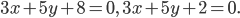
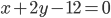 найдите точки, равноудаленные от прямых
найдите точки, равноудаленные от прямых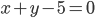 и
и 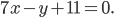
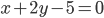 и
и 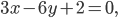 в котором лежит начало координат.
в котором лежит начало координат.
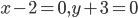 и
и 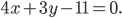 Составьте уравнения вписанной и вневписанных окружностей.
Составьте уравнения вписанной и вневписанных окружностей.
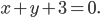 Дойдя до прямой
Дойдя до прямой 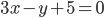 луч отразился. Составьте уравнение прямой, на которой оказался отраженный луч.
луч отразился. Составьте уравнение прямой, на которой оказался отраженный луч.
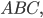 зная уравнения двух биссектрис
зная уравнения двух биссектрис 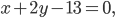
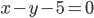 и координаты вершины
и координаты вершины 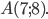
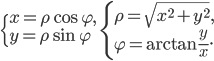
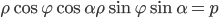
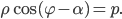
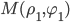 и
и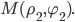 Вычислите расстояние между ними.
Вычислите расстояние между ними.
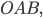 если
если 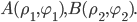
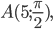
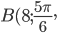
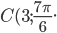 Докажите, что треугольник
Докажите, что треугольник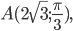
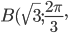
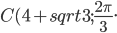 Докажите, что
Докажите, что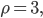 б)
б) 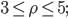
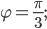 г)
г) 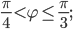
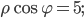 е)
е)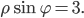
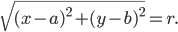
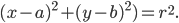
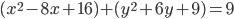
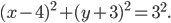
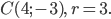
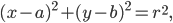 то
то 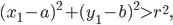 а если внутри окружности, то
а если внутри окружности, то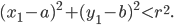 Докажите это.
Докажите это.
 и
и 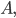 в одном и том же
в одном и том же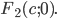
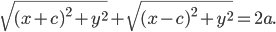
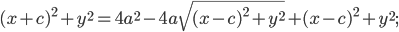
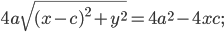
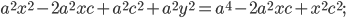
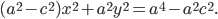
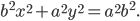
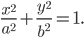
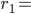
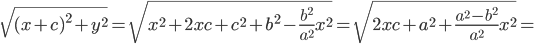
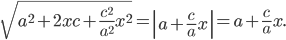
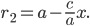
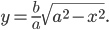
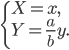
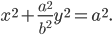
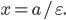
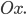
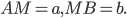
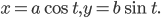
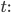
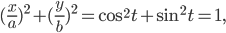
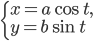
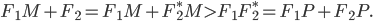
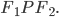
 Определите длину этой хорды.
Определите длину этой хорды.
 для которой
для которой 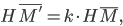
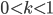 и
и 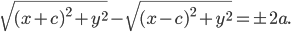
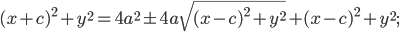
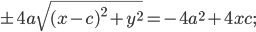
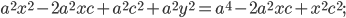
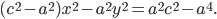
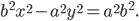
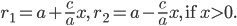
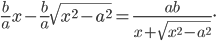
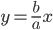
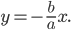
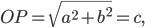
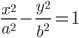 в точке
в точке 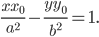
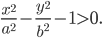
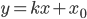 с
с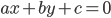 с
с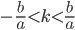 , то прямая не может касаться
, то прямая не может касаться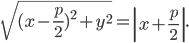
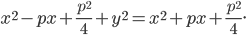
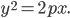
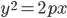 в точке
в точке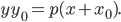
 .
.
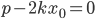 . Докажите это.
. Докажите это.
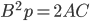 . Докажите это.
. Докажите это.
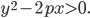
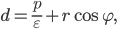
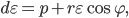
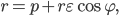
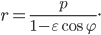
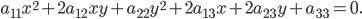
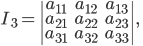
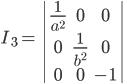
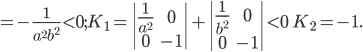
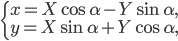
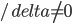 . Докажите, что координаты центра
. Докажите, что координаты центра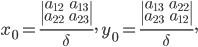
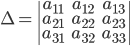
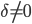 и
и 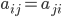 для
для 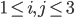 ю
ю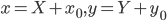 уравнение (1) приобрело вид
уравнение (1) приобрело вид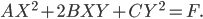
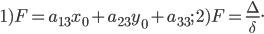
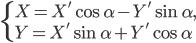
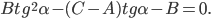
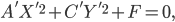
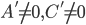 и
и 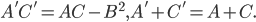
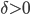 ,
,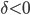 и параболическим, если
и параболическим, если 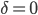 .
.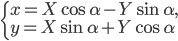
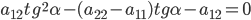 .
.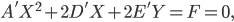
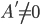 , либо вид
, либо вид