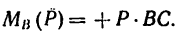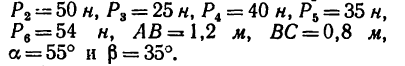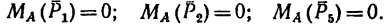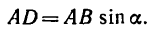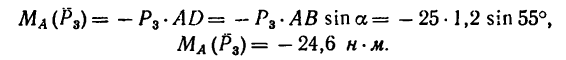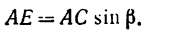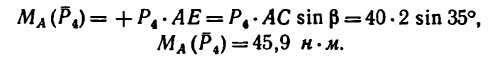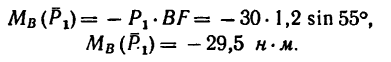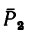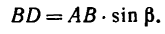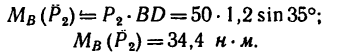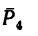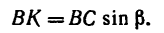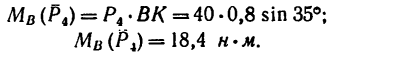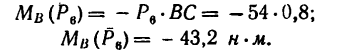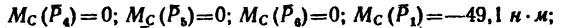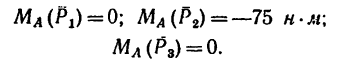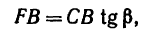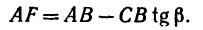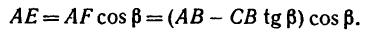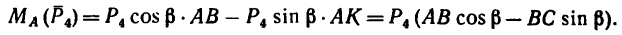iSopromat.ru
Правила знаков для моментов и проекций сил на оси координат:
Правило знаков проекций сил
То есть, для уравнений сумм проекций сил на оси:
Проекции сил и нагрузок на координатную ось имеющие одинаковое направление принимаются положительными, а проекции усилий противоположного направления – отрицательными.
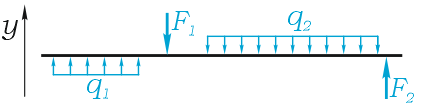
Например, для такой схемы нагружения:
уравнение суммы сил имеет вид
А так как суммы проекций разнонаправленных сил равны, то данное уравнение можно записать и так:
Здесь F(q) – равнодействующая от распределенной нагрузки, определяемая произведением интенсивности нагрузки на ее длину.
Правило знаков для моментов
Сосредоточенные моменты и моменты сил стремящиеся повернуть систему относительно рассматриваемой точки по ходу часовой стрелки записываются в уравнения с одним знаком, и соответственно моменты, имеющие обратное направление с противоположным знаком.

Например, для суммы моментов относительно точки A
или, что одно и то же
Здесь m(F) – моменты сил F относительно точки A.
M(q) – моменты распределенных нагрузок q относительно рассматриваемой точки.
При составлении уравнений статики для систем находящихся в равновесии (например при определении опорных реакций) правила знаков могут быть упрощены до следующего вида:
Нагрузки направленные в одну сторону принимаются положительными, а соответственно, нагрузки обратного направления записываются со знаком минус.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Как составить силовые уравнения
В задачах динамики учитывают силы, действующие на тело. Векторы сил могут действовать в различных направлениях. Большинство школьных задач можно решить, располагая векторы сил в одной плоскости. Поэтому, в статье будем рассматривать векторы, лежащие в одной плоскости — компланарные векторы.
Что такое равнодействующая
Равнодействующий вектор – это вектор, который мы получаем, когда складываем несколько векторов сил.
Результат сложения может дать:
- вектор, имеющий длину,
- или вектор, не имеющий длины.
Примечание: Когда у вектора отсутствует длина, говорят, что вектор равен нулю. На рисунке нулевой вектор можно изобразить одной точкой. Длины у точки нет – т. е. длина нулевая, а направление может быть любым.
Длина вектора содержит сумму квадратов всех его проекций на оси.
Где ( a_ ) и ( a_ ) — это проекции вектора (ссылка) ( vec ) на оси Ox и Oy.
Когда вектор равен нулю, равна нулю каждая его проекция на осях.
Длина вектора отлична от нуля, когда хотя бы одна его проекция ненулевая.
Левая часть силового уравнения
В левой части силового уравнения записываем силы, действующие на тело.
Когда векторы сил направлены вдоль параллельных прямых, проводим на рисунке одну ось. Если векторы сил не параллельные, проводим две оси на плоскости. Раскладываем векторы на проекции по осям. Для каждой оси составляем отдельное уравнение. Количество уравнений совпадает с количеством осей.
Если сила сонаправлена с осью, то она войдет в левую часть уравнения со знаком «+», а если она направлена против оси — то со знаком «минус».
Правая часть силового уравнения
В правой части уравнения записываем равнодействующую. В задаче может присутствовать несколько осей, вдоль каждой оси направляем отдельную проекцию равнодействующей.
Примечание: Тело может вдоль одной оси двигаться с ускорением, а вдоль другой оси двигаться без ускорения, или, вообще, покоиться. Например, тело может двигаться по вертикали под действием силы тяжести, а по горизонтали при этом не смещаться.
Когда проекция равнодействующей вдоль какой-либо оси не равна нулю, тело по оси будет двигаться с ускорением. Это следует из второго закона Ньютона.
Тогда в правой части уравнения запишем:
- (ma), если ускорение направлено туда же, куда направлена ось;
- (- ma), если ускорение направлено противоположно оси;
А когда проекция равнодействующей на ось нулевая, ускорение вдоль оси отсутствует. Тогда вдоль этой оси тело движется с неизменной скоростью, или же, вдоль этой оси движение отсутствует. Это следует из первого закона Ньютона.
В правой части уравнения запишем ноль (0 = ускорения нет).
Векторы сил параллельны
В случае, когда векторы направлены вдоль одной прямой, достаточно выбрать и провести единственную ось.
Выясним, как выглядит силовое уравнение для задачи, в которой векторы сил направлены вдоль единственной оси. Например, парашютист спускается вертикально вниз (рис. 1) на парашюте под действием силы тяжести.
Проведем на рисунке ось, направим ее вверх.
Примечание: Мы можем направить ось вниз, если захотим. При таком направлении оси знаки проекций векторов изменятся на противоположные, но на конечный ответ это никак не повлияет.
Составим левую часть уравнения. В левой части мы запишем силы, действующие на парашютиста:
Сила ( F_<text<сопр>>) направлена по оси, поэтому войдет в уравнение со знаком «+». А сила ( m cdot g ) вошла в уравнение со знаком «минус», так как направлена против оси.
В правую часть уравнения поместим равнодействующую.
Размеры парашюта рассчитаны так, что парашютист опускается вниз с постоянной (неизменной, т. е. одной и той же) скоростью. Значит, скорость есть, она не меняется, ускорения нет.
Математики запишут, что ускорение есть, но оно – нулевое (vec=0).
То есть, вдоль вертикальной оси тело движется без ускорения, значит, силы компенсировались. По первому закону Ньютона, равнодействующая равна нулю и, в правой части уравнения запишем ноль.
Примечания:
- На рисунке 1 скорость обозначена красным вектором, направленным вниз и обозначенным, как (vec>). Обычно математики дописывают нижний индекс к величине, которая не должна меняться. Так как у вектора скорости этот индекс есть, скорость считаем неизменной.
- На рисунке векторы скоростей и ускорений нужно рисовать отдельно от векторов сил! Решая задачу, мы будем складывать векторы (ссылка), имеющие одинаковую размерность. Силы измеряют в Ньютонах, поэтому их можно складывать. А ускорения и скорости измеряют в других единицах, с Ньютонами их сложить не получится. Именно поэтому, чтобы не запутаться, ускорения и скорости рисуем на небольшом расстоянии от тела, отдельно от векторов сил.
Итоговое силовое уравнение имеет вид:
[large F_<text<сопр>> — m cdot g = 0 ]
Зная массу парашютиста, можно вычислить силу сопротивления воздуха. А зная эту силу, можно рассчитать и размеры парашюта.
Векторы сил не параллельны
Когда векторы направлены вдоль разных прямых, будем проводить две взаимно перпендикулярные оси на плоскости.
Разберем задачу равнозамедленного движения тела по горизонтальной шероховатой поверхности (рис. 2).
Поверхность шероховатая, это намек на то, что есть сила трения. А если в условии напишут, что поверхность гладкая, значит, силы трения нет.
Движение равнозамедленное (ссылка), значит, скорость тела уменьшается и есть вектор ускорения, который направлен против вектора скорости.
Нарисуем взаимно перпендикулярные оси. Ось Ox проведем горизонтально, а ось Oy – вертикально. Рассмотрим оси и проекции векторов на них по очереди.
Горизонтальная ось. Пусть движение тела происходит в положительном направлении оси Ox. Сила трения всегда направлена против движения, поэтому направим ее влево. Скорость тела направлена вправо и будет уменьшаться, значит, ускорение, так же, направим влево. Вектор ускорения рисуем отдельно от векторов сил.
Наличие ускорения говорит о том, что вдоль оси Ox равнодействующая имеет не нулевую проекцию. Ускорение направлено против оси, запишем (- ma) в правой части уравнения.
Так выглядит уравнение для горизонтальной оси
Вертикальная ось. Вниз направлена сила тяжести, а вверх – сила реакции опоры. Так как поверхность горизонтальная и тело не движется ни вверх, ни вниз, то движения вдоль оси Oy нет. Значит, сила тяжести и реакция опоры компенсировались и нет ускорения вдоль оси Oy. В правой части уравнения для вертикальной оси запишем ноль.
Для вертикальной оси уравнение выглядит так:
[large N — m cdot g = 0 ]
Система, пригодная для решения задачи, состоит из двух уравнений
Куда направить оси
Разберем равнозамедленное движение тела вверх по наклонной шероховатой плоскости (рис. 3).
Силы, действующие на тело в этой задаче, не параллельные, направлены вдоль разных прямых. Поэтому для составления уравнений нужно использовать две взаимно перпендикулярные оси. Попробуем для начала провести ось Oy вертикально, а ось Ox горизонтально.
Из рисунка 3 видно, вдоль оси направлен только один вектор (mg). Остальные векторы сил не параллельны ни одной из осей. Такие векторы придется раскладывать на проекции, это усложнит конечную систему уравнений.
Если выберем оси так, как показано на рисунке 3, на проекции нужно будет разложить три вектора.
Попробуем теперь провести оси так, чтобы как можно большее количество векторов оказались параллельными осям (рис. 4). Из рисунка видно, что только один вектор (mg) окажется ненаправленным вдоль какой-либо оси. Остальные векторы сил параллельны осям.
При таком выборе осей раскладывать на проекции придется только один вектор. Это позволит быстрее решить задачу и решать более простые уравнения.
Примечание: Если мы выбререм оси так, как это представлено на рисунке 3, получим более сложные уравнения. Но решив их, мы получим точно такой же ответ, как и в случае выбора осей на рисунке 4.
Выводы:
- Выбор осей на конечный результат не влияет! А влияет только на сложность полученных уравнений.
- Оси проводим так, чтобы как можно больше векторов оказались направленными вдоль осей.
Движение по наклонной плоскости
Составим систему уравнений для решения такой задачи:
Велосипедист подъезжает с начальной скоростью к подъему, посыпанному песком и, едет в гору на велосипеде по инерции, не крутя педали. Масса велосипедиста с велосипедом, начальная скорость его, коэффициент сопротивления поверхности и угол наклона известны.
Нужно составить систему силовых уравнений, чтобы найти ускорение велосипедиста. А после, зная начальную скорость и ускорение, найти путь, который велосипедист сможет проехать по инерции в горку.
Выражение для ускорения
Составим рисунок, на котором изобразим силы, действующие на велосипедиста (рис. 5)
Мы провели оси так, чтобы пришлось разложить на проекции только один вектор и система силовых уравнений оказалась достаточно простой.
Пользуясь осями координат, составляем теперь уравнения в проекциях.
Уравнение для проекций векторов на ось Ox:
[ large — F_<text<трен>> – m cdot g_ = — m cdot a ]
Уравнение для проекций векторов на ось Oy:
[ large N – m cdot g_ = 0 ]
Разложим теперь силу тяжести — вектор (mg) на проекции. Чтобы проделать это разложение, нужно отметить угол (alpha ) межу вектором (mg) и одной из осей. В нашем случае, это угол между вектором (mg) и осью Oy.
[ large begin m cdot g_ = mg cdot cos left(alpha right) \ m cdot g_ = mg cdot sin left(alpha right) end ]
Подставив разложение вектора (mg) в уравнения для осей, получим такую систему уравнений
[ large begin — F_<text<трен>> – mg cdot sin left(alpha right) = — m cdot a \ N – mg cdot cos left(alpha right) = 0 end ]
Дополним эту систему выражением для силы трения.
Запишем эти уравнения в систему и выразим из нее уравнение для ускорения.
[ large begin N = mg cdot cos left(alpha right) \ F_<text<трен>> = mu cdot mg cdot cos left(alpha right) \ mu cdot mg cdot cos left(alpha right) + mg cdot sin left(alpha right) = m cdot a end ]
Поделим нижнее уравнение системы на массу велосипедиста и запишем окончательно уравнение для ускорения:
[ large mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a ]
Выражение для пройденного пути
Запишем выражения для связи скоростей и пройденного пути. Велосипедист движется по инерции в гору и его скорость уменьшается из-за силы тяжести и силы сопротивления поверхности, посыпанной песком. Когда скорость велосипедиста обратится в ноль, он, проехав часть пути в гору, остановится. Используем систему двух уравнений, она описывает путь при учете уменьшения скорости до нуля:
[ large begin 0 = v_ <0>— a cdot t \ S = v_ <0>cdot t — a cdot frac <2>end ]
Получим теперь уравнение для пути, в котором будут присутствовать только начальная скорость и ускорение и, будет отсутствовать время.
Упрощенная система для решения задачи теперь включает всего два уравнения
[ large begin mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a \ S = v_ <0>cdot frac> — frac> <2>cdot frac> end ]
Подставив в эту систему известные значения начальной (v_<0>) скорости велосипедиста, коэффициент (mu) сопротивления поверхности и угол (alpha) наклона плоскости, сможем посчитать путь, пройденный велосипедистом до его полной остановки.
Теоретическая механика. В помощь студенту
Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.
Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.
Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.
Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.
Статика твердого тела
Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.
-
Основные понятия и законы статики
Сила как вектор характеризуется точкой приложения, направлением действия и абсолютным значением. Единица измерения модуля силы – Ньютон.
Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины).
Размерность распределенной нагрузки – Н/м 3 (Н/м 2 , Н/м).
Принятое обозначение:
 .
. .
. .
.Принятое обозначение:
 .
. Под действием пары сил тело будет совершать вращательное движение.
Проекция положительна, если направление отрезка совпадает с положительным направлением оси.
Равномерное и прямолинейное движение материальной точки является движением по инерции. Под состоянием равновесия материальной точки и твердого тела понимают не только состояние покоя, но и движение по инерции. Для твердого тела существуют различные виды движения по инерции, например равномерное вращение твердого тела вокруг неподвижной оси.
Эти две силы называются уравновешивающимися.
Вообще силы называются уравновешивающимися, если твердое тело, к которому приложены эти силы, находится в покое.
Следствие. Не нарушая состояния твердого тела, силу можно переносить по ее линии действия в любую точку тела.
Две системы сил называются эквивалентными, если одну из них можно заменить другой, не нарушая состояния твердого тела.
диагонали.
По модулю равнодействующая равна:

Следует иметь в виду, что действие — сила, приложенная к телу Б, и противодействие — сила, приложенная к телу А, не уравновешиваются, так как они приложены к разным телам.
Не следует при этом забывать, что условия равновесия, являющиеся необходимыми и достаточными для твердого тела, являются необходимыми, но недостаточными для соответствующего нетвердого тела.
-
Связи и их реакции
- Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности.
- Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры.
- Шарнирная неподвижная опора противодействует любому перемещению в плоскости, перпендикулярной оси вращения.
- Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня.
- Глухая заделка противодействует любому перемещению и вращению в плоскости. Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.
-
Момент силы относительно точки
- Абсолютное значение момента равно произведению модуля силы на кратчайшее расстояние h от центра вращения до линии действия силы. Расстояние h называют плечом силы.
- Момент считают положительным, если сила стремится вращать плечо h против хода часовой стрелки и отрицательным при вращении по ходу часовой стрелки.
- Свойства момента силы относительно точки:
1) Момент силы не изменится при переносе точки приложения силы вдоль линии действия силы.
2) Момент силы равен нулю, если линия действия силы проходит через точку приложения силы.
3) Момент равнодействующей силы относительно точки равен сумме моментов слагаемых сил относительно этой точки.,
где
-
Момент силы относительно оси
- Момент силы относительно оси — это момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Момент считается положительным, если с положительного конца оси поворот, который сила стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки. - Чтобы найти момент силы относительно оси, нужно:
1) Провести плоскость перпендикулярную оси z.
2) Спроецировать силу на эту плоскость и вычислить величину проекции.
3) Провести плечо h из точки пересечения оси с плоскостью на линию действия проекции силыи вычислить его длину.
4) Найти произведение этого плеча и проекции силы с соответствующим знаком. - Свойства момента силы относительно оси.
Момент силы относительно оси равен нулю, если:
1), то есть сила параллельна оси.
2) h=0, то есть линия действия силы пересекает ось.
-
Момент пары сил
- Момент пары сил равен произведению одной силы на кратчайшее расстояние между линиями действия сил пары, которое называется плечом пары (пара сил оказывает на тело вращающее действие)
,
где:— силы, составляющие пару;
h — плечо пары.
Момент пары считают положительным, если силы стремятся вращать плечо против хода часовой стрелки. - Свойства пары сил.
1) Сумма проекций сил пары на любую ось равна нулю.
2) Не изменяя момента пары можно одновременно соответственно изменять значение сил и плечо пары.
3) Пару можно переносить в плоскости ее действия при этом действие пары на тело не изменится.
-
Преобразование произвольной системы сил
- Теорема: силу, приложенную к твердому телу, можно, не изменяя оказываемого ею действия, перенести параллельно в другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы относительно точки, в которую она переносится.
В результате указанного преобразования получается сходящаяся система сил и сумма моментов пар сил. Действие сходящейся системы сил заменяют действием суммарной силы, действие моментов — суммарным моментом.
Суммарный вектор— это главный вектор системы сил.
Суммарный момент — это главный момент системы сил.
Вывод: произвольная система сил в результате тождественного преобразования приводится к главному вектору и главному моменту системы сил. - Аналитически главный вектор и главный момент системы сил могут быть определены через их проекции на оси координат:
,
-
Условия равновесия систем сил
- Равновесие системы сходящихся сил
Действие системы сходящихся сил эквивалентно действию одной равнодействующей силы.
Для равновесия тела необходимо и достаточно, чтобы равнодействующая равнялась нулю .
Из формулы следует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю: - Для равновесия плоской сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y равнялась нулю:
-
Равновесие произвольной системы сил.
- Действие произвольной системы сил эквивалентно действию главного вектора и главного момента. Для равновесия необходимо и достаточно выполнения условия:
. - Для равновесия произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси X,Y,Z и суммы моментов всех сил относительно осей X,Y,Z равнялись нулю:
- Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций главного вектора на оси X,Y, и алгебраическая сумма моментов сил относительно центра О были равны нулю:
Кинематика
Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.
-
Основные понятия кинематики
-
Способы задания движения точки
- Задать движение точки — значит задать изменение ее положения по отношению к выбранной системе отсчета. Существуют три основные системы отсчета: векторная, координатная, естественная.
- В векторной системе положение точки относительно начала отсчета задается радиус-вектором.
Закон движения: . - В системе координат OXYZ положение точки задается тремя координатами X, Y, Z.
Закон движения: x = x(t), y = y(t); z = z(t). - В естественной системе отсчета положение точки задается расстоянием S от начала отсчета до этой точки вдоль траектории.
Закон движения: .
Движение точки, при естественном способе задания движения, определено если известны:
1) Траектория движения.
2) Начало и направление отсчета дуговой координаты.
3) Уравнение движения.
При естественном способе задания движения, в отличии от других способов, используются подвижные координатные оси, движущиеся вместе с точкой по траектории. Такими осями являются:
Касательная (τ) – направлена в сторону возрастания дуговой координаты по касательной к траектории.
Главная нормаль (n) – направлена в сторону вогнутости кривой.
Бинормаль (b) – направлена перпендикулярно к осям τ, n.
-
Определение кинематических характеристик точки
- Траектория точки
В векторной системе отсчета траектория описывается выражением: .
В координатной системе отсчета траектория определяется по закону движения точки и описывается выражениями z = f(x,y) — в пространстве, или y = f(x) – в плоскости.
В естественной системе отсчета траектория задается заранее. - Определение скорости точки в векторной системе координат
При задании движения точки в векторной системе координат отношение перемещения к интервалу времени называют средним значением скорости на этом интервале времени: .
Принимая интервал времени бесконечно малой величиной, получают значение скорости в данный момент времени (мгновенное значение скорости): .
Вектор средней скорости направлен вдоль вектора в сторону движения точки, вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки.
Вывод:скорость точки – векторная величина, равная производной от закона движения по времени.
Свойство производной:производная от какой либо величины по времени определяет скорость изменения этой величины. - Определение скорости точки в координатной системе отсчета
Скорости изменения координат точки:
.
Модуль полной скорости точки при прямоугольной системе координат будет равен:
.
Направление вектора скорости определяется косинусами направляющих углов:
,
где — углы между вектором скорости и осями координат. - Определение скорости точки в естественной системе отсчета
Скорость точки в естественной системе отсчета определяется как производная от закона движения точки: .
Согласно предыдущим выводам вектор скорости направлен по касательной к траектории в сторону движения точки и в осях определяется только одной проекцией .
-
Ускорение точки
- По определению ускорение характеризует изменение скорости, то есть скорость изменения скорости.
- Ускорения точки в векторной системе отсчета
На основании свойства производной:
.
Вектор скорости может изменяться по модулю и направлению.
Вектор ускорения направлен по линии приращения вектора скорости, т. е. в сторону искривления траектории. - Ускорение точки в координатной системе отсчета
Ускорение изменения координат точки равно производной по времени от скоростей изменения этих координат:
.
Полное ускорение в прямоугольной системе координат будет определяться выражением:
.
Направляющие косинусы вектора ускорения:
. - Ускорение точки в естественной системе отсчета Приращение вектора скорости можно разложить на составляющие, параллельные осям естественной системы координат:
.
Разделив левую и правую части равенства на dt, получим:
,
где — тангенциальное ускорение;
— нормальное ускорение;
R — радиус кривизны траектории в окрестности точки.
-
Кинематика твердого тела
- В кинематике твердых тел решаются две основные задачи:
1) задание движения и определение кинематических характеристик тела в целом;
2) определение кинематических характеристик точек тела. - Поступательное движение твердого тела
Поступательное движение — это движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению.
Теорема:при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения.
Вывод:поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки. - Вращательное движение твердого тела вокруг неподвижной оси
Вращательное движение твердого тела вокруг неподвижной оси — это движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.
Положение тела определяется углом поворота . Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)
Закон вращательного движения тела вокруг неподвижной оси .
Угловую скорость и угловое ускорение тела определим методом дифференцирования:
— угловая скорость, рад/с;
— угловое ускорение, рад/с².
Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точку М, то точка М будет описывать вокруг точки С окружность радиуса R. За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние .
Модуль линейной скорости:
.
Ускорение точки М при известной траектории определяется по его составляющим :
,
где .
В итоге, получаем формулы
тангенциальное ускорение: ;
нормальное ускорение: .
-
Плоско-параллельное движение твердого тела
- Плоско-параллельное движение твердого тела — это движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных одной неподвижной плоскости.
Движение сечения S в своей плоскости можно рассматривать как сложное, состоящее из двух элементарных движений:
1) поступательного и вращательного;
2) вращательного относительно подвижного (мгновенного) центра. - В первом варианте движение сечения может быть задано уравнениями движения одной его точки (полюса) и вращением сечения вокруг полюса.
В качестве полюса может быть принята любая точка сечения.
Уравнения движения запишутся в виде:
.
Ускорение точки движущейся плоской фигуры складывается из ускорения полюса относительно неподвижной системы отсчета и ускорения за счет вращательного движения вокруг полюса. - Во втором варианте движение сечения рассматривается как вращательное вокруг подвижного (мгновенного) центра P.
В этом случае скорость любой точки В сечения будет определяться по формуле для вращательного движения:
.
Угловая скорость вокруг мгновенного центра Р может быть определена если известна скорость какой либо точки сечения, например точки А.
. - Положение мгновенного центра вращения может быть определено на основании следующих свойств:
1) вектор скорости точки перпендикулярен радиусу;
2) модуль скорости точки пропорционален расстоянию от точки до центра вращения ();
3) скорость в центре вращения равна нулю. - Теорема:проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки, равны между собой и одинаково направлены.
Доказательство: расстояние АВ изменяться не может, следовательно, не может быть больше или меньше .
Вывод:.
-
Сложное движение точки
- Относительное движение — это движение точки относительно подвижной системы.
Переносное движение — это движение точки вместе с подвижной системой.
Абсолютное движение — это движение точки относительно неподвижной системы.
Соответственно называют скорости и ускорения:
— относительные;
— переносные;
— абсолютные. - Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей (согласно теореме о сложении скоростей):
.
Абсолютное значение скорости определяется по теореме косинусов:
. - Ускорение по правилу параллелограмма определяется только при поступательном переносном движении
.
. - При непоступательном переносном движении появляется третья составляющая ускорения, называемое поворотным или кориолисовым.
,
где .
Кориолисово ускорение численно равно:
,
где – угол между векторами и .
Направление вектора кориолисова ускорения удобно определять по правилу Н.Е. Жуковского: вектор спроектировать на плоскость, перпендикулярную оси переносного вращения, проекцию повернуть на 90 градусов в сторону переносного вращения. Полученное направление будет соответствовать направлению кориолисова ускорения.
Динамика
Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.
-
Основные понятия динамики
где mk, xk, yk, zk — масса и координаты k-той точки механической системы, m — масса системы.
В однородном поле тяжести положение центра масс совпадает с положением центра тяжести.
Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси:
.
Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек:
где — ускорение центра масс тела.
.
Полный импульс силы за Δt равен интегралу от элементарных импульсов:
.
Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов:
,
где α — угол между направлениями векторов перемещения и силы.
.
Единица измерения работы — Джоуль (1 Дж = 1 Н·м).
.
или
,
где m — масса механической системы, — вектор скорости центра масс системы.
.
.
-
Аксиомы динамики
- Первая аксиома — это закон инерции.
Если на свободную материальную точку не действуют никакие силы или действует уравновешенная система сил, то точка будет находиться в состоянии покоя или равномерного прямолинейного движения. - Вторая аксиома — закон пропорциональности ускорения.
Ускорение, сообщаемое материальной точке действующей на неё силой, пропорционально этой силе и по направлению совпадает с направлением силы: — это основной закон динамики. - Третья аксиома — это закон противодействия.
Силы, с которыми действуют друг на друга две материальные точки, равны по модулю и направлены вдоль прямой, соединяющей эти точки, в противоположные стороны:
. - Четвертая аксиома — закон независимости действия сил.
При действии на материальную точку системы сил полное ускорение этой точки равно геометрической сумме ускорений от действия каждой силы:
-
Дифференциальные уравнения динамики
- Дифференциальные уравнения движения точки связывают ускорение точки с действующими на нее силами. Фактически дифференциальные уравнения являются записью основного закона динамики в явной дифференциальной форме.
Для абсолютного движения точки (движение в инерциальной системе отсчета) дифференциальное уравнение имеет вид:
. - Векторное уравнение может быть записано в проекциях на оси прямоугольной инерциальной системы координат:
- При известной траектория движения точки уравнение может быть записано в проекциях на оси естественной системы координат:
С учетом того, что ,
где — тангенциальное ускорение;
— нормальное ускорение,
уравнения примут вид:
-
Общие теоремы динамики
- Общие теоремы динамики устанавливают зависимость между мерами механического движения и механического взаимодействия. Выводы теорем являются результатом тождественного преобразования основного закона динамики.
- Теорема об изменении количества движения: изменение количества движения материальной точки (механической системы) за конечный промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени — для материальной точки;
— для механической системы. - Теорема об изменении кинетической энергии: изменение кинетической энергии точки (механической системы) при её перемещении равно сумме работ всех действующих внешних сил на этом перемещении — для материальной точки;
— для механической системы. - Кинетическая энергия механической системы определяется в соответствии с , при этом для твердых тел выведены следующие зависимости:
— при поступательном движении тела;
— при вращательном движении тела;
— при плоско-параллельном движении тела. - Момент инерции цилиндра относительно его оси:
. - Момент инерции стержня относительно оси z:
. - Момент инерции прямоугольной пластины относительно осей х и y: .
- Момент инерции шара определяется по формуле:
. - Работа силы тяжести:
,
где P — сила тяжести;
h — изменение положения тела по вертикали. - Работа силы при вращательном движении тела
,
где M — момент силы,
w — угловая скорость тела.
Следует иметь в виду, что работа, как скалярная величина, может быть положительной или отрицательной. Работа будет положительной если направление действия силы совпадает с направлением движения.
-
Принцип Даламбера
- Формулировка принципа Даламбера: если в любой момент времени к действующим на точку силам присоединить силы инерции, то полученная система сил будет уравновешенной:
. - Для механической системы:
.
Примеры решения задач
Решение примеров по теме: «Статика твердого тела»
Пример 1. Условия равновесия
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.
Дано: P = 10 Н; α = 45°
Найти: N, T — ?
Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.
Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).
Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).
При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).
В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:
После подстановки в формулы числовых значений, получим:
.
Ответ: .
Решение примеров по теме: «Кинематика»
Пример 2. Уравнение траектории точки
Дано:
Движение точки задано уравнениями ;
(x, у — в сантиметрах, t — в секундах).
Найти: уравнение траектории точки в координатной форме.
Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:
.
Опуская промежуточные выражения, получаем уравнение траектории:
.
Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).
Ответ: .
Решение примеров по теме: «Динамика»
Пример 3. Основной закон динамики точки
Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.
Дано: m = 10 кг; a = 0,5 м/с 2 .
Найти: F — ?
Решение.
Согласно основному закону динамики: .
Подставив значения в формулу, получим:
Ответ: сила, сообщающая массе, равной 10 кг,
ускорение 0,5 м/с 2 , равна 5 Н.
В помощь студенту
-
Формулы, правила, законы, теоремы, уравнения, примеры решения задач
Список литературы:
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах.
Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие.
[spoiler title=”источники:”]
[/spoiler]
Вопрос по теоретической механике… Как составлять уравнения моментов сил относительно каких-либо точек?
Мастер
(2295),
закрыт
4 года назад
Евгений Кондратюк
Гений
(78083)
4 года назад
1. Задаёмся положительным направлением момента. Обычно, против часовой стрелки – положительное.
2. Суммируем произведения сил на плечо.
2.1. Плечо силы – это кратчайшее расстояние от точки или от оси, относительно которой определяем момент, до линии действия этой силы.
2.2. Зачастую, когда вектор силы не параллелен ни одной из координатных осей, для удобства (чтобы не вычислять плечо), векторы сил раскладывают на составляющие, проецируя их на координатные оси, которые могут быть и локальными.
3. Приравниваем эту сумму к нулю, если система находится в равновесии. К этому сводятся задачи.
4. Решаем уравнение или систему уравнений, относительно неизвестных величин, которые находим в результате этих вычислений.
——————————————————————————
Вот и всё!
——————————————————————————
P.S.: Если остались какие-то неясности, пишите. Поясню.
Источник: опыт и знания…
Бгс .Знаток (421)
5 месяцев назад

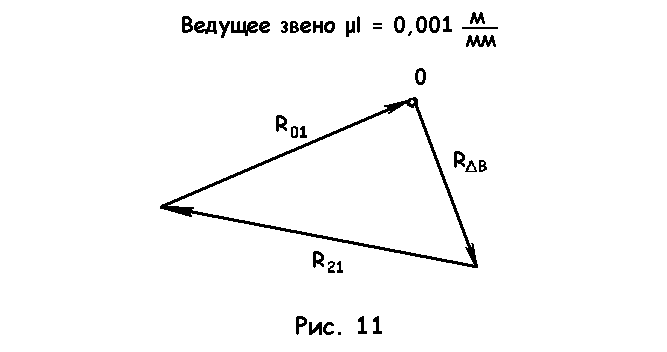
Σm0(1)= 0 = Рдв* OA + P1* h1-R21*h
Отсюда:
Далее строим план сил для ведущего звена
ΣFi(361)= 0 = Р1+R1u+ Рдв+R21+R01
С использованием масштабного коэффициента
μр = 5 Н/мм (рис.11).
Построение
плана сил начинаем с точки 0, откладываем
силу Рдв
(так как силы Р1
и R1u
изображаются отрезком менее 2 мм, их не
показываем), затем от нее откладываем
R21
с точкой 0, получаем неизвестную реакцию
R01,
которую находим и по величине:
R01 = (отрезок)
·μр = 56
·5 = 280 Н
В результате
приведенного силового расчета определили
реакции в кинематических парах и движущую
силу, пренебрегая силами трения. Получили:
R12τ
= 7,14 Н; R12n
=335 Н; R12
= 335 Н; R8
= 400 Н;
Рдв = 179,6 Н; R01
= 280 Н; R03
= 277,5 Н.
5.6.2. Силовой расчет с учетом сил трения
Силовой расчет с учетом сил трения
приводится после расчета без учета сил
трения, для уточнения реакций в
кинематических парах в следующей
последовательности:
1. Находим силу трения и направляющие:
F = R03
f = 277,5 ·
0,15 = 41,6 Н,
где f= 0,15 – коэффициент
трения.
Прикладываем ее к поршню по направлению
противоположно перемещению поршня (см.
рис.8, сила Fпоказана
пунктиром).
Находим моменты трения во вращательных
кинематических парах:
M32B
= M23B
= RB
r f΄ = RB
r (4/3) f =
= 400·0,02·(4/3)·0,15 = 1,6 Нм,
M12А
= M21А
= R12 r
f΄ = R12
r(4/3) f
=
= 335·0,02·(4/3)·0,15 = 1,34 Нм,
M010
= M01 r
f΄ = R01
r (4/3) f
=
= 280·0,02·(4/3)· 0,15 = 1,12 Нм,
здесь r = 20 мм =0,02 м– радиус цапфы подшипника;
f΄ =
(4/3)f– коэффициент
трения для приработавшихся цапф;
M32B– момент сил трения в точке В со стороны
3-го звена на 2-ое.
Прикладываем
найденные моменты в точках 0, А и В в
направлении, противоположном относительному
вращениюзвеньев.
Так, например, шатун АВ относительно
поршня поворачивается против часовой
стрелки, (тогда момент M32B
будет направлен по часовой стрелке).
Направление моментов показано пунктиром
на рис.8 и 10.
3. Составляем для группы 2-3 уравнение
моментов относительно точки В для сил,
приложенных к звену 2 (см. соответствующее
уравнение без учета сил трения, но в
него дополнительно войдут M12АиM32B:
рис.8).
Имеем:
ΣmB(2)
=0= R12τ·ABμl+P2h2μl–M2u–R2uhμl+
M12А
+ M32B
Отсюда:
Знак «-» также говорит о неправильном
направлении R12τ.
В действительности она будет направлена
вверх (рис.8).
Далее строим план сил для группы 2-3
(рис.12), который будет отличаться от
плана сил (рис. 9)введением силы трения
Fи несколько другой
величиной реакцииR12τ.
Σ
R12τ
+ R2u
+ P2 +
Pnc +F
+P3 + R3u
+ R03 +
R12n
Построение
плана сил аналогично описанному ранее
для этой же группы Ассура. Масштабный
коэффициент μр
= 5 Н/мм.
Из плана сил находим:
R12n
= (отрезок) μр
= 73 · 5 = 365 Н
R03
= (отрезок)
μр
= 53 · 5 = 265 Н
Геометрически
суммируя
и
,
находим
R12 = (отрезок)
μр = 73,5
· 5 = 367,5 Н
Геометрически
суммируя,
находим
RВ
= (отрезок) μр
= 86 · 5 = 430 Н
-
Составляем
уравнение моментов для кривошипа (рис.
10), в которое дополнительно войдут
моменты сил трения M21А
= 1,34 Нм и M010
= 1,12 Нм,
показанные пунктиром:
Σm0(1)
=0= РдвОAμl
+ P1h1μl
– R21hμl
– M010
– M21А
Отсюда:

строим план сил для ведущего звена
(рис.13):
ΣFi(гр)=
0 = Р1 +R1u
+ Рдв +R21
+R01
с
использованием масштабного коэффициента
μр
= 5 Н/мм.
Поскольку силы Р1
и R1u
изображаются отрезком менее 2 мм, то их
на плане сил не показываем.
Из плана сил находим:
R01
= (отрезок)
μр
= 64 · 5 = 320 Н
В результате
приведенного расчета определили реакции
в кинематических парах и движущую силу
с учетом сил трения.
Получили:
R12τ
= 20,5 Н; R12n
= 365 Н; R12
= 367,5 Н;
RВ
= 430 Н; Рдв
= 246,7 Н; R01
= 320 Н;
R03
= 265 Н.
Сравнивая эти
значения с соответствующими, найденными
без учета сил трения, видим, что они
несколько изменили свою величину в
основном в сторону увеличения.
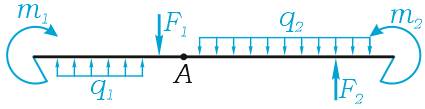
Рассмотрим решение задачи по составлению и определению суммы моментов внешних сил приложенных к заданной системе относительно её точек.
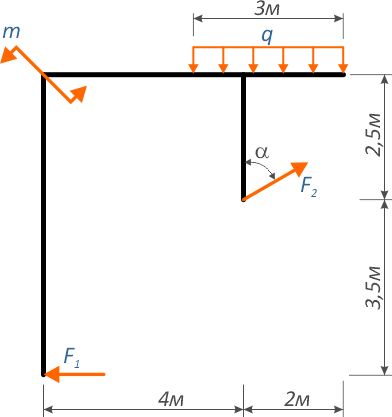
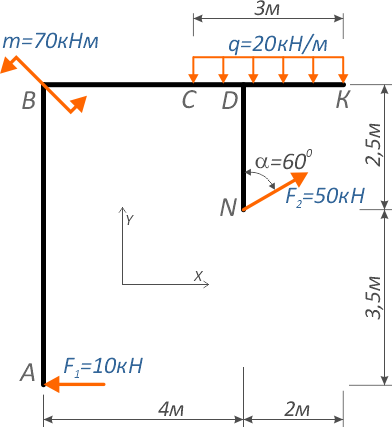
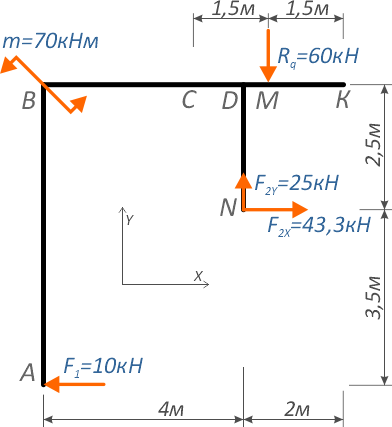
Задача
К составной планке, показанной на рисунке
приложены следующие нагрузки:
- Внешние сосредоточенные силы F1=10кН и F2=50кН расположенная под углом
- Сосредоточенный момент m=70кНм
- Равномерно-распределённая нагрузка q интенсивностью 20кН/м
Требуется составить и определить алгебраическую сумму моментов относительно точек A, B и D.
Решение
Обозначим характерные точки системы буквами и покажем систему координат x-y.
Для записи и расчета уравнений суммы моментов надо мысленно закрепить систему в рассматриваемой точке и записать все внешние усилия, которые стремятся повернуть систему.
Момент силы определяется по формуле
где h — расстояние от точки до линии действия силы называемое плечом.
Другие видео
При этом, по правилу знаков, нагрузки, поворачивающие систему против хода часовой стрелки записываются положительными и наоборот.
При записи уравнений суммы моментов:
- Силы умножаются на плечо;
- Равномерно распределенные нагрузки умножаются на длину (получается равнодействующая сила), полученное произведение умножается на плечо, которым служит расстояние от её середины до рассматриваемой точки;
- Сосредоточенный момент в сумме моментов записывается как есть (с учётом знака).
Примеры составления суммы моментов сил
Определим алгебраические суммы моментов сил относительно произвольных точек системы.
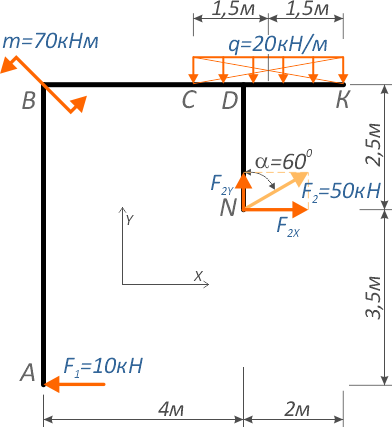
Для некоторого упрощения решения задачи, распределенную нагрузку можно заменить её равнодействующей
которая при равномерном распределении приложена посередине:
а сосредоточенную силу F2 можно разложить на составляющие, спроецировав её на оси x и y.
Получается упрощенная расчетная схема:
Расчет суммы моментов относительно точки, к которой приложена сила
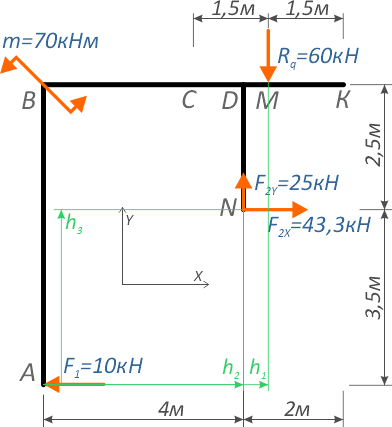
Для точки A:
Силы Rq и F2X создают момент, вращающий по ходу часовой стрелки, поэтому будут записаны со знаком минус.
Сила F2Y относительно точки A имеет обратное направление и создает положительный момент.
Здесь h1, h2 и h3 плечи моментов соответствующих сил и равнодействующей распределенной нагрузки относительно точки A.
Линия действия силы F1 проходит через саму точку A, следовательно, плечо равно нулю, поэтому момент этой силой в данном случае не создается.
Таким образом, относительно точки A уравнение суммы моментов будет иметь вид:
Здесь сумма моментов относительно точки A отрицательна, поэтому, если данную систему закрепить в этой точке, она будет вращаться по ходу часовой стрелки.
Определение суммы моментов относительно точки, в которой приложен момент
Для точки B надо помнить что момент приложенный в точке, относительно которой записывается сумма, в уравнении участвует.
Поэтому алгебраическая сумма моментов относительно точки B равна:
Знак «-» так же показывает на вращение системы по ХЧС.
Сумма моментов относительно точки, где действует распределенная нагрузка
Для точки D:
Здесь надо смотреть, как расположена равнодействующая нагрузки по отношению к рассматриваемой точке.
В данном случае она находится справа от точки и направлена вниз, следовательно, создает вращение по ходу часовой стрелки.
Плечом момента нагрузки служит расстояние между равнодействующей и точкой.
Уравнение суммы моментов для точки под распределенной нагрузкой (в точке D) запишется в виде:
Положительный результат показывает вращение системы против ХЧС.
Направления определенных сумм моментов относительно заданных точек
При определении суммы моментов следует помнить, что в отличие от сил и распределенных нагрузок, сосредоточенный момент будет иметь один и тот же знак относительно любой точки системы.
Уравнения суммы моментов можно составить относительно любых других точек системы, в том числе точек, которые лежат вне заданной системы. Но, как правило, при решении задач этого не требуется.
Для статичных, геометрически неизменяемых систем сумма моментов всегда равна нулю.
Другие примеры решения задач статики >
Содержание:
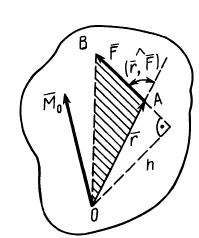
Моменты силы относительно точки и оси:
Для рассмотрения различных систем сил необходимо ввести понятия алгебраического и векторного моментов силы относительно точки и момента силы относительно оси. Введем эти характеристики действия силы на твердое тело и рассмотрим их свойства.
Алгебраический момент силы относительно точки
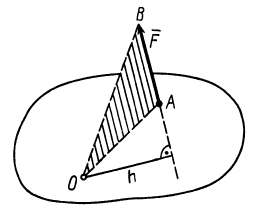
При рассмотрении плоской системы сил, приложенных к твердому телу, используется понятие алгебраического момента силы относительно точки.
Рис. 19
Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки (рис. 19), взятое со знаком плюс или минус.
Плечом 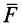

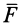
Обозначим 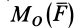
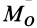
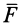

Если сила стремится вращать тело вокруг моментной точки (точки, относительно которой вычисляют алгебраический момент силы) против часовой стрелки, то берем знак плюс, если по часовой стрелке — знак минус.
Алгебраический момент силы представляет собой произведение силы на длину (в 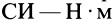
Из определения алгебраического момента силы относительно точки следует, что он не зависит от переноса силы вдоль ее линии действия. Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Сумма алгебраических моментов относительно точки двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой, равна нулю. Численно алгебраический момент относительно точки равен удвоенной площади треугольника, построенного на силе 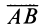
Векторный момент силы относительно точки
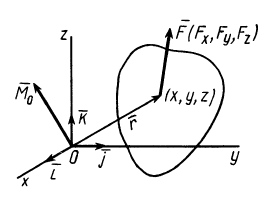
При рассмотрении пространственной системы сил, приложенных к твердому телу, применяется понятие векторного момента силы относительно точки.
Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки (рис. 20).
Плечом 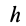

Рис. 20
Условимся векторный момент силы 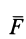


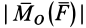
Как и для алгебраического момента, векторный момент силы относительно точки равен удвоенной площади треугольника, построенного на силе и моментной точке:
Справедлива формула
где 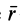

Чтобы убедиться в справедливости формулы (3), достаточно показать, что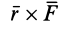

Как показано на рис. 20, 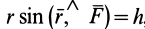
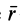
что совпадает с векторным моментом силы относительно точки 
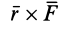
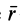
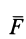
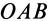

Направление 

Векторный момент силы относительно точки не изменяется от переноса силы вдоль ее линии действия. Он станет равным
нулю, если линия действия силы пройдет через моментную точку.
Рис. 21
Если сила 
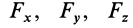
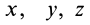
где 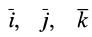
Используя формулу (4), можно выделить проекции 
Модуль векторного момента 
В формулах (6) числовую величину 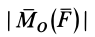
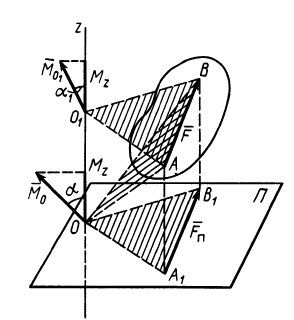
Момент силы относительно оси
Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью (рис. 22). Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси (проекция силы на плоскость является вектором), стремится вращать тело вокруг положительного направления оси против часовой стрелки, и отрицательным, если она стремится вращать тело по часовой стрелке. Момент силы, например, относительно оси 
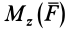
Рис. 22
По определению,
где 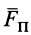
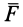





Из определения момента силы относительно оси следует, что введенный выше алгебраический момент силы относительно точки можно считать моментом силы относительно оси, проходящей через эту точку, перпендикулярно плоскости, в которой лежат сила и моментная точка. Момент силы относительно оси можно выразить через площадь треугольника, построенного на проекции силы 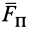

Из формулы (8) можно получить следующие важные свойства момента силы относительно оси:
- Момент силы относительно оси равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси.
- Момент силы относительно оси равен нулю, если линия действия силы пересекает эту ось. В этом случае линия действия проекции силы на плоскость, перпендикулярную оси, проходит через точку пересечения оси с плоскостью и, следовательно, равно нулю плечо силы
относительно точки
.
В обоих этих случаях ось и сила лежат в одной плоскости. Объединяя их, можно сказать, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
Связь момента силы относительно оси с векторным моментом силы относительно точки на оси
Используя формулу (8), имеем (рис. 23)
Векторный момент силы 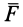



Векторный момент 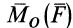
причем векторный момент 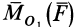
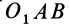
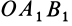

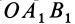

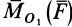
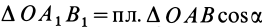
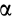
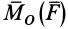

причем знак 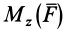
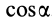
Аналогично,
т. е.
где 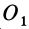

Формулы (11) и (12) отражают искомую связь между моментом силы относительно оси и векторными моментами силы относительно точек, лежащих на этой оси: момент силы относительно оси равен проекции на эту ось векторного момента силы относительно любой точки на оси.
Эту зависимость между моментом силы относительно оси и векторным моментом силы относительно точки на оси можно принять за определение момента силы относительно оси.
Рис. 23
Формулы для моментов силы относительно осей координат
Используя связь момента силы относительно оси с векторным моментом силы относительно точки на оси, можно получить формулы для вычисления моментов относительно осей координат, если даны проекции силы на оси координат и координаты точки приложения силы. Для оси 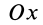
Согласно (5),
следовательно,
Аналогично, для осей 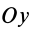
Окончательно
По формулам (13) можно вычислить моменты силы относительно прямоугольных осей координат.
По этим формулам получаются необходимые знаки для 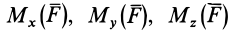
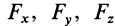
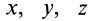
При решении задач момент силы относительно какой-либо оси часто получают, используя его определение, т. е. проецируя силу на плоскость, перпендикулярную оси, и вычисляя затем алгебраический момент этой проекции относительно точки пересечения оси с этой плоскостью.
Момент пары сил. Сложение пар сил. Равновесие пар сил
При изучении теоретической механики необходимо совершенно отчетливо уяснить, что в статике рассматриваются два простейших элемента: сила и пара сил. Любые две силы, кроме сил, образующих пару, всегда можно заменить одной —сложить их (найти равнодействующую). Пара сил нс поддается дальнейшему упрощению, она не имеет равнодействующей и является простейшим элементом.
Действие пары сил на тело характеризуется ее моментом — произведением одной из сил пары на ее плечо (на кратчайшее расстояние между линиями действия сил, образующих пару).
Единицей момента пары сил в Международной системе служит 1 нм (ньютон-метр = 1 н-1ж), а в системе МКГСС (технической)— 1 кГ-м.
Несколько пар сил, действующих на тело в одной плоскости, можно заменить одной парой сил (равнодействующей парой), момент которой равен алгебраической сумме моментов данных пар:
При равновесии пар сил
Если пары сил действуют в одной плоскости, то при решении задач достаточно рассматривать моменты пар как алгебраические величины. Причем знак момента определяется в зависимости от направления вращающего действия пары сил.
Дальнейшее изложение основано на правиле, т. е. считается момент положительным, если пара сил действует против хода часовой стрелки, если же пара сил действует на тело но ходу часовой стрелки, то момент считается отрицательным.
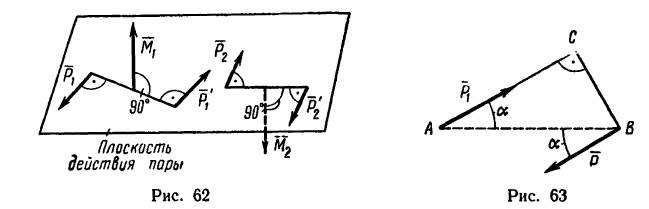
В том случае когда пары сил действуют на тело будучи расположенными в различных плоскостях, гораздо удобнее рассматривать пару сил как вектор, направленный перпендикулярно
к плоскости действия пары сил (рис. 62). Направление вектора в зависимости от направления вращательного действия пары определяется по направлению движения винта с правой нарезкой.
Задача 1.
Определить момент пары сил (рис. 63), если 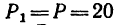
Решение.
1. При определении момента пары сил нужно прежде всего правильно определить плечо пары. При этом необходимо различать следующие понятия: плечо пары сил и расстояние между точками приложения сил нары.
Так как в механике твердого тела сила—скользящий вектор, то действие силы не изменяется при переносе точки ее приложения вдоль линии ее действия. Значит расстояние между точками приложения сил, образующих пару, можно изменять неограниченно. Но плечо пары при этом переносе остается неизменным.
В частном случае расстояние между точками приложения сил, образующих пару, может быть равно плечу.
Чтобы определить плечо данной пары из точки приложения одной из сил, например из точки В, восставим перпендикуляр ВС к линии действия другой силы. Расстояние ВС и есть плечо данной пары сил. Расстояние между точками приложения сил, образующих пару, АВ=0,5 м.
Легко видеть, что
2. Найдем момент пары сил:
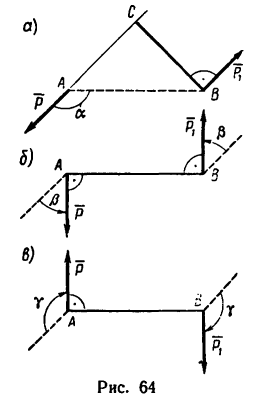
Задача 2.
Как изменится момент пары сил 
повернуть силы 
1. Найдем момент пары при заданном положении ее сил (рис. 64, а).
Из точки В восставим перпендикуляр ВС к линиям действия сил 
Момент пары при заданном положении сил
2. Повернем силы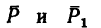
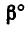
3. Сравнивая полученные результаты, видим, что после поворота сил момент пары увеличивается на 20—14,5 = 5,85 н-м.
4. Легко заметить, что силы 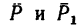
Момент пары сил изменяет свой знак.
Задача 3.
К точкам А, С и В, D, образующим вершины квадрата со стороной 0,5 м (рис. 65, а), приложены равные по модулю силы (Р = 12н) таким образом, что они образуют две пары сил
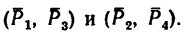
Решение 1.
Плечи у обеих пар сил равны стороне квадрата поэтому
Решение 2.
1. Перенесем силы 
2. Сложим попарно эти силы у каждой из точек В и D. В обоих случаях
3. Силы R, модули которых теперь известны, направлены перпендикулярно к диагонали BD квадрата. Значит эта диагональ является плечом вновь образовавшейся пары сил 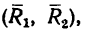
4. Найдем момент пары
и, следовательно,
Эту пару в соответствии со вторым решением можно представить в виде пары 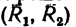
Но можно равнодействующую пару представить и в любом другом виде, например в виде сил Q = 24 и, приложенных к двум любым вершинам квадрата ABCD (рис. 65, в)
- Заказать решение задач по теоретической механике
Задача 4.
На прямоугольник ABCD (рис. 67) вдоль его длинных сторон действует пара сил 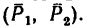
Решение.
1. Момент данной пары сил
необходимо уравновесить парой, момент которой обозначим Л1м. Тогда, согласно условию равновесия,
Откуда
2. Обозначив силы, образующие искомую пару 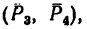
Отсюда
•Значит к прямоугольнику необходимо приложить пару сил с положительным (направленным против хода часовой стрелки) моментом, равным 48 н м. Силы, образующие эту пару, равняются
20 н каждая и одна из них должна действовать вдоль стороны АВ от А к В, вторая — вдоль стороны CD от С к D.
Задача 5.
Прямолинейный стержень АВ должен находиться в равновесии в положении, показанном на рис. 68, а (угол а = 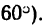
Решение.
1. Пару сил можно уравновесить только парой сил. Поэтому в точках С и D к стержню необходимо приложить две равные силы так, чтобы они образовали пару сил с моментом, равным моменту пары 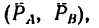
Так как пара 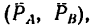
2. Применяем условие равновесия:
Или, подставив значения моментов,
где
Отсюда
Следовательно, в точках С и D необходимо приложить силы 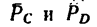
Момент силы относительно точки
Момент силы относительно точки при решении задач по статике, а затем и по динамике имеет не менее важное значение, чем проекции сил. Поэтому нужно уметь определять эту величину безошибочно. Обычно его числовое значение находят неправильно из-за ошибок, допускаемых при определении плеча.
Чтобы не допускать ошибок при определении моментов сил относительно точки, рекомендуется придерживаться следующего порядка:
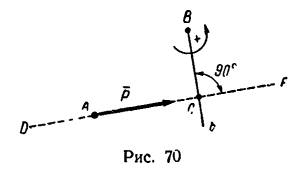
- Прежде всего нужно научиться «видеть» силу, момент которой определяем, и центр моментов – точку, относительно которой определяем момент (рис. 70 – сила
и центр моментов – точка В).
- Затем из центра момента проводим прямую ВЬ перпендикулярно к линии действия силы DF. Длина перпендикуляра ВС от центра момента до линии действия силы и есть плечо.
- Потом находим знак момента. При этом если сила стремится повернуть плечо вокруг центра момента против хода часовой стрелки, то считаем момент положительным; если по ходу часовой стрелки, то отрицательным (тоже правило, что и при определении знака момента пары сил).
- Находим числовое значение момента силы относительно точки, умножив модуль силы на плечо.
По рис. 70
В частном случае момент силы может равняться нулю. Это происходит тогда, когда центр моментов лежит на линии действия силы, при этом плечо равняется нулю. По рис. 70 момент силы 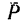
Задача 6.
Определить моменты шести заданных сил (рис. 71) относительно точек А, В и С, если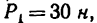
Решение 1 — определение моментов гнести заданных сил относительно точки А (рис. 71, а).
1. Центр моментов в точке А. Через точку А проходят линии действия трех сил 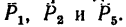
2. Находим момент силы 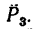
силы 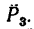
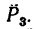
3. Величина момента отрицательная (сила 
4. Находим момент силы 
Величина момента положительная (плечо АЕ поворачивается около точки А силой 
5. Находим момент силы 
Решение 2 — определение моментов сил относительно точки В (рис. 71, б).
1. Центр моментов в точке В.
2. Через точку В проходят линии действия двух сил: 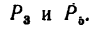
3. Находим момент силы 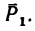
Величина момента отрицательная:
4. Находим момент силы 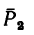
Момент отрицательный:
5. Находим момент силы 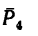
Величина момента положительная:
6. Находим момент силы 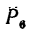
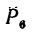
Решение 3 — определение моментов сил относительно точки С (рис. 71, в) рекомендуется выполнить самостоятельно.
Ответ.
В задаче силы расположены так, что либо их плечи определяются очень просто – как катеты прямоугольных треугольников, в которых даны гипотенузы, либо плечи заданы в условии задачи (ВС и АС).
Но иногда некоторые силы заданной системы оказываются расположенными относительно выбранного центра моментов так, что определить длину плеча трудно и требуется, например, предварительно вычислить длины еще одного-двух отрезков. В таких случаях целесообразно силу разложить на две составляющие и применить для определения ее момента теорему Вариньона.
Задача 7.
Определить моменты относительно точки 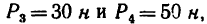

Решение.
1. Относительно точки А моменты сил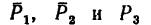
2. Находим момент силы 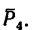
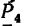
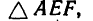
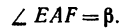
AF = AB – FB.
Величину FB находим из 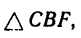
следовательно,
И теперь можем определить плечо АЕ:
Раскрываем скобки и заменяем
Момент положительный, следовательно:
Вариант 2-й. Чтобы избежать определения плеча АЕ, которое в данном случае находится после предварительного вычисления двух отрезков (FB и AF), необходимо момент силы 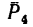
Разложим силу 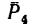
Модуль первой составляющей 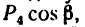
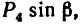
Применяя теорему Вариньона, получаем
Как видно, получено точно такое же значение момента, что и в первом варианте решения:
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил
- Аксиомы и теоремы статики
- Система сходящихся сил
- Плоское движение тела
- Принцип виртуальных перемещений

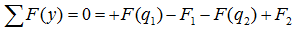
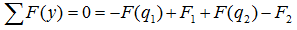






 ,
, 

 .
.  , то есть сила параллельна оси.
, то есть сила параллельна оси.  ,
,  — силы, составляющие пару;
— силы, составляющие пару;  — это главный вектор системы сил.
— это главный вектор системы сил. 




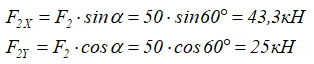
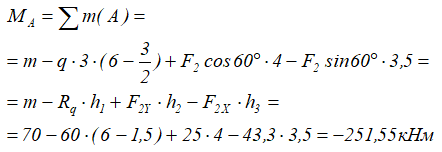
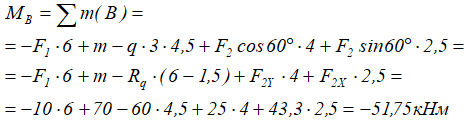
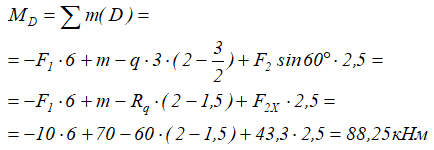

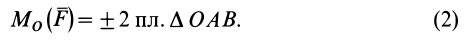
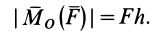
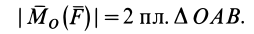

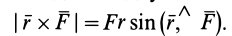
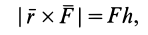
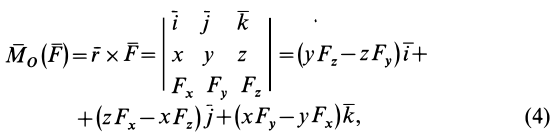
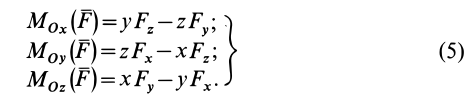
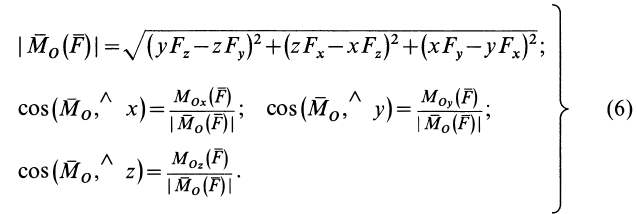
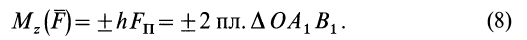
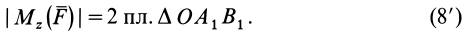
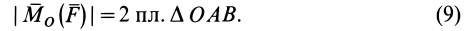
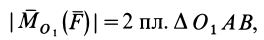
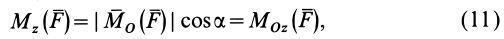
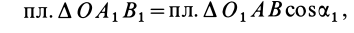
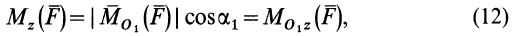
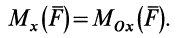
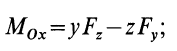
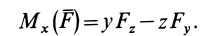
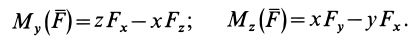
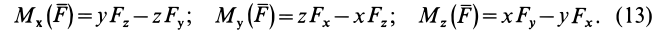
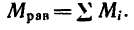
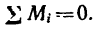
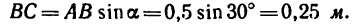
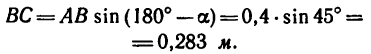
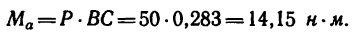
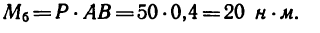
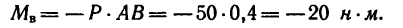
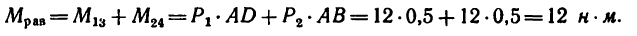
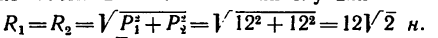
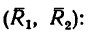
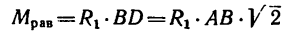
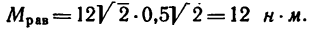
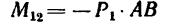
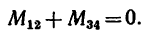
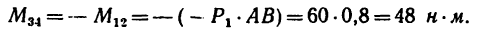
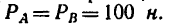
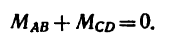
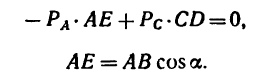
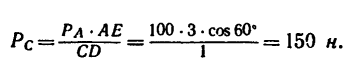
 и центр моментов – точка В).
и центр моментов – точка В).