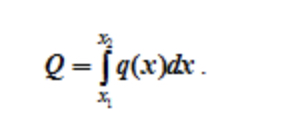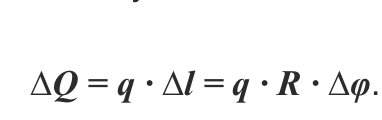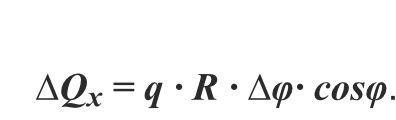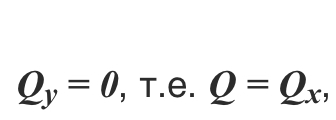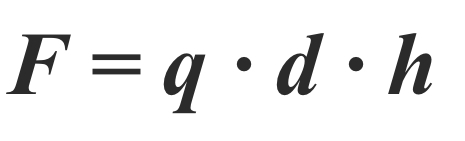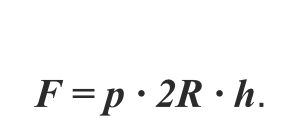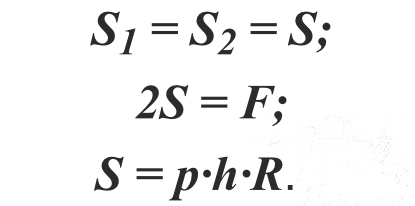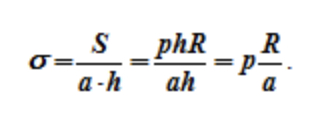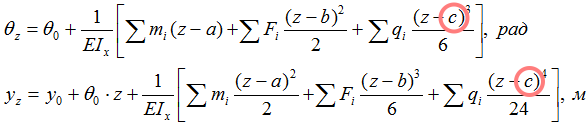Взаимодействия с деталями, отдельными элементами и конструкциями механизма задается с помощью нагрузок. В плоскости задается интенсивность взаимодействия конструкции по длине, а в пространстве – по её площади.
Распределённая нагрузка на балку задается площадью, обозначается буквой q и измеряется в [H/м3] для объемной конструкции, в [H/м2] — для площади, для линейной – в [H/м].
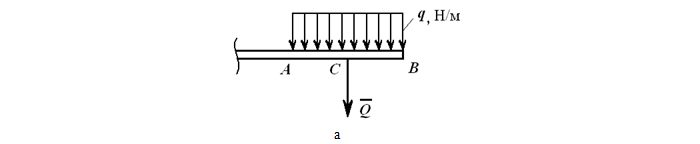
Продемонстрируем это на рисунке:
Нагрузку также можно заменить тягой, рассредоточенной по всей поверхности. Значение определяется по формуле:
Q = q ∗ AB⌈H⌉
здесь AB является тяжестью, q – интенсивностью, которая измеряется в [H/м].
Примечательно, что сила приложена к середине данного отрезка AB.
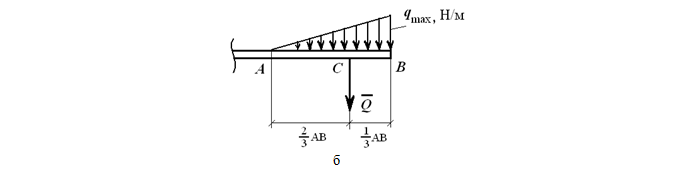
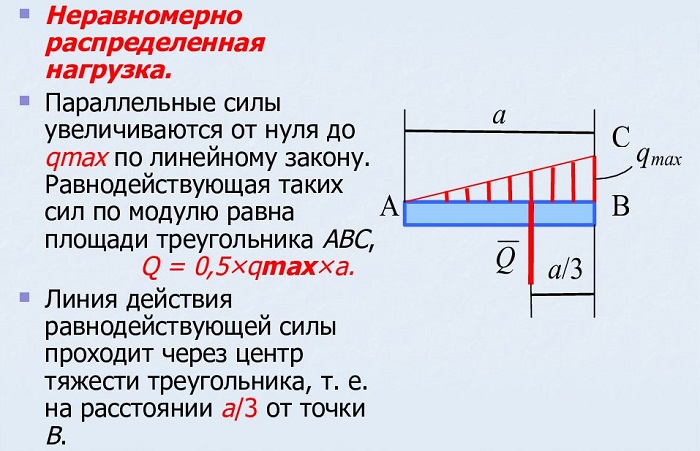
На данном рисунке представлен расчёт возрастающей нагрузки, которую можно заменить равнодействующей единицей, рассчитываемое по формуле:
Q = qmax ∗ AB/2
где qmax – максимальная интенсивность [Н/м].
Q приложена к точке C, где AC равно: AC = 2/3 AB
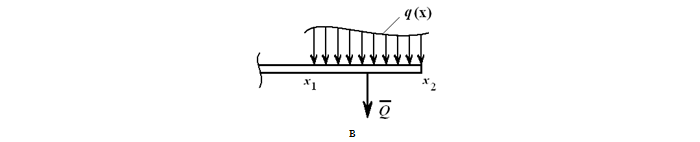
Рассматривая функцию q(x), представленную на рисунке:
можно высчитать значение эквивалентной силы по формуле:
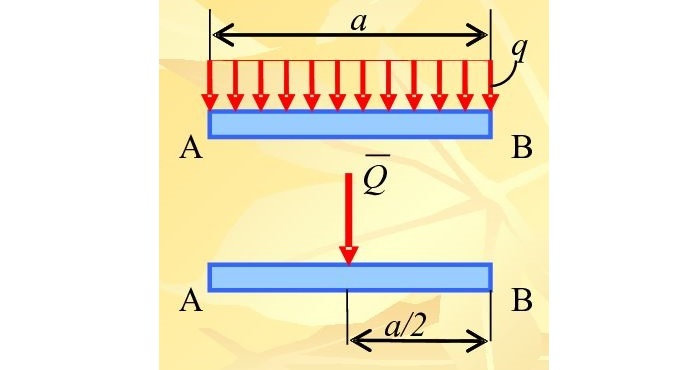
Равномерно и неравномерно распределенная нагрузка на балку
Распределение сил, которые лежат в одной плоскости, задается равномерно распределенной тяжестью. Основным обозначением является интенсивность q – предельная тяга, несущая равнодействующую на единицу длины нагруженного участка АВ длиной а.
Единицы измерения распределённой нагрузки [Н/м].
Её также можно заменить на величину Q, которая приложена в середину AB.
Составим формулу: Q = q∗a
Неравномерно распределённую нагрузку чаще всего упрощают, приводя её к эквивалентной равномерно распределенной, чтобы упростить расчеты.
При построении также следует учитывать максимальный прогиб балки, её прочность, расчетную опорную реакцию и моментальную опору.
Пример решения задач с распределенной нагрузкой
Рассмотрим пример распределенной нагрузки на балку. Им может послужить тяга, благодаря которой происходит разрыв стальной стенки баллона с некоторым газом.
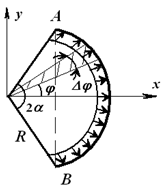
Для начала определяем результирующую давления в металлической трубе. Интенсивность равна q, радиус этого сектора трубы – R, ось симметрии Оx, а 2α – это центральный угол. Представим это на рисунке:
Выделим элемент сектора трубы ∆ϕ.
Затем определим единицу силы ∆Q. Она действует на плоскость дуги. Составим формулу:
Проекция результирующей тяги на ось Оx является:
Исходя из вышесказанного, можно найти проекцию этой же силы на ось Оy:
AB является хордой, которая стягивает дугу.
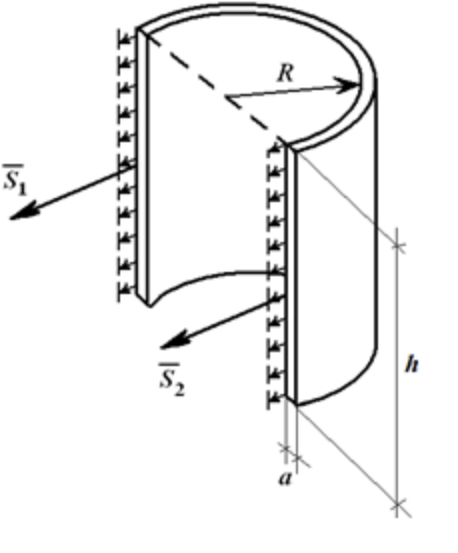
В нашей задаче сосуд – это ёмкость цилиндрической формы с высотой H, внутренним давлением P, действующим на стенки, и нагрузкой q = p [Н/м2].
Разделим цилиндр вдоль его диаметра.
Исходя из этого, равнодействующая результирующих сил определяется по формуле:
где d – это внутренний диаметр цилиндра, h — его высота.
Формулу также можно записать следующим образом:
Итак, почему баллон имеет способность разрываться? На его стенки действуют значения S1, S2, S3 (площади), а также F, p (плотность), h (высота цилиндра) и R (его радиус). Рассчитаем их по формулам:
Изобразим баллон в момент разрыва:
Учтём a – толщину ёмкости. Таким образом напряжение, которое растягивает баллон, (усилия распространяются в том числе на крышку и дно цилиндра) равно:
Важную роль при решении практических задач также играет эпюра распределенной нагрузки – плоская фигура, которая ограничена графиком. Величина, действующая на балку, называется интенсивностью – силой, которая распространяется на единицы площади, объема или длины.
В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).


Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:
Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:
Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:


Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:
Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉
Построение эпюр для консольной балки
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:
Как видишь, поперечная сила будет постоянна на первом участке:
Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:
Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:
Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:
Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке
Первым делом, нам потребуется определить реакции в заделке:

Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:

Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила QA будет равна:
Изгибающий момент Mизг, A будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:
Рассчитаем значения на эпюре поперечных сил:


Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:


На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюр для двухопорной балки
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:

Рассчитываем первый участок:
Строим эпюры на первом участке:

Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:
Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:
Определение экстремума:


Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
При
решении практических задач далеко не
всегда можно считать, что действующая
на тело сила приложена в одной точке.
Часто силы бывают приложены на целом
участке тела (например снеговая
нагрузка, ветровая и т.д.). Такая нагрузка
называется распределенной. Равномерно
распределенная нагрузка характеризуется
интенсивностью q (рис.1.29). Интенсивность
– это суммарная нагрузка, приходящаяся
на единицу длины конструкции.
|
|
Единица
измерения интенсивности [H/м], [кН/м]. При
решении задач статики распределенную
нагрузку можно заменить ее равнодействующей,
которая равна произведению интенсивности
на длину участка, на который действует
распределенная нагрузка, и которая
приложена в середине этого участка.
1.13. Решение задач на плоскую систему сил
Пример
(рис.1.30). Определить реакции шарнирно
опертой балки, нагруженной силой
и парой сил с моментом М.
|
|
Решение.
Воспользуемся тем же планом, который
применялся для решение задач на
сходящуюся систему сил. Объектом
равновесия является вся балка, нагрузка
на которую показана на чертеже. Отбросим
связи – шарниры А и В. Реакцию неподвижного
шарнира А разложим на две составляющих
–
и
,
а реакция подвижного шарнира В направлена
перпендикулярно опорной плоскости.
Таким образом, на балку действует
плоская произвольная система сил, для
которой можно составить три уравнения
равновесия. Выберем оси координат и
составим эти уравнения. Уравнения
проекций:
1.
Fkx
= 0; Rax
-Fcos(60)
= 0;
2.
Fky
=
0; Ray
+
RB
–
Fcos(30)
= 0;
(пара
в уравнение проекций не входит, так как
сумма проекций сил пары на любую ось
равна нулю).
Уравнение
моментов составляем относительно точки
А, поскольку в ней пересекаются две
неизвестных силы. При нахождении момента
пары относительно точки А помним, что
сумма моментов сил пары относительно
любой точки равен моменту пары, а знак
момента будет положительным, поскольку
пара стремится повернуть тело против
часовой стрелки. Для нахождения момента
силы
удобно разложить ее на вертикальную и
горизонтальную составляющие:
Fx=Fcos(60),
Fy=Fcos(30)
и
воспользоваться теоремой Вариньона,
причем следует учесть, что момент от
силы
относительно
точки А равен нулю, поскольку ее линия
действия проходит через эту точку.
Тогда уравнение моментов примет вид:
3.
; Rв.3-FBcos(30)2
+ M = 0.
Решая это уравнение
получим:
Из уравнения (2)
находим:
Ray
=
Fcos(30)
– RB
=
20,867
– 4=-2,67 кН,
а
из уравнения (1) Rax
= Fcos(60)
= 20,5
= 1 кН.
|
Пример |
|
Решение.
Заменим равномерно распределенную
нагрузку ее равнодействующей Q = 3q
= 310
= 30 кН. Она будет приложена в середине
пролета, то есть на расстоянии АС = 1,5
м. Рассматриваем равновесие балки АВ.
Отбрасываем связь – жесткую заделку, а
вместо нее прикладываем две составляющие
реакции Rах
и Rау
и реактивный момент Mа.
На балку будет действовать плоская
произвольная система сил, для которой
можно составить три уравнения равновесия,
из которых можно найти искомые
неизвестные.
Fкх
= 0; Rах =
0;
Fку
= 0; Rау
– Q = 0; Rау
= Q = 30 кН;
Mа(Fк)
= 0; Mа
– 1,5Q
= 0; Mа =
1,5Q
= 1,530
= 45 кHм.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Сосредоточенные силы и распределенные нагрузки
- Плоская система параллельных сил
- Равновесие системы тел
- Статически обозначенные и статически неопределенные задачи
- Методика решения задач на равновесие системы тел
Такие силы называются сосредоточенными. Однако в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности или линии по тому или иному закону. Распределенные силы прежде всего характеризуются интенсивностью q, т.е. величиной силы, приходящейся на единицу поверхности или линии.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Сосредоточенные силы и распределенные нагрузки
Мы рассматривали силы, которые были представлены в виде вектора, приложенного к точке. Однако в природе существует большое количество взаимодействий тел, осуществляются не в точке и которые нельзя представить в виде вектора, приложенного к точке.
Такими силовыми факторами являются силы давления жидкости или газа в поверхность твердых тел, силы тяжести, как массовые силы, электромагнитные силы тому подобное. Поэтому в теоретической механике вводится понятие о распределенных силах, которые делятся на поверхностные и объемные.
Поверхностные силы действуют на некоторую поверхность тела. Объемные силы действуют на каждый элемент объема тела, рассматривается. Примером последних сил является сила притяжения.
В теоретической механике рассматривается воздействие на тело только сосредоточенных сил, приложенных к абсолютно твердым телам. А потому
распределенную нагрузку необходимо заменить его равнодействующей, то есть
сосредоточенной силой. Введем несколько общих положений.
Распределенная нагрузка характеризуется его интенсивностью 
силовых схемах оно изображается в виде эпюры элементарных сил, то есть графика интенсивности нагрузки, приложенная к линейному элементу тела.
В общем случае распределенная нагрузка изображается в виде определенной кривой, отражающей данный закон изменения интенсивности нагрузки на участке тела (рис. 1.20). Направление действия нагрузки показывается стрелками.
Сначала рассмотрим равномерно распределенную нагрузку и нагрузку, распределенную по линейному закону. Заменяем распределенную нагрузку сосредоточенной силой.
Рассмотрим эти два случая:
— равномерно распределенная нагрузка (или нагрузка, распределенная по закону прямоугольника) изображается на схемах в виде прямоугольника, размеры которого таковы: высота — это интенсивность нагрузки 

Q = q · l,
где q — интенсивность нагрузки, Н/м; l — длина участка тела, на которой приложенная нагрузка, м.
Точка C приложения равнодействующей силы 

— нагрузка распределена по линейному закону (то есть по закону треугольника). В этом случае (рис. 1.22) интенсивность распределенной нагрузки на участке l меняется от 0 до максимального значения qmax. Равнодействующая сила 
Точка C приложения равнодействующей 


Плоская система параллельных сил
Когда линии действия всех сил параллельны, то всегда в плоскости можно так
расположить оси координат, одна из них будет обязательно параллельной заданным силам, а вторая — перпендикулярной. А потому, чтобы тело под действием плоской системы параллельных сил находилось в равновесии, необходимо приравнять к нулю алгебраическую сумму проекций всех сил на параллельную ось и алгебраическую сумму моментов всех сил относительно произвольной точки. В данном случае система условий равновесия (1.54) упрощается и будет иметь такой вид
Для равновесия тела, находящегося под действием системы параллельных сил
на плоскости, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил
на ось, параллельная силам, и алгебраическая сумма моментов всех сил относительно произвольной точки А плоскости равны нулю.
Для системы параллельных сил на плоскости можно использовать и такие условия равновесия
Для равновесия тела, находящегося под действием системы параллельных сил на плоскости, необходимо и достаточно, чтобы алгебраические суммы моментов всех
сил относительно любых двух точек плоскости равны нулю.
Однако для этих условиях существует ограничение: линия АВ, которой можно соединить
центры моментов, не должна быть параллельной силам.
Данные условия наиболее пригодны при расчетах двухопорных балок. Используя эти условия, составляют алгебраические суммы моментов всех сил относительно точек A и B, в которых установлены опоры балки.
Рассмотрим примеры задач на равновесие тела под действием плоской системы произвольных сил.
Пример:
Однородная балка АВ прямоугольного сечения весом 400 Н имеет один конец А, который закреплен шарнирно, и опирается на точечную опору O (рис. 1.23). Ко второму концу балки В подвешен груз весом 200 Н. Длина балки 4 м, точечная опора расположена на расстоянии ¾ длины балки от шарнирной опоры. Угол наклона балки к горизонту составляет α = 30º.
Определить реакции опор балки.
Краткое условие задачи:
G = 400 H ;
Q = 200 H ;
AB = 4 м;
AO = 3/4 AB = 3 м ;
α = 30º.
RA = ?
Rо = ?
Решение.
Составляем расчетно–силовую схему задачи. Приложим к оси балки заданные активные силы: силу тяжести 



Далее условно освобождаем балку от связей и заменяем их соответствующими реакциями связей. В точке A размещена неподвижная шарнирная опора, она имеет
две составляющие реакции 

координат. В точке O — точечная опора, которая имеет одну реакцию 
Таким образом, балка находится в равновесии под действием плоской системы произвольных сил. Для решения этой задачи используем условия равновесия (1.54),
Поскольку оси координат x и y заданные по условию задачи, то составим соответствующие уравнения равновесия
Если подставить значения известных величин в эти уравнения равновесия, то получим
С третьего уравнения вычислим реакцию Ro:
Ro = 
и подставим ее значение в первые два уравнения. Будем иметь
ХА = 
YА = 400 + 200 – 0,866 · 461,86 = 160,04 Н.
Поскольку определены две составляющие реакции, приложенные в точке A, — ХА и YА, то геометрическим добавлением можно вычислить модуль полной реакции RA. А именно:
Таким образом определении все искомые реакции.
Ответ: RA = 280,97 Н;
Rо = 461,86 Н.
Пример.
Определить реакции опоры однородной балки АВ прямоугольного сечения, один конец которого A жестко закреплен в стене и находящийся под действием сосредоточенной силы P = 4,0 kH, пары сил с моментом m = 2,0 kH · м и равномерно распределенной нагрузки интенсивностью q = 1,5 
нагрузка действует на участке 3 м от точки A. Угол наклона сосредоточенной силы 
Краткое условие задачи:
P = 4,0 kH;
m = 2,0 kH · м;
q = 1,5 
АВ = 5 м;
AС = 3 м;
α = 30º
RA = ?
МA = ?
Решение.
Составляем расчетно-силовую схему. Покажем все силы, приложенные к балке АВ. Прежде всего, это заданные активные силы — сила 


Сила 
Далее условно освобождаем балку от вязи и заменяем ее соответствующими реакциями вязи. В точке A — жесткое закрепление балки в стене, а потому оно имеет две составляющие реакции: 

координат, и реактивный момент MA. Направление этого неизвестного момента
показываем на силовой схеме произвольно, например, — против направления стрелки
часов. Если же при окончательном определении момента MA получим отрицательный знак, то получим, что действительное направление момента — противоположно. Покажем на силовой схеме линейные и угловые размеры. Оси координат показаны на схеме.
Как видно из построенной расчетно–силовой схемы, балка находится под действием плоской системы произвольных сил. Используем условия равновесия (1.54). А именно = 0.
Составим соответствующие уравнения равновесия
Если подставить значения известных величин в эти уравнения равновесия, то получаем
Из первого уравнения вычислим XA:
XA = 4,0

Из второго уравнения вычислим YA:
YA = 4,5 + 4,0 · 
С третьего уравнения вычислим MA:
MA = 2,0 + 4,5 

Поскольку составляющие реакций XA и YA, приложенных в точке A, вычислены, то можно найти модуль RA полной реакции в точке A. Будем иметь
Таким образом, определены все искомые реакции.
Ответ: RA = 4,30 kH; MA = 18,75 kH.
Равновесие системы тел
Системой тел называется совокупность нескольких тел, или которые опираются друг на друга, или соединены шарнирами, которые дают возможность относительного движения тел.
При решении задач на систему тел различают силы внешние и внутренние.
Внешние силы — это силы взаимодействия тел данной системы с другими телами, которые не входят в состав системы.
Внутренние силы — это силы взаимодействия между отдельными телами, которые входят в состав данной системы. Внутренние силы существуют попарно, как действие и
противодействие.
Статически обозначенные и статически неопределенные задачи
Задача является статически обозначенной, если для нее можно составить такое
количество уравнений равновесия материальной системы, не меньше, чем число
неизвестных.
Задача, является статически неопределенной, если число уравнений равновесия
системы меньше, чем число неизвестных.
В теоретической механике рассматриваются только статически обозначенные
материальные системы.
Методика решения задач на равновесие системы тел
Равновесие системы тел можно рассматривать в целом под действием только
внешних сил. Но может так случиться, что количество уравнений равновесия будет
меньше, чем количество неизвестных. Тогда необходимо рассматривать равновесие
отдельных тел системы, условно разделяя ее обязательно по внутренним связям. Причем необходимо учитывать, что внутренние силы реакций входят попарно, как действие и противодействие.
Рассмотрим пример решения задач на равновесие системы тел.
Пример.
На трех-шарнирную арку А В С (рис. 1.25) действует вертикальная сила Р = 10 kH. Вес каждой части балки Q1 = Q2 = 6 kH. Определить реакции шарниров А, В, С арки, размеры которой данные на рисунке.
Решение.
Как видно из схемы, заданная система тел состоит из двух пиварок I и II, которые соединены шарниром в точке С. Составим расчетно–силовую схему, где покажем заданные активные силы Q1, Q2, 












Покажем оси прямоугольной декартовой системы координат Axy.
Условно разделяем систему тел на два отдельных тела по шарниру С. Действие отброшенной части заменяем двумя реакциями 

Теперь рассмотрим отдельно равновесие каждого тела, для чего составим две системы уравнений равновесия. Используем условия равновесия.
Для первого тела (левая половина арки):



Для второго тела (правая половина арки):



Как видно из полученных шести уравнений равновесия, в них содержатся шесть неизвестных: ХА, ХB, ХС, YA, YB, YC .
Определим эти неизвестные величины. С третьего уравнения второй системы определим Y´C . Перепишем это уравнение следующим образом:
5Y´C = 4Х´С – Q2,
откуда находим реакцию Y´C :
Поскольку численно Y´C = YC , а ХС = Х´С, то подставив значения этих реакций в третье уравнение первой системы, получаем
или
8ХС = Q1 + Q2 + 4P,
откуда
Теперь есть возможность определить неизвестную реакцию Y´C . Подставив значение XC в третье уравнение второй системы, будем иметь
Из первого уравнения первой системы имеем XA = XC = 6,5 kH. А с первого уравнения второй системы должны XB = – X´C = – 6,5 kH. Направление этой реакции противоположно показанному на силовой схеме. Из второго уравнения первой системы получаем
YA = Q1 + P – YC = 6,0 + 10,0 – 4,0 = 12,0 kH.
Из второго уравнения второй системы вычислим последнюю неизвестную реакцию YB. Она будет равняться YB = Y´C + Q2 = 4,0 + 6,0 = 10,0 kH.
Таким образом вычислено все искомые величины.
Ответ:
XA = 6,5 kH; YA = 12,0 kH; XB = – 6,5 kH; YB = 10,0 kH; XC = 6,5 kH; YC = 4,0 kH.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Продление и компенсация распределенной нагрузки требуются корректного составления универсальных уравнений метода начальных параметров (МНП).
При составлении универсальных уравнений метода начальных параметров в некоторых случаях требуются дополнительные действия, связанные с распределенной нагрузкой.
Дело в том, что уравнения МНП учитывают только то, где начинается действие нагрузки (переменная «c»), т.е. подразумевается, что она при этом продолжается до конца балки.
В тех случаях, когда это не так, ее действие продолжают до окончания рассматриваемой балки, вследствие чего начальная схема нагружения меняется.
Другие видео
Чтобы вернуться к исходной схеме, на всем участке балки, где была добавлена распределенная нагрузка, прикладывают компенсирующую нагрузку той же величины но обратного направления.
В сторону начала координат (НК) нагрузка не добавляется.
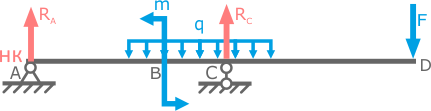
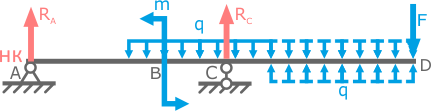
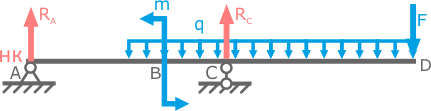
Пример 1
Начало координат слева (в точке A)
Добавленную и компенсирующую нагрузки проводят до крайнего правого сечения.
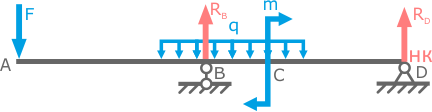
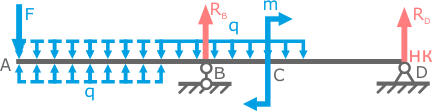
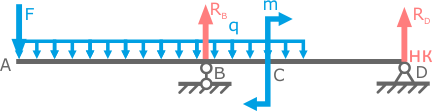
Пример 2
Начало координат справа
Добавление и компенсация распределенной нагрузки производится влево.
В случаях, когда распределенная нагрузка изначально продолжается до конца балки (сечения противоположного НК) добавленную и компенсирующую нагрузки не прикладывают.
В составляемых уравнениях МНП добавленная нагрузка учитывается вместе с основной, компенсирующая записывается как отдельная.
Расчет деформации балки методом начальных параметров >
Краткая теория по сопромату >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее