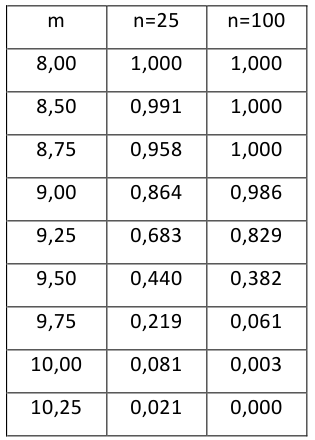
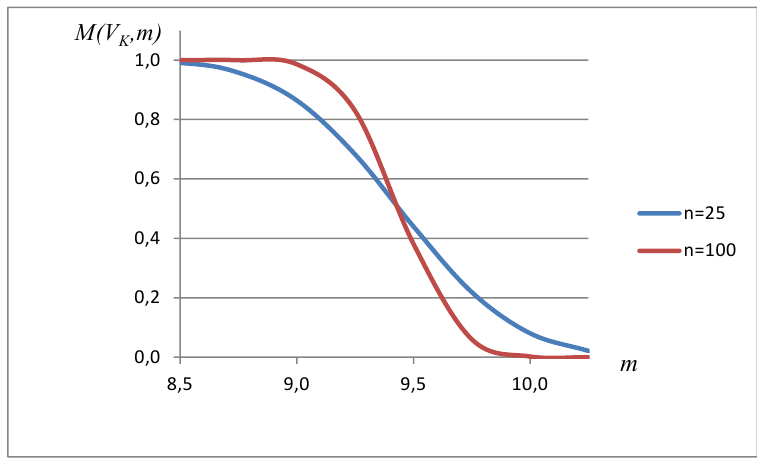
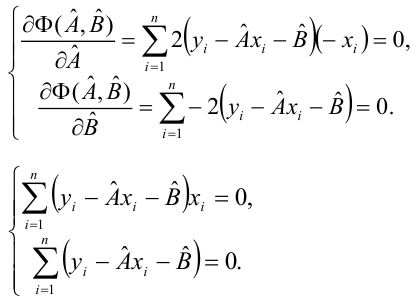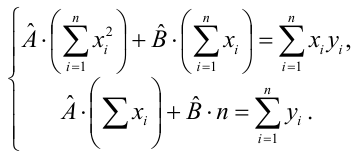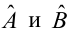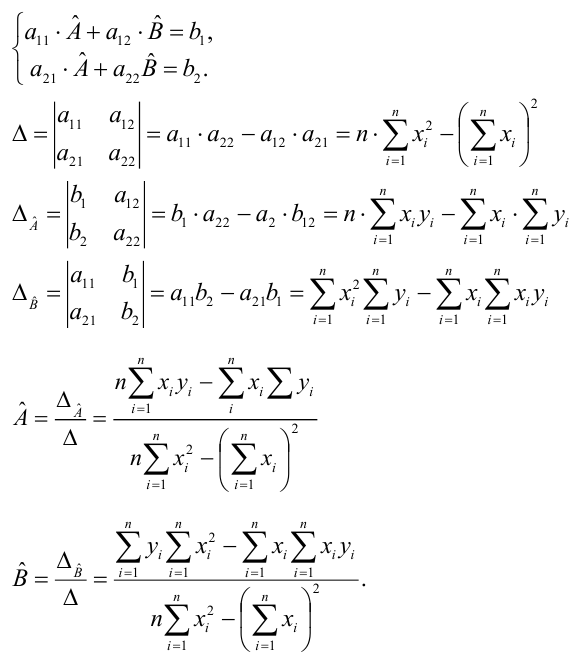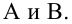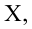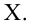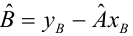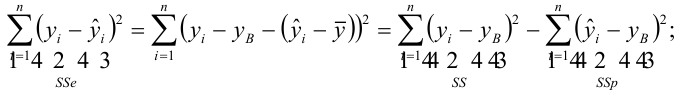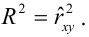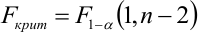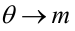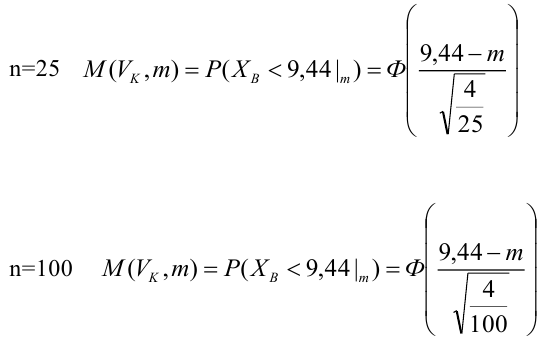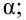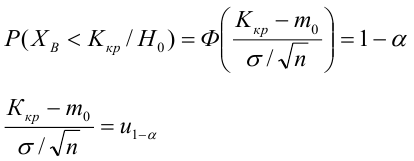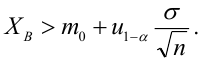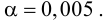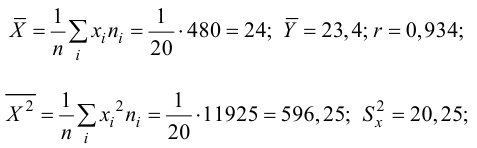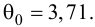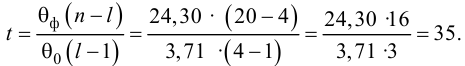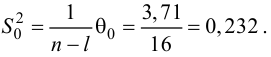Нелинейные модели парной регрессии
- Параболическая регрессия
- Гиперболическая регрессия
- Показательная (экспоненциальная) регрессия)
- Степенная регрессия
Параболическая регрессия
Уравнение регрессии в
форме параболы второго порядка имеет следующий вид:
Если при линейной связи
среднее изменение результативного признака на единицу фактора постоянно по всей
области вариации фактора, то при параболической корреляции изменение признака
меняется
равномерно с изменением величины фактора. В результате связь может даже
поменять знак на противоположный, из прямой превратится в обратную, из обратной в прямую. Такой характер связи присущ многим системам. Например, с увеличением дозы
удобрений урожайность сельхозкультур сначала
повышается, но если превысить оптимальную величину дозы, то при дальнейшем
росте дозы удобрения растения угнетаются и урожайность снижается.
Нормальные уравнения
метода наименьших квадратов (МНК) для параболы 2-го порядка таковы:
Ввиду симметричности
кривой парабола второй степени далеко не всегда пригодна в конкретных
исследованиях. Чаще исследователь имеет дело лишь с отдельными сегментами
параболы, а не с полной параболической формой.
Кроме того, параметры
параболической связи не всегда могут быть логически истолкованы. Поэтому если
график зависимости не демонстрирует четко выраженной параболы второго порядка
(нет смены направленности связи признаков), то она может быть заменена другой
нелинейной функцией, например степенной. В частности, в литературе часто
рассматривается парабола второй степени для характеристики зависимости
урожайности от количества внесенных удобрений. Данная форма связи мотивируется
тем, что с увеличением количества внесенных удобрений урожайность растет лишь
до достижения оптимальной дозы вносимых удобрений. Дальнейший же рост их дозы
оказывается вредным для растения, и урожайность снижается. Несмотря на несомненную
справедливость данного утверждения, следует отметить, что внесение в почву
минеральных удобрений производится на основе учета достижений агробиологической
науки. Поэтому на практике часто данная зависимость представлена лишь сегментом
параболы, что и позволяет использовать другие нелинейные функции.
Задача 1
Постройте
криволинейную регрессионную модель (параболу) для следующих исходных данных.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение параболической
регрессии имеет вид:
Составим
расчетную таблицу:
Для
нахождения коэффициентов параболы необходимо решить систему уравнений:
Подставляя
в систему уравнений, получаем:
Решая
систему уравнений, получаем:
Уравнение
параболической регрессии имеет вид:
Коэффициент
детерминации:
Коэффициент эластичности:
Гиперболическая регрессия
Уравнение регрессии в
форме гиперболы имеет следующий вид:
Гиперболические
зависимости характерны для связей, в которых результативный признак не может
варьировать неограниченно, его вариация имеет односторонний предел. Например,
совершенствуя двигатель, можно увеличивать его КПД, но не выше предела, допускаемого
данным видом преобразования энергии. Или таков характер связи между уровнем
душевого дохода в семье и долей семей, имеющих телевизоры – он приближен к
пределу (100%) в наиболее обеспеченной группе семей.
Если величина
положительна, то при увеличении значений
факторного признака
значения
результативного признака уменьшаются, причем это уменьшение все время
замедляется, и при
средняя
величина признака
будет
равна
. Классическим примером является кривая Филлипса, характеризующая нелинейное соотношение между
нормой безработицы
и
процентом прироста заработной платы.
Если же параметр
отрицателен,
то значения результативного признака с ростом фактора возрастают, причем их
рост замедляется, и в пределе при
. Примером может служить взаимосвязь доли
расходов на товары длительного пользования и общих сумм расходов.
Математическое описание подобного рода взаимосвязей получило название кривых Энегеля.
Нормальные уравнения
метода наименьших квадратов (МНК) для гиперболы таковы:
Легко увидеть, что эти
уравнения, по существу, те же, что для линейной связи. Линеаризация гиперболического
уравнения достигается заменой
на
новую переменную, которую можно обозначить
. Тогда уравнение гиперболической регрессии
примет вид
.
Задача 2
Постройте
криволинейную регрессионную модель (гиперболу) для следующих исходных данных.
|
|
0,96 | 0,75 | 0,64 | 0,55 | 0,68 | 0,71 | 0,95 | 0,45 | 0,71 | 0,63 |
|
|
1,95 | 2,6 | 4,28 | 6,52 | 4,55 | 2,91 | 1,81 | 8,21 | 2,84 | 4,38 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение гиперблической регрессии имеет вид:
Составим
расчетную таблицу:
Расчетная вспомогательная таблица
| № |
|
|
|
|
|
|
|
|
| 1 | 0,96 | 1,95 | 1,042 | 1,085 | 2,031 | 1,436 | 6,598 | 4,223 |
| 2 | 0,75 | 2,6 | 1,333 | 1,778 | 3,467 | 3,105 | 0,809 | 1,974 |
| 3 | 0,64 | 4,28 | 1,563 | 2,441 | 6,688 | 4,417 | 0,169 | 0,076 |
| 4 | 0,55 | 6,52 | 1,818 | 3,306 | 11,855 | 5,880 | 3,514 | 6,325 |
| 5 | 0,68 | 4,55 | 1,471 | 2,163 | 6,691 | 3,891 | 0,013 | 0,297 |
| 6 | 0,71 | 2,91 | 1,408 | 1,984 | 4,099 | 3,535 | 0,221 | 1,199 |
| 7 | 0,95 | 1,81 | 1,053 | 1,108 | 1,905 | 1,499 | 6,279 | 4,818 |
| 8 | 0,45 | 8,21 | 2,222 | 4,938 | 18,244 | 8,192 | 17,527 | 17,682 |
| 9 | 0,71 | 2,84 | 1,408 | 1,984 | 4,000 | 3,535 | 0,221 | 1,357 |
| 10 | 0,63 | 4,38 | 1,587 | 2,520 | 6,952 | 4,559 | 0,306 | 0,141 |
| Итого | 7,03 | 40,05 | 14,905 | 23,306 | 65,932 | 40,048 | 35,658 | 38,092 |
Для
нахождения коэффициентов гиперболической регрессии необходимо решить систему
уравнений:
Подставляя
в систему уравнений, получаем:
Решая
систему уравнений, получаем:
Искомое уравнение гиперболической
регрессии:
Коэффициент
детерминации:
Коэффициент эластичности:
Показательная (экспоненциальная) регрессия
Уравнение регрессии в
показательной форме имеет следующий вид:
Данное
уравнение является нелинейным по коэффициенту
и относится к классу моделей регрессии,
которые можно с помощью преобразований привести к линейному виду.
Показательная функция
является внутренне линейной, поэтому оценки неизвестных параметров её
линеаризованной формы можно рассчитать с помощью классического метода
наименьших квадратов
Нормальные уравнения
метода наименьших квадратов (МНК) для показательной регрессии:
Отсюда:
Задача 3
Постройте
криволинейную регрессионную модель (показательная функция) для следующих
исходных данных.
|
|
1,95 | 2,58 | 3,26 | 4,51 | 5,14 | 5,92 | 6,81 | 7,45 | 8,02 | 8,75 |
|
|
6,1 | 8,51 | 10,82 | 17,92 | 24,21 | 33,1 | 45,51 | 61,21 | 72,38 | 95,24 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение показательной
регрессии имеет вид:
Составим
расчетную таблицу:
Расчетная вспомогательная таблица
| № |
|
|
|
|
|
|
|
|
| 1 | 1,95 | 6,1 | 3,803 | 1,808 | 3,526 | 6,433 | 0,104 | 985,960 |
| 2 | 2,58 | 8,51 | 6,656 | 2,141 | 5,524 | 8,292 | 0,048 | 840,420 |
| 3 | 3,26 | 10,82 | 10,628 | 2,381 | 7,763 | 10,904 | 0,007 | 711,822 |
| 4 | 4,51 | 17,92 | 20,340 | 2,886 | 13,015 | 18,041 | 0,015 | 383,376 |
| 5 | 5,14 | 24,21 | 26,420 | 3,187 | 16,380 | 23,252 | 0,918 | 176,624 |
| 6 | 5,92 | 33,1 | 35,046 | 3,500 | 20,717 | 31,835 | 1,600 | 19,360 |
| 7 | 6,81 | 45,51 | 46,376 | 3,818 | 26,000 | 45,561 | 0,003 | 64,160 |
| 8 | 7,45 | 61,21 | 55,503 | 4,114 | 30,652 | 58,959 | 5,066 | 562,164 |
| 9 | 8,02 | 72,38 | 64,320 | 4,282 | 34,341 | 74,176 | 3,226 | 1216,614 |
| 10 | 8,75 | 95,24 | 76,563 | 4,556 | 39,869 | 99,532 | 18,423 | 3333,908 |
| Итого | 54,39 | 375 | 345,654 | 32,674 | 197,788 | 29,408 | 8294,409 |
Для
нахождения коэффициентов показательной регрессии необходимо решить систему
уравнений:
Подставляя
в систему уравнений, получаем:
Решая
систему уравнений, получаем:
Искомое уравнение показательной
регрессии:
Коэффициент
детерминации:
Коэффициент эластичности:
Степенная регрессия
В моделях, нелинейных по
оцениваемым параметрам, но приводимых к линейному виду, метод наименьших
квадратов и его требования применяются не к исходным данным результативного
признака, а к их преобразованным величинам.
Так, в степенной функции:
метод наименьших квадратов
применяется к преобразованному уравнению:
Система линейных уравнений
будет иметь вид:
Отсюда:
Степенная регрессия широко
используется в исследованиях при изучении эластичности спроса от цен.
Задача 4
По данным постройте
степенную регрессию:
|
|
2,21 | 17,45 | 8,6 | 61,05 | 5,76 | 33,38 | 16,22 | 3,88 | 0,75 | 149,3 |
|
|
9,63 | 25,92 | 31,6 | 17,71 | 14,87 | 44,03 | 13,7 | 9,13 | 3,86 | 170,45 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение степенной
регрессии имеет вид:
Составим
расчетную таблицу:
Расчетная вспомогательная таблица
| № |
|
|
|
|
|
|
|
|
|
| 1 | 2,21 | 9,63 | 0,793 | 0,629 | 2,265 | 1,796 | 8,690 | 105,030 | 86,655 |
| 2 | 17,45 | 25,92 | 2,859 | 8,176 | 3,255 | 9,307 | 20,871 | 3,733 | 48,736 |
| 3 | 8,6 | 31,6 | 2,152 | 4,630 | 3,453 | 7,430 | 15,461 | 12,093 | 160,304 |
| 4 | 61,05 | 17,71 | 4,112 | 16,906 | 2,874 | 11,818 | 35,494 | 274,065 | 1,510 |
| 5 | 5,76 | 14,87 | 1,751 | 3,066 | 2,699 | 4,726 | 13,045 | 34,739 | 16,556 |
| 6 | 33,38 | 44,03 | 3,508 | 12,306 | 3,785 | 13,277 | 27,478 | 72,911 | 629,564 |
| 7 | 16,22 | 13,7 | 2,786 | 7,763 | 2,617 | 7,293 | 20,234 | 1,677 | 27,446 |
| 8 | 3,88 | 9,13 | 1,356 | 1,838 | 2,212 | 2,999 | 11,033 | 62,506 | 96,214 |
| 9 | 0,75 | 3,86 | -0,288 | 0,083 | 1,351 | -0,389 | 5,496 | 180,711 | 227,373 |
| Итого | 149,3 | 170,45 | 19,029 | 55,397 | 24,511 | 58,257 | 747,465 | 1294,358 |
Для
нахождения коэффициентов степенной регрессии необходимо решить систему
уравнений:
Подставляя
в систему уравнений, получаем:
Решая
систему уравнений, получаем:
Искомое уравнение
степенной регрессии:
Коэффициент
детерминации:
Коэффициент эластичности:
Соотношения
между социально-экономическими явлениями
и процессами далеко не всегда можно
выразить линейными функциями, так как
при этом могут возникать неоправданно
большие ошибки. В таких случаях используют
нелинейную регрессию. Таким образом,
если
между экономическими явлениями существуют
нелинейные
соотношения, то они выражаются с помощью
соответствующих
нелинейных функций: например, равносторонней
гиперболы

параболы
второй степени
и
др.
Различают
два
класса нелинейных регрессий:
• регрессии,
нелинейные относительно включенных в
анализ объясняющих
переменных, но линейные по оцениваемым
параметрам;
• регрессии,
нелинейные по оцениваемым параметрам.
Примером
нелинейной регрессии по включаемым в
нее объясняющим
переменным могут служить следующие
функции:
-
полином
второй степеней,
-
полином
третьей –
;
-
равносторонняя
гипербола
.
К
нелинейным регрессиям по оцениваемым
параметрам относятся
функции:
-
степенная
;
-
показательная
;
-
экспоненциальная
.
Нелинейная
регрессия по включенным переменным не
таит каких-либо
сложностей в оценке ее параметров. Она
определяется,
как и в линейной регрессии, методом
наименьших квадратов (МНК), ибо эти
функции линейны по параметрам. Так. в
параболе
второй степени

заменяя
переменные


получим
двухфакторное уравнение
линейной регрессии:
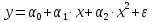
для
оценки параметров которого, как будет
показано в гл. 3, используется
МНК.
Соответственно
для полинома третьего порядка

при
замене

получим трехфакторную модель линейной
регрессии:

а
для полинома

порядка

получим
линейную модель множественной регрессии
с k
объясняющими
переменными:

Следовательно,
полином любого порядка сводится к
линейной регрессии с ее методами
оценивания параметров и проверки
гипотез.
Как показывает опыт большинства
исследователей, среди
нелинейной полиномиальной регрессии
чаще всего используется
парабола второй степени; в отдельных
случаях — полином третьего
порядка. Ограничения в использовании
полиномов более
высоких степеней связаны с требованием
однородности исследуемой
совокупности: чем выше порядок полинома,
тем больше
изгибов имеет кривая и соответственно
менее однородна совокупность
по результативному признаку.
Парабола
второй степени целесообразна к применению,
если для определенного интервала
значений фактора меняется характер
связи рассматриваемых признаков: прямая
связь меняется на обратную
или обратная на прямую. В этом случае
определяется значение
фактора, при котором достигается
максимальное (или минимальное)
значение результативного признака:
приравниваем
к нулю первую производную параболы
второй степени:

т. е.

Если
же исходные данные не обнаруживают
изменения направленности
связи, то параметры параболы второго
порядка становятся
трудно интерпретируемыми, а форма связи
часто заменяется
другими нелинейными моделями.
Применение
МНК для оценки параметров параболы
второй степени
приводит к следующей системе нормальных
уравнений:

Решают
эту систему тем или другим способами
получают числовые значения неизвестных
параметров

Пример
3.3. По
данным табл. 13.4 исследовать зависимость
урожайности зерновых культур Y
(ц/га)
от количества осадков Х
(см), выпавших в вегетационный период.
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
Количество
|
25 |
27 |
30 |
35 |
36 |
38 |
39 |
41 |
42 |
45 |
46 |
47 |
50 |
52 |
53 |
|
Урожайность |
23 |
24 |
27 |
27 |
32 |
31 |
33 |
35 |
34 |
32 |
29 |
28 |
25 |
24 |
25 |
Решение.
Из качественных соображений можно
предположить, что увеличение
количества выпавших осадков приводит
к увеличению урожайности до некоторого
предела, после чего урожайность будет
снижаться. Поэтому можно предположить,
что наиболее подходящим уравнением
регрессии будет уравнение параболы

При

кривая
симметрична относительно высшей точки
т.
е. точки перелома кривой, изменяющей
направление а
именно рост на падение. Такого рода
функцию можно наблюдать
в экономике труда при изучении зависимости
заработной
платы работников физического труда от
возраста — с увеличением
возраста повышается заработная плата
ввиду одновременного
увеличения опыта и повышения квалификации
работника. Однако с определенного
возраста ввиду старения организма и
снижения
производительности труда дальнейшее
повышение возраста может приводить
к снижению заработной платы работника.
Если
параболическая
форма связи демонстрирует сначала рост,
а затем
снижение уровня значений результативного
признака, то определяется
значение фактора, при котором достигается
максимум.
Так, предполагая, что потребление товара
А (единиц) в зависимости от уровня
дохода семьи (тыс. руб.) характеризуется
уравнением
вида

Приравнивая
к нулю первую производную

найдем величину дохода, при которой
потребление максимально, т. е. при

При


второго порядка симметрична относительно
своей низшей точки, что позволяет
определять минимум
функции в точке, меняющей направление
связи, т. е. снижение на рост. Так, если
в зависимости от объема выпуска продукции
затраты на производство характеризуются
уравнением

то
наименьшие затраты достигаются при
выпуске продукции


В
этом можно убедиться, подставляя в
уравнение значения х.
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
800 |
782 |
768 |
758 |
752 |
750 |
752 |
758 |
Ввиду
симметричности кривой парабола второй
степени далеко
не всегда пригодна в конкретных
исследованиях. Чаще исследователь
имеет дело лишь с отдельными сегментами
параболы,
а не с полной параболической формой.
Кроме того, параметры
параболической связи не всегда могут
быть логически истолкованы.
Поэтому если график зависимости не
демонстрирует четко
выраженной параболы второго порядка
(нет смены направленности
связи признаков), то она может быть
заменена другой нелинейной функцией,
например степенной. В частности, в
литературе
часто рассматривается парабола второй
степени для характеристики
зависимости урожайности от количества
внесенных
удобрений. Данная форма связи мотивируется
тем, что с увеличением
количества внесенных удобрений
урожайность растет лишь
до достижения оптимальной дозы вносимых
удобрений. Дальнейший
же рост их дозы оказывается вредным для
растения, и урожайность снижается.
Несмотря на несомненную справедливость
данного утверждения, следует отметить,
что внесение в почву
минеральных удобрений производится на
основе учета достижений
агробиологической науки. Поэтому на
практике часто
данная зависимость представлена лишь
сегментом параболы, что
и позволяет использовать другие
нелинейные функции. В качестве
примера рассмотрим табл. 3.3.
Таблица
3.3
Зависимость
урожайности озимой пшеницы от количества
внесенных удобрений
|
№ |
Внесено |
Урожайность, |
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 2 3 4 5 |
1 2 3 4 5 |
6 9 10 12 13 |
1 4 9 16 25 |
1 8 27 64 125 |
1 16 81 256 625 |
6 18 30 48 65 |
6 36 90 192 325 |
6,2 8,5 10,4 11,9 13,0 |
|
|
15 |
50 |
55 |
225 |
979 |
167 |
649 |
50,0 |
Поданным
табл. 3.3 система нормальных уравнений
составит:
Решая
ее методом определителей, получим:

Откуда параметры искомого уравнения
составят:
==
3,4;
=2,986;

а уравнение параболы
второй степени примет вид

Подставляя
в это уравнение последовательно значения
х,
найдем
теоретические значения

Как
видно
из табл. 3.3, уравнение параболы второго
порядка хорошо описывает рассматриваемую
зависимость. Сумма квадратов отклонений
остаточных величин

Ввиду того, что данные табл. 3.3
демонстрируют лишь сегмент параболы
второго порядка, то рассматриваемая
зависимость может бытьохарактеризована
и другой функцией. Используя, в частности,
степенную
функцию

было
получено уравнение регрессии

Для него
что означает еще лучшую сходимость
фактических и расчетных значенийy.
Среди
класса нелинейных функций, параметры
которых без особых
затруднений оцениваются МНК, следует
назвать хорошо
известную
в эконометрике равностороннюю гиперболу:
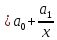
Она
может быть использована не только, как
уже указывалось в
параграфе (3.2), для характеристики связи
удельных расходов сырья, материалов,
топлива с объемом выпускаемой продукции,
времени
обращения товаров от величины
товарооборота, т.е. на микроуровне,
но и на макроуровне. Классическим ее
примером является
кривая
Филлипса, характеризующая
нелинейное соотношение
между нормой безработицы x
и процентом прироста заработной
платы у:

Английский
экономист А. В. Филлипс, анализируя
данные
более
чем за 100-летний период, в конце 50-х гг.
XX
в. установил
обратную зависимость
процента прироста заработной платы
от
уровня
безработицы.
Для
равносторонней гиперболы вида №№,
заменив
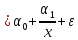
заменив

z,
получим
линейное уравнение регрессии
оценка параметров которого может быть
дана МНК. Система нормальных уравнений
составит:
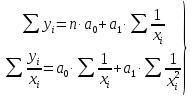
(3.34)
При
>
0 имеем обратную зависимость, которая
при

т. е. минимальным предельным
значением у,
оценкой
которого служит параметр a.
Так,
для
кривой
Филипса
величина параметра
a,
равная
0,00679, означает, что с ростом уровня
безработицы темп прироста заработной
платы в пределе стремится к нулю.
Соответственно
можно определить тот уровень безработицы,
при котором
заработная плата оказывается стабильной
и темп ее прироста
равен нулю.
При
<
0 имеем медленно повышающуюся функцию
с верхней асимптотой при

т. е. с максимальным предельным
уровнем
у,
оценку
которого в уравнении
дает
пара метр

Примером
может служить взаимосвязь доли расходов
на товары
длительного пользования и общих сумм
расходов (или доходов).
Математическое описание подобного рода
взаимосвязей получило название
кривых
Энгеля. В
1857
г. немецкий статистик
Э. Энгель на основе исследования семейных
расходов сформулировал
закономерность — с ростом дохода доля
доходов,
расходуемых на продовольствие,
уменьшается. Соответственно
с увеличением дохода доля доходов,
расходуемых на непродовольственные
товары, будет возрастать. Однако это
увеличение
не беспредельно, ибо на все товары сумма
долей не может быть больше единицы,
или 100%, а на отдельные непродовольственные
товары этот предел может характеризоваться
величиной
параметра а
для
уравнения вида

где у
—
доля расходов на непродовольственные
товары;
х —
доходы (или общая сумма расходов как
индикатор дохода).
Правомерность
использования равномерной гиперболы

доказывается.
Соответственно
можно определить границу величины
дохода, дальнейшее
увеличение которого не приводит с росту
доли расходов на отдельные
непродовольственные товары.
Вместе
с тем равносторонняя гипербола
не
является
единственно возможной функцией для
описания кривой Энгеля.
В 1943 г. Уоркинг и в 1964 г. Лизер для этих
целей использовали полулогарифмическую
кривую

Заменив

опять
получим линейное уравнение:
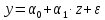
Данная
функция, как и предыдущая, линейна по
параметрам
и нелинейна по объясняющей переменной
х.
Оценка
параметров
и
может
быть найдена МНК. Система нормальных
уравнений
при этом окажется следующей:

Применим
полулогарифмическую функцию зависимости
доли
расходов на товары длительного пользование
в общих расходах
семьи от дохода семьи
(табл.
3.4).
Таблица
3.4
Доля
расходов на товары длительного пол в
зависимости от дохода семьи
|
Среднемесячный |
1 |
2 |
3 |
4 |
5 |
6 |
|
Процент |
10 |
13,4 |
15,4 |
16,5 |
18,6 |
19,1 |
Суммы,
необходимые для расчета, составили:

Решая
систему нормальных уравнений

мы
получили уравнение регрессии

которое
достаточно хорошо описывает исходные
соотношения дохода
семьи и доли расходов на товары длительного
пользования, что
видно из сравнения фактических и
теоретических значений у:
|
|
9,9 |
13,4 |
15,5 |
17,0 |
18,1 |
19,1 |
Сумма |
|
y |
0,1 |
0,0 |
-0,1 |
-0,5 |
0,5 |
0,0 |
0,0 |
|
|
0,01 |
0,0 |
0,01 |
0,25 |
0,25 |
0,0 |
0,52* |
|
*При |
Возможны
и иные модели, нелинейные по объясняющим
переменным.
Например,

Соответственно
система нормальных уравнений для оценки
параметров составит:

(3.36)
Уравнения
с квадратными корнями использовались
в исследованиях
урожайности, трудоемкости
сельскохозяйственного производства.
В работе Н. Дрейпера и Г. Смита справедливо
отмечено,
что если нет каких-либо теоретических
обоснований в использовании
данного вида кривых, то основная цель
подобных преобразований
состоит в том, чтобы для преобразованных
переменных
получить более простую модель регрессии,
чем для исходных
данных.
Иначе
обстоит дело с регрессией, нелинейной
по
оцениваемым
параметрам. Данный класс нелинейных
моделей
подразделяется
на два типа: нелинейные модели внутренне
линейные
и нелинейные
модели внутренне нелинейные. Если
нелинейная
модель
внутренне линейна, то
она с помощью соответствующих
преобразований
может быть приведена к линейному виду.
Если же нелинейная
модель внутренне нелинейна, то
она не может
быть сведена
к линейной функции. Например, в
эконометрических
исследованиях при изучении эластичности
спроса от цен
широко используется
степенная функция:
где

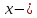
случайная ошибка.
Данная
модель нелинейна относительно оцениваемых
параметров,
ибо включает параметры а
и
b
не
аддитивно. Однако ее можно
считать внутренне линейной, ибо
логарифмирование данного
уравнения по основанию е
приводит
его к л шейному виду:

Соответственно
оценки параметров a
и
b
пут
быть найдены МНК. В рассматриваемой
степенной функции предполагается, что
случайная
ошибка е мультипликативно связана с
объясняющей переменной
х.
Если
же модель представить в виде

она становится внутренне нелинейной,
ибо ее невозможно превратить
в линейный вид.
Внутренне
нелинейной будет и модель вила
или
модель

ибо
эти уравнения не могут быть преобразованы
в уравнения, линейные
по коэффициентам.
В
специальных исследованиях по регрессионному
анализу часто
к нелинейным относят модели, только
внутренне нелинейные
по оцениваемым параметрам, а все другие
модели, которые внешне
нелинейные, но путем преобразований
параметров могут быть
приведены к линейному виду, относятся
к классу
линейных моделей.
В этом
плане к линейным относят, например,
экспоненциальную
модель

ибо
логарифмируя ее по натуральному
основанию, получим линейную форму модели

Если
модель внутренне нелинейна по параметрам,
то для оценки
параметров используются итеративные
процедуры, успешность
которых зависит от вида уравнений и
особенностей применяемого
итеративного подхода. Модели внутренне
нелинейные по параметрам могут иметь
место в эконометрических исследованиях.
Однако гораздо большее распространение
получили
модели, приводимые к линейному виду.
Решение такого типа
моделей реализовано в стандартных
пакетах прикладных программ.
Среди них, в частности, можно назвать и
обратную модель вида
Обращая
обе части равенства, получим линейную
форму модели
для переменной

Среди
нелинейных функций, которые могут быть
приведены к
линейному виду, в эконометрических
исследованиях очень широко
используется степенная функция

Связано
это с тем, что параметр
в
ней имеет четкое экономическое
истолкование,
т. е. он является коэффициентом
эластичности.
Это значит, что
величина коэффициента
показывает,
на сколько процентов изменится в среднем
результат, если фактор изменится на 1
%. Так,
если зависимость спроса от цен
характеризуется уравнением вида

то, следовательно, с увеличением цен на
1 % спрос снижается в среднем на 1,12 %. О
правомерности подобного истолкования
параметра
для
степенной функции
расчета коэффициента
эластичности
где
первая
производная, характеризующая соотношение
приростов
результата и фактора для соответствующей
формы связи.
Для
степенной функции она составит:

Соответственно
коэффициент эластичности окажется
равным:
Коэффициент
эластичности, естественно, можно
определять и при
наличии других форм связи, но только
для степенной функции он представляет
собой постоянную величину, равную
параметру

В
других функциях коэффициент эластичности
зависит
от значений фактора х.
Так,
для линейной регрессии
функция
и эластичность следующие:

В
силу того что коэффициент эластичности
для линейной функции
не является величиной постоянной, а
зависит от соответствующего
значения х,
то
обычно рассчитывается средний
показатель
эластичности по
формуле
Для
оценки параметров степенной функции

к линеаризованному уравнению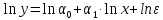
т.е. решается система нормальных
уравнений:
Параметр
определяется
непосредственно из системы, а параметр
—
косвенным путем после потенцирования
величины

Так, решая систему нормальных уравнений
зависимости спроса от цен, было получено
уравнение
потенцировать его, получим:

Поскольку
параметр
экономически
не интерпретируется, то нередко
зависимость записывается в виде
логарифмически линейной.
В виде степенной функции изучается
не только эластичность спроса, но и
предложения. При этом
обычно эластичность спроса характеризуется
параметром
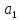
0,
а эластичность предложения:
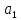
0.
Поскольку
коэффициенты эластичности представляют
экономический
интерес, а виды моделей не ограничиваются
только степенной
функцией, приведем формулы
расчета коэффициентов эластичности
для наиболее распространенных типов
уравнений регрессии
(табл.
3.5).
Таблица 3.5
Коэффициенты
эластичности для ряда математических
функций
|
Вид функции, |
Первая производная, |
Коэффициенты |
|
Линейная |
|
|
|
Парабола второго |
|
|
|
Гипербола |
|
|
|
Показательная |
|
|
|
Степенная |
|
|
|
Полулогарифмическая |
|
|
|
Логарифмическая
|
|
|
|
Обратная
|
|
|
Несмотря
на широкое использование в эконометрике
коэффициентов
эластичности, возможны случаи, когда
их расчет экономического
смысла не имеет. Это происходит тогда,
когда для рассматриваемых признаков
бессмысленно определение изменения
значений в процентах. Например, вряд ли
кто будет определять,
на сколько процентов может измениться
заработная плата с ростом
стажа работы на 1 %. Или, например, на
сколько процентов
изменится урожайность пшеницы, если
качество почвы, измеряемое
в баллах, изменится на 1 %. В такой ситуации
степенная
функция, даже если она оказывается
наилучшей по формальным
соображениям (исходя из наименьшего
значения остаточной
вариации), не может быть экономически
интерпретирована. Например, изучая
соотношение ставок межбанковского
кредита у
(в
процентах годовых) и срока его
предоставления х (в днях), было
получено уравнение регрессии

(0,9895). Коэффициент эластичности 0,352%
лишен смысла, ибо срок предоставления
кредитане
измеряется в процентах. Значительно
больший интерес для этой
зависимости может представить линейная
функция

имеющая
более низкий показатель корреляции
0,85. Коэффициент регрессии 0,403 показывает
в процентных
пунктах изменение ставок кредита с
увеличением срока их предоставления
на один день.
В
моделях, нелинейных по оцениваемым
параметрам, но приводимых
к линейному виду, МНК применяется к
преобразованным
уравнениям. Если в линейной модели и
моделях, нелинейных
по переменным, при оценке параметров
исходят из критерия

то в моделях, нелинейных по оцениваемымпараметрам,
требование МНК применяется не к исходным
данным
результативного признака, а к их
преобразованным величинам,
т. е.

Так,
в степенной функции
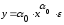
уравнению
Это
значит, что оценка параметров основывается
на минимизации
суммы квадратов отклонений в логарифмах.
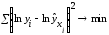
Соответственно
если в линейных моделях (включая
нелинейные
по переменным)

то в моделях, нелинейных пооцениваемым
параметрам,

Вследствие
этого оценка параметров для линеаризуемых
функций МНК оказываются несколько
смещенной.
Возьмем,
например, показательную кривую:
или
равносильную ей экспоненту

Прологарифмировав,
имеем:

Применяя
МНК, минимизируем

Система
нормальных
уравнений составит:
Из
первого уравнения видно, что
Предположим,
что фактические данные сложились так,
что

Тогда
или

т.
е. параметр
представляет
собой среднюю геометрическую из значений
переменной у.
Между
тем в линейной зависимости
при

т.
е. средней арифметической. Поскольку
средняя геометрическая
всегда меньше средней арифметической,
то и оценки параметров,
полученные из минимизации

будут
несколько
смещены (занижены).
Практическое
применение экспоненты возможно, если
результативный
признак не имеет отрицательных значений.
Поэтому
если исследуется, например, финансовый
результат деятельности
предприятий, среди которых наряду с
прибыльными есть и убыточные,
то данная функция не может быть
использована. Если
экспонента строится как функция
выравнивания по динамическому
ряду для характеристики тенденции с
постоянным темпом,
то

где
у
—
уровни динамического ряда; t
–
хронологические даты, параметр b
означает
средний за период коэффициент роста.
В уравнении
этот
смысл приобретает величина антилогарифма
параметра

При
исследовании взаимосвязей среди функций,
использующих

в
эконометрике преобладают степенные
зависимости — это
и кривые спроса и предложения, и кривые
Энгеля, и производственные функции,
и кривые освоения для характеристики
связи
между трудоемкостью продукции и
масштабами производства
в период освоения выпуска нового вида
изделий, и зависимость валового
национального дохода от уровня занятости.
В
отдельных случаях может использоваться
и нелинейная модель
вида
так
называемая обратная модель, являющаяся
разновидностью
гиперболы.
Но если в равносторонней гиперболе
преобразованию
подвергается объясняющая переменная


то
для по.
В
результате обратная модель оказывается
внутренне
нелинейной и требование МНК выполняется
не для
фактических значений признака у,
а
для их обратных
величин

а именно:
Соответственно
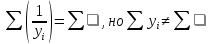
Проанализируем
зависимость рентабельности продукции
от ее
трудоемкости по данным семи предприятий
(табл. 3.6).
Таблица 3.6
Зависимость
рентабельности продукции y
(%) от ее
трудоемкости x
(
|
x |
y |
|
|
|
|
|
|
|
|
1,0 |
32 |
0,0312 |
0,0312 |
1,00 |
0,0285 |
35,1 |
0,0027 |
-3,1 |
|
1,2 |
28 |
0,0357 |
0,0428 |
1,44 |
0,0341 |
29,3 |
0,0016 |
-1,3 |
|
1,5 |
22 |
0,0455 |
0,0682 |
2,25 |
0,0424 |
23,6 |
0,0031 |
-1,6 |
|
2,0 |
20 |
0,0500 |
0,1000 |
4,00 |
0,0563 |
17,7 |
-0,0063 |
2,3 |
|
2,5 |
16 |
0,0625 |
0,1563 |
6,25 |
0,0703 |
14,2 |
-0,0078 |
1,8 |
|
2,7 |
15 |
0,0667 |
0,1800 |
7,29 |
0,0758 |
13,2 |
-0,0091 |
1,8 |
|
3,0 |
10 |
0,1000 |
0,3000 |
9,00 |
0,0842 |
11,9 |
0,0158 |
-1,9 |
|
|
143 |
0,3916 |
0,8785 |
31,23 |
0,3936 |
145,0 |
0,0000 |
-2,0 |
Для
оценки параметров исследуемой функции
по
МНК система нормальных уравнений примет
вид:
Исходя
из данных табл. 2.6, имеем:
Решая
эту систему уравнений, получим оценки
параметров искомой функции:
=
0,0007;
= 0,0278.
Соответственно уравнение регрессии
составит:
Сравним
последние две графы табл. 2.6. Получим

тогда как для обратных значений эта
величина равна
нулю.
Кроме того, заметим, что положительные
отклонения фактических
и теоретических обратных значений
сменяются на отрицательные
значения для аналогичных показателей
по исходным данным. Уравнение отражает
обратную связь рассматриваемых
признаков: чем выше трудоемкость, тем
ниже рентабельность.
Поскольку данное уравнение линейно
относительно
величин

то если обратные значения
смысл,
коэффициент регрессии
интерпретируется,
так же как в линейном
уравнении регрессии. Если, например,
под y
подразумеваются
затраты на 1 руб. продукции, а под х
— производительность
труда (выработка продукции на одного
работника), то обратная величина
характеризует затратоотдачу и параметр
имеет
экономическое содержание — средний
прирост продукции в стоимостном
измерении на 1 руб. затрат с ростом
производительности труда на единицу
своего измерения.
Уравнение вида

признака от фактора. Оно целесообразно
при
очень медленном повышении уровней
результативного признака
с ростом значений фактора.
Возможно
и одновременное использование
логарифмирования,
и преобразование в обратные величины:
Прологарифмировав, получим:
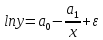
Далее заменим
и
тогда для оценки параметров к линейному
уравнению
может быть применен МНК.
При
всех положительных значениях х
функция
возрастает; при
кривая
имеет точку перегиба — ускоренный рост
при
сменяется
на замедленный рост при

Подобного
типа
функции используются при анализе
статистических данных о
бюджетах потребителей, где выдвигается
гипотеза о существовании
асимптотического уровня расходов, об
изменении предельной
склонности к потреблению товара, о
существовании «порогового
уровня дохода». В этом случае при
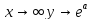
При
использовании линеаризуемых функций,
затрагивающих
преобразования зависимой переменной
у,
следует
особенно проверять
наличие предпосылок
МНК
(они будут рассмотрены в п.
3, 10), чтобы они не нарушались при
преобразовании. При не линейных
соотношениях рассматриваемых признаков,
приводимых к линейному виду, возможно
интервальное оценивание параметров
нелинейной функции. Так, для показательной
кривой
сначала
строятся доверительные интервалы для
параметров нового преобразованного
уравнения

т.
е. для


Далее
с помощью обратного преобразования
определяются
доверительные интервалы для параметров
в исходном
соотношении. В степенной функции
доверительный
интервал для параметра b
строится
так же. как в линейной функции, т. е.

Отличие
состоит лишь в том. что при определении
стандартной ошибки параметра b,

не исходные
данные, а их логарифмы:
(2.28)
Уравнение нелинейной регрессии
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
Виды нелинейной регрессии
Здесь ε – случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка – это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. – трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. – тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) – 49694.9535
Эконометрика
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ
Кафедра экономико-метематических моделей
Тема 4. Множественная регрессия.
Вопросы
1. Нелинейная регрессия. Нелинейные модели и их линеаризация.
Нелинейная регрессия
При рассмотрении зависимости экономических показателей на основе реальных статистических данных с использованием аппарата теории вероятности и математической статистики можно сделать выводы, что линейные зависимости встречаются не так часто. Линейные зависимости рассматриваются лишь как частный случай для удобства и наглядности рассмотрения протекаемого экономического процесса. Чаще встречаются модели которые отражают экономические процессы в виде нелинейной зависимости.
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.
Различают два класса нелинейных регрессий:
-
регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам: регрессии, нелинейные по оцениваемым параметрам.
Нелинейные регрессии по включаемым в нее объясняющим переменным, но линейные по оцениваемым параметрам
Данный класс нелинейных регрессий включает уравнения, в которых зависимая переменная линейно связана с параметрами. Примером могут служить:
полиномы разных степеней



При оценке параметров регрессий нелинейных по объясняющим переменным используется подход, именуемый «замена переменных». Суть его состоит в замене «нелинейных» объясняющих переменных новыми «линейными» переменными и сведение нелинейной регрессии к линейной регрессии. К новой «преобразованной» регрессии может быть применен обычный метод наименьших квадратов (МНК).
Полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез.
Среди нелинейной полиноминальной регрессии чаще всего используется парабола второй степени; в отдельных случаях — полином третьего порядка. Ограничение в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, менее однородна совокупность по результативному признаку.
Равносторонняя гипербола, для оценки параметров которой используется тот же подход «замены переменных» (1/x заменяют на переменную z) хорошо известна в эконометрике.
Она может быть использована, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции. Также примером использования равносторонней гиперболы являются кривые Филлипса и Энгеля..
Регрессии нелинейные по оцениваемым параметрам
К данному классу регрессий относятся уравнения, в которых зависимая переменная нелинейно связана с параметрами. Примером таких нелинейных регрессий являются функции:
• степенная – 
• показательная – 
• экспоненциальная –
Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду (например, логарифмированием и заменой переменных). Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции и для оценки её параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.
Примером нелинейной по параметрам регрессии внутренне линейной является степенная функция, которая широко используется в эконометрических исследованиях при изучении спроса от цен: 
Данная модель нелинейна относительно оцениваемых параметров, т. к. включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду 
Широкое использование степенной функции 
Коэффициент эластичности можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру b.
По семи предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений ( Х, млн. руб. ).
Тема 11. Нелинейные регрессии и их линеаризация
Аннотация.Данная тема раскрывает особенности построения нелинейных моделей регрессии.
Ключевые слова.Нелинейная регрессия, индекс корреляции, коэффициент эластичности, подход Бокса-Кокса.
Методические рекомендации по изучению темы
· Тема содержит лекционную часть, где даются общие представления по теме.
· В качестве самостоятельной работы предлагается ознакомиться с решениями типовых задач, выполнить практические задания и ответить на вопросы для самоконтроля.
· Для проверки усвоения темы имеется тест для самоконтроля.
· Для подготовки к экзамену имеется контрольный тест.
Рекомендуемые информационные ресурсы:
2. Эконометрика: [Электронный ресурс] Учеб. пособие / А.И. Новиков. – 3-e изд., испр. и доп. – М.: ИНФРА-М, 2014. – 272 с.: (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=1#none) С. 41-45.
3.Уткин, В. Б. Эконометрика [Электронный ресурс] : Учебник / В. Б. Уткин; Под ред. проф. В. Б. Уткина. – 2-е изд. – М.: Издательско-торговая корпорация «Дашков и К°», 2012. – 564 с.
(http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С. 383-399.
4. Эконометрика. Практикум: [Электронный ресурс] Учебное пособие / С.А. Бородич. – М.: НИЦ ИНФРА-М; Мн.: Нов. знание, 2014. – 329 с. (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С.172-174.
Глоссарий
Бокса-Кокса подход – способ подбора линеаризующего преобразования.
Индекс корреляции–показатель корреляции, который определяется для нелинейных регрессий.
Коэффициент эластичности показывает, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 процент.
Линеаризация нелинейных моделей – процедура, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований.
Нелинейная модель, внутренне линейная, с помощью преобразований может быть приведена к линейному виду.
Нелинейная модель, внутренне нелинейная, не может быть сведена к линейной функции.
Вопросы для изучения
1. Классы и виды нелинейных регрессий.
2. Линеаризация нелинейных моделей. Выбор формы модели.
3. Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса).
Классы и виды нелинейных регрессий. Различают два класса нелинейных регрессий: регрессии, нелинейные относительно включенных в анализ объясняющих переменных; регрессии, нелинейные по оцениваемым параметрам. Нелинейная модель, внутренне линейная, с помощью преобразований может быть приведена к линейному виду. Нелинейная модель, внутренне нелинейная, не может быть сведена к линейной функции. При анализе нелинейных регрессионных зависимостей наиболее важным вопросом применения классического МНК является способ их линеаризации.
Линеаризация нелинейных моделей. Выбор формы модели. В нелинейных зависимостях, не являющихся классическими полиномами, обязательно проводится предварительная линеаризация, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований. Рассмотрим некоторые классы таких зависимостей.
Рис. 11.1. Способы линеаризации
Замена переменных заключается в замене нелинейных объясняющих переменных новыми линейными переменными и сведении нелинейной регрессии к линейной. Логарифмирование обеих частей уравнения применяется обычно, когда мультипликативную модель необходимо привести к линейному виду. К классу степенных функций относятся: кривые спроса и предложения, производственная функция Кобба-Дугласа, кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения и выпуска нового вида изделий, зависимость валового национального дохода от уровня занятости.
Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса). Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции:
Здесь 
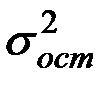

Следует обратить внимание на то, что разности в соответствующих суммах 


Если разные модели используют разные функциональные формы для зависимой переменной, то проблема выбора модели становится более сложной, так как нельзя непосредственно сравнивать коэффициенты R 2 или суммы квадратов отклонений. Например, нельзя сравнивать эти статистики для линейного и логарифмического вариантов. Пусть в линейной модели в качестве зависимой переменной используется заработок, а в нелинейной – логарифм заработка. Тогда R 2 в одном уравнении измеряет объясненную регрессией долю дисперсии заработка, а в другом – объясненную регрессией долю дисперсии логарифма заработка. В случае, если значения R 2 для двух моделей близки друг к другу, проблема выбора усложняется. Здесь следует использовать тест Бокса – Кокса. При сравнении моделей с использованием в качестве зависимой переменной y и lny проводится такое преобразование масштаба наблюдений y, при котором можно непосредственно сравнивать суммы квадратов отклонений в линейной и логарифмической моделях. Здесь выполняются следующие шаги. Вычисляется среднее геометрическое значений y в выборке. Оно совпадает с экспонентой среднего арифметического логарифмов y. Все значения y пересчитываются делением на среднее геометрическое, получаем значения y*. Оцениваются две регрессии: для линейной модели с использованием y* в качестве зависимой переменной и для логарифмической модели с использованием ln y* вместо ln y. Во всех других отношениях модели должны оставаться неизменными. Теперь значения СКО для двух регрессий сравнимы, и модель с меньшей остаточной СКО обеспечивает лучшее соответствие исходным данным. Для проверки, обеспечивает ли одна из моделей значимо лучшее соответствие, можно вычислить величину (n/2)lnz, где z – отношение значений остаточной СКО в перечисленных регрессиях. Эта статистика имеет распределение хи – квадрат с одной степенью свободы. Если она превышает критическое значение при выбранном уровне значимости α, то делается вывод о наличии значимой разницы в качестве оценивания.
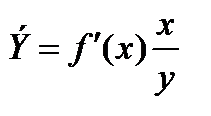
В заключение приведем формулы расчета коэффициентов эластичности для наиболее распространенных уравнений регрессии:
| Вид уравнения регрессии | Коэффициент эластичности |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
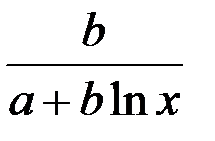 |
  |
 |
 |
Вопросы и задания для самоконтроля
1. Какие модели являются нелинейными относительно: а) включаемых переменных; б) оцениваемых параметров?
2. Какие преобразования используются для линеаризации нелинейных моделей?
3. Чем отличается применение МНК к моделям, нелинейным относительно включаемых переменных, от применения к моделям, нелинейным по оцениваемым параметрам?
4. Как определяются коэффициенты эластичности по разным видам регрессионных моделей?
5. Какие показатели корреляции используются при нелинейных соотношениях рассматриваемых признаков?
6. В каких случаях используют обратные и степенные модели?
Задача 1.По группе предприятий, производящих однородную продукцию известно, как зависит себестоимость единицы продукции (Y) от факторов, приведенных в таблице:
| Признак-фактор | Уравнение парной регрессии | Среднее значение фактора |
Объем производства,  млн. руб. млн. руб. |
 |
 |
Трудоемкость единицы продукции,  чел/час чел/час |
 |
 |
Оптовая цена за 1т энергоносителя,  , млн. руб. , млн. руб. |
 |
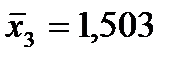 |
Доля прибыли, изымаемая государством,  ,% ,% |
 |
 |
1) определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат;
2) ранжировать факторы по силе влияния на результат.
Задача 2. По группе из 10 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости единицы продукции 


Доля остаточной дисперсии в общей составила 0,19.
1) определить коэффициент эластичности, предполагая, что стоимость активных производственных фондов составляет 200 тыс. руб.;
2) вычислить индекс корреляции;
3) оценить значимость уравнения регрессии с помощью 
[spoiler title=”источники:”]
http://pandia.ru/text/77/203/77731.php
http://poisk-ru.ru/s16268t6.html
[/spoiler]
Нелинейная регрессия — это вид регрессионного анализа, в котором экспериментальные данные моделируются функцией, являющейся нелинейной комбинацией параметров модели и зависящей от одной и более независимых переменных. Данные аппроксимируются методом последовательных приближений.
Общие положения[править | править код]
Данные состоят из свободных от ошибок независимых переменных x и связанных наблюдаемых зависимых переменных (откликов) y. Каждая переменная y моделируется как случайная величина со средним значением, задаваемым нелинейной функцией f(x,β). Методическая погрешность может присутствовать, но её обработка выходит за границы регрессионного анализа. Если независимые переменные не свободны от ошибок, модель становится моделью с ошибками в переменных[en] и также выходит за рамки рассмотрения.
Например, модель Михаэлиса — Ментен для ферментативной кинетики
можно записать как
где 





Другими примерами нелинейных функций служат показательные функции, логарифмические функции, тригонометрические функции, степенные функции, гауссова функция и кривые Лоренца. Регрессионный анализ с такими функциями, как показательная или логарифмическая, иногда может быть сведён к линейному случаю и может быть применена стандартная линейная регрессия, но применять её следует осторожно. Подробнее в разделе «Линеаризация» ниже.
В общем случае представления в замкнутом виде (как в случае линейной регрессии) может и не быть. Обычно для определения наилучших оценок параметров используются оптимизационные алгоритмы. В отличие от линейной регрессии может оказаться несколько локальных минимумов оптимизируемой функции и глобальный минимум даже может дать смещённую оценку. На практике используются оценочные значения[en] параметров совместно с оптимизационным алгоритмом в попытке найти глобальный минимум суммы квадратов.
Подробнее о нелинейном моделировании см. «Метод наименьших квадратов» и «Нелинейный метод наименьших квадратов[en]».
Регрессионная статистика[править | править код]
Предположение, лежащее в основе этой процедуры, заключается в возможности аппроксимации модели линейной функцией.
где 
Статистика нелинейной регрессии вычисляется и используется как статистика линейной регрессии, но вместо X в формулах используется J. Линейная аппроксимация вносит смещение в статистику, поэтому следует более осторожно интерпретировать статистики, полученные из нелинейной модели.
Обычный и взвешенный метод наименьших квадратов[править | править код]
Лучшей аппроксимирующей кривой часто предполагается та, что минимизирует сумму квадратов невязок[en]. Это подход (обычного) метода наименьших квадратов (МНК). Однако, в случае, когда зависимая переменная не имеет постоянной дисперсии, можно минимизировать сумму взвешенных квадратов. Каждый вес, в идеальном случае, должен быть равен обратной величине от дисперсии наблюдений, однако веса могут пересчитываться в итеративном алгоритме взвешенных наименьших квадратов на каждой итерации.
Линеаризация[править | править код]
Преобразование[править | править код]
Некоторые задачи нелинейной регрессии могут быть сведены к линейным путём подходящего преобразования формулировки модели.
Например, рассмотрим задачу нелинейной регрессии
с параметрами a и b и с мультипликативным множителем ошибки U. Если взять логарифм от обеих частей, мы получим
где u = ln(U). Из этого можно получить оценку неизвестных параметров с помощью линейной регрессии ln(y) от x и вычисления не потребуют итеративной оптимизации. Однако использование нелинейного преобразования требует осторожности. Влияние значений данных изменится, меняется структура ошибок модели и интерпретация любых полученных результатов, что может привести к нежелательным результатам. С другой стороны, в зависимости от наибольшего источника ошибки, нелинейное преобразование может распределять ошибки в виде распределения Гаусса, так что при применении нелинейного преобразования необходимо учитывать модель.
Например, для уравнения Михаэлиса — Ментен широко используется линейное представление Лайнуивер-Берка[en]
.
Тем не менее, из-за сильной чувствительности к ошибкам данных, а также вследствие сильного смещения, это не рекомендуется.
Для распределений ошибок, принадлежащих семейству экспоненциальных распределений, может быть использована связывающая функция для преобразования параметров под обобщённую линейную модель.
Сегментация[править | править код]
Зависимость урожайности горчицы от засолённости почвы
Независимая переменная (скажем, X) может быть разбита на классы или сегменты и может быть осуществлена линейная регрессия посегментно. Сегментированная регрессия с анализом достоверности может дать результат, в котором зависимая переменная или отклик (скажем, Y) ведёт себя различно в различных сегментах[1] .
График справа показывает, что засолённость почвы[en] (X) начально не оказывает никакого влияния на урожайность (Y) горчицы, пока не будет достигнуто критического или порогового значения, после которого сказывается отрицательное влияние на урожайность[2]
Примеры[править | править код]
Правило Тициуса — Боде в виде математической формулы представляет собой одномерное уравнение нелинейной регресии, связывающее порядковые номера планет солнечной системы, считая от Солнца, с приближёнными значениями больших полуосей их орбит. Точность вполне удовлетворительная не для астрономических целей.
См. также[править | править код]
- Нелинейный метод наименьших квадратов[en]
- Приближение с помощью кривых
- Обобщённая линейная модель
- Локальная регрессия[en]
Примечания[править | править код]
- ↑ Oosterbaan, 1994, с. 175—224.
- ↑ (Oosterbaan 2002) Иллюстрация сделана программой SegReg[en]
Литература[править | править код]
- R.J.Oosterbaan. Frequency and Regression Analysis // Drainage Principles and Applications / H.P.Ritzema. — Wageningen, The Netherlands: International Institute for Land Reclamation and Improvement (ILRI), 1994. — Т. 16. — С. 175—224. — ISBN 90-70754-33-9.
- R.J.Oosterbaan. Drainage research in farmers’ fields: analysis of data. Part of project “Liquid Gold” of the International Institute for Land Reclamation and Improvement (ILRI). — Wageningen, The Netherlands, 2002.
Литература для дальнейшего чтения[править | править код]
- R. M. Bethea, B. S. Duran, T. L. Boullion. Statistical Methods for Engineers and Scientists. — New York: Marcel Dekker, 1985. — ISBN 0-8247-7227-X.
- N. Meade, T. Islam. Prediction Intervals for Growth Curve Forecasts // Journal of Forecasting. — 1995. — Т. 14, вып. 5. — С. 413—430. — doi:10.1002/for.3980140502.
- K. Schittkowski. Data Fitting in Dynamical Systems. — Boston: Kluwer, 2002. — ISBN 1402010796.
- G. A. F. Seber, C. J. Wild. Nonlinear Regression. — New York: John Wiley and Sons, 1989. — ISBN 0471617601.
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии 
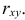
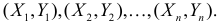
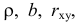
Неизвестная нам линия регрессии 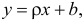

Такие значения 
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.
и
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 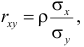
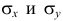
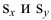
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 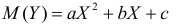
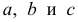
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
По формулам (3.7.1) и (3.7.2) получим
Итак, оценка линии регрессии имеет вид 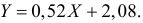
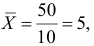
Аналогично, 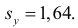
Ответ.
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 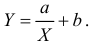
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 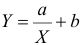
Необходимые условия экстремума приводят к системе из двух уравнений:
Откуда
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров
На основе опытных данных вычисляем:
В итоге получаем систему уравнений (?????) и (?????) в виде
Эта система имеет решения
Ответ.
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 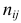
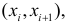
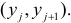
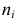
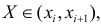
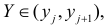
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 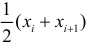
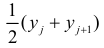
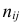
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.
Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 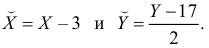
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 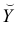
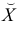
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33):
Тогда
В новом масштабе оценка линии регрессии имеет вид 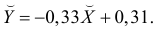
Для оценки 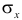
Подобным же образом можно оценить 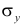
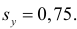
Вернемся к старому масштабу:
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ.
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 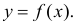
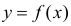
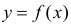
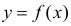
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 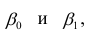
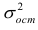
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей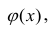
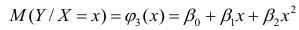
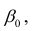
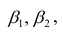
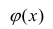
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 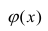
по переменным. Оценки параметров модели (2.1) 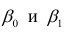
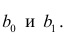
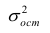
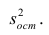
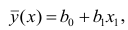
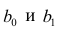
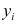
Составим систему нормальных уравнений: первое уравнение
откуда
второе уравнение
откуда
Итак,
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно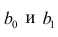
Остаётся получить оценку параметра 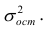
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы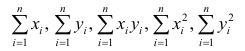
где 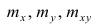
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
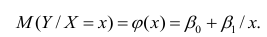
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
где 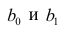
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
или
Дифференцируя последнее равенство по 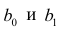
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 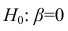
имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 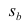
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение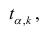
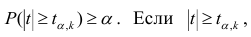
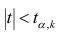
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
где 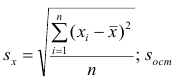
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
где а — уровень значимости, находим
Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 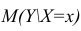
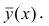
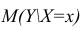
построить доверительный интервал в точке
Известно, что 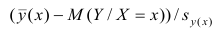
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания
Оценку дисперсии условного среднего вычисляют по формуле
или для интервального ряда
Доверительный интервал находят из условия
где а — уровень значимости. Отсюда
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
Из рис. 2.2 видно, что в точке 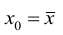
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 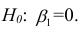
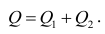
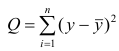
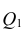
X) и 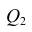
Для проверки нулевой гипотезы вычисляют статистику 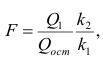
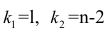
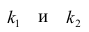
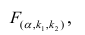
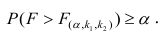
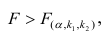
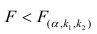
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 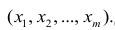
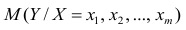
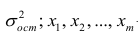
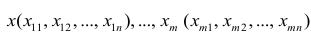
Оценке подлежат параметры 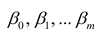
Заменив параметры их оценками, запишем уравнение регрессии
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 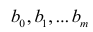

Как и в двумерном случае, составляют систему нормальных уравнений
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 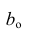
Подставим в остальные уравнения системы вместо 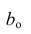
Пусть С — матрица коэффициентов при неизвестных параметрах 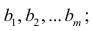
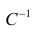
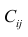
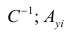
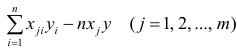
запишем окончательные выражения для параметров:
Оценкой остаточной дисперсии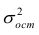
где 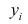
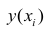
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику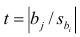
где 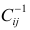
го столбца;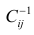
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 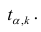
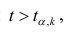
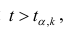
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: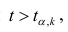
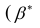
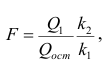
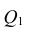
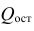
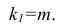
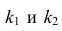
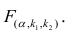
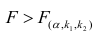
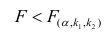
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 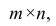
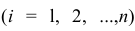
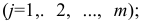
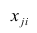
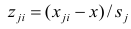
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
где 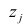
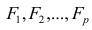
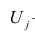
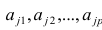
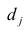
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 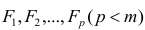
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков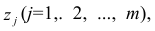
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы
Факторные нагрузки 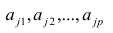
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
где 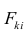
Дисперсию признака 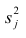
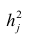
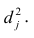
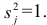
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
где 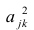
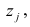
Полный вклад k-го фактора в суммарную дисперсию признаков
Вклад общих факторов в суммарную дисперсию
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
где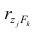
м фактором;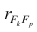
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
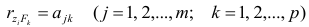
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам:
где 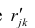
и к-м признаком. Остаточный коэффициент корреляции
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
где 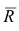
Результаты факторного анализа удобно представить в виде табл. 2.10.
Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции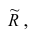
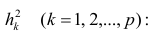
Редуцированная и полная матрицы связаны соотношением
где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 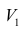
где 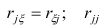
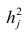
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора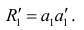
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 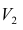
где 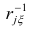
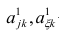
Факторный анализ учитывает суммарную общность. Исходная суммарная общность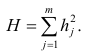
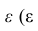
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 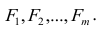
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
где 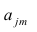
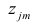
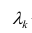
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t – распределения Стьюдента
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 
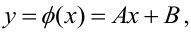
Диаграмма рассеяния (разброса, рассеивания)
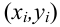
Выборочное уравнение прямой линии регрессии 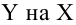
Задача: подобрать 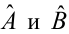
Для того, что бы провести прямую 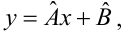
чтобы
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
подчинены нормальному закону распределения.
- Дисперсия
постоянна и не зависит от номера измерения.
- Результаты наблюдений
в разных точках независимы.
- Входные переменные
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 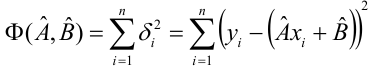
Решив систему, получим искомые значения
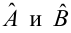
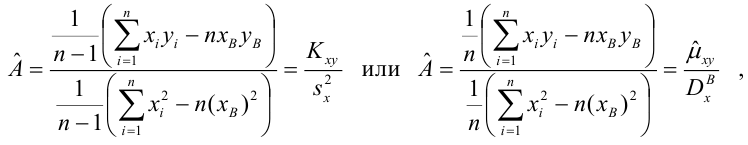
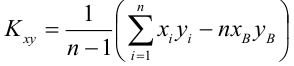
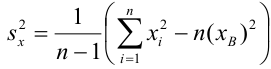
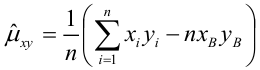
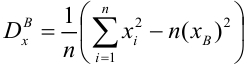
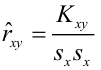
Коэффициент детерминации
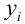
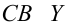
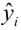
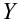
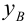
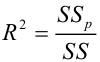
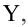
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
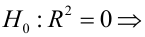
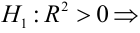
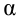
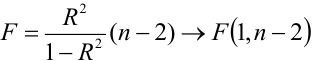
Критическая область – правосторонняя;
Если 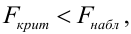
Мощность статистического критерия. Функция мощности
Определение. Мощностью критерия 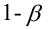
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода
Пример:
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 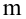
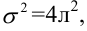
3) Уровень значимости
4) Статистический критерий
5) Критическая область – левосторонняя
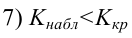
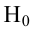
Пример:
В условиях примера 1 предположим, что наряду с 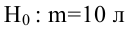
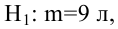
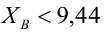
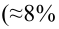
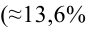
Определение. Пусть проверяется 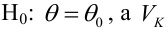
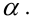
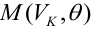
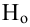
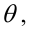
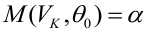
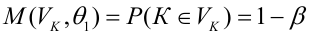
Пример:
Построить график функции мощности из примера 2 для

Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить
Лемма Неймана-Пирсона.
При проверке простой гипотезы 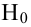
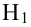
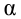
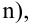
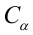
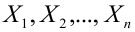
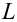
Пример:
Случайная величина 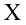
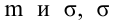
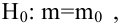
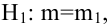
Решение:
Ошибка первого рода:
НКО:
Пример:
Для зависимости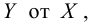
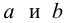
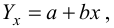
Решение. Воспользуемся предыдущими результатами
Согласно формуле (24), уравнение регрессии будет иметь вид 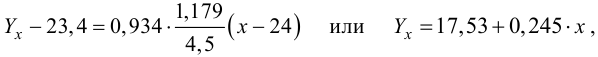
Для выяснения значимости уравнения регрессии вычислим суммы 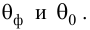
Из (27) и (28) по данным таблицы получим
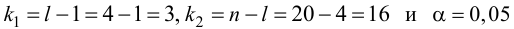
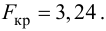
Вычислим статистику
Так как 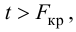
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез

 ,
, ;
;  .
. ;
; ;
; .
.


 (см)
(см) (ц/га)
(ц/га)






























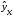



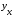










































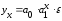
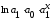




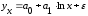


















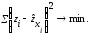


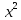




 13,9
13,9
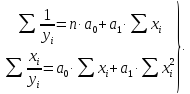


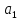


















![{displaystyle v={frac {V_{max } [{mbox{S}}]}{K_{m}+[{mbox{S}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddb07a5f0c5464d685c5ab5072a8bee836260b6d)





![{displaystyle {frac {1}{v}}={frac {1}{V_{max }}}+{frac {K_{m}}{V_{max }[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb44905c5bb097edbf610f26176e996180c36ac7)

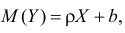
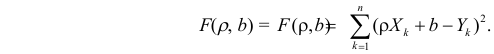
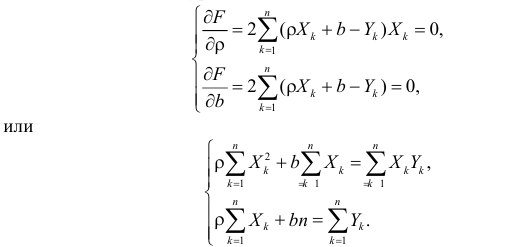
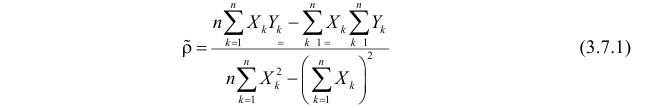
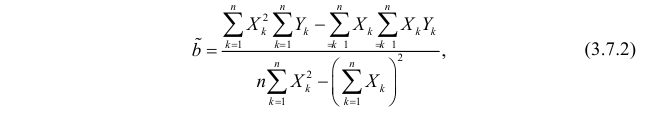
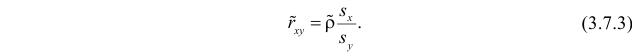
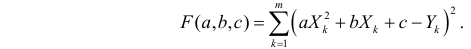

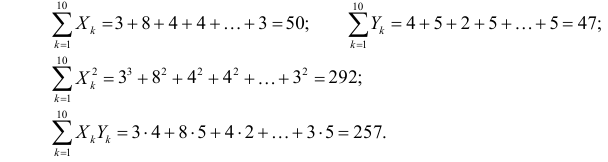
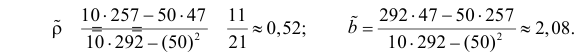
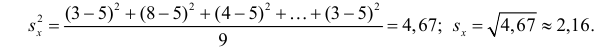
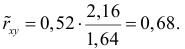
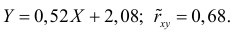

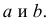
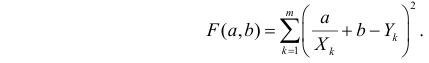
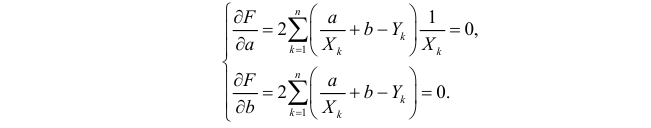
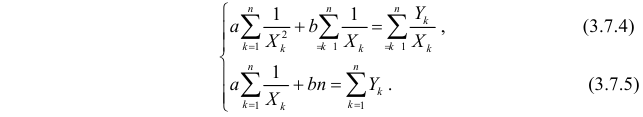
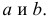
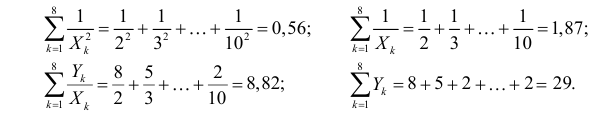
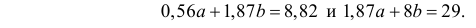
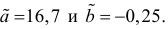
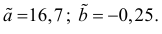

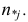



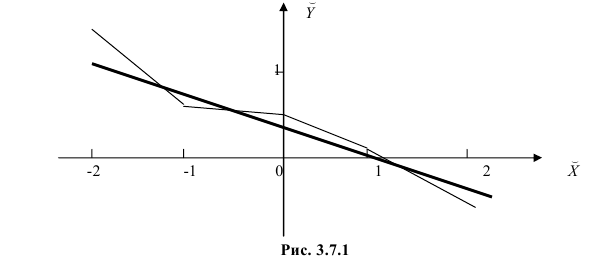
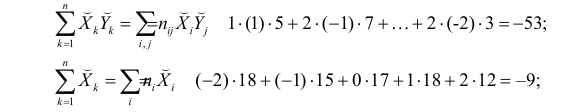
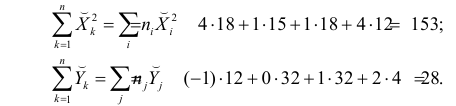
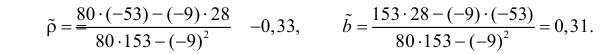
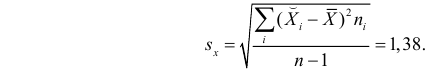
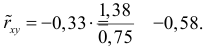
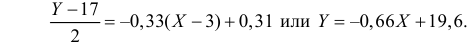
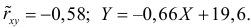
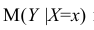 можно представить в виде
можно представить в виде 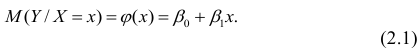
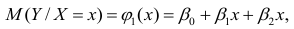
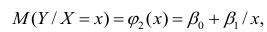
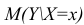 можно представить в виде (2.1).
можно представить в виде (2.1).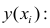
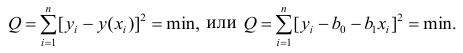
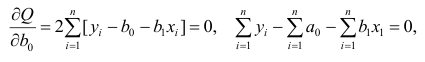
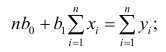
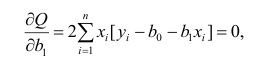
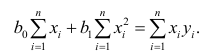
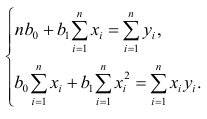
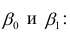
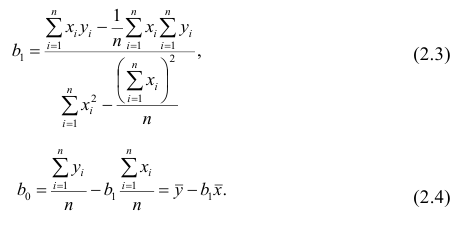
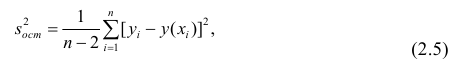
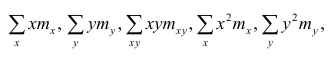
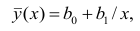
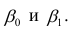
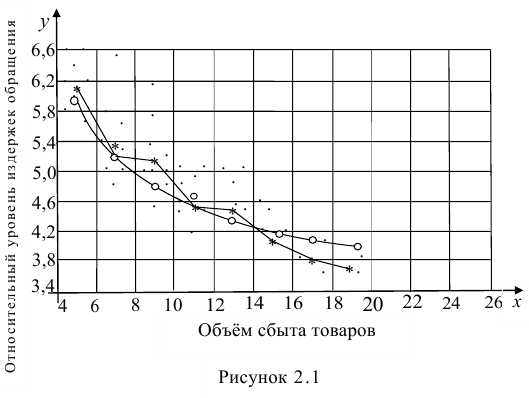
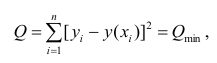
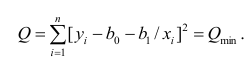
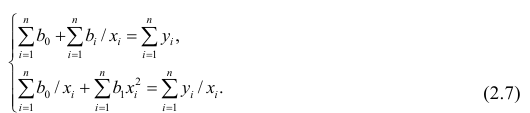
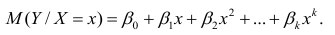
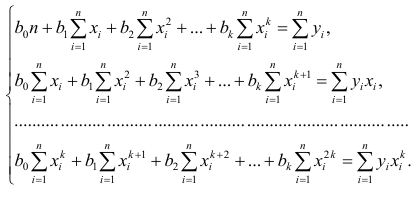

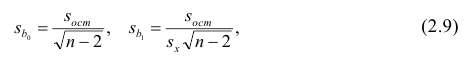
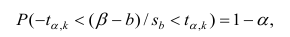

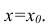
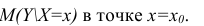
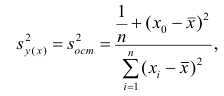
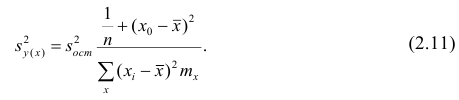
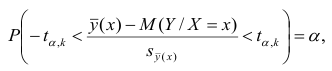
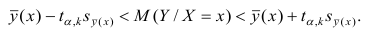
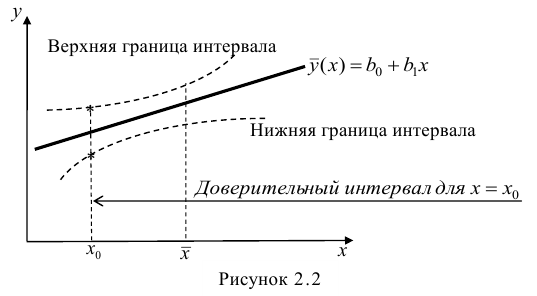
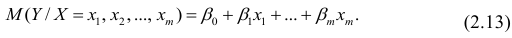
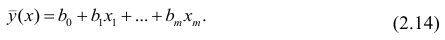
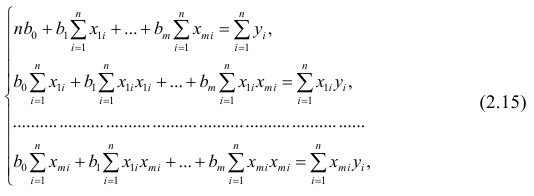
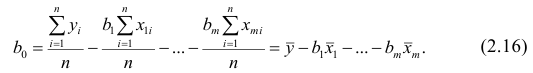
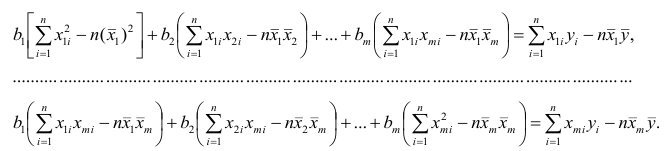
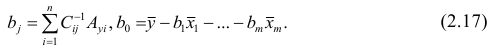
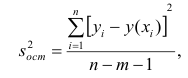
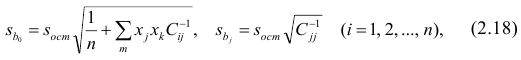
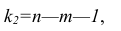
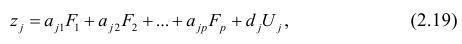
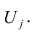
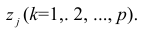
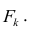
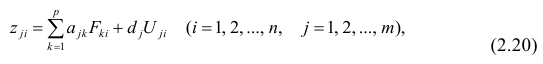
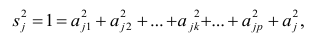
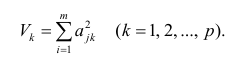
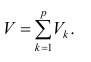
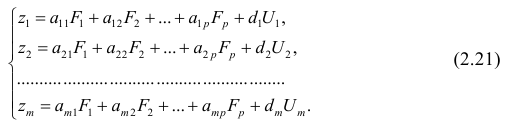
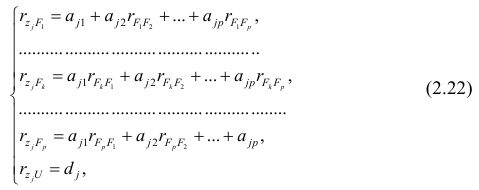
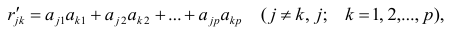
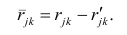
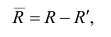

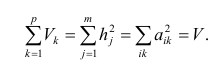
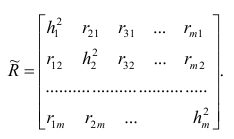


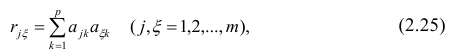

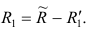

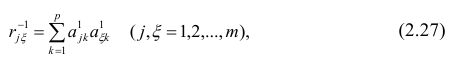
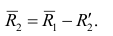
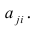
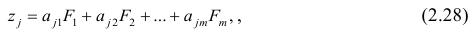
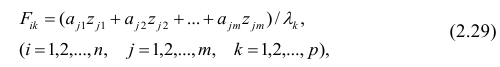
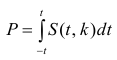
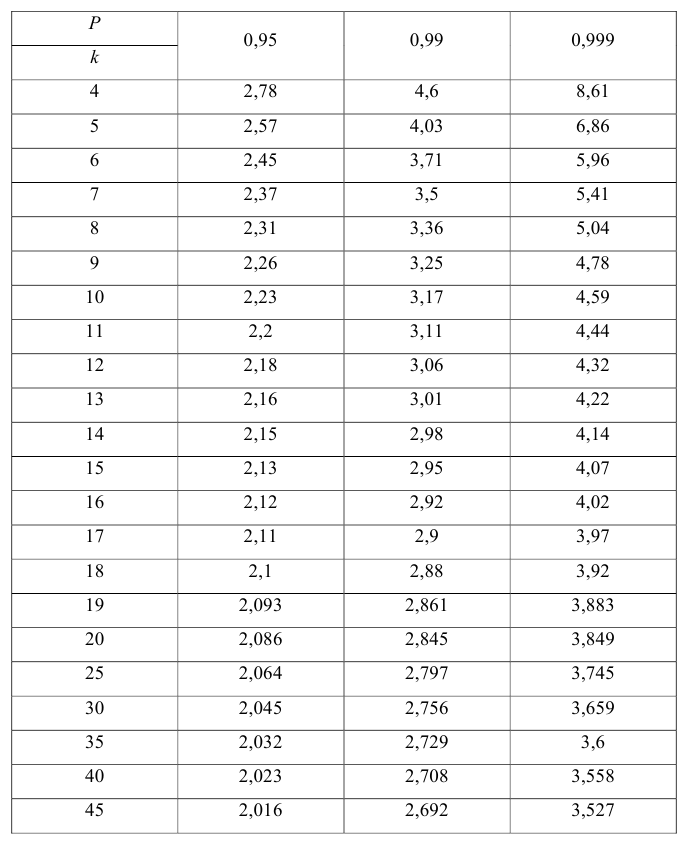
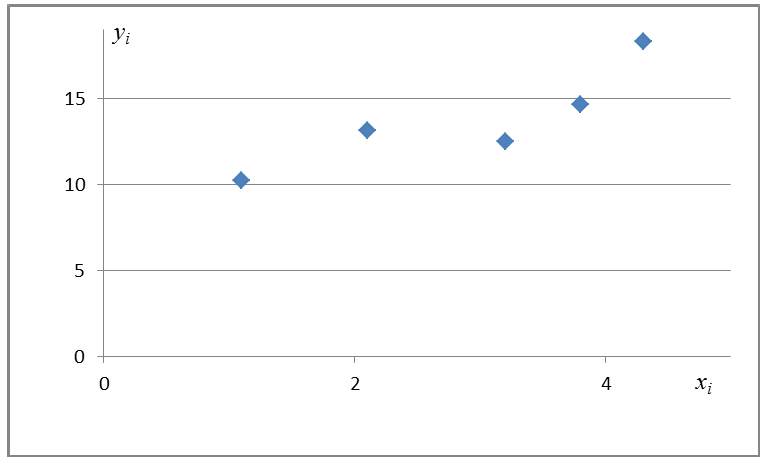
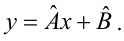
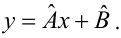
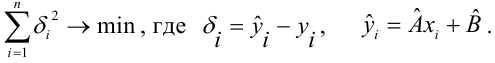
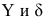 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.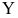 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения.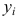 в разных точках независимы.
в разных точках независимы. независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.