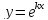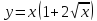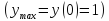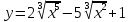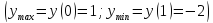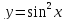Касательная и нормаль к графику функции
Основные формулы
Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной
Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓
Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓
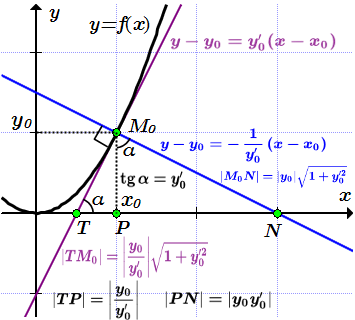
Определения
Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.
Определение касательной приводится здесь. Уравнение касательной:
.
 Касательная TM0, нормаль M0N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
Касательная TM0, нормаль M0N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .
Полезные формулы из аналитической геометрии
Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.
Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.
Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .
Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :
Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.
Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.
Уравнение прямой в отрезках, пересекающей оси координат в точках :
.
Примеры решения задач
Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓
Пример 1
Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.
Находим значение функции при :
.
Находим производную:
.
Находим производную в точке :
;
.
Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .
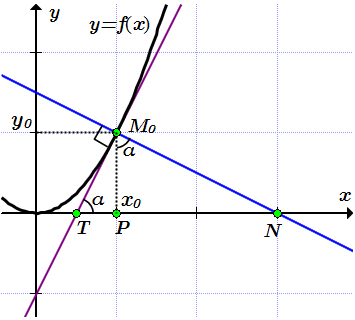 Касательная и нормаль к графику функции y=x 2 в точке M0(1;1).
Касательная и нормаль к графику функции y=x 2 в точке M0(1;1).
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.
Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .
Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.
Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка поднормали . Из прямоугольника имеем:
.
Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.
Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .
Пример 2
Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .
Находим значения переменных при .
;
.
Обозначим эту точку как .
Находим производные переменных x и y по параметру t .
;
;
;
;
.
Подставляя , находим производную y по x в точке .
.
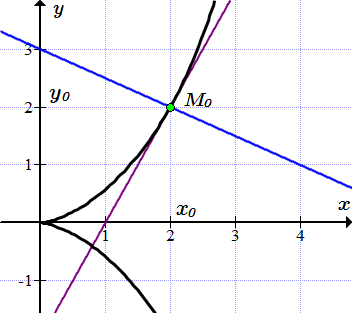 Касательная и нормаль к циссоиде в точке (2;2).
Касательная и нормаль к циссоиде в точке (2;2).
Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.
Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.
Уравнение касательной: .
Уравнение нормали: .
Пример 3
Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .
Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.
Находим производную в заданной точке, подставляя .
;
.
Находим уравнение касательной по формуле (2).
;
;
;
.
Находим уравнение нормали по формуле (3).
;
;
;
.
Касательная и нормаль к циссоиде изображены на рисунке ⇑.
Уравнение касательной: .
Уравнение нормали: .
Пример 4
Найти угол между кривыми и .
Найдем множество точек пересечения кривых, решая систему уравнений.
Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .
Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.
Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.
Вывод формулы для угла между кривыми
Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .
Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .
Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.
В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .
На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .
При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.
1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).
2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:
.
Этот случай изображен на рисунке ⇑.
3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).
Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.
Автор: Олег Одинцов . Опубликовано: 30-06-2021
Уравнение касательной и уравнение нормали к графику функции
Как получить уравнение касательной и уравнение нормали
Касательная – это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.
Уравнение касательной выводится из уравнения прямой.
Выведем уравнение касательной, а затем – уравнение нормали к графику функции.
В нём k – угловой коэффициент.
Отсюда получаем следующую запись:
Значение производной f ‘(x 0 ) функции y = f(x) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f(x 0 ) . В этом состоит геометрический смысл производной.
Таким образом, можем заменить k на f ‘(x 0 ) и получить следующее уравнение касательной к графику функции:
В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.
Теперь об уравнении нормали. Нормаль – это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:
Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).
Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет “холодным душем”.
Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .
Решаем задачи вместе
Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции (функция представляет собой многочлен и её производную можно найти по формулам 1, 2 и 3 в таблице производных):
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем
В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:
На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.
Следующий пример – тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг – приведение уравнения к общему виду.
Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Подставляем все полученные данные в “формулу-болванку” и получаем уравнение касательной:
Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):
Составляем уравнение нормали:
Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Находим уравнение касательной:
Перед тем, как привести уравнение к общему виду, нужно его немного “причесать”: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:
Составляем уравнение нормали:
Решить задачи самостоятельно, а затем посмотреть решения
Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Снова решаем задачи вместе
Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Распространённая ошибка при составлении уравнений касательной и нормали – не заметить, что функция, данная в примере, – сложная и вычислять её производную как производную простой функции. Следующие примеры – уже со сложными функциями (соответствующий урок откроется в новом окне).
Пример 7. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Внимание! Данная функция – сложная, так как аргумент тангенса ( 2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции (потребуется формула 9 в таблице производных сложной функции):
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 8. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Как и в предыдущем примере, данная функция – сложная, так как степень () сама является функцией. Поэтому найдём производную функции как производную сложной функции (используя формулу 1 в таблице производных сложной функции):
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Геометрическое применение производной: уравнения касательной и нормали, угол между кривыми
Касательная и нормаль к кривой
Касательная прямая – прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.
Если кривая определена уравнением $y=f(x)$, то уравнение касательной к ней в точке $M(x_0;y_0)$ имеет вид:
а уравнение нормали:
Задание. Написать уравнение касательной и нормали к кривой $y=x^2-3x+4$ в точке с абсциссой $x_0=0$.
Решение. Находим значение функции в заданной точке:
Далее вычислим значение производной функции в точке $x_0=0$:
а тогда уравнение касательной запишется в виде:
или после упрощения:
$$y-4=-frac<1><-3>(x-0) Rightarrow x-3 y+12=0$$
Ответ. Уравнение касательной: $3x+y-4=0$
Уравнение нормали: $x-3y+12=0$
Угол между кривыми
Углом между кривыми на плоскости в их общей точке $M(x_0;y_0)$ называется наименьший из двух возможных углов между касательными к этим кривым в данной точке. Если уравнения касательных, проведенных к кривым $y=f_1(x)$ и $y=f_2(x)$, соответственно $y=k_<1>x+b_<1>$ и $y=k_<2>x+b_2$, то тангенс угла между кривыми определяется соотношением:
Задание. Найти тангенс угла между кривыми $y=x^2-1$ и $y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.
Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:
Таким образом, искомая точка $x=1$.
Далее находим производные заданных функций в найденной точке:
Итак, искомый тангенс:
Ответ. $operatorname phi=frac<1><7>$
[spoiler title=”источники:”]
http://function-x.ru/derivative_and_tangent.html
http://www.webmath.ru/poleznoe/formules_8_10.php
[/spoiler]
Рассмотрим
кривую, уравнение которой имеет вид

Уравнение
касательной к данной кривой в точке
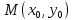 имеет вид:
имеет вид:
 (34)
(34)
Нормалью
к кривой в данной точке называется
прямая, проходящая через данную точку,
перпендикулярную к касательной в этой
точке.
Уравнение
нормали к данной кривой в точке
 имеет вид:
имеет вид:
 (35)
(35)
Длина
отрезка касательной, заключенного между
точкой касания и осью абсцисс называется
длиной
касательной,
проекция этого отрезка на ось абсцисс
называется подкасательной.
Длина
отрезка нормали, заключенного между
точкой касания и осью абсцисс называется
длиной
нормали,проекция
этого отрезка на ось абсцисс называется
поднормалью.
Пример
17
Написать
уравнения касательной и нормали к кривой
 в точке, абсцисса которой равна
в точке, абсцисса которой равна .
.
Решение:
Найдем
значение функции в точке
 :
:

Найдем
производную заданной функции в точке

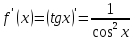

Уравнение
касательной найдем по формуле (34):

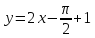
Уравнение
нормали найдем по формуле (35):


Ответ:
Уравнение
касательной :
Уравнение
нормали : .
.
Пример
18
Написать
уравнения касательной и нормали, длины
касательной и подкасательной, длины
нормали и поднормали для эллипса

в
точке
 ,
,
для которой .
.
Решение:
Найдем
 как производную функции, заданной
как производную функции, заданной
параметрически по формуле (10):



Найдем
координаты точки касания
 :
:
и значение производной в точке касания
 :
:



Уравнение
касательной найдем по формуле (34):

Найдем
координаты
 точки
точки пересечения
пересечения
касательной с осью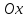 :
:

Длина
касательной равна длине отрезка
 :
:
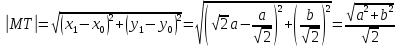
Согласно
определению, подкасательная
 равна
равна

Где
угол
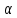 – угол между касательной и осью
– угол между касательной и осью . Поэтому,
. Поэтому, – угловой коэффициент касательной,
– угловой коэффициент касательной,
равный

Таким
образом, подкасательная
 равна
равна
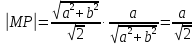
Уравнение
нормали найдем по формуле (35):

Найдем
координаты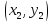 точки
точки пересечения нормали с осью
пересечения нормали с осью :
:

Длина
нормали равна длине отрезка
 :
:
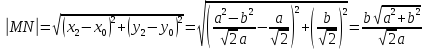
Согласно
определению, поднормаль
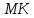 равна
равна

Где
угол
 – угол между нормалью и осью
– угол между нормалью и осью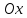 . Поэтому,
. Поэтому, – угловой коэффициент нормали, равный
– угловой коэффициент нормали, равный
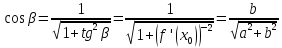
Поэтому,
поднормаль
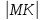 равна:
равна:

Ответ:
Уравнение
касательной :

Уравнение
нормали :
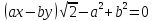
Длина
касательной
 ;
;
подкасательная ;
;
Длина
нормали
 ; поднормаль
; поднормаль
Задания
7. Написать
уравнения касательной и нормали:
1. К параболе в точке, абсцисса которой
 .
.
2.
К окружности
 в точках пересечения её с осью абсцисс
в точках пересечения её с осью абсцисс
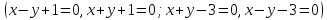 .
.
3.
К циклоиде
 в точке, для которой
в точке, для которой
 .
.
4.
В каких точках кривой
 касательная параллельна:
касательная параллельна:
а)
оси Оx; б) прямой
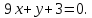
 .
.
10.
Промежутки монотонности функции.
Экстремумы функции.
Условие
монотонности функции:
Для
того, чтобы дифференцируемая на
 функция
функция не возрастала, необходимо и достаточно,
не возрастала, необходимо и достаточно,
чтобы во всех точках, принадлежащих ее производная была неположительна .
ее производная была неположительна .
 (36)
(36)
Для
того, чтобы дифференцируемая на
 функция
функция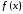 не убывала, необходимо и достаточно,
не убывала, необходимо и достаточно,
чтобы во всех точках, принадлежащих ее производная была неотрицательна.
ее производная была неотрицательна.
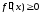 (37)
(37)
Промежутки,
на которых производная функции сохраняет
определенный знак, называются промежутками
монотонности
функции

Пример
19
Найти
промежутки монотонности функции
 .
.
Решение:
Найдем
производную функции
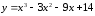 .
.

Найдем
промежутки знакопостоянства полученной
производной. Для этого
разложим полученный
квадратный трехчлен на множители:
 .
.
Исследуем
знак полученного выражения, используя
метод интервалов.

Таким
образом, получаем согласно (36), (37),что
заданная функция возрастает на
 и убывает на
и убывает на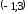 .
.
Ответ:
Заданная
функция
 возрастает на
возрастает на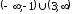 и убывает на
и убывает на .
.
Определение
Функция
 имеет в точке
имеет в точке локальный
локальный
максимум (минимум),
если существует такая окрестность
точки

 ,
,
что для всех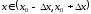 выполняется условие
выполняется условие
( ).
).
Локальный
минимум или максимум функции
 называетсялокальным
называетсялокальным
экстремумом.
Необходимое
условие существования экстремума.
Пусть
функция
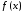 определена в некоторой окрестности
определена в некоторой окрестности
точки .
.
Если функция имеет
имеет
в точке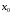 экстремумом, то производная
экстремумом, то производная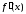 в точке
в точке либо равна нулю, либо не существует.
либо равна нулю, либо не существует.
Точка
 называетсякритической
называетсякритической
точкой
функции
 ,
,
если производная в точке
в точке либо равна нулю, либо не существует.
либо равна нулю, либо не существует.
Достаточные
условия наличия экстремума в критической
точке
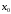 .
.
Пусть
точка
 является критической.
является критической.
Первое
достаточное условие экстремума:
Пусть
функция
 непрерывна в некоторой окрестности
непрерывна в некоторой окрестности точки
точки и дифференцируема в каждой точке
и дифференцируема в каждой точке .
.
Точка
 является локальным максимумом, если
является локальным максимумом, если
при переходе через
производная
функции меняет знак с плюса на минус.
Точка
 является локальным минимумом, если при
является локальным минимумом, если при
переходе через
производная
функции меняет знак с минуса на плюс.
Пример
20
Найти
экстремумы функции
 .
.
Решение:
Найдем
производную заданной функции

Приравнивая
в полученной производной к нулю числитель
и знаменатель, найдем критические точки:

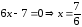
Исследуем
знак производной, используя метод
интервалов.


Из
рисунка видно, что при переходе через
точку
 производная меняет знак с плюса на
производная меняет знак с плюса на
минус. Следовательно, в точке –
–
локальный максимум.
При
переходе через точку
 производная меняет знак с минуса на
производная меняет знак с минуса на
плюс.
Следовательно,
в точке
 –
–
локальный минимум.
При
переходе через точку
 производная не меняет знак. Следовательно,
производная не меняет знак. Следовательно,
критическая точка не является экстремумом заданной
не является экстремумом заданной
функции.
Ответ:
 –
–
локальный максимум,
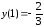 –
–
локальный минимум.
Второе
достаточное условие экстремума:
Если
первые
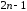 производные функции
производные функции в точке
в точке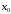 равны нулю, а
равны нулю, а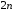 -ная
-ная
производная функции в точке
в точке отлична от нуля, то точка
отлична от нуля, то точка является экстремумом функции
является экстремумом функции ,
,
причем,
если
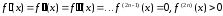 ,
,
(38)
то
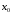 -локальный
-локальный
минимум
если
 ,
,
(39)
то
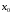 -локальный
-локальный
максимум.
Пример
21
Найти
экстремумы функции, пользуясь второй
производной
 .
.
Решение:
ОДЗ:
 .
.
Найдем
первую производную заданной функции
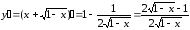
Найдем
критические точки функции:

Точку
 мы не рассматриваем, так как функция
мы не рассматриваем, так как функция
определена только в левой окрестности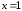 .
.
Найдем
вторую производную
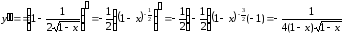
Находим

Таким
образом, на основании (39) делаем вывод
о том, что при
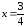
 – локальный максимум.
– локальный максимум.
Ответ:
 –
–
локальный максимум.
Задания
8.
Исследовать
на возростание и убывание функции:
|
1. |
2. |
3. |
|
4. |
5. |
6. |
Исследовать
на экстремумы функции:
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задание. Найти тангенс угла между кривыми $y=x^2-1$ и
$y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.
Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:
$$begin{array}{c}
left{begin{array}{l}
y_{1}=x^{2}-1 \
y_{2}=x^{3}-1
end{array} Rightarrow x^{2}-1=x^{3}-1 Rightarrow x^{3}-x^{2}=0 Rightarrowright. \
Rightarrow x_{1,2}=0, x_{3}=1
end{array}$$
Таким образом, искомая точка $x=1$.
Далее находим производные заданных функций в найденной точке:
$$begin{array}{c}
y_{1}^{prime}=left(x^{2}-1right)^{prime}=left(x^{2}right)^{prime}-(1)^{prime}=2 x-0=2 x, y_{1}^{prime}(1)=2 \
y_{2}^{prime}=left(x^{3}-1right)^{prime}=left(x^{3}right)^{prime}-(1)^{prime}=3 x^{2}-0=3 x^{2}, y_{2}^{prime}(1)=3
end{array}$$
Итак, искомый тангенс:
$$operatorname{tg} phi=frac{3-2}{1+2 cdot 3}=frac{1}{7}$$
Ответ. $operatorname{tg} phi=frac{1}{7}$
Назначение сервиса. Данный сервис предназначен для нахождения уравнения нормали к кривой. Решение оформляется в формате Word. Для получения уравнения необходимо выбрать вид заданной функции.
Функция задана в явном виде
Функция задана в неявном виде
Функция задана в параметрическом виде
Пример
Задание №1
Найти уравнение нормали к параболе y = 1/2*x2 в точке (-2;2).
Решение находим с помощью калькулятора.
Запишем уравнения нормали в общем виде:
![]()
По условию задачи x0 = -2, тогда y0 = 2
Теперь найдем производную:
y’ = (1/2•x2)’ = x
следовательно:
f'(-2) = -2 = -2
В результате имеем:
![]()
или
yk = 1/2•x+3
Задание №2
Написать уравнения нормали к кривой y2-1/2*x3-8 в точке M0(0;2).
Решение.
Поскольку функция задана в неявном виде, то производную ищем по формуле:
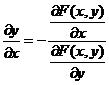
Для нашей функции:
![]()
![]()
Тогда:

или
![]()
следовательно:
Fx‘(0;2) = 3/4•02/2 = 0
В результате имеем:
![]()
или
x = 0
Задание №3
Написать уравнения нормали к эллипсу, заданному в параметрической форме: x = 5*sqrt(2)*cos(t);y = 3*sqrt(2)*sin(t) в точке M0(-5;3).
Решение.
Запишем уравнения нормали в для функции, заданной в параметрической форме:
(x – x0)x’ + (y – y0)y’ = 0
Данной точке M0(-5;3) соответствует значение t = 3/4•π
Для нашей функции:
![]()
![]()
следовательно: