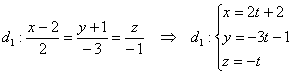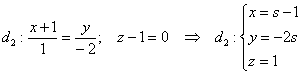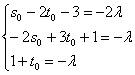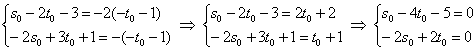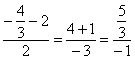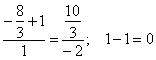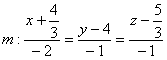Как составить уравнение общего перпендикуляра двух прямых

Макеты страниц



5.5.3. Как найти прямую, содержащую общий перпендикуляр?

в) Эта задачка посложнее будет. «Чайникам» рекомендую пропустить данный пункт, не хочу охлаждать вашу искреннюю симпатию к

аналитической геометрии =) Кстати, и более подготовленным читателям, возможно, лучше тоже повременить – дело в том, что по сложности эту задачу

надо бы поставить последней в параграфе, но по логике изложения она должна располагаться здесь. …Впрочем, танцуйте читайте все! 🙂

Итак, требуется найти уравнения прямой , которая содержит общий

перпендикуляр скрещивающихся прямых.

Общий перпендикуляр скрещивающихся прямых – это отрезок, соединяющий данные прямые и перпендикулярный данным прямым:

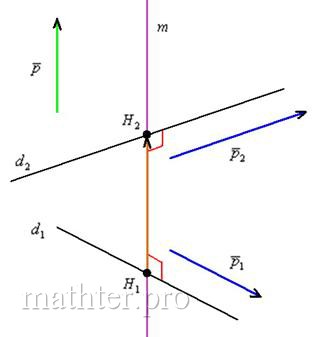
Вот наш красавец:  – общий перпендикуляр прямых . Он

единственный. Другого такого нет. Нам же требуется составить уравнения прямой ,

которая содержит данный отрезок.

Что известно о прямой «эм»? Известен её направляющий вектор , найденный

в предыдущем пункте. Но, к сожалению, мы не знаем ни одной точки, принадлежащей прямой «эм», не знаем и концов перпендикуляра – точек . Где эта перпендикулярная прямая пересекает две исходные прямые? В Африке, в

Антарктиде? Из первоначального обзора и анализа условия вообще не видно, как решать задачу….

Но есть хитрый ход, связанный с использованием параметрических уравнений прямой.

Решение оформим по пунктам:

1) Перепишем уравнения первой прямой в параметрической форме:

Рассмотрим точку . Координат мы не знаем. НО. Если точка

принадлежит данной прямой, то её координатам  соответствует вполне

конкретное значение параметра, обозначим его через . Тогда координаты

точки запишутся в виде:
, или:

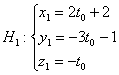
Жизнь налаживается, одна неизвестная – это всё-таки не три неизвестных.

2) Аналогичные действия проведём со второй прямой. Перепишем её уравнения в параметрическом

виде:

Если точка  принадлежит данной прямой, то при вполне конкретном

значении  её координаты должны удовлетворять

параметрическим уравнениям:
, или:

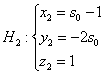
3) Запишем вектор . Ну и что, что нам не известны координаты точек – это же не

мешает из координат конца вектора  вычесть соответствующие координаты начала :

4) Вектор , как и ранее найденный вектор , является направляющим вектором прямой . Таким образом, они коллинеарны, и один вектор можно линейно

выразить через другой с некоторым коэффициентом пропорциональности «лямбда»:
или покоординатно:

Получилась самая, что ни на есть обычная система линейных уравнений с тремя неизвестными , которая стандартно разрешима, например, методом Крамера. Но так извращаться мы, конечно, не будем. Выразим из

3-го уравнения  и подставим эту «лямбду» в первые два уравнения:

Из 2-го уравнения выразим  и подставим в 1-е уравнение:
, а «лямбда» нам не потребуется.

То, что значения параметров получились одинаковыми – чистая случайность.

5) Небо полностью проясняется, подставим найденные значения  в наши

точки:
       

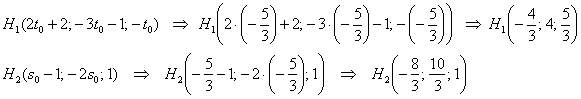
Сам вектор  нам не нужен, так как уже найден его коллега .

И после длинного пути всегда интересно выполнить проверку. Подставим координаты точки  в уравнения :

 –  получены верные равенства.

Подставим координаты  в уравнения :

 – получены верные равенства.

Вывод: найденные точки действительно принадлежат соответствующим прямым.

6) Заключительный аккорд: составим уравнения прямой  по точке  (можно взять ) и направляющему вектору :

В принципе, можно подобрать «хорошую» точку с целыми координатами, но это уже косметика.

5.5.4. Как найти расстояние между скрещивающимися прямыми?

5.5.2. Скрещивающиеся прямые

| Оглавление |



Автор: Aлeксaндр Eмeлин

Общий перпендикуляр к двум скрещивающимся прямым. Расстояние между скрещивающимися прямыми

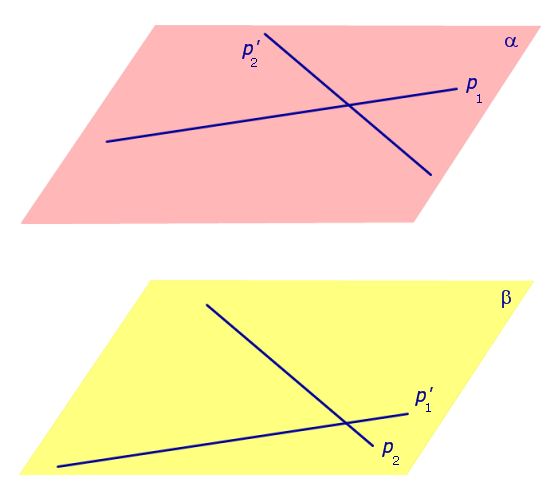
Теорема. Пусть p₁ и p₂ – две произвольные скрещивающиеся прямые скрещивающиеся прямые . Если рассмотреть всевозможные прямые A₁A₂, такие, что точка A₁ лежит на прямой p₁, а точка A₂ лежит на прямой p₂, то будут выполнены следующие два утверждения:

1. Среди всех прямых A₁A₂ существует единственная прямая, перпендикулярная к прямой p₁ и к прямой p₂ ( общий перпендикуляр к двум скрещивающимся прямым ).
2. Среди всех отрезков A₁A₂наименьшую длину имеет отрезок общего перпендикуляра к двум скрещивающимся прямым.

Доказательство. Докажем сначала существование общего перпендикуляра к двум скрещивающимся прямым.

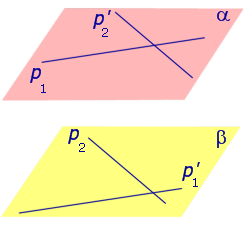
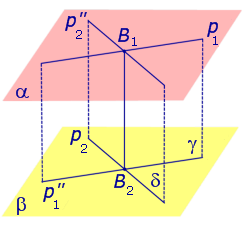
Через произвольную точку прямой p₁ проведем прямую , параллельную прямой параллельную прямой p₂ , а через произвольную точку прямой p₂ проведем прямую , параллельную прямой параллельную прямой p₁ . Обозначим буквой α плоскость, проходящую через прямые p₁ и , а буквой β плоскость, проходящую через прямые p₂ и (рис 1).

Поскольку прямая p₁ параллельна прямой , лежащей на плоскости β , то по признаку параллельности прямой и плоскости прямая p₁ параллельна плоскости β. Точно так же, поскольку прямая параллельна прямой p₂ , лежащей на плоскости β , то прямая по признаку параллельности прямой и плоскости параллельна плоскости β. Таким образом, плоскость α содержит две пересекающиеся прямые p₁ и , паралельные плоскости β. В силу признака параллельности плоскостей заключаем, что плоскости α и β параллельны.

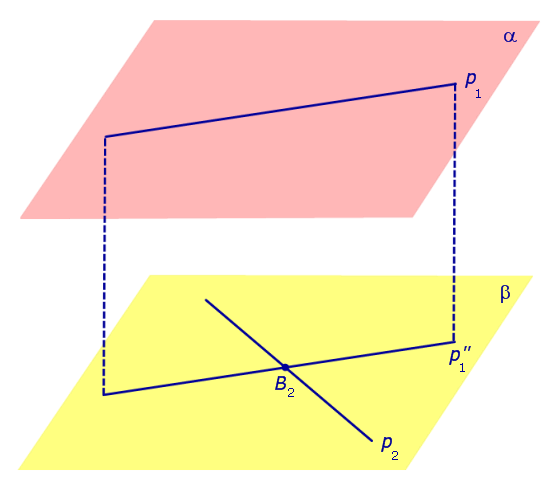
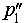
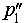
Спроектируем прямую p₁ на плоскость β. Получим прямую , являющуюся проекцией прямой проекцией прямой p₁, и обозначим точку пересечения прямых p₂ и буквой B₂ (рис. 2).

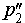
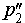
Спроектируем теперь прямую p₂ на плоскость α . Получим прямую , являющуюся проекцией прямой проекцией прямой p₂ , и обозначим точку пересечения прямых p₁ и буквой B₁ (рис. 3).

Доказательство существования общего перпендикуляра к двум скрещивающимся прямым завершено.

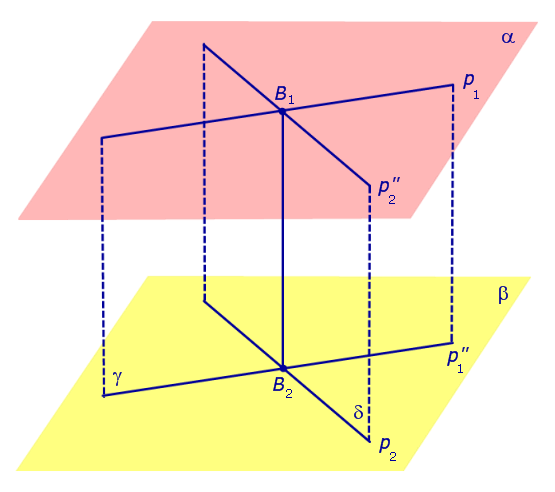
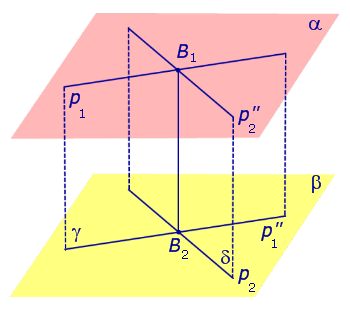
Докажем, что построенная прямая B₁B₂ является единственным общим перпендикуляром к прямым p₁ и p₂ .

Таким образом, общий перпендикуляр к прямым p₁ и p₂ является линией пересечения плоскостей γ и δ, то есть прямой B₁B₂ .

Доказательство единственности общего перпендикуляра к двум скрещивающимся прямым завершено. Утверждение 1 доказано.

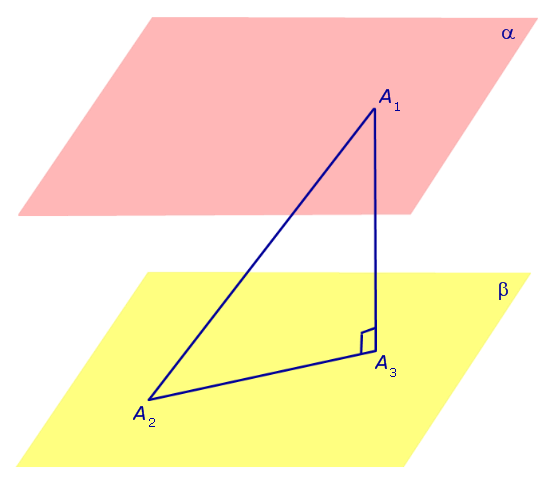
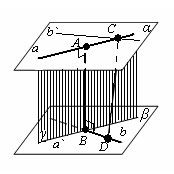
Перейдем к доказательству утверждения 2. Для этого рассмотрим произвольный отрезок A₁A₂ , у которого конец A₁ лежит на плоскости α , а конец A₂ лежит на плоскости β . Опустим перпендикуляр из точки A₁ на плоскость β и обозначим основание этого перпендикуляра символом A₃ (рис. 4).

Если отрезок A₁A₂ не является перпендикуляром к плоскостям α и β, то точка A₃ не совпадет с точкой A₂ , и треугольник A₁A₂A₃ будет прямоугольным треугольником с гипотенузой A₁A₂ и катетом A₁A₃. Поскольку в прямоугольном треугольнике длина катета меньше длины гипотенузы, то

Условие перпендикулярности прямых

I. Выясним условие перпендикулярности двух прямых y=k₁x+b₁ и y=k₂x+b₂.

Пусть прямые y=k₁x+b₁ и y=k₂x+b₂ образуют с положительным направлением оси Ox углы α₁ и α₂ соответственно.

Обозначим точки пересечения прямых с осью абсцисс через A и B, точку пересечения прямых — C.

Так как α₂ — внешний угол при вершине B треугольника ABC, то

Отсюда угловой коэффициент второй прямой

условие перпендикулярности прямых:

прямые, заданные уравнениями y=k₁x+b₁ и y=k₂x+b₂ перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку:

и условие перпендикулярности прямых в этом случае имеет вид:

Уравнение перпендикулярной прямой

Альтернативная формула
Прямая, проходящая через точку M₁(x₁; y₁) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).

Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /₉x – 1 /₃ (a = 4 /₉). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .

Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .

[spoiler title=”источники:”]

http://math.semestr.ru/line/perpendicular.php

[/spoiler]

Общий перпендикуляр к двум скрещивающимся прямым. Расстояние между скрещивающимися прямыми

Теорема. Пусть p₁ и p₂ – две произвольные скрещивающиеся прямые скрещивающиеся прямые . Если рассмотреть всевозможные прямые A₁A₂, такие, что точка A₁ лежит на прямой p₁, а точка A₂ лежит на прямой p₂, то будут выполнены следующие два утверждения:

1. Среди всех прямых A₁A₂ существует единственная прямая, перпендикулярная к прямой p₁ и к прямой p₂ ( общий перпендикуляр к двум скрещивающимся прямым ).
2. Среди всех отрезков A₁A₂наименьшую длину имеет отрезок общего перпендикуляра к двум скрещивающимся прямым.

Доказательство. Докажем сначала существование общего перпендикуляра к двум скрещивающимся прямым.

Через произвольную точку прямой p₁ проведем прямую , параллельную прямой параллельную прямой p₂ , а через произвольную точку прямой p₂ проведем прямую , параллельную прямой параллельную прямой p₁ . Обозначим буквой α плоскость, проходящую через прямые p₁ и , а буквой β плоскость, проходящую через прямые p₂ и (рис 1).

Поскольку прямая p₁ параллельна прямой , лежащей на плоскости β , то по признаку параллельности прямой и плоскости прямая p₁ параллельна плоскости β. Точно так же, поскольку прямая параллельна прямой p₂ , лежащей на плоскости β , то прямая по признаку параллельности прямой и плоскости параллельна плоскости β. Таким образом, плоскость α содержит две пересекающиеся прямые p₁ и , паралельные плоскости β. В силу признака параллельности плоскостей заключаем, что плоскости α и β параллельны.

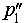
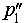
Спроектируем прямую p₁ на плоскость β. Получим прямую , являющуюся проекцией прямой проекцией прямой p₁, и обозначим точку пересечения прямых p₂ и буквой B₂ (рис. 2).

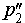
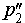
Спроектируем теперь прямую p₂ на плоскость α . Получим прямую , являющуюся проекцией прямой проекцией прямой p₂ , и обозначим точку пересечения прямых p₁ и буквой B₁ (рис. 3).

Доказательство существования общего перпендикуляра к двум скрещивающимся прямым завершено.

Докажем, что построенная прямая B₁B₂ является единственным общим перпендикуляром к прямым p₁ и p₂ .

Таким образом, общий перпендикуляр к прямым p₁ и p₂ является линией пересечения плоскостей γ и δ, то есть прямой B₁B₂ .

Доказательство единственности общего перпендикуляра к двум скрещивающимся прямым завершено. Утверждение 1 доказано.

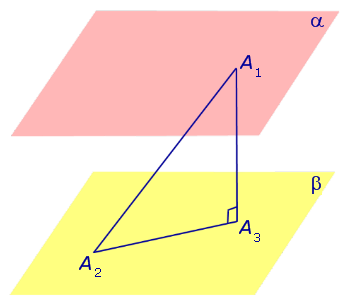
Перейдем к доказательству утверждения 2. Для этого рассмотрим произвольный отрезок A₁A₂ , у которого конец A₁ лежит на плоскости α , а конец A₂ лежит на плоскости β . Опустим перпендикуляр из точки A₁ на плоскость β и обозначим основание этого перпендикуляра символом A₃ (рис. 4).

Если отрезок A₁A₂ не является перпендикуляром к плоскостям α и β, то точка A₃ не совпадет с точкой A₂ , и треугольник A₁A₂A₃ будет прямоугольным треугольником с гипотенузой A₁A₂ и катетом A₁A₃. Поскольку в прямоугольном треугольнике длина катета меньше длины гипотенузы, то

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home

Расстояние между двумя скрещивающимися прямыми.

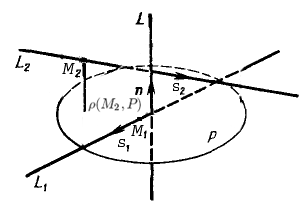
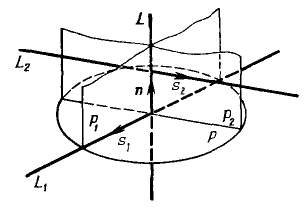
Пусть $L_1: frac=frac=frac$ и $L_2: frac=frac=frac$ — две скрещивающиеся прямые. Расстояние $rho(L_1, L_2)$ между прямыми $L_1$ и $L_2$ можно найти по следующей схеме:

1) Находим уравнение плоскости $P,$ проходящей через прямую $L_1,$ параллельно прямой $L_2:$

Плоскость $P$ проходит через точку $M_1(x_1, y_1, z_1),$ перпендикулярно вектору $overline n=[overline s_1, overline s_2]=(n_x, n_y, n_z),$ где $overline s_1=(m_1, l_1, k_1)$ и $overline s_2=(m_2, l_2, k_2)$ — направляющие вектора прямых $L_1$ и $L_2.$ Следовательно, уравнение плоскости $P: n_x(x-x_1)+n_y(y-y_1)+n_z(z-z_1)=0.$

2) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_2$ до плоскости $P:$

Нахождение общего перпендикуляра скрещивающихся прямых.

Для нахождения общего перпендикуляра прямых $L_1$ и $L_2,$ необходимо найти уравнения
плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0;$

Тогда уравнение общего перпендикуляра имеет вид

Пример.

2.214.

а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;

б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$

в) вычислить расстояние между прямыми;

г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$

Решение.

а) Если прямые $L_1$ и $L_2$ лежат в одной плоскости, то их направляющие вектора $overline(3, 4, -2),$ $overline(6, -4, -1),$ и вектор $overline l,$ соединяющий произвольную точку прямой $L_1$ и произвольную точку прямой $L_2$ компланарны. В качестве такого вектора $overline$ можно выбрать $overline(x_2-x_1, y_2-y_1, z_2-z_1).$ Проверим будут ли эти вектора компланарны.

Следовательно, вектора не компланарны и прямые не лежат в одной плоскости.

б) Запишем уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1.$ Эта плоскость проходит через точку $M_2(21, -5, 2)$ перпендикулярно вектору $overline n=[overline s_1, overline s_2].$

Таким образом, вектор $overline n$ имеет координаты $overline n(-12, -9, -36).$

Находим уравнение плоскости $$P:,, -12(x-21)-9(y+5)-36(z-2)=0Rightarrow$$ $$Rightarrow-12x-9y-36z+252-45+72=0Rightarrow -12x-9y-36z+279=0Rightarrow$$ $$Rightarrow 4x+3y+12z-93=0.$$

в) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_1$ до плоскости $P:$

Ответ: $frac<76><13>.$

г) Найдем уравнения плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$

Имеем, $M_1=(-7, -4, -3)in P_1,$

Таким образом, $$P_1: 54(x+7)-44(y+4)-7(z+3)=54x-44y-7z+378-176-21=$$ $$=54x-44y-7z+181=0.$$

Аналогично находим $P_2:$

Имеем, $M_2=(21, -5, 2)in P_2,$

Таким образом, $$P_1: -45(x-21)-76(y+5)+34(z-2)=-45x-76y+34z+945-380-68=$$ $$=-45x-76y+34z+497=0.$$

Ответ: $left<begin54x-44y-7z+181=0;\ -45x-76y+34z+497=0.endright. $

2.215.

а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;

б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$

в) вычислить расстояние между прямыми;

г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$

Ответ: б) $4x+12y+12z+76=0;$

г) $left<begin53x-7y-44z-429=0;\ 105x-23y-48z+136=0.endright. $

Как составить уравнение общего перпендикуляра к двум прямым

Признак

a α, b α = A , A a (чертеж 2.1.2). Допустим, что прямые a и b не скрещивающиеся, то есть они пересекаются. Тогда существует плоскость β, которой принадлежат прямые a и b . В этой плоскости β лежат прямая a и точка A . Поскольку прямая a и точка A вне ее определяют единственную плоскость, то β = α. Но b β и b α, следовательно, равенство β = α невозможно.

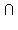
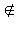
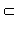
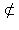
Теорема

Две скрещивающиеся прямые имеют общий перпендикуляр, и при том только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.

Доказательство

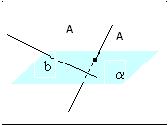
Пусть a и b – данные скрещивающиеся прямые. Проведем через них параллельные плоскости α и β. Прямые, пересекающие прямую a и перпендикулярные плоскости α, лежат в одной плоскости (γ). Эта плоскость пересекает плоскость β по прямой a`, параллельной a. Пусть B – точка пересечения прямых a` и b. Тогда прямая AB, перпендикулярная плоскости α, перпендикулярна и плоскости β, так как β параллельна α. Отрезок AB – общий перпендикуляр плоскостей α и β, а значит, и прямых a и b.
Докажем, что этот общий перпендикуляр единственный. Допустим, что у прямых a и b есть другой общий перпендикуляр CD. Проведем через точку С прямую b`, параллельную b. Прямая CD перпендикулярна прямой b, а значит, и b`. Так как она перпендикулярна прямой a, то она перпендикулярна плоскости α, а значит, параллельна прямой AB. Выходит, что через прямые AB и CD, как через параллельные, можно провести плоскость. В этой плоскости будут лежать наши скрещивающиеся прямые AC и BD, а это невозможно, что и требовалось доказать.

Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра.

1007 Составить канонические
уравнения прямой, проходящей через точку М₁(2; 0; -3) параллельно: 1007.1 вектору a={2; -3;
5}; 1007.2 прямой ; 1007.3 оси Ох; 1007.4 оси Оу; 1007.5 оси Oz. 1008 Составить
канонические уравнения прямой, проходящей через
данные точки: 1008.1 (1; -2; 1), (3; 1; -1); 1008.2 (3; -1; 0), (1; 0; -3); 1008.3 (0; -2; 3), (3; -2; 1); 1008.4 (1; 2; -4), (-1; 2; -4). 1009 Составить
параметрические уравнения прямой, проходящей
через точку М₁(1; -1; -3) параллельно: 1009.1 вектору a={2; -3;
4}; 1009.2 прямой ; 1009.3 прямой , , . 1010 Составить
параметрические уравнения прямой, проходящей
через данные точки: 1010.1 (3; -1; 2), (2; 1; 1); 1010.2 (1; 1; -2), (3; -1; 0); 1010.3 (0; 0; 1), (0; 1; -2). 1011 Через точки М₁(-6; 6; -5), М₂(12;
-6; 1) проведена прямая. Определить
точки пересечения этой прямой с координатными
плоскостями.
1012 Даны вершины
треугольника А(3; 6; -7), В(-5; 2; 3), С(4; -7; -2). Составить
параметрические уравнения его медианы,
проведенной из вершины С. 1013 Даны вершины
треугольника А(3; -1; -1), В(1; 2; -7), С(-5; 14; -3). Составить
канонические уравнения биссектрисы его
внутреннего угла при вершине С. 1014 Даны вершины
треугольника А(2; -1; -3), В(5; 2; -7), С(-7; 11; 6). Составить
канонические уравнения биссектрисы его внешнего
угла при вершине А. 1015 Дан вершины
треугольника А(1; -2; -4), В(3; 1; -3), С(5; 1; -7). Составить
параметрические уравнения его высоты,
опущенного из вершины В на противоположную
сторону. 1016 Дана прямая , . Вычислить
проекции какого-нибудь ее направляющего вектора
а на координатные оси. Найти общее выражение
проекций произвольного направляющего вектора
этой прямой на координатные оси. 1017 Дана прямая , . Найти
разложение какого-нибудь ее направляющего
вектора а по базису i, j, k. Выразить в общем виде
разложение произвольного направляющего вектора
этой прямой по базису i, j, k. 1018 Составить
канонические уравнения прямой, проходящей через
точку М₁(2; 3; -5) параллельно
прямой , . 1019 Составить
канонические уравнения следующих прямых: 1019.1 , ; 1019.2 , ; 1019.3 , . 1020 Составить
параметрические уравнения следующих прямых: 1020.1 , ; 1020.2 , . 1021 Доказать
параллельность прямых: 1021.1 и , ; 1021.2 , , и , ; 1021.3 , и ,
. 1022 Доказать
перпендикулярность прямых: 1022.1 и , ; 1022.2 , , и , ; 1022.3 , и ,
. 1023 Найти острый
угол между прямыми , . 1024 Найти тупой
угол между прямыми , , и , , . 1025 Определить
косинус угла между прямыми , и , . 1026 Доказать, что
прямые, заданные параметрическими уравнениями , , и , , , пересекаются. 1027 Даны прямые , ; при
каком значении l они пересекаются? 1028  

Доказать,
что условие, при котором две прямые и лежат в одной плоскости, может быть
представлено в следующем виде:

.

1029 Составить
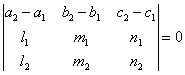
уравнения прямой, которая проходит через точку М₁(-1;
2; -3) перпендикулярно к вектору a={6;
-2; -3} и пересекает прямую . 1030 Составить
уравнения прямой, которая проходит через точку
М(-4; -5; 3) и пересекает две прямые , .
1031 Составить
параметрические уравнения общего
перпендикуляра двух прямых, заданных
уравнениями , , и, ,. 1032 Даны
уравнения движения точки М(x; y; z): , , . Определить скорость v. 1033 Даны
уравнения движения точки М(x; y; z): , , . Определить расстояние d, которое
пройдет эта точка за промежуток времени от t₁=0
до t₂=7. 1034 Составить
уравнения движения точки М(x; y; z), которая, имея
начальное положение М₀(3; -1; -5), движется прямолинейно и равномерно
в направлении вектора s={-2; 6; 3} со скоростью v=21. 1035 Составить
уравнения движения точки М(x; y; z), которая,
двигаясь прямолинейно и равномерно, прошла
расстояние от точки М₁(-7; 12; 5) до точки М₂(9; -4; -3) за промежуток времени от t₁=0
до t₂=4. 1036 Точка М(x; y; z)
движется прямолинейно и равномерно из
начального положения М₀(20; -18; -32)
в направлении, противоположном
вектору s={3; -4; -12}, со скоростью v=26. Составить
уравнения движения точки М и определить точку, с
которой она совпадает в момент времени t=3. 1037 Точки М(x; y; z)
и N(x, y, z) движутся прямолинейно и равномерно:
первая из начального положения М₀(-5;
4; -5) со скоростью v_M=14 в направлении вектора s={3; -6; 2}, вторая
из начального положения N₀(-5; 16; -6) со скоростью v_N=13 в направлении, противоположном
вектору r={-4; 12; -3}. Составить уравнения движения
каждой из точек и, убедившись, что их траектории
пересекаются, найти: 1037.1 точку Р
пересечения их траекторий; 1037.2 время,
затраченное на движение точки М от М₀
до Р; 1037.3 время,
затраченное на движение точки N от N₀
до Р; 1037.4 длины
отрезков M₀P и N₀P.