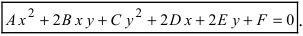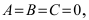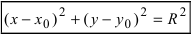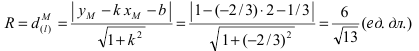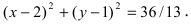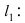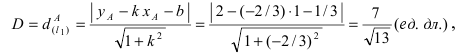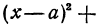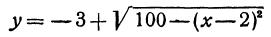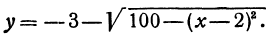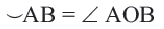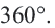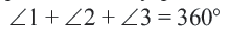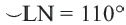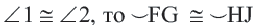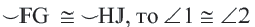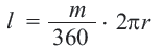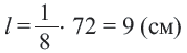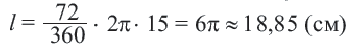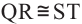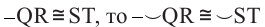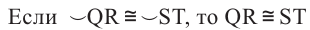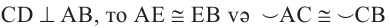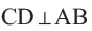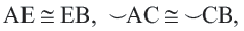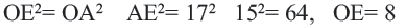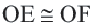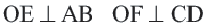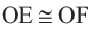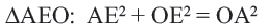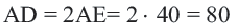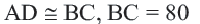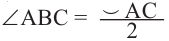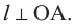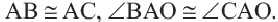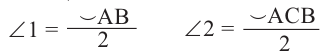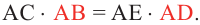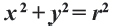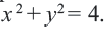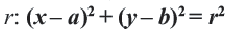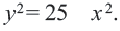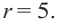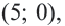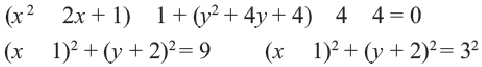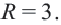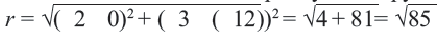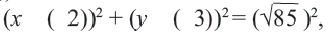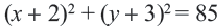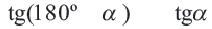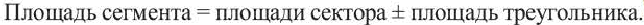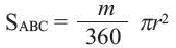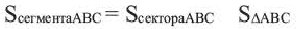Как составить уравнение окружности через диаметр

Написать уравнение окружности

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

Следовательно, уравнение данной окружности

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

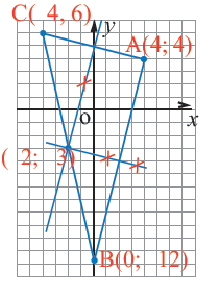
4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

получаем систему уравнений:

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

Приравняем правые части 2-го и 3-го уравнений:

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

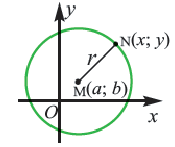
Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x – 2 ) 2 + (y – ( -3 )) 2 = 4 2
или
(x – 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x – 2) 2 + (y + 3) 2 = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение ( x – 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x – 2) 2 + ( y + 3) 2 = 16
( 2 – 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

[spoiler title=”источники:”]

http://www.calc.ru/Uravneniye-Okruzhnosti.html

http://profmeter.com.ua/communication/learning/course/course7/chapter0552/

[/spoiler]

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Решение:

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

   

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

   

   

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Решение:

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

   

   

   

Следовательно, уравнение данной окружности

   

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Решение:

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

   

   

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

   

   

   

Таким образом, уравнение окружности с диаметром AB —

   

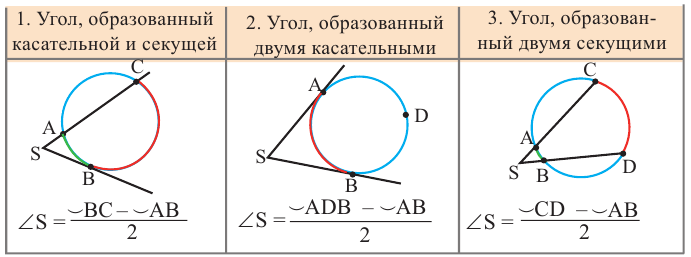
4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Решение:

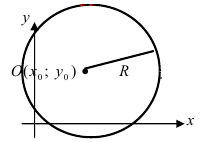
Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

   

получаем систему уравнений:

   

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

   

   

   

   

Приравняем правые части 2-го и 3-го уравнений:

   

   

   

Умножив уравнение

   

на -1 и сложив результат почленно с уравнением

   

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

   

   

получаем R²=100.

Следовательно, уравнение окружности, проходящей через три данные точки —

   

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

   

Прежде всего,
давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что
уравнение с двумя переменными x и y
называется уравнением линии l, если этому уравнению
удовлетворяют координаты любой точки линии l и не
удовлетворяют координаты никакой точки, не лежащей на этой линии.

Сегодня на уроке мы
попробуем по геометрическим свойствам линии найти ее уравнение.

В качестве линии
рассмотрим окружность радиуса  с
центром в точке .

Пусть центр
окружности имеет координаты . Возьмем на
окружности произвольную точку . Запишем формулу
расстояния между точками C и M.
Мы знаем, что длина отрезка, который соединяет любую точку на окружности с
центром окружности – это радиус. Поэтому можно записать, что MC
равно r. Возведем MC в квадрат
и получим уравнение MC² = r².
Заменим MC² квадрат на выражение  и получим, что если
точка лежит на окружности с радиусом r и центром в
точке C, то координаты этой точки удовлетворяют
уравнению . Если точка не
лежит на окружности, то расстояние от этой точки до центра окружности не равно
радиусу, поэтому координаты таких точек не будут удовлетворять полученному
уравнению. Поэтому можно сказать, что в прямоугольной системе координат уравнение
окружности радиуса r с центром в точке C с координатами  имеет вид: .

Задача. Записать
уравнение окружности с радиусом  и центром в начале
координат.

Решение.

Начало координат
имеет координаты (0;0). Подставим их в уравнение окружности и получим, что
уравнение окружности с радиусом r и
центром в начале координат имеет вид

 

.

Задача. Начертить
окружность, заданную уравнением .

Решение.

Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего,
определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь
давайте определим величину радиуса окружности.

Поскольку в правой
части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо
извлечь квадратный корень из 4. Получим 2.

 Значит наша
формула задает окружность с центром в точке с координатами пять три и радиусом
равным двум.

Задача. Начертить
окружность, заданную уравнением .

Решение.

Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего
определимся с координатами центра окружности.

Это будут числа -4
и 2. Теперь давайте определим величину радиуса окружности.

Задача. Начертить
окружность, заданную уравнением .

Решение. Уравнениями
такого типа описываются окружности с центром в начале координат. Теперь давайте
определим величину радиуса окружности. Поскольку в правой части формулы стоит
квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень
из 9.

Значит наша формула
задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.

Теперь давайте
попробуем решить задачу обратную данным.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Как и в предыдущих
задачах мы начнем с определения координат центра окружности. Сделать это
нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр
окружности имеет координаты (0;0).

Нетрудно заметить,
что радиус окружности равен 4.

Запишем уравнение
окружности и подставим найденные значения.

 

 

 

Ответ: .

Решим еще одну
задачу.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Решение.

 – центр окружности

 – радиус окружности

Ответ:.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Решение.

 – центр окружности

 – радиус окружности

 

 

 

Ответ:.

Решая задачи, мы с
вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот
порядок.

Для того, что
бы составить уравнение окружности и построить ее надо:

1. Найти координаты
центра окружности.

2. Найти длину
радиуса этой окружности.

3. Записать уравнение
окружности.

4. Подставить
полученные значения в уравнение окружности.

5. Построить
окружность, если это требуется для решения задачи.

Рассмотрим еще одну
задачу.

Написать уравнение
окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм
имеет координаты шесть три.

Задача. Написать
уравнение окружности с диаметром , если , .

Решение.

Найдем координаты
центра окружности. Центр окружности является серединой диаметра. Воспользуемся
формулами для нахождения координат середины отрезка.

Получим, что центр
окружности имеет координаты .

Теперь определим
радиус окружности. Для этого найдем расстояние от центра окружности до концов
диаметра.

 

 

Запишем общее
уравнение окружности и подставим в него найденные значения. Тогда получим, что
уравнение данной окружности имеет вид:

Ответ: .

Подведем итоги
урока.

На сегодняшнем
уроке мы познакомились с формулой, которая задает окружность с центром в точке С
(x₀; y₀)
и радиусом r.

Также мы
познакомились с формулой, которая задает окружность с центром в начале
координат и радиусом r.

Мы рассмотрели
задачи на составление уравнения окружности по рисунку и на построение
окружности по заданному уравнению.

Содержание:

Окружность:

Определение: Кривой второго порядка называется линия, описываемая уравнением

Замечание: Если коэффициенты

При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.

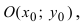
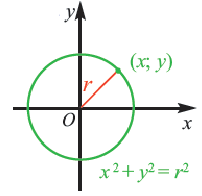
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки называемой центром окружности, на расстояние R, которое называется радиусом окружности.

Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:

Рис. 27. Вывод уравнения окружности.

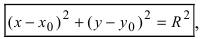
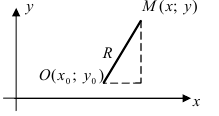
Из рисунка видно, что по теореме Пифагора которое определяет уравнение окружности (Рис. 28):

Рис. 28. Окружность.

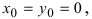
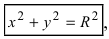
Если то уравнение принимает вид который называется каноническим уравнением окружности.

Пример:

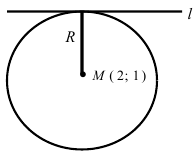
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 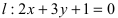является касательной к окружности.

Решение:

Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.

В уравнении окружности 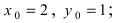таким образом оно имеет вид:

Пример:

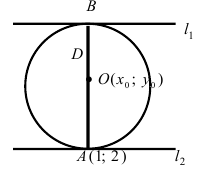
Составить уравнение окружности, касающейся двух параллельных прямых 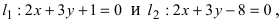причем одной из них в т. А (1; 2).

Решение:

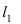
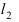
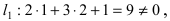
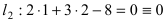
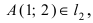
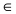
Прежде всего определим, на какой из прямых или лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых

следовательно, точка A(1; 2) принадлежит линии (в сокращенной форме это предложение пишут так: где значок означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой

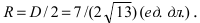
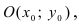
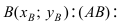
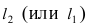
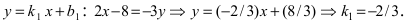
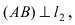
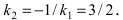
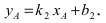
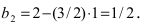
а радиус окружности Найдём координаты центра окружности точки которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки перейдем от общего уравнения прямой к уравнению прямой с угловым коэффициентом Так как прямаято её угловой коэффициент Прямая (АВ) проходит через известную точку A(1;2), следовательно, Отсюда находим Таким образом,уравнение прямой (АВ):

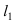
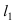
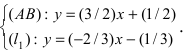
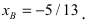
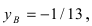
Найдем координаты точки B, которая является пересечением прямых и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых и (АВ): (В): Подставим выражение для переменной у из второго у равнения в первое, получим Подставив это значение во второе уравнение системы, найдем т.е.

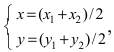
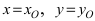
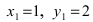
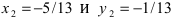
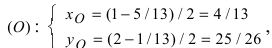
Для вычисления координат точки О применим формулы деления отрезка пополам (О): в этой формуле (координаты точки О), (координаты точки А), (координаты точки В), следовательно, т.е. координаты точки О

Таким образом, уравнение искомой окружности имеет вид:

Окружность в высшей математике

Рассмотрим уравнение

которое получается из уравнения (I), если положить , .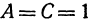

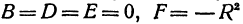
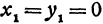
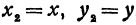
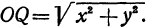
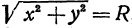
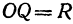
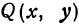
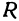
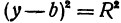
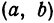
Если в формулу, выражающую расстояние между двумя точками, подставить , , то получим Из уравнения (1) находим, что , т. е. . Это значит, что все точки , координаты которых удовлетворяют уравнению (1), находятся на расстоянии от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса с центром в начале координат. Аналогично получаем, что уравнение определяет окружность радиуса с центром в точке .

Пример:

Найдем уравнение окружности с центром в точке и радиусом, равным 10.

Решение:

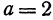
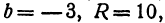
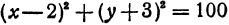
Полагая, получим .

Разрешим это уравнение относительно 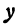, будем иметь

и

Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.

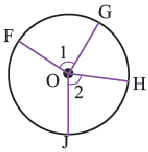
Центральный угол. Градусная мера дуги

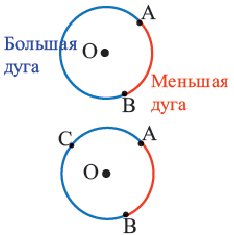
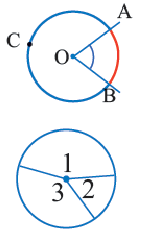
Дуга окружности. Если отметить на окружности точки и , то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка является какой-либо точкой дуги , то . Если точки и являются концами диаметра, го каждая дуга является полуокружностью.

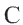
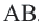
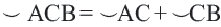
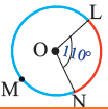
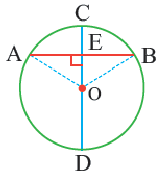
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла:

Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна

Дуги окружности и их величины

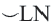
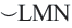
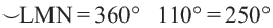
Пример: минорная дуга:

мажорная дуга:

Конгруэнтные дуги

В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.

Если

Если

Длина дуги

Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.

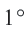
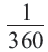
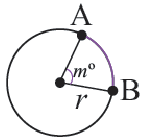
Длина дуги в равна части длины окружности.

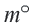
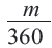
Длина дуги, соответствующей центральному углу с градусной мерой , составляет части длины окружности:

Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)

Пример №1

Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу .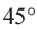

Решение:

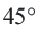
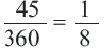
Так как центральный угол составляет часть полного угла, то длина искомой дуги:

Пример №2

Найдите длину дуги, соответствующей центральному углу 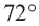в окружности радиусом 15 см.

Решение: подставляя значения 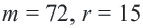в формулу длины дуги находим:

Окружность и хорда

Теорема о конгруэнтных хордах

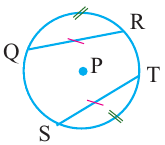
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.

Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.

1)Если 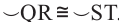, то

2)Если

Доказательство теоремы 1:

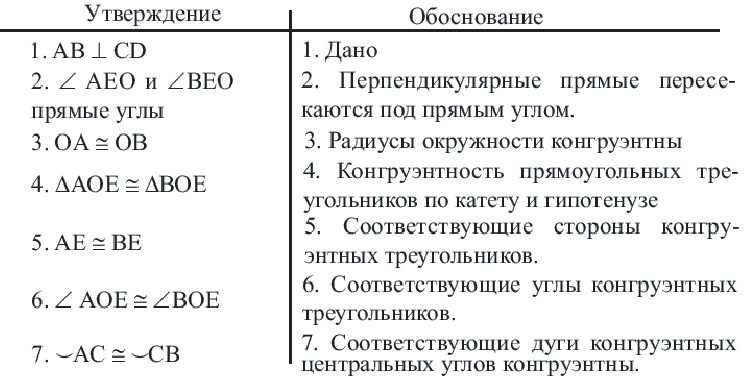
Теорема о серединном перпендикуляре хорд

Теорема 2.

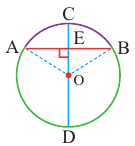
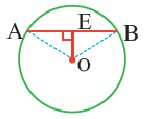
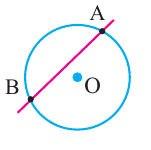
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.

Если

Доказательство теоремы 2.

Дано: – центральный угол,

Докажите:

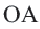
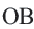
Начертите радиусы и окружности.

Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.

Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.

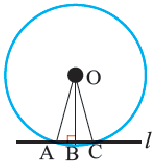
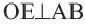
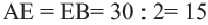
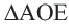
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если , то . Из по теореме Пифагора имеем:

Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности

Теорема 3.

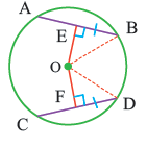
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.

Если 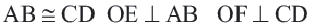, то

Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.

Доказательство теоремы 3

Дано: Окружность с центром

Докажите:

Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам. и – серединные перпендикуляры конгруэнтных хорд и . , так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности и : . Прямоугольные треугольники, и конгруэнтны (по катету и гипотенузе). Так как и являются соответствующими сторонами данных треугольников, то они конгруэнтны: . Теорема доказана.

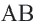
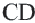
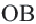
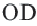
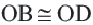
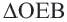
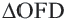
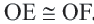
Задача. Хорды и находятся на одинаковом расстоянии от центра окружности. . Если радиус окружности равен 41 единице, то найдите .

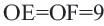
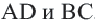
Решение: Так как хорды и находятся на одинаковом расстоянии от центра, то они конгруэнтны: Соединим точки и с точкой В прямоугольном треугольнике ; ; ;

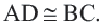
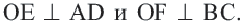
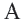
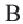
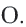
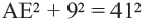
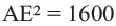
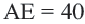
Так как

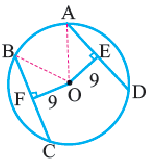
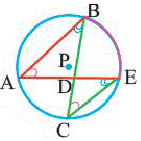
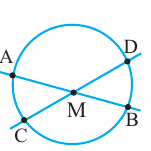
Угол, вписанный в окружность

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.

является углом вписанным в окружность с центром , а дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.

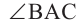
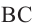
Угол, вписанный в окружность:

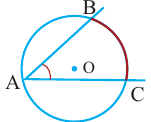
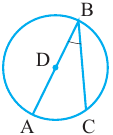
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается.

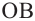
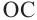
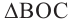
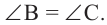
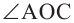
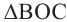
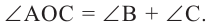
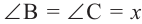
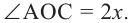
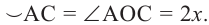
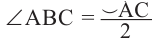
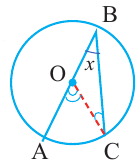
Доказательство (текстовое): и радиусы окружности и равнобедренный треугольник. Значит, Так как является внешним углом , Если примем, что , то Так как градусные меры центрального угла и опирающейся на него дуги равны, то Следовательно, .

Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.

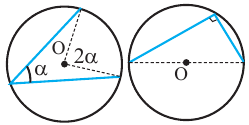
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.

Конгруэнтные углы, вписанные в окружность

Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. , .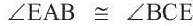

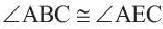
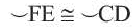
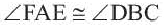
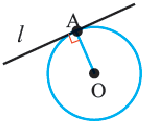
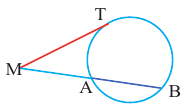
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если , то .

Касательная к окружности

Касательная. Признак касательной

Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

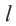
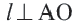
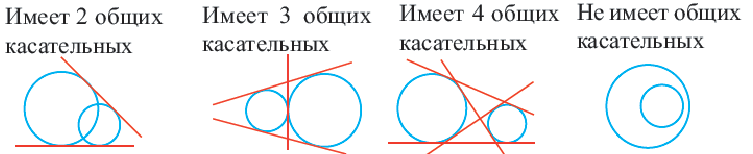
Прямая является касательной к окружности. Значит, Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.

Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.

Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.

Доказательство теоремы 1. Если прямая – касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая не перпендикулярна радиусу Проведем и на прямой выделим отрезок Тогда так как Значит, точка также находится на окружности. То есть прямая имеет с окружностью две общие точки, что противоречит условию. Значит,

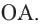
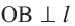
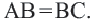
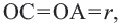
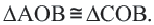
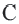
Свойства касательных, проведенных к окружности из одной точки

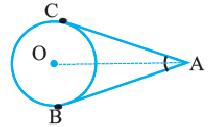
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.

и касательные, проведенные из точки к окружности с центром

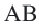
Углы, образованные секущими и касательными

Прямая, имеющая две общие точки с окружностью, называется секущей окружности.

Углы между двумя секущими

Вершина угла находится внутри окружности

Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному.

Углы между касательной и секущей

Вершина угла находится на окружности

Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.

Углы, образованные касательной и секущей

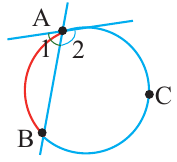
Вершина угла находится вне окружности

Теорема 1.

Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.

Отрезки секущих и касательных

Длина отрезков, секущих окружность

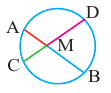
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.

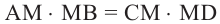
Теорема 2. Если из точки провести две прямые, пересекающие окружность соответственно в точках и , и то верно равенство

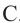
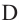
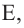
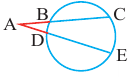
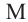
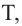
Теорема 3. Если из точки проведены прямая, которая пересекает окружность в точках и и касательная к окружности в точке то верно равенство:

Уравнение окружности

Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом и с центром в начале координат. Расстояние между центром окружности и ее любой точкой равно радиусу окружности.

Расстояние между двумя точками

Упрощение

Возведение обеих частей в квадрат

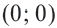
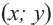
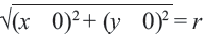
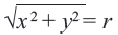
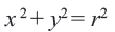
Уравнение окружности с центром в начале координат и радиусом :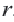

Например, уравнение окружности с центром в начале координат 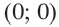и радиусом 2 имеет вид:

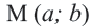
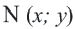
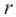
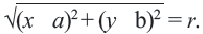
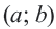
По формуле расстояния между центром окружности и точки на окружности радиуса имеем Возведя в квадрат обе части, получаем уравнение окружности с центром в точке и радиусом

Например, уравнение окружности с центром в точке 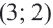и радиусом 4 имеет вид:

Пример №3

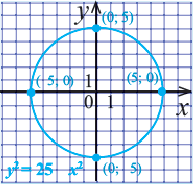
Постройте на координатной плоскости окружность, заданную уравнением

Решение: Напишем уравнение в виде 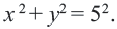Как видно,

Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 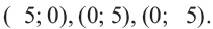Проведем окружность через эти точки.

Пример №4

Точка 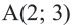находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.

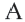
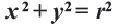
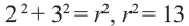
Решение: Записав координаты точки в уравнении , получим: Уравнение этой окружности:

Пример №5

Найдем центр и радиус окружности, заданной уравнением

Решение:

Центр окружности точка 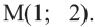Радиус

Пример №6

Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 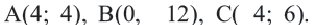На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.

Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 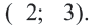Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности,

Уравнение окружности:

Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.

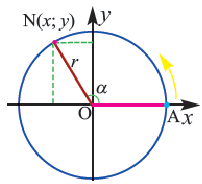
Координаты точек, находящихся на окружности, и тригонометрические отношения

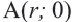
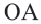
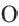
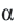
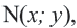
Если точка при повороте радиуса вокруг точки против движения часовой стрелки на угол преобразуется в точку то

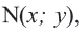
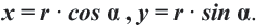
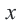
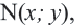
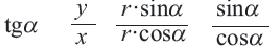
Для координат точки соответствующей углу поворота на окружности, верны формулы В этих формулах – угол, отсчитываемый от положительной оси против движения часовой стрелки. Если точка не находится на оси ординат, то .

Синусы смежных углов равны, а косинусы взаимно противоположны.

Из этих формул при 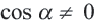почленным делением получаем:

С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.

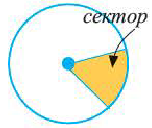
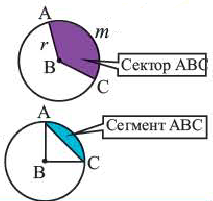
Сектор и сегмент

Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.

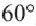
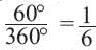
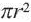
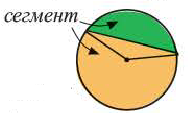
Например, часть круга, соответствующая центральному углу , составляет часть всего круга. Так как площадь круга , то площадь этого сектора будет Сегмент часть круга, ограниченная хордой и соответствующей дугой.

Площадь сектора

Площадь сектора:

Площадь сегмента:

Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь

 Формулы окружности 

• Длины окружности и диаметр:

(С=pi*D)

• Длина окружности:

(C = 2*pi*R)

• Площадь круга:

(S=pi*r^2)

• Площадь через диаметр:

(frac{pi*D}{4})

• Уравнение окружности:

(r^2 = x^2 + y^2)

• Выразим (R) из формулы  (C = 2*pi*R) (–>) (R=frac{c}{2*pi}) подставим (R) в формулу (S=pi*r^2) (–>) (S=frac{C^2}{4*pi}). Получаем формулу площади через длину окружности и (pi):

(S=frac{C^2}{4*pi})