Решение задач по темам “Уравнение окружности” и “Уравнение прямой”
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

На прошлых уроках мы вывели уравнение окружности и решили некоторые задачи на уравнение окружности, вывели уравнение прямой и решили соответствующие задачи. На этом уроке мы продолжим решение задач на уравнение окружности и уравнение прямой.
Касательная к окружности

О чем эта статья:
Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).
Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.
Свойства касательной к окружности
Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
- окружность с центральной точкой А;
- прямая а — касательная к ней;
- радиус АВ, проведенный к касательной.
Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.
Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.
В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.
Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Задача
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.
Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.
Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.
∠АОС = 180° – ∠САО – ∠АСО = 180° – 90° – 28° = 62°
Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.
Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.
Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.
Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.
Задача 1
У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.
Решение
Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).
Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:
∠BDC = ∠BDA × 2 = 30° × 2 = 60°
Итак, угол между касательными составляет 60°.
Задача 2
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.
Решение
Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.
Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.
∠МNК = (180° – ∠МКN) : 2 = (180° – 50°) : 2 = 65°
Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
Задача 1
Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.
Решение
Исходя из соотношения касательной и секущей МА 2 = МВ × МС.
Найдем длину внешней части секущей:
МС = МВ – ВС = 16 – 12 = 4 (см)
МА 2 = МВ × МС = 16 х 4 = 64
Задача 2
Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.
Решение
Допустим, что МО = у, а радиус окружности обозначим как R.
В таком случае МВ = у + R, а МС = у – R.
Поскольку МВ = 2 МА, значит:
МА = МВ : 2 = (у + R) : 2
Согласно теореме о касательной и секущей, МА 2 = МВ × МС.
(у + R) 2 : 4 = (у + R) × (у – R)
Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:
Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).
Ответ: MO = 10 см.
Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.
Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.
Задача 1
Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.
Решение
Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.
АВ = ∠АВС × 2 = 32° × 2 = 64°
Задача 2
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Решение
Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:
КМ = 2 ∠МКВ = 2 х 84° = 168°
Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.
∠ОКМ = ∠ОМК = (180° – ∠КОМ) : 2
Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:
∠ОМК = (180° – ∠КОМ) : 2 = (180° – 168°) : 2 = 6°
Написать уравнение окружности
Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.
1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.
Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:
Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:
2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).
Так как центр окружности — точка A(8; -3), то a=8, b=-3.
Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.
Следовательно, уравнение данной окружности
3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).
Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка
Центр окружности — точка O(1;-2). Значит, a=1, b=-2.
Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,
Таким образом, уравнение окружности с диаметром AB —
4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).
Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение
получаем систему уравнений:
Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим
Приравняем правые части 2-го и 3-го уравнений:
на -1 и сложив результат почленно с уравнением
получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:
Следовательно, уравнение окружности, проходящей через три данные точки —
5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).
Решение аналогично решению задания 4. В результате получим уравнение
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/kasatelnaya-k-okruzhnosti
[/spoiler]
в каждом из следующих случаев:
совпадает с началом координат и ее радиус R=3;
совпадает с точкой С(2; -3) и ее радиус R=7;
проходит через начало координат и ее центр
совпадает с точкой С(6; -8);
проходит через точку А(2; 6) и ее центр совпадает с
точкой С(-1; 2);
являются концами одного из диаметров окружности;
совпадает с началом координат и прямая
совпадает с точкой С(1; -1) и прямая
касательной к окружности;
проходит через точки А(3; 1) и В(-1; 3), а ее центр
лежит на прямой
проходит через три точки А(1; 1), В(1; -1), С(2; 0);
проходит через три точки: М1(-1;
5), М2(-2; -2). М3(5; 5).
является центром окружности, отсекающей на
прямой
6. Составить уравнение этой окружности.
окружностей радиуса
прямой
уравнение окружности, касающейся прямых
одна из них – в точке А(2; 1).
уравнения окружностей, которые проходят через
точку А(1; 0) и касаются прямых
уравнение окружности, которая, имея центр на
прямой
касается прямых
уравнения окружностей, касающихся прямых
одной из них – в точке М1(1; 2).
уравнения окружностей, проходящих через начало
координат и касающихся прямых
уравнение окружностей, которые, имея центры на
прямой
касаются прямых
окружностей, проходящих через точку А(-1; 5) и
касающихся прямых
окружностей, касающихся прямых
окружностей, касающихся прямых
нижеприводимых уравнений определяют окружности?
Найти центр С и радиус R каждой из них:
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
расположена точка А(1; -2) относительно каждой из
следующих окружностей – внутри, вне или на
контуре:
уравнение линии центров двух окружностей,
заданных уравнениями:
уравнение диаметра окружности
к прямой
кратчайшее расстояние от точки до окружности в
каждом из следующих случаев:
координаты точек пересечения прямой
окружности
расположена прямая относительно окружности
(пересекает ли, касаетлся или проходит вне ее),
если прямая и окружность заданы следующими
уравнениями:
каких значениях углового коэффициента k прямая
окружность
окружности;
окружности.
при котором прямая
диаметра окружности
через середину хорды, отсекаемой на прямой
уравнение хорды окружности
в точке М(8,5; 3,5) пополам.
хорды окружности
А(1; 2) пополам.
пучка прямых
на которых окружность
длиною
в точках М1(x1, y1), М2(x2, y2). Доказать, что любая окружность,
проходящая через точки М1, М2, а также
прямая М1М2 могут быть определены уравнением
вида
уравнение окружности, проходящей через точку А(1;
-1) и точки пересечения окружностей
уравнение окружности, проходящей через начало
координат и точки пересечения окружностей
уравнение прямой, проходящей через точки
пересечения окружностей
расстояние от центра окружности
прямой, проходящей через точки пересечения
окружностей
общей хорды окружностей
лежит на прямой
уравнение этой окружности, если известно, что она
проходит через точки пересечения окружностей
уравнение касательной к окружности
точке А(-1; 2).
уравнение касательной к окружности
точке А(-5; 7).
вычислить расстояние d от точки М1 до этой прямой.
y1) лежит на окружности
уравнение касательной к этой окружности в точке
М1.
y1) лежит на окружности
уравнение касательной к этой окружности в точке
М1.
угол, образованный при пересечении прямой
и окружности называется угол между прямой и
касательной к окружности, проведенной к точке их
пересечения).
каким углом пересекаются окружности
окружностями называется угол между их
касательными в точке пересечения).
при котором окружности
прямым углом.
окружности
проведены касательной к окружности
их уравнения.
проведены касательные к окружности
их уравнения.
пучка прямых
которые касаются окружности
проведены касательные к окружности
угол, образованный этими касательными.
проведены касательные к окружности
уравнение хорды, соединяющий точки касания.
проведены касательные к окружности
расстояние d от точки С до хорды, соединяющей
точки касания.
проведены касательные к окружности
расстояние d от центра окружности до хорды,
соединяющей точки касания.
проведены касательные к окружности
длину d хорды, соединяющей точки касания.
касательной, проведенной из точки А(1; -2) к
окружности
уравнение касательных к окружности
прямой
уравнения касательных к окружности
к прямой
уравнение окружности в полярных координатах в
полярных координатах по данному радиусу R и
полярным координатам центра C(R,
уравнение окружности в полярных координатах по
данному радиусу R и полярным координатам центра
окружности:
полярные координаты центра и радиус каждой из
следующих окружностей:
уравнениями в полярных координатах. Составить их
уравнения в декартовых прямоугольных
координатах при условии, что полярная ось
совпадает с положительной полуосью Ох, а полюс –
с началом координат.
Окружности
заданы уравнениями в декартовых прямоугольных
координатах. Составить уравнения этих
окружностей в полярных координатах при условии,
что полярная ось совпадает с положительной
полуосью Ох, а полюс – с началом координат.
уравнение касательной к окружности
точке М1(R,
Содержание:
Окружность:
Определение: Кривой второго порядка называется линия, описываемая уравнением 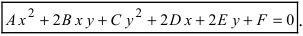
Замечание: Если коэффициенты 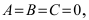
При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки 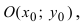 называемой центром окружности, на расстояние R, которое называется радиусом окружности.
называемой центром окружности, на расстояние R, которое называется радиусом окружности.
Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:
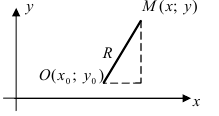
Рис. 27. Вывод уравнения окружности.
Из рисунка видно, что по теореме Пифагора 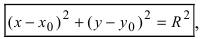 которое определяет уравнение окружности (Рис. 28):
которое определяет уравнение окружности (Рис. 28): 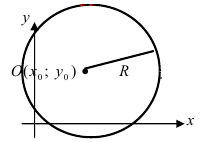
Рис. 28. Окружность. 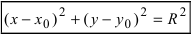
Если 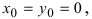 то уравнение принимает вид
то уравнение принимает вид 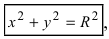 который называется каноническим уравнением окружности.
который называется каноническим уравнением окружности.
Пример:
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 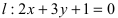 является касательной к окружности.
является касательной к окружности.
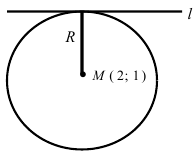
Решение:
Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.
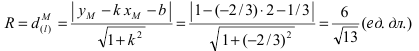
В уравнении окружности 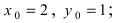 таким образом оно имеет вид:
таким образом оно имеет вид: 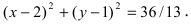
Пример:
Составить уравнение окружности, касающейся двух параллельных прямых 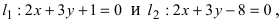 причем одной из них в т. А (1; 2).
причем одной из них в т. А (1; 2).
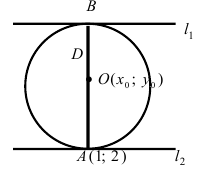
Решение:
Прежде всего определим, на какой из прямых 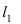 или
или 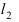 лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых
лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых 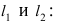
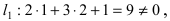 следовательно, точка A(1; 2) принадлежит линии
следовательно, точка A(1; 2) принадлежит линии 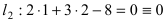 (в сокращенной форме это предложение пишут так:
(в сокращенной форме это предложение пишут так: 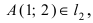 где значок
где значок 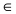 означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой
означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой 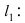
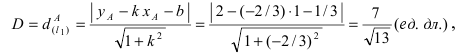
а радиус окружности 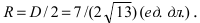 Найдём координаты центра окружности точки
Найдём координаты центра окружности точки 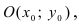 которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки
которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки 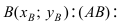 перейдем от общего уравнения прямой
перейдем от общего уравнения прямой 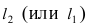 к уравнению прямой с угловым коэффициентом
к уравнению прямой с угловым коэффициентом 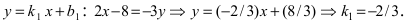 Так как прямая
Так как прямая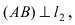 то её угловой коэффициент
то её угловой коэффициент 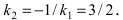 Прямая (АВ) проходит через известную точку A(1;2), следовательно,
Прямая (АВ) проходит через известную точку A(1;2), следовательно, 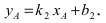 Отсюда находим
Отсюда находим 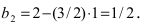 Таким образом,уравнение прямой (АВ):
Таким образом,уравнение прямой (АВ):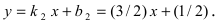
Найдем координаты точки B, которая является пересечением прямых 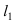 и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых
и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых 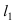 и (АВ): (В):
и (АВ): (В): 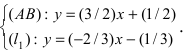 Подставим выражение для переменной у из второго у равнения в первое, получим
Подставим выражение для переменной у из второго у равнения в первое, получим 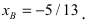 Подставив это значение во второе уравнение системы, найдем
Подставив это значение во второе уравнение системы, найдем 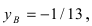 т.е.
т.е. 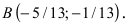
Для вычисления координат точки О применим формулы деления отрезка пополам (О): 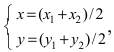 в этой формуле
в этой формуле 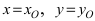 (координаты точки О),
(координаты точки О), 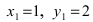 (координаты точки А),
(координаты точки А), 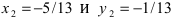 (координаты точки В), следовательно,
(координаты точки В), следовательно, 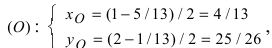 т.е. координаты точки О
т.е. координаты точки О 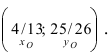
Таким образом, уравнение искомой окружности имеет вид: 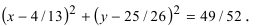
Окружность в высшей математике
Рассмотрим уравнение

которое получается из уравнения (I), если положить 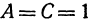 ,
, 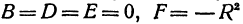 .
.
Если в формулу, выражающую расстояние между двумя точками, подставить 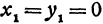 ,
, 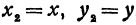 , то получим
, то получим 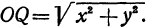 Из уравнения (1) находим, что
Из уравнения (1) находим, что 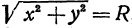 , т. е.
, т. е. 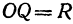 . Это значит, что все точки
. Это значит, что все точки 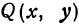 , координаты которых удовлетворяют уравнению (1), находятся на расстоянии
, координаты которых удовлетворяют уравнению (1), находятся на расстоянии 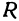 от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса
от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса  с центром в начале координат. Аналогично получаем, что уравнение
с центром в начале координат. Аналогично получаем, что уравнение 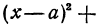
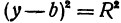 определяет окружность радиуса
определяет окружность радиуса  с центром в точке
с центром в точке 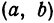 .
.
Пример:
Найдем уравнение окружности с центром в точке  и радиусом, равным 10.
и радиусом, равным 10.
Решение:
Полагая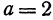 ,
, 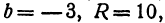 получим
получим 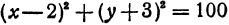 .
.
Разрешим это уравнение относительно 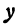 , будем иметь
, будем иметь
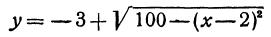
и
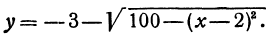
Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.
Центральный угол. Градусная мера дуги
Дуга окружности. Если отметить на окружности точки  и
и  , то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка
, то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка 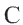 является какой-либо точкой дуги
является какой-либо точкой дуги 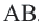 , то
, то 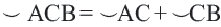 . Если точки
. Если точки  и
и  являются концами диаметра, го каждая дуга является полуокружностью.
являются концами диаметра, го каждая дуга является полуокружностью.
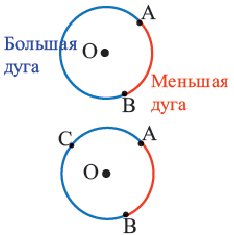
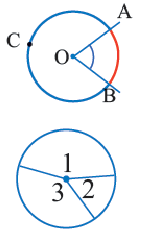
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла: 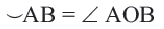
Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна 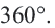
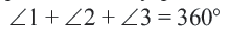
Дуги окружности и их величины

Пример: 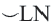 минорная дуга:
минорная дуга: 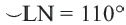
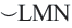 мажорная дуга:
мажорная дуга: 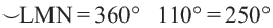
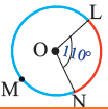
Конгруэнтные дуги
В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.
Если 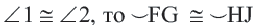
Если 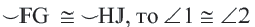
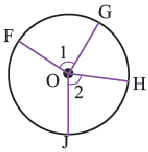
Длина дуги
Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.
Длина дуги в 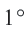 равна
равна 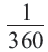 части длины окружности.
части длины окружности.
Длина дуги, соответствующей центральному углу с градусной мерой 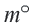 , составляет
, составляет 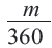 части длины окружности:
части длины окружности: 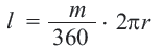
Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)
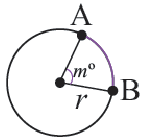
Пример №1
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу 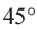 .
.
Решение:
Так как центральный угол 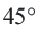 составляет
составляет 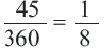 часть полного угла, то длина искомой дуги:
часть полного угла, то длина искомой дуги: 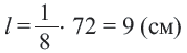
Пример №2
Найдите длину дуги, соответствующей центральному углу 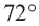 в окружности радиусом 15 см.
в окружности радиусом 15 см.
Решение: подставляя значения 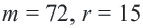 в формулу длины дуги находим:
в формулу длины дуги находим: 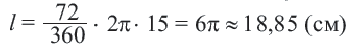
Окружность и хорда
Теорема о конгруэнтных хордах
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.
Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.
1)Если 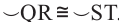 , то
, то 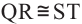
2)Если 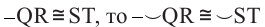
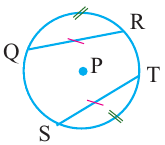
Доказательство теоремы 1:
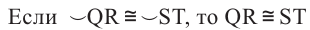

Теорема о серединном перпендикуляре хорд
Теорема 2.
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.
Если 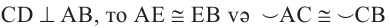
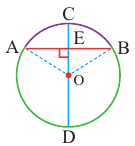
Доказательство теоремы 2.
Дано:  – центральный угол,
– центральный угол, 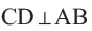
Докажите: 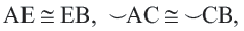
Начертите радиусы 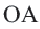 и
и 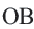 окружности.
окружности.
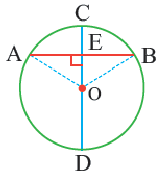
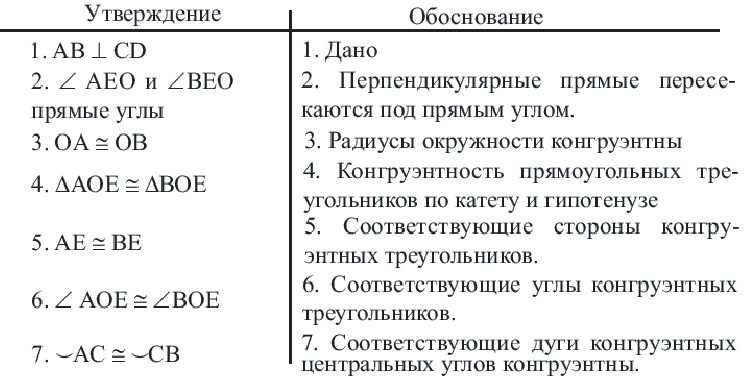
Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.
Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если 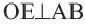 , то
, то 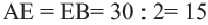 . Из
. Из 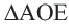 по теореме Пифагора имеем:
по теореме Пифагора имеем: 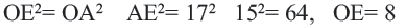
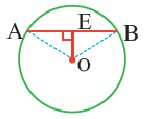
Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности
Теорема 3.
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.
Если 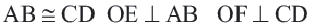 , то
, то 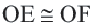
Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.
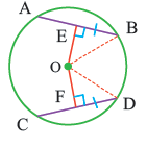
Доказательство теоремы 3
Дано: Окружность с центром 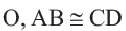
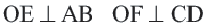
Докажите: 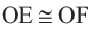
Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам.  и
и  – серединные перпендикуляры конгруэнтных хорд
– серединные перпендикуляры конгруэнтных хорд 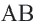 и
и 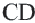 .
.  , так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности
, так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности 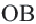 и
и 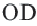 :
: 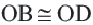 . Прямоугольные треугольники,
. Прямоугольные треугольники, 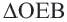 и
и 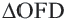 конгруэнтны (по катету и гипотенузе). Так как
конгруэнтны (по катету и гипотенузе). Так как  и
и  являются соответствующими сторонами данных треугольников, то они конгруэнтны:
являются соответствующими сторонами данных треугольников, то они конгруэнтны: 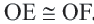 . Теорема доказана.
. Теорема доказана.
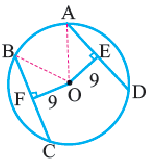
Задача. Хорды  и
и  находятся на одинаковом расстоянии от центра окружности.
находятся на одинаковом расстоянии от центра окружности. 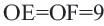 . Если радиус окружности равен 41 единице, то найдите
. Если радиус окружности равен 41 единице, то найдите 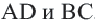 .
.
Решение: Так как хорды  и
и  находятся на одинаковом расстоянии от центра, то они конгруэнтны:
находятся на одинаковом расстоянии от центра, то они конгруэнтны: 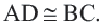
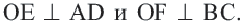 Соединим точки
Соединим точки 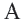 и
и 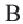 с точкой
с точкой 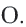 В прямоугольном треугольнике
В прямоугольном треугольнике 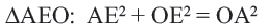
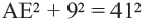 ;
; 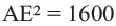 ;
; 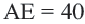 ;
; 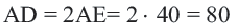
Так как 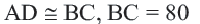
Угол, вписанный в окружность
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.
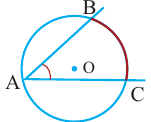
 является углом вписанным в окружность с центром
является углом вписанным в окружность с центром  , а
, а 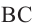 дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
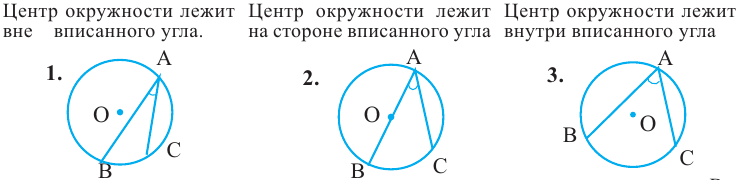
Угол, вписанный в окружность:
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается. 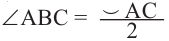
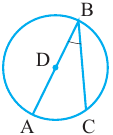
Доказательство (текстовое): 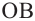 и
и 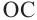 радиусы окружности и
радиусы окружности и 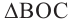 равнобедренный треугольник. Значит,
равнобедренный треугольник. Значит, 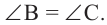 Так как
Так как 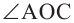 является внешним углом
является внешним углом 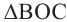 ,
, 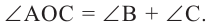 Если примем, что
Если примем, что 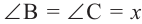 , то
, то 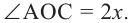 Так как градусные меры центрального угла и опирающейся на него дуги равны, то
Так как градусные меры центрального угла и опирающейся на него дуги равны, то 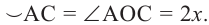 Следовательно,
Следовательно, 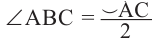 .
.
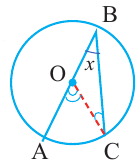
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.
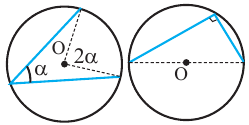
Конгруэнтные углы, вписанные в окружность
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. 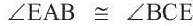 ,
, 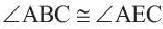 .
.
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если 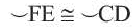 , то
, то 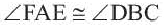 .
.
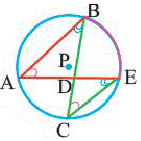

Касательная к окружности
Касательная. Признак касательной
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
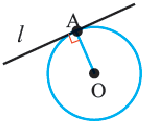
Прямая 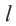 является касательной к окружности. Значит,
является касательной к окружности. Значит, 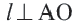 Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.

Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.
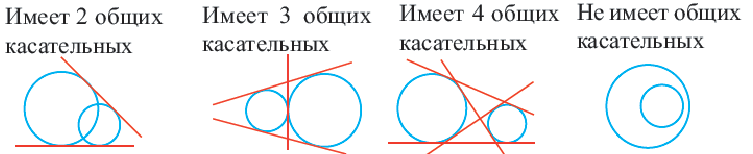
Доказательство теоремы 1. Если прямая  – касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая
– касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая  не перпендикулярна радиусу
не перпендикулярна радиусу 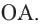 Проведем
Проведем 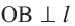 и на прямой
и на прямой  выделим отрезок
выделим отрезок 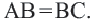 Тогда
Тогда 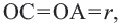 так как
так как 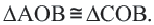 Значит, точка
Значит, точка 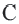 также находится на окружности. То есть прямая
также находится на окружности. То есть прямая  имеет с окружностью две общие точки, что противоречит условию. Значит,
имеет с окружностью две общие точки, что противоречит условию. Значит, 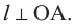
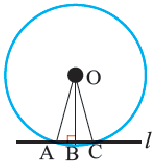
Свойства касательных, проведенных к окружности из одной точки
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.
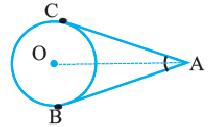
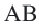 и
и 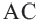 касательные, проведенные из точки
касательные, проведенные из точки 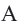 к окружности с центром
к окружности с центром 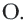
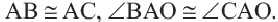
Углы, образованные секущими и касательными
Прямая, имеющая две общие точки с окружностью, называется секущей окружности.
Углы между двумя секущими
Вершина угла находится внутри окружности
Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному. 
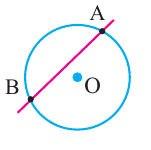
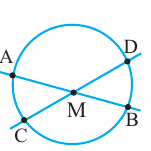
Углы между касательной и секущей
Вершина угла находится на окружности
Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.
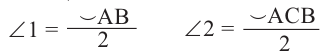
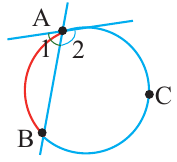
Углы, образованные касательной и секущей
Вершина угла находится вне окружности
Теорема 1.
Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.
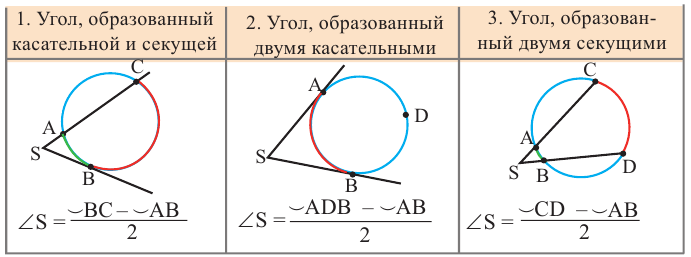
Отрезки секущих и касательных
Длина отрезков, секущих окружность
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.
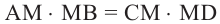
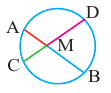
Теорема 2. Если из точки  провести две прямые, пересекающие окружность соответственно в точках
провести две прямые, пересекающие окружность соответственно в точках  и
и 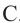 ,
, 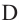 и
и 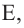 то верно равенство
то верно равенство 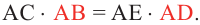
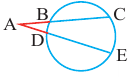
Теорема 3. Если из точки 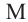 проведены прямая, которая пересекает окружность в точках
проведены прямая, которая пересекает окружность в точках  и
и  и касательная к окружности в точке
и касательная к окружности в точке 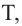 то верно равенство:
то верно равенство: 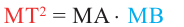
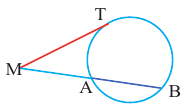
Уравнение окружности
Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом  и с центром в начале координат. Расстояние между центром окружности
и с центром в начале координат. Расстояние между центром окружности 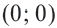 и ее любой точкой
и ее любой точкой 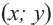 равно радиусу
равно радиусу  окружности.
окружности.
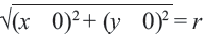 Расстояние между двумя точками
Расстояние между двумя точками
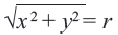 Упрощение
Упрощение
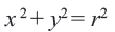 Возведение обеих частей в квадрат
Возведение обеих частей в квадрат
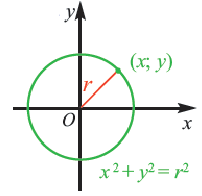
Уравнение окружности с центром в начале координат и радиусом 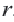 :
: 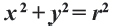
Например, уравнение окружности с центром в начале координат 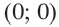 и радиусом 2 имеет вид:
и радиусом 2 имеет вид: 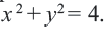
По формуле расстояния между центром окружности 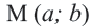 и точки
и точки 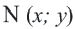 на окружности радиуса
на окружности радиуса 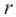 имеем
имеем 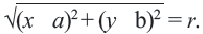 Возведя в квадрат обе части, получаем уравнение окружности с центром в точке
Возведя в квадрат обе части, получаем уравнение окружности с центром в точке 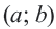 и радиусом
и радиусом 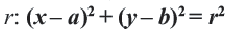
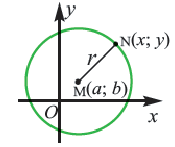
Например, уравнение окружности с центром в точке 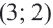 и радиусом 4 имеет вид:
и радиусом 4 имеет вид: 
Пример №3
Постройте на координатной плоскости окружность, заданную уравнением 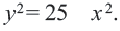
Решение: Напишем уравнение в виде 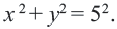 Как видно,
Как видно, 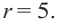
Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 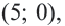
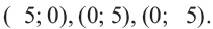 Проведем окружность через эти точки.
Проведем окружность через эти точки.
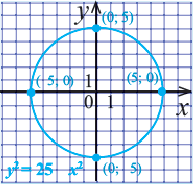
Пример №4
Точка 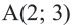 находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
Решение: Записав координаты точки 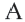 в уравнении
в уравнении 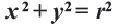 , получим:
, получим: 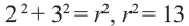 Уравнение этой окружности:
Уравнение этой окружности: 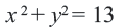
Пример №5
Найдем центр и радиус окружности, заданной уравнением 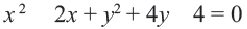
Решение: 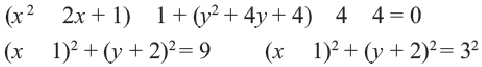
Центр окружности точка 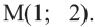 Радиус
Радиус 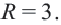
Пример №6
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 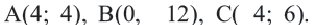 На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 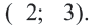 Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности,
Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности, 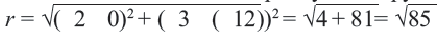
Уравнение окружности: 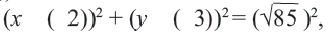
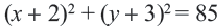
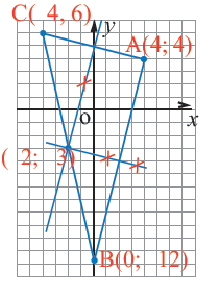
Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.
Координаты точек, находящихся на окружности, и тригонометрические отношения
Если точка 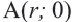 при повороте радиуса
при повороте радиуса 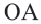 вокруг точки
вокруг точки 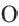 против движения часовой стрелки на угол
против движения часовой стрелки на угол 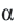 преобразуется в точку
преобразуется в точку 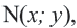 то
то 
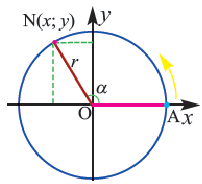
Для координат точки 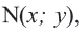 соответствующей углу поворота
соответствующей углу поворота  на окружности, верны формулы
на окружности, верны формулы 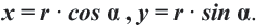 В этих формулах
В этих формулах  – угол, отсчитываемый от положительной оси
– угол, отсчитываемый от положительной оси 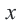 против движения часовой стрелки. Если точка
против движения часовой стрелки. Если точка 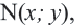 не находится на оси ординат, то
не находится на оси ординат, то 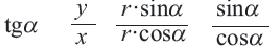 .
.
Синусы смежных углов равны, а косинусы взаимно противоположны.

Из этих формул при 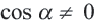 почленным делением получаем:
почленным делением получаем:
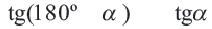
С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.
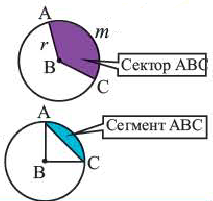
Сектор и сегмент
Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.
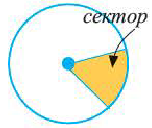
Например, часть круга, соответствующая центральному углу 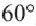 , составляет
, составляет 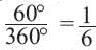 часть всего круга. Так как площадь круга
часть всего круга. Так как площадь круга 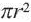 , то площадь этого сектора будет
, то площадь этого сектора будет  Сегмент часть круга, ограниченная хордой и соответствующей дугой.
Сегмент часть круга, ограниченная хордой и соответствующей дугой.
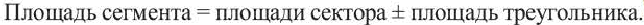
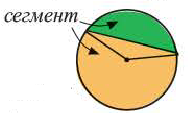
Площадь сектора
Площадь сектора: 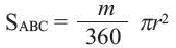
Площадь сегмента: 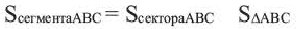
Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь 
- Эллипс
- Гипербола
- Парабола
- Многогранник
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
Уравнение окружности и прямой — как между собой связаны
Определение
Окружностью называют замкнутую плоскую кривую, состоящую из всех точек на плоскости, которые равноудалены от заданной точки, лежащей в аналогичной плоскости, что и кривая. Данная точка является центром окружности.
Записать уравнение окружности можно, используя известные свойства геометрической фигуры:
- Любые точки окружности равноудалены от ее центра. Расстояние является радиусом.
- Зная координаты точек, можно записать формулу для определения расстояния между ними: (|AB|=sqrt{(x_{A}−x_{B})^{2}+(y_{A}−y_{B})^{2}}). Таким образом, квадрат расстояния равен (AB^{2}=(x_{A}−x_{B})^{2}+(y_{A}−y_{B})).
Уравнение для описания окружности, которая имеет радиус R, а ее центр совпадает с точкой (O(x_0;y_0)), имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
((x-x_0)^2+(y-y_0)^2 = R^2)
В том случае, когда центр окружности лежит в точке начала координат, уравнение окружности приобретает упрощенную форму:
(x^2+y^2=R^2)
Предположим, что существует уравнение некой окружности:
((x-1)^2+(y+2)^2=4)
Центром данной геометрической фигуры является точка C(1;-2). Радиус окружности равен R=2.
Определение
Прямая представляет собой линию, которая не имеет начала и не имеет конца, и при этом не искривляется.
Каждую прямую на плоскости можно представить в виде уравнения прямой первой степени. Формула имеет следующий вид:
Ax + By + C = 0
В данном случае А и В не могут одновременно принимать нулевые значения.
С учетом углового коэффициента общее уравнение прямой при значении b, не равном нулю, записывают следующим образом:
y = kx + b
Здесь k является угловым коэффициентом, который можно посчитать, как тангенс угла между рассматриваемой прямой и положительным направлением оси ОХ.
Рассмотрим случай, когда прямая пересекает оси ОХ и ОУ в точках, имеющих следующие координаты:
((a; 0) и (0; b))
Найти рассматриваемую прямую можно с помощью уравнения прямой в отрезках:
(frac{x}{a}+frac{y}{b}=1)
Предположим, что прямая пересекает пару точек (A(x_1;y_1)) и (B(x_2; y_2),) удовлетворяющих данным условиям:
(x_1 ≠ x_2 и y_1 ≠ y_2)
В таком случае уравнение прямой рассчитывают по формуле:
(frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1})
Например, существует некая прямая в прямоугольной системе координат. Данная прямая пересекает пару точек:
(M_1(1;1)) и (M_2(4;2))
Уравнение прямой, проходящей через две обозначенные точки, имеет вид:
(frac{x-1}{4-1}=frac{y-1}{2-1} Leftrightarrow frac{x-1}3=frac{y-1}1)
Преобразуем полученное уравнение:
(frac{x-1}3=frac{y-1}1 Leftrightarrow 1cdot (x-1)=3cdot(y-1) Leftrightarrow x-3y+2=0)
Как составить уравнение прямой, проходящей через центр окружности
Применяя записанные ранее уравнения для прямой и окружности, можно найти уравнение прямой, которая проходит через центр окружности:
(x^2+y^2-6x-8y+16=0)
(x^2+y^2+10x+4y+13=0)
В первую очередь следует рассчитать радиусы и определить координаты центров окружностей:
(x^2 + y^2 – 6x – 8y + 16 = 0)
((x^2 – 6x + 9) + (y^2 – 8y + 16) = 9)
((x – 3)^2 + (y – 4)^2 = 3^2)
(r1 = 3)
(O_1(3;4))
(x^2 + y^2 + 10x + 4y + 13 = 0)
((x^2 + 10x + 25) + (y^2 + 4y + 4) = 16)
((x + 5)^2 + (y + 2)^2 = 4^2)
(r2 = 4)
(O_2(-5;-2))
Уравнение прямой, проходящей через точки (O_1(3;4)) и (O_2(-5;-2)), можно записать следующим образом:
(frac{(x – 3)}{(3 + 5)}=frac{(y – 4)}{(4 + 2)})
(frac{(x – 3)}{8}=frac{(y – 4)}{6})
(3(x – 3) = 4(y – 4))
(3x – 9 = 4y – 16)
(4y = 3x + 7)
(y = frac{3x}{4}+frac{7}{4})
В результате уравнение прямой принимает такой вид:
(y = frac{3x}{4}+frac{7}{4})
Решение задач по теме, примеры
Задача 1
Требуется определить, где находится центр окружности, и чему равен ее радиус. Уравнение окружности:
(x^{2}+(y-3)^{2}=49)
Необходимо представить график окружности в осях абсцисс и ординат.
Решение
Каноническое уравнение окружности имеет вид:
((x-h)^{2}+(y-k)^{2}=r^{2})
В данном случае, центр соответствует О:(h, k), а радиус окружности равен r.
По условиям задачи: (x^{2}+(y-3)^{2}=49)
Таким образом:
(O:(0, 3)qquad r=7)
График:
Ответ: центр совпадает с точкой, имеющей координаты ((0, 3)qquad r=7)
Задача 2
Нужно определить, в какой точке расположен центр окружности, и чему равен ее радиус. Уравнение окружности:
((x+2)^{2}+y^{2}=36)
Решение
В первую очередь следует записать каноническое уравнение окружности:
((x-h)^{2}+(y-k)^{2}=r^{2})
В данном случае, центр окружности совпадает с точкой, имеющей координаты (h, k), а ее радиус равен r.
Согласно условиям задачи:
((x+2)^{2}+y^{2}=36)
Таким образом:
(O:(-2, 0)qquad r=6)
График:
Ответ: центр окружности совпадает с точкой (-2, 0), а ее радиус равен 6.
Задача 3
Требуется преобразовать уравнение в сумму квадратов для расчета радиуса и определения центра окружности:
(2x^{2}+2y^{2}+4x+16y+1=0)
Решение
(2x^{2}+2y^{2}+4x+16y+1=0Longrightarrow x^{2}+y^{2}+2x+8y+frac{1}{2}=0)
В таком случае:
(left(x+1right)^{2}+left( y+4right)^{2}-1-16+frac{1}{2}=0Longrightarrow left(x+1right) ^{2}+left(y+4right) ^{2}=frac{33}{2})
В результате расчетов получим:
центр находится в (-1,-4)
радиус равен (sqrt{frac{33}{2}})
Ответ: (O (-1,-4) и r=sqrt{frac{33}{2}})
Задача 4
Центр окружности совпадает с точкой (4,-5). Необходимо записать уравнение данной окружности, учитывая, что она проходит через точку с координатами (7,-3).
Решение
Каноническое уравнение окружности:
((x-h)^{2}+(y-k)^{2}=r^{2})
Центр находится в точке:
(4,-5)
Радиус соответствует r.
Таким образом:
((x-4)^{2}+(y+5)^{2}=r^{2}Longrightarrow r=sqrt{(x-4)^{2}+(y+5)^{2}})
Учитывая, что окружность проходит через точку (7,-3), запишем:
(r=sqrt{left(3right)^{2}+left(2right)^{2}}=sqrt{13})
Ответ: уравнение окружности имеет вид ((x-4)^{2}+(y+5)^{2}=13)
Задача 5
Необходимо записать уравнение окружности, центр которой соответствует точке O(2,-1), касающейся прямой r:y=x+2. Требуется начертить график.
Решение
Зная, что радиус r является расстоянием, на которое удалены точка O:(h, k) и прямая y-x-2=0, запишем:
(O:(2,-1))
(r=d(O,L)=frac{leftvert -2-1-2rightvert }{sqrt{1^{2}+left( -1right) ^{2}}}=frac{5}{sqrt{2}})
Получим уравнение окружности:
((x-h)^{2}+(y-k)^{2}=r^{2}Longrightarrow (x-2)^{2}+(y+1)^{2}=frac{25}{2})
График:
Ответ: ((x-2)^{2}+(y+1)^{2}=frac{9}{5})
Задача 6
Требуется записать уравнение, описывающее прямую с угловым коэффициентом (k= frac{3}{2}). Искомая прямая пересекает точку А (3;2).
Решение
В первую очередь следует записать стандартную формулу:
(y-y_{0}=k(x-x_{0}))
Применительно к условиям задачи, получим:
(y-(-2)= frac{3}{2} (x-3))
(y+2= frac{3}{2}х-frac{9}{2})
(y= frac{3}{2}х-frac{13}{2})
Ответ: (y= frac{3}{2}х-frac{13}{2})
![]()
![]()
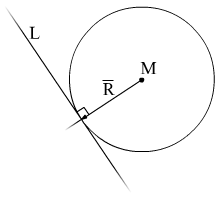
Для построения
окружности необходимо знать центр
окружности и радиус.
Центр окружности
нам задан, а радиус окружности – это
расстояние от центра к касательной.
Найдем расстояние
от точки M
до прямой L.
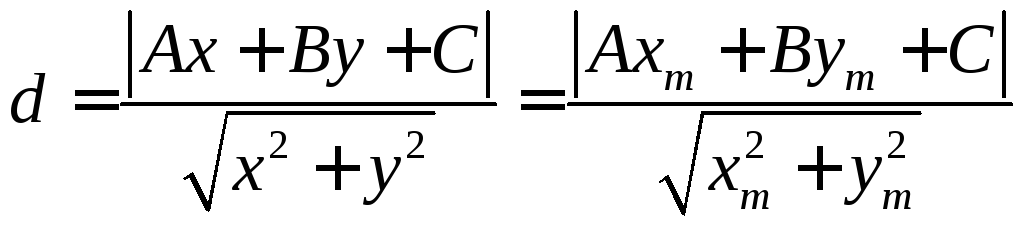 ,
,
где
A = 2, B = 3, C = 1

Составим уравнение
окружности
![]()
![]()
Ответ:
![]()
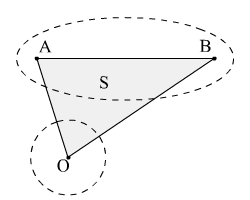
10.2. Найти площадь треугольника, две вершины которого находятся в фокусах данного эллипса, а третья – в центре окружности.
![]()
![]()
Для нахождения
площади треугольника необходимо найти
его три точки. Эти точки можно получить,
если привести уравнения кривых к
каноническому виду.
По одному только
виду трудно сразу сказать, к какому типу
кривой принадлежит уравнение. Сначала
его необходимо привести к каноническому
виду.
![]()
![]() –уравнение
–уравнение
окружности
![]()
![]() –одну точку нашли
–одну точку нашли
Приведём к
каноническому виду уравнение
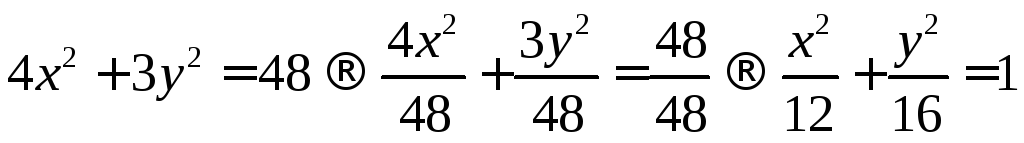
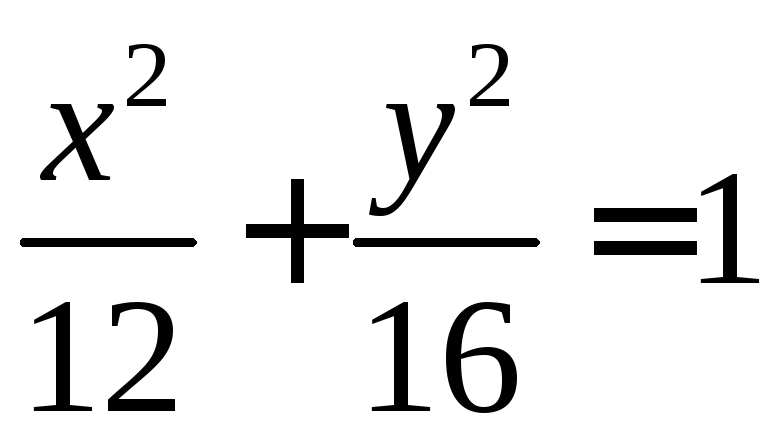 –уравнение эллипса
–уравнение эллипса
![]()
Найдём фокусное
расстояние
![]()
![]()
Так как параметр
![]() ,
,
то эллипс расположен вдоль оси OY:
![]()
Мы получили три
точки треугольника, найдём его площадь
![]() ,
,
![]() ,
,![]() .
.
![]()
![]()
![]()
Ответ: 10.
Примечание.
Всегда нужно смотреть на соотношение
коэффициентов a и b. Если a > b, то эллипс
(гипербола), вытянута по горизонтали и
фокусы, соответственно, на горизонтальной
прямой. Если a < b, то вытянута по
вертикали.
10.3. Найти уравнения гиперболы, вершины которой находятся в фокусах, а фокусы – в вершинах данного эллипса.
![]()
Приведём уравнение
к каноническому виду
![]()
![]() ,
,
![]() .
.
Найдём фокусы
эллипса
![]()
![]()
Теперь рассмотрим
для гиперболы
![]() ,
, ![]()
Найдём параметр
b
гиперболы
![]()
Составим уравнение
гиперболы
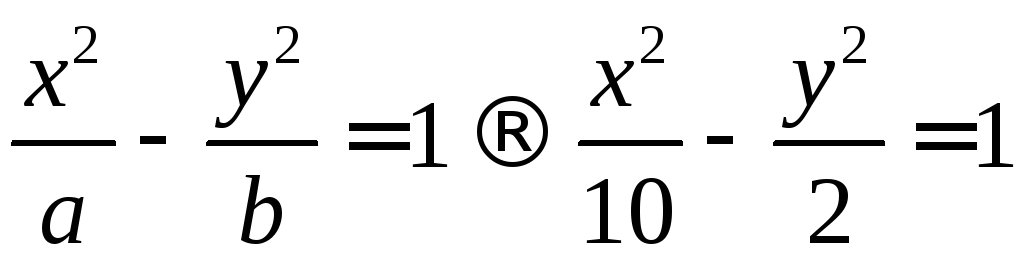
Ответ:
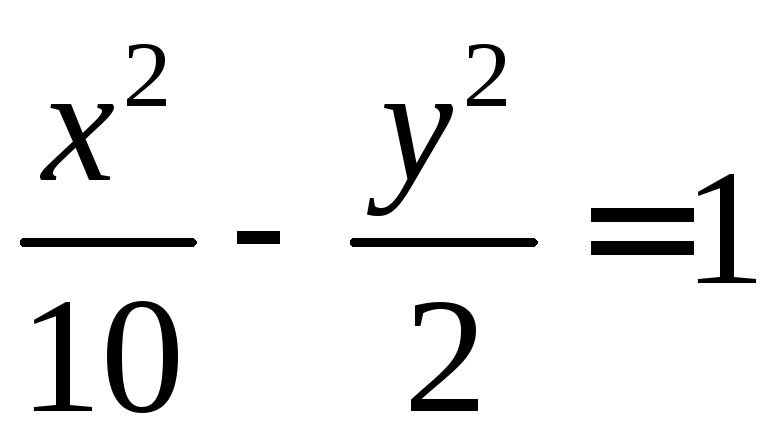
10.4. Составить
каноническое уравнение параболы, фокус
которой лежит на оси OX слева от начала
координат, а параметр P равен расстоянию
от фокуса данной гиперболы до асимптоты.
![]()
Приведём к
каноническому виду уравнение гиперболы
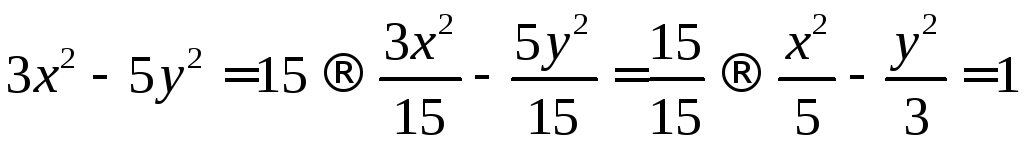
Получим:
![]()
![]()
![]()
Гипербола имеет
две асимптоты, но расстояние от любого
фокуса до любой из них одинаково.
Асимптота проходит
через начало координат и точку (a,
b)
Составим уравнение
прямой
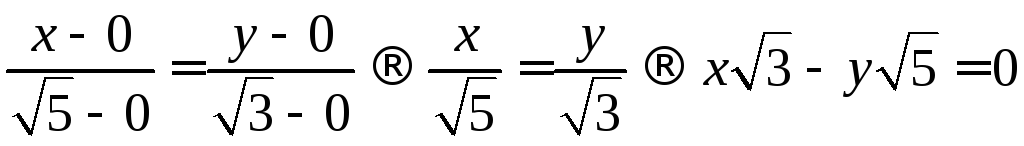
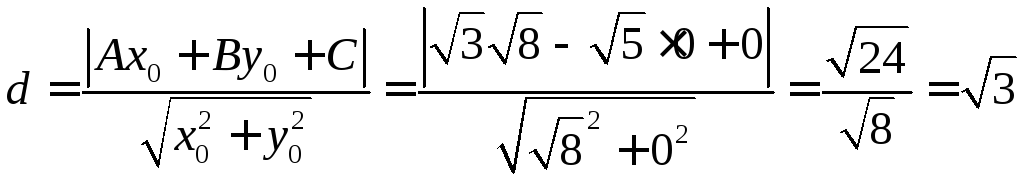
![]()
Составим уравнение
параболы, следует также учесть что, по
заданию фокус лежит на оси ОХ, слева от
начала координат.
![]()
Ответ:
![]() .
.
10.5. Составить
каноническое уравнение параболы, фокусы
которой совпадают с фокусами данного
эллипса. Написать уравнение директрисы.
![]()

Приведём к
каноническому виду
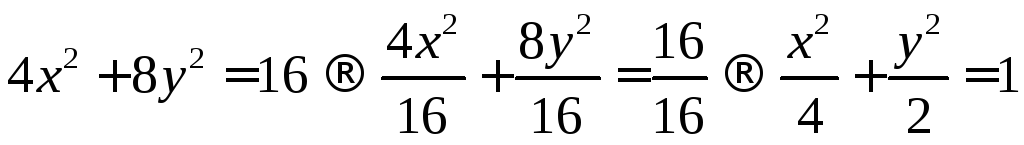
![]()
![]()
Фокус параболы
находится
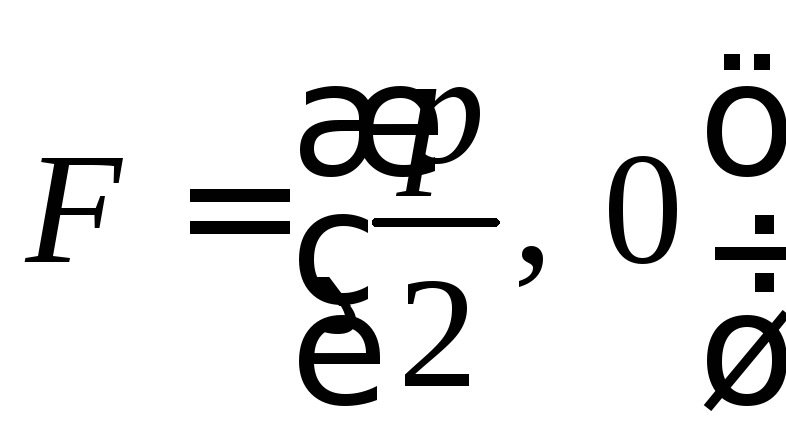
Отсюда находим
параметр P.
![]()
Составим уравнение
параболы
![]()
Составим уравнение
директрисы. Директриса – это прямая, в
данном случае вертикальная.
Уравнение директрисы
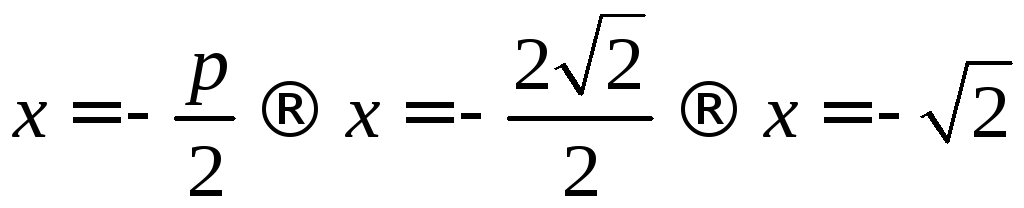
Ответ:
![]() ,
,![]()
-
Полярная система координат
11.1. Построить
в полярной системе координат кривую.
Написать ее уравнение в декартовых
координатах.
![]()
Составим таблицу
соответствий и построим график данной
функции
|
|
0 |
15 |
30 |
45 |
60 |
75 |
90 |
105 |
120 |
135 |
150 |
165 |
180 |
|
|
1 |
0.5 |
0.13 |
0 |
0.13 |
0.5 |
1 |
1.5 |
1.87 |
2 |
1.87 |
1.5 |
1 |
Э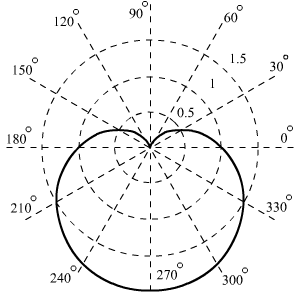 то
то
график кардиоиды.
Напишем уравнение
функции в декартовых координатах.
Если полюс полярной
системы координат находится в начале
прямоугольной системы координат, а
положительная ось ОХ совпадает с полярной
осью, а ось ОУ перпендикулярна ОХ, то
зависимость между координатами следующая:
![]()
![]()
![]() –в заданной
–в заданной
функции содержится синус, который можем
выразить из формулы
![]() и подставить в исходную функцию:
и подставить в исходную функцию:![]() .
.
Заменим![]() и
и
получим функцию, заданную в полярной
системе координат в неявном виде.
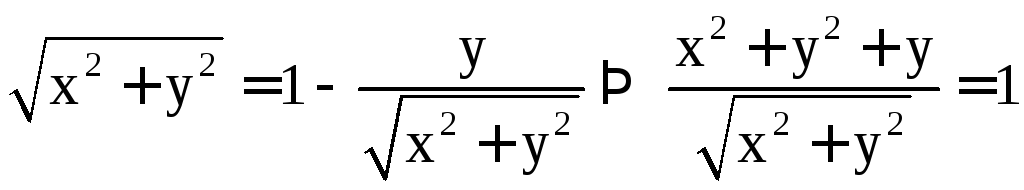
Ответ:
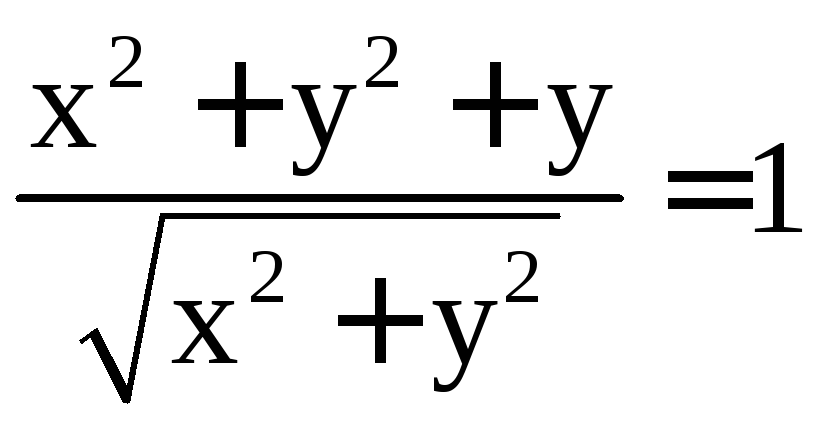 .
.
0
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2016959.94 Кб5PT.pdf
- #
