Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm<frac1x>) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график – ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm <(x-2)^2+(y-1)^2=9>$$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<7>=-frac<2> + 2 > ) – это прямая
б) xy + 4 = 0
Выразим y из уравнения: ( mathrm> ) – это гипербола
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm=2> )
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<5>> ) – это парабола
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<5>=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) (mathrm<frac<|x-1|><2>+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.
Как задать окружность на графике
Как построить окружность?
Как построить окружность?
Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соединяющей точку окружности с ее центром.
Чтобы построить окружность необходимо знать уравнение окружности:
(х – а) 2 + (у – b) 2 = R 2
Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:
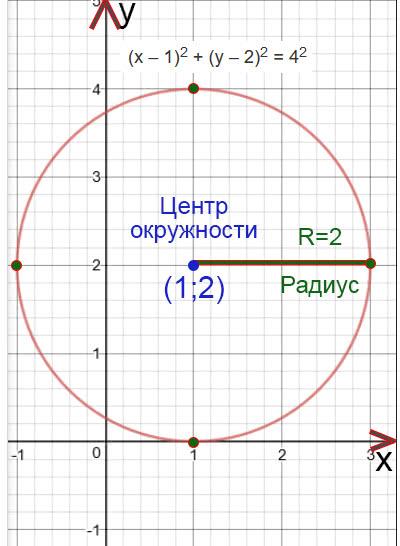
Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2
Найдем центр окружности:
х – 1=0
x=1
Центр окружности будет находится в точке (1;2)
Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2
Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.
Пример №2:
х 2 + (у + 1) 2 =1
Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2
Найдем центр окружности:
х=0
Центр окружности будет находится в точке (0;–1)
Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1
Построим окружность.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm ) – гипербола.
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm ) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm $$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm =-frac + 2 > ) – это прямая
б) xy + 4 = 0
Выразим y из уравнения: ( mathrm > ) – это гипербола
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm =2> )
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm > ) – это парабола
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm =-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) (mathrm +2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.
Построение графиков функций
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
при х ≠ -1.
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
Как построить окружность?
Как построить окружность?
Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соединяющей точку окружности с ее центром.
Чтобы построить окружность необходимо знать уравнение окружности:
(х – а) 2 + (у – b) 2 = R 2
Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:
Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2
Найдем центр окружности:
х – 1=0
x=1
Центр окружности будет находится в точке (1;2)
Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2
Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.
Пример №2:
х 2 + (у + 1) 2 =1
Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2
Найдем центр окружности:
х=0
Центр окружности будет находится в точке (0;–1)
Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1
Построим окружность.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/kak-zadat-okruzhnost-na-grafike
http://tutomath.ru/uroki/kak-postroit-okruzhnost.html
[/spoiler]
Download Article
Download Article
The equation of a circle gives you the center coordinates and radius, allowing you to represent all of the literally infinite points around the boundary of the circle. But how exactly do you write it? Read on to learn how to write the equation of a circle in standard form, as well as how to convert general form to standard form. Once you’ve got that down, you can try your hand at some sample problems and check your answers. Let’s get started!
Things You Should Know
-
1
-
2
The general form of the equation of a circle is
. This equation technically has all the same information the standard form has, it’s just expressed differently. Let’s break it down:[2]
Advertisement
-
1
-
2
Plug in values for the radius and center coordinates to complete a standard equation. This is probably the simplest type of problem you’ll have dealing with the equation of a circle. Just place the values where they go in the the standard form
.[4]
-
3
Advertisement
-
1
-
2
Move the constant to the other side of the equation. Since the number is moving to the other side of the equation, the sign in front of it changes. So if it was negative on the left side, it’ll be positive on the right side (and vice versa).[7]
-
3
-
4
-
5
-
6
Add the numbers to both sides of the equation. Keeping your groups together on the left side of the equation, add your third number to each parenthetical expression. Then, add each of those numbers to the right side of the equation to maintain equality.[11]
-
7
Solve the
and
groups. Now you have what you may recognize as a basic trinomial in each parenthesis. Use the quadratic formula to find the number you need for each parenthetical expression in the standard equation of a circle.[12]
-
8
Simplify the right side of the equation. Almost there! Add the numbers on the right side, then square them. The equation you’re left with will be the standard form for the equation of a circle. From here, you can easily determine the center points and radius if you need to graph the circle.[13]
Advertisement
-
1
Write the equation of the circle with center
and radius
.[14]
- Hint: pay attention to the negative signs in front of the center coordinates.
-
2
Find the center coordinates of the circle with the equation
.[15]
- Hint: look at the signs in the parentheses and compare them to the standard form for the equation.
-
3
Find the center coordinates and radius for the circle
.[16]
- Hint: complete the square twice to convert general form to standard form. Don’t forget that anything you add on the left side you also have to add on the right side.
-
4
Is
the equation of a circle? Why or why not?[17]
- Hint: a circle can never have a negative radius.
Advertisement
-
1
-
2
The center coordinates are
. You’re given the equation of the circle
. Since the signs in the parentheses in the standard form are
, the
signs in this equation tell you that the center coordinates must be negative.[19]
-
3
-
4
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 1,175 times.
Did this article help you?
Каждое уравнение с
двумя переменными х и у определяет некоторое множество пар (х; у) значений
переменных, которые являются решениями этого уравнения, т. е. задаёт некоторое
отношение между значениями переменной х и значениями
переменной у. График отношения, заданного уравнением с двумя
переменными, или, короче, график уравнения с двумя переменными, есть, как
известно, множество точек плоскости, координаты которых служат решениями
уравнения. Мы знаем, что графиком уравнения вида ax + by = c,
где a ≠ 0 или b ≠ 0,
служит прямая линия, график уравнения вида
y = ax2 +
bx + c (a ≠ 0)
парабола, график
уравнения вида
xy = k
гипербола.
На рисунку
изображён график уравнения
х2 + 9у2
= 81.
Кривая такого вида
называется эллипсом.
Графиком уравнения
(x – a)2 +
(y – b)2 =
r2
является окружность на координатной плоскости хОу с центром в точке О’(a; b) и радиусом
r (r
> 0).
Уравнением фигуры
на плоскости в декартовых координатах
называется уравнение с двумя переменными
х и у, которые будут координатами любой точки фигуры. И наоборот:
любые два числа, которые будут решением этого уравнения, будут координатами некоторой
точки фигуры.
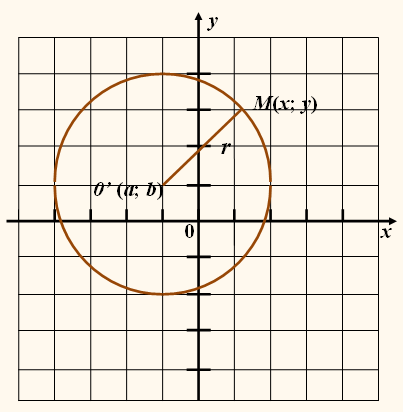
Составим уравнение окружности
с центром в точке А0(а; b) и радиусом R.
Возьмём произвольную
точку А(х; у) на окружности. Расстояние от неё до
центра А0 равно R. Квадрат расстояния от точки А до А0 равен:
(х – a)2
+ (у – b)2.
Таким образом, координаты х, у каждой точки А окружности будут корнями уравнения:
(х – a)2
+ (у – b)2 = R2.
Наоборот: любая
точка А, координаты которой будут решениями уравнения, принадлежат окружности, так как расстояние
от неё до точки А0 равно R. Отсюда вытекает, что это уравнение будет уравнением окружности
с центром А0 и радиусом
R.
Обратите внимание, что
когда центром окружности будет начало координат, то уравнение окружности имеет
вид:
х2 + у2 = R2.
ПРИМЕР:
Какая геометрическая фигура задано уравнением ?
х2 + у2
+ ах + bу + с = 0.
РЕШЕНИЕ:
видим, что искомая фигура – окружность с центром
ПРИМЕР:
Построить график уравнения:
х2 + у2
= 16.
Перепишем уравнение в виде
(х – 0)2 + (у – 0)2 = 42.
Графиком этого уравнения является окружность с центром в
точке О(0;
0) и
радиусом 4.
ПРИМЕР:
Построить график уравнения:
(х – 1)2 + (у – 2)2 = 9.
Перепишем уравнение в виде
(х – 1)2 + (у – 2)2 = 32.
Графиком этого уравнения является окружность с центром в
точке (1;
2) и
радиусом 3.
ПРИМЕР:
Построить график уравнения:
х2 + у2
+ 4х = 0.
Перепишем уравнение в виде
х2 +
4х + 4 + у2 = 4,
(х + 2)2 + у2
= 4,
(х – (–2))2 + (у – 0)2 = 22,
Графиком этого уравнения является окружность с центром в
точке (–2;
0) и
радиусом 2.
От графиков функций
необходимо отличать графики уравнений.
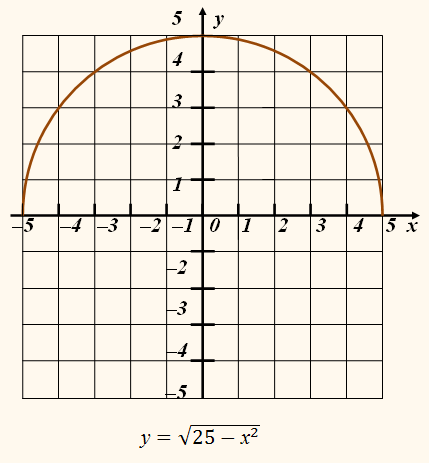
ПРИМЕР:
На координатной плоскости изображена окружность радиусом r = 5 с центром в начале координат. Уравнение этой окружности:
х2 + у2
= 25.
Можно сказать и так: графиком уравнения
х2 + у2
= 25
будет окружность, изображённая на рисунку.
А можно график уравнения
х2 + у2
= 25
считать графиком некоторой функции ? Нет. Если переменные х и у связаны соотношением
х2 + у2
= 25,
то одному значению
х = 3 соответствует два
разных значения переменной у: 4 и –4.
А соотношение между переменными х и у только тогда считается функцией, когда каждому
значению х из области определения соответствует одно
значение у.
График уравнения только тогда будет графиком некоторой функции, если каждая
прямая, параллельная оси у, пересекает
его не больше чем в одной точке.
ПРИМЕР:
Изображённые на рисунке полуокружности – графики функций
Их объединение – вся окружность – график не функции, а уравнения
у2 = 25 – х2, или
у2 +
х2 = 25.
Задания к уроку 27
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x2 + 2x – 1 – парабола, (mathrm{y=frac1x}) – гипербола.
Если записать такое выражение: x2(x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Все записанные выражения являются уравнениями с двумя переменными.
В общем случае их принято записывать в виде F(x; y) = 0.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm{frac1x}) – y = 0 – гипербола
F(x; y)=x2(x + y) + y – 1 = 0 – некоторая кривая (график – ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
F(–x; y) = 0
Симметричное отображение относительно оси OY
F(x; –y) = 0
Симметричное отображение относительно оси OX
F(–x; –y) = 0
Центральная симметрия относительно начала координат
F(x – a; y) = 0
a > 0
Параллельный перенос графика на a единиц вправо
F(x + a; y) = 0
a > 0
Параллельный перенос графика на a единиц влево
F(x; y – b) = 0
b > 0
Параллельный перенос графика на b единиц вниз
F(x; y + b) = 0
b > 0
Параллельный перенос графика на b единиц вверх
F(ax; y) = 0
a > 1
Сжатие графика к оси OY в a раз
F(ax; y) = 0
0 < a < 1
Растяжение графика от оси OY в $frac{1}{a}$ раз
F(x; by) = 0
b > 1
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 < b < 1
Растяжение графика от оси OX в (mathrm{frac{1}{b}}) раз
F(|x|; y) = 0
Зеркальное отображение в левой полуплоскости части графика begin{gather*} left{ begin{array}{ l } mathrm{F(x;y)=0} & \ mathrm{xgt y} & end{array}right. , end{gather*}расположенного в правой полуплоскости.
F(x; |y|) = 0
Зеркальное отображение в нижней полуплоскости части графика begin{gather*} left{ begin{array}{ l } mathrm{F(x;y)=0} & \ mathrm{ygt y} & end{array}right. , end{gather*}расположенного в верхней полуплоскости.
п.3. Уравнение окружности
Окружность с центром в точке O($x_0, y_0$) и радиусом R в прямоугольной системе координат задаётся уравнением: $$ mathrm{(x-x_0)^2+(y-y_0)^2=R^2} $$
Например:
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm{(x-2)^2+(y-1)^2=9} $$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm{y=frac{-2x+14}{7}=-frac{2}{x} + 2 } ) – это прямая
б) xy + 4 = 0
Выразим y из уравнения: ( mathrm{y=frac{-4}{x}} ) – это гипербола
в) ( x+ 2)2 + y2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm{R=sqrt{4}=2} )
г) x2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm{y=frac{-x^2+2}{5}} ) – это парабола
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm{y=frac{-2|x|+10}{5}=-frac25|x|+2} )
Строим график для ( mathrm{xgt 0: y=-frac25 x+2} ), а затем отражаем его относительно оси OY в левую полуплоскость.
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) (mathrm{frac{|x-1|}{2}+2|y-2|=4})
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x2 + y2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x2 + 4x + 4) + (y2 – 6y + 9) – 9 = 0
(x + 2)2 + (y – 3)2 = 32 – уравнение окружности с центром (–2; 3), радиусом 3.
б) (mathrm{x^2+y^2-x+8y+15frac14=0})
Выделим полные квадраты:
(mathrm{left(x^2-x+frac14right)+(y^2+8y+16)-1=0})
(mathrm{left(x-frac12right)^2+(y+4)^2=1}) – уравнение окружности с центром (mathrm{left(frac12; -4right)}), радиусом 1
Уравнение
x−a2+y−b2=r2
графически представляется окружностью с центром в точке ((a; b)) и радиусом (r).
Пример:
дано уравнение
x+12+y−32=4
. Выполнить его график.
Запишем уравнение в виде
x−−12+y−32=22
.
Изобразим окружность с центром в точке ((-1; 3)) и радиусом (2).