Как составить уравнение окружности по заданной точке - Сайт, где вы сможете решить свои вопросы

Написать уравнение окружности

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

Следовательно, уравнение данной окружности

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

получаем систему уравнений:

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

Приравняем правые части 2-го и 3-го уравнений:

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

Как составить уравнение окружности по одной точке

Написать уравнение окружности

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Следовательно, уравнение данной окружности

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

получаем систему уравнений:

Приравняем правые части 2-го и 3-го уравнений:

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Уравнения окружностей имеющих одну общую точку

Уравнение окружности.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

Отметим произвольную точку М(х; у) на этой окружности.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

§ 3. Уравнения окружности и прямой

При изучении алгебры мы строили графики некоторых функций в прямоугольной системе координат, например график функции у-х. Известно, что графиком этой функции является прямая, проходящая через точки О (0; 0) и А(1;1) (рис. 284). Координаты любой точки М (х; у), лежащей на прямой О А, удовлетворяют уравнению у = х (так как ММ₁ = ММ₂), а координаты любой точки, не лежащей на прямой ОА, этому уравнению не удовлетворяют. Говорят, что уравнение у = х является уравнением прямой О А. Введём теперь понятие уравнения произвольной линии.

Пусть на плоскости задана прямоугольная система координат Оху и дана некоторая линия L (рис. 285). Уравнение с двумя переменными х и у называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

При изучении линий методом координат возникают две задачи: 1) по геометрическим свойствам данной линии найти её уравнение; 2) обратная задача: по заданному уравнению линии исследовать её геометрические свойства. В следующем пункте мы рассмотрим первую из этих задач применительно к окружности. Вторая задача рассматривалась в курсе алгебры при построении графиков функций.

Уравнение окружности

Выведем уравнение окружности радиуса г с центром С в заданной прямоугольной системе координат. Пусть точка С имеет координаты (x₀; у₀) (рис. 286). Расстояние от произвольной точки М (х; у) до точки С вычисляется по формуле Если точка М лежит на данной окружности, то МС = r, МС 2 = r 2 , т. е. координаты точки М удовлетворяют уравнению

Если же точка М (х; у) не лежит на данной окружности, то МС 2 ≠ r 2 , и, значит, координаты точки М не удовлетворяют уравнению (1). Следовательно, в прямоугольной системе координат уравнение окружности радиуса r с центром в точке С (х₀; у₀) имеет вид:

(х — х₁) 2 + (у — у₀) 2 = r 2 .

В частности, уравнение окружности радиуса r с центром в начале координат имеет вид:

Найти уравнение окружности с центром в точке (-3; 4), проходящей через начало координат.

Центр окружности имеет координаты (-3; 4). Поэтому уравнение этой окружности можно записать в виде (х + 3) 2 + (у — 4) 2 = r 2 , где r — пока неизвестный радиус окружности. Найдём его. Для этого воспользуемся тем, что окружность проходит через начало координат, т. е. координаты точки О (0; 0) удовлетворяют этому уравнению: (0 + 3) 2 + (0 — 4) 2 = r 2 . Отсюда r 2 = 25, и, значит, r = 5. Итак, искомое уравнение окружности имеет вид (х + 3) 2 + (у — 4) 2 = 25.

Если раскрыть скобки и привести подобные члены, то получится уравнение х 2 + у 2 + 6х — 8у = 0, которое также является уравнением данной окружности.

Уравнение прямой

Выведем уравнение данной прямой l в заданной прямоугольной системе координат. Отметим две точки А (x₁; у₁) и В (х₂; у₂) так, чтобы прямая l была серединным перпендикуляром к отрезку АВ (рис. 287, а). Если точка М (х; у) лежит на прямой l, то АМ = ВМ, или AM 2 = ВМ 2 , т. е. координаты точки М удовлетворяют уравнению

Если же точка М (x; у) не лежит на прямой l, то AM 2 ≠ ВМ 2 , и, значит, координаты точки М не удовлетворяют уравнению (2). Следовательно, уравнение (2) является уравнением прямой I в заданной системе координат. После возведения выражений в скобках в квадрат и приведения подобных членов уравнение (2) принимает вид

где а = 2 (х₁ — х₂), b = 2(у₁ — у₂), Так как А (x₁; у₁) и В (x₂; y₂) — различные точки, то хотя бы одна из разностей (х₁ — х₂) и (у₁ — у₂) не равна нулю, т. е. хотя бы один из коэффициентов а и b отличен от нуля. Таким образом, уравнение прямой в прямоугольной системе координат является уравнением первой степени.

Если в уравнении (3) коэффициент b отличен от нуля, то это уравнение можно записать так:

где Число k называется угловым коэффициентом прямой, заданной этим уравнением. Докажите самостоятельно, что:

две параллельные прямые, не параллельные оси Оу, имеют одинаковые угловые коэффициенты; вели две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны.

Выведем уравнение прямой l, проходящей через точку М₀ (x₀; у₀) и параллельной оси Оу (рис. 287, б). Абсцисса любой точки М (х; у) прямой l равна x₀, т. е. координаты любой точки М (x; у) прямой l удовлетворяют уравнению х = х₀. В то же время координаты любой точки, не лежащей на прямой l, этому уравнению не удовлетворяют. Следовательно, уравнение х = х₀ является уравнением прямой l.

Ясно, что ось Ох имеет уравнение у = О, а ось Оу — уравнение х = 0.

Взаимное расположение двух окружностей

Исследуем взаимное расположение двух окружностей в зависимости от их радиусов r, R и расстояния d между их центрами. Для определённости будем считать, что r ≤ R.

Если центры окружностей совпадают, т. е. d = 0, то окружности называются концентрическими, и окружность радиуса г лежит внутри круга радиуса R (рис. 288, а).

Пусть d > 0. Введём прямоугольную систему координат Оху так, чтобы точка О была центром первой окружности, а точка с координатами (d; 0) — центром второй окружности. В этой системе координат уравнения первой и второй окружностей имеют вид

х 2 + у 2 = R 2 , (х — d) 2 + у 2 = r 2 . (4)

Если система уравнений (4) имеет решением пару чисел х = х₀, у = у₀, то точка М0 (х₀; у₀) является общей точкой данных окружностей (рис. 288, б), и обратно: если М₀ (x₀; у₀) — общая точка данных окружностей, то пара чисел х = х₀, у = у₀ является решением системы уравнений (4).

Пусть система (4) имеет решением пару чисел x = х₀, у = у₀, т. е. справедливы числовые равенства

Вычитая из первого равенства второе, подучаем равенство 2x₀d — d 2 = R 2 — r 2 , откуда

Заметим, что х₀ > 0, поскольку R ≥ r и d > 0. Кроме того, как следует из первого равенства (5), х₀ = т. е. для величин R, r и d должно выполняться неравенство или R 2 + d 2 — r 2 ≤ 2dR. Последнее неравенство запишем в виде (d — R) 2 ≤ r 2 . Отсюда следует, что -r ≤ d — R ≤ r, или

Отметим, что х₀ = R, если d = R — r или d = R + r, и x₀ R + r (рис. 288, г). В этом случае говорят, что одна окружность лежит вне другой.

Если неравенства (7) выполнены, то возможны три случая:

3) d = R — r, при этом R > r, поскольку d > 0. Как уже было отмечено, в этом случае x₀ = R, поэтому из первого из равенств (5) следует, что y₀ = 0. Непосредственной проверкой можно убедиться в том, что пара чисел x = R, у = 0 есть решение системы (4). Таким образом, в данном случае окружности имеют ровно одну общую точку, и их взаимное расположение изображено на рисунке 288, д. Говорят, что окружности касаются изнутри.

4) d = R + r. В этом случае также х₀ = R, поэтому y₀ = 0, и непосредственно проверяется, что пара чисел x = R, у = 0 есть решение системы (4). Таким образом, в данном случае, как и в случае 3, окружности имеют ровно одну общую точку, но их взаимное расположение иное (рис. 288, е). Говорят, что окружности касаются извне.

5) R — r 2 + у 2 = 9; б) (х — 1) 2 + (у + 2) 2 = 4; в) (х + 5) 2 + (у — 3) 2 = 25; г) (х — 1) 2 + у 2 = 4; д) х 2 + (у + 2) 2 = 2.

960. Какие из точек А (3; -4), В (1; 0), С (0; 5), D (0; 0) и Е (0; 1) лежат на окружности, заданной уравнением:

а) х 2 + у 2 = 25; б) (х — 1) 2 + (у + 3) 2 = 9; в) (х — 0,5) 2 — у 2 = 0,25;

961. Окружность задана уравнением (х + 5) 2 + (у — 1) 2 = 16. Не пользуясь чертежом, укажите, какие из точек А (-2; 4), В (-5; -3), С (-7; -2) и D (1; 5) лежат:

а) внутри круга, ограниченного данной окружностью;
6) на окружности;
в) вне круга, ограниченного данной окружностью.

962. Даны окружность х 2 + у 2 = 25 и две точки А (3; 4) и В (4;-3). Докажите, что АВ — хорда данной окружности.

963. На окружности, заданной уравнением х 2 + у 2 = 25, найдите точки: а) с абсциссой -4; б) с ординатой 3.

964. На окружности, заданной уравнением (x — 3) 2 + (у — 5) 2 = 25, найдите точки: а) с абсциссой 3; б) с ординатой 5.

965. Напишите уравнения окружностей с центром в начале координат и радиусами r₁ = 3, r₂ = √2, r₂ = 5/2.

966. Напишите уравнение окружности радиуса r с центром А, если: а) А (0; 5), r = 3; б) А (-1;2), r = 2; в) А (-3;-7), r = 1/2; г) А (4;-3), r =10.

967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).

968. Напишите уравнение окружности с центром в точке А (0; 6), проходящей через точку В (-3; 2).

969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5), N (7; -3); б) М (2; -1), N (4; 3).

970. Напишите уравнение окружности, проходящей через точку А (1;3), если известно, что центр окружности лежит на оси абсцисс, а радиус равен 5. Сколько существует таких окружностей?

971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и В (0; 9), если известно, что центр окружности лежит на оси ординат.

972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2); б) С (2; 5) и D (5; 2); в) М (0; 1) и N (-4; -5).

а) Уравнение прямой АВ имеет вид ах + by + с = 0. Так как точки А и В лежат на прямой АВ, то их координаты удовлетворяют этому уравнению:

а • 1 + b • (-1) + с = 0, а • (-3) + b • 2 + с = 0,
или а — b + с = 0, -3а + 2b + с = 0.

Из этих уравнений выразим коэффициенты а и b через с: а = 3с, b = 4с. Подставив эти значения в уравнение прямой, получим 3сх + 4су + с = 0. При любом с ≠ 0 это уравнение является уравнением прямой АВ. Сократив на с, запишем искомое уравнение в виде 3х + 4у + 1 = 0.

973. Даны координаты вершин треугольника АВС: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнение прямой, содержащей медиану СМ.

974. Даны координаты вершин трапеции ABCD: А (-2; -2), В (-3;1), С (7; 7) и D (3; 1). Напишите уравнения прямых, содержащих: а) диагонали АС и BD трапеции; б) среднюю линию трапеции.

975. Найдите координаты точек пересечения прямой 3х — 4у + 12 = О с осями координат. Начертите эту прямую.

976. Найдите координаты точки пересечения прямых 4х + 3у — 6 = О и 2х + у — 4 = 0.

977. Напишите уравнения прямых, проходящих через точку М (2; 5) и параллельных осям координат.

978. Начертите прямую, заданную уравнением: а) у = 3; б) х = -2; в) у = -4; г) х = 7.

979. Найдите ординату точки М, лежащей на прямой АВ, если известно, что А (-8; -6), В (-3; -1) и абсцисса точки М равна 5.

980 Напишите уравнения прямых, содержащих стороны ромба, диагонали которого равны 10 см и 4 см, если известно, что его диагонали лежат на осях координат.

Использование уравнений окружности и прямой при решении задач

981. Даны две точки А и В. Найдите множество всех точек, для каждой из которых расстояние от точки А в два раза больше расстояния от точки В.

Введём прямоугольную систему координат так, как показано на рисунке 289,а. Тогда точки А и В имеют координаты А (0; 0), В (а; 0), где а = АВ.

Найдём расстояния от произвольной точки М (х; у) до точек А и В:

Если точка М (х; у) принадлежит искомому множеству, то

AM = 2ВМ, или AM 2 = 4ВМ 2 .

Поэтому её координаты удовлетворяют уравнению

х 2 + у 2 = 4 ((х — а) 2 + у 2 ). (8)

Если же точка М не принадлежит искомому множеству, то её координаты не удовлетворяют этому уравнению.

Следовательно, уравнение (8) и есть уравнение искомого множества точек в выбранной системе координат. Раскрывая скобки и группируя слагаемые соответствующим образом, приводим уравнение (8) к виду

Таким образом, искомым множеством точек является окружность радиуса 2/3a с центром в точке C(4/3a; 0). Эта окружность изображена на рисунке 289, б.

Аналогично можно доказать, что множеством всех точек М, удовлетворяющих условию AM = kBM, где k — данное положительное число, не равное единице, является окружность радиуса с центром в точке

Эти окружности, соответствующие различным значениям k ≠ 1, называют окружностями Аполлония, поскольку они рассматривались ещё древнегреческим математиком Аполлонием в его трактате «О кругах» во II в. до н. э.

Если k = 1, то задача сводится к известной нам задаче о нахождении множества всех точек, равноудалённых от точек А и В. Таким множеством, как мы знаем, является серединный перпендикуляр к отрезку АВ.

982. Точка В — середина отрезка АС, длина которого равна 2. Найдите множество всех точек М, для каждой из которых: a) AM 2 + ВМ 2 + СМ 2 = 50; б) AM 2 + 2ВМ 2 + 3СМ 2 = 4.

983. Даны две точки А и В. Найдите множество всех точек М, для каждой из которых AM 2 + ВМ 2 = k 2 , где k — данное число.

984. Даны две точки А и В. Найдите множество всех точек М, для каждой из которых AM 2 — ВМ 2 = k, где k — данное число.

Введём прямоугольную систему координат так, чтобы точка А была началом координат, а точка В имела координаты (а; 0), где а = АВ. Найдём расстояния от произвольной точки М (х; у) до точек А и В:

Если точка М (х; у) принадлежит искомому множеству, то AM 2 — ВМ 2 = k, поэтому координаты точки М удовлетворяют уравнению х 2 + у 2 — (х — а) 2 — у 2 = k, или 2ах — а 2 — k = 0.

Если же точка М не принадлежит искомому множеству, то её координаты не удовлетворяют этому уравнению. Итак, полученное уравнение является уравнением искомого множества точек. Но этим уравнением определяется прямая, параллельная оси Оу, если а 2 + k ≠ 0, и сама ось Оу, если a 2 + k = 0. Таким образом, искомым множеством точек является прямая, перпендикулярная к прямой АВ.

985. Даны две точки А и B. Найдите множество всех точек М, для каждой из которых ВМ 2 — AM 2 = 2АВ 2 .

986. Дан прямоугольник ABCD. Найдите множество всех точек М, для каждой из которых

(AM 2 + DM 2 ) — (ВМ 2 + СМ 2 ) = 2АВ 2 .

987.* Дан ромб ABCD, диагонали которого равны 2а и 2Ь. Найдите множество всех точек М, для каждой из которых

AM 2 + DM 2 = ВМ 2 + СМ 2 .

Ответы к § 3

960. а) А и С; б) В; в) В и D.

961. а) С; б) В; в) А и D.

963. а) (-4; -3), М;3);б) (4; 3), (-4; 3).

964. а) (3; 0), (3; 10); б) (-2; 5), (8; 5).

965. 1) х 2 + у 2 = 9; 2) х 2 + у 2 = 2; 3)

966. а) х 2 + (у-5) 2 = 9; б) (х + 1) 2 + (y — 2) 2 = 4; в) г) (х — 4) 2 + (y + 3) 2 = 100.

967. х 2 + у 2 = 10.

968. х 2 + (у — 6) 2 = 25.

969. а) (х — 2) 2 + (y — 1) 2 = 41; б) (х — 3) 2 + (у — 1) 2 = 5.

970. (х — 5) 2 + у 2 = 25, (х + 3) 2 + у 2 = 25; две окружности.

971. х 2 + (у — 4) 2 = 25.

972. б) х + у- 7 = 0; в) 3х — 2у + 2 = 0.

973. 7х — у + 3 = 0.

974. а) х — у = 0, у — 1 = 0; б) 3х — 5у + 5 = 0.

977. х = 2 и у = 5.

980. 5х + 2у — 10 = 0, 5х — 2у — 10 = 0, 5х + 2у + 10 = 0, 5х — 2у + 10 = 0 или 2х + 5у- 10 = 0, 2х — 5у -10 = 0, 2х + 5y + 10 = 0, 2х — 5у+ 10 = 0.

982. а) Окружность радиуса 4 с центром В; б) окружность радиуса 1/3 с центром D, лежащим на отрезке ВС, причём BD = 1/3

983. Окружность с центром в точке О радиуса , если k 2 > 2а 2 , и точка О, если k 2 = 2а 2 , где О — середина отрезка АВ и Если k 2 2 , то точек, удовлетворяющих условию задачи, не существует.

985. Серединный перпендикуляр к отрезку АВ’, где В’ и В — точки, симметричные относительно точки А.

986. Прямая ВС. Указание. Выбрать прямоугольную систему координат так, чтобы точки А и В лежали на оси Ох и были симметричны относительно оси Оу.

987. Прямая, проходящая через точку пересечения диагоналей ромба и перпендикулярная к стороне ромба.

Геометрия. 9 класс

Две окружности могут пересекаться, не пересекаться либо касаться друг друга.
Перейдем к анализу возможных случаев расположения двух окружностей.
Рассмотрим окружность с центром О₁ и окружность с центром О₂. Тогда расстояние между их центрами равно О₁О₂.
I. Пересекающиеся окружности имеют две общие точки.
Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов:
II. Не пересекающиеся окружности не имеет общих точек.

Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:
Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов:
III. Касающиеся окружности имеют одну общую точку – точку касания.
При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:
При внутреннем касании расстояние между центрами равно разности радиусов:
Если центры окружностей совпадают, то такие окружности называются концентрическими.
Концентрические окружности разного радиуса не пересекаются: О₁О₂ = 0
В случае равенства радиусов они совпадают.
Если же радиусы этих окружностей не равны, то одна из них лежит внутри другой – образуется кольцо.

Кольцом называют фигуру, заключенную между концентрическими окружностями.

НАШИ ПАРТНЁРЫ

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x – 2 ) 2 + (y – ( -3 )) 2 = 4 2
или
(x – 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x – 2) 2 + (y + 3) 2 = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение ( x – 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x – 2) 2 + ( y + 3) 2 = 16
( 2 – 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

[spoiler title=”источники:”]

http://b4.cooksy.ru/articles/kak-sostavit-uravnenie-okruzhnosti-po-odnoy-tochke

http://profmeter.com.ua/communication/learning/course/course7/chapter0552/

[/spoiler]

Источник

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Решение:

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

$[{(x - a)^2} + {(y - b)^2} = {R^2}]$

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

$[{(x - 5)^2} + {(y - ( - 1))^2} = {7^2},]$

$[{(x - 5)^2} + {(y + 1)^2} = 49.]$

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Решение:

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

$[R = AC = sqrt {{{({x_C} - {x_A})}^2} + {{({y_C} - {y_A})}^2}} ]$

$[R = AC = sqrt {{{(3 - 8)}^2} + {{( - 6 - ( - 3))}^2}} = sqrt {25 + 9} = sqrt {34} ,]$

$[{R^2} = 34.]$

Следовательно, уравнение данной окружности

$[{(x - 8)^2} + {(y + 3)^2} = 34.]$

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Решение:

$[{x_O} = frac{{{x_A} + {x_B}}}{2},{y_O} = frac{{{y_A} + {y_B}}}{2}]$

$[{x_O} = frac{{ - 4 + 6}}{2} = 1,{y_O} = frac{{ - 9 + 5}}{2} = - 2]$

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

$[R = OA = sqrt {{{({x_A} - {x_O})}^2} + {{({y_A} - {y_O})}^2}} ]$

$[R = OA = sqrt {{{( - 4 - 1)}^2} + {{( - 9 - ( - 2))}^2}} = sqrt {25 + 49} = sqrt {74} ,]$

$[{R^2} = 74.]$

Таким образом, уравнение окружности с диаметром AB —

$[{(x - 1)^2} + {(y + 2)^2} = 74.]$

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Решение:

$[{(x - a)^2} + {(y - b)^2} = {R^2},]$

получаем систему уравнений:

$[left{ begin{array}{l} {(4 - a)^2} + {( - 5 - b)^2} = {R^2}\ {(8 - a)^2} + {(3 - b)^2} = {R^2}\ {( - 8 - a)^2} + {(11 - b)^2} = {R^2} end{array} right.]$

$[{(4 - a)^2} + {( - 5 - b)^2} = {(8 - a)^2} + {(3 - b)^2}]$

$[16 - 8a + {a^2} + 25 + 10b + {b^2} = 64 - 16a + {a^2} + 9 - 6b + {b^2}]$

Приравняем правые части 2-го и 3-го уравнений:

$[{(8 - a)^2} + {(3 - b)^2} = {( - 8 - a)^2} + {(11 - b)^2}]$

$[64 - 16a + {a^2} + 9 - 6b + {b^2} = 64 + 16a + {a^2} + 121 - 22b + {b^2}]$

Умножив уравнение

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

$[{(4 + 2)^2} + {( - 5 - 3)^2} = {R^2}]$

$[{(4 + 2)^2} + {( - 5 - 3)^2} = {R^2},]$

получаем R²=100.

Следовательно, уравнение окружности, проходящей через три данные точки —

$[{(x + 2)^2} + {(y - 3)^2} = 100.]$

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

$[{(x - 5)^2} + {(y - 2)^2} = 25.]$

Источник

Как составить уравнение окружности

Окружность — совокупность точек, лежащих на расстоянии R от заданной точки (центра окружности). Уравнением окружности в декартовых координатах называется такое уравнение, что для любой точки, лежащей на окружности, ее координаты (x, y) удовлетворяют этому уравнению, а для любой точки, не лежащей на окружности — не удовлетворяют.

Инструкция

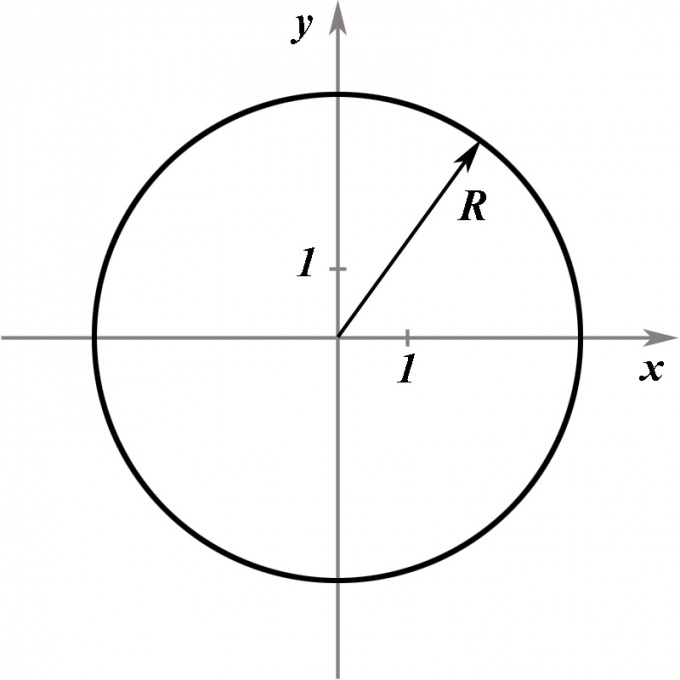
Предположим, что ваша задача — составить уравнение окружности заданного радиуса R, центр которой находится в начале координат. Окружность, по определению — множество точек, находящихся на заданном расстоянии от центра. Это расстояние как раз и равно радиусу R.

Расстояние от точки (x, y) до центра координат равно длине отрезка, соединяющего ее с точкой (0, 0). Этот отрезок вместе с его проекциями на координатные оси составляют прямоугольный треугольник, катеты которого равны x0 и y0, а гипотенуза, по теореме Пифагора, равна √(x^2 + y^2).

Чтобы получить окружность, вам нужно уравнение, определяющее все точки, для которых это расстояние будет равно R. Таким образом:√(x^2 + y^2) = R, а следовательно,
x^2 + y^2 = R^2.

Аналогичным способом составляется уравнение окружности радиусом R, центр которой находится в точке (x0, y0). Расстояние от произвольной точки (x, y) до заданной точки (x0, y0) равно √((x – x0)^2 + (y – y0)^2). Следовательно, уравнение нужной вам окружности будет выглядеть так:(x – x0)^2 + (y – y0)^2 = R^2.

Вам может понадобиться также составить уравнение окружности с центром в точке координат, проходящей через заданную точку (x0, y0). В этом случае радиус искомой окружности не задан в явном виде, и его придется вычислять. Очевидно, он будет равен расстоянию от точки (x0, y0) до начала координат, то есть √(x0^2 + y0^2). Подставляя это значение в уже выведенное уравнение окружности, вы получите:x^2 + y^2 = x0^2 + y0^2.

Если вам предстоит построить окружность по выведенным формулам, то их придется разрешать относительно y. Даже самое простое из этих уравнений при этом превращается в:y = ±√(R^2 – x^2).Знак ± необходим здесь потому, что квадратный корень числа всегда неотрицателен, а это значит, что без знака ± такое уравнение описывает только верхнюю полуокружность.Чтобы построить окружность, удобнее составить ее параметрическое уравнение, в котором обе координаты x и y зависят от параметра t.

Согласно определению тригонометрических функций, если гипотенуза прямоугольного треугольника равна 1, а один из углов при гипотенузе равен φ, то прилежащий к нему катет равен cos(φ), а противолежащий — sin(φ). Таким образом, sin(φ)^2 + cos(φ)^2 = 1 для любого φ.

Предположим, вам дана окружность единичного радиуса с центром в начале координат. Возьмем любую точку (x, y) на этой окружности и проведем от нее отрезок к центру. Этот отрезок образует угол с положительной полуосью x, который может быть равен от 0 до 360° или от 0 до 2π радиан. Обозначая этот угол t, вы получите зависимость:x = cos(t),
y = sin(t).

Эту формулу можно обобщить на случай окружности радиуса R с центром в произвольной точке (x0, y0):x = R*cos(t) + x0,
y = R*sin(t) + y0.

Источники:

уравнение окружности с заданным центром и радиусом

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Метод координат
Уравнение окружности

Выведем уравнение окружности радиуса 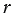с центром 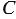в заданной прямоугольной системе координат. Пусть точка 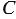имеет координаты :

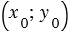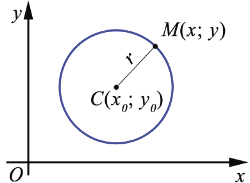
Расстояние от произвольной точки 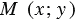до точки 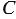вычисляется по формуле 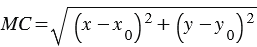. Если точка 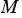лежит на данной окружности, то 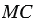= 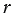, , 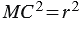т.е. координаты точки 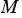удовлетворяют уравнению

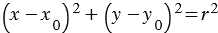(1)

Если же точка 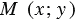не лежит на данной окружности, то 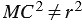, и, значит, координаты точки 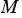не удовлетворяют уравнению (1).

Частный случай: уравнение окружности радиуса 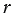с центром в начале координат: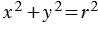

Задача

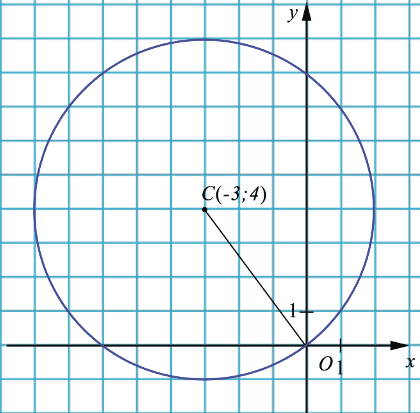
Найти уравнение окружности с центром в точке (-3; 4), проходящей через начало координат.

Дано: окр.(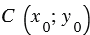), 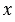₀= -3, 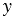₀ = 4,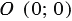 окр.()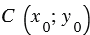

Найти: уравнение окр.()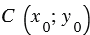

Решение:

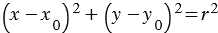, следовательно, для данной окружности имеем, что 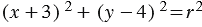(2).

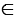Найдем : т.к. окр.(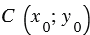), т.е. координаты точки 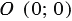удовлетворяют уравнению (2):

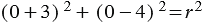Отсюда 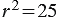или .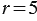

Итак, искомое уравнение окружности имеет вид .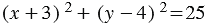

Раскроем скобки и приведем подобные члены, получим, что: 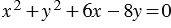. Полученное уравнение также является уравнением данной окружности.

Советуем посмотреть:

Разложение вектора по двум неколлинеарным векторам

Координаты вектора

Связь между координатами вектора его начала и конца

Простейшие задачи в координатах

Уравнение линии на плоскости

Уравнение прямой

Взаимное расположение двух окружностей

Метод координат

Правило встречается в следующих упражнениях:

7 класс

Задание 959,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 981,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 24,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1001,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1010,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1012,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 5,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1264,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1265,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Прежде всего,
давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что
уравнение с двумя переменными x и y
называется уравнением линии l, если этому уравнению
удовлетворяют координаты любой точки линии l и не
удовлетворяют координаты никакой точки, не лежащей на этой линии.

Сегодня на уроке мы
попробуем по геометрическим свойствам линии найти ее уравнение.

В качестве линии
рассмотрим окружность радиуса с
центром в точке .

Пусть центр
окружности имеет координаты . Возьмем на
окружности произвольную точку . Запишем формулу
расстояния между точками C и M.
Мы знаем, что длина отрезка, который соединяет любую точку на окружности с
центром окружности – это радиус. Поэтому можно записать, что MC
равно r. Возведем MC в квадрат
и получим уравнение MC² = r².
Заменим MC² квадрат на выражение и получим, что если
точка лежит на окружности с радиусом r и центром в
точке C, то координаты этой точки удовлетворяют
уравнению . Если точка не
лежит на окружности, то расстояние от этой точки до центра окружности не равно
радиусу, поэтому координаты таких точек не будут удовлетворять полученному
уравнению. Поэтому можно сказать, что в прямоугольной системе координат уравнение
окружности радиуса r с центром в точке C с координатами имеет вид: .

Задача. Записать
уравнение окружности с радиусом и центром в начале
координат.

Решение.

Начало координат
имеет координаты (0;0). Подставим их в уравнение окружности и получим, что
уравнение окружности с радиусом r и
центром в начале координат имеет вид

Задача. Начертить
окружность, заданную уравнением .

Решение.

Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего,
определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь
давайте определим величину радиуса окружности.

Поскольку в правой
части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо
извлечь квадратный корень из 4. Получим 2.

Значит наша
формула задает окружность с центром в точке с координатами пять три и радиусом
равным двум.

Задача. Начертить
окружность, заданную уравнением .

Решение.

Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего
определимся с координатами центра окружности.

Это будут числа -4
и 2. Теперь давайте определим величину радиуса окружности.

Задача. Начертить
окружность, заданную уравнением .

Решение. Уравнениями
такого типа описываются окружности с центром в начале координат. Теперь давайте
определим величину радиуса окружности. Поскольку в правой части формулы стоит
квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень
из 9.

Значит наша формула
задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.

Теперь давайте
попробуем решить задачу обратную данным.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Как и в предыдущих
задачах мы начнем с определения координат центра окружности. Сделать это
нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр
окружности имеет координаты (0;0).

Нетрудно заметить,
что радиус окружности равен 4.

Запишем уравнение
окружности и подставим найденные значения.

Ответ: .

Решим еще одну
задачу.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Решение.

– центр окружности

– радиус окружности

Ответ:.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Решение.

– центр окружности

– радиус окружности

Ответ:.

Решая задачи, мы с
вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот
порядок.

Для того, что
бы составить уравнение окружности и построить ее надо:

1. Найти координаты
центра окружности.

2. Найти длину
радиуса этой окружности.

3. Записать уравнение
окружности.

4. Подставить
полученные значения в уравнение окружности.

5. Построить
окружность, если это требуется для решения задачи.

Рассмотрим еще одну
задачу.

Написать уравнение
окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм
имеет координаты шесть три.

Задача. Написать
уравнение окружности с диаметром , если , .

Решение.

Найдем координаты
центра окружности. Центр окружности является серединой диаметра. Воспользуемся
формулами для нахождения координат середины отрезка.

Получим, что центр
окружности имеет координаты .

Теперь определим
радиус окружности. Для этого найдем расстояние от центра окружности до концов
диаметра.

Запишем общее
уравнение окружности и подставим в него найденные значения. Тогда получим, что
уравнение данной окружности имеет вид:

Ответ: .

Подведем итоги
урока.

На сегодняшнем
уроке мы познакомились с формулой, которая задает окружность с центром в точке С
(x₀; y₀)
и радиусом r.

Также мы
познакомились с формулой, которая задает окружность с центром в начале
координат и радиусом r.

Мы рассмотрели
задачи на составление уравнения окружности по рисунку и на построение
окружности по заданному уравнению.

Источник

Написать уравнение окружности

Как составить уравнение окружности по одной точке

Написать уравнение окружности

Уравнение окружности.

Уравнения окружностей имеющих одну общую точку

Уравнение окружности.

§ 3. Уравнения окружности и прямой

Уравнение окружности

Уравнение прямой

Взаимное расположение двух окружностей

Использование уравнений окружности и прямой при решении задач

Ответы к § 3

Геометрия. 9 класс

НАШИ ПАРТНЁРЫ

Уравнение окружности.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Задача. Принадлежит ли точка уравнению окружности

Как составить уравнение окружности

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Вам также может понравиться

Муж как нашел девушку

У меня злое лицо как исправить

Как найти личное дело деда

Добавить комментарий Отменить ответ