Окружность в полярных координатах
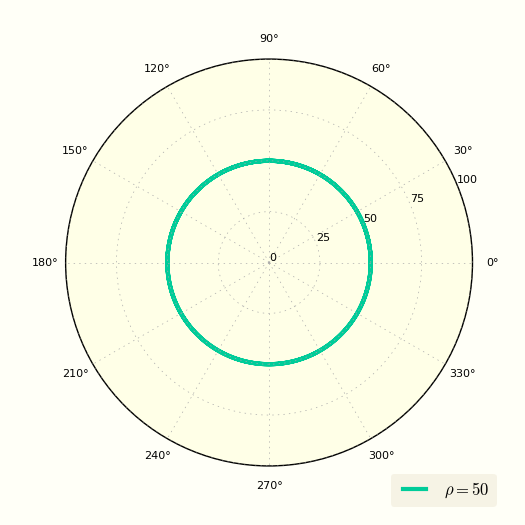
Уравнение окружности в полярных координатах выглядит очень просто
[ ρ = R = htmlStyle{color: DarkOrange;}{const} ]
Это уравнение показывает, что ρ вообще не зависит от угла φ.
Построение окружности по простому уравнению в полярной системе координат
Еще одно уравнение окружности в полярных координатах
Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.
Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:
[ (x-R)^2 + y^2 = R^2 ]
Также известны
формулы перевода декартовых координат в полярные
Используя эти формулы и подставив их в (1) мы получим:
Уравнение окружности в полярных координатах
Изначально после подстановки имеем
[ ρ^{2} – 2Rρcos(φ) = 0 ]
И этого уравнения получается система
[
begin{cases}
ρ = 0 \
ρ = 2Rcos(φ)
end{cases}
]
Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
В итоге получаем:
[ ρ = 2Rcos(φ) ]
Построение окружности в полярной системе координат
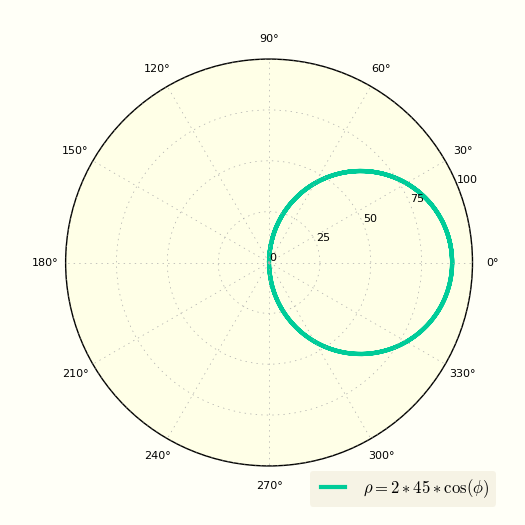
Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах
В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.
При таком смещении окружность описывается уравнением:
[ x^2 + (y-R)^2 = R^2 ]
Снова используем
формулы перевода декартовых координат в полярные
получаем:
[ ρ^{2} – 2Rρsin(φ) = 0 ]
И этого уравнения получается система
[
begin{cases}
ρ = 0 \
ρ = 2Rsin(φ)
end{cases}
]
Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
В итоге получаем:
[ ρ = 2Rsin(φ) ]
Построение окружности в полярной системе координат смещенной вверх относительно полюса
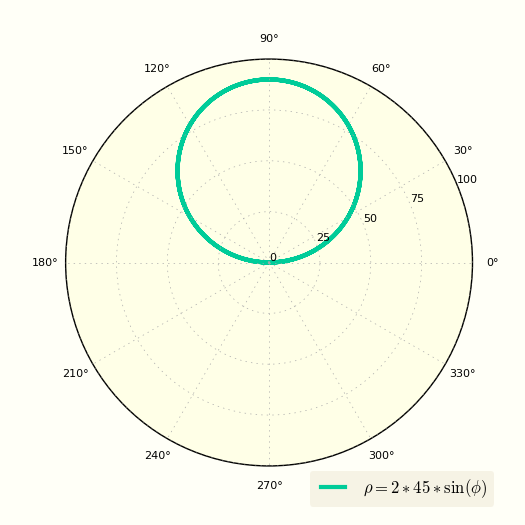
Окружность в полярных координатах |
стр. 124 |
|---|
Окружность в полярных координатах
Уравнение окружности в полярных координатах выглядит очень просто
Это уравнение показывает, что ρ вообще не зависит от угла φ.
Построение окружности по простому уравнению в полярной системе координат

Еще одно уравнение окружности в полярных координатах
Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.
Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:
Используя эти формулы и подставив их в (1) мы получим:
Уравнение окружности в полярных координатах
Изначально после подстановки имеем
И этого уравнения получается система
Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
В итоге получаем:
Построение окружности в полярной системе координат

Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах
В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.
При таком смещении окружность описывается уравнением:
И этого уравнения получается система
Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
Полярные координаты – определение и вычисление с примерами решения
Содержание:
Полярные координаты. параметрические уравнения линии
Полярные координаты
Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.
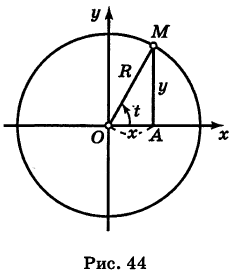
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).
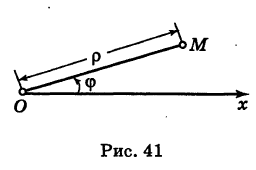
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол 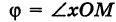
Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до 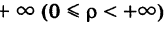 и значения ф от 0 до
и значения ф от 0 до 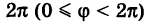 , при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие
, при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие 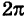 , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.
, а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.
Связь между прямоугольными и полярными координатами
Рассмотрим переход от полярных координат к прямоугольным и обратно.
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).
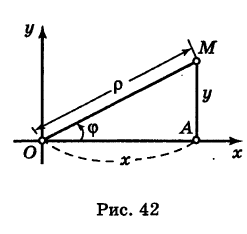
Тогда для произвольной точки М имеем
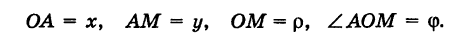
Считая угол ф острым, из прямоугольного треугольника АОМ находим
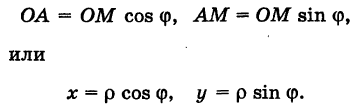
Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем
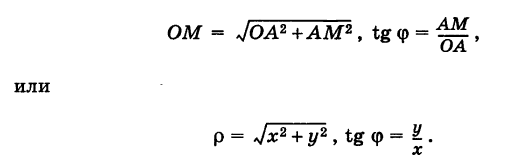
Так выражаются полярные координаты точки через ее прямоугольные координаты.
Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.
Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.
Пример:
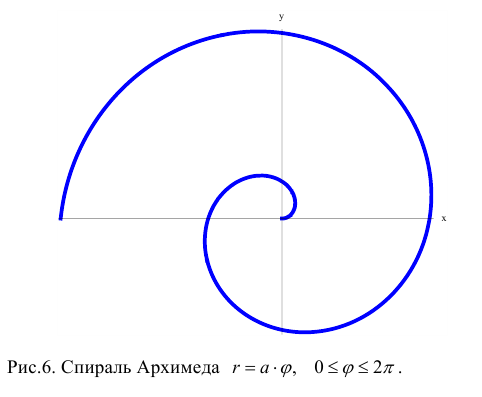
Рассмотрим кривую 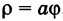 , где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:
, где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:
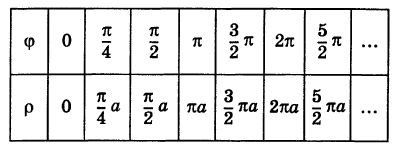
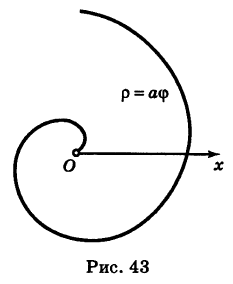
По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).
Параметрические уравнения линии
Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 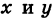 , рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).
, рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).
Пример:
Выведем параметрические уравнения окружности.
Пусть М 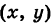 — произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства
— произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства
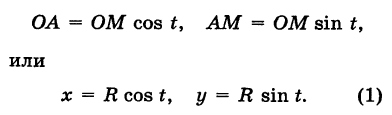
Это и есть параметрические уравнения окружности.
Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:
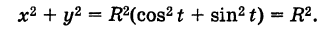
Пример:
Выведем параметрические уравнения эллипса.
Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где

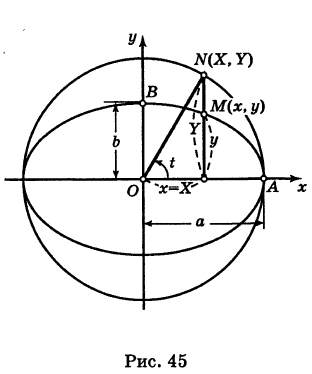 За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох:
За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: 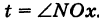 . Используя формулы (2), имеем
. Используя формулы (2), имеем
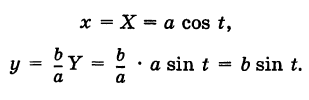
Таким образом, параметрические уравнения эллипса с полуосями а и b есть
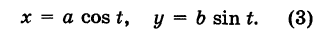 Исключив из уравнений (3) параметр получим каноническое уравнение эллипса
Исключив из уравнений (3) параметр получим каноническое уравнение эллипса
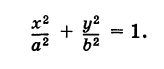
Имея параметрические уравнения линии, можно по точкам построить ее.
Пример:

Решение:
Составляем таблицу значений:
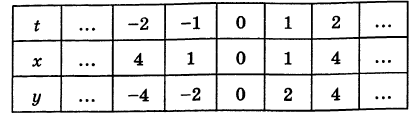
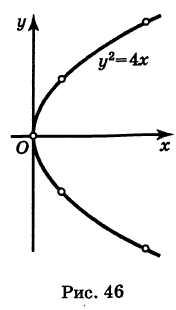 Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).
Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 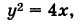 т. е. каноническое уравнение параболы.
т. е. каноническое уравнение параболы.
Параметрические уравнения циклоиды
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).
Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем
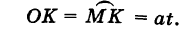
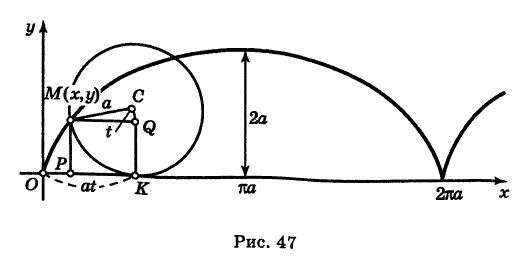
Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:
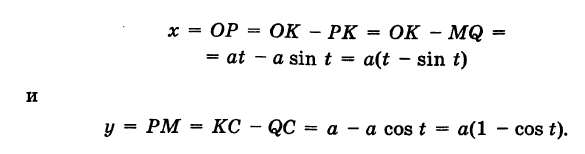
Таким образом, параметрические уравнения циклоиды есть
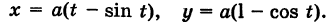
Полярная система координат
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 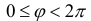 . Точка О при этом называется
. Точка О при этом называется
полюсом, а полуось Ох – полярной осью.
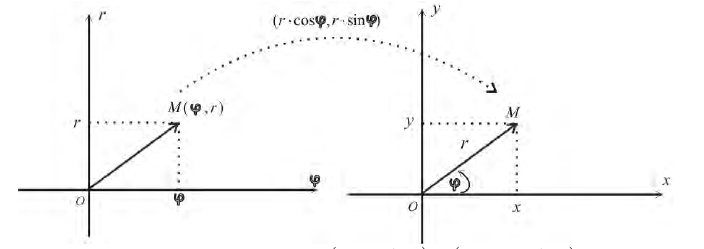
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 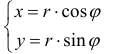 (1)
(1)
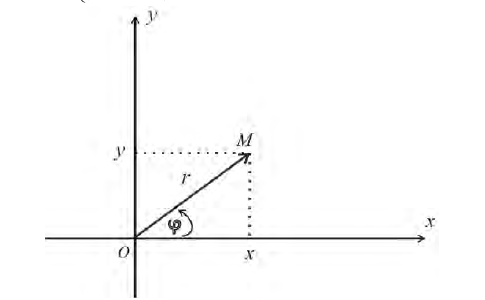
Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:
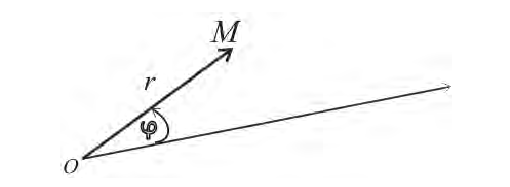
Пример 1.
Построим на плоскости линию, заданную уравнением:
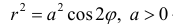 − лемниската.
− лемниската.
Решение.
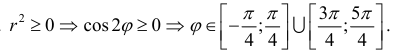
Вычислим значения r при различных значениях ϕ : 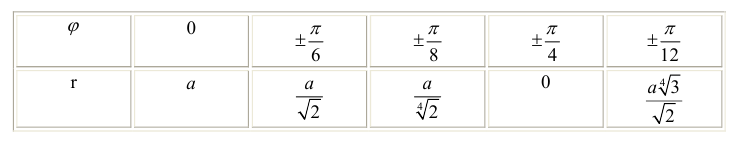
Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :
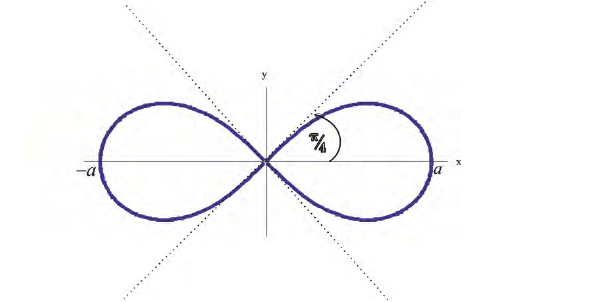
Рис.3. Лемниската 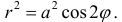
Пример 2.
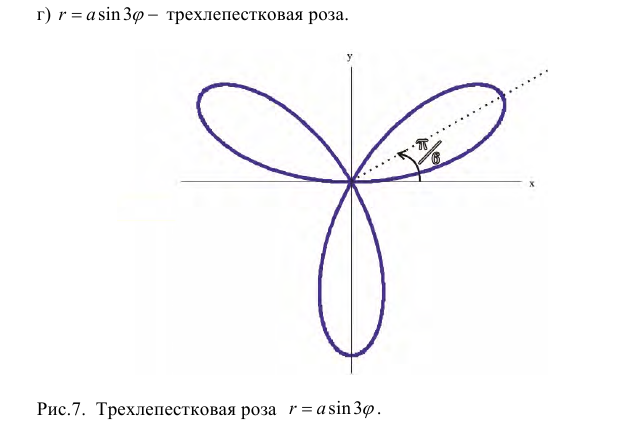
а) Построим кривую 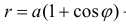 − кардиоида. Рассуждая, как в примере 1 получим:
− кардиоида. Рассуждая, как в примере 1 получим: 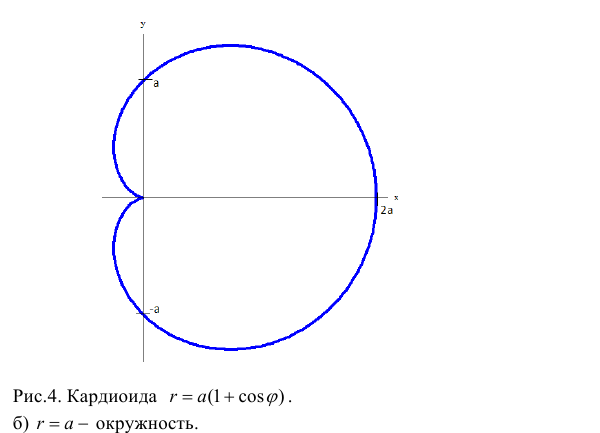
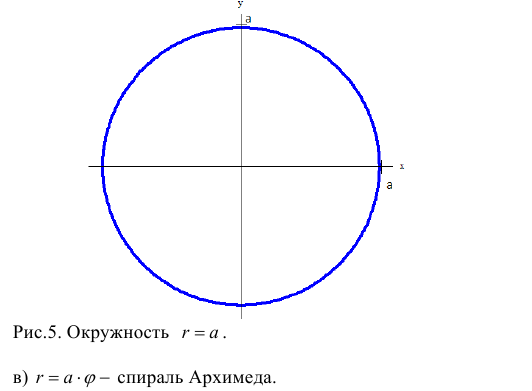
Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).
При этом, если r > 0, то векторы 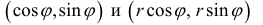 сонаправлены, если r
сонаправлены, если r
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Уравнение окружности в полярной системе координат.
Определим уравнение окружности, проходящей через полюс системы координат, центр которой C расположен на полярной оси, а радиус равен R. Выполним построения:
Далее отметим на окружности любую точку А и В, причем точка В – конец диаметра. Соединим выбранную пару точек. Угол ОАВ – прямой, а потому, так как диаметр равен 2R, из прямоугольного треугольника АОВ имеем:
Если же центр является началом координат, то уравнение принимает вид:
Так же уравнение может принимать вид:
Для ситуации, когда центр окружности расположен на прямой перпендикулярной полярной оси и проходящей через полюс:
[spoiler title=”источники:”]
http://www.evkova.org/polyarnyie-koordinatyi
http://www.calc.ru/Uravneniye-Okruzhnosti-V-Polyarnoy-Sisteme-Koordinat.html
[/spoiler]
Уравнение линии в полярных координатах. Простейшие примеры
По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса от полярного угла (аргумента). При этом полярный угол учитывается в радианах (!) и
непрерывно принимает значения от до (иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от до ).
Каждому значению угла «фи», которое входит в область определения
функции , соответствует единственное значение
полярного радиуса.
Полярную функцию можно сравнить со своеобразным радаром – когда луч света, исходящий из полюса, вращается против часовой стрелки и «прорисовывает»
линию.
«Дежурным» примером полярной кривой является Архимедова спираль . На
следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до :
Далее, пересекая полярную ось в точке , спираль продолжит раскручиваться, бесконечно далеко удаляясь от полюса. Но подобные случаи на
практике встречаются довольно редко; более типичная ситуация, когда на всех последующих оборотах мы «пройдёмся по той же самой линии», которая
получена в диапазоне .
В первом же примере мы сталкиваемся и с понятием области определения полярной функции: поскольку полярный радиус неотрицателен , то отрицательные углы у функции рассматривать нельзя.
! Примечание: в ряде случаев принято использовать обобщённые полярные координаты, где радиус может быть отрицательным, и
такой подход мы вкратце изучим чуть позже
Кроме спирали Архимеда, есть множество других известных кривых, но искусством, как говорится, сыт не будешь, поэтому я подобрал примеры, которые
очень часто встречаются в реальных практических заданиях.
Сначала простейшие уравнения и простейшие линии:
Уравнение вида задаёт луч, исходящий из полюса. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было
Действительно, вдумайтесь, если значение угла всегда (каким бы ни было
«эр») постоянно, то какая это линия?
Примечание: в обобщённой полярной системе координат данное уравнение задаёт прямую, проходящую через полюс.
Уравнение вида определяет… догадайтесь с первого раза – если для
любого угла «фи» радиус остаётся постоянным? Фактически это определение окружности с центром в полюсе радиуса .
Например, . Для наглядности найдём уравнение этой линии в прямоугольной
системе координат. Используя полученную ранее формулу , проведём замену:
Возведём обе части в квадрат:
– уравнение окружности с центром в начале координат радиуса 2, что и
требовалось проверить.
А теперь оценИте удобство – с окружностью значительно выгоднее работать именно в полярных координатах по причине предельной простоты уравнения .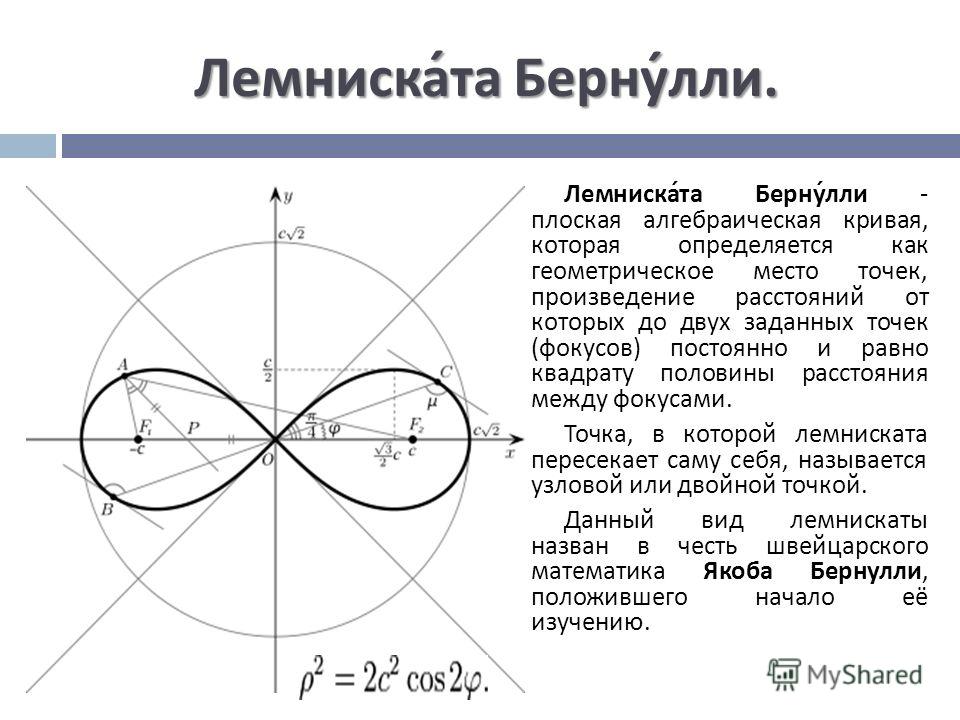
Рассмотрим более содержательные задачи на построение:
Задача 116
Построить линию
Решение: в первую очередь найдём область определения. Так как полярный радиус неотрицателен, то должно выполняться
неравенство . Можно вспомнить школьные правила решения тригонометрических
неравенств, но в простых случаях как этот,
я советую более быстрый графический метод решения:
– Посмотрим на график функции (см. Приложение
Тригонометрия). Что означает неравенство ? Оно
означает, что нас устраивает тот кусок графика, который не ниже оси абсцисс , а именно, его часть на отрезке . И,
соответственно, интервал не подходит. Таким образом, область определения нашей
функции: , то есть график расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).
В полярных координатах часто бывает смутное представление о том, какую линию определяет то или уравнение, поэтому чтобы её построить, необходимо
найти принадлежащие ей точки – и чем больше, тем лучше. Обычно ограничиваются десятком-другим (а то и меньшим количеством). Проще всего, конечно
же, взять табличные значения угла.
Для бОльшей ясности к отрицательным значениям угла я буду «прикручивать» один оборот
(левая колонка), и в силу чётности косинуса соответствующие положительные значения можно заново не считать (справа):
Изобразим полярную систему координат и отложим найденные точки, при этом одинаковые значения «эр» удобно откладывать за один раз, делая парные
засечки циркулем по рассмотренной ранее технологии:
В принципе, линия отчётливо прорисовывается, но чтобы
стопроцентно подтвердить догадку, давайте найдём её уравнение в декартовой системе координат. Можно применить недавно выведенные формулы , но я расскажу вам о более хитром приёме.
Можно применить недавно выведенные формулы , но я расскажу вам о более хитром приёме.
Обе части уравнения искусственно домножаем на «эр»: и используем более компактные формулы перехода:
Выделяя полный квадрат, приводим уравнение к понятному виду:
– уравнение окружности с центром в
точке , радиуса 2.
Коль скоро по условию требовалось просто выполнить построение и всё, плавно соединяем найденные точки линией. Ничего страшного, если получится
немного неровно, вы же не обязаны были знать, что это окружность 😉
Почему мы не рассмотрели значения угла вне промежутка ?
Ответ прост: нет
смысла. Ввиду периодичности функции нас ждёт бесконечный «бег» по
построенной окружности.
Несложно провести нехитрый анализ и прийти к выводу, что уравнение вида задаёт окружность диаметра с центром в точке .
Образно говоря, все такие окружности «сидят» на полярной оси и обязательно проходят через полюс. Если же , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).
Если же , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).
Похожая задача для самостоятельного решения:
Задача 117
Построить линию и найти её уравнение в декартовой системе координат.
Систематизируем порядок решения задачи:
Находим область определения функции, для этого удобно посмотреть на синусоиду (Приложение Тригонометрия), чтобы
сразу же понять, где синус неотрицателен.
На втором шаге рассчитываем полярные координаты точек, используя табличные значения углов; проанализируйте, нельзя ли сократить количество
вычислений?
На третьем шаге откладываем точки в полярной системе координат и аккуратно соединяем их линией.
И, наконец, находим уравнение линии в декартовой системе координат.
Примерный образец решения в конце книги.
Общий алгоритм и технику построения в полярных координатах мы детализируем и существенно ускорим совсем скоро, но перед этим
познакомимся ещё с одной распространённой линией:
4. 5. Полярная роза
5. Полярная роза
4.3. Взаимосвязь прямоугольной и полярной системы координат
| Оглавление |
Автор: Aлeксaндр Eмeлин
Полярные координаты — определение и вычисление с примерами решения
Содержание:
Полярные координаты
Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол
Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до и значения ф от 0 до , при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.
Связь между прямоугольными и полярными координатами
Рассмотрим переход от полярных координат к прямоугольным и обратно.
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).
Тогда для произвольной точки М имеем
Считая угол ф острым, из прямоугольного треугольника АОМ находим
Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты.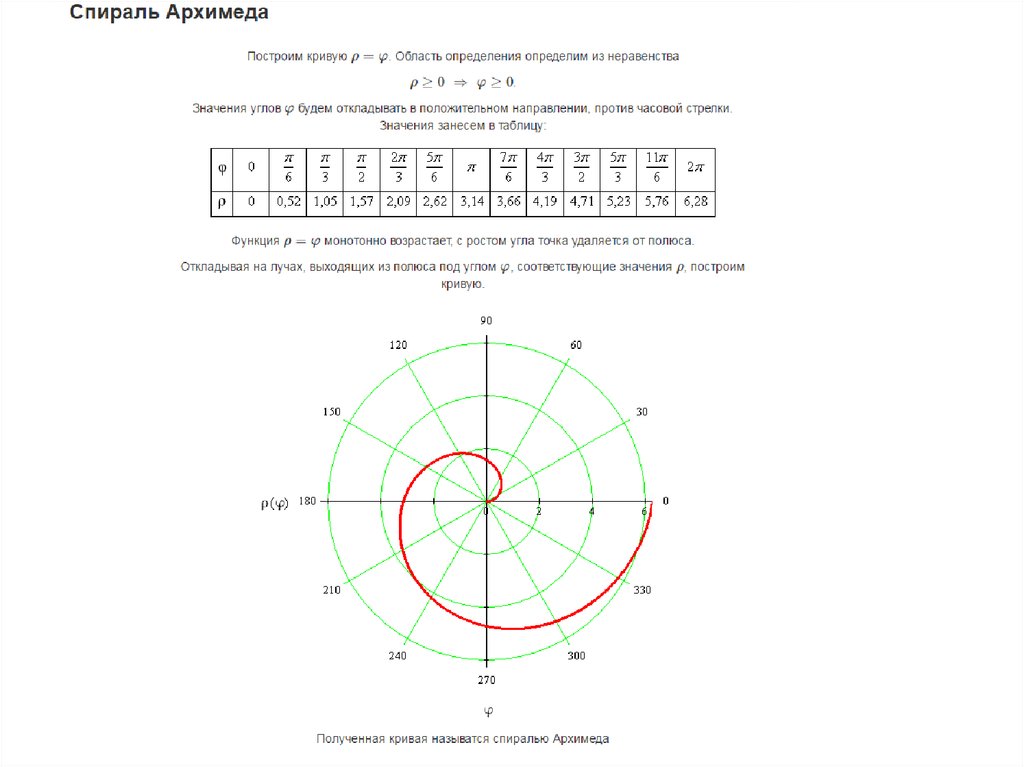 Далее, из этого же прямоугольного треугольника АОМ получаем
Далее, из этого же прямоугольного треугольника АОМ получаем
Так выражаются полярные координаты точки через ее прямоугольные координаты.
Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.
Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.
Пример:
Рассмотрим кривую , где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:
По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).
Параметрические уравнения линии
Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты , рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра).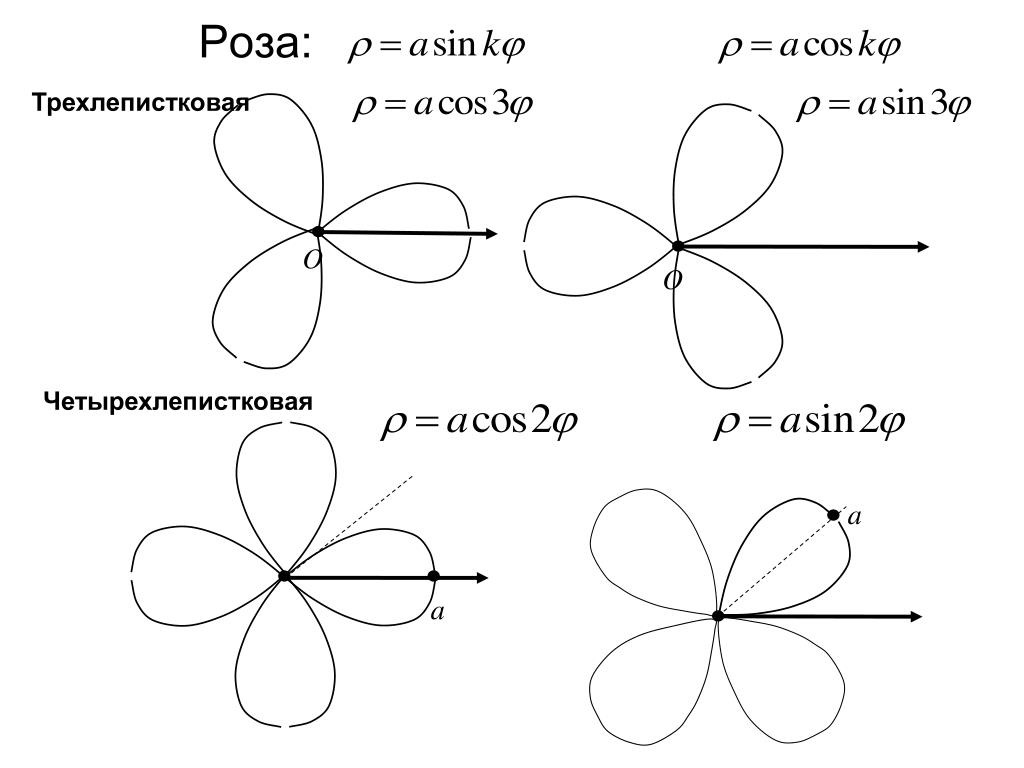 Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).
Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).
Пример:
Выведем параметрические уравнения окружности.
Пусть М — произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства
Это и есть параметрические уравнения окружности.
Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:
Пример:
Выведем параметрические уравнения эллипса.
Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где
За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: . Используя формулы (2), имеем
Используя формулы (2), имеем
Таким образом, параметрические уравнения эллипса с полуосями а и b есть
Исключив из уравнений (3) параметр получим каноническое уравнение эллипса
Имея параметрические уравнения линии, можно по точкам построить ее.
Пример:
Построить кривую
Решение:
Составляем таблицу значений:
Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим т. е. каноническое уравнение параболы.
Параметрические уравнения циклоиды
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).
Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем
За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем
Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:
Таким образом, параметрические уравнения циклоиды есть
——-
Полярная система координат
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), . Точка О при этом называется
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: (1)
Рис.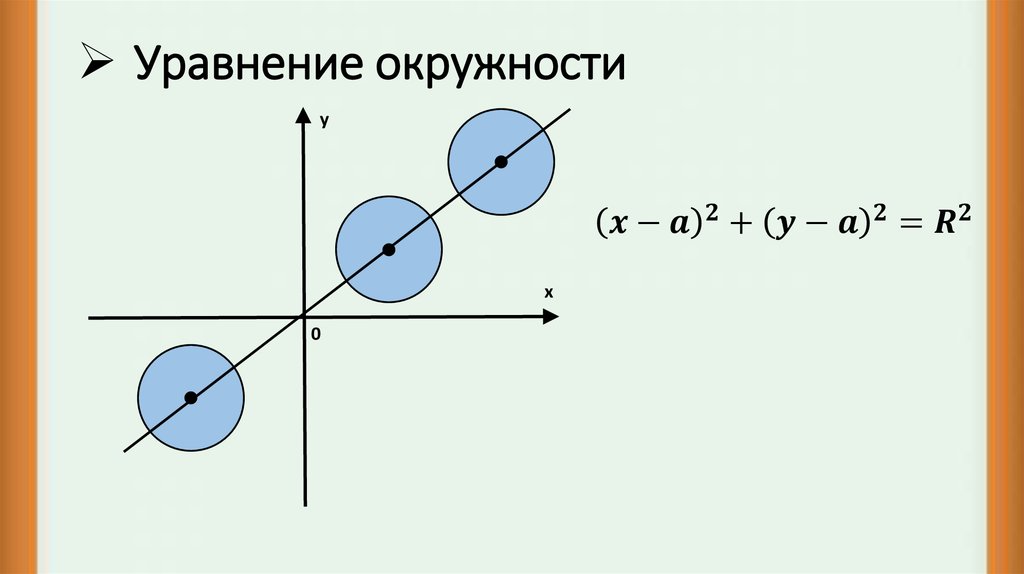
1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:
Пример 1.
Построим на плоскости линию, заданную уравнением:
− лемниската.
Решение.
Вычислим значения r при различных значениях ϕ :
Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :
Рис.3. Лемниската
- Заказать решение задач по высшей математике
Пример 2.
а) Построим кривую − кардиоида. Рассуждая, как в примере 1 получим:
Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).
При этом, если r > 0, то векторы сонаправлены, если r
Тогда, с учетом (1), кривую r= r(ϕ) можно рассматривать как заданную параметрически в виде:
ϕ — параметр.
В этом случае на кривой получаются два дополнительных
лепестка, когда соответствующие случаю r
(см.пример 9 § 30).
На кривой каждый из лепестков проходится дважды и
задается параметрически формулами:
(см.пример 10 § 30).
Пусть r = r(ϕ) – кривая в полярной системе координат, r (ϕ) – непрерывна при . Рассмотрим на плоскости ( x, O, y) криволинейный сектор
Найдем его площадь. Заметим, что сектору Ф
соответствует обычная криволинейная трапеция на плоскости (O, r, ϕ)
Разобьем фигуру Ф на n частичных фигур лучами На плоскости (O, r, ϕ) получаем обычное разбиение
трапеции:
Рассмотрим, например, нижние суммы Дарбу:
Каждое слагаемое в нижней сумме равно площади обычного кругового
сектора радиуса
таким образом,
(2) для нижних сумм и (3) для верхних сумм Дарбу, где Суммы (2) и (3) – суммы Дарбу для функции (см.формулы (5) § 24), поэтому (4)
Пример 3.
Найти площадь ограниченную лемнискатой (см.пример 1).
Решение.
По формуле (4):
площадь одного лепестка.
Поэтому
Пример 4.
Найти площадь фигуры ограниченной линиями: и (вне круга).
Решение. Найдем точки пересечения кривых: По формуле (4):
Пример 3.
r=2cosϕ. Вычислим
− окружность радиуса 1 с центром в точке (1; 0).
При изменении ϕ от 0 до 2 π окружность проходится дважды и оба раза против
часовой стрелки, поэтому (см. § 30) найденное значение интеграла задает
удвоенную площадь круга.
Полярная система координат
Содержание статьи
1. Образование полярной системы координат
2. Связь между прямоугольными и полярными координатами
3. Некоторые важнейшие кривые
Образование полярной системы координат
На плоскости, кроме декартовой прямоугольной системы координат, используют также полярную систему координат.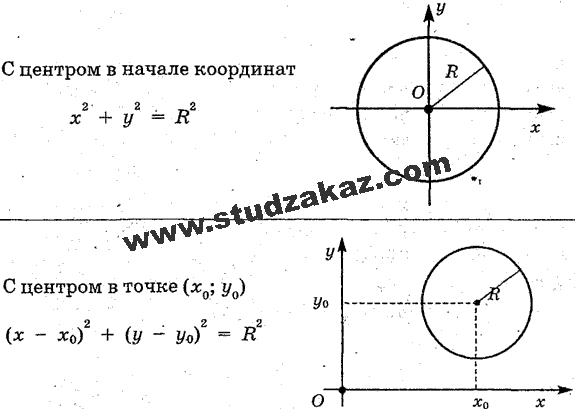 {2} $. Уравнение той же окружности в полярной системе координат: $rho =R$.
{2} $. Уравнение той же окружности в полярной системе координат: $rho =R$.
Полярная система координат вводится следующим образом. На плоскости вибираем некоторую точку $O$, которая называется полюсом. Из этой точки проводим луч $Ox$, который называется полярной осью. Выбираем линейный масштаб для измерения длин отрезков. Для измерения углов выбираем или градусную, или радианную меру.
Положение точки $M$ на плоскости определяют два числа: число $rho $ — расстояние точки $M$ от полюса (полярный радиус $OM$), а также число $phi $ — угол, образованный полярным радиусом с полярной осью (полярный угол). Положительным направлением отсчета угла $phi $ считается направление против часовой стрелки.
Числа $rho $ и $phi $ называются полярными координатами точки $Mleft(rho ,; phi right)$. При этом полярный радиус $rho ge 0$, а полярный угол $0le phi
Связь между прямоугольными и полярными координатами
Между полярными и декартовыми прямоугольными координатами точки $M$ можно установить связь. {3} }{a-x} } $.
{3} }{a-x} } $.
При построении графика строфоиды поступаем аналогично.
Для построения графиков кардиоиды и лемнискаты такой прием не подходит, так как разрешить их уравнения в декартовой прямоугольной системе координат относительно $y$ невозможно.
Поэтому рекомендуется использовать уравнения этих кривых в полярных координатах по следующей схеме: задать значение угла $phi $ в градусах (так удобнее), перевести это значение в радианы, в соответствии с уравнением кривой вычислить значение $rho $, вычислить декартовы координаты $x$ и $y$ по формулам $x=rho cdot cos phi $ и $y=rho cdot sin phi $. Теперь можно строить график обычным образом.
Сообщество экспертов Автор24
Автор этой статьи
Дата последнего обновления статьи: 25.11.2021
Проект «Исследование полярной системы координат»
Министерство образования и науки Российской Федерации
Муниципальное автономное образовательное учреждение
«Лицей №14 имени Заслуженного учителя Российской Федерации А. М. Кузьмина».
М. Кузьмина».
ПРОЕКТ
на тему: «Исследование полярной системы координат».
Выполнила:
Учащаяся 11 класса «Б»
Бросалина Татьяна Витальевна
Подпись ____________
Научный руководитель:
Ондрикова Елена Вячеславовна,
учитель математики
Оценка ______________
Дата ________________
Подпись _____________
Тамбов, 2016
СОДЕРЖАНИЕ
- Введение………………………………………………………………….
 ……. 3
……. 3 - Полярная система координат………………………………………….……..4
- Связь между полярными и декартовыми координатами………………….. 6
- Уравнения кривых в полярных координатах………………………………..8
4.1 Окружность………………………………………………………………..8
4.2 Спираль Архимеда………………………………………………………..9
4.3 Логарифмическая спираль ………………………………………………10
4.4 Гиперболическая спираль………………………………………………..12
4.5 Семейство роз Гранди …………………………………………………..13
4.6 Улитка Паскаля и кардиоида………………………………………………15
5. Вывод …………………………………………………………………………20
- Список используемой литературы………………………………………….21
ВВЕДЕНИЕ
Любая точка на плоскости может быть задана координатами и легко определяется в пространстве с помощью различных систем координат. Не во всех случаях рационально и удобно использовать привычную нам прямоугольную декартовую систему координат. Существуют и другие способы определения точки на плоскости или в пространстве.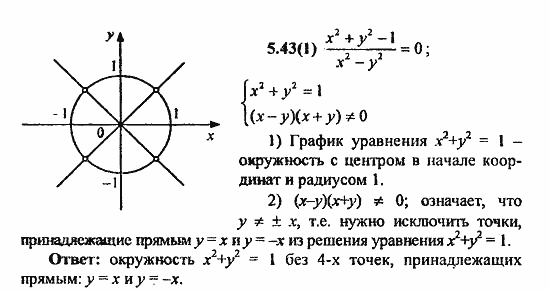 Выбор этих способов зависит от разнообразных факторов, например, от желаемой наглядности полученного результата. Наиболее часто используются полярные, цилиндрические и сферические координаты.
Выбор этих способов зависит от разнообразных факторов, например, от желаемой наглядности полученного результата. Наиболее часто используются полярные, цилиндрические и сферические координаты.
Именно полярная система координат и является объектом исследования данной работы. Такая система координат хорошо и естественно отображает природные формы, и может познакомить учащихся с красивейшими результатами математической науки. Различные кривые, построенные в такой системе координат, имеют сходства с растениями и животными окружающего мира, и вследствие этого обладают эстетической привлекательностью. Таким образом, предметом исследования выбраны уравнения кривых, заданные в полярной системе координат.
Данная тема является актуальной на сегодняшний день, т.к. не каждая школьная программа включает в себя изучение полярной системы координат, несмотря на то, что не все графики удобно строить в декартовой системе. Правильный выбор системы координат может значительно упростить решение той или иной задачи.
Целью данной исследовательской работы является изучение полярной системы координат, ознакомление с важнейшими математическими кривыми, а также приобретение навыка решения простейших задач в полярной системе координат.
Задачи, требующие выполнения в ходе исследовательской работы:
- изучить основную теорию о полярной системе координат
- сравнить полярную систему координат с декартовой
- рассмотреть важнейшие математические кривые и их применение в жизни
- научиться решать простейшие задачи в полярной системе координат
ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ
Полярная система координат — двухмерная система координат, каждая точка в которой однозначно определяется на плоскости двумя числами — полярным радиусом и полярным углом.
Чтобы определить полярную систему координат на плоскости следует отметить произвольную точку O, которая называется полюсом, и луч OX, называемый полярной осью. Также следует задать масштабный отрезок, с помощью которого и будет измеряться расстояние от какой-либо точки на плоскости до полюса. Как правило, задается единичный вектор , длина которого и является масштабным отрезком. Направление данного вектора задает положительное направление полярной оси.
Как правило, задается единичный вектор , длина которого и является масштабным отрезком. Направление данного вектора задает положительное направление полярной оси.
Рис.1
Положение любой точки M определяется в полярной системе координат полярным радиусом — расстоянием r от точки M, до полюса, т.е. r = ||, и полярным углом — углом φ между вектором и полярной осью. Полярные радиус и угол составляют полярные координаты точки M, что записывается в виде M(r,φ).
Полярный радиус можно определить для любой точки области, при этом он, так как расстояние не может быть отрицательным, всегда будет больше либо равен нулю (r ≥0).
Полярный угол можно определить для любой точки плоскости, кроме самого полюса О, при этом он, как правило, изменяется в пределах –π
Полярный угол отсчитывается от полярной оси в положительном направлении, т.е. против часовой стрелки, если значение угла положительное, а в отрицательном направлении, т.е. по часовой стрелке, если значение угла отрицательное.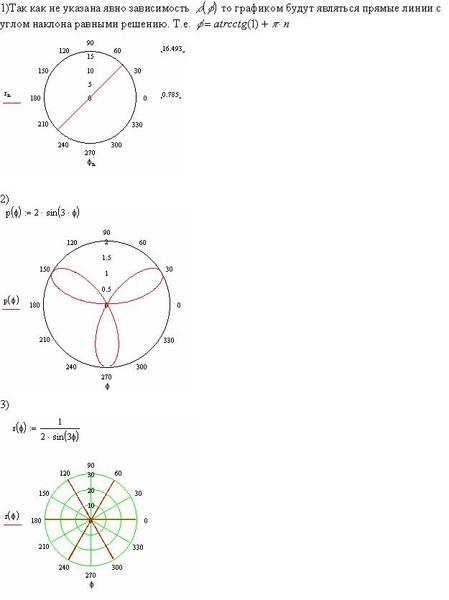 Измеряется в радианах.
Измеряется в радианах.
Таким образом, точка с координатами (5, 30°) на графике – это точка, принадлежащая лучу, который лежит под углом 30° к полярной оси, на расстоянии пяти единичных отрезков. Точка с координатами (5, -330) будет расположена на том же месте. В этом заключается одна из главнейших особенностей полярной системы координат – одна и та же очка может быть представлена бесконечным количеством разных способов.
Принято считать, что термин «полярные координаты» ввел итальянский математик, Грегорио Фонтана. В английский же язык термин перешел в 1816 году, когда Джордж Пикок перевел трактат «Дифференциальное и интегральное исчисление», написанный Сильвестром Лакруа. Французский математик Алекси Клеро впервые применил полярные координаты для трехмерного пространства, а Леонард Эйлер был первым ученым, разработавшим систему таких координат.
СВЯЗЬ МЕЖДУ ПОЛЯРНЫМИ И ДЕКАРТОВЫМИ КООРДИНАТАМИ
В школе ученики обычно строят графики функций в декартовой системе координат. Однако точно такие же построения можно совершать и в полярной системе, что особенно удобно, когда переменная φ не только изображается, но и фактически является углом.
Однако точно такие же построения можно совершать и в полярной системе, что особенно удобно, когда переменная φ не только изображается, но и фактически является углом.
Полярную систему координат Oxφ можно связать с более привычной декартовой системой O следующим способом.
Для перехода из одной системы координат в другую начало декартовой системы O должно совпадать с полюсом полярной системы, а ось абсцисс с полярной осью, сохранив направление вектора. Следом, перпендикулярно оси абсцисс, достраивается ось ординат так, чтобы, проходя через точку O, она образовывала декартовую систему координат, как показано на рисунке.
Рис.2 Рис.3
И, наоборот, из декартовой системы координат можно легко перейти в полярную. Для этого следует принять положительную ось абсцисс за полярную ось.
Теперь рассмотрим связь полярных и декартовых координат точки. Из рисунка 3 можно увидеть, что вектор является диагональю в прямоугольнике, со сторонами x и y, которые являются декартовыми координатами точки M. Из этого следует, что искомое расстояние r можно найти с помощью теоремы Пифагора по формуле . Кроме того, из рисунка видно, что
Из этого следует, что искомое расстояние r можно найти с помощью теоремы Пифагора по формуле . Кроме того, из рисунка видно, что
Таким образом, можно найти декартовые координаты, если известны полярные. В противоположном случае действуют следующие формулы:
При определении главного значения полярного угла следует помнить:
- если r = 0, то может принимать любые значения и является произвольным действительным числом;
- если r ≠0, то ограничивают интервалом в 2, обычно выбирают интервал (-π;π] или (0;2π].
Для определения главного значения полярного угла используют следующие формулы:
Углы в полярной системе координат могу измеряться как в градусах, так и в радианах. Выбор единиц измерения зависит, как правило, от области применения. В то время как в математике и почти во всех областях физики наиболее часто используют радианы, в навигации предпочтение отдается именно градусам.
УРАВНЕНИЯ КРИВЫХ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
В полярной системе координат, благодаря ее радиальной природе, многие кривые могут быть описаны гораздо более просто и менее громоздко, нежели в декартовой системе.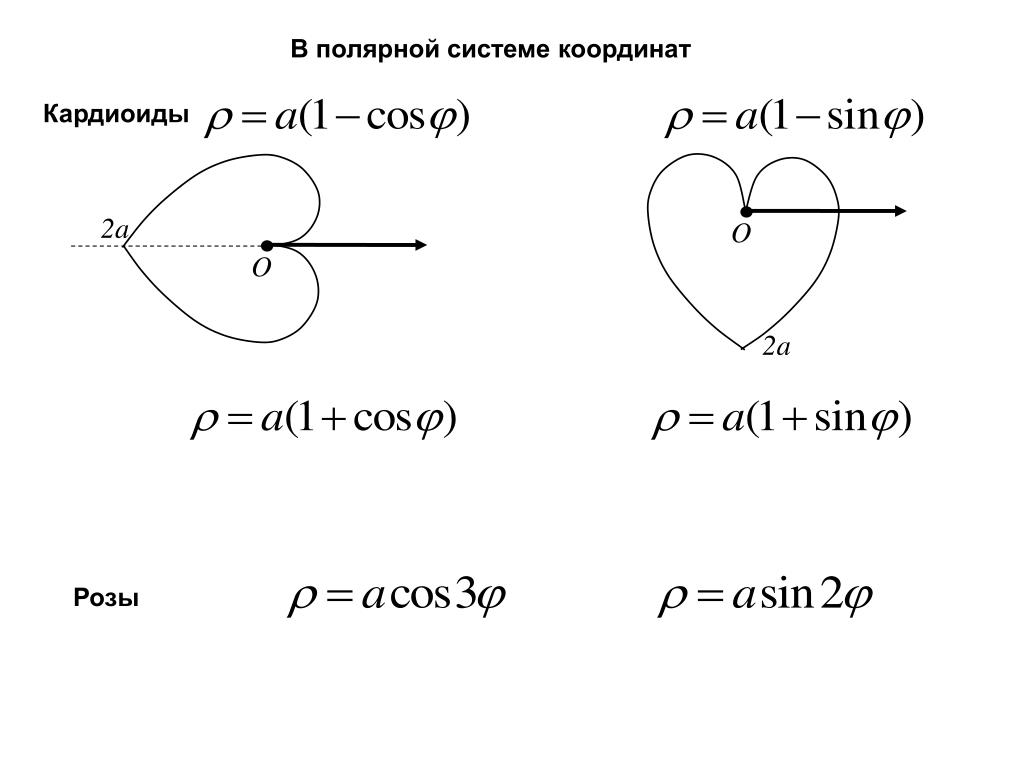 Рассмотрим самые распространенные из них.
Рассмотрим самые распространенные из них.
- ОКРУЖНОСТЬ
Уравнение окружности с центром в полюсе и радиусом a имеет вид r(φ)=a
Очевидно, что графиком этой функции является совокупность точек, расположенных на равном расстоянии от полюса при любом угле, т.е. окружность.
Для того, чтобы ее построить, зададим несколько значений для полярного угла и найдем соответствующие значения радиуса.
|
φ |
0 |
π |
2π |
||||||
|
r |
а |
а |
а |
а |
а |
а |
а |
а |
а |
На графике ниже можно увидеть построение окружности r(φ)=а.
Окружность, центром которой не является полюс, можно построить по точкам, или уравнением +=, центр окружности в таком случае находится в точке (;.
- СПИРАЛЬ АРХИМЕДА
Чтобы представить спираль Архимеда, отметим точку на секундной стрелке часов и будем перемещать ее вдоль этой стрелки, независимо от движения самой стрелки. Тогда точка опишет кривую, которая носит название «спираль Архимеда».
Данная кривая задается уравнением r=aφ, где a – коэффициент пропорциональности.
Пусть a=1. Для того, чтобы построить такую спираль, зададим несколько значений для полярного угла и найдем соответствующие значения радиуса.
|
φ |
0 |
π |
2π |
||
|
r |
0 |
π |
2π |
Отметим на лучах φ=0, φ=, и т.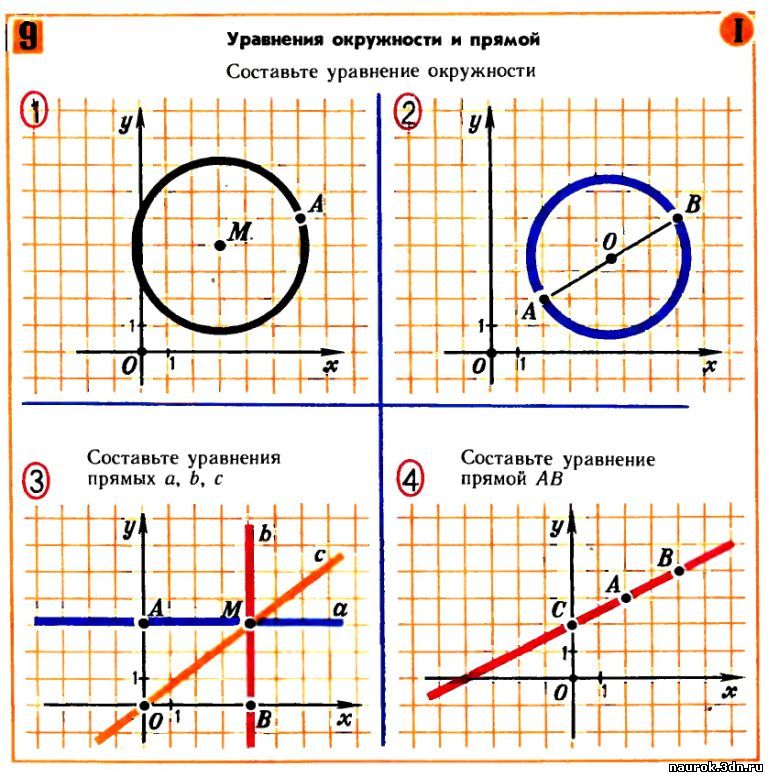 д. соответствующие значения r. Можно заметить, что при увеличении φ будет возрастать и r, что можно увидеть на графике ниже.
д. соответствующие значения r. Можно заметить, что при увеличении φ будет возрастать и r, что можно увидеть на графике ниже.
Открытие данной кривой приписывается Коннону Самосскому, но впервые описал все ее свойства именно Архимед. Главное из этих свойств заключается в том, что расстояние между двумя витками в данной спирали всегда остается постоянной величиной. Благодаря этому свойству, с помощью спирали Архимеда можно легко разделить любой угол на равные части.
В технической области спираль Архимеда применяется в кулачковых механизмах, преобразующих вращательное движение шайбы и поступательное движения стержня. Также форму спирали Архимеда играет и звуковая дорожка на пластинке.
- ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ
Логарифмическую спираль описывает точка, отмеченная на секундной стрелке, которая движется по этой стрелке не с постоянной скоростью, как в спирали Архимеда, а с возрастающей пропорционально расстоянию от центра часов.
Данная кривая задается уравнением r=a, где k – это коэффициент, который отвечает за расстояние между витками.
Пусть k=1. Для того, чтобы построить такую спираль, зададим несколько значений для полярного угла и найдем соответствующие значения радиуса.
|
φ |
0 |
π |
2π |
||
|
r |
а |
4,78а |
22,88а |
110,56а |
523,65а |
Логарифмическая спираль имеет несколько интересных свойств:
- Расстояния между последовательными витками составляют геометрическую прогрессию.
- Образующиеся в результате отсекания кривой радиусами секторы подобны друг другу.
- Последовательность длин радиусов, которые составляют одинаковые углы друг с другом, так же образуют геометрическую прогрессию
- Не изменяет своей природы при таких преобразованиях, как ее сжатие или растяжение относительно полюса, или при ее повороте на определенный угол.
В математике логарифмическая спираль впервые упоминается Декартом в 1638 году. Он описал ее, как линию, отношение длины дуги которой к соответствующему радиусу остается константой.
На свойстве логарифмической спирали пересекать все свои радиус-векторы под одним углом основаны ее применения в технике. Например, вращающиеся ножи нередко имеют схожую форму, вследствие чего угол резания по всей поверхности ножа остается постоянным, что делает его менее изнашиваемым.
- ГИПЕРБОЛИЧЕСКАЯ СПИРАЛЬ
Гиперболическая спираль задается уравнением r=, которое является обратным для уравнения спирали Архимеда.
Пусть a=1. Для того, чтобы построить такую спираль, зададим несколько значений для полярного угла и найдем соответствующие значения радиуса.
|
φ |
π |
2π |
||
|
r |
0,31 |
0,15 |
Особенностью гиперболической спирали является тот факт, что при φ, r, то есть полюс является асимптотической точкой данной кривой.
Более того, из треугольника MNO видно, что отрезок MN= r.
Таким образом, при φ, MN, то есть прямая, проходящая параллельно полярой оси и удаленная от нее на расстояние a, является асимптотой данной спирали.
- СЕМЕЙСТВО РОЗ ГРАНДИ
Роза – это плоская кривая, которая формой напоминает изображение цветка. Она задается формулой r = a, где a – постоянная, определяющая размер лепестков, а – постоянная, определяющая количество лепестков данной розы.
При вся кривая расположена внутри окружности радиусом a, а график состоит из одинаковых по форме и размеру лепестков. Причем, если четное, то количество лепестков будет 2, а если нечетное, то просто
При кривая расположена вне окружности и образована точкой, движущейся по внешней стороне окружности.
На данном рисунке можно увидеть, как изменяется роза в зависимости от .
Рассмотрим графики четырех- и трехлепестковых роз.
Трехлепестковая кривая задается уравнением r=a.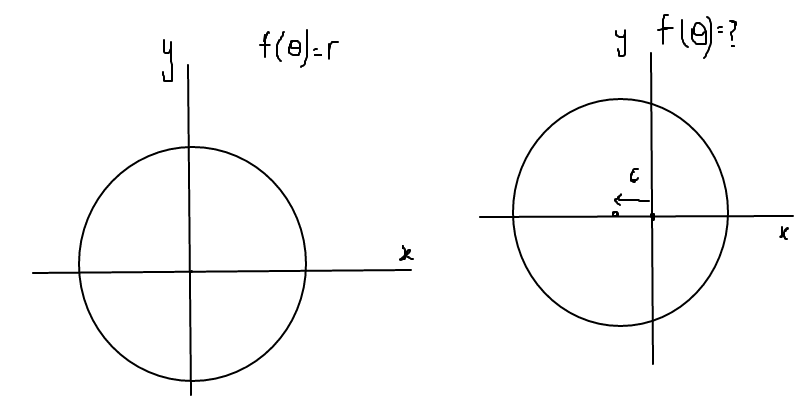
Пусть a=1. Для того, чтобы построить такую кривую, зададим несколько значений для полярного угла и найдем соответствующие значения радиуса.
Так как все лепестки розы одинаковы, то можно найти значения радиуса лишь для одного лепестка и отобразить полученный график.
Найдем область определения функции. Поскольку полярный радиус неотрицателен, то должно выполняться неравенство sin3φ≥0, решая которое находим область допустимых углов: φ[0; ][][]
|
φ |
0 |
||||
|
3φ |
0 |
||||
|
0 |
0,7 |
1 |
0,7 |
0 |
Четырехлепестковая кривая задается уравнением r=a.
Пусть a=1. Для того, чтобы построить такую кривую, зададим несколько значений для полярного угла и найдем соответствующие значения радиуса.
Так как все лепестки розы одинаковы, то можно найти значения радиуса лишь для одного лепестка и отобразить полученный график.
|
φ |
0 |
||||||
|
2φ |
0 |
||||||
|
0 |
0,5 |
0,86 |
1 |
0,86 |
0,5 |
0 |
Семейство роз Гранди было открыто в XVIII в. итальянским геометром Гвидо Гранди. Эти кривые нашли широко применяются в технике. Напимер, если некоторая точка совершает колебание вдоль прямой, вращающейся с постоянной скоростью вокруг неподвижной точки, которая называется центром колебаний, то траектория этой точки будет описываться именно розой Гранди.
итальянским геометром Гвидо Гранди. Эти кривые нашли широко применяются в технике. Напимер, если некоторая точка совершает колебание вдоль прямой, вращающейся с постоянной скоростью вокруг неподвижной точки, которая называется центром колебаний, то траектория этой точки будет описываться именно розой Гранди.
- УЛИТКА ПАСКАЛЯ
Улитка Паскаля задается уравнением r=2R, где R – радиус данной окружности.
Построим кривую при a=2R. В таком случае уравнение принимает вид r=1). График такой функции является частным случаем улитки Паскаля и называется кардиоидой.
Пусть a=1. Для того, чтобы построить такую кривую, зададим несколько значений для полярного угла и найдем соответствующие значения радиуса.
|
φ |
0 |
|||||||
|
1 |
0,86 |
0,7 |
0 |
-0,5 |
-0,7 |
-0,86 |
-1 |
|
|
1) |
2 |
1,86 |
1,7 |
1 |
0,5 |
0,3 |
0,14 |
0 |
Стоит отметить, что если в уравнении r=2R, , то радиус будет находиться по формуле r=2R, которая является уравнением окружности с радиусом r.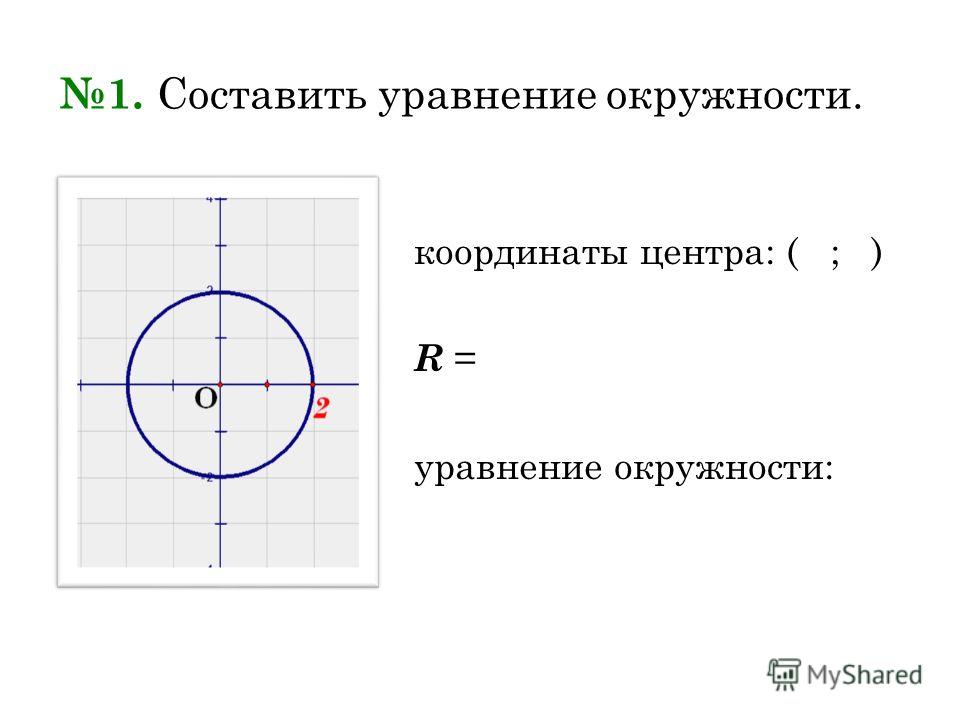
ЗАДАЧИ
Задача 1. Найти полярные координаты точки М (1; ) , если полюс совпадает с началом координат, а полярная ось — с положительным направлением оси абсцисс.
Решение:
Из теории известно, что . Кроме того, из рисунка видно, что
, следовательно =.
На основании этих равенств находим = ; =. Очевидно, что точка М лежит в IV четверти и, следовательно, =.
Итак, М (2;).
Ответ: (2;).
Задача 2. Найти прямоугольные координаты точки А (; ). если полюс совпадает с началом координат, а полярная ось направлена по оси абсцисс.
Решение:
Из теории известно, что , следовательно:
х==2;
y==2.
Таким образом, А (2;2).
Ответ: (2;2).
Задача 3. Определить расстояние между точками (3; ) и (4; ).
Решение:
Рассмотрим треугольник O. По теореме косинусов:
= =) = =5.
Ответ: 5
Задача 4.1. Точка М равномерно перемещается по лучу, вращающемуся равномерно около полюса. Составить уравнение линии, описанной точкой М, если в начальный момент вращающийся луч совпадает с полярной осью, а точка М – с полюсом; при повороте же луча на угол = 1 радиан, точка М удалилась от полюса на расстояние а.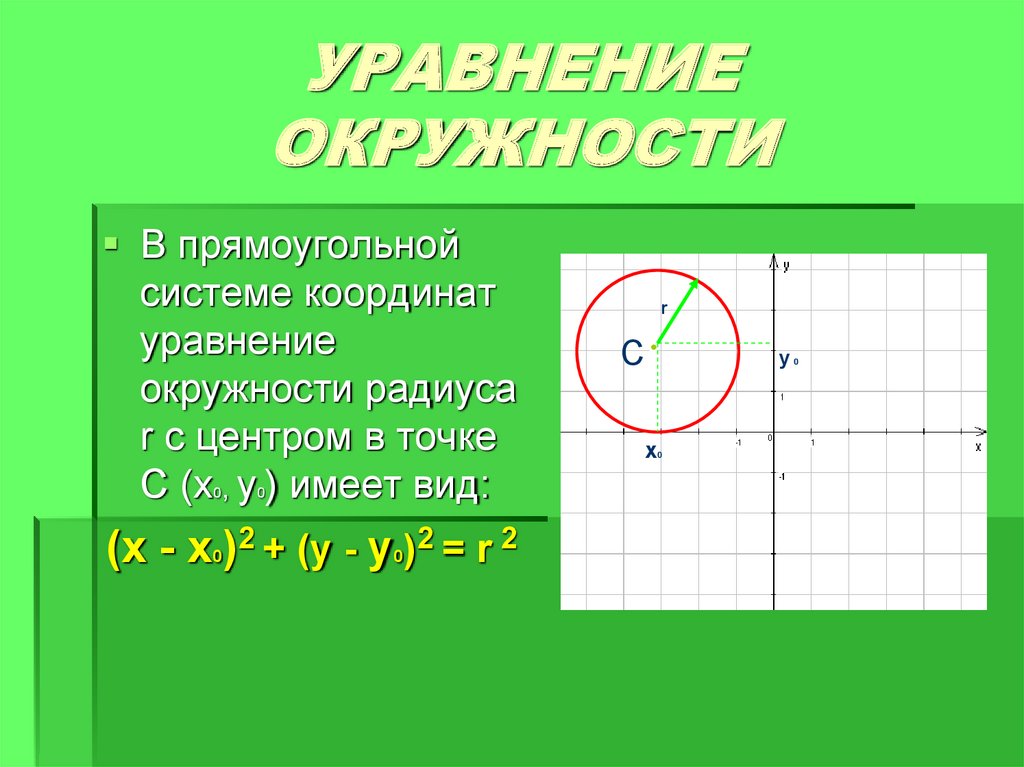
Решение: Поскольку в начальный момент величины r и равны нулю, а затем обе возрастают пропорционально времени, легко заметить, что они связаны прямой пропорциональной зависимостью: =const. Но r = а при = 1, следовательно, =, т.е. r =. Кривая r = называется спиралью Архимеда. Построение данной кривой рассматривалось в этой исследовательской работе ранее.
Задача 4.2. Окружность диаметра а катится без скольжения по внешней стороне другой окружности такого же диаметра. Составить в полярных координатах уравнение линии, описанной некоторой фиксированной точкой катящейся окружности.
Решение:
На рисунке – это первоначальное положение центра катящейся окружности, A — первоначальное положение точки, описывающей искомую линию. Причем точка А диаметрально противоположна точке В, где в начальный момент соприкасаются окружности, -центр неподвижной окружности, — центр катящейся окружности в новом положении, — новое положение точки , описывающей искомую линию. После перемещения окружности в положение точка займет положение . Точка займет положение .
Точка займет положение .
Так как качение происходит без скольжения, то = , =. На чертеже показано положение полюса О и пол󠆻ярной оси Ох. Требуется составить уравнение, которому удовлетворяют координаты любой точки М (r; ) искомой линии. Можно заметить, что = O, в силу чего четырехугольник O является равнобедренной трапецией с меньшим основанием = а, ; и перпендикуляры, опущенные из точек и на прямую О.
Итак, r =++= + a+ =a(1+).
Таким образом, уравнение искомой линии в полярных координатах имеет вид r = a(1+). Эта кривая называется кардиоидой. Построение данной кривой рассматривалось в этой исследовательской работе ранее.
Задача 5. Вычислить площадь, заключенную внутри лемнискаты Бернулли r2 = a2cos 2φ
Решение:
В полярной системе координат площадь фигуры, ограниченной дугой кривой r = f(φ) и двумя полярными радиусами φ1 = и φ2 = , выразится следующим интегралом:
S =d.
В силу симметрии кривой определяем сначала одну четвертую искомой площади:
S = d = = .
Следовательно, вся площадь равна S = a2.
Ответ: a2
ВЫВОД
Таким образом, цели, поставленные в данной работе, достигнуты. Основная теория о полярной системе координат изучена. В ходе данной исследовательской работы были рассмотрены важнейшие математические кривые и их применение в жизни, а также были приобретены навыки решения простейших задач, связанных с полярной системой координат, что значительно упрощает решение некоторых задач.
СПИСОК ЛИТЕРАТУРЫ
- В.К. Егерев, Б.А. Радунский, Д.А.Тальский. «Методики построения графиков функций»
- А.А. Гусак. «Пособие к решению задач по высшей математике»
- Д.В. Клетеник. «Сборник задач по аналитической геометрии»
- П.Е. Данко, А.Г. попов, Т.Я. Кожевникова «Высшая математика в упражнениях и задачах».
- Б.П. Демидович «Сборник задач и упражнений по математическому анализу».
Замена переменной в двойном интеграле. Полярная система координат.
|
Заглавная страница КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 6 из 15Следующая ⇒ Замена переменной в интеграле состоит в переходе от переменных xиyк новым переменным u иv, связанных соотношениями x= X (u, v), y = Y (u,v), (u,v) D. (3.4) При выполнении условий, что отображение (3.4) взаимно однозначно, а функции в соотношении (3.4) непрерывно-дифференцируемы, то якобиан отображения – определитель, составленный из первых частных производных: тогда имеет место формула: (3. 5) Обычно замена переменных производится с целью упрощения области интегрирования. Соотношения (3.4) называют переходом от прямоугольных декартовых координат к криволинейным. Примером криволинейных координат являются полярные координаты, связанные с прямоугольными формулами: , , , (3. ; В полярных координатах полюс совпадает с началом координат, полярная ось – с положительным направлением оси Ох, угол φ (положительный) отсчитывается от полярной оси против часовой стрелки. Якобиан преобразования равен: Если D = , то (3.7) Пример: построить область интегрирования и перейти к полярной системе координат Порядок интегрирования соответствует формуле (3.1): ; верхняя граница Возводя в квадрат правую и левую части и дополняя до полного квадрата разности, получили уравнение окружности с центром ( т.к. в верхнем пределе перед корнем нет знака, то приписывается знак плюс. Т.е. верхняя граница области D – верхняя часть окружности Нижняя граница: Переносим в левую часть и возводим правую и левую часть в квадрат Получили уравнение окружности с центром радиуса Рис. Область интегрирования D — область между двумя выше указанными окружностями. Точка пересечения A ( ). Вся область D находится в первом квадранте, следовательно , но область ограничена двумя разными окружностями. Проведем луч из начала координат в точку А. Тогда область разделится на две части. , следовательно, . Тогда в полярной системе координат область интегрирования и сам двойной интеграл разбиваются на две части: 0≤φ≤π/6 и π/6≤φ≤π/2. Окружность в полярной системе примет вид Окружность в полярной системе примет вид Студентам рекомендуется запомнить следующее правило. Если центр окружности сдвинут по оси Ох вправо, ровно на радиус окружности R, то в полярной системе координат уравнение такой окружности , если влево на радиус, то . Если центр окружности сдвинут на радиус по оси Оy вверх – уравнение окружности в полярной системе , если же центр окружности сдвинут ровно на радиус вниз, то . Окончательно в полярной системе координат двойной интеграл примет вид: I= Пример: начертить область на которую, распространяется двойной интеграл, изменить порядок интегрирования, записать интеграл в полярной системе координат. Рис. 3.9 Уравнение нижней окружности: Уравнение верхней окружности: x ²+ y ²=2. В декартовой системе координат заданный интеграл примет вид: порядок интегрирования изменен, где (нижний предел интегрирования во внутреннем интеграле). Используя вышеприведенное правило в полярной системе координат при π≤φ≤7π/6 двойной интеграл примет вид: — двойной интеграл в полярной системе координат. Геометрические и физические приложения двойного интеграла. Пусть G – материальная пластинка (квадрируемая фигура) на плоскости с плотностью 1. 2. Масса пластины m= 3. Статические моменты пластинки относительно осей Ox и Oy 4. Координаты центра тяжести пластинки 5. Моменты инерции пластинки относительно осей Ox и Oy , 6. Момент инерции пластинки относительно начала координат Пример: вычислить площадь пластины ограниченной линиями: y=x; y=0; y ²-4 y + x ²=0; y ²-8 y + x ²=0 Запишем уравнения линий, ограничивающих область интегрирования: y ² — 4 y + x ² =0 y Окружность с центром, Окружность с центром, сдвинутым по у на 4 единицы сдвинутым по у на 2 единицы Рис. 3.10 Уравнения окружностей, в соответствии с вышеизложенным правило примут вид: ρ=4∙ sinφи ρ=8∙sinφ. Пример: вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением Проведем замену переменных: x=ρcosφ, y= ρsinφ. Тогда заданная кривая в полярной системе координат примет вид: где Рис.3.11 Тогда С учетом того, что cos2 имеет период Т=π, и ρ≥0 параметр С учетом симметрии фигуры (рис. 3.11), вычислим площадь четвертой части и результат умножим на четыре. Вычислим площадь по формуле Площадь всей фигуры, ограниченной данной линией, S=2 . Пример: найти массу пластинка G, если она задана ограничивающими её кривыми (рис. 3.12): x = 0, y = 0, , — поверхностная плотность. Рис. 3.12 Пластинка расположена в прямоугольной системе координат таким образом, что центры окружностей совпадают с началом координат. . Перейдем в двойном интеграле к полярным координатам при этом область G преобразуется в прямоугольную область в полярной системе координат: 2≤ρ≤3, -π/2 ≤φ≤0, поверхностная плотность: Масса плоской пластины вычисляется по формуле: Пример: найти статические моменты относительно координатных осей Ох и Oy однородной фигуры, ограниченной кривыми y²=ax, y=x (рис. 3.13) Т.к. фигура однородная, примем поверхностную плотность μ=const=1. Рис.3.13 Статический момент относительно оси Ох Статический момент относительно оси Оу Тройные интегралы Задача о массе пространственного тела переменной плотности f(x,y,z) приводит к понятию тройного интеграла. Под областью “V”,на которую распространен тройной интеграл, понимается ограниченная замкнутая пространственная область, ограниченная снизу и сверху поверхностями , а с боков – цилиндрической поверхностью с образующими, параллельными оси OZ. Свойства тройного интеграла аналогичны свойствами двойного интеграла. Предыдущая123456789101112131415Следующая Читайте также: Алгоритмические операторы Matlab Конструирование и порядок расчёта дорожной одежды Исследования учёных: почему помогают молитвы? Почему терпят неудачу многие предприниматели? |
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 105; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Фигуры в криволинейных координатах
Фигуры в криволинейных координатах
Криволинейные координаты
Примеры для статьи — polar.zip
Кроме привычной нам прямоугольной декартовой системы координат, в математике используются и другие способы задания положения точки в пространстве или на плоскости. Чаще всего применяются полярные, цилиндрические и сферические координаты. Все эти системы родственны. В них присутствует центральная точка или полюс, от которого расходятся концентрические окружности (полярная система координат), цилиндры (цилиндрическая система) или сферы (сферические координаты). Положение точки определяется при помощи луча, выходящего из полюса и пересекающего в заданном месте соответствующую окружность, цилиндр или сферу. В такие координаты очень естественно укладываются многие природные формы.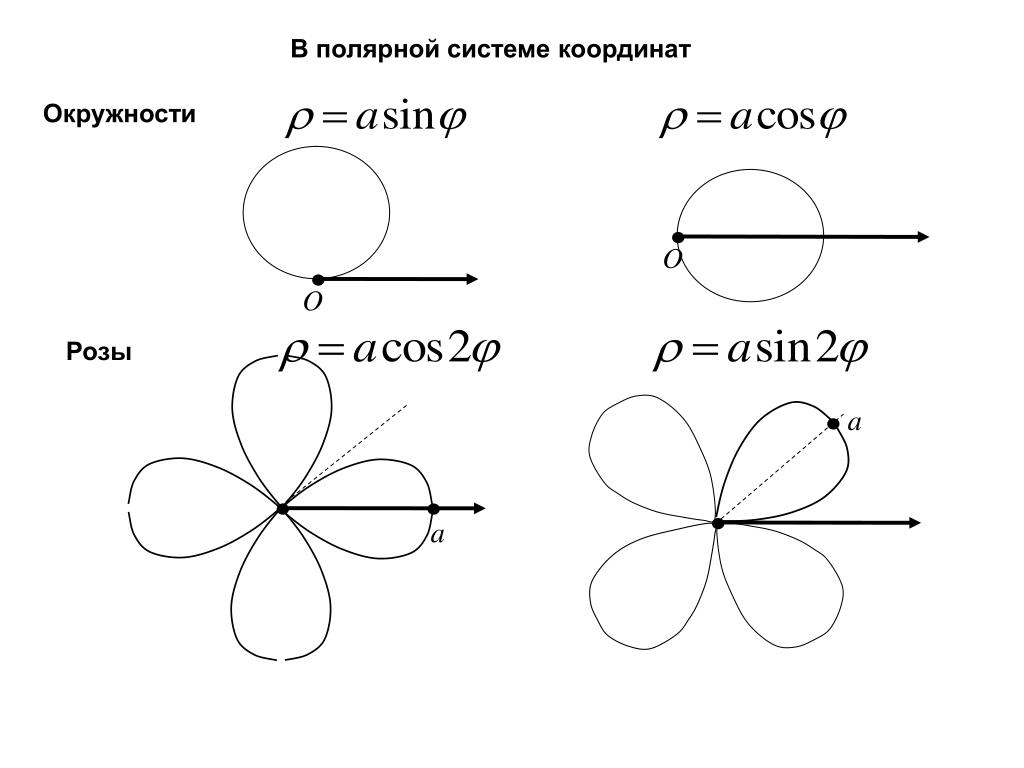 Перечисленные криволинейные системы координат идеально приспособлены для отображения форм, построенных вокруг единой центральной точки. Такая организация характерна для многих биологических объектов. Их формы порой самым удивительным образом напоминают фигуры, образуемые в криволинейных координатах достаточно простыми и лаконичными математическими выражениями. Это сходство указывает на то, что тела живых организмов, биологические структуры, образуются по принципам, сходным с принципами построения «полярных» объектов. Живой организм «начинается» из одной исходной точки, и затем развивается и растет во все стороны по определенному математическому закону. По крайней мере такое предположение совсем не противоречит наблюдаемому в природе обилию «математических», «полярных» форм. Природа как бы сама использует полярные координаты, что особенно бросается в глаза на примере растений, примитивных многоклеточных животных и насекомых. Вероятно поэтому фигуры, построенные в полярных координатах, обладают неповторимой эстетической привлекательностью.
Перечисленные криволинейные системы координат идеально приспособлены для отображения форм, построенных вокруг единой центральной точки. Такая организация характерна для многих биологических объектов. Их формы порой самым удивительным образом напоминают фигуры, образуемые в криволинейных координатах достаточно простыми и лаконичными математическими выражениями. Это сходство указывает на то, что тела живых организмов, биологические структуры, образуются по принципам, сходным с принципами построения «полярных» объектов. Живой организм «начинается» из одной исходной точки, и затем развивается и растет во все стороны по определенному математическому закону. По крайней мере такое предположение совсем не противоречит наблюдаемому в природе обилию «математических», «полярных» форм. Природа как бы сама использует полярные координаты, что особенно бросается в глаза на примере растений, примитивных многоклеточных животных и насекомых. Вероятно поэтому фигуры, построенные в полярных координатах, обладают неповторимой эстетической привлекательностью. Они плотно ассоциируются с формами цветов, бабочек, словом, всем тем, что так много удовольствия доставляет нашему взору в живой природе.
Они плотно ассоциируются с формами цветов, бабочек, словом, всем тем, что так много удовольствия доставляет нашему взору в живой природе.
Полярная система координат
В полярной системе координат положение точки определяется полярным радиусом R и углом theta, образуемым полярным радиусом с полярной осью. Если в декартовой системе координат предельно простое выражение y=kx определяет прямую линию, то это же выражение, переписанное в форме R=k*theta, уже превращается в спираль. Фигуры в полярных координатах образуются как след конца бегающего по кругу полярного радиуса переменной длины. Длина полярного радиуса определяется величиной угла, который в данный момент времени он образует с полярной осью. В цилиндрической системе к полярному радиусу и углу добавляется еще одна координата — z, которую можно интерпретировать как высоту точки над плоскостью, в которой вращается полярный радиус.
Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы:
X=R* Cos (theta) Y=R* Sin(theta)
Соответственно, для перехода от декартовой системы к полярной применяют формулу:
R=Sqr(X*X+Y*Y)
и угол вычисляется как Atn(Y/X) (если X не равен 0)
Фигуры в полярных координатах
Формулы кривых, записанных в полярной системе координат, вычисляются гораздо проще, чем в декартовой. Например, уравнение окружности с радиусом 0.9 вокруг точки отчета выглядит очень просто
Например, уравнение окружности с радиусом 0.9 вокруг точки отчета выглядит очень просто
R=0.9, что подразумевает следующие вычисления:
R*Cos(theta) R*Sin(theta)
где угол theta изменяется от 0 до 2π радиан и определяет декартовы координаты X и Y окружности в полярной системе
Для объяснения вышесказанного приведем небольшой листинг программы, рисующей окружность:
Dim x As Single, y As Single Dim twoPi As Single, I As Single, R As Single twoPi = Atn(1) * 8 Scale (-2, 2)-(2, -2) For I = 0 To twoPi Step 0.05 R = 0.9 x = R * Cos(I) y = R * Sin(I) PSet (x, y) Next I
Полярные координаты позволяют рисовать намного более сложные и красивые фигуры. Например, можно нарисовать четырехлистный клевер. Его формула выглядит как R = Cos (2*theta), где угол theta меняется от 0 до 2π радиан (от 0 до 360 градусов)
Листинг для клевера
Dim x As Single, y As Single Dim twoPi As Single, I As Single, R As Single twoPi = Atn(1) * 8 Scale (-2, 2)-(2, -2) For I = 0 To twoPi Step 0.01 R = Cos(2 * I) x = R * Cos(I) y = R * Sin(I) PSet (x, y) Next I
Для трехлистного цветка используйте формулу R = Cos (3*theta)
На протяжении многих лет ученые собирали информацию о формулах, рисующих разные фигуры. Многие фигуры получили свои названия. Список таких названий внушителен.
- Дельтоида
- Астроида
- Кардиоида
- Лимакона (Улитка Паскаля)
- Спираль Архимеда
- Логарифмическая спираль
- Кохлеоида
- Строфоида
- Freeth’s Nephroid
- Овалы Кассини
- Лемниската Бернулли
Окружность
Итак, формула R=a определяет обычную окружность, а коэффициент a влияет на ее радиус
«Пируэты» окружности
Возьмем теперь одну окружность и поместим ее внутрь другой. Все кривые, которые будет вычерчивать точка на окружности, катящейся внутри другой окружности, будут относиться к семейству гипоциклоид (от греч. гипо — под, внизу и киклоидес — кругообразный). 3 рисует астроиду,
3 рисует астроиду,
где коэффициент a влияет на вытянутость фигуры.
Эпициклоиды
Рассмотрим другой случай. Будем вращать окружность не внутри другой (опорной) окружности, а по ее внешней стороне. Теперь, все получаемые кривые будут относиться к семейству эпициклоиды (греч.эпи — на, над). К таким фигурам относятся кардиодида и улитка Паскаля
Реклама
Уравнение окружности — Формула, Примеры
Уравнение окружности обеспечивает алгебраический способ описания окружности с учетом центра и длины радиуса окружности. Уравнение окружности отличается от формул, которые используются для вычисления площади или длины окружности. Это уравнение используется во многих задачах окружностей в координатной геометрии.
Чтобы изобразить окружность на декартовой плоскости, нам потребуется уравнение окружности. На листе бумаги можно нарисовать окружность, если известны ее центр и длина радиуса. Точно так же на декартовой плоскости мы можем нарисовать окружность, если знаем координаты центра и его радиус. Круг может быть представлен во многих формах:
Круг может быть представлен во многих формах:
- Общая форма
- Типовая форма
- Параметрическая форма
- Полярная форма
В этой статье давайте узнаем об уравнении окружности, его различных формах с графиками и решенными примерами.
| 1. | Что такое уравнение окружности? |
| 2. | Различные формы уравнения окружности |
| 3. | Уравнение окружности Формула |
| 4. | Вывод уравнения окружности |
| 5. | График уравнения окружности |
| 6. | Как найти уравнение окружности? |
| 7. | Преобразование общей формы в стандартную форму |
| 8. | Преобразование стандартной формы в общую форму |
| 9. | Часто задаваемые вопросы по уравнению окружности |
Что такое уравнение окружности?
Уравнение окружности представляет положение окружности на декартовой плоскости. Зная координаты центра окружности и длину ее радиуса, мы можем написать уравнение окружности. Уравнение окружности представляет собой все точки, лежащие на окружности окружности. 92).
Различные формы уравнения окружности
Уравнение окружности представляет положение окружности на декартовой плоскости. На листе бумаги можно нарисовать окружность, зная ее центр и длину радиуса. Используя уравнение окружности, как только мы найдем координаты центра окружности и ее радиус, мы сможем нарисовать окружность на декартовой плоскости. Существуют различные формы представления уравнения окружности,
- Общая форма
- Типовая форма
- Параметрическая форма
- Полярная форма
Давайте рассмотрим здесь две распространенные формы уравнения окружности — общий вид и стандартную форму уравнения окружности, а также полярную и параметрическую формы в деталях.
Общее уравнение окружности
Общая форма уравнения окружности: x 2 + y 2 + 2gx + 2fy + c = 0. Эта общая форма используется для определения координат центра окружности и радиуса, где g, f, c — константы. В отличие от стандартной формы, которую легче понять, общая форма уравнения окружности затрудняет поиск каких-либо значимых свойств любой данной окружности. Итак, мы будем использовать формулу заполнения квадрата, чтобы сделать быстрое преобразование из общей формы в стандартную форму. 92)
Рассмотрим этот пример уравнения окружности (x — 4) 2 + (y — 2) 2 = 36 — это окружность с центром в точке (4,2) и радиусом 6.
Параметрическое уравнение окружности
Мы знаем, что уравнение окружности в общем виде имеет вид x 2 + y 2 + 2hx + 2ky + C = 0. Берем общую точку на границе окружности, сказать (х, у). Линия, соединяющая эту общую точку и центр окружности (-h, -k), образует угол (theta). Параметрическое уравнение окружности можно записать в виде x 2 + y 2 + 2hx + 2ky + C = 0, где x = -h + rcosθ и y = -k + rsinθ.
Полярное уравнение окружности
Полярная форма уравнения окружности почти аналогична параметрической форме уравнения окружности. Обычно мы пишем полярную форму уравнения окружности для окружности с центром в начале координат. Возьмем точку P(rcosθ, rsinθ) на границе круга, где r — расстояние точки от начала координат. Мы знаем, что уравнение окружности с центром в начале координат и радиусом «p» равно x 2 + у 2 = р 2 .
Подставьте значения x = rcosθ и y = rsinθ в уравнение окружности.
(rcosθ) 2 + (rsinθ) 2 = p 2
r 2 cos 2 θ + r 2 sin 2 θ = p 2
r 2 (cos 2 θ + sin 2 θ) = p 2
г 2 (1) = р 2
г = р
где р — радиус окружности.
Пример: Найти уравнение окружности в полярной форме при условии, что уравнение окружности в стандартной форме: уравнение окружности в полярной форме, замените значения (x) и (y) на:
x = rcosθ
у = rsinθ
х = rcosθ
у = rsinθ
х 2 + у 2 = 9
(rcosθ) 2 + (rsinθ) 2 = 9
r 2 cos 2 θ + r 2 sin 2 θ = 9
r 2 (cos 2 θ + sin 2 θ) = 9
г 2 (1) = 9
г = 3
Уравнение окружности Формула
Формула уравнения окружности используется для расчета уравнения окружности. 2).
- Для этого нам нужно всего лишь изменить константу 9, чтобы она соответствовала r 2 как (x -3) 2 + (y — 2) 2 = 3 2 .
- Здесь мы должны отметить, что одной из распространенных ошибок является рассмотрение (x_{1}) как -3, а (y_{1}) как -2.
- В уравнении окружности, если знак перед (x_{1}) и (y_{1}) отрицателен, то (x_{1}) и (y_{1}) равны положительные значения и наоборот.
- Здесь (x_{1}) = 3, (y_{1}) = 2 и r = 3
Таким образом, окружность, представленная уравнением (x -3) 2 + (y — 2) 2 = 3 2 , имеет центр в точке (3, 2) и радиус 3. На приведенном ниже изображении показан график, полученный из этого уравнения окружности.
Как найти уравнение окружности?
Существует множество различных способов представления уравнения окружности в зависимости от положения окружности на декартовой плоскости. Мы изучили формы представления уравнения окружности при заданных координатах центра окружности. Существуют определенные особые случаи, основанные на положении окружности в координатной плоскости. Давайте узнаем о методе нахождения уравнения окружности для общего и этих частных случаев. 92} = г).
Уравнение окружности с центром в начале координат
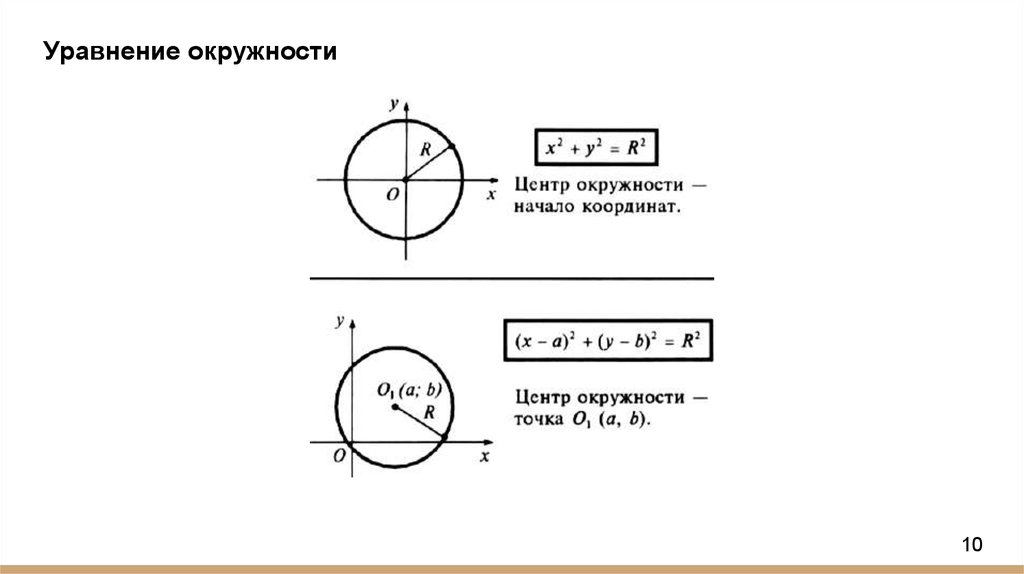
В простейшем случае центр окружности находится в начале координат (0, 0), радиус которого равен r. (x, y) — произвольная точка на окружности.
Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками. 92).
Если центр находится в начале координат, то (x_1)= 0 и (y_1)= 0.
Ответ: Уравнение окружности, если ее центр находится в начале координат, равно x 2 + y 2 = г 2 .
Уравнение окружности с центром на оси x
Рассмотрим случай, когда центр окружности находится на оси x: (a, 0) — центр окружности с радиусом r. (x, y) — произвольная точка на окружности.
Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками. 92)
Уравнение касания окружности с осью x
Рассмотрим случай, когда длина окружности касается оси x в некоторой точке: (a, r) — центр окружности с радиусом r. Если окружность касается оси x, то координата y центра окружности равна радиусу r.
(x, y) — произвольная точка на окружности. Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками. 92)
Уравнение касания окружности с осью y
Рассмотрим случай, когда длина окружности касается оси y в некоторой точке: (r, b) — центр окружности с радиусом r. Если окружность касается оси y, то координата x центра окружности равна радиусу r.
(x, y) — произвольная точка на окружности. Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками. 92)
Уравнение окружности, касающейся обеих осей
Рассмотрим случай, когда окружность касается обеих осей в некоторой точке: (r, r) — центр окружности с радиусом r. Если окружность касается и оси x, и оси y, то обе координаты центра окружности становятся равными радиусу (r, r).
(x, y) — произвольная точка на окружности. Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками. 92 = 16
г = 4 )
Преобразование общей формы в стандартную форму
Это стандартное уравнение окружности с радиусом r и центром в (a,b): (x — a) 2 + (y — b) 2 = r 2 и рассмотрим общую форму как : x 2 + y 2 + 2gx + 2fy + c = 0. Вот шаги, которые нужно выполнить, чтобы преобразовать общую форму в стандартную:
Шаг 1: Объединить подобные члены и взять константу на другая сторона как х 2 + 2gx + y 2 + 2fy = — c -> (1)
Шаг 2: Использование тождества с совершенным квадратом (x + g) 2 = x 2 + 2gx + g 2 найти значения выражения x 2 + 2gx и y 2 + 2fy как:
(x + g) 2 = x 2 + 2gx + g 2 + 907 x 2 90 2gx = (x + g) 2 — g 2 -> (2)
(y + f) 2 = y 2 + 2fy + f 2 ⇒ y 2 + 2fy = (y + f) 2 — f 2 -> (3)
Подставляя (2) и (3) в (1), получаем уравнение в виде:
(x+g) 2 — g 2 + (y+f) 2 — f 2 = — c
(x+g) 2 + (y+f) 2 = g 2 + f 2 — c
Сравнивая это уравнение со стандартной формой: (x — a) 2 + (y — b) 2 = r 2 получаем,
Центр = (-g,-f) и радиус = (sqrt{g^2+f^2 — c}) 9{2} — 9}) = (sqrt{9 + 16 — 9}) = (sqrt{16}) = 4. Итак, радиус r = 4,
Преобразование стандартной формы в общую форму
Мы можем использовать алгебраическую формулу тождества (a — b) 2 = a 2 + b 2 — 2ab, чтобы преобразовать стандартную форму уравнения окружности в общую форму. Давайте посмотрим, как сделать это преобразование. Для этого расширьте стандартную форму уравнения окружности, как показано ниже, используя алгебраические тождества для квадратов: 92 + 2gx + 2fy + с = 0), где g, f, с — константы.
Статьи по теме Уравнение окружности
Ознакомьтесь со следующими страницами, посвященными уравнению окружности
- Уравнение окружности Калькулятор
- Длина окружности
- Все формулы круга
- Отношение длины окружности к диаметру
Важные примечания к уравнению окружности
Вот несколько моментов, которые следует помнить при изучении уравнения окружности 92 + axy + C = 0), то это не уравнение окружности. В уравнении окружности нет члена (xy).
Примеры уравнений окружности
-
Пример 1: Найдите уравнение окружности в стандартной форме для окружности с центром (2,-3) и радиусом 3.
Решение:
Уравнение окружности в стандартной форме запишется как: (x — x (_1)) 2 + (у — у(_1)) 2 = г 2 . Здесь (x(_1), y(_1)) = (2, -3) — центр окружности и радиус r = 3.
Представим эти значения в стандартной форме уравнения окружности :
(х — 2) 2 + (у — (-3)) 2 = (3) 2
(x — 2) 2 + (y + 3) 2 = 9 — искомая стандартная форма уравнения данной окружности. -
Пример 2: Запишите уравнение окружности в стандартной форме для окружности с центром (-1, 2) и радиусом, равным 7.
Решение:
Уравнение окружности в стандартной форме записывается как: (х — х(_1)) 2 + (у — у(_1)) 2 = г 2 . Здесь (x(_1), y(_1)) = (-1, 2) — центр окружности и радиус r = 7.
Представим эти значения в стандартной форме уравнения окружности:
(х — (-1)) 2 + (у — 2) 2 = 7 2
(x + 1) 2 + (y — 2) 2 = 49 — искомая стандартная форма уравнения данной окружности. -
Пример 3: Найти уравнение окружности в полярной форме при условии, что уравнение окружности в стандартной форме: x 2 + y 2 = 16.
Решение:
Чтобы найти уравнение окружности в полярной форме, подставьте значения x и y на:
x = rcosθ
y = rsinθx 2 + y 2 = 16
(rcosθ) 2 + (rsinθ) 2 = 16
r 2 cos 2 θ + r 2 sin 2 θ = 16
r 2 (1) = 4
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по уравнению окружности
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по уравнению окружности
Что такое уравнение окружности в геометрии? 92).
Каково уравнение окружности, когда центр находится в начале координат?
В простейшем случае центр окружности находится в начале координат (0, 0), радиус которого равен r. (x, y) — произвольная точка на окружности. Уравнение окружности, когда центр находится в начале координат: x 2 + y 2 = r 2 .
Что такое общее уравнение окружности?
Общая форма уравнения окружности: x 2 + y 92 + 2hx + 2ky + C = 0), где (x = -h +rcos theta) и (y = -k +rsin theta)
Что такое C в общем уравнении окружности?
Общая форма уравнения окружности: x 2 + y 2 + 2gx + 2fy + c = 0. 2 = 2).
Что такое полярное уравнение окружности?
Полярное уравнение окружности с центром в начале координат: r = p, где p – радиус окружности.
Предварительное вычисление алгебры — Полярное уравнение окружности
спросил
10 лет, 3 месяца назад
Изменено
7 лет, 2 месяца назад
Просмотрено
44к раз
92 sintheta = 0$$
Теперь я застрял, я думаю, что должен был заполнить квадрат или что-то в этом роде. Кто-нибудь может закончить мою мысль?
алгебра-предварительное исчисление тригонометрия круги полярные координаты
$endgroup$
1
$begingroup$
Я думаю, что ваши замены из первой строки во вторую не совсем правильные. 2$
добавление этих двух уравнений, равных нулю, дает уравнение в декартовой форме, как показано выше Джерри Майерсоном. Я просто добавляю подробности для тех, кто может не понять.
$endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Документ без названия
Документ без названия
Полярные уравнения
на
Хи Юнг Ким
На плоскости две системы координат:
декартова система координат и полярная система координат. Любая точка в
плоскость может иметь декартовы координаты (x, y) или полярные координаты
(r, θ) в соответствующей системе. Полярные координаты (r, θ) точки
состоит из радиальной координаты r и угловой координаты θ. Координата r
представляет собой направленное расстояние от источника, называемого полюсом, и
Координата θ представляет угол против часовой стрелки от начального луча
называется полярной осью. Полярная ось обычно совпадает с осью абсцисс.
Декартова система координат.
Когда мы перекрываем две системы координат, мы можем
легко преобразовать полярные координаты (r, θ) точки в декартовы координаты
(х, у).
х = r cos θ
y = r sin θ
I. Теперь давайте исследуем
поведение графика полярного уравнения r = 2 a sin ( k θ)
+ b варьируя значения (отличные от нуля) a , b ,
и к с .
1.1. Эффект
Установим b = 0 и k
= 1, и посмотрите на график r = 2 a sinθ при изменении a .
На анимации ниже и варьируются от 0 до 10.
График r = 2 a sinθ представляет собой окружность
с центром (0, 1) и радиусом 1. Это также можно показать алгебраически, преобразовав
полярное уравнение в уравнение в декартовой системе координат.
Разновидность и (будь то и
> 0 или a < 0) изменяет центр и радиус
круг уравнения r = 2 a sin θ. На самом деле это центр
( a , 0) и радиус a .
Вот несколько графиков, когда a <
0.
Следовательно, мы заметили, что и есть
только относительно центра и радиуса на графике r = 2 а грех
( k θ), когда k = 1. Если a
> 0, кружок находится над осью абсцисс, а если a < 0, то
круг находится ниже оси Y. Поскольку функция синуса является нечетной функцией (f(-x)
= – f(x)), r = a sin(-θ) совпадает с r = — a sinθ.
Следовательно, когда b = 0 и k = -1, мы имеем
аналогичный результат, за исключением того, что если a < 0, кружок находится выше
ось абсцисс, а если a > 0, кружок ниже оси Y.
1.2. Эффект к
Когда k = 1, r = 2 a sin
( k θ) — это круг. Когда k не равно 1,
график по-прежнему круг? Нет, это уже не круг, а на самом деле
n-листная роза. Когда k четно, граф симметричен с
относительно оси x (при условии, что мы перекрываем две системы координат), поэтому r
= 2 a sin ( k θ) и r = 2 a sin
(- k θ) = -2asin ( k θ) имеют то же самое
график.
Когда k нечетно, графики r
= 2 a sin ( k θ) и r = 2 a sin
(- k θ) различны и симметричны относительно
ось х.
На следующих рисунках показано, что и
по-прежнему связано с размером графика, и чем больше | и |
то есть, тем больше растяжение графика.
Теперь исправьте на = 1, чтобы увидеть больше
влияние k на график.
Из приведенных выше цифр можно сказать, что
r = 2sin ( k θ)
это 2 | k |-листовая роза, если k четно
r = 2sin ( k θ)
это | k |-листовая роза if k странно.
1.3. Эффект б
Теперь изменим значение b
of r = 2 a sin ( k θ) + b . Напоминание
влияние константы , скажем, c на график y = f(x) + c в декартовой
системе координат, можно предположить, что b может быть связано с
сдвиг. Но если это правильно, то вопрос «вдоль чего?». Давайте исправим на
= 1 и k = 1 для простоты и рассмотрим несколько графиков. Первый
всего, находим, что r = 2 a sin θ + b и r
= 2 a sin θ — b имеют такие же графики.
В общем, если k нечетно, графики
r = 2 a sin ( k θ) + b и
r = 2 a sin ( k θ) — b совпадают,
которые симметричны относительно оси y (при условии, что мы перекрываем
две системы координат, декартова и полярная координаты).
С другой стороны, если к четно,
r = 2 a sin ( k θ) + b и r
= 2 a sin ( k θ) — b симметричны
относительно оси y (при условии, что мы перекрываем две системы координат,
декартовы и полярные координаты).
На следующих графиках показано, что начальное предположение
для эффекта b было неправильно, значит b
не имеет отношения к сдвигу графика.
Чем больше |b| это «больше»
«размер» графика. (Строго говоря, это объяснение очень интуитивно
и не совсем математически правильно, потому что форма каждого графика различна.)
Например, при изменении b график r = 2sin (2θ) + b
это:
Подводя итог, имеем следующее:
r = 2 a sin ( k θ)
и г = 2 a sin (- k θ) = -2 a sin ( k θ) есть
тот же график, если к даже
r = 2 a sin ( k θ)
и r = 2 a sin (- k θ) равны
симметричен относительно оси x, если k нечетно
r = 2 a sin ( k θ)
является кругом, если | к | = 1
и выше | и | есть, чем больше
круг есть.
Когда k = 1, если a > 0, кружок находится над осью x, а если a < 0,
круг находится ниже оси Y.
Когда k = -1, если a > 0, кружок внизу
ось x, и если a > 0, кружок находится над осью y.
r = 2 a sin ( k θ)
это 2 | k |-листовая роза, если к четно.
r = 2 a sin ( k θ)
это | k |-листовая роза, если k нечетно (исключая
1 и -1).
r = 2 a sin ( k θ)
+ b и r = 2 a sin ( k θ) —
b имеют тот же график, если k нечетно.
r = 2 a sin ( k θ)
+ b и r = 2 a sin ( k θ) —
b симметричны относительно оси y, если k
даже.
II. Сравнение графика r =
2 a sin ( k θ) + b , исследуем
поведение графика r = 2 a cos ( k θ)
+ b варьируя значения (отличные от нуля) a , b ,
и к с .
Поскольку функция косинуса четная,
r = 2 a cos ( k θ) и r = 2 a cos (- k θ)) имеют одинаковый график для любых k .
Поэтому будем рассматривать только положительное значение k .
На анимации выше, когда и варьировались от -5 до 5, мы обнаружили, что
r = 2 a cos ( k θ)
является кругом, если | к | = 1
и выше | и | есть, чем больше
круг есть.
Когда | к | = 1, если a > 0, кружок находится справа от оси y, а если a < 0,
круг находится в левой части оси Y.
r = 2 a cos ( k θ) и r = -2 a cos ( k θ) имеют один и тот же график для любых k (исключая
1 и -1).
r = 2 a cos ( k θ)
это | k |-листовая роза, если k нечетно (исключая
1 и -1).
r = 2 a cos ( k θ)
это 2 | k |-листовая роза, если k четно.
Из приведенных выше графиков имеем:
r = 2 a cos ( k θ)
+ б и г = 2 а cos ( k θ) — b имеют тот же график, если k нечетно.
Соотношение между графиками r = 2 a sin ( k θ)
+ b и r = 2 a sin ( k θ) — b при k даже включает поворот на некоторые углы относительно начала координат, хотя формы графиков совпадают.
III. Как насчет графика ?
3.1. Варьируем c
с a = b и k = 1. Когда
а = б = 1, имеем:
Когда a = b = -3,14,
у нас есть:
До a = b
и k = 1, график
является прямой линией, а c относится к точкам пересечения с осью y. Если и
= b = 1 или -1, (0, c ) и (0, — c )
являются y-пересечениями графика.
С ,
можно сказать, что линии и
имеют одинаковые наклоны, поэтому они параллельны. В самом деле, полярное уравнение
эквивалентно a rcosθ + a rsinθ = c ,
поэтому, используя эквивалентное соотношение с декартовыми уравнениями, мы имеем a x
+ a y = c , что равно линейное уравнение
а у = — а х +
с
у = — х + к/к
с наклоном -1 и точкой пересечения с осью Y (0, c/a ).
Вот почему чем бы ни было , поскольку а = b
и k = 1, прямые параллельны
с уклоном -1.
3.2. Поменяем к
где a = b и c = 1.
Когда a = b =
с =1,
имеет
2| к | параболы с 2| к | асимптоты, если k
даже
имеет
| к | параболы с | к | асимптоты, если k
нечетное (кроме 1)
Для любой c, когда
a = b = 1, мы можем иметь те же формы:
имеет 2 | к | параболы с 2| к | асимптоты, если
к это даже
имеет
| к | параболы с | к | асимптоты, если k
нечетное (кроме 1)
3. 3. Поскольку k = 1, для любых ненулевых a , b и c график представляет собой линию, потому что
Когда к = 2,
графики выше показывают, что для любых ненулевых a и b , и имеют один и тот же график.
Кроме того,
вариация c не влияет на форму графика, и чем больше | с | есть, тем больше график.
В заключение, мы имеем для любого ненулевого a , b и c , и ненулевое целое число k :
имеет
| к | параболы с | к | асимптоты, если k нечетно (исключая 1)
имеет
2| к | параболы с 2| к | асимптоты, если k равно
8.
2: Полярные координаты — Математика LibreTexts
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 13876
- Дэвид Липпман и Мелони Расмуссен
- The OpenTextBookStore
7
Система координат, с которой мы лучше всего знакомы, называется декартовой системой координат, прямоугольной плоскостью, разделенной на четыре квадранта горизонтальной и вертикальной осями.
В предыдущих главах мы часто находили декартовы координаты точки на окружности под заданным углом от положительной горизонтальной оси. Иногда этот угол, наряду с расстоянием точки от начала координат, обеспечивает более полезный способ описания местоположения точки, чем обычные декартовы координаты.
ПОЛЯРНЫЕ КООРДИНАТЫ
Полярные координаты точки состоят из упорядоченной пары ((r),(theta)), где (r) — расстояние от точки до начала координат, а ( theta) — угол, измеренный в стандартном положении.
Обратите внимание, что если бы мы разметили плоскость в полярных координатах, это выглядело бы как график справа, с кругами с возрастающими радиусами и лучами, нарисованными с возрастающими углами.
Пример (PageIndex{1})
Постройте полярную точку ((3, dfrac{5pi}{6})).
Решение
Эта точка будет находиться на расстоянии 3 от начала координат под углом (dfrac{5pi}{6}). Построение этого
Пример (PageIndex{2})
Постройте полярную точку ((-2, dfrac{pi}{4})).
Решение
Обычно мы используем положительные значения (r), но иногда мы сталкиваемся со случаями, когда (r) отрицательно. На обычной числовой прямой мы измеряем положительные значения справа и отрицательные значения слева. Аналогично нанесем эту точку. Для начала мы поворачиваем на угол (dfrac{pi}{4}).
Перемещение в этом направлении в первый квадрант даст положительные значения r . Для отрицательных r значений, мы движемся в противоположном направлении, в третий квадрант. График:
Обратите внимание, что результирующая точка совпадает с полярной точкой ((2, dfrac{5pi}{4})). На самом деле, любую декартову точку можно представить бесконечным числом различных полярных координат, добавляя или вычитая из этих точек полные обороты. Например, одна и та же точка может быть представлена как ((2, dfrac{13pi}{4})).
Упражнение (PageIndex{1})
Нанесите следующие точки, заданные в полярных координатах, и подпишите их.
а. (A = (3, dfrac{pi}{6}))
б. (B = (-2, dfrac{pi}{3}))
c. (C = (4, dfrac{3pi}{4}))
- Ответ
Конверсионные баллы
Чтобы преобразовать полярные координаты в декартовы координаты, мы вспоминаем отношения, которые мы разработали еще в главе 5.
ПРЕОБРАЗОВАНИЕ МЕЖДУ ПОЛЯРНЫМИ И ДЕКРАТОВЫМИ КООРДИНАТАМИ
Для преобразования между полярными ((r, theta)) и декартовыми ((x, y)) координатами мы используем отношения 9{2}]
Исходя из этих соотношений и наших знаний об единичной окружности, если (r = 1) и (theta = dfrac{pi}{3}), полярные координаты будут ((r, theta ) = (1, dfrac{pi}{3})), и соответствующие декартовы координаты ((x, y) = (dfrac{1}{2}, dfrac{sqrt{3}} {2})).
Запоминание значений единичного круга очень пригодится при преобразовании между декартовыми и полярными координатами.
Пример (PageIndex{3})
Найти декартовы координаты точки с полярными координатами ((r, theta) = (5, dfrac{2pi}{3})).
Решение
Чтобы найти (x) и (y) координаты точки,
[x = rtext{cos} (theta) = 5 cos (dfrac{ 2pi}{3}) = 5(-dfrac{1}{2}) = -dfrac{5}{2}nonumber]
[y = rtext{sin} (theta ) = 5 sin ( dfrac {2 pi} {3}) = 5 (- dfrac { sqrt {3}} {2}) = — dfrac {5 sqrt {3}} {2} nonumber]
Декартовы координаты: ((-dfrac{5}{2}, dfrac{5sqrt{3}}{2})).
Пример (PageIndex{4})
Найти полярные координаты точки с декартовыми координатами (−3,−4) . 9{text{rd}}) квадранта, мы можем определить, что второй угол и есть тот, который нам нужен. Полярные координаты этой точки равны ((r, theta) = (5, 4,069)).
Упражнение (PageIndex{2})
Преобразуйте следующее.
а. Преобразуйте полярные координаты ((r, theta) = (2, pi)) в ((x, y)).
б. Преобразуйте декартовы координаты ((x, y) = (0, -4)) в ((r, theta)).
- Ответить
-
а. ((r, theta) = (2, pi)) преобразуется в ((x, y) = (2cos(pi), 2sin(pi)) = (-2, 0 )) 92) описывает связь между значениями (x) и (y) на декартовой сетке, можно написать полярное уравнение, описывающее связь между значениями (r) и (theta) на полярной сетка.
Пример (PageIndex{5})
Нарисуйте график полярного уравнения (r = theta).
Решение
Уравнение (r = theta) описывает все точки, для которых радиус (r) равен углу.
Чтобы визуализировать эту связь, мы можем создать таблицу значений.
(тета) 0 (пи/4) (пи/2) (3пи/4) (пи) (5пи/4) (3пи/2) (7пи/4) (2пи) (р) 0 (пи/4) (пи/2) (3пи/4) (пи) (5пи/4) (3пи/2) (7пи/4) (2пи) Мы можем нанести эти точки на плоскость, а затем нарисовать кривую, соответствующую этим точкам. Полученный график представляет собой спираль.
Обратите внимание, что результирующий график не может быть результатом функции вида (y = f(x)), так как он не проходит тест на вертикальную линию, даже если он является результатом функции, дающей (r ) в терминах (тета).
Хотя приятно видеть полярные уравнения на полярных сетках, полярные графики чаще изображаются в декартовой системе координат, поэтому остальные полярные уравнения будут отображаться соответственно.
Здесь показан приведенный выше спиральный график на декартовой сетке.
Пример (PageIndex{6})
Нарисуйте график полярного уравнения (r = 3).
Решение
Вспомните, что когда переменная не появляется в уравнении, это означает, что не имеет значения, какое значение имеет эта переменная; результат уравнения останется прежним. Например, декартово уравнение (y = 3) описывает все точки, где (y = 3), независимо от значений x, образуя горизонтальную линию.
Аналогично, это полярное уравнение описывает все точки на расстоянии 3 от начала координат, независимо от угла, создавая график круга.
Нормальные настройки графических калькуляторов и графических программ в декартовой системе координат, где (y) является функцией (x), где графическая утилита запрашивает (f(x)), или просто ( у =).
Для построения полярных уравнений вам может потребоваться изменить режим калькулятора на полярный. Вы будете знать, что вам удалось изменить режим, если теперь у вас есть (r) как функция (theta), где графическая утилита запрашивает (r(theta)), или просто (г =).
Пример (PageIndex{7})
Нарисуйте график полярного уравнения (r = 4 cos(theta)) и найдите интервал, на котором оно завершает один цикл.
Решение
Хотя мы могли бы снова создать таблицу, нанести на нее соответствующие точки и соединить точки, мы также можем обратиться к технологии, чтобы напрямую изобразить ее. Используя технологию, мы производим показанный здесь график, окружность, проходящую через начало координат.
Поскольку этот график замыкает цикл и повторяется, мы можем спросить, какой интервал значений (theta) дает весь график. В (theta = 0), (r = 4cos(0) = 4), что дает точку (4, 0). Нам нужно следующее значение (theta), когда график вернется к точке (4, 0).
Решение для случая (x = 4) эквивалентно решению (rcos(theta) = 4). 9{2}(theta)= 1nonumber]У этого есть решения, когда
[cos(theta) = 1text{ или }cos(theta) = -1nonumber]Решение этих решений дает решения
[theta = 0text{ or }theta = pinonumber]Это показывает нам, что при 0 радианах мы находимся в точке (0, 4), и снова при (pi) радианах мы находимся в точке (0, 4), совершив один полный оборот.
Этот интервал (0 le theta < pi) дает одну полную итерацию окружности.
Упражнение (PageIndex{3})
Нарисуйте график полярного уравнения (r = 3 sin (theta)) и найдите интервал, на котором оно совершает один цикл.
- Ответить
-
[3 sin(theta) = 0text{ at }theta = 0text{ и }theta = pinonumber]
Он завершает один цикл на интервале (0 le theta < pi).
Последние несколько примеров были кругами. Далее мы рассмотрим два других «именных» полярных уравнения, лимасон и розы .
Пример (PageIndex{8})
Нарисуйте график полярного уравнения (r = 4sin(theta) + 2). Какой интервал значений (theta) соответствует внутреннему циклу?
Solution
Этот тип графика называется limaçon .
Используя технологию, мы можем нарисовать график. Внутренний цикл начинается и заканчивается в начале координат, где (r = 0). Мы можем найти значения (theta), для которых (r = 0).[0 = 4sin(theta) + 2nonnumber]
[-2 = 4sin(theta)nonnumber]
[sin(theta) = -dfrac{ 1}{2}nonumber]
[theta = dfrac{7pi}{6}text{ или }theta = dfrac{11pi}{6}nonumber]Это говорит нам, что (r = 0), поэтому график дважды проходит через начало координат на интервале ([0, 2pi)).
Внутренняя петля возникает из интервала (dfrac{7pi}{6} le theta le dfrac{11pi}{6}).
Это соответствует тому, где функция (r = 4 sin(theta) + 2) принимает отрицательные значения, как мы могли бы видеть, если бы построили график функции в плоскости (r theta).
Пример (PageIndex{9})
Нарисуйте график полярного уравнения (r = cos(3theta)). Какой интервал значений (theta) описывает одну маленькую петлю графика?
Решение
Этот тип графа называется трехлистной розой .
Мы можем использовать технологию для создания графика. Интервал ([0, pi)) дает один цикл этой функции. Как и в последней задаче, мы можем заметить, что существует интервал, на котором одна петля этого графа начинается и заканчивается в начале координат, где (r = 0). Решение для (тета),
[0 = cos(3theta)nonumber]Подстановка (u = 3theta)
[0 = cos(u)nonumber]
[u = dfrac{ pi}{2}text{ или }u = dfrac{3pi}{2}text{ или }u = dfrac{5pi}{2}nonumber]Отменить замену,
[3 theta = dfrac{pi}{2}text{ или}3 theta = dfrac{3pi}{2}text{ или}3 theta = dfrac{5pi {2}nonumber]
[theta = dfrac{pi}{6}text{ или }theta = dfrac{pi}{2}text{ или }theta = dfrac{5pi}{6}nonumber]
Есть 3 решения на (0 le theta < pi), которые соответствуют 3 раза, когда график возвращается в начало координат, но первые два решения мы решили выше, достаточно, чтобы сделать вывод, что
одна петля соответствует интервалу (dfrac{pi}{6} le theta < dfrac{pi}{2}).
Если мы хотим получить представление о том, как компьютер нарисовал этот график, рассмотрим, когда (theta = 0).
(r = cos(3theta) = cos(0) = 1), поэтому график начинается с (1, 0). Как мы обнаружили выше, при (theta = dfrac{pi}{6}) и (theta = dfrac{pi}{2}) график находится в начале координат. Глядя на уравнение, обратите внимание, что любой угол между (dfrac{pi}{6}) и (dfrac{pi}{2}), например, при (theta = dfrac{ pi}{3}), дает отрицательное значение (r): [r = cos(3 cdot dfrac{pi}{3}) = cos(pi) = -1nonumber ]
Обратите внимание, что при отрицательном значении (r) и угле с конечной стороной в первом квадранте соответствующая декартова точка будет в третьем квадранте. Поскольку (r = cos(3theta)) отрицательно на (dfrac{pi}{6} le theta < dfrac{pi}{2}), этот интервал соответствует петля графика в третьем квадранте.
Упражнение (PageIndex{4})
Нарисуйте график полярного уравнения (r = sin(2theta)).
Вы бы назвали эту функцию limaçon 9?0004 или роза ?
- Ответить
-
Это 4-хлистная роза.
Преобразование уравнений
Несмотря на то, что многие полярные уравнения невозможно красиво выразить в декартовой форме (и наоборот), может быть полезно конвертировать между двумя формами, когда это возможно. Для этого мы используем те же отношения, которые мы использовали для преобразования точек между системами координат.
92 — 6rsin(theta) = 0nonnumber]Множитель
[r (r — 6sin(theta)) = 0nonnumber] Используйте теорему о нулевом множителе
[r = 6sin (theta)text{ или }r = 0nonumber] Поскольку (r = 0) — это всего лишь точка, мы отвергаем это решение.Решение (r = 6sin(theta)) очень похоже на то, что мы изобразили в примере 7. Фактически, это уравнение описывает окружность с низом в начале координат и вершиной в точке (0, 6).
Пример (PageIndex{11})
Перепишите декартово уравнение (y = 3x + 2) как полярное уравнение.
Решение
[y = 3x + 2nonnumber]Используйте (y = rsin(theta)) и (x = rcos(theta))
[r sin(theta) = 3rcos(theta) + 2nonumber] Переместить все термины с (r) в одну сторону
[rsin(theta) — 3rcos(theta) = 2nonumber] Вынести на множители (r)
[r(sin(theta) — 3cos(theta)) = 2nonumber] Разделить
[r = dfrac{2} {sin(theta) — 3cos(theta)}nonumber]В этом случае полярное уравнение более громоздко, чем декартово уравнение, но все же бывают случаи, когда это уравнение может быть полезным.
Пример (PageIndex{12})
Перепишите полярное уравнение (r = dfrac{3}{1- 2cos(theta)}) как декартово уравнение.
Решение
Мы хотим исключить (theta) и (r) и ввести (x) и (y). Обычно проще всего начать с очистки дроби и поиска подстановочных значений, которые исключат (theta).
[r = dfrac{3}{1 — 2cos(theta)}nonumber]Очистить дробь
[r(1 — 2cos(theta)) = 3nonumber] Используйте (cos(theta) = dfrac{x}{r}), чтобы исключить (theta) 9{2/3}номер]- Декартова система координат
- Полярная система координат
- Нанесение точек в полярных координатах
- Преобразование координат между системами
- Полярные уравнения: спирали, круги, лимасоны и розы Преобразование уравнений между системами
Эта страница под заголовком 8.2: Полярные координаты публикуется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Дэвидом Липпманом и Мелони Расмуссен (The OpenTextBookStore) посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или страница
- Автор
- Дэвид Липпман и Мелони Расмуссен
- Лицензия
- CC BY-SA
г.
- Версия лицензии
- 4,0
- Показать страницу Содержание
- нет
-
- Теги
-
- полярные координаты
- источник@http://www.opentextbookstore.com/details.php?id=30
Полярные координаты
Полярные координаты
Определение полярных координат
Напомним, что мы определяем точку (x,y) на плоскости как
x единиц вправо
от начала координат и у единиц слева от начала координат. Это отлично работает
для линий и парабол, но у окружностей есть несколько запутанные уравнения. В качестве
в качестве альтернативы мы определяем новую систему координат, где первая координата
r — расстояние от начала координат до точки и вторая координата q
это угол, который луч из начала координат в точку составляет с
положительная ось x.Из тригонометрии имеем
В вашем калькуляторе есть специальный режим для полярных координат. Мы используем
калькулятор для построения графикаг = потому что (
)
кругов
Окружность с центром в начале координат имеет уравнение
x 2 + y 2 = R 2 В полярной форме имеем
г = р
Например, круг радиуса 3 с центром в (0,0) имеет полярное уравнение
р = 3
90 250 Линии 90 251
Если
у = мх + б
мы можем написать
г грех (д) =
m r cos q + bили
Конические сечения
Напомним, что коническое сечение определяется следующим образом:
Пусть f (называемая фокусом ) будет фиксированной точкой на плоскости,
м (так называемый
директриса )
быть фиксированной линией, а e (называется эксцентриситет ) положительная постоянная.затем
множество точек P на плоскости спо
|ПФ|
= е
|Пм|является коническим сечением. Если e < 1, то сечение представляет собой эллипс, если
e = 1, то это a
парабола,
а также
если e = 0, то это гипербола.Примечание. Если F – исходная точка, m
х = d, тогда|ПФ| = r, |Pm| = д —
r cos qтак что уравнение становится
г = е (d — rcos (q)) = ed —
рекос(к)или
Производные в полярных координатах
Теорема
Пусть r = r(q) представляет собой полярную кривую, тогда
ды
dy/dq r’ sinq
+ г cosq
знак равно
=
дх
дх/дк
r ‘cosq
— г синкdy r’ sinq
+ г cosq
=
дх
r ‘cosq
— г синк
Доказательство:Так как
x = r cosq,
и y = r sinq,мы можем подставить в r = r(q), чтобы получить
x = r cosq
Взяв производную,
x’ = r’ cosq —
r sinqи
y’ = r’ sinq +
р коскв.Начиная с
день
dy/dq
=
дх
dx/dqделение дает результат.
Пример
Пусть
dy
(раковина
+ q cosq) sinq
+ q sinq cosq
=
дх
(раковина
+ qcosq) cosq
— q sinq sinq
sin 2 q + 2qsinqcosq
=
Синк Коскв +
qcos 2 q — qsin 2 qsinq cosq
+ qcos(2q)
=
грех 2 д
+ qsin(2q)
Назад к полярному и параметрическому
Страница уравненийНазад
на домашнюю страницу Math 107Назад на домашнюю страницу математического факультета
электронная почта
Вопросы и предложенияПолярные координаты
Полярные координаты
Преобразование полярных координат
Если мы выберем луч l как положительную ось x , то
точка P на плоскости имеет как декартовы координаты ( x , y ), так и полярные координаты ( r , q).Определение функций синуса и косинуса подразумевает, что ( x , y ) задается в терминах ( р ,q) по
x = r cos(q) , y = r sin(q)
(1) Решение для r и q дает тождества
r 2 = x 2 + y 2 и tan(q) = г
x(2) ПРИМЕР 3 Преобразование точки ( 4, p/4) из
полярные координаты в декартовы координаты, а затем показать, что (2)
преобразует его обратно в полярный .Решение: Для этого положим r = 4 и q = p/4 в (1), чтобы получить
х = 4cos æ
èп
4ö
ø= 2…2, y = 4sin æ
èп
4ö
ø= 2…2 Чтобы отобразить обратно, мы замечаем, что
р 2 = x 2 + y 2 = 8 + 8 = 16, R = 4
и что y/x
и что y/x =
и что y/x = Q) = Q) Q) Q) Q).
1, д = р/4.
Если мы подставим x = r cos(q) и y = r sin(q) в кривую g ( x,y ) = k , то 60 результат
g ( r cos(q), r sin(q) ) = k
называется откатом кривой в полярные координаты.
Тождество r 2 = x 2 + y 2
часто используется для перевода кривой обратно в полярные координаты.Для
например, x 2 + y 2 = R 2 для
константа R > 0 имеет откатТочно так же строки формы y = m x становятся
r sin(q) = m r cos(q) Þ sin(q) = m cos(q) Þ tan(q) = м
Это соответствует примеру 4 в предыдущем разделе, в котором мы видели, что координата
кривые для преобразования полярных координатТ ( г , д ) =
á r cos(q), r sin(q)
–представляют собой окружности с центром в начале координат и линии, проходящие через начало координат,
соответственно.
Кроме того, это показывает, что всякий раз, когда это возможно, мы должны решить для r значение
получить функцию вида r = f (q) .ПРИМЕР 4 Преобразование кривой x 2 +
( г — 1) 2 =
1 в полярный
координаты, а затем решить для р , если можно.Решение: Расширение приводит к x 2 + y 2 —
2 y + 1 = 1 , так что для этого заменим y r 2 и пусть x = r cos( q) :Решение на r тогда получается
То есть r = 2
sin(q) — окружность
радиус 1 с центром в ( 1,0) .
Уравнение кривых в полярных координатах
Благодаря
радиальной природе полярной системы
координат, некоторые кривые могут быть
достаточно просто описаны полярным
уравнением, тогда как уравнение в
прямоугольной системе координат были
бы намного сложнее. Среди самых известных
кривых: полярная
роза, архимедова
спираль, Лемниската, улитка
Паскаля и кардиоида.
Окружность

![]()
Круг,
заданный уравнением ![]() .
.
Общее
уравнение окружности с центром в (![]() )
)
и радиусом ![]() имеет
имеет
вид:
![]()
Это
уравнение может быть упрощено для
частных случаев, например
![]()
является
уравнением, определяющим окружность с
центром в полюсе и радиусом ![]() .[15]
.[15]
Прямая
Радиальные прямые (те,
которые проходят через полюс) определяются
уравнением
![]()
где ![]() —
—
угол, на который прямая отклоняется от
полярной оси, то есть, ![]() где
где ![]() —
—
наклон прямой в прямоугольной системе
координат. Нерадиальная прямая,
перпендикулярно пересекает радиальную
прямую ![]() в
в
точке ![]() определяется
определяется
уравнением
![]()
Полярная роза

![]()
Полярная
роза задана
уравнением ![]() .
.
Полярная
роза —
известная математическая кривая,
похожая на цветок с лепестками. Она
может быть определена простым уравнением
в полярных координатах:
![]()
для
произвольной постоянной ![]() (включая
(включая
0). Если ![]() —
—
целое число, то это уравнение будет
определять розу с ![]() лепестками
лепестками
для нечётных ![]() ,
,
либо с![]() лепестками
лепестками
для чётных ![]() .
.
Если ![]() —
—
рациональное, но не целое, график,
заданный уравнением, образует фигуру,
подобную розе, но лепестки будут
перекрываться. Розы с 2, 6, 10, 14 и т. д.
лепестками этим уравнением определить
невозможно. Переменная ![]() определяет
определяет
длину лепестков.
Если
считать, что радиус не может быть
отрицательным, то при любом натуральном ![]() мы
мы
будем иметь ![]() –
–
лепестковую розу. Таким образом,
уравнение ![]() будет
будет
определять розу с двумя лепестками. С
геометрической точки зрения радиус –
это расстояние от полюса до точки и он
не может быть отрицательным.
Спираль Архимеда

![]()
Одна
из ветвей спирали Архимеда, задаваемая
уравнением ![]() для
для ![]() .
.
Архимедова
спираль названа
в честь её изобретателя, древнегреческого
математика Архимеда.
Эту спираль можно определить с помощью
простого полярного уравнения:
![]()
Изменения
параметра ![]() приводят
приводят
к повороту спирали, а параметра ![]() —
—
расстояния между витками, которое
является константой для
конкретной спирали. Спираль Архимеда
имеет две ветви, одну для ![]() а
а
другую для ![]() .
.
Две ветви плавно соединяются в полюсе.
Зеркальное отображение одной ветви
относительно прямой, проходящей через
угол 90°/270°, даст другую ветвь. Эта кривая
интересна тем, что была описана в
математической литературе одной из
первых, после конического
сечения,
и лучше других определяется именно
полярным уравнением.
Конические сечения
![]()
Эллипс.
Коническое
сечение, один из полюсов которого
находится в полюсе, а другой где-то на
полярной оси (так, что малая полуось
лежит вдоль полярной оси) задаётся
уравнением:
![]()
где ![]() — эксцентриситет,
— эксцентриситет,
а ![]() —
—
фокальный параметр. Если ![]() ,
,
это уравнение определяет гиперболу;
если ![]() ,
,
то параболу; если ![]() ,
,
то эллипс. Отдельным случаем является ![]() ,
,
определяющее окружность с радиусом ![]() .
.
86. Вычисление определенного интеграла. Применение его к вычислению площадей плоских фигур, длины дуги кривой.
Вычисление
площадей и длин дуг кривых в декартовых
координатах
Пусть
на плоскости x0y задана область, ограниченная
снизу кривой y=f1(x) ,
заданной в декартовых координатах,
сверху – кривой y=f2(x)
, слева – прямой x=a (ее может и не быть,
если f1(a)=f2(a) ),
справа – прямой x=b.
Исходя
из геометрического
смысла определенного интеграла,
площадь этой области можно вычислить
по формуле
![]()
Здесь
не нужно заботиться, какая из функций
и где положительная, а какая отрицательная.
Если, например, f1(x)<0,
то формула сама прибавит нужную площадь.
Более сложные области всегда можно
разбить так, чтобы выполнялись указанные
условия.
Пусть
на отрезке [a,b] уравнением y=f(x) задана
плоская кривая. Ее длина вычисляется
по формуле
![]()
Пример 1 :: ![]()
![]() Вычисление
Вычисление
площадей и длин дуг в декартовых
координатах
Вычислим
площадь области, ограниченной кривыми
![]() и
и
длину границы этой области.
Вычисление
площадей и длин дуг при параметрическом
задании кривых
Если
область на плоскости снизу ограничена кривой,
заданной параметрически,
то есть
![]()
при
этом x1()=b,
x1()=b,
а сверху – кривой
![]()
Тогда
площадь такой плоской фигуры вычисляем
по формуле
![]()
Эта
формула совпадает с формулой вычисления
площади в декартовых координатах, если
учесть, что x'(t)dt=dx.
Пусть
кривая на плоскости задана параметрически
![]()
Тогда
длина этой кривой вычисляется по формуле
![]()
Пример 2 :: ![]()
![]() Вычисление
Вычисление
площадей и длин дуг при параметрическом
задании кривых.
Вычислим
площадь фигуры, ограниченной кривыми
 ,
,  ,
, ![]() .
.
Вычислим длину дуги циклоиды  ,
, ![]() .
.
Вычисление
площадей и длин дуг кривых в полярных
координатах
Когда
кривая, ограничивающая область, задана
в полярных
координатах =(),
то площадь этой области вычисляем по
формуле
![]()
Основная
трудность в использовании этой формулы
заключается в определении пределов
интегрирования , .
Здесь нужно понимать, что кривая =()
определена только, если >0.
Поскольку в формуле присутствует 2 ,
то она учтет и не существующую площадь,
когда .
Решив уравнение ()=0
, найдем пределы интегрирования.
Если
кривая, ограничивающая область, задана
в полярных координатах =(),
то ее длина вычисляется по формуле
![]()
Пределы
интегрирования определяются из тех же
соображений, что и при вычислении
площади.

Полярная сетка, на которой отложено несколько углов с пометками в градусах
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой декартовой, или прямоугольной, системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся лучом, который называют нулевым лучом, или полярной осью.
Точка, из которой выходит этот луч, называется началом координат, или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой.
Радиальная координата (обычно обозначается 

Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
История[править | править код]
Понятие угла и радиуса были известны ещё в первом тысячелетии до нашей эры. Греческий астроном Гиппарх (190—120 до н. э.) создал таблицу, в которой для разных углов приводились длины хорд. Существуют свидетельства применения им полярных координат для определения положения небесных тел[2]. Архимед в своём сочинении «Спирали» описывает так называемую спираль Архимеда, функцию, радиус которой зависит от угла. Работы греческих исследователей, однако, не развились в целостное определение системы координат.
В IX веке персидский математик Хаббаш аль-Хасиб (аль-Марвази́) применял методы картографических проекций и сферической тригонометрии для преобразования полярных координат в другую систему координат с центром в некоторой точке на сфере, в этом случае, для определения Киблы — направления на Мекку[3]. Персидский астроном Абу Райхан Бируни (973—1048) выдвинул идеи, которые выглядят как описание полярной системы координат. Он был первым, кто, примерно в 1025 году, описал полярную экви-азимутальную равнопромежуточную проекцию небесной сферы[4].
Существуют разные версии о введении полярных координат в качестве формальной системы координат. Полная история возникновения и исследования описана в работе профессора из Гарварда Джулиан Лоувел Кулидж «Происхождение полярных координат»[5]. Грегуар де Сен-Венсан и Бонавентура Кавальери независимо друг от друга пришли к похожей концепции в середине XVII века. Сен-Венсан описал полярную систему в личных заметках в 1625 году, напечатав свои труды в 1647; а Кавальери напечатал свои труды в 1635 году, и исправленную версию в 1653 году. Кавальери применял полярные координаты для вычисления площади, ограниченной спиралью Архимеда. Блез Паскаль впоследствии использовал полярные координаты для вычисления длин параболических дуг.
В книге «Метод флюксий» (англ. Method of Fluxions, написана в 1671 году, напечатана в 1736 году) сэр Исаак Ньютон исследовал преобразование между полярными координатами, которые он обозначал как «Седьмой способ; Для спиралей» («англ. Seventh Manner; For Spirals»), и девятью другими системами координат[6]. В статье, опубликованной в 1691 году в журнале Acta eruditorum, Якоб Бернулли использовал систему с точкой на прямой, которые он назвал полюсом и полярной осью соответственно. Координаты задавались как расстояние от полюса и угол от полярной оси. Работа Бернулли была посвящена проблеме нахождения радиуса кривизны кривых, определённых в этой системе координат.
Введение термина «полярные координаты» приписывают Грегорио Фонтана. В XVIII веке он входил в лексикон итальянских авторов. В английский язык термин попал через перевод трактата Сильвестра Лакруа «Дифференциальное и интегральное исчисление», выполненного в 1816 году Джорджем Пикоком[7][8] Для трёхмерного пространства полярные координаты впервые предложил Алекси Клеро, а Леонард Эйлер был первым, кто разработал соответствующую систему[5].
Графическое представление[править | править код]

Точка в полярной системе координат
Каждая точка в полярной системе координат может быть определена двумя полярными координатами, что обычно называются 






Полярный радиус определен для любой точки плоскости и всегда принимает неотрицательные значения 



- в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
- в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Например, точка с координатами 

Одной из важных особенностей полярной системы координат является то, что одна и та же точка может быть представлена бесконечным количеством способов. Это происходит потому, что для определения азимута точки нужно повернуть полярную ось так, чтобы она указывала на точку. Но направление на точку не изменится, если осуществить произвольное число дополнительных полных оборотов. В общем случае точка 



Для обозначения полюса используют координаты 




![(-180^{circ },;180^{circ }]](https://wikimedia.org/api/rest_v1/media/math/render/svg/535196b36d3271ec1d81408cf666971e69c412a8)

![(-pi ,;pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d42d585d0cc7e452cd100efa4127cc28bedceb)
Углы в полярных координатах задаются либо в градусах, либо в радианах, при этом 
Связь между декартовыми и полярными координатами[править | править код]
Пару полярных координат 




в то время как две декартовы координаты 


(по теореме Пифагора).
Для определения угловой координаты 
Для вычисления 


.
Для вычисления 
![(-pi ,;pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d42d585d0cc7e452cd100efa4127cc28bedceb)
.
Учитывая, что для вычисления полярного угла недостаточно знать отношение 

atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты 


Уравнение кривых в полярных координатах[править | править код]
Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат было бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.
Окружность[править | править код]

Окружность, заданная уравнением
Общее уравнение окружности с центром в (

Это уравнение может быть упрощено для частных случаев, например
является уравнением, определяющим окружность с центром в полюсе и радиусом 
Прямая[править | править код]
Радиальные прямые (те, которые проходят через полюс) определяются уравнением
,
где 




Полярная роза[править | править код]

Полярная роза задана уравнением
Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:
для произвольной постоянной 








Если считать, что радиус не может быть отрицательным, то при любом натуральном 

будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.
Спираль Архимеда[править | править код]

Одна из ветвей спирали Архимеда, задаваемая уравнением 
Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:
Изменения параметра 



Конические сечения[править | править код]

Коническое сечение, один из фокусов которого находится в полюсе, а другой где-то на полярной оси (так, что большая полуось лежит вдоль полярной оси) задаётся уравнением:
,
где 






Комплексные числа[править | править код]

Пример комплексного числа 

Пример комплексного числа, нанесённого на график, с использованием формулы Эйлера
Каждое комплексное число может быть представлено точкой на комплексной плоскости, и, соответственно, эта точка может определяться в декартовых координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число 
,
где 
и отсюда:
,
где 

Для перехода между прямоугольным и полярным представлением комплексных чисел, могут использоваться указанные выше формулы преобразования между системами координат.
Операции умножения, деления и возведения в степень с комплексными числами, как правило, проще проводить в полярной форме. Согласно правилам возведения в степень:
- Умножение:
- Деление:
- Возведение в степень (формула Муавра):
В математическом анализе[править | править код]
Операции математического анализа тоже можно сформулировать, используя полярные координаты[16][17].
Дифференциальное исчисление[править | править код]
Справедливы следующие формулы:
Чтобы найти тангенс угла наклона касательной к любой данной точке полярной кривой 
Дифференцируя оба уравнения по 
Разделив эти уравнения (второе на первое), получим искомый тангенс угла наклона касательной в декартовой системе координат в точке 
Интегральное исчисление[править | править код]

Область 


Пусть 





Область 


Такой результат можно получить следующим образом. Сначала разобьём интервал ![[a,;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e682a8a7d3222e237401e57d673fd362523662cd)










Если число подынтервалов 


Обобщение[править | править код]
Используя декартовы координаты, площадь бесконечно малого элемента может быть вычислена как 
Для полярной системы координат, определитель матрицы Якоби равен 
Следовательно, площадь элемента в полярных координатах можно записать так:
Теперь, функция, записанная в полярных координатах, может быть интегрирована следующим образом:
Здесь область 



Формула для вычисления площади, описанная в предыдущем разделе, получена в случае 
Векторный анализ[править | править код]
Для полярных координат можно применить элементы векторного анализа. Любое векторное поле 
в направлении 
Связь между декартовыми компонентами поля 

Соответствующим образом в полярной системе координат определяются операторы векторного анализа. Например, градиент скалярного поля 
Всё это работает за исключением одной особой точки — полюса, для которой 
Трёхмерное расширение[править | править код]
Полярная система координат распространяется в третье измерение двумя системами: цилиндрической и сферической, обе содержат двумерную полярную систему координат как подмножество. По сути, цилиндрическая система расширяет полярную добавлением ещё одной координаты расстояния, а сферическая — ещё одной угловой координаты.
Цилиндрические координаты[править | править код]

Точка 
Цилиндрическая система координат, грубо говоря, расширяет плоскую полярную систему добавлением третьей линейной координаты, называемой «высотой» и равной высоте точки над нулевой плоскостью подобно тому, как декартова система расширяется на случай трёх измерений. Третья координата обычно обозначается как 

Тройку цилиндрических координат можно перевести в декартову систему следующими преобразованиями:
Сферические координаты[править | править код]
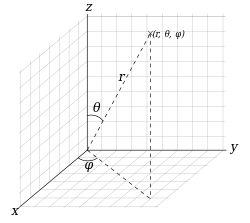
Точка начертана в сферической системе координат
Также полярные координаты можно расширить на случай трёх измерений путём добавления угловой координаты 











Тройку сферических координат можно перевести в декартову систему следующими преобразованиями:
Обобщение на n измерений[править | править код]
Полярную систему координат можно расширить на случай 






Для перевода обобщённых 
Как можно показать, случай 

Якобиан преобразования полярных координат в декартовы даётся формулой:
,
где 
Применение[править | править код]
Полярная система координат двумерная и поэтому может применяться только в тех случаях, когда местонахождение точки определяется на плоскости, или для случая однородности свойств системы в третьем измерении, например, при рассмотрении течения в круглой трубе. Лучшим контекстом применения полярных координат являются случаи, тесно связанные с направлением и расстоянием от некоторого центра. Например, в приведённых выше примерах видно, что простых уравнений в полярных координатах достаточно для определения таких кривых как спираль Архимеда, уравнения которых в прямоугольной системе координат гораздо сложнее. Кроме того, многие физические системы — такие, которые содержат тела, движущиеся вокруг центра, либо явления, распространяющиеся из некоторого центра — гораздо проще моделировать в полярных координатах. Поводом создания полярной системы координат было исследование орбитального и движения по кругу, впоследствии оказалось, что она крайне удобна иногда и для исследования некругового движения (см. Кеплерова задача).
Позиционирование и навигация[править | править код]
Полярную систему координат часто применяют в навигации, поскольку пункт назначения можно задать как расстояние и направление движения от отправной точки. Например, в авиации, для навигации применяют несколько изменённую версию полярных координат. В этой системе, обычно используемой для навигации, луч 0° называют направлением 360, а углы отсчитываются в направлении по часовой стрелке. Направление 360 соответствует магнитному северу, а направления 90, 180, и 270 соответствуют магнитным востоку, югу и западу[19]. Так, самолёт, летящий 5 морских миль на восток можно описать как самолёт, летящий 5 единиц в направлении 90 (центр управления полётами назовёт его найн-зиро)[20].
Применение в физике[править | править код]

Cечение комптоновского рассеяния от угла рассеяния (для разной энергии фотона)
Системы с радиальной симметрией очень хорошо подходят для описания в радиальных координатах, где полюс системы координат совпадает с центром симметрии. В качестве примера можно привести уравнение тока грунтовых вод в случае радиально симметричных колодцев. Системы с центральными силами также подходят для моделирования в полярных координатах. К таким системам относятся гравитационные поля, подчиняющиеся закону обратно-квадратичной зависимости, и вообще центральные силы. Также существенное удобство полярные координаты предоставляют при работе с системами, имеющими точечные (или приближенно точечные) источники энергии, такие как радиоантенны — при исследовании их излучения на сравнительно больших расстояниях от антенны, распространение звука или света — в особенности (но не обязательно) сферически- или цилиндрически-симметричное.
В определенных задачах, в том числе из числа упомянутых выше, использование сферических или цилиндрических координат (являющихся для этих задач естественными) по сути сводится к использованию просто двумерных полярных координат.
Полярные координаты как для вычислений, так и для наглядного изображения их результатов, бывают достаточно полезны не только в случаях, когда симметрия задачи близка в целом к осевой или сферической, но и в случаях, когда симметрия явно далека от таковой, например, для вычисления поля диполя. В этом случае применение полярных координат имеет мотивировку в малом размере источника поля (заряды диполя расположены очень близко друг к другу), к тому же поле каждого такого заряда просто выражается в полярных координатах, особенно если поместить полюс в один из этих зарядов (поле второго будет отличаться, кроме знака, лишь на малую поправку).
В квантовой механике и химии полярные координаты (наряду со сферическими для более сложных случаев) используются для изображения угловой зависимости волновой функции электрона в атоме, в том числе в целях качественного анализа и наглядности при преподавании.
Применение в прикладных целях, диаграммы направленности[править | править код]

Диаграмма направленности (азимутальная) типичной направленной антенны

Фронт мощности звуковой волны промышленного громкоговорителя показан в сферических координатах при шести частотах
В разных прикладных областях, полярные координаты применяются как способами, близкими к применяемым в соответствующих областям фундаментальной физики, так и самостоятельным образом.
Трёхмерное моделирование звука динамиков может использоваться для прогнозирования их эффективности. Необходимо сделать несколько диаграмм в полярных координатах для широкого диапазона частот, поскольку фронт существенно меняется в зависимости от частоты звука. Полярные диаграммы помогают увидеть, что многие громкоговорители с понижением частоты звука теряют направленность. В случае излучателя, имеющего строгую осевую симметрию или слабо от нее отклоняющегося, достаточно использовать не сферические, а обычные (двумерные) полярные координаты, так как во всех плоскостях, проходящих через ось симметрии, зависимость будет одинаковой или почти одинаковой. Если такой симметрии нет, то какое-то представление о звуковом потоке в разных направлениях может дать пара (для каждой частоты) полярных диаграмм в перпендикулярных плоскостях, для эллиптического или прямоугольного излучателя — связанного с его главными осями.
В полярных координатах также принято представлять характеристику направленности микрофонов, определяемую отношением чувствительности при падении звуковой волны под углом относительно акустической оси микрофона к его осевой чувствительности.
В принципе, полярные диаграммы могут использоваться для представления практически любых зависимостей. Но на практике обычно этот вид представления выбирается в случаях, когда речь идет от зависимости от реального геометрического направления (см. например Роза ветров, Диаграмма рассеяния, зависимость отраженного светового потока от угла в фотометрии, диаграмма направленности антенн, светодиодов и других светоизлучателей, фотодатчиков, акустических систем итп). Также довольно нередко можно встретиться с применением полярных координат в случаях, когда одна из переменных имеет циклический характер (в полярных координатах ее довольно естественно представлять углом).
Могут применяться и областях, не связанных прямо с физикой (хотя иногда можно проследить более или менее прямую аналогию в этом плане), например, можно использовать полярные диаграммы, аналогичные розе ветров, например, для изучения направлений миграций животных. Такое использование достаточно удобно и наглядно.
См. также[править | править код]
- Системы координат в элементарной математике
Примечания[править | править код]
- ↑ 1 2 Brown, Richard G. Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis (англ.) / Andrew M. Gleason. — Evanston, Illinois: McDougal Littell (англ.) (рус., 1997. — ISBN 0-395-77114-5.
- ↑ Friendly, Michael Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization. Дата обращения: 10 сентября 2006. Архивировано из оригинала 26 апреля 2001 года.
- ↑ T. Koetsier, L. Bergmans (2005), Mathematics and the Divine, Elsevier, с. 169, ISBN 0444503285
- ↑ David A. King (1996), «Astronomy and Islamic society: Qibla, gnomics and timekeeping», in Roshdi Rashed (ed.), Encyclopedia of the History of Arabic Science, Vol. 1, pp. 128—184 [153], Routledge, London and New York
- ↑ 1 2 Coolidge, Julian (англ.) (рус.. The Origin of Polar Coordinates (англ.) // American Mathematical Monthly : journal. — 1952. — Vol. 59. — P. 78—85. — doi:10.2307/2307104.
- ↑ Boyer, C. B. Newton as an Originator of Polar Coordinates (англ.) // American Mathematical Monthly : journal. — 1949. — Vol. 56. — P. 73—78. — doi:10.2307/2306162.
- ↑ Miller, Jeff Earliest Known Uses of Some of the Words of Mathematics. Дата обращения: 10 сентября 2006. Архивировано 15 февраля 2012 года.
- ↑ Smith, David Eugene. History of Mathematics, Vol II (неопр.). — Boston: Ginn and Co., 1925. — С. 324.
- ↑ Polar Coordinates and Graphing (PDF) (недоступная ссылка — история) (13 апреля 2006). Дата обращения: 22 сентября 2006. Архивировано 15 февраля 2012 года.
- ↑ Lee, Theodore; David Cohen, David Sklar. Precalculus: With Unit-Circle Trigonometry (англ.). — Fourth Edition. — Thomson Brooks/Cole, 2005. — ISBN 0534402305.
- ↑ Stewart, Ian; David Tall. Complex Analysis (the Hitchhiker’s Guide to the Plane) (англ.). — Cambridge University Press, 1983. — ISBN 0521287634.
- ↑ Serway, Raymond A.; Jewett, Jr., John W. Principles of Physics (неопр.). — Brooks/Cole—Thomson Learning, 2005. — ISBN 0-534-49143-X.
- ↑ Torrence, Bruce Follett; Eve Torrence. The Student’s Introduction to Mathematica® (англ.). — Cambridge University Press, 1999. — ISBN 0521594618.
- ↑ Claeys, Johan Polar coordinates (недоступная ссылка — история). Дата обращения: 25 мая 2006. Архивировано 15 февраля 2012 года.
- ↑
Smith, Julius O. Euler’s Identity // Mathematics of the Discrete Fourier Transform (DFT) (англ.). — W3K Publishing, 2003. — ISBN 0-9745607-0-7. - ↑ Husch, Lawrence S. Areas Bounded by Polar Curves. Дата обращения: 25 ноября 2006. Архивировано из оригинала 11 октября 2014 года.
- ↑ Lawrence S. Husch. Tangent Lines to Polar Graphs. Дата обращения: 25 ноября 2006. Архивировано из оригинала 2 июля 2015 года.
- ↑ Wattenberg, Frank Spherical Coordinates (недоступная ссылка — история) (1997). Дата обращения: 16 сентября 2006. Архивировано 15 февраля 2012 года.
- ↑ Santhi, Sumrit Aircraft Navigation System (недоступная ссылка — история). Дата обращения: 26 ноября 2006. Архивировано 15 февраля 2012 года.
- ↑ Emergency Procedures (PDF). Дата обращения: 15 января 2007. Архивировано 15 февраля 2012 года.
Литература[править | править код]
- Гельфанд И. М., Глаголева Е. Г., Кириллов А. А. Метод координат. (недоступная ссылка) Издание пятое, стереотипное. Серия: Библиотечка физико-математической школы. Математика. Выпуск 1. М.: Наука, 1973, стр. 47-50.
Ссылки[править | править код]
- Программы для рисования графиков в каталоге ссылок Curlie (dmoz)
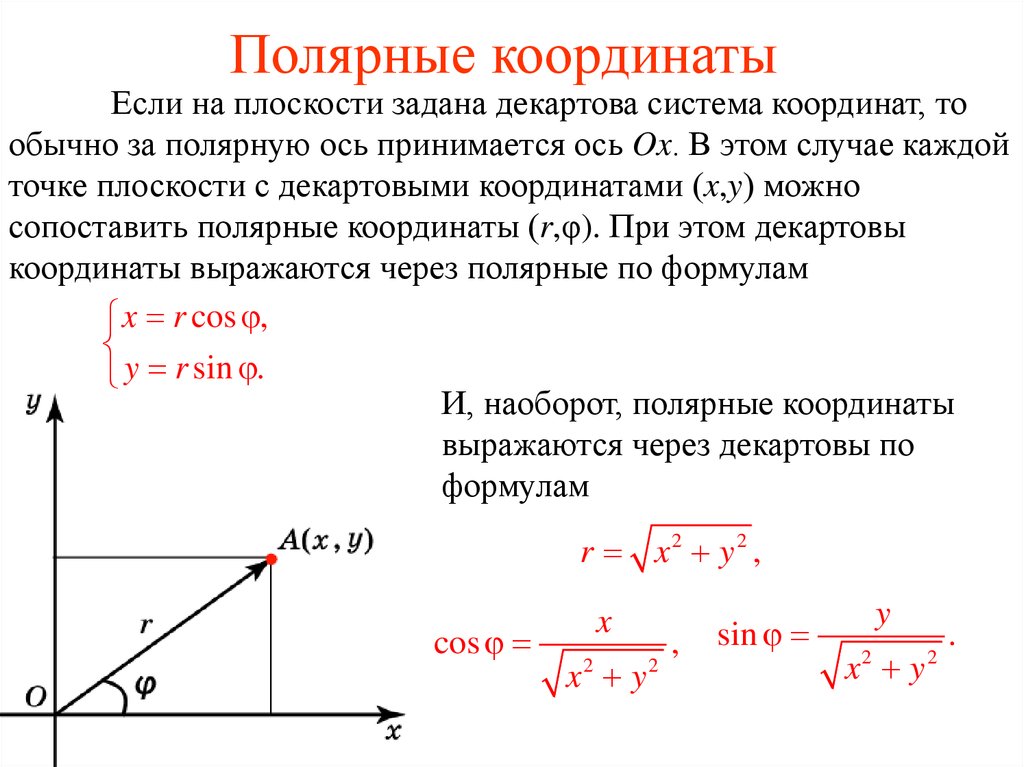
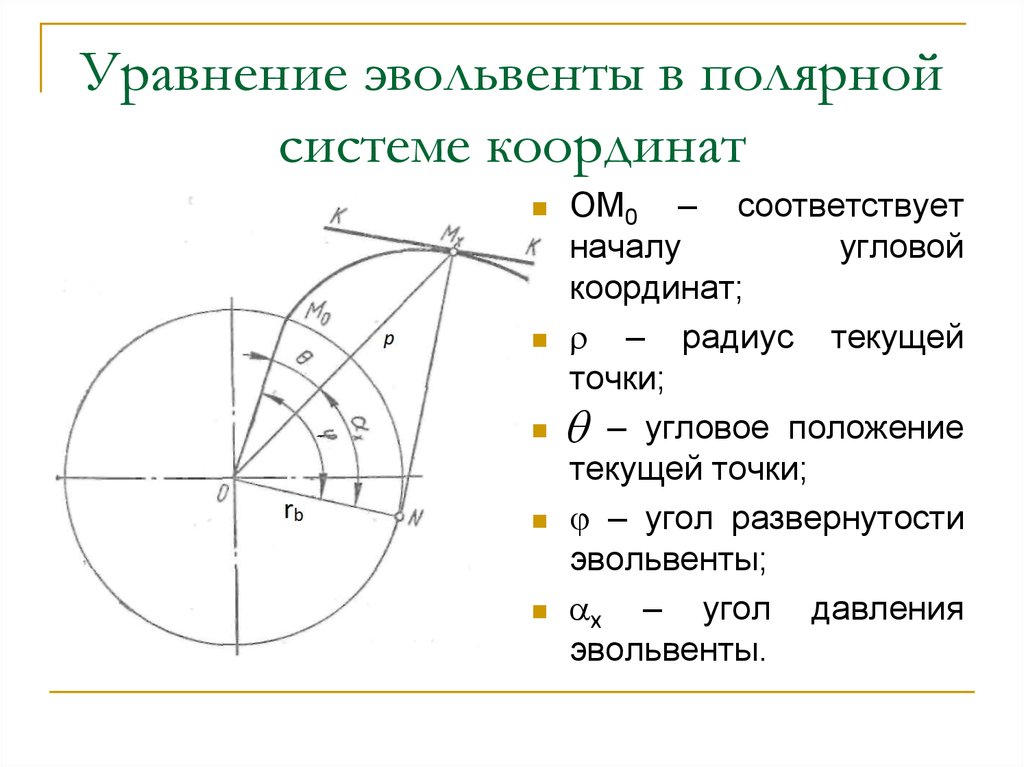 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 6)
6)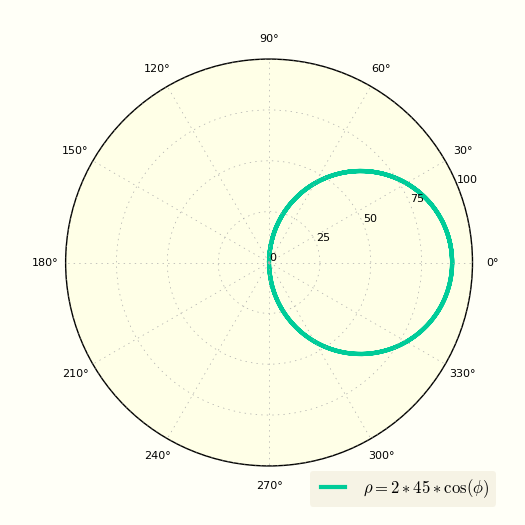 3.8
3.8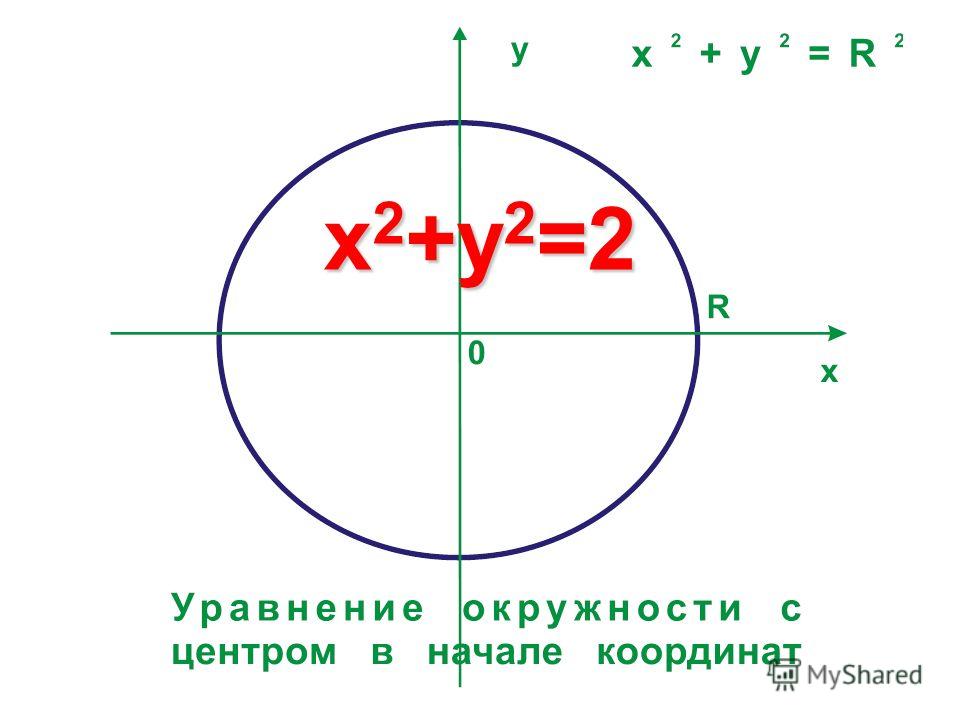 Это правило легко выводится из соотношений (3.6).
Это правило легко выводится из соотношений (3.6).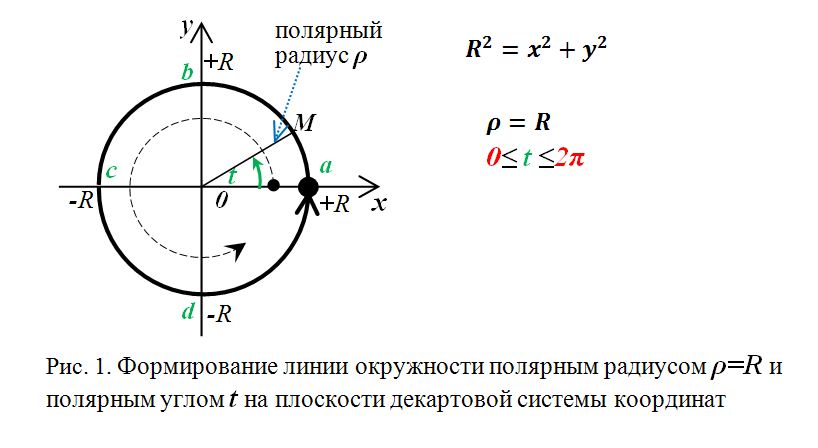 Площадь пластины
Площадь пластины 

 Переменные x и y изменяются в плоской области , которая является проекцией на плоскость xoy пространственной области “V”. Функция f(x,y,z), стоящая под интегралом должна быть непрерывной и ограниченной в области “V”.
Переменные x и y изменяются в плоской области , которая является проекцией на плоскость xoy пространственной области “V”. Функция f(x,y,z), стоящая под интегралом должна быть непрерывной и ограниченной в области “V”.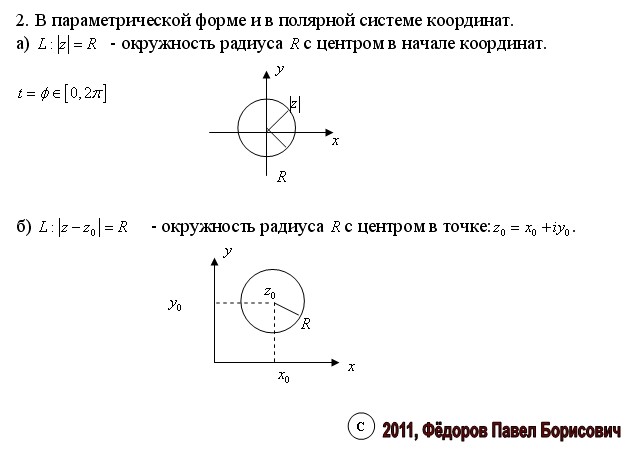 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.016 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.016 с.) 






















![{frac {1}{2}}int limits _{a}^{b}[r(varphi )]^{2},dvarphi .](https://wikimedia.org/api/rest_v1/media/math/render/svg/266e820a4d162bf3999f98de23e8237ad757c5ee)

![lim _{{Delta varphi to 0}}sum _{{i=1}}^{infty }{frac {1}{2}}r(varphi _{i})^{2},Delta varphi ={frac {1}{2}}int limits _{a}^{b}[r(varphi )]^{2},dvarphi .](https://wikimedia.org/api/rest_v1/media/math/render/svg/9889d1586d04c6f806776f20f2e9e4f0407d694c)
















