Уравнение окружности.
Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.
В формулировке окружности упоминается расстояние между точкой окружности и центром.
Формула расстояния между двумя точками М1(х1; у1) и М2(х2; у2) имеет вид:
,
Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х0; у0) и радиусом r.
Отметим произвольную точку М(х; у) на этой окружности.
.
Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.
Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х0 ) 2 +(у – у0 ) 2 = r 2 .
Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х0; у0) и радиусом r имеет вид:
В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):
Уравнение окружности.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:
Уравнение окружности
(Әйләнә тигезләмәсе)
17.03.14
Составила: учитель математики
Саттарова Р.Д.
Образовательные: Вывести уравнение окружности, рассмотрев решение этой задачи как одну из возможностей применения метода координат. Уметь: – Распознать уравнение окружности по предложенному уравнению, научить учащихся составлять уравнение окружности по готовому чертежу, строить окружность по заданному уравнению.
Цели урока:
Формулу нахождения координат середины отрезка.
Уравнение фигуры – это уравнение
с двумя переменными х и у, которому
удовлетворяют координаты любой
точки фигуры.
Пусть дана окружность.
А(а;b) – центр окружности,
С(х ; у) – точка окружности.
d 2 = АС 2 = (х – а)2 + (у – b)2,
d = АС = R, следовательно
R 2 = (х – а)2 + (у – b)2
Формула I
(х – а)2 + (у – b)2 = R2
уравнение окружности, где
А(а;b) − центр, R − радиус,
х и у – координаты точки окружности.
__________________________
А(2;4) – центр, R = 3, то
(х – 2)2 + (у – 4)2 = 32;
(х – 2)2 + (у – 4)2 = 9.
Формула II
(х – а)2 + (у – b)2 = R 2 .
Центр окружности О(0;0),
(х – 0)2 + (у – 0)2 = R 2,
х2 + у2 = R 2 − уравнение
окружности с центром в
начале координат. .
О (0;0) – центр, R = 4, тогда
х2 + у2 = 42;
х2 + у2 = 16.
1) узнать координаты центра;
2) узнать длину радиуса;
3) подставить координаты центра (а;b)
и длину радиуса R
в уравнение окружности
(х – а)2 + (у – b)2 = R2.
Для того чтобы составить уравнение
окружности, нужно:
№1. Составить уравнение окружности.
№2. Составить уравнение окружности.
№3. Составить уравнение окружности.
№4. Составить уравнение окружности.
№5. Составить уравнение окружности.
№6. Составить уравнение окружности.
№7. Заполните таблицу.
(х – 5)2 + (у + 3)2 = 36;
2) (х + 1)2 + (у – 7)2 = 49.
№8. Постройте в тетради окружности, заданные уравнениями:
№9. Найдите координаты центра и радиус, если АВ – диаметр данной окружности.
№10. Составьте уравнение окружности, проходящей через точку К(−12;5), с центром в начале координат.
№11. Составьте уравнение окружности с центром в точке С(3;−1), проходящей через начало координат.
№12. Составьте уравнение окружности с центром А(3;2), проходящей через В(7;5).
№13. Проверьте, лежат ли на окружности, заданной уравнением (х + 3)2 + (у − 4)2 = 25, точки А(1;−1), В(0;8), С(−3;−1).
№1. Даны точки С(−2;5) и D(0;3). Начертите окружность, для которой CD является радиусом. Составьте уравнение этой окружности.
№2. Даны точки С(−2;5) и D(0;3). Начертите окружность, для которой CD является диаметром. Составьте уравнение этой окружности.
Домашнее задание: п.73, 74, №17, 19, 22, 23, 26, решить задачи
Рисуем белку (единичный отрезок 2 клетки)
Краткое описание документа:
двумя переменными х и у,
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 931 человек из 79 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 309 человек из 67 регионов
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 496 075 материалов в базе
Дистанционные курсы для педагогов
Другие материалы
- 30.03.2014
- 3274
- 30.03.2014
- 3439
- 30.03.2014
- 823
- 30.03.2014
- 1108
- 30.03.2014
- 4057
- 30.03.2014
- 5348
- 30.03.2014
- 920
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 30.03.2014 2563 –> –> –> –>
- PPTX 3.2 мбайт –> –>
- Оцените материал:
Настоящий материал опубликован пользователем Саттарова Рания Дамировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 8 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 5898
- Всего материалов: 2
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Петербурге дали рекомендации по переводу школьников на дистант
Время чтения: 3 минуты
«Учителя года» проведут открытые занятия для педагогов России
Время чтения: 1 минута
Орловские школы переведут на дистанционное обучение с 24 января
Время чтения: 1 минута
Школы Сургута переведут на дистанционное обучение с 24 января
Время чтения: 1 минута
Санкт-Петербургский госуниверситет переходит на дистанционное обучение
Время чтения: 1 минута
Крупнейшие вузы Татарстана откроют цифровые кафедры в 2022 году
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Уравнение окружности.
Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.
В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.
Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.
Геометрическая интерпретация уравнения окружности – это линия окружности.
Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.
Окружность с центром в точке А и радиусом R поместим в координатную плоскость.
Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:
Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.
Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:
Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.
Примеры решения задач про уравнение окружности
Задача. Составить уравнение заданной окружности
Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.
Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2
Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3
Получаем:
(x – 2 ) 2 + (y – ( -3 )) 2 = 4 2
или
(x – 2 ) 2 + (y + 3 ) 2 = 16 .
Задача. Принадлежит ли точка уравнению окружности
Проверить, принадлежит ли точка A(2;3) уравнению окружности (x – 2) 2 + (y + 3) 2 = 16.
Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.
В уравнение ( x – 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3
Проверим истинность полученного равенства
( x – 2) 2 + ( y + 3) 2 = 16
( 2 – 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно
Таким образом, заданная точка не принадлежит заданному уравнению окружности.
[spoiler title=”источники:”]
http://infourok.ru/material.html?mid=48705
http://profmeter.com.ua/communication/learning/course/course7/chapter0552/
[/spoiler]
Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.
1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.
Решение:
Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:
![]()
Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:
![]()
![]()
2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).
Решение:
Так как центр окружности — точка A(8; -3), то a=8, b=-3.
Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.
![]()
![]()
![]()
Следовательно, уравнение данной окружности
![]()
3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).
Решение:
Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка
![]()
![]()
Центр окружности — точка O(1;-2). Значит, a=1, b=-2.
Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,
![]()
![]()
![]()
Таким образом, уравнение окружности с диаметром AB —
![]()
4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).
Решение:
Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение
![]()
получаем систему уравнений:
![Rendered by QuickLaTeX.com [left{ begin{array}{l} {(4 - a)^2} + {( - 5 - b)^2} = {R^2}\ {(8 - a)^2} + {(3 - b)^2} = {R^2}\ {( - 8 - a)^2} + {(11 - b)^2} = {R^2} end{array} right.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-1b6af6ba9c2f16e2223e654fc885b160_l3.png)
Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим
![]()
![]()
![]()
![]()
Приравняем правые части 2-го и 3-го уравнений:
![]()
![]()
![]()
Умножив уравнение
![]()
на -1 и сложив результат почленно с уравнением
![]()
получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:
![]()
![]()
получаем R²=100.
Следовательно, уравнение окружности, проходящей через три данные точки —
![]()
5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).
Решение аналогично решению задания 4. В результате получим уравнение
![]()
Написать уравнение окружности
Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.
1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.
Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:
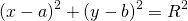
Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:
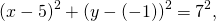
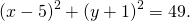
2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).
Так как центр окружности — точка A(8; -3), то a=8, b=-3.
Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.
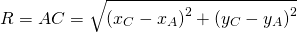
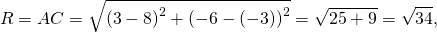
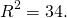
Следовательно, уравнение данной окружности
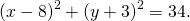
3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).
Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка
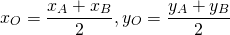
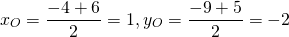
Центр окружности — точка O(1;-2). Значит, a=1, b=-2.
Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,
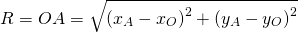
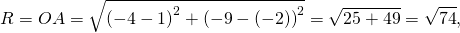
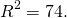
Таким образом, уравнение окружности с диаметром AB —
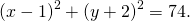
4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).
Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение
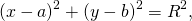
получаем систему уравнений:
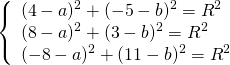
Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим
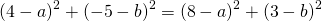
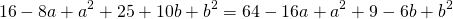
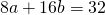
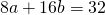
Приравняем правые части 2-го и 3-го уравнений:
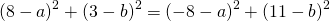
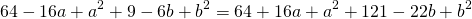
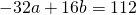
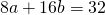
на -1 и сложив результат почленно с уравнением
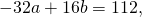
получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:
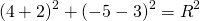
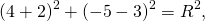
Следовательно, уравнение окружности, проходящей через три данные точки —
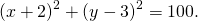
5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).
Решение аналогично решению задания 4. В результате получим уравнение
Уравнение окружности
Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.
Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности
Равенство (1) есть уравнение окружности радиуса R с центром в точке С.
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.
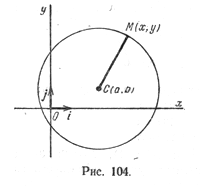
Так как |СМ| = ( sqrt <(x — a)^2 + (у — b)^2>), то уравнение (1) можно записать так:
(x — a) 2 + (у — b) 2 = R 2 (2)
Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение
есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).
Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид
Уравнение (3) называют каноническим уравнением окружности.
Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.
Непосредственной подстановкой значения радиуса в уравнение (3) получим
Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).
Подставив значение координат точки С и значение радиуса в формулу (2), получим
(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.
Задача 3. Найти центр и радиус окружности
Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.
Задача 4. Доказать, что уравнение
является уравнением окружности. Найти ее центр и радиус.
Преобразуем левую часть данного уравнения:
Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.
Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).
Напишем уравнение прямой АВ:
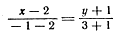 или 4х + 3y —5 = 0.
или 4х + 3y —5 = 0.
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:
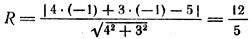
Напишем уравнение искомой окружности
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).
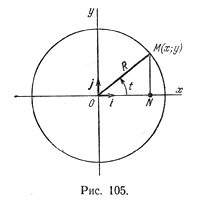
Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t
(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем
Уравнение окружности по заданному центру и радиусу в различных формах
Этот онлайн-калькулятор показывает уравнение окружности в стандартной, параметрической и общей формах, по заданному центру и радиусу окружности. Описание и формулы приведены под калькулятором

Уравнение окружности по заданному центру и радиусу в различных формах
Центр окружности
Уравнение окружности
Уравнение окружности — это алгебраический способ описания всех точек, лежащих на некоторой окружности. То есть если координаты точки x и y обращают уравнение окружности в равенство — эта точка принадлежит данной окружности. Существуют разные формы записи уравнения окружности:
- общее уравнение окружности
- стандартное уравнение окружности 1
- параметрическое уравнение окружности
- уравнение окружности в полярных координатах
Общее уравнение окружности
Общее уравнение окружности с центром и радиусом выглядит так:
,
где
В таком виде довольно сложно судить о свойствах заданной этим уравнением окружности, а именно, о координатах центра и радиусе. Но эту форму достаточно легко привести к стандартной форме (ниже), которая гораздо нагляднее.
Стандартное уравнение окружности
Стандартное уравнение окружности с центром и радиусом выглядит так:
Переход от общей формы к стандартной заключается в применении метода выделения полного квадрата. Получив стандартную форму, можно легко узнать координаты центра и радиус. Подробнее можно посмотреть здесь — Метод выделения полного квадрата и здесь — Нахождение центра и радиуса окружности по общему уравнению окружности.
Параметрическое уравнение окружности
Параметрическое уравнение окружности с центром и радиусом выглядит так:
Уравнение называется «параметрическим», потому что и x и y зависят от «параметра» тета. Это переменная, которая может принимать любые значения (но конечно это должно быть одно и то же значение в обоих уравнениях). Для параметрического уравнения используется определение синуса и косинуса в прямоугольном треугольнике построенном на радиусе и перпендикуляров от точки на окружности до координатных осей.
Уравнение окружности в полярных координатах
Для записи уравнения окружности в полярных координатах требуются полярные координаты центра окружности по отношению к началу координат. Если полярные координаты центра окружности — это , то полярные координаты точки окружности должны удовлетворять следующему уравнению:
,
где a — радиус окружности.
Так, во всяком случае, его называют в англоязычной литературе. Насчет русского термина я не уверен, по-моему эту форму рассматривают просто как еще один способ записи общего уравнения окружности, тем более что переход от общего уравнения к стандартному довольно простой. ↩
источники:
http://razdupli.ru/teor/31_uravnenie-okruzhnosti.php
http://planetcalc.ru/8115/
Download Article
Download Article
The equation of a circle gives you the center coordinates and radius, allowing you to represent all of the literally infinite points around the boundary of the circle. But how exactly do you write it? Read on to learn how to write the equation of a circle in standard form, as well as how to convert general form to standard form. Once you’ve got that down, you can try your hand at some sample problems and check your answers. Let’s get started!
Things You Should Know
-

1
-

2
The general form of the equation of a circle is
. This equation technically has all the same information the standard form has, it’s just expressed differently. Let’s break it down:[2]
Advertisement
-

1
-

2
Plug in values for the radius and center coordinates to complete a standard equation. This is probably the simplest type of problem you’ll have dealing with the equation of a circle. Just place the values where they go in the the standard form
.[4]
-

3
Advertisement
-

1
-

2
Move the constant to the other side of the equation. Since the number is moving to the other side of the equation, the sign in front of it changes. So if it was negative on the left side, it’ll be positive on the right side (and vice versa).[7]
-

3
-

4
-

5
-

6
Add the numbers to both sides of the equation. Keeping your groups together on the left side of the equation, add your third number to each parenthetical expression. Then, add each of those numbers to the right side of the equation to maintain equality.[11]
-

7
Solve the
and
groups. Now you have what you may recognize as a basic trinomial in each parenthesis. Use the quadratic formula to find the number you need for each parenthetical expression in the standard equation of a circle.[12]
-

8
Simplify the right side of the equation. Almost there! Add the numbers on the right side, then square them. The equation you’re left with will be the standard form for the equation of a circle. From here, you can easily determine the center points and radius if you need to graph the circle.[13]
Advertisement
-

1
Write the equation of the circle with center
and radius
.[14]
- Hint: pay attention to the negative signs in front of the center coordinates.
-

2
Find the center coordinates of the circle with the equation
.[15]
- Hint: look at the signs in the parentheses and compare them to the standard form for the equation.
-

3
Find the center coordinates and radius for the circle
.[16]
- Hint: complete the square twice to convert general form to standard form. Don’t forget that anything you add on the left side you also have to add on the right side.
-

4
Is
the equation of a circle? Why or why not?[17]
- Hint: a circle can never have a negative radius.
Advertisement
-

1
-

2
The center coordinates are
. You’re given the equation of the circle
. Since the signs in the parentheses in the standard form are
, the
signs in this equation tell you that the center coordinates must be negative.[19]
-

3
-

4
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 1,175 times.
Did this article help you?
Прежде всего,
давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что
уравнение с двумя переменными x и y
называется уравнением линии l, если этому уравнению
удовлетворяют координаты любой точки линии l и не
удовлетворяют координаты никакой точки, не лежащей на этой линии.
Сегодня на уроке мы
попробуем по геометрическим свойствам линии найти ее уравнение.
В качестве линии
рассмотрим окружность радиуса с
центром в точке .
Пусть центр
окружности имеет координаты . Возьмем на
окружности произвольную точку . Запишем формулу
расстояния между точками C и M.
Мы знаем, что длина отрезка, который соединяет любую точку на окружности с
центром окружности – это радиус. Поэтому можно записать, что MC
равно r. Возведем MC в квадрат
и получим уравнение MC2 = r2.
Заменим MC2 квадрат на выражение и получим, что если
точка лежит на окружности с радиусом r и центром в
точке C, то координаты этой точки удовлетворяют
уравнению . Если точка не
лежит на окружности, то расстояние от этой точки до центра окружности не равно
радиусу, поэтому координаты таких точек не будут удовлетворять полученному
уравнению. Поэтому можно сказать, что в прямоугольной системе координат уравнение
окружности радиуса r с центром в точке C с координатами имеет вид:
.
Задача. Записать
уравнение окружности с радиусом и центром в начале
координат.
Решение.
Начало координат
имеет координаты (0;0). Подставим их в уравнение окружности и получим, что
уравнение окружности с радиусом r и
центром в начале координат имеет вид
.
Задача. Начертить
окружность, заданную уравнением .
Решение.
Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего,
определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь
давайте определим величину радиуса окружности.
Поскольку в правой
части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо
извлечь квадратный корень из 4. Получим 2.
Значит наша
формула задает окружность с центром в точке с координатами пять три и радиусом
равным двум.
Задача. Начертить
окружность, заданную уравнением .
Решение.
Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего
определимся с координатами центра окружности.
Это будут числа -4
и 2. Теперь давайте определим величину радиуса окружности.
Задача. Начертить
окружность, заданную уравнением .
Решение. Уравнениями
такого типа описываются окружности с центром в начале координат. Теперь давайте
определим величину радиуса окружности. Поскольку в правой части формулы стоит
квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень
из 9.
Значит наша формула
задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.
Теперь давайте
попробуем решить задачу обратную данным.
Задача. Составить
уравнение окружности, которая показана на рисунке.
Как и в предыдущих
задачах мы начнем с определения координат центра окружности. Сделать это
нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр
окружности имеет координаты (0;0).
Нетрудно заметить,
что радиус окружности равен 4.
Запишем уравнение
окружности и подставим найденные значения.
Ответ: .
Решим еще одну
задачу.
Задача. Составить
уравнение окружности, которая показана на рисунке.
Решение.
– центр окружности
– радиус окружности
Ответ:.
Задача. Составить
уравнение окружности, которая показана на рисунке.
Решение.
– центр окружности
– радиус окружности
Ответ:.
Решая задачи, мы с
вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот
порядок.
Для того, что
бы составить уравнение окружности и построить ее надо:
1. Найти координаты
центра окружности.
2. Найти длину
радиуса этой окружности.
3. Записать уравнение
окружности.
4. Подставить
полученные значения в уравнение окружности.
5. Построить
окружность, если это требуется для решения задачи.
Рассмотрим еще одну
задачу.
Написать уравнение
окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм
имеет координаты шесть три.
Задача. Написать
уравнение окружности с диаметром , если
,
.
Решение.
Найдем координаты
центра окружности. Центр окружности является серединой диаметра. Воспользуемся
формулами для нахождения координат середины отрезка.
Получим, что центр
окружности имеет координаты .
Теперь определим
радиус окружности. Для этого найдем расстояние от центра окружности до концов
диаметра.
Запишем общее
уравнение окружности и подставим в него найденные значения. Тогда получим, что
уравнение данной окружности имеет вид:
Ответ: .
Подведем итоги
урока.
На сегодняшнем
уроке мы познакомились с формулой, которая задает окружность с центром в точке С
(x0; y0)
и радиусом r.
Также мы
познакомились с формулой, которая задает окружность с центром в начале
координат и радиусом r.
Мы рассмотрели
задачи на составление уравнения окружности по рисунку и на построение
окружности по заданному уравнению.
