Как составить уравнение параллелограмма по координатам

Задача 59148 Подскажите как правильно решать! Найти.

Условие

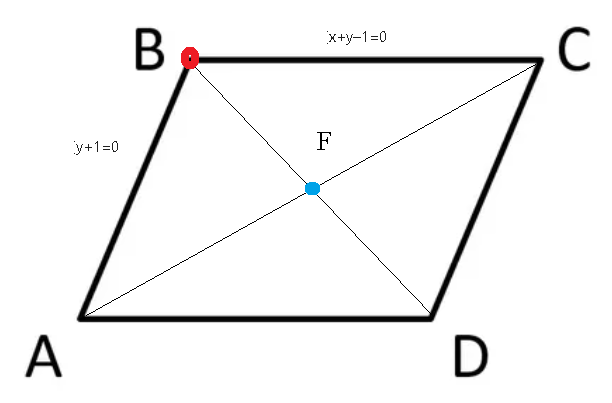
Подскажите как правильно решать! Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон x+y-1=0 если у+1=0 если известно что диагональ параллелограмма пересекается в точке F(-1, 0) И надо ли в этой задаче чертить рисунок?

Решение

Можно нарисовать схематический чертеж, чтобы понять как решать задачу ( cм. рис)

Противоположные стороны параллелограмма параллельны.

Даны уравнения смежных сторон. Это может быть АВ и ВС

1) чтобы найти точку пересечения сторон АВ и ВС

Это и есть координаты точки B.

2)
Составить уравнение прямой, проходящей через две точки:
(2;-1) и F(–1, 0)

Это можно сделать двумя способами:

Уравнение прямой с угловым коэффициентом имеет вид:
y=kx+b

Подставляем координаты точек:
-1=k*2+b
0=k*(-1)+b
находим k и b

[b]x+3y+1=0[/b] — это ответ.

Второй способ
Уравнение прямой, проходящей через две точки имеет вид: ( cм. скрин)

Подставляем координаты точек

и получаем пропорцию:

[b]x+3y+1=0[/b]- ответ.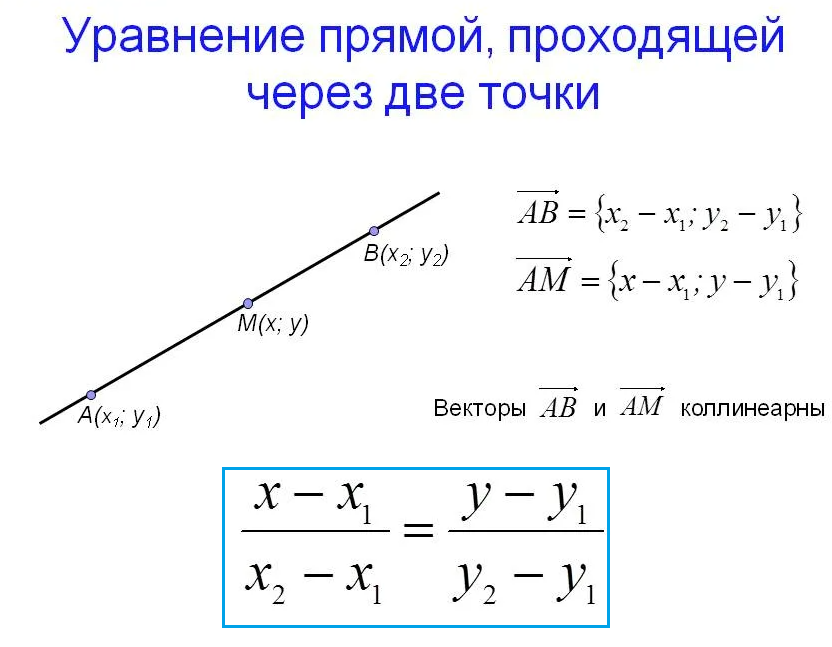

Найти четвертую вершину параллелограмма

Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?

В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.

Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.

Дано: ABCD — параллелограмм,

1) Найдём координаты точки O — середины диагонали AC.

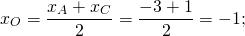
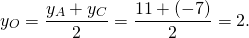
2) По свойству диагоналей параллелограмма, точка O также является серединой BD:

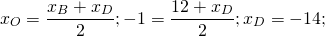
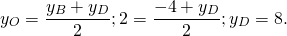
Дано: ABCD — параллелограмм,

1) Ищем координаты точки O — середины отрезка BD:

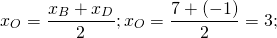
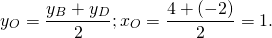
2) Точка O также является серединой AC:

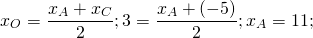
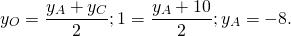
2 Comments

А как вы получили -14 в первом примере.

Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.

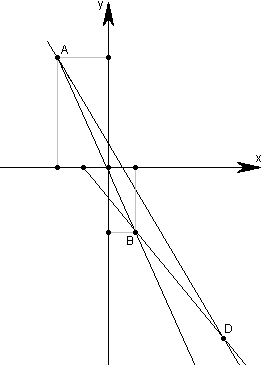
Даны уравнения двух сторон параллелограмма 8х+3у+1=0, 2х+у-1=0 и уравнение одной из его диагоналей 3х+2у+3=0. Определить координаты вершин этого параллелограмма.

Выразим у:

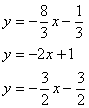Мы видим, что в уравнениях сторон коэффициенты при х не равны, значит прямые, определяемые этими уравнениями, не параллельны. То есть пересекаются, образуя одну из вершин. Пусть это будет вершина А. И пусть первое уравнение – сторона АВ, второе – А D .

Для нахождения точки А приравняем эти два уравнения:

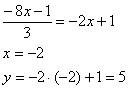А(-2;5)

Мы видим, что уравнение 3х+2у+3=0 задает диагональ BD . Поэтому, приравняв сначала 1 и 3, а затем 2 и 3 уравнения, найдем соответственно точки D и В.

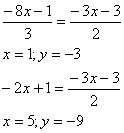Итак В (1;-3) D (5;-9)

Как известно в параллелограмме противоположные стороны параллельны, то есть коэффициенты k при х равны. Поэтому для сторон ВС и CD остаются неизвестными только свободные члены d . Найдем их, подставив в уравнения прямых их известные точки D и В соответственно:

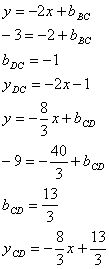Теперь для нахождения точки С приравняем уравнения сторон BC и CD

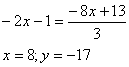С(8;-17)

источники:

http://www.treugolniki.ru/najti-koordinaty-vershiny-parallelogramma/

http://methmath.ru/zadatcha9.html

Источник

Тема: Составить уравнение диагоналей параллелограмма (Прочитано 6110 раз)

0 Пользователей и 1 Гость просматривают эту тему.

В общем задача весьма простая с изюминкой,не пойму как её решить.Даны координаты параллелограмма ABCD.Известны координаты точек A(2;4),B(3;-7),C(-6;6).Составить уравнение диагоналей АС и BD.Насколько я понимаю чтобы составить ур-е диагоналей нужно найти точку D,а её я даже не пойму как найти.

« Последнее редактирование: 31 Мая 2011, 23:52:37 от Dlacier »

Найдите уравнение прямой СD по точке С и направляющему вектору прямой AB
Найдите уравнение прямой AD по точке A и направляющему вектору прямой BC

Найдите точку D как пересечение прямых BD и AC, составив предварительно их уравнения по 2 точкам.

Решение задач – практическое искусство; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь….

Найдите уравнение прямой СD по точке С и направляющему вектору прямой AB
Найдите уравнение прямой AD по точке A и направляющему вектору прямой BC

Найдите точку D как пересечение прямых СD и AD, составив предварительно их уравнения по 2 точкам. Дальше дело техники.

Поправка.

Источник

Уравнение параллелограмма (также закон параллелограмма или тождество параллелограмма ) – это математическая теорема, которая берет свое начало и свое название от элементарной геометрии , но также применяется в очень похожей формулировке к комплексным числам и векторам во внутренних пространствах продуктов .

Применение в геометрии

Обозначения на параллелограмме

предложение

В параллелограмме с длинами сторон a , b и диагоналями e , f применяется:

2 влево (a ^ 2 + b ^ 2 right) = e ^ 2 + f ^ 2.

доказательства

Теорема непосредственно и особенно просто следует из теоремы Пифагора . Для этого расширяем соседний рисунок на высоту с левой стороны по диагонали f с участками q . Двойное применение теоремы Пифагора дает два уравнения
Ха}

${ displaystyle (a + q) ^ {2} + h_ {a} ^ {2} = e ^ {2}}$

${ displaystyle (aq) ^ {2} + h_ {a} ^ {2} = f ^ {2}}$

Сумма этих двух уравнений дает . Третье приложение обеспечивает доказательство теоремы.
${ displaystyle 2 (a ^ {2} + q ^ {2} + h_ {a} ^ {2}) = e ^ {2} + f ^ {2}}$ ${ displaystyle q ^ {2} + h_ {a} ^ {2} = b ^ {2}}$

Доказательство очень просто с помощью закона косинуса :

$begin {align} e ^ 2 + f ^ 2 & = (a ^ 2 + b ^ 2-2ab cos ( beta)) + (c ^ 2 + b ^ 2-2cb cos ( gamma) ) \ & = 2 (a ^ 2 + b ^ 2) end {align}$

там и есть.
с = а

Два вектора и создаем параллелограмм

В линейной алгебре в школе подходит доказательство с векторами и скалярным произведением :

С и применяется

$color {красный} e ^ 2 color {черный} + color {синий} f ^ 2 color {черный} = color {красный} a ^ 2 + 2 vec a cdot vec b + b ^ 2 color {черный} + color {синий} a ^ 2-2 vec a cdot vec b + b ^ 2 color {black} = 2 a ^ 2 + 2 b ^ 2$

Обобщение и обращение

Следующее относится к любому плоскому квадрату с данными обозначениями:

a ^ 2 + b ^ 2 + c ^ 2 + d ^ 2 = e ^ 2 + f ^ 2 + 4 x ^ 2,

где обозначает расстояние между центрами двух диагоналей.
Икс

Если квадрат представляет собой параллелограмм, два диагональных центра совпадают. Таким образом, уравнение параллелограмма является частным случаем.
х = 0

И наоборот: если уравнение параллелограмма выполнено, то . Две диагонали делят друг друга пополам, квадрат представляет собой параллелограмм.
х = 0

Приложение для комплексных чисел

предложение

Для двух комплексных чисел z, w:

2 слева (| z | ^ 2 + | w | ^ 2 right) = | z + w | ^ 2 + | zw | ^ 2.

доказательство

Справедливость теоремы очевидна, если интерпретировать числа в гауссовой плоскости чисел , в которой z и w затем образуют параллелограмм с диагоналями z + w и zw. Однако его также можно получить непосредственно математически. Используя для каждого комплексного числа, мы имеем:
$left | z right | ^ 2 = z overline {z}$

$left | z + w right | ^ 2 + left | zw right | ^ 2 = (z + w) overline {(z + w)} + (zw) overline {(zw)}$

= (z + w) ( overline {z} + overline {w}) + (zw) ( overline {z} - overline {w})

= (z overline {z} + w overline {z} + z overline {w} + w overline {w}) + (z overline {z} -w overline {z} -z overline { w} + w overline {w})

= 2 влево | г вправо | ^ 2 + 2 влево | ш вправо | ^ 2

Уравнение в векторных пространствах

Рассмотрение в Prähilberträumen представляет собой наиболее абстрактный курс вида, заявление двух предыдущих разделов с теперь следующей теорема может быть доказана (один с помощью. Аналитическая геометрия , другое по переработке двухмерного – векторное пространства в разделе Определение умножения и нормы), но соответствующие доказательства, конечно, не лишние с доступными средствами.

предложение

В предгильбертовых пространствах , то есть векторных пространствах, в которых определено скалярное произведение (или в векторных пространствах, по крайней мере, с одним положительным полуопределенным внутренним произведением) применяется следующее:

| x + y | ^ 2 + | xy | ^ 2 = 2 ( | x | ^ 2 + | y | ^ 2)

где норма индуцированная с помощью скалярного произведения (неотрицательно скалярное произведения) ( пол-норма ).

доказательство

Для доказательства нужен только тот факт, что скалярный продукт каждого внутреннего пространства продукта линейен относительно сложения для обоих аргументов (см. Определение скалярного продукта и полуторалинейной формы ). Тогда получаем:

| x + y | ^ 2 + | xy | ^ 2 = langle x + y, x + y rangle + langle xy, xy rangle

= langle x, x + y rangle + langle y, x + y rangle + langle x, xy rangle - langle y, xy rangle

= langle x, x rangle + langle x, y rangle + langle y, x rangle + langle y, y rangle + langle x, x rangle - langle x, y rangle - langle y, x rangle + langle y, y rangle

= 2 langle x, x rangle + 2 langle y, y rangle = 2 ( | x | ^ 2 + | y | ^ 2)

разворот

Уравнение параллелограмма не применяется в нормированных векторных пространствах , норма которых не определяется скалярным произведением. Это набор Джордана-фон Неймана (после Паскуаля Джордана и Джона фон Неймана ): применяет в нормализованном векторном пространстве параллелограмм, существует скалярное произведение , которое генерирует норму, то есть для всех применимых
х в V

Это скалярное произведение может быть определено формулой поляризации , в реальном случае, например, как

$langle x, y rangle = frac 14 left ({ | x + y | ^ 2- | xy | ^ 2} right)$

а в сложном случае –

$langle x, y rangle = frac {1} {4} left ( | x + y | ^ 2- | xy | ^ 2 right) + frac {i} {4} left ( | x + iy | ^ 2- | x-iy | ^ 2 right).$

источники

Дирк Вернер : Функциональный анализ . 6-е, исправленное издание, Springer-Verlag, Берлин 2007, ISBN 978-3-540-72533-6 , страницы 203-204.

веб ссылки

Источник

Помогаю со студенческими работами здесь

Найти координаты всех вершин параллелограмма, если известны координаты одной вершины и уравнения двух его сторон
Найти координаты всех вершин параллелограмма, если известны координаты одной вершины А=(12;-7) и…

Уравнения сторон параллелограмма
Дано 2 смежные вершины А(-3,-1) и В(2,2) параллелограмма АВСD и точка М(2,-3) пересечение его…

Вычислить площадь параллелограмма ABCD по координатам трех его вершин в репере
Вычислить площадь параллелограмма ABCD по координатам трех его вершин в репере (O, ): 1) A(3,1),…

Составить уравнения двух сторон параллелограмма
В параллелограмме известны точка пересечения диагоналей М(7;6) и уравнение двух смежных сторон :…

Составить уравнения трех сторон параллелограмма
Если известны: уравнение стороны AB: 3x+4y-12=0, уравнение диагонали AC: x+12y-12=0 и середина…

Составить уравнения двух других сторон параллелограмма
Прямые 3х – 4у + 17 = 0 и 4х – у – 12 = 0 являются сторонами параллелограмма, а точка Р (2; 7 ) –…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

Источник

Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?

В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.

Примеры.

Дано: ABCD — параллелограмм,

A(-3;11), B(12;-4), C(1;-7)

Найти: D.

Решение:

1) Найдём координаты точки O — середины диагонали AC.

По формуле координат середины отрезка

$[x_O = frac{{x_A + x_C }}{2} = frac{{ - 3 + 1}}{2} = - 1;]$

$[y_O = frac{{y_A + y_C }}{2} = frac{{11 + ( - 7)}}{2} = 2.]$

То есть O(-1;2).

2) По свойству диагоналей параллелограмма, точка O также является серединой BD:

$[x_O = frac{{x_B + x_D }}{2}; - 1 = frac{{12 + x_D }}{2};x_D = - 14;]$

$[y_O = frac{{y_B + y_D }}{2};2 = frac{{ - 4 + y_D }}{2};y_D = 8.]$

Ответ: D (-14; 8).

Дано: ABCD — параллелограмм,

B(7;4), C(-5;10), D(-1;-2)

Найти: A.

Решение:

1) Ищем координаты точки O — середины отрезка BD:

$[x_O = frac{{x_B + x_D }}{2};x_O = frac{{7 + ( - 1)}}{2} = 3;]$

$[y_O = frac{{y_B + y_D }}{2};x_O = frac{{4 + ( - 2)}}{2} = 1.]$

Итак, O (3;1).

2) Точка O также является серединой AC:

$[x_O = frac{{x_A + x_C }}{2};3 = frac{{x_A + ( - 5)}}{2};x_A = 11;]$

$[y_O = frac{{y_A + y_C }}{2};1 = frac{{y_A + 10}}{2};y_A = - 8.]$

Ответ: A (11;-8).

Источник

Задача 59148 Подскажите как правильно решать! Найти.

Условие

Решение

Найти четвертую вершину параллелограмма

2 Comments