Как составить уравнение плоскости а1а2а3

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.

Для того, чтобы однозначно построить плоскость, необходимы три точки, которые не лежат на одной прямой.

Общее уравнение плоскости принимает вид:

Общее уравнение плоскости

Ax+By+Cz+D=0Ax+By+Cz+D=0,

где A,B,C,DA, B, C, D — коэффициенты, задающие плоскость. Они не могут быть одновременно равны нулю.

Здесь будет калькулятор

Составление уравнения плоскости по трем точкам

Текст цитаты

Заголовок

Текст цитаты

В случае, когда известны координаты всех трех точек, уравнение плоскости, проходящей через эти точки составляется с помощью определителя:

Уравнение плоскости через определитель

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0,

где (x1;y1;z1),(x2;y2;z2),(x3;y3;z3)(x_1;y_1;z_1), (x_2;y_2;z_2), (x_3;y_3;z_3) — координаты точек, через которые проходит данная плоскость, а (x;y;z)(x; y; z) — всевозможные координаты точек этой плоскости.

Задача 1

Составить уравнения плоскости проходящей через три точки с координатами (1;3;0),(5;6;4),(−1;−4;0)(1;3;0), (5;6;4), (-1;-4;0).

Решение

Пусть:

x1=1x_1=1
y1=3y_1=3
z1=0z_1=0
x2=5x_2=5
y2=6y_2=6
z2=4z_2=4
x3=−1x_3=-1
y3=−4y_3=-4
z3=0z_3=0

Составляем определитель:

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0

∣x−15−1−1−1y−36−3−4−3z−04−00−0∣=0begin{vmatrix}
x-1 & 5-1 & -1-1 \
y-3 & 6-3 & -4-3 \
z-0 & 4-0 & 0-0 \
end{vmatrix}=0

∣x−14−2y−33−7z40∣=0begin{vmatrix}
x-1 & 4 & -2 \
y-3 & 3 & -7 \
z & 4 & 0 \
end{vmatrix}=0

28x−8y−22z−4=028x-8y-22z-4=0 — уравнение искомой плоскости.

Ответ

28x−8y−22z−4=028x-8y-22z-4=0

Уравнение плоскости по точке и вектору нормали

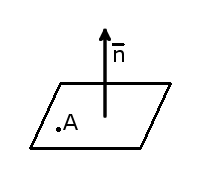
Если дана точка, лежащая на плоскости и вектор нормали к этой плоскости, то сама плоскость задается уравнением:

Уравнение плоскости по точке и нормали

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0,

где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, принадлежащей плоскости, а (n1;n2;n3)(n_1;n_2;n_3) — координаты вектора нормали к этой плоскости.

Задача 2

Выпишите уравнение плоскости, если даны: координата точки плоскости (8;−2;9)(8;-2;9) и вектор нормали (1;3;5)(1;3;5).

Решение

x0=8x_0=8
y0=−2y_0=-2
z0=9z_0=9
n1=1n_1=1
n2=3n_2=3
n3=5n_3=5

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0

(x−8)⋅1+(y−(−2))⋅3+(z−9)⋅5=0(x-8)cdot 1+(y-(-2))cdot 3+(z-9)cdot 5=0

x−8+3y+6+5z−45=0x-8+3y+6+5z-45=0

x+3y+5z−47=0x+3y+5z-47=0 — уравнение плоскости.

Проверка

Чтобы убедиться в том, что задача решена правильно, без ошибок, необходимо в полученное уравнение подставить координаты точки, которые даны в условии задачи:

8+3⋅(−2)+5⋅9−47=08+3cdot(-2)+5cdot9-47=0

0=00=0 — верно, значит ответ правильный.

Ответ

x+3y+5z−47=0x+3y+5z-47=0

Уравнение плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку “Решить”.

Уравнение плоскости, проходящей через три точки

Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы и 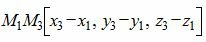не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M₁, M₂, M₃ тогда и тольно тогда, когда векторы M₁M₂, M₁M₃ и компланарны. Но векторы M₁M₂, M₁M₃, M₁M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов M₁M₂, M₁M₃, M₁M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:

Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M₁, M₂, M₃:

Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).

Решение.

Уравнение плоскости, проходящей через точки A(x₁, y₁, z₁), B(x₂, y₂, z₂) и C(x₃, y₃, z₃) имеет следующий вид:

Подставляя координаты точек A, B, C в (1), получим:

Упростим:

Разложим определитель по первому столбцу:

Упростим выражение:

или

Ответ:

Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:

Уравнение плоскости, проходящей через одну точку и имеющий нормаль n

Пример 2. Построить плоскость, проходящую через точку M₀(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).

Решение.

Уравнение плоскости, проходящей через точку M₀(x₀, y₀, z₀) и имеющей нормаль n(A, B, C) имеет следующий вид:

Подставляя координаты векторов M₀ и n в (2), получим:

или

Уравнение плоскости, проходящей через три точки.

Для того, чтобы через
три какие- либо точки пространства можно
было провести единственную плоскость,
необходимо, чтобы эти точки не лежали
на одной прямой.

Рассмотрим
точки М₁(x₁,
y₁,
z₁),
M₂(x₂,
y₂,
z₂),
M₃(x₃,
y₃,
z₃)
в общей декартовой системе координат.

Для
того, чтобы произвольная точка М(x,
y,
z)
лежала в одной плоскости с точками М₁,
М₂,
М₃
необходимо, чтобы векторы
были компланарны.

()
= 0

Таким
образом,

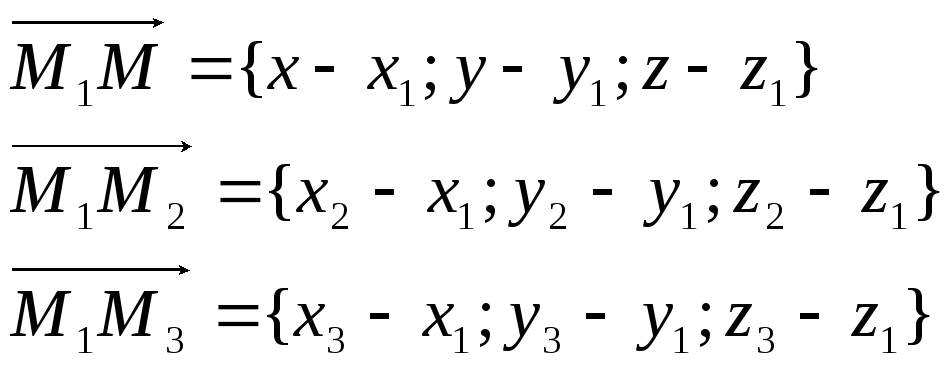
Уравнение
плоскости, проходящей через три точки:

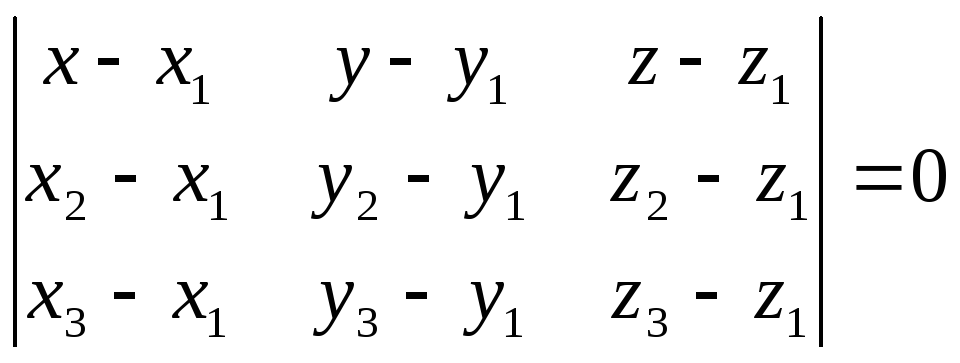
Уравнение
плоскости по двум точкам и вектору,
коллинеарному плоскости.

Пусть заданы точки
М₁(x₁,y₁,z₁),M₂(x₂,y₂,z₂)
и вектор.

Составим
уравнение плоскости, проходящей через
данные точки М₁
и М₂
и произвольную точку М(х, у, z)
параллельно вектору .

Векторы
и
вектордолжны быть
компланарны, т.е.

()
= 0

Уравнение
плоскости:

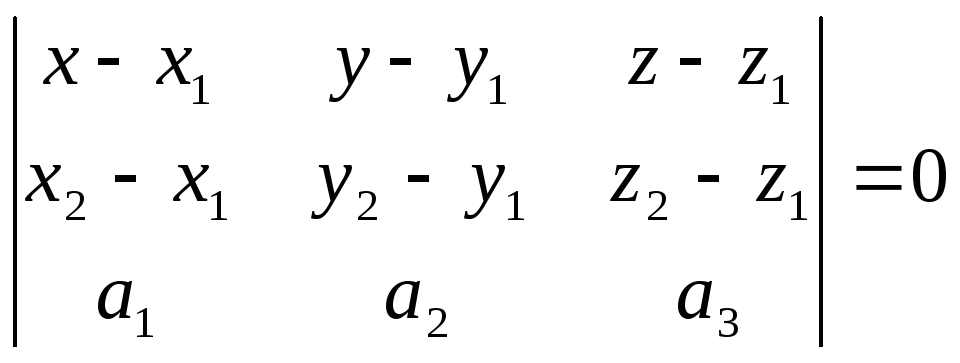
Уравнение
плоскости по одной точке и двум векторам,

коллинеарным
плоскости.

Пусть заданы два
вектора
и,
коллинеарные плоскости. Тогда для
произвольной точки М(х, у,z),
принадлежащей плоскости, векторыдолжны быть компланарны.

Уравнение
плоскости:

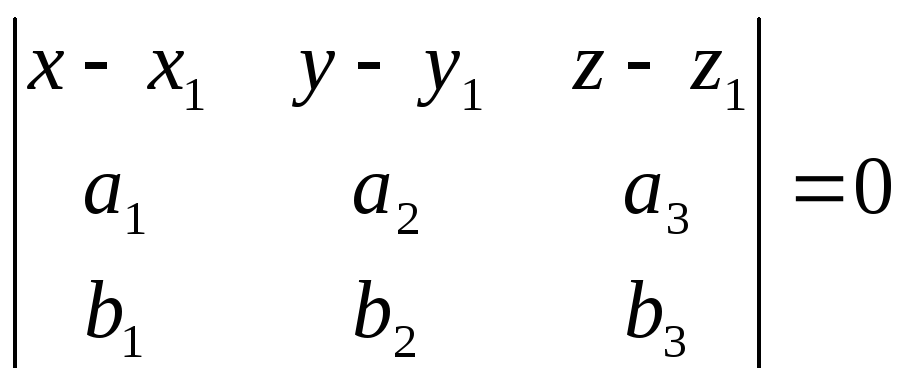
Уравнение
плоскости по точке и вектору нормали.

Теорема.
Если в пространстве задана точка М₀(х₀,
у₀,
z₀),
то уравнение плоскости, проходящей
через точку М₀
перпендикулярно вектору нормали
(A,
B,
C)
имеет вид:

A(x
– x₀)
+ B(y
– y₀)
+ C(z
– z₀)
= 0.

Доказательство.
Для произвольной точки М(х, у, z),
принадлежащей плоскости, составим
вектор
.
Т.к. вектор

– вектор нормали, то он перпендикулярен
плоскости, а, следовательно, перпендикулярен
и вектору
.
Тогда скалярное произведение

=
0

Таким
образом, получаем уравнение плоскости

Теорема
доказана.

Уравнение плоскости в отрезках.

Если
в общем уравнении Ах + Ву + Сz
+ D
= 0 поделить обе части на (-D)

,

заменив
,
получим уравнение плоскости в отрезках:

Числа
a,
b,
c
являются точками пересечения плоскости
соответственно с осями х, у, z.

Уравнение плоскости в векторной форме.

где

–
радиус- вектор текущей точки М(х, у, z),

–
единичный вектор, имеющий направление,
перпендикуляра, опущенного на плоскость
из начала координат.

,

и 
– углы, образованные этим вектором с
осями х, у, z.

p
– длина этого перпендикуляра.

В
координатах это уравнение имеет вид:

xcos
+ ycos
+ zcos
– p
= 0.

Расстояние от точки до плоскости.

Расстояние
от произвольной точки М₀(х₀,
у₀,
z₀)
до плоскости Ах+Ву+Сz+D=0
равно:

Пример.
Найти уравнение плоскости, зная, что
точка Р(4; -3; 12) – основание перпендикуляра,
опущенного из начала координат на эту
плоскость.

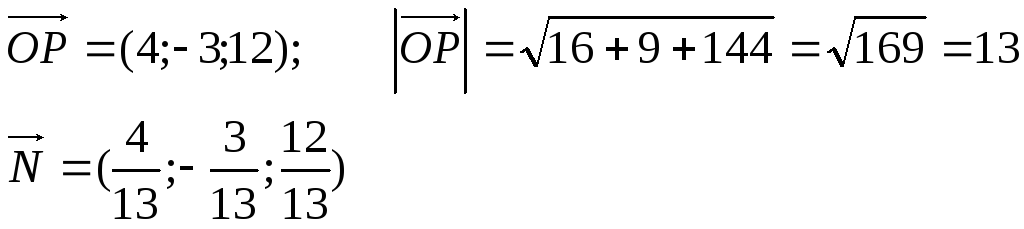
Таким
образом, A
= 4/13; B
= -3/13; C
= 12/13, воспользуемся формулой:

A(x
– x₀)
+ B(y – y₀)
+ C(z – z₀)
= 0.

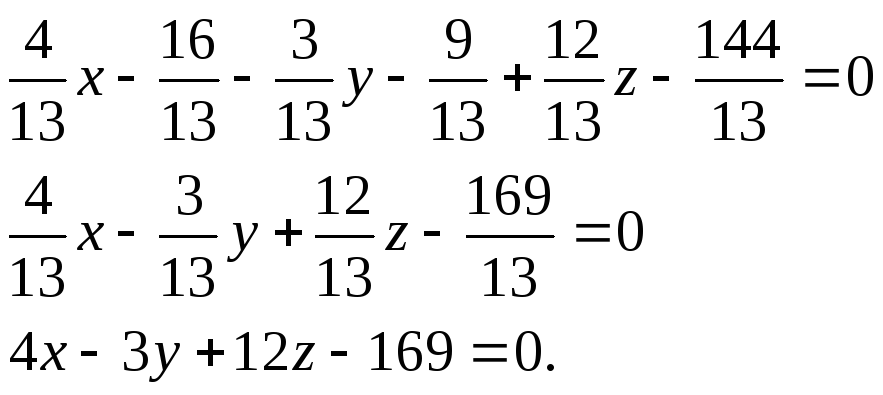
Пример.
Найти уравнение плоскости, проходящей
через две точки P(2;
0; -1) и

Q(1;
-1; 3) перпендикулярно плоскости 3х + 2у –
z
+ 5 = 0.

Вектор
нормали к плоскости 3х + 2у – z
+ 5 = 0
параллелен
искомой плоскости.

Получаем:

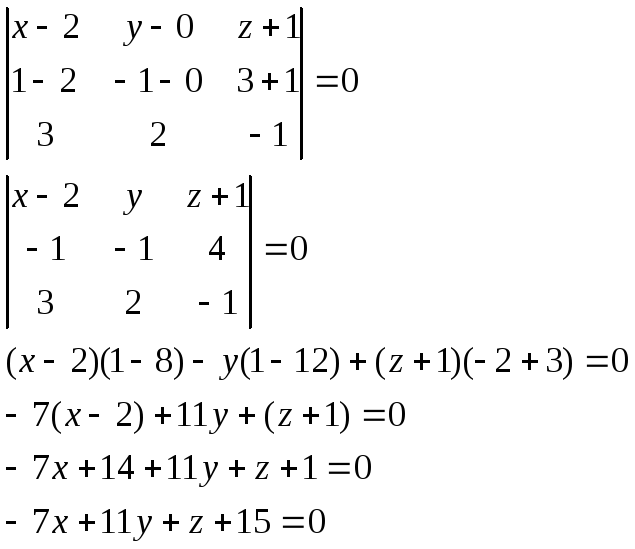
Пример.
Найти уравнение плоскости, проходящей
через точки А(2, -1, 4) и

В(3,
2, -1) перпендикулярно плоскости х
+ у
+ 2z
– 3 = 0.

Искомое
уравнение плоскости имеет вид: Ax
+ By
+ Cz
+ D
= 0, вектор нормали к этой плоскости
(A,
B,
C).
Вектор
(1,
3, -5) принадлежит плоскости. Заданная
нам плоскость, перпендикулярная искомой
имеет вектор нормали(1,
1, 2). Т.к. точки А и В принадлежат обеим
плоскостям, а плоскости взаимно
перпендикулярны, то

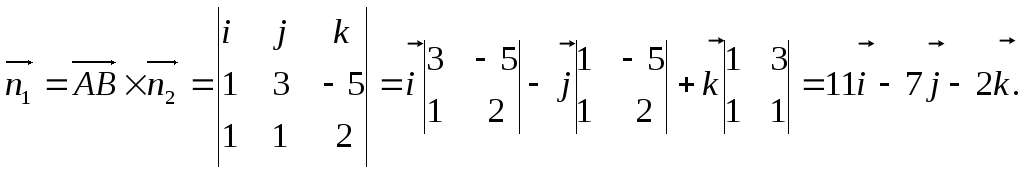
Таким образом, вектор нормали
(11,
-7, -2). Т.к. точка А принадлежит искомой
плоскости, то ее координаты должны
удовлетворять уравнению этой плоскости,
т.е. 112 + 71
– 24 +D= 0;D= -21.

Итого,
получаем уравнение плоскости: 11x
– 7y
– 2z
– 21 = 0.

Пример.
Найти уравнение плоскости, зная, что
точка Р(4, -3, 12) – основание перпендикуляра,
опущенного из начала координат на эту
плоскость.

Находим
координаты вектора нормали
=
(4, -3, 12). Искомое уравнение плоскости
имеет вид: 4x
– 3y
+ 12z
+ D
= 0. Для нахождения коэффициента D
подставим в уравнение координаты точки
Р:

16
+ 9 + 144 + D
= 0

D
= -169

Итого,
получаем искомое уравнение: 4x
– 3y
+ 12z
– 169 = 0

Пример.
Даны координаты вершин пирамиды А₁(1;
0; 3), A₂(2;
-1; 3), A₃(2;
1; 1),

A₄(1;
2; 5).

1. Найти
   длину ребра А₁А₂.

1. Найти
   угол между ребрами А₁А₂
   и А₁А₄.

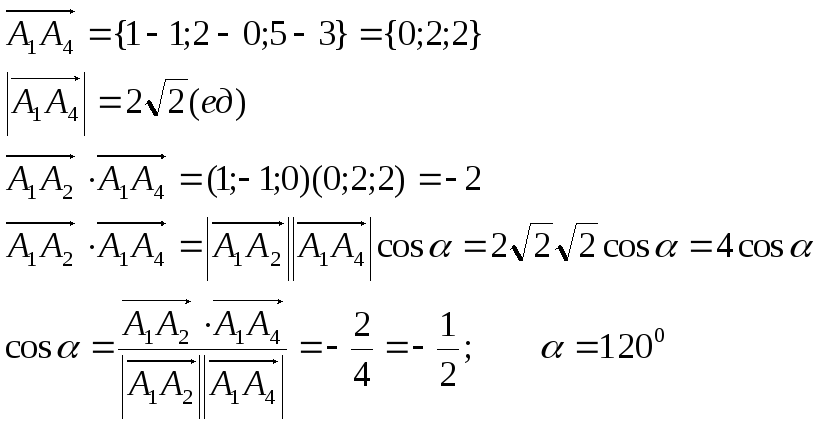
1. Найти
   угол между ребром А₁А₄
   и гранью А₁А₂А₃.

Сначала
найдем вектор нормали к грани А₁А₂А₃
как векторное произведение векторови.

=
(2-1;
1-0; 1-3) = (1; 1; -2);

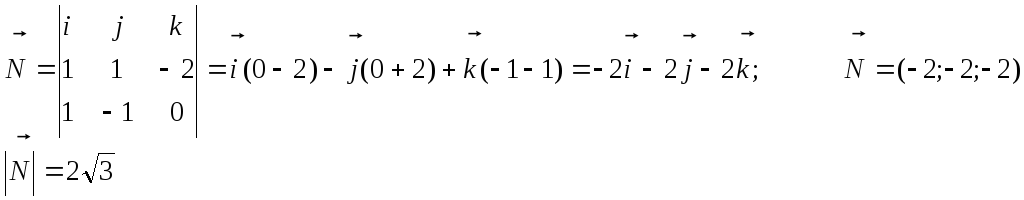
Найдем
угол между вектором нормали и вектором
.

-4
– 4 = -8.

Искомый
угол 
между вектором и плоскостью будет равен

= 90⁰
– .

1. Найти
   площадь грани А₁А₂А₃.

1. Найти
   объем пирамиды.

(ед³).

1. Найти
   уравнение плоскости А₁А₂А₃.

Воспользуемся
формулой уравнения плоскости, проходящей
через три точки.

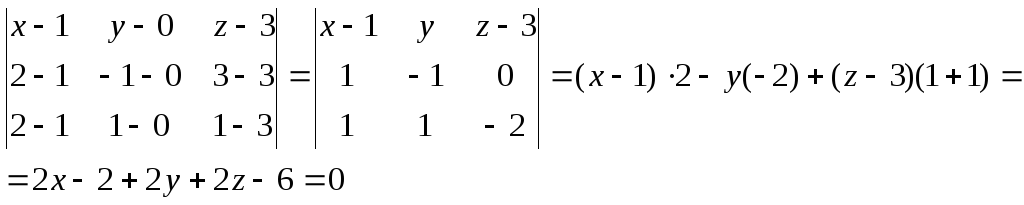
2x
+ 2y
+ 2z
– 8 = 0

x
+ y
+ z
– 4 = 0;

При
использовании компьютерной версии
“Курса высшей
математики”
можно запустить программу, которая
решит рассмотренный выше пример для
любых координат вершин пирамиды.

Для
запуска программы дважды щелкните на
значке:

В
открывшемся окне программы введите
координаты вершин пирамиды и, нажимитеEnter.
Таким образом, поочередно могут быть
получены все пункты решения.

Примечание:
Для запуска программы необходимо чтобы
на компьютере была установлена программа
Maple
(
Waterloo
Maple
Inc.)
любой версии, начиная с MapleV
Release
4.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #