Как составить уравнение плоскости oxy

Общее уравнение плоскости

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.

Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:

где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz. Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x₀, y₀, z₀. Действительно. Пусть из коэффициентов A≠0. Возьмем произвольные числа y₀, z₀. Тогда

Таким образом, существует точка M₀(x₀, y₀, z₀), координаты которой удовлетворяют уравнению (1):

Вычитая из уравнения (1) тождество (2), получим

которая эквивалентна уравнению (1).

Покажем, что (3) определяет некоторую плоскость, проходящую через точку M₀(x₀, y₀, z₀) и перпендикулярную вектору n={A,B,C} (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).

Если точка M₀(x₀, y₀, z₀) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n={A,B,C} и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

Если же точка M(x, y, z) не лежит на плоскости α, то векторы n={A,B,C} и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.

Вектор n=(A,B,C) называется нормальным вектором плоскости, определяемой линейным уравнением (1).

Утверждение 2. Если два общих уравнения плоскости

и

определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства

Доказательство. Так как уравнения (4) и (5) определяют одну и ту же плоскость, то нормальные векторы n₁={A₁,B₁,С₁} и n₂={A₂,B₂, С₂} коллинеарны. Так как векторы n₁≠0, n₂≠0, то существует такое число λ, что n₂=n₁λ. Отсюда имеем: A₂=A₁λ, B₂=B₁λ, С₂=С₁λ. Докажем, что D₂=D₁λ. Очевидно, что совпадающие плоскости имеют общую точку M₀(x₀, y₀, z₀), так что

и

Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:

Так как выполнены первые три равенства из выражений (6), то D₁λ−D₂=0. Т.е. D₂=D₁λ. Утверждение доказано.

Неполные уравнения плоскости

Определение 1. Общее уравнение плоскости (1) называется полным, если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным.

Рассмотрим все возможные варианты неполных уравнений плоскости:

При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.

При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n={0,B,C} лежит на координатной плоскости Oyz.

При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).

При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).

При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).

При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).

При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).

При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).

При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.

Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя координаты точки M в (3), получим:

Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n={A,B,C}={0,0,1}, т.е. A=0, B=0, C=1.

Подставляя коэффициенты A,B,C в (9), получим:

или

Ответ:

Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n=={2,3,1}.

Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:

Так как плоскость имеет нормальный вектор n={A,B,C}={2,3,1}, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:

или

Ответ:

Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.

Уравнение плоскости в пространстве

Рассмотрим
трехмерное пространство

с фиксированной декартовой системой
координат Oxyz.

Координатная
плоскость Oxy
в нем является подпространством
размерности два. Изученная нами прямая
и кривые 2-го порядка, лежащие в плоскости
Oxy,
в пространстве также могут быть
определены. Для этого необходимо задать
саму плоскость Oxy
в нем.

Очевидно,
что если в пространстве задана система
координат Oxyz,
то плоскость Oxy
определяется
в ней уравнением
.

Но
плоскость в пространстве в системе
координат может быть определена
по-разному, поскольку она не обязательно
долж-на проходить через начало или быть
перпендикулярной другим ко-ординатным
плоскостям.

Естественно
возникает вопрос об уравнении плоскости
в пространстве.

Справедливы
утверждения:

1. Если
   в пространстве (размерности
   )
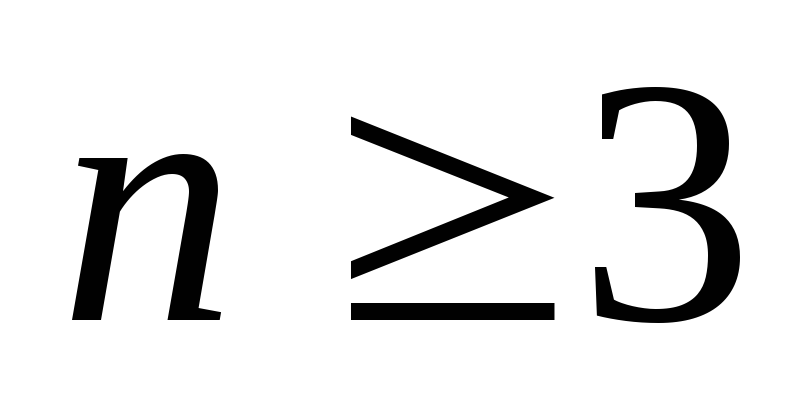   задана произвольная плоскость и
   фиксирована произвольная декартовая
   система координат Oxyz,
   то плоскость определяется в ней
   уравнением 1-й
   степени.

2. Если в пространстве
   (размерности
   )
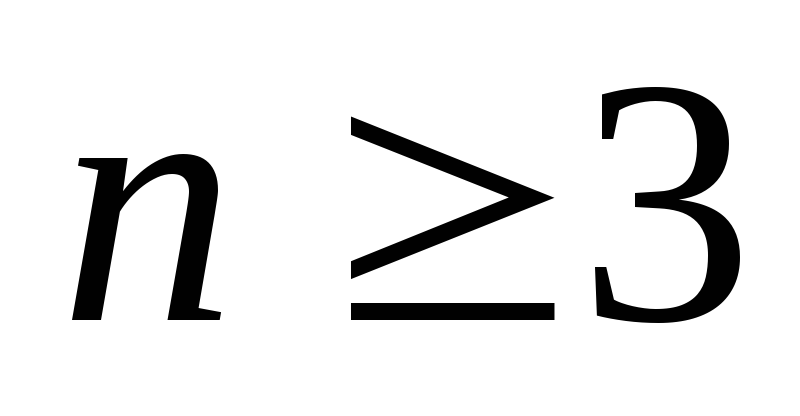   фикси-рована произвольная декартовая
   прямоугольная система коор-динат Oxyz,
   то всякое уравнение 1-й
   степени с переменными x,
   y,
   z
   определяет в ней плоскость.

Ниже мы эти
утверждения сформулируем в виде теорем.

Пусть
Р
– произвольная плоскость в пространстве.
Всякий перпендикулярный ей ненулевой
вектор

называется нормальным
вектором
этой
плоскости (рис. 7.2).

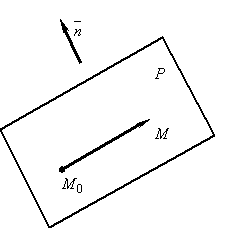
Рис. 7.2

Если
известна какая-нибудь точка

плоскости P
и какой-нибудь ее нормальный вектор
,
то этими двумя условиями плоскость в
пространстве вполне определена (через
данную точку можно провести единственную
плоскость, перпендикулярную данному
вектору).

В самом деле,
возьмем на плоскости P
произвольную точку М
с переменными координатами x,
y,
z.
Эта точка принадлежит плоскости только
в том случае, когда вектор

перпендикулярен вектору
,
а для этого необходимо и достаточно,
чтобы скалярное произведение этих
векторов равнялось нулю, то есть
.

Вектор

задан по условию, найдем координаты
вектора:

и запишем скалярное произведение этих
векторов в координатной форме:

.
(12)

Так
как точка

выбрана на плоскости произвольно, то
последнему уравнению удовлетворяют
координаты любой точки, лежащей на
плоскости Р.
Для точки N,
не лежащей
на заданной плоскости,

и равенство (12) нарушается. Следовательно,
уравнение (12), являясь уравнением 1-й
степени, определяет плоскость, проходящую
через точку

и пер-пендикулярную вектору

Пример 7.1. Составить
уравнение плоскости, проходящей через
точку

и перпендикулярной вектору
.

Решение. Используя
формулу (12), имеем


откуда
после преобразований получим
.

Это
уравнение 1-й степени и есть искомое
уравнение плоскости.

Уравнение
плоскости, проходящей через три точки.
Пусть даны три точки
,

и
.
Если точки не лежат на одной прямой, то
через них всегда можно провести
единственную
плоскость. Обозначим (х,
у,
z)
координаты произвольной точки М
пространства и рассмотрим три вектора:
,
,
.
Точка М
лежит на плоскости М₁М₂М₃
в том и только в том случае, когда
перечисленные три вектора компланарны,
а значит,
,
т. е. определитель, составленный из их
координат, равен нулю:

.

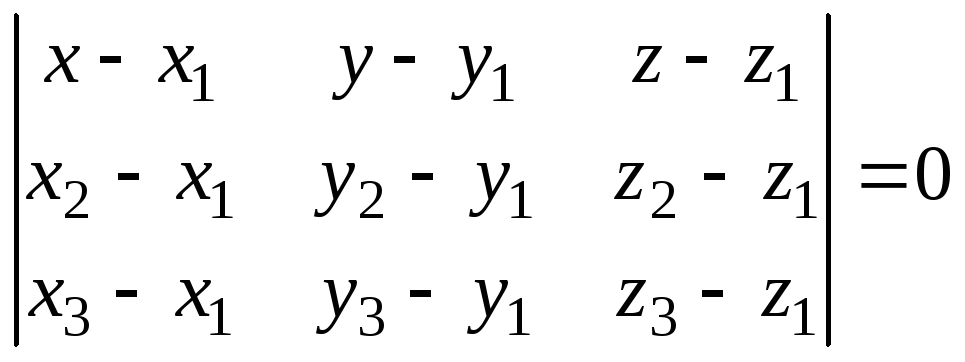Пример 7.2.
Написать уравнение плоскости, проходящей
через точки
,
и

Решение.
Пусть

– произвольная точка плоскости, тогда
векторы
,
,

компланарны, поэтому:

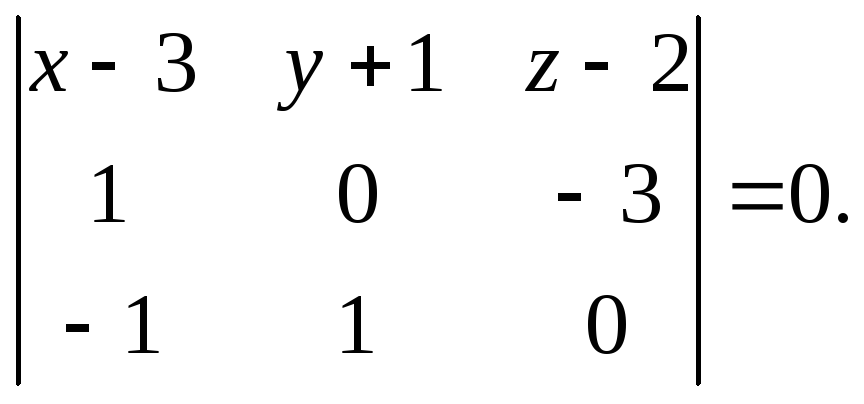
Вычисляя определитель
по правилу треугольников, получим:

или
.

Теорема 7.1. В
пространстве

всякая плоскость выража-ется уравнением
1-й степени
,

Доказательство.
В предыдущем пункте было установлено,
что всякая плоскость может быть задана
уравнением вида (12):

,

Раскрыв
скобки и обозначив
,
получим общее уравнение 1-й степени
относительно x,
y,
z:

,
эквивалентное уравнению (12). Поэтому
оно определяет ту же плоскость, что и
уравнение (12), и называется общим
уравнением плоскости.
Коэффициенты при переменных в этом
уравнении сохраняют тот же геометрический
смысл, что и в равенстве (12),
то есть являются координатами нормального
вектора

плоскости. Так как нормальный вектор
плоскости является ненулевым, то
коэффициенты A,
B
и
C
не могут быть одновременно равны нулю.
Итак, мы доказали, что всякая плоскость
в

определяется уравнением 1-й степени
относительно переменных координат x,
y,
z.

Теорема 7.2
(обратная).
Всякое
линейное уравнение с тремя переменными


определяет плоскость в пространстве

,
если хотя бы один из коэффициентов при
переменных не равен нулю.

Доказательство.
Пусть x₀,
y₀,
z₀
– какое-либо решение данного уравнения.
Тогда
,
откуда
.
Подставляя в данное уравнение вместо
D
его значение и группируя члены, получим

Это
уравнение плоскости, проходящей через
точку

и
имеющей нормальный вектор

Следовательно, и равносильное ему
уравнение

определяет плоскость, перпендикулярную
вектору

Пример
7.3. Построить
в прямоугольной системе ко-ординат
плоскость, заданную уравнением
.

Решение.
Для построения плоскости необходимо и
достаточ-но знать какие-либо три ее
точки, не лежащие на одной прямой,
нап-ример, точки пересечения плоскости
с осями координат. Полагая в заданном
уравнении
,
получим
.
Следовательно, за-данная плоскость
пересекает ось Oz
в точке

Ана-логично при

получим
,
то есть точку
;
при

получим
,
то есть точку
.
По трем точкам
,
,

строим заданную плоскость (рис. 7.3).

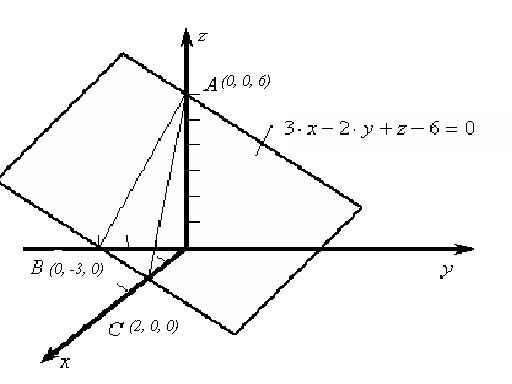
Рис. 7.3

Частные
случаи общего уравнения плоскости.
Рассмотрим особенности расположения
плоскости в тех случаях, когда те или
иные коэффициенты общего уравнения
обращаются в нуль.

1. При

уравнение

определяет плоскость, проходящую через
начало координат, так как ко-ординаты
точки

удовлетворяют этому уравнению.

2. При

уравнение

определяет плоскость, параллельную оси
Ох,
поскольку нормальный вектор

этой плоскости перпендикулярен оси Ох
(его проек-ция на ось Ох
равна нулю). Аналогично при

плоскость

параллельна оси Оу,
а при

плоскость

параллельна оси Оz.

3.
При

уравнение

определяет плоскость, проходящую через
ось Ох,
поскольку она параллельна оси Ох
()
и проходит через начало координат ().
Аналогично плоскость

проходит через ось Оу,
а плоскость

– через ось Оz.

4.
При

уравнение

определяет плоскость, параллельную
координатной плоскости Оxу,
поскольку она параллельна осям Oх
()
и Оу
().
Аналогично плоскость

параллельна плоскости уОz,
а плоскость

– плоскости Оxz.

5. При

уравнение

(или
)
определяет координатную плоскость Оxу,
так как она параллельна плоскости Оxу
()
и проходит через начало координат

Аналогично уравнение

в пространстве определяет координатную
плоскость Оxz,
а уравнение

– координатную плоскость Оyz.

Пример 7.4. Составить
уравнение плоскости P,
проходящей через ось Оу
и точку
.

Решение.
Уравнение плоскости, проходящей через
ось Оу,
имеет вид
.
Для определения коэффициентов A
и C
воспользуемся
тем, что точка

принадлежит плоскости P.
Поэтому ее координаты удовлетворяют
написанному выше урав-нению плоскости:

Û
,
откуда

Подставив найденное значение A
в уравнение
,
получим:

или
.

Это и есть искомое
уравнение.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Для того, чтобы однозначно построить плоскость, необходимы три точки, которые не лежат на одной прямой.

Общее уравнение плоскости принимает вид:

Общее уравнение плоскости

Ax+By+Cz+D=0Ax+By+Cz+D=0,

где A,B,C,DA, B, C, D — коэффициенты, задающие плоскость. Они не могут быть одновременно равны нулю.

Здесь будет калькулятор

Составление уравнения плоскости по трем точкам

Текст цитаты

Заголовок

Текст цитаты

В случае, когда известны координаты всех трех точек, уравнение плоскости, проходящей через эти точки составляется с помощью определителя:

Уравнение плоскости через определитель

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0,

где (x1;y1;z1),(x2;y2;z2),(x3;y3;z3)(x_1;y_1;z_1), (x_2;y_2;z_2), (x_3;y_3;z_3) — координаты точек, через которые проходит данная плоскость, а (x;y;z)(x; y; z) — всевозможные координаты точек этой плоскости.

Задача 1

Составить уравнения плоскости проходящей через три точки с координатами (1;3;0),(5;6;4),(−1;−4;0)(1;3;0), (5;6;4), (-1;-4;0).

Решение

Пусть:

x1=1x_1=1
y1=3y_1=3
z1=0z_1=0
x2=5x_2=5
y2=6y_2=6
z2=4z_2=4
x3=−1x_3=-1
y3=−4y_3=-4
z3=0z_3=0

Составляем определитель:

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0

∣x−15−1−1−1y−36−3−4−3z−04−00−0∣=0begin{vmatrix}
x-1 & 5-1 & -1-1 \
y-3 & 6-3 & -4-3 \
z-0 & 4-0 & 0-0 \
end{vmatrix}=0

∣x−14−2y−33−7z40∣=0begin{vmatrix}
x-1 & 4 & -2 \
y-3 & 3 & -7 \
z & 4 & 0 \
end{vmatrix}=0

28x−8y−22z−4=028x-8y-22z-4=0 — уравнение искомой плоскости.

Ответ

28x−8y−22z−4=028x-8y-22z-4=0

Уравнение плоскости по точке и вектору нормали

Если дана точка, лежащая на плоскости и вектор нормали к этой плоскости, то сама плоскость задается уравнением:

Уравнение плоскости по точке и нормали

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0,

где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, принадлежащей плоскости, а (n1;n2;n3)(n_1;n_2;n_3) — координаты вектора нормали к этой плоскости.

Задача 2

Выпишите уравнение плоскости, если даны: координата точки плоскости (8;−2;9)(8;-2;9) и вектор нормали (1;3;5)(1;3;5).

Решение

x0=8x_0=8
y0=−2y_0=-2
z0=9z_0=9
n1=1n_1=1
n2=3n_2=3
n3=5n_3=5

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0

(x−8)⋅1+(y−(−2))⋅3+(z−9)⋅5=0(x-8)cdot 1+(y-(-2))cdot 3+(z-9)cdot 5=0

x−8+3y+6+5z−45=0x-8+3y+6+5z-45=0

x+3y+5z−47=0x+3y+5z-47=0 — уравнение плоскости.

Проверка

Чтобы убедиться в том, что задача решена правильно, без ошибок, необходимо в полученное уравнение подставить координаты точки, которые даны в условии задачи:

8+3⋅(−2)+5⋅9−47=08+3cdot(-2)+5cdot9-47=0

0=00=0 — верно, значит ответ правильный.

Ответ

x+3y+5z−47=0x+3y+5z-47=0