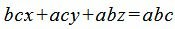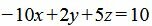Как составить уравнение плоскости в отрезках - Сайт, где вы сможете решить свои вопросы

Данный раздел будет полностью посвящен теме «Уравнение плоскости в отрезках». Мы последовательно рассмотрим, какой вид имеет уравнение плоскости в отрезках, применение этого уравнения для построения заданной плоскости в прямоугольной системе координат, переход от общего уравнения плоскости к уравнению плоскости в отрезках. В статье мы рассмотрим большое количество примеров, которые облегчат усвоение информации.

Уравнение плоскости в отрезках – описание и примеры

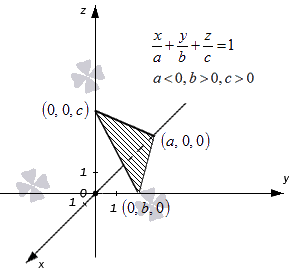
Уравнение плоскости в отрезках имеет вид xa+yb+zc=1 , где a, b и c – это действительные числа, отличные от нуля. Абсолютные величины чисел a, b и c равны длинам отрезков, которые отсекаются плоскостью на осях координат Oх, Oу и Oz в трехмерной системе координат Oхуz. Откладываются длины отрезков от начала координат. Направление, в котором необходимо отложить длину отрезка, определяет знак, стоящий перед числом. Наличие «-» свидетельствует о том, что отрезок надо откладывать от нуля в отрицательном направлении оси.

Действительно, координаты точек a, 0, 0, 0, b, 0, 0, 0, c удовлетворяют уравнению плоскости в отрезках:

aa+0b+0c=1=1⇔1=10a+bb+0c=1=1⇔1=10a+0b+cc=1=1⇔1=1

Поясним этот момент, расположив заданные точки на графике.

Проиллюстрируем описанное выше примером.

Пример 1

Плоскость проходит через точки -2, 0, 0, 0, 3, 0 и 0, 0, -12 на осях координат в прямоугольной системе координат Oxyz. Необходимо записать уравнение плоскости в отрезках.

Решение

Определим положение отрезков, отсекаемых плоскостью на осях координат. На оси абсцисс откладываем в отрицательном направлении отрезок длиной 2 единицы. На оси ординат в положительном направлении откладываем отрезок длиной 3 . На оси аппликат в отрицательном направлении откладываем отрезок длиной 12 .

При этом, уравнение плоскости в отрезках будет иметь вид: x-2+y3+z-12=1 .

Ответ: x-2+y3+z-12=1

Уравнение плоскости в отрезках удобно использовать для построения чертежей. Проиллюстрируем это утверждение примером.

Пример 2

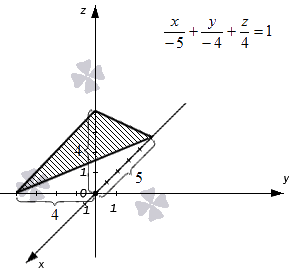
Плоскость в прямоугольной системе координат Oхуz задана уравнением плоскости в отрезках вида x-5+y-4+z4=1 . Необходимо изобразить эту плоскость на графике.

Решение

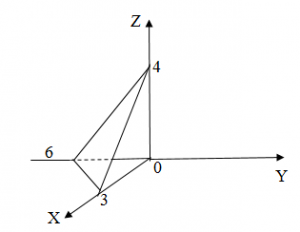
Изобразим оси координат, обозначаем начало координат и единичные отрезки на осях. Отмечаем длины отрезков, отсекаемых плоскостью, на каждой из осей. Соединяем концевые точки отрезков прямыми линиями. Полученная плоскость имеет вид треугольника. Она соответствует заданному уравнению плоскости в отрезках x-5+y-4+z4=1 .

Ответ:

Плоскость может быть задана уравнением плоскости другого вида. Для того, чтобы изобразить заданную плоскость на чертеже, можно сначала перейти к уравнению плоскости в отрезках. Получив уравнение плоскости в отрезках, нам останется лишь отметить точки a, 0, 0, 0, b, 0, 0, 0, c и соединить их прямыми линиями.

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Мы имеем общее уравнение плоскости в пространстве вида Ax+By+Cz+D=0 . И мы можем получить уравнение плоскости в отрезках. Сделать это можно в том случае, если плоскость пересекает все координатные оси, причем не в начале координат.

Не получится перевести общее уравнение плоскости в пространстве в уравнение плоскости в отрезках в тех случаях, когда плоскость проходит через одну из координатных осей или располагается параллельно оси. Другими словами, мы можем работать лишь с полным уравнением плоскости вида Ax+By+Cz+D=0, где A≠0, B≠0, C≠0, D≠0 .

Приведение общего уравнения плоскости к уравнению плоскости в пространстве производится следующим образом. Переносим слагаемое D в правую часть уравнения с противоположным знаком.

Ax+By+Cz+D=0⇔Ax+By+Cz=-D

Так как D≠0 , то обе части полученного уравнения можно разделить на –D: A-Dx+B-Dy+C-Dz=1 .

Так как A≠0, B≠0, C≠0 , то мы можем отправить в знаменатели коэффициенты перед переменными x, y и z. Последнее уравнение эквивалентно равенству x-DA+y-DB+z-DC=1 . При этом мы использовали очевидное равенство pq=1qp, p, q∈R, p≠0, q≠0 .

В итоге, мы получаем уравнение плоскости в отрезках. Это становится хорошо видно в том случае, если обозначить -DA=a, -DB=b, -DC=c.

Разберем решение примера.

Пример 3

Плоскость в прямоугольной системе координат Oxyz в пространстве задана уравнением вида 3x+9y-6z-6=0 . Переведем это уравнение в уравнение плоскости в отрезках.

Решение

Данное в условии задачи уравнение является полным уравнением плоскости. Это дает нам возможность привески его к уравнению плоскости в отрезках. Перенесем -6 в правую часть равенства, а затем разделим обе части равенства на 6:

3x+9y-6z-6=0⇔3x+9y+6z=63x+9y-6z=6⇔12x+32y-z=1

Коэффициенты при переменных x, y и z отправим в знаменатели: 12x+32y-z=1⇔x2+y23+z-1=1 . Полученное уравнение и есть уравнение плоскости в отрезках.

Ответ: x2+y23+z-1=1

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Уравнение плоскости в отрезках

В данной статье мы рассмотрим уравнение плоскости в отрезках. Представим методы преобразования уравнения плоскости в отрезках в уравнение плоскости в общем виде и обратно. Рассмотрим численные примеры.

Уравнение плоскости в отрезках представляется следующей формулой:

где a, b, c отличные от нуля числа.

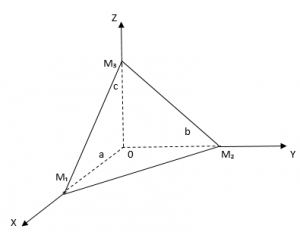
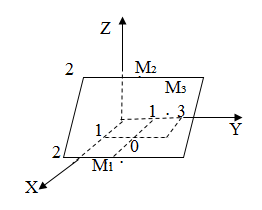
Отметим, что числа a, b, c в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает плоскость на осях Ox, Oy, Oz (Рис.1, Рис.2).

Действительно. Подставляя в (1) y=0, z=0 получим x=a, если же подставить в (1) x=0, y=0 то получим z=c, подставвляя, наконец, x=0, z=0 получим y=b. Таким образом плоскость, определяемая уравнением (1) проходит через точки M₁(a, 0, 0), M₂(0, b, 0) и M₃(0, 0, с).

Пример 1. Составить уравнение прямой, которая пересекает оси Ox, Oy и Oz в точках −1,3 и 7, соответственно.

Решение. Подставляя значения a=−1, b=3 и c=7 в (1), получим:

Ответ:

Приведение уравнения плоскости в отрезках к общему виду

Левая часть уравнения (1) приведем к общему знаменателю:

Далее, умножив обе части уравнения на abc, получим:

или

Пример 2. Уравнение плоскости в отрезках представлено следующим уравнением:

Перевести уравнение к общему виду.

Решение. Приведем левую часть уравнения к общему знаменателю:

Умножив обе части уравнения на 10, получим:

или

Ответ:

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Пусть задано общее уравнение плоскости:

где A, B, C, D − отличные от нуля числа, т.е. уравнение плокости является полным (о полных и неполных уравнениях плоскости смотрите здесь).

Сделаем следующие преобразования. Переведем свободный член D на правую часть уравнения и разделим обе части уравнения на −D:

Уравнение (2) можно переписать в следующем виде:

Сделаем следующие обозначения:

Тогда получим уравнение прямой в отрезках (1).

Пример 3. Привести общее уравнение прямой

к уравнению прямой в отрезках.

Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение плоскости в отрезках. Воспользуемся формулой (3). Имеем: A=−2, B=3, C=5, D=−4. Подставив эти значения в формулу (3), получим:

или

Ответ:

Источник

После
того как были получены уравнения
плоскости, определяемой принадлежащими
ей тремя произвольными
точками, возникает интерес к частным
случаям расположения этих точек. Особый
интерес вызывает случай, когда в качестве
заданных точек
,,
выступают точки, расположенные на осях
координат
,,
системы
:
ожидаем существенное упрощение в
используемых аналитических выражениях
и снижение вычислительных трудностей!

Пусть
плоскость

определяют три точки:
=,=,=.

Это
значит, что плоскость пересекает все
три оси системы координат
,
то есть не параллельна ни одной из осей
координат
,,.
Построим векторы:

==,

==
. (1)

Вычислим
вектор нормали плоскости: ====.
Воспользуемся уравнение плоскости,
заданной нормалью
и точкой
=:

=0
→
=0. (2)

Разделим
последнее равенство на число
.
Получаем легко запоминаемое уравнение
плоскости: :

, (3)

числа

определяют отрезки (длина со знаком!),
отсекаемые плоскостью на осях координат

:
поэтому и называют (3) – уравнение
в отрезках.

Теперь
рассмотрим частные случаи уравнения
(3), когда плоскость

параллельна одной или двум осям системы
координат
.
В таблице представлены все возможные
случаи параллельности

с осями
,,.


→.	→.	→.

→.	→.	→.

Замечание:
получение уравнений плоскости для
частных случаев, определяемых
параллельностью плоскости осям координат

,,,
не представляет труда, если считать,
что параллельности соответствует
бесконечно удалённая точка пересечения!

Продолжим применение
формул, определяющих плоскость в
пространстве, в примерах и задачах
аналитической геометрии.

☺☺

Пример 4–08:
Вычислить площадь треугольника,
отсекаемого плоскостью
:=0
от координатного угла
.

Решение:

Замечание: в
этом примере применим не эскиз, отражающий
исходные данные, а чертёж, который
максимально соответствует используемой
геометрической фигуре и её расположению
в пространстве
!

1). Воспользуемся
уравнением плоскости

для нахождения отсекаемых на осях
координатного угла

отрезков. Принимая
,
вычисляем:
=–24.
Для значений

имеем

=20.

2). Имея

и
,
вычислим площадь
треугольника:

=|
=240.

Ответ:

=240.

Пример 4–09:
Вычислить объём пирамиды, ограниченной
плоскостью
:=0
и координатными плоскостями.

Решение:

Замечание: положение
плоскости

на рисунке соответствует заданному в
примере уравнению; для нахождения объёма
пирамиды мы не станем пользоваться
смешанным произведением векторов

=,=,=,
так как достаточно воспользоваться
формулой для вычисления объёма пирамиды,
вычислив параметры:
.

1).
Воспользуемся уравнением плоскости

для нахождения отсекаемых на осях
координатного угла

отрезков. Принимая
,
вычисляем:
=6.
Для значений

имеем

=–4,
для значений

имеем
=2.

2).
Вычисляем объём пирамиды:
===8.

Ответ:
=8.

Пример 4–10:
Плоскость проходит через точку
(6,–10_,1)
и отсекает на оси

=–3,
на оси

=2.
Составить для этой плоскости уравнение
в отрезках.

Решение:

Замечание: исходные
условия задачи вполне позволяют построить
общее уравнение плоскости
,
а затем превратить его в уравнение в
отрезках.

1).
Воспользуемся уравнением в отрезках
при условии, что известны параметры

и
.
Это значит, что нам известно уравнение

2).
Учитывая, что точка

принадлежит плоскости
,
вычисляем:
=–4
и записываем окончательное выражение

Ответ:
.

Пример
4–11:
Составить уравнение плоскости, отсекающей
на оси

отрезок
=–5
и перпендикулярной к вектору =(–2,1,3).

Решение:

Замечание: исходные
условия задачи вполне позволяют построить
общее уравнение плоскости
;
представляет интерес решить задачу
несколькими способами.

Способ
первый:

1).
Воспользуемся уравнением плоскости:

=0,
где используется вектор нормали =
и точка
=,
принадлежащая этой плоскости.

2). Заменяя
(для удобства!) вектор
на =(2,–1,–3)
и учитывая заданную точку
=(0,0,–5),

получаем: .

Способ
второй:

1). Запишем
уравнение плоскости в виде уравнения
в отрезках:
,
где учтено значение
=–5
, и составим вектор нормали плоскости
для этой записи: =.

2).
Приравнивая векторы ,
имеем:
=(–2,1,3),
откуда:
=,

=–15.
Получаем: ––=1,
или .

Ответ:
.

Пример 4–12:
Составить уравнение плоскости,
параллельной вектору =(2,1,–1)
и отсекающей на координатных осях
,

отрезки
=3,

=–2.

Решение:

Способ
первый:

1).
Обозначим:
(0,–2,0),

(3,0,0)
и вычислим вектор
==(3,2,0).
Так как векторы
и
не параллельны, построим вектор нормали:
===(2,
–3,1).

2).
Воспользуемся уравнением плоскости:

=0,
где используется вектор нормали =
и точка
=(0,–2,0),
принадлежащая этой плоскости. После
несложных вычислений получаем:

Способ
второй:

1). Запишем
уравнение плоскости в виде уравнения
в отрезках:
,
где учтены значения
=3,

=–2.
, и составим вектор нормали плоскости
для этой записи: =.

2).
Учитывая, что векторы
и
ортогональны, имеем:
·==0,
откуда:
=–6.
Получаем:
,
или .

Ответ:
,
или.

Замечание: решение
одной и той же задачи несколькими
способами представляет большой интерес,
так как вырабатывает навыки импровизации
в применении теоретических знаний и
развивает динамику (быстроту) мышления.

☻

Соседние файлы в папке ЛА и АГ пособие

Источник

При построении плоскости в пространстве можно использовать аналогии для прямой линии на плоскости. Также можно утверждать, что между множеством всех плоскостей пространства и множеством линейных уравнений относительно трёх переменных x, y, z однозначно существует соответствие. Об этом и поговорим.

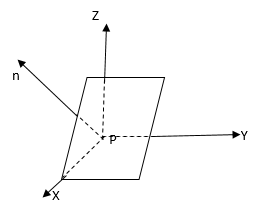
Уравнение плоскости через точку и нормальный вектор. Общее уравнение плоскости
Исследование общего уравнения плоскостей
Уравнение плоскости в отрезках
Уравнение плоскости проходящей через три точки
Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
Примеры задач по уравнению плоскости
- Составление уравнения плоскости
- Составление уравнения в отрезках
- Уравнение плоскости через три точки
- Вычисление угла между плоскостями

Уравнение плоскости через точку и нормальный вектор. Общее уравнение плоскости

Рассмотрим уравнение плоскости через точку на примере, так как будет более понятно, чем определения и термины.

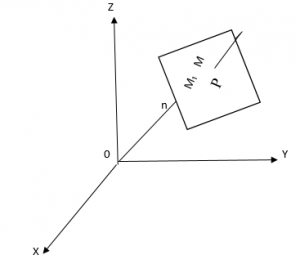
Пусть в пространстве задана точка $M_{1}(x_{1}, y_{1}, z_{1})$ и ненулевой вектор . Через точку $M_{1}$ можно провести единственную плоскость перпендикулярно вектору . Чтобы получить уравнение плоскости, выберем на ней произвольную точку и рассмотрим вектор $overline{M_{1}M} = (x - x_{1}, y - y_{1}, z - z_{1})$ (см. рис. 1)

Рис. 1

Точка тогда и только тогда, когда

$overline{M_{1}M}perpoverline{n}tooverline{M_{1}M} * overline{n}$ =

${A(x - x_{1}) + B(y - y_{1}) + C(z - z_{1}) = 0$

(1)

– уравнение плоскости, которая проходит через данную точку с нормальным вектором.

Открыв скобки в (1) у нас получается:

(2}

– это общее уравнение плоскости, где обозначено: $overline{D} = -Ax_{1} - By_{1} - Cz_{1}$ .

Значит, плоскости отвечает линейное уравнение (2). Наоборот, если задано линейное уравнение вида (2), тогда нетрудно найти точку $M_{1}(x_{1}, y_{1}, z_{1})$ , координаты которой удовлетворяют это уравнение, и записать вектор Вектор и точка определяют плоскость .

Исследование общего уравнения плоскостей

Рассматриваются частные случаи размещения плоскостей:

когда некоторые из чисел равняются нулю.

1. Если , тогда уравнение выглядит так: , плоскость проходит через начало координат перпендикулярно вектору .

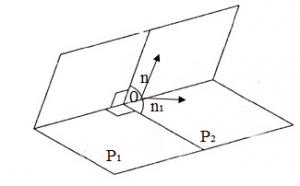
2. Если , тогда у нас получается уравнение , вектор принадлежит плоскости . Так как плоскость , или же (см. рис. 2). Уравнения плоскости – это уравнение следа в плоскости .

Рис. 2

3. Если же , тогда плоскость проходит через ось .

4. Если же , тогда уравнение плоскости выглядит так: , принадлежит плоскости . Плоскость (см. рис. 3)

Рис. 3

5. Если же , тогда плоскость проходит через всю ось .

6. Если , тогда получается уравнение , , или .

7. Если же , тогда плоскость проходит через ось .

Вывод:

На основании 2, 4 и 6 получается, что плоскость параллельна той координатной оси, переменная которой в уравнении отсутствует.

8. , плоскость , либо же , где . Вектор = направленный вдоль оси , поэтому плоскость перпендикулярна к оси в точке

В частности, если , тогда – уравнение координатной плоскости .

9. Если , тогда у нас есть плоскость , либо , где . Вектор направляющий вдоль оси . Плоскость перпендикулярна оси в точке .

В частности, если , тогда – уравнение координатной плоскости .

10. На конец, если , тогда , где

При получается – уравнение координатной плоскости .

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Подробнее

Уравнение плоскости в отрезках

Прежде чем записывать уравнение плоскости в отрезках, вспомним общее уравнение:

если ни одно из чисел не равняется нулю, тогда плоскость можно построить за тремя точками пересечения её с координатными осями:

$M_{1}(a, 0, 0)$ , $M_{2}(0, b, 0)$ , $M_{3}(0, 0, c)$ , где , , – отрезки, которые отсекают плоскость на координатных осях (см. рис. 4)

Рис. 4

Уравнение плоскости в отрезках запишется:

(3)

Так, например, если плоскость , тогда в этой плоскости уравнения следа $M_{1}M_{2}$ запишется:

Аналогично и до остальных следов.

Уравнение плоскости проходящей через три точки

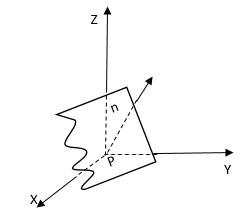
Пусть заданы три точки $M_{1} (x_{1}, y_{1}, z_{1}), M_{2}(x_{2}, y_{2}, z_{2}), M_{3}(x_{3}, y_{3}, z_{3})$ , которые не лежат на одной линии. Произвольная точка отлична от $M_{1}, M_{2}, M_{3}$ , будет находиться в плоскости точек $M_{1}, M_{2}, M_{3}$ тогда, и только тогда, когда векторы $overline{M_{1}M}$ = $(x - x_{1}, y - y_{1}, z - z_{1})$ , $overline{M_{1}M_{2}} = (x_{2} - x_{1}, y_{2} - y_{1}, z_{2} - z_{1}), overline{M_{1}M_{3}} = (x_{3} - x_{1}, y_{3} - y_{1}, z_{3} - z_{1})$

компланарные, то есть их смешанное произведение $(overline{M_{1}M}$ x $overline{M_{1}M_{2}})overline{M_{1}M_{3}} = 0$

В координатной форме запишется:

$begin{vmatrix} x - x_{1}&y - y_{1}&z - z_{1}\ x_{2} - x_{1}&y_{2} - y_{1}&z_{2} - z_{1}\ x_{3} - x_{1}&y_{3} - y_{1}&z_{3} - z_{1} end{vmatrix} = 0 right$

(4)

– уравнение плоскости проходящее через три точки.

Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей

Если для однозначности угол между двумя плоскостями называть один из меньших двугранных углов между ними, а соответственно к этому самый маленький из углов назовём углом между двумя векторами, тогда между двумя плоскостями есть угол между их нормальными векторами.

Рис. 5

= ${overline{n_{1}}}{overline{n_{2}}}over{overline{|n_1|}overline{|n_{2|}}$ = $A_{1}A_{2} + B_{1}B_{2} + C_{1}C_{2}over{sqrt{A_{1}^2 + B_{1}^2 + C_{1}^2} * sqrt{A_{2}^2 + B_{2}^2 + C_{2}^2}$ ,

(5)

где $overline{n_{1}}(A_{1}, B_{1}, C_{1}})$ , $overline{{n_2}}(A_{2}, B_{2}, C_{2})$ – нормальные векторы плоскости

$A_{1}x + B_{1}y + C_{1}z + D = 0$ – $(P_{1})$ ,

$A_{2}x + B_{2}y + C_{2}z + D_{2} = 0$ – $P_{2}$ .

Если $P_{1}perp{P_{2}}$ , тогда =

И тогда:

$A_{1}A_{2} + B_{1}B_{2} + C_{1}C_{2} = 0$

(6)

– условие перпендикулярности двух плоскостей.

Когда же $P_{1}||{P_{2}}$ , тогда получим:

$A_{1}over{A_{2}}$ = $B_{1}over{B_{2}}$ = $C_{1}over{C_{2}}$

(7)

– условие параллельности двух плоскостей.

Расстояние от точки до плоскости

Расстояние от точки до плоскости рассмотрим при помощи примера, формул и рисунка.

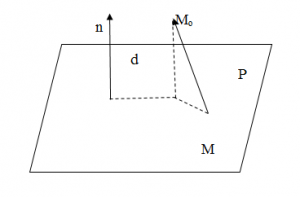
Расстояние от точки $M_{0}(x_{0}, y_{0}, z_{0})$ до плоскости , выражается формулой:

= $|Ax_{0} + By_{0} + Cz_{0} + D|over{sqrt{A^2 + B^2 + C^2}}$

(8)

Действительно, на рисунке 6:

Рис. 6

видим, что для произвольной точки

= $|{pr_overline{n}}{overline{MM_{0}}}$ = $|overline{n} * overline{MM_{0}}|over{overline{n}}$ ,

где $overline{MM_{0}} = (x_{0} - x, y_{0} - y, z_{0} - z)$ , .

Так как $overline{n} * overline{MM_{0}}$ = $A(x_{0} - x) + B(y_{0} - y) + C{z_{0} - z)$ = $Ax_{0} + By_{0} + Cz_{0} + (-Ax - By - Cz)$ = $Ax_{0} + By_{0} + Cz_{0} + D$ ,

потому что , а $overline{|n|} = sqrt{A^2 + B^2 + C^2}$ , тогда формула (5) доказана.

Примеры задач по уравнению плоскости

Чтобы ещё лучше понять вышеописанную тему, необходимо решить много задач. Поэтому предлагаем вам ознакомиться с примерами и их решениями.

Составление уравнения плоскости

Задача

Даны точки и . Составить уравнение плоскости, которая проходит через точку и перпендикулярна к вектору .

Решение

По условию вектор – это нормальный вектор плоскости. Найдём его координаты.

= .

Подставляя в уравнение (1) , а также $x_{1} = -4, y_{1} = 6, z = -6$

У нас получается:

Составление уравнения в отрезках

Задача

Построить плоскость и записать её уравнение в отрезках, а также уравнение следов на соответствующих координатных плоскостях.

Решение:

Положим , тогда . Аналогично при находим , при , , тогда уравнение в отрезках запишется:

(рис. 7)

Рис. 7

Уравнение следов:

Уравнение плоскости через три точки

Задача

Составить уравнение и построить плоскость, которая проходит через точки $M_{1}(2, 1, 0), M_{2}(0, 1, 2), M_{3}(1, 3, 1)$

Решение

По формуле (4)

$begin{vmatrix} x-2&y - 1&z - 0\ 0 - 2&1 - 1&2 - 0\ 1 - 2&3 - 1&1 - 0 end{vmatrix} = 0 to{-4(x - 2) - 0(y - 1) - 4z}= 0to{x + z - 2 = 0 right$

Плоскость параллельна (рис. 8)

Рис. 8

Вычисление угла между плоскостями

Задача

Найти угол между плоскостями и

Решение

Подставим в формулу вычисления угла между плоскостями соответствующие коэффициенты:

= $|2 * 4 + 4 * 3 + (-4) * 0|over{sqrt{2^2 + 4^2 + (-4)^2}} * sqrt{4^2 + 3^2 + 0^2$ = = =

Вы заметили, что в этом примере мы воспользовались исключительно одной формулой? В нашем случае – (5) формула. Никаких других формул мы не использовали и смогли найти угол между двумя плоскостями.

Источник

Уравнение плоскости в отрезках

Уравнение плоскости в отрезках представляется следующей формулой:

(1)

где a, b, c отличные от нуля числа.

Пример 1. Составить уравнение прямой, которая пересекает оси Ox, Oy и Oz в точках −1,3 и 7, соответственно.

Решение. Подставляя значения a=−1, b=3 и c=7 в (1), получим:

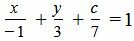
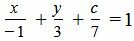
Приведение уравнения плоскости в отрезках к общему виду

Левая часть уравнения (1) приведем к общему знаменателю:

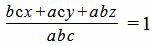
Далее, умножив обе части уравнения на abc, получим:

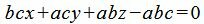
Пример 2. Уравнение плоскости в отрезках представлено следующим уравнением:

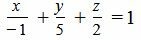
Перевести уравнение к общему виду.

Решение. Приведем левую часть уравнения к общему знаменателю:

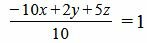
Умножив обе части уравнения на 10, получим:

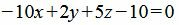
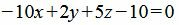
Приведение общего уравнения плоскости к уравнению плоскости в отрезках

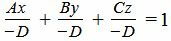(2)

Уравнение (2) можно переписать в следующем виде:

(3)

Сделаем следующие обозначения:

Тогда получим уравнение прямой в отрезках (1).

Пример 3. Привести общее уравнение прямой

к уравнению прямой в отрезках.

Уравнение плоскости в отрезках: описание, примеры, решение задач

Уравнение плоскости в отрезках – описание и примеры

Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 , где a , b и c – это действительные числа, отличные от нуля. Абсолютные величины чисел a , b и c равны длинам отрезков, которые отсекаются плоскостью на осях координат O х , O у и O z в трехмерной системе координат O х у z . Откладываются длины отрезков от начала координат. Направление, в котором необходимо отложить длину отрезка, определяет знак, стоящий перед числом. Наличие «-» свидетельствует о том, что отрезок надо откладывать от нуля в отрицательном направлении оси.

Действительно, координаты точек a , 0 , 0 , 0 , b , 0 , 0 , 0 , c удовлетворяют уравнению плоскости в отрезках:

a a + 0 b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + b b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + 0 b + c c = 1 = 1 ⇔ 1 = 1

Поясним этот момент, расположив заданные точки на графике.

Проиллюстрируем описанное выше примером.

Плоскость проходит через точки – 2 , 0 , 0 , 0 , 3 , 0 и 0 , 0 , – 1 2 на осях координат в прямоугольной системе координат O x y z . Необходимо записать уравнение плоскости в отрезках.

Решение

При этом, уравнение плоскости в отрезках будет иметь вид: x – 2 + y 3 + z – 1 2 = 1 .

Ответ: x – 2 + y 3 + z – 1 2 = 1

Плоскость в прямоугольной системе координат O х у z задана уравнением плоскости в отрезках вида x – 5 + y – 4 + z 4 = 1 . Необходимо изобразить эту плоскость на графике.

Решение

Ответ:

Плоскость может быть задана уравнением плоскости другого вида. Для того, чтобы изобразить заданную плоскость на чертеже, можно сначала перейти к уравнению плоскости в отрезках. Получив уравнение плоскости в отрезках, нам останется лишь отметить точки a , 0 , 0 , 0 , b , 0 , 0 , 0 , c и соединить их прямыми линиями.

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Мы имеем общее уравнение плоскости в пространстве вида A x + B y + C z + D = 0 . И мы можем получить уравнение плоскости в отрезках. Сделать это можно в том случае, если плоскость пересекает все координатные оси, причем не в начале координат.

A x + B y + C z + D = 0 ⇔ A x + B y + C z = – D

Так как D ≠ 0 , то обе части полученного уравнения можно разделить на – D : A – D x + B – D y + C – D z = 1 .

Так как A ≠ 0 , B ≠ 0 , C ≠ 0 , то мы можем отправить в знаменатели коэффициенты перед переменными x , y и z . Последнее уравнение эквивалентно равенству x – D A + y – D B + z – D C = 1 . При этом мы использовали очевидное равенство p q = 1 q p , p , q ∈ R , p ≠ 0 , q ≠ 0 .

В итоге, мы получаем уравнение плоскости в отрезках. Это становится хорошо видно в том случае, если обозначить – D A = a , – D B = b , – D C = c .

Разберем решение примера.

Плоскость в прямоугольной системе координат O x y z в пространстве задана уравнением вида 3 x + 9 y – 6 z – 6 = 0 . Переведем это уравнение в уравнение плоскости в отрезках.

Решение

Данное в условии задачи уравнение является полным уравнением плоскости. Это дает нам возможность привески его к уравнению плоскости в отрезках. Перенесем – 6 в правую часть равенства, а затем разделим обе части равенства на 6 :

3 x + 9 y – 6 z – 6 = 0 ⇔ 3 x + 9 y + 6 z = 6 3 x + 9 y – 6 z = 6 ⇔ 1 2 x + 3 2 y – z = 1

Коэффициенты при переменных x, y и z отправим в знаменатели: 1 2 x + 3 2 y – z = 1 ⇔ x 2 + y 2 3 + z – 1 = 1 . Полученное уравнение и есть уравнение плоскости в отрезках.

Ответ: x 2 + y 2 3 + z – 1 = 1

Глава 31. Уравнение плоскости, проходящей через три точки. Уравнение плоскости в отрезках

Уравнение плоскости, проходящей через три точки

Если точки M0(x0;y0;z0), M1(x1;y1;z1), M2(x2;y2;z2) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

Написать уравнение плоскости, проходящей через три точки: M0(1;2;3), M1(2;1;2), M2(3;3;1).

Данные точки не лежат на одной прямой, так как векторы <1,–1,–1>и <2,1,–2>не коллинеарны. Плоскость M0M1M2 представляется уравнением т. е. x+z–4=0.

Уравнение плоскости в отрезках

А=D/A; B= D/B, C= D/A,

Называется Уравнением плоскости в отрезках, a, b и c –соответственно абсцисса, ордината и аппликата пересечения плоскости с осями Ox, Oy и Oz (рис. 2.17.1).

Написать уравнение плоскости 3x – 6y +2z – 12 = 0 в отрезках.

Очевидно, что a=4, b=–2, c=6. Тогда уравнение плоскости в отрезках есть

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-v-otrezkah/

http://matica.org.ua/metodichki-i-knigi-po-matematike/vysshaia-matematika-uchebnoe-posobie/glava-31-uravnenie-ploskosti-prokhodiashchei-cherez-tri-tochki-uravnenie-ploskosti-v-otrezkakh

[/spoiler]

Источник

Уравнение плоскости в отрезках – описание и примеры

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Уравнение плоскости в отрезках

Приведение уравнения плоскости в отрезках к общему виду

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Уравнение плоскости через точку и нормальный вектор. Общее уравнение плоскости

Исследование общего уравнения плоскостей

Уравнение плоскости в отрезках

Уравнение плоскости проходящей через три точки

Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей

Примеры задач по уравнению плоскости

Составление уравнения плоскости

Составление уравнения в отрезках

Уравнение плоскости через три точки

Вычисление угла между плоскостями

Уравнение плоскости в отрезках

Приведение уравнения плоскости в отрезках к общему виду

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Уравнение плоскости в отрезках: описание, примеры, решение задач

Уравнение плоскости в отрезках – описание и примеры

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Глава 31. Уравнение плоскости, проходящей через три точки. Уравнение плоскости в отрезках

Вам также может понравиться

Как составить модель к задаче по математике

Не слышно в ватсапе свои голосовые сообщения как исправить

Физика как найти давление твердого тела

Добавить комментарий Отменить ответ