В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат Oxyz в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x, y, и z, которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Любую плоскость, заданную в прямоугольной системе координат Oxyz трехмерного пространства, можно определить уравнением Ax + By + Cz + D = 0. В свою очередь, любое уравнение Ax + By + Cz + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A, B, C, D – некоторые действительные числа, и числа A, B, C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида Ax + By + Cz + D = 0. Допустим, задана некоторая плоскость и точка M0(x0, y0, z0), через которую эта плоскость проходит. Нормальным вектором этой плоскости является n→= (A, B, C). Приведем доказательство, что указанную плоскость в прямоугольной системе координат Oxyz задает уравнение Ax + By + Cz + D = 0.
Возьмем произвольную точку заданной плоскости M(x, y, z).В таком случае векторы n→= (A, B, C) и M0M→=(x-x0, y-y0, z-z0) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n→, M0M→=Ax-x0+B(y-y0)+C(z-z0)=Ax+By+Cz-(Ax0+By0+Cz0)
Примем D=-(Ax0+By0+Cz0) , тогда уравнение преобразуется в следующий вид: Ax + By + Cz + D = 0. Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида Ax + By + Cz + D = 0 задает некоторую плоскость в прямоугольной системе координат Oxyz трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А, B, C одновременно не являются равными нулю. Тогда существует некоторая точка M0(x0, y0, z0), координаты которой отвечают уравнению Ax + By + Cz + D = 0, т.е. верным будет равенство Ax0 + By0 + Cz0 + D = 0. Отнимем левую и правую части этого равенства от левой и правой частей уравнения Ax + By + Cz + D = 0. Получим уравнение вида
A(x-x0) + B(y-y0) + C(z-z0) + D = 0, и оно эквивалентно уравнению Ax + By + Cz + D = 0. Докажем, что уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает некоторую плоскость.
Уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n→=(A, B, C) и M0M→=x-x0, y-y0, z-z0. Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A(x-x0) + B(y-y0) + C(z-z0) + D = 0 множество точек M(x, y, z) задает плоскость, у которой нормальный вектор n→=(A, B, C). При этом плоскость проходит через точку M(x0, y0, z0). Иначе говоря, уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает в прямоугольной системе координат Oxyz трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение Ax + By + Cz + D = 0 также определяет эту плоскость. Теорема доказана полностью.
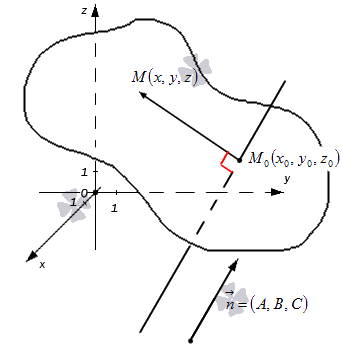
Уравнение вида Ax + By + Cz + D = 0 называют общим уравнением плоскости в прямоугольной системе координат Oxyz трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ·Ax+λ·By+λ·Cz+λ·D=0, где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением Ax+By+Cz+D=0, поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x-2·y+3·z-7=0 и -2·x+4·y-23·z+14=0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида Ax+By+Cz+D=0( при конкретных значениях чисел A, B, C, D). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
Укажем пример как иллюстрацию этих утверждений.
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4x + 5y – 5z + 20 = 0, и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4x + 5y – 5z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
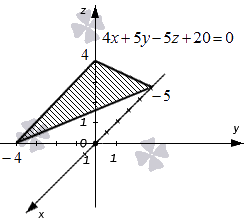
Общее уравнение плоскости, проходящей через точку
Повторимся: точка M0(x0, y0, z0) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением Ax+By+Cz+D=0 в том случае, когда подставив координаты точки M0(x0, y0, z0) в уравнение Ax+By+Cz+D=0, мы получим тождество.
Заданы точки M0(1, -1, -3) и N0(0, 2, -8) и плоскость, определяемая уравнением 2x+3y-z-2=0. Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М0 в исходной уравнение плоскости:
2·1+3·(-1)-(-3)-2=0⇔0=0
Мы видим, что получено верное равенство, значит точка M0(1, -1, -3) принадлежит заданной плоскости.
Аналогично проверим точку N0. Подставим ее координаты в исходное уравнение:
2·0+3·2-(-8)-2=0⇔12=0
Равенство неверно. Таким, образом, точка N0(0, 2, -8) не принадлежит заданной плоскости.
Ответ: точка М0 принадлежит заданной плоскости; точка N0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n→=(A, B, C) – нормальный вектор для плоскости, определяемой уравнением Ax+By+Cz+D=0. Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2x+3y-z+5=0. Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x, y, z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n→ исходной плоскости имеет координаты 2, 3, -1 . В свою очередь, множество нормальных векторов запишем так:
λ·n→=λ·2, λ·3, -λ, λ∈R, λ≠0
Ответ: λ·2, λ·3, -λ, λ∈R, λ≠0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n→=(A, B, C)является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M0(x0, y0, z0), принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n→=(A, B, C) будет выглядеть так: Ax+By+Cz+D=0. По условию задачи точка M0(x0, y0, z0) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство:Ax0+By0+Cz0+D=0
Вычитая соответственно правые и левые части исходного уравнения и уравнения Ax0+By0+Cz0+D=0, получим уравнение вида A(x-x0)+B(y-y0)+C(z-z0)=0. Оно и будет уравнением плоскости, проходящей через точку M0(x0, y0, z0) и имеющей нормальный вектор n→=(A, B, C).
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М (x, y, z) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n→=(A, B, C) и M0M→=(x-x0, y-y0, z-z0) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n→, M0M→=A(x-x0)+B(y-y0)+C(z-z0)=0
Задана точка М0(-1, 2, -3), через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n→=(3, 7, -5). Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x0=-1, y0=2, z0=-3, A=3, B=7, C=-5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A(x-x0)+B(y-y0)+C(z-z0)=0
И получим:
3(x-(-1))+7(y-2)-5(z-(-3))=0⇔3x+7y-5z-26=0
- Допустим, М (x, y, z) – некоторая точки заданной плоскости. Определим координаты вектора M0M→ по координатам точек начала и конца:
M0M→=(x-x0, y-y0, z-z0)=(x+1, y-2, z+3)
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n→, M0M→=0⇔3(x+1)+7(y-2)-5(z+3)=0⇔⇔3x+7y-5z-26=0
Ответ: 3x+7y-5z-26=0
Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А, B, C, D отличны от нуля, общее уравнение плоскости Ax+By+Cz+D=0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
- В случае, когда D = 0, мы получаем общее неполное уравнение плоскости: Ax+By+Cz+D=0⇔Ax+By+Cz=0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О (0, 0, 0), то придем к тождеству:
A·0+B·0+C·0=0⇔0≡0
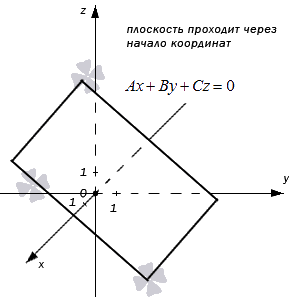
- Если А = 0, В ≠ 0, С ≠ 0, или А ≠ 0, В = 0, С ≠0, или А ≠ 0, В ≠ 0, С = 0, то общие уравнения плоскостей имеют вид соответственно: By+Cz+D=0, или Ax+Cz+D=0, или Ax+By+D=0. Такие плоскости параллельны координатным осям Оx, Oy, Oz соответственно. Когда D=0, плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей By+Cz+D=0, Ax+Cz+D=0 и Ax+By+D=0 задают плоскости, которые перпендикулярны плоскостям Oyz, Oxz, Ozy соответственно.

- При А=0, В=0, С≠0, или А=0, В≠0, С=0, или А≠0, В=0, С=0 получим общие неполные уравнения плоскостей: Cz+D=0 ⇔z+DC=0⇔z=-DC⇔z=λ, λ∈R или By+D=0⇔y+DB=0⇔y=-DB⇔y=λ, λ∈R или Ax+D=0⇔x+DA=0⇔x=-DA⇔x=λ, λ∈R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям Oxy, Oxz, Oyz соответственно и проходят через точки 0, 0, -DC, 0, -DB, 0 и -DA, 0, 0 соответственно. При D=0 уравнения самих координатных плоскостей Oxy, Oxz, Oyz выглядят так: z=0, y=0, x=0
соответственно.

Задана плоскость, параллельная координатной плоскости Oyz и проходящая через точку М0(7, -2, 3). Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости Oyz, а, следовательно, может быть задана общим неполным уравнением плоскости Ax+D=0, A≠0⇔x+DA=0. Поскольку точка M0(7, -2, 3) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x+DA=0, иначе говоря, должно быть верным равенство 7+DA=0 . Преобразуем: DA=-7, тогда требуемое уравнение имеет вид: x-7=0.
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости Oyz. Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости Oyz: i→=(1, 0, 0). Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A(x-x0)+B(y-y0)+C(z-z0)=0⇔⇔1·(x-7)+0·(y+2)+0·(z-3)=0⇔⇔x-7=0
Ответ: x-7=0
Задана плоскость, перпендикулярная плоскости Oxy и проходящая через начало координат и точку М0(-3, 1, 2).
Решение
Плоскость, которая перпендикулярна координатной плоскости Oxy определяется общим неполным уравнением плоскости Ax+By+D=0 (А≠0, В≠0). Условием задачи дано, что плоскость проходит через начало координат, тогда D=0 и уравнение плоскости принимает вид Ax+By=0⇔x+BAy=0.
Найдем значение BA. В исходных данных фигурирует точка М0(-3, 1, 2), координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: -3+BA·1=0, откуда определяем BA=3.
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x+3y=0.
Ответ: x+3y=0.
Для того, чтобы однозначно построить плоскость, необходимы три точки, которые не лежат на одной прямой.
Общее уравнение плоскости принимает вид:
Ax+By+Cz+D=0Ax+By+Cz+D=0,
где A,B,C,DA, B, C, D — коэффициенты, задающие плоскость. Они не могут быть одновременно равны нулю.
Здесь будет калькулятор
Составление уравнения плоскости по трем точкам
Текст цитаты
Заголовок Текст цитаты
В случае, когда известны координаты всех трех точек, уравнение плоскости, проходящей через эти точки составляется с помощью определителя:
∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0,
где (x1;y1;z1),(x2;y2;z2),(x3;y3;z3)(x_1;y_1;z_1), (x_2;y_2;z_2), (x_3;y_3;z_3) — координаты точек, через которые проходит данная плоскость, а (x;y;z)(x; y; z) — всевозможные координаты точек этой плоскости.
Составить уравнения плоскости проходящей через три точки с координатами (1;3;0),(5;6;4),(−1;−4;0)(1;3;0), (5;6;4), (-1;-4;0).
Решение
Пусть:
x1=1x_1=1
y1=3y_1=3
z1=0z_1=0
x2=5x_2=5
y2=6y_2=6
z2=4z_2=4
x3=−1x_3=-1
y3=−4y_3=-4
z3=0z_3=0
Составляем определитель:
∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0
∣x−15−1−1−1y−36−3−4−3z−04−00−0∣=0begin{vmatrix}
x-1 & 5-1 & -1-1 \
y-3 & 6-3 & -4-3 \
z-0 & 4-0 & 0-0 \
end{vmatrix}=0
∣x−14−2y−33−7z40∣=0begin{vmatrix}
x-1 & 4 & -2 \
y-3 & 3 & -7 \
z & 4 & 0 \
end{vmatrix}=0
28x−8y−22z−4=028x-8y-22z-4=0 — уравнение искомой плоскости.
Ответ
28x−8y−22z−4=028x-8y-22z-4=0
Уравнение плоскости по точке и вектору нормали
Если дана точка, лежащая на плоскости и вектор нормали к этой плоскости, то сама плоскость задается уравнением:
(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0,
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, принадлежащей плоскости, а (n1;n2;n3)(n_1;n_2;n_3) — координаты вектора нормали к этой плоскости.
Выпишите уравнение плоскости, если даны: координата точки плоскости (8;−2;9)(8;-2;9) и вектор нормали (1;3;5)(1;3;5).
Решение
x0=8x_0=8
y0=−2y_0=-2
z0=9z_0=9
n1=1n_1=1
n2=3n_2=3
n3=5n_3=5
(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0
(x−8)⋅1+(y−(−2))⋅3+(z−9)⋅5=0(x-8)cdot 1+(y-(-2))cdot 3+(z-9)cdot 5=0
x−8+3y+6+5z−45=0x-8+3y+6+5z-45=0
x+3y+5z−47=0x+3y+5z-47=0 — уравнение плоскости.
Проверка
Чтобы убедиться в том, что задача решена правильно, без ошибок, необходимо в полученное уравнение подставить координаты точки, которые даны в условии задачи:
8+3⋅(−2)+5⋅9−47=08+3cdot(-2)+5cdot9-47=0
0=00=0 — верно, значит ответ правильный.
Ответ
x+3y+5z−47=0x+3y+5z-47=0

1. Общее уравнение плоскости
Определение. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0 , где А, В, С – координаты вектора
N = Ai + Bj + Ck -вектор нормали к плоскости. Возможны следующие частные случаи:
A = 0 – плоскость параллельна оси Ох
B = 0 – плоскость параллельна оси Оу C = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
A = B = 0 – плоскость параллельна плоскости хОу A = C = 0 – плоскость параллельна плоскости хОz B = C = 0 – плоскость параллельна плоскости yOz A = D = 0 – плоскость проходит через ось Ох
B = D = 0 – плоскость проходит через ось Оу C = D = 0 – плоскость проходит через ось Oz
A = B = D = 0 – плоскость совпадает с плоскостью хОу A = C = D = 0 – плоскость совпадает с плоскостью xOz B = C = D = 0 – плоскость совпадает с плоскостью yOz
2. Уравнение поверхности в пространстве
Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.
3. Уравнение плоскости, проходящей через три точки
Для того, чтобы через три какиелибо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе
|
координат. |
||||||
|
Для того, чтобы произвольная точка M (x, y, z) |
лежала в одной плоскости с точками |
|||||
|
M1, M2 , M3 необходимо, чтобы векторы M1M 2 , M1M 3 , M1M были компланарны, т.е |
||||||
|
M1M = {x − x1 ; y − y1 ; z − z1} |
||||||
|
( M1M 2 , M1M 3 , M1M ) = 0. Таким образом, M1M 2 |
= {x2 − x1 ; y2 |
− y1 ; z2 − z1} |
||||
|
M1M 3 |
= {x3 − x1 ; y3 − y1 ; z3 − z1} |
|||||
|
x − x1 |
y − y1 |
z − z1 |
||||
|
Уравнение плоскости, проходящей через три точки: |
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 |
||
|
x3 − x1 |
y3 − y1 |
z3 − z1 |
35

4. Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости
Пусть заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и векторa = (a1, a2 , a3 ) .
Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную
|
точку М(х, у, z) параллельно вектору a . |
||||||||||
|
Векторы M1M = {x − x1 ; y − y1 ; z − z1} |
и вектор a = (a , a |
2 |
, a |
3 |
) |
должны быть |
||||
|
M1M 2 = {x2 − x1 ; y2 − y1 ; z2 − z1} |
1 |
|||||||||
|
x − x1 |
y − y1 |
z − z1 |
||||||||
|
компланарны, т.е. ( M1M , M1M 2 , a ) = 0.Уравнение плоскости: |
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 |
||||||
|
a1 |
a2 |
a3 |
5. Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости
Пусть заданы два вектора a = (a1, a2 , a3 ) и b = (b1,b2 ,b3 ) , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы a,b, MM1 должны быть компланарны.
|
x − x1 |
y − y1 |
z − z1 |
|||
|
Уравнение плоскости: |
a1 |
a2 |
a3 |
= 0 . |
|
|
b1 |
b2 |
b3 |
6. Уравнение плоскости по точке и вектору нормали
Теорема. Если в пространстве задана точка M0 (x0 , y0 , z0 ) , то уравнение плоскости, проходящей через точку M0 перпендикулярно вектору нормали N ( A, B,C) имеет вид: A(x − x0 ) + B ( y − y0 ) + C (z − z0 ) = 0 .
7. Уравнение плоскости в отрезках
Если в общем уравнении Ax + By + Cz + D = 0 поделить обе части на (-D)
|
− |
A |
x − |
B |
y − |
C |
z − 1 = 0 , заменив − |
D |
= a, |
− |
D |
= b, |
− |
D |
= c , получим уравнение плоскости |
||||||||
|
A |
B |
C |
||||||||||||||||||||
|
D |
D |
D |
||||||||||||||||||||
|
в отрезках: |
x |
+ |
y |
+ |
z |
= 1 . Числа a, b, c являются точками пересечения плоскости соответственно |
||||||||||||||||
|
a |
b |
c |
||||||||||||||||||||
с осями х, у, z.
8. Уравнение плоскости в векторной форме
r n = p, где r = xi + yj + zk – радиусвектор текущей точки M (x, y, z) ,
n = i cosα + j cos β + k cosγ – единичный вектор, имеющий направление, перпендикуляра,
опущенного на плоскость из начала координат. α, β и γ – углы, образованные этим вектором с осями х, у, z. p – длина этого перпендикуляра. В координатах это уравнение имеет вид:
x cosα + y cos β + z cosγ − p = 0
36
9. Расстояние от точки до плоскости
Расстояние от произвольной точки M0 (x0 , y0 , z0 ) до плоскости Ax + By + Cz + D = 0 равно:
d = Ax0 + By0 + Cz0 + D
 A2 + B2 + C 2
A2 + B2 + C 2
Пример. Найти уравнение плоскости, проходящей через точки А(2,-1,4) и В(3,2,-1) перпендикулярно плоскости x + y + 2z − 3 = 0 .
Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0 , вектор нормали к этой плоскости n1 (A,B,C). Вектор AB (1,3,-5) принадлежит плоскости. Заданная нам плоскость,
перпендикулярная искомой имеет вектор нормали n2 (1,1,2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то
|
n = AB × n |
i |
j |
k |
= i |
3 |
− 5 |
− j |
1 |
− 5 |
+ k |
1 |
3 |
= 11i − 7 j − 2k. |
||||||||
|
2 |
= |
1 |
3 |
− 5 |
|||||||||||||||||
|
1 |
1 |
2 |
1 |
2 |
1 |
1 |
|||||||||||||||
|
1 |
1 |
2 |
|||||||||||||||||||
Таким образом, вектор нормали n1 (11,-7,-2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е.
11.2+ 7.1− 2.4 + D = 0; D = −21. Итого, получаем уравнение плоскости: 11x − 7 y − 2z − 21 = 0
10.Уравнение линии в пространстве
Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:
F(x, y, z) = 0 . Это уравнение называется уравнением линии в пространстве.
Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана какимлибо уравнением.
Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.
F(x, y, z) = 0
Тогда пару уравнений Ф(x, y, z) = 0 назовем уравнением линии в пространстве.
11. Уравнение прямой в пространстве по точке и направляющему вектору
Возьмем произвольную прямую и вектор S (m, n, p), параллельный данной прямой. Вектор S называется направляющим вектором прямой.
На прямой возьмем две произвольные точки M0 (x0 , y0 , z0 ) и M (x, y, z) .
z
37
z
S M1
M0
r0 r
Обозначим радиусвекторы этих точек как r0 и r , очевидно, что r − r0 = M0 M .
Т.к. векторы М0 М и S коллинеарны, то верно соотношение М0 М = St , где t – некоторый параметр. Итого, можно записать: r = r0 + St .
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
x = x0 + mt
Это векторное уравнение может быть представлено в координатной форме: y = y0 + nt
z = z0 + pt
Преобразовав эту систему и приравняв значения параметра t, получаем канонические
|
уравнения прямой в пространстве: |
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
m |
n |
|||||
|
p |
Определение. Направляющими косинусами прямой называются направляющие косинусы вектора S , которые могут быть вычислены по формулам:
|
cosα = |
m |
; cos β = |
n |
; cosγ = |
p |
. |
||
|
+ n2 |
+ p2 |
+ n2 + p2 |
m2 + n2 + p2 |
|||||
|
m2 |
m2 |
Отсюда получим: m : n : p = cosα : cos β : cosγ .
Числа m , n , p называются угловыми коэффициентами прямой. Т.к. S – ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
12. Уравнение прямой в пространстве, проходящей через две точки
Если на прямой в пространстве отметить две произвольные точки M1 (x1, y1, z1 ) и
M2 (x2 , y2 , z2 ), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
|
x2 − x1 |
= |
y2 − y1 |
= |
z2 − z1 |
. |
|
m |
n |
||||
|
p |
38
Содержание:
Плоскость в пространстве
Общее уравнение плоскости
Определение: Уравнение вида 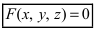
Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин.
Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости.
Рассмотрим частные случаи приведенного уравнения:
1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 36). 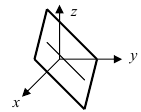
Рис. 36. Плоскость, проходящая через начало координат.
2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 37). 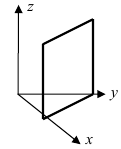
Рис. 37. Плоскость, проходящая параллельно оси аппликат.
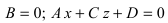 – плоскость параллельна оси ординат (Оу);
– плоскость параллельна оси ординат (Оу);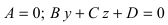 – плоскость параллельна оси абсцисс (Ох).
– плоскость параллельна оси абсцисс (Ох).
Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.
3. С=0; D=0; Ах+ By=0 – плоскость проходит через начало отсчета параллельно оси аппликат (Рис. 38). 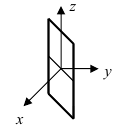
Рис. 38. Плоскость, проходящая через начало координат параллельно оси аппликат.
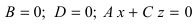 – плоскость проходит через начало координат параллельно оси ординат;
– плоскость проходит через начало координат параллельно оси ординат;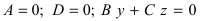 – плоскость проходит через начало координат параллельно оси абсцисс.
– плоскость проходит через начало координат параллельно оси абсцисс.
4. 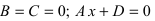 – плоскость проходит через точку
– плоскость проходит через точку 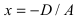 параллельно плоскости
параллельно плоскости 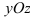 (Pис. 39).
(Pис. 39). 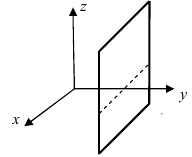
Рис. 39. Плоскость, проходящая параллельно координатной плоскости 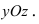
5. В = С = D = 0; Ах = 0=>х = 0 – уравнение описывает плоскость 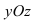 (Рис. 40).
(Рис. 40).
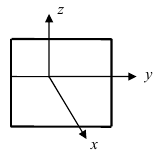
Рис. 40. Координатная плоскость 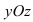 .
.
Другие уравнения плоскости
1. Уравнение плоскости в отрезках. Пусть в уравнении 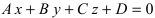 коэффициент
коэффициент 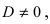 тогда выполним следующие преобразования
тогда выполним следующие преобразования
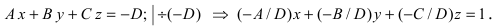
Введем следующие обозначения 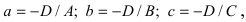 тогда уравнение примет вид
тогда уравнение примет вид 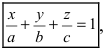 которое называется уравнением плоскости в отрезках. Найдем точки пересечения плоскости с координатными осями:
которое называется уравнением плоскости в отрезках. Найдем точки пересечения плоскости с координатными осями: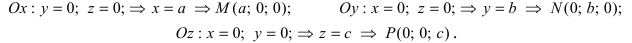
Откладывая на координатных осях точки М, N и Р, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры а, b, с положительные) (Рис. 41): 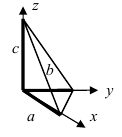
Рис. 41. Отрезки, отсекаемые плоскостью на координатных осях.
Из рисунка видно, что числа а, b, с показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.
2. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка 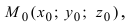 через которую проходит плоскость перпендикулярно к заданному вектору
через которую проходит плоскость перпендикулярно к заданному вектору 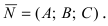 ОЗ. Вектор
ОЗ. Вектор 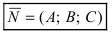 называется нормальным вектором плоскости, если он перпендикулярен любой паре неколлинеарных векторов, лежащих на плоскости.
называется нормальным вектором плоскости, если он перпендикулярен любой паре неколлинеарных векторов, лежащих на плоскости.
Возьмем на плоскости произвольную точку 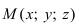 и образуем вектор
и образуем вектор 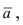 соединяющий точку
соединяющий точку 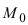 с точкой М (Рис. 42). Тогда
с точкой М (Рис. 42). Тогда 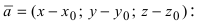
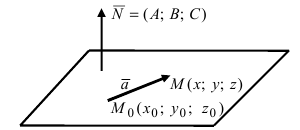
Рис. 42. Плоскость, проходящая через заданную точку перпендикулярно к нормальному вектору.
В силу того, вектор 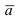 лежит в плоскости, то он перпендикулярен нормальному вектору
лежит в плоскости, то он перпендикулярен нормальному вектору 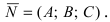 Используя условие перпендикулярности векторов
Используя условие перпендикулярности векторов 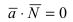 в проекциях перемножаемых векторов, получим уравнение плоскости, проходящая через заданную точку перпендикулярно к нормальному вектору:
в проекциях перемножаемых векторов, получим уравнение плоскости, проходящая через заданную точку перпендикулярно к нормальному вектору: 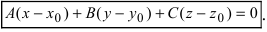
Пример:
Составить уравнение плоскости, проходящей через т. 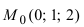 параллельно плоскости
параллельно плоскости 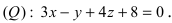
Решение:
Так как искомая плоскость параллельна плоскости (Q), то нормальный вектор этой плоскости 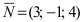 (см. коэффициенты при переменных величинах х, у и z в уравнении плоскости
(см. коэффициенты при переменных величинах х, у и z в уравнении плоскости 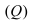 ) перпендикулярен к искомой плоскости и может быть взят в качестве нормального вектора этой плоскости. Используя уравнение плоскости, проходящей через заданную точку перпендикулярно к данному вектору, получаем:
) перпендикулярен к искомой плоскости и может быть взят в качестве нормального вектора этой плоскости. Используя уравнение плоскости, проходящей через заданную точку перпендикулярно к данному вектору, получаем: 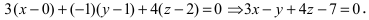
Пример:
Составить уравнение плоскости, проходящей через точки А(—1; 1 ;2) и В(0; —1; —1) параллельно вектору 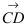 = (0; 0; -2):
= (0; 0; -2):
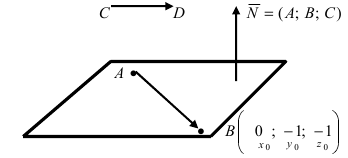
Решение:
Построим на искомой плоскости вектор 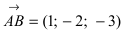 и вычислим нормальный вектор
и вычислим нормальный вектор 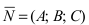 как векторное произведение векторов
как векторное произведение векторов 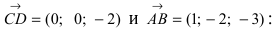
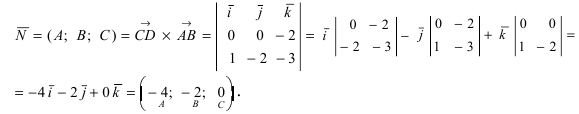
Уравнение плоскости, проходящей через заданную точку 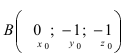 перпендикулярно к заданному вектору
перпендикулярно к заданному вектору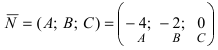 имеет вид:
имеет вид: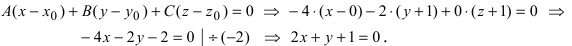
Отметим, что при выборе точки, через которую проходит искомая плоскость из точек 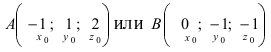 брать как точку, через которую проходит искомая плоскость.
брать как точку, через которую проходит искомая плоскость.
3. Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через 3 известные точки 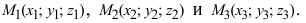 Возьмем произвольную точку плоскости М(х; у; z) и образуем векторы
Возьмем произвольную точку плоскости М(х; у; z) и образуем векторы 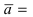
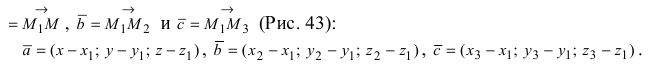
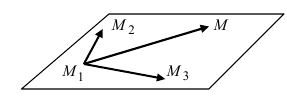
Рис. 43. Плоскость, проходящая через три заданные точки.
Вектора 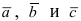 компланарные, используя условие компланарности векторов
компланарные, используя условие компланарности векторов 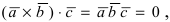 получим уравнение плоскости, проходящей через 3 известные точки:
получим уравнение плоскости, проходящей через 3 известные точки: 
Замечание: Полученный определитель третьего порядка раскрывается по элементам первой строки.
Пример:
Составить уравнение плоскости, проходящей через три заданные точки 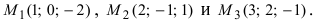
Решение:
Составим определитель третьего порядка 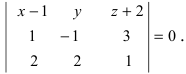 Раскроем определитель по элементам первой строки
Раскроем определитель по элементам первой строки 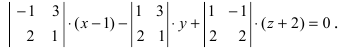 Вычислим определители второго порядка: -7(x-l) + 5y + 4(z + 2) = 0. Умножив уравнение на (-1) и раскрыв скобки, получим окончательный ответ:
Вычислим определители второго порядка: -7(x-l) + 5y + 4(z + 2) = 0. Умножив уравнение на (-1) и раскрыв скобки, получим окончательный ответ: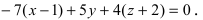
Основные задачи о плоскости в пространстве
1. Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости 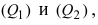 которые имеют нормальные векторы
которые имеют нормальные векторы
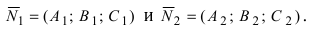
Пусть линия пересечения плоскостей определяется прямой (l). Из одной точки этой прямой проведем два перпендикулярных к прямой вектора 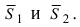 Меньший угол между этими векторами определяет угол между плоскостями (Рис.44):
Меньший угол между этими векторами определяет угол между плоскостями (Рис.44):
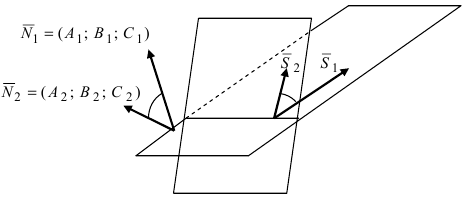
Рис.44. Угол между плоскостями.
В силу того, что 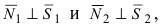 то угол между нормальными векторами равен углу между векторами
то угол между нормальными векторами равен углу между векторами 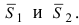 Из векторной алгебры известно, что угол между векторами определяется формулой:
Из векторной алгебры известно, что угол между векторами определяется формулой: 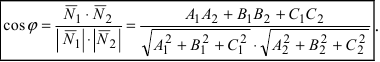
Следствие: Если плоскости перпендикулярны (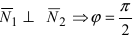 ), то условием перпендикулярности плоскостей является равенство:
), то условием перпендикулярности плоскостей является равенство: 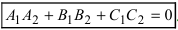 .
.
Следствие: Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей: 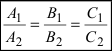
2. Расстояние от данной точки до заданной плоскости. Расстояние от данной точки 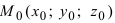 до заданной плоскости
до заданной плоскости 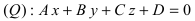 определяется по формуле:
определяется по формуле: 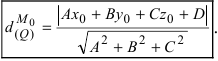
Пример:
На каком расстоянии от плоскости 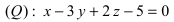 находится точка
находится точка 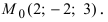
Решение:
Воспользуемся приведенной формулой: 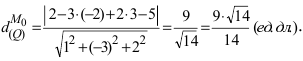
Прямая в пространстве
Общее уравнение прямой
Прямая в пространстве может быть задана как пересечение двух плоскостей: 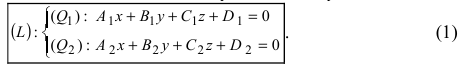
Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.
Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, 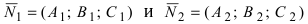 были неколлинеарными, т.е. выполняется одно из неравенств:
были неколлинеарными, т.е. выполняется одно из неравенств: 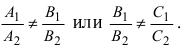
Пусть прямая проходит через точку 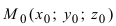 параллельно вектору
параллельно вектору 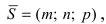 который называется направляющим вектором прямой (см. Лекцию Ле 7), тогда ее уравнение называется каноническим и имеет вид:
который называется направляющим вектором прямой (см. Лекцию Ле 7), тогда ее уравнение называется каноническим и имеет вид:

Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Пример:
Как расположена прямая 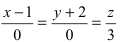 относительно координатных осей.
относительно координатных осей.
Решение:
Согласно замечанию эта прямая будет перпендикулярна осям абсцисс и ординат (параллельна оси аппликат) и будет проходить через точку 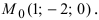 Приравняв каждую дробь уравнения (2) параметру t, получим параметрическое уравнение прямой:
Приравняв каждую дробь уравнения (2) параметру t, получим параметрическое уравнение прямой:
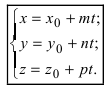
Пример:
Записать уравнение прямой 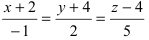 в параметрическом виде.
в параметрическом виде.
Решение:
Приравняем каждую дробь к параметру t: 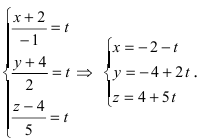 Если прямая проходит через две известные точки
Если прямая проходит через две известные точки 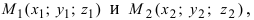 то ее уравнение имеет вид:
то ее уравнение имеет вид: 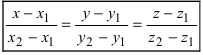 и называется уравнением прямой, проходящей через две заданные точки.
и называется уравнением прямой, проходящей через две заданные точки.
Пример:
Составить канонические и параметрические уравнения прямых, проходящих через точки А (— 1; 1; 2 ), В (0; -1; -1) И С (1; 0; -1), D (l; 0; 1 ).
Решение:
Составим каноническое уравнение прямой линии, проходящей через точки 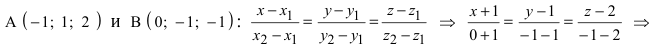
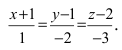 Перейдём к параметрическому уравнению
Перейдём к параметрическому уравнению 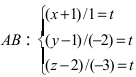 или
или 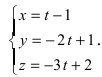 Составим каноническое уравнение прямой линии, проходящей через точки
Составим каноническое уравнение прямой линии, проходящей через точки 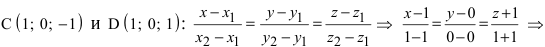
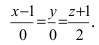 Перейдём к параметрическому уравнению прямой
Перейдём к параметрическому уравнению прямой 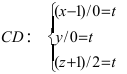
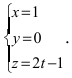
Основные задачи о прямой в пространстве
1. Переход от общего уравнения прямой к каноническому. Пусть прямая задана общим уравнением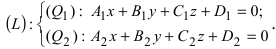 Для того, чтобы перейти от этого уравнения прямой к каноническому, поступают следующим образом:
Для того, чтобы перейти от этого уравнения прямой к каноническому, поступают следующим образом:
Пример:
Записать уравнение прямой 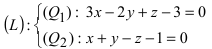 в каноническом и параметрическом виде.
в каноническом и параметрическом виде.
Решение:
Положив х = 0, получим СЛАУ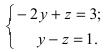 Складывая уравнения, найдем у = -4. Подставив это значение переменной у во второе уравнение системы, получим z = —5. Таким образом, прямая проходит через точку
Складывая уравнения, найдем у = -4. Подставив это значение переменной у во второе уравнение системы, получим z = —5. Таким образом, прямая проходит через точку 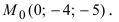 Найдем направляющий вектор прямой как векторное произведение нормальных векторов заданных плоскостей:
Найдем направляющий вектор прямой как векторное произведение нормальных векторов заданных плоскостей:
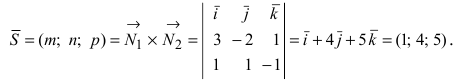
Запишем каноническое 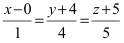 и параметрическое уравнения прямой:
и параметрическое уравнения прямой:
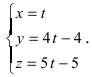
Угол между пересекающимися прямыми
Угол между двумя пересекающимися прямыми определяется как угол между их направляющими векторами. Если прямые 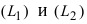 имеют направляющие вектора
имеют направляющие вектора
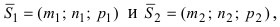
соответственно, то угол между прямыми определяется по формуле: 
Следствие: Если прямые перпендикулярны (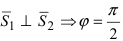 ), то условием перпендикулярности прямых является равенство:
), то условием перпендикулярности прямых является равенство: 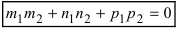
Следствие: Если прямые параллельны, то направляющие вектора коллинеарны, следовательно, условие параллельности прямых: 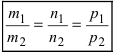
Координаты точки пересечения прямой и плоскости
Пусть прямая (L) задана общим уравнением 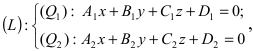 а плоскость (Q) уравнением Ax+By+Cz+D=0. Так как точка пересечения прямой и плоскости принадлежит одновременно обоим этим объектам, то ее координаты находят из системы уравнений:
а плоскость (Q) уравнением Ax+By+Cz+D=0. Так как точка пересечения прямой и плоскости принадлежит одновременно обоим этим объектам, то ее координаты находят из системы уравнений: 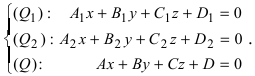 Если прямая (L) задана каноническим уравнением
Если прямая (L) задана каноническим уравнением 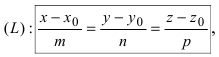 а плоскость (Q)
а плоскость (Q)
Рассмотрим возможные случаи:
- если выполняются условия
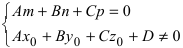 , то прямая не пересекает плоскость (прямая параллельна плоскости);
, то прямая не пересекает плоскость (прямая параллельна плоскости); - при условиях
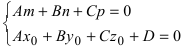 прямая лежит на плоскости;
прямая лежит на плоскости; - если
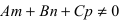 , прямая пересекает плоскость в одной точке.
, прямая пересекает плоскость в одной точке.
Пример:
Найти координаты точки пересечения прямой (L), заданной уравнением 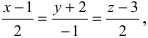 и плоскости (Q): 2x-y+3z-4=0.
и плоскости (Q): 2x-y+3z-4=0.
Решение:
Перепишем уравнение прямой (L) в параметрическом виде 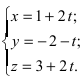 Подставим найденные величины в уравнение плоскости (Q)? получим
Подставим найденные величины в уравнение плоскости (Q)? получим
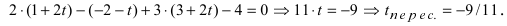
Найденное значение параметра 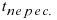 подставим в параметрическое уравнение прямой
подставим в параметрическое уравнение прямой 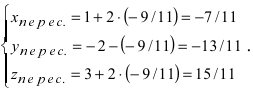 Таким образом, прямая пересекает заданную плоскость в точке
Таким образом, прямая пересекает заданную плоскость в точке 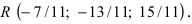
- Заказать решение задач по высшей математике
Угол между прямой и плоскостью
Пусть дана плоскость (Q) с нормальным вектором 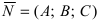 и пересекающая ее прямая (L) с направляющим вектором
и пересекающая ее прямая (L) с направляющим вектором 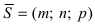 (Рис.45).
(Рис.45). 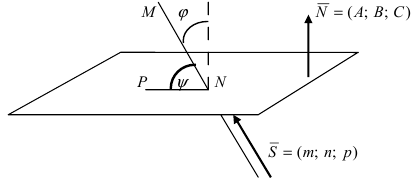
Рис. 45. Угол между прямой и плоскостью.
Угол 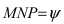 является углом между прямой (L) и плоскостью (Q). Угол между нормальным вектором плоскости и прямой обозначим через
является углом между прямой (L) и плоскостью (Q). Угол между нормальным вектором плоскости и прямой обозначим через 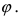 Из рисунка видно, что
Из рисунка видно, что 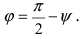 Следовательно,
Следовательно,
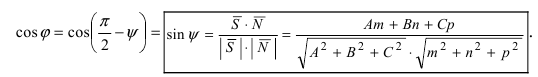
Следствие: Если прямая перпендикулярна плоскости (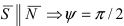 ), то условие перпендикулярности прямой и плоскости имеет вид:
), то условие перпендикулярности прямой и плоскости имеет вид: 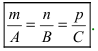
Следствие: Если прямая параллельна плоскости (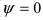 ), то направляющий вектор прямой и нормальный вектор плоскости перпендикулярны (
), то направляющий вектор прямой и нормальный вектор плоскости перпендикулярны (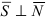 ), следовательно, условие параллельности прямой и плоскости:
), следовательно, условие параллельности прямой и плоскости: 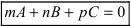 .
.
Плоскость и прямая в пространстве
Всякое уравнение первой степени относительно координат 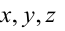
 задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
Вектор 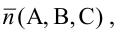 ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты А, В, С одновременно не равны 0.
ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты А, В, С одновременно не равны 0.
Особые случаи уравнения (3.1):
- D = 0, Ах + By + Cz = 0 – плоскость проходит через начало координат.
- С = 0, Ах + By + D = 0 – плоскость параллельна оси Oz.
- С = D = 0, Ах + By = 0 – плоскость проходит через ось Oz.
- С = В = 0, Ах + D = 0 – плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: 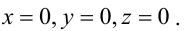
Прямая в пространстве может быть задана:
- как линия пересечения двух плоскостей, т.е. системой уравнений:
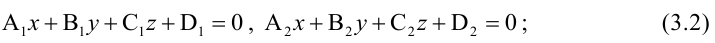
- двумя своими точками
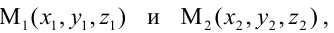 тогда прямая, через них проходящая, задается уравнениями:
тогда прямая, через них проходящая, задается уравнениями: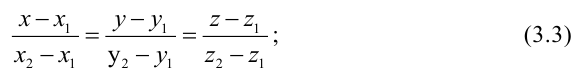
- точкой
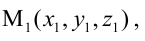 ей принадлежащей, и вектором
ей принадлежащей, и вектором 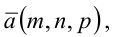 ей коллинеарным.
ей коллинеарным.
Тогда прямая определяется уравнениями: 
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор 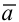 называется направляющим вектором прямой.
называется направляющим вектором прямой.
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: 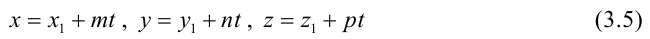 Решая систему (3.2) как систему линейных уравнений относительно неизвестных х и у, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой.
Решая систему (3.2) как систему линейных уравнений относительно неизвестных х и у, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой.
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения: 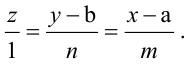
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор 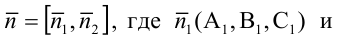
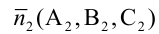 – нормальные векторы заданных плоскостей. Если один из знаменателей
– нормальные векторы заданных плоскостей. Если один из знаменателей 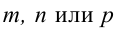 в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система
в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система 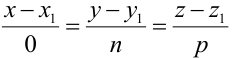 равносильна системе
равносильна системе 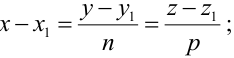 такая прямая перпендикулярна к оси Ох. Система
такая прямая перпендикулярна к оси Ох. Система 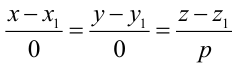 равносильна системе
равносильна системе 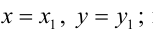 прямая параллельна оси Oz.
прямая параллельна оси Oz.
Пример:
Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение:
По условию задачи вектор 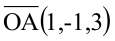 является нормальным вектором плоскости, тогда ее уравнение можно записать в виде
является нормальным вектором плоскости, тогда ее уравнение можно записать в виде 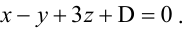 Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D:
Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D: 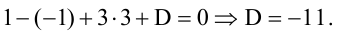 Итак,
Итак, 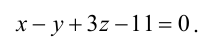
Пример:
Составьте уравнение плоскости, проходящей через ось Oz и образующей с плоскостью 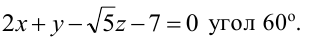
Решение:
Плоскость, проходящая через ось Oz, задается уравнением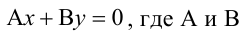 одновременно не обращаются в нуль. Пусть В не равно 0,
одновременно не обращаются в нуль. Пусть В не равно 0, 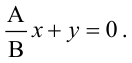 По формуле косинуса угла В между двумя плоскостями
По формуле косинуса угла В между двумя плоскостями 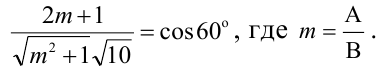
Решая квадратное уравнение 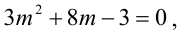 находим его корни
находим его корни 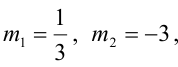 откуда получаем две плоскости
откуда получаем две плоскости 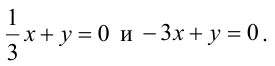
Пример:
Составьте канонические уравнения прямой: 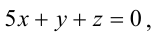
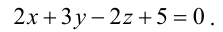
Решение:
Канонические уравнения прямой имеют вид:
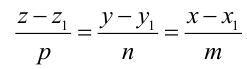 где
где 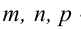 – координаты направляющего вектора прямой,
– координаты направляющего вектора прямой, 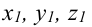 – координаты какой-либо точки, принадлежащей прямой. Прямая задана как линия пересечения двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируют одну из координат (проще всего положить, например, х = 0) и полученную систему решают как систему линейных уравнений с двумя неизвестными. Итак, пусть х = 0, тогда у + z = 0, Зу-2z + 5 = 0 , откуда у = -l, z = l. Координаты точки
– координаты какой-либо точки, принадлежащей прямой. Прямая задана как линия пересечения двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируют одну из координат (проще всего положить, например, х = 0) и полученную систему решают как систему линейных уравнений с двумя неизвестными. Итак, пусть х = 0, тогда у + z = 0, Зу-2z + 5 = 0 , откуда у = -l, z = l. Координаты точки 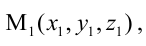 принадлежащей данной прямой, мы нашли: М(0,-1,1). Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей
принадлежащей данной прямой, мы нашли: М(0,-1,1). Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей 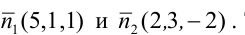 Тогда
Тогда
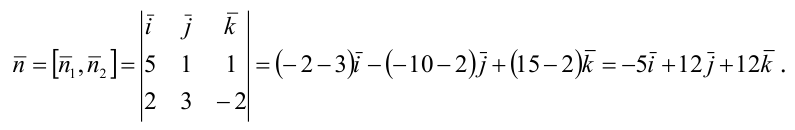 Канонические уравнения прямой имеют вид:
Канонические уравнения прямой имеют вид: 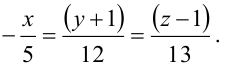
Пример:
В пучке, определяемом плоскостями 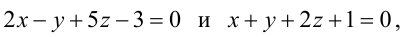 найти две перпендикулярные плоскости, одна из которых проходит через точку М (1,0,1).
найти две перпендикулярные плоскости, одна из которых проходит через точку М (1,0,1).
Решение:
Уравнение пучка, определяемого данными плоскостями, имеет вид 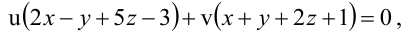 где
где 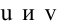 не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом:
не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом: 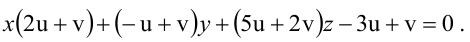
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим: 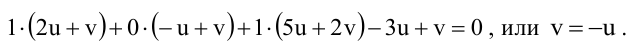
Тогда уравнение плоскости, содержащей М, найдем, подставив 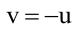 в уравнение пучка:
в уравнение пучка: 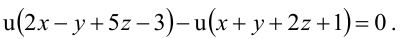
Т.к. и 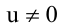 (иначе v=0, а это противоречит определению пучка), то имеем уравнение плоскости
(иначе v=0, а это противоречит определению пучка), то имеем уравнение плоскости 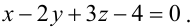 Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей:
Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей: 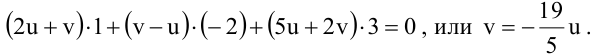
Значит, уравнение второй плоскости имеет вид: 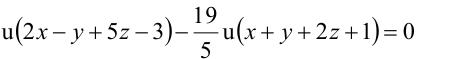 или
или 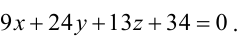
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
23 ноября 2012
В этом уроке мы рассмотрим, как с помощью определителя составить уравнение плоскости. Если вы не знаете, что такое определитель, зайдите в первую часть урока — «Матрицы и определители». Иначе вы рискуете ничего не понять в сегодняшнем материале.
Уравнение плоскости по трем точкам
Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:
Задача. В пространстве даны три точки, не лежащие на одной прямой. Их координаты:
M = (x1, y1, z1);
N = (x2, y2, z2);
K = (x3, y3, z3);Требуется составить уравнение плоскости, проходящей через эти три точки. Причем уравнение должно иметь вид:
Ax + By + Cz + D = 0
где числа A, B, C и D — коэффициенты, которые, собственно, и требуется найти.
Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ — подставить координаты в уравнение Ax + By + Cz + D = 0. Получится система из трех уравнений, которая легко решается.
Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.
Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием без каких-либо обоснований и доказательств.
Уравнение плоскости через определитель
Хватит лирики, приступаем к делу. Для начала — теорема о том, как связаны определитель матрицы и уравнение плоскости.
Теорема. Пусть даны координаты трех точек, через которые надо провести плоскость: M = (x1, y1, z1); N = (x2, y2, z2); K = (x3, y3, z3). Тогда уравнение этой плоскости можно записать через определитель:
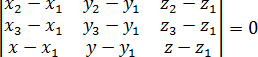
Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:
Задача. Составьте уравнение плоскости, проходящей через точки:
A1 = (0, 0, 1);
B = (1, 0, 0);
C1 = (1, 1, 1);
Составляем определитель и приравниваем его к нулю:
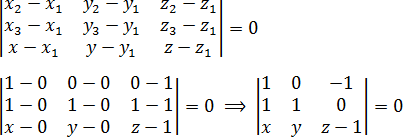
Раскрываем определитель:
a = 1 · 1 · (z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · (z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;
Как видите, при расчете числа d я немного «причесал» уравнение, чтобы переменные x, y и z шли в правильной последовательности. Вот и все! Уравнение плоскости готово!
Задача. Составьте уравнение плоскости, проходящей через точки:
A = (0, 0, 0);
B1 = (1, 0, 1);
D1 = (0, 1, 1);
Сразу подставляем координаты точек в определитель:
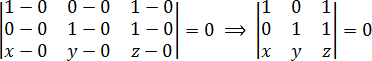
Снова раскрываем определитель:
a = 1 · 1 · z + 0 · 1 · x + 1 · 0 · y = z;
b = 1 · 1 · x + 0 · 0 · z + 1 · 1 · y = x + y;
d = a − b = z − (x + y) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;
Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно, но все-таки рекомендуется — чтобы упростить дальнейшее решение задачи.
Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель — и все, уравнение готово.
На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит x2 или x3, а в какой — просто x. Чтобы окончательно разобраться с этим, давайте проследим, откуда берется каждое число.
Откуда берется формула с определителем?
Итак, разбираемся, откуда возникает такое суровое уравнение с определителем. Это поможет вам запомнить его и успешно применять.
Все плоскости, которые встречаются в задаче C2, задаются тремя точками. Эти точки всегда отмечены на чертеже, либо даже указаны прямо в тексте задачи. В любом случае, для составления уравнения нам потребуется выписать их координаты:
M = (x1, y1, z1);
N = (x2, y2, z2);
K = (x3, y3, z3).
Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:
T = (x, y, z)
Берем любую точку из первой тройки (например, точку M) и проведем из нее векторы в каждую из трех оставшихся точек. Получим три вектора:
MN = (x2 − x1, y2 − y1, z2 − z1);
MK = (x3 − x1, y3 − y1, z3 − z1);
MT = (x − x1, y − y1, z − z1).
Теперь составим из этих векторов квадратную матрицу и приравняем ее определитель к нулю. Координаты векторов станут строчками матрицы — и мы получим тот самый определитель, который указан в теореме:
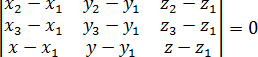
Эта формула означает, что объем параллелепипеда, построенного на векторах MN, MK и MT, равен нулю. Следовательно, все три вектора лежат в одной плоскости. В частности, и произвольная точка T = (x, y, z) — как раз то, что мы искали.
Замена точек и строк определителя
У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2. Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:
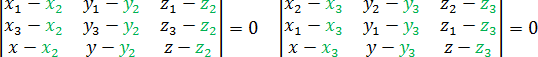
Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки T = (x; y; z) в самом верху. Пожалуйста, если вам так удобно:
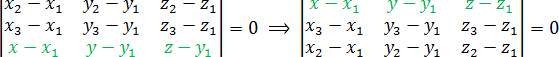
Некоторых смущает, что в одной из строчек присутствуют переменные x, y и z, которые не исчезают при подстановке точек. Но они и не должны исчезать! Подставив числа в определитель, вы должны получить вот такую конструкцию:
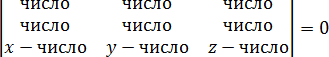
Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:
Ax + By + Cz + D = 0
Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.
Задача. Составьте уравнение плоскости, проходящей через точки:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1).
Итак, рассматриваем 4 точки:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1);
T = (x, y, z).
Для начала составим стандартный определитель и приравниваем его к нулю:
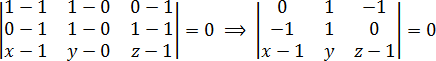
Раскрываем определитель:
a = 0 · 1 · (z − 1) + 1 · 0 · (x − 1) + (−1) · (−1) · y = 0 + 0 + y;
b = (−1) · 1 · (x − 1) + 1 · (−1) · (z − 1) + 0 · 0 · y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;
Все, мы получили ответ: x + y + z − 2 = 0.
Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными x, y, z не внизу, а вверху:
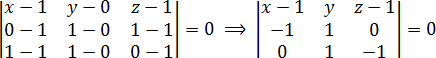
Вновь раскрываем полученный определитель:
a = (x − 1) · 1 · (−1) + (z − 1) · (−1) · 1 + y · 0 · 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) · 1 · 0 + y · (−1) · (−1) + (x − 1) · 1 · 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;
Мы получили точно такое же уравнение плоскости: x + y + z − 2 = 0. Значит, оно действительно не зависит от порядка строк. Осталось записать ответ.
Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.
В рассмотренной выше задаче мы использовали точку B1 = (1, 0, 1), но вполне можно было взять C = (1, 1, 0) или D1 = (0, 1, 1). В общем, любую точку с известными координатами, лежащую на искомой плоскости.
Смотрите также:
- Видеоурок по задачам C2: уравнение плоскости через определитель

- Уравнение плоскости в задаче C2. Часть 1: матрицы и определители

- Тест к уроку «Что такое числовая дробь» (легкий)

- Сводный тест по задачам B15 (1 вариант)

- Однородные тригонометрические уравнения: общая схема решения

- Задача B4: тарифы на сотовую связь

