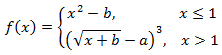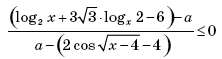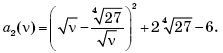Как составить уравнение по графику сложной функции

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

• х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

• стационарные и критические точки;
• точки экстремума;
• нули функции;
• точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

1. Найти область определения функции.
2. Найти область допустимых значений функции.
3. Проверить не является ли функция четной или нечетной.
4. Проверить не является ли функция периодической.
5. Найти нули функции.
6. Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
7. Найти асимптоты графика функции.
8. Найти производную функции.
9. Найти критические точки в промежутках возрастания и убывания функции.
10. На основании проведенного исследования построить график функции.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

1. 
2. 
3. 

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Построение графиков сложных функций

В работе описаны основные методы построения элементарных функций с преобразованиями и рассмотрено построение графиков сложных функций (без производной): «y=f(v(x))», «y=f(x)+g(x)», «y=f(x)*g(x)».

Скачать:

Вложение	Размер
Презентация к работе «Построение графиков сложных функций»	250.5 КБ
В работе описаны основные методы построения элементарных функций с преобразованиями и рассмотрено построение графиков сложных фу	463.5 КБ

Предварительный просмотр:

Подписи к слайдам:

Графики сложных функций Работу выполнил: ученик 11 класса МОУ «Гимназия № 36 «Золотая горка» Закиев Ринат Руководитель: Шапеева А.В. – учитель математики МАОУ «ЛИИТ №36»

Цели Выявить способы построения графиков сложных функций

Задачи изучить основные методы построения элементарных функций и приемы их преобразования; выделить способы построения графиков сложных функций, опираясь на графики элементарных функций, и научиться их строить. Объектом исследования является сложная функция, а предметом исследования — графики сложных функций.

Прием №1 График функции у = f ( x )+ b получается из графика функции у = f ( x ) (рис.1) на вектор (0, b ) вдоль оси ординат у = f ( x ) у = f ( x )+ b

Прием №2 График функции у = f ( x + b ) получается из графика функции у = f ( x ) на вектор (- b ,0) вдоль оси абсцисс у = f ( x + b ) у = f ( x ) у = f ( x )+ b

Прием №3 График функции у = — f ( x ) получается симметрией графика функции у = f ( x ) относительно оси абсцисс у = f ( x ) у = — f ( x )

Прием №4 График функции у = f (а x ) получается сжатием графика функции у = f ( x ) к оси ординат в а раз, если a > 1, и растяжением от оси ординат в раз, если 0 1, и сжатием к оси абсцисс в раз, если 0 Муниципальное образовательное учреждение

«Гимназия № 36 «Золотая горка»

Построение графиков сложных функций

Выполнил: ученик 11 класса

МОУ «Гимназия № 36 «Золотая горка»

Шапеева А.В., учитель математики

МОУ «Гимназия № 36 «Золотая горка»

1. Методы построения элементарных функций…………………………..6
2. Метод построения функции y = f(v(x))………………………………….9
3. Метод построения функции у = f(x) + g(x)……………………………..16
4. Метод построения функции у = f(x)∙g(x). ……………………………. 18

При решении неравенств и уравнений иногда приходится использовать функционально – графический метод. Суть метода: найти абсциссы точек пересечения графиков функций, стоящих в левой и правой частях уравнения. При этом реализация метода основывается на выполнении следующих действий:

1. Преобразовать исходное уравнение к виду f(x)=g(x). Где f(x) и g(x) функции, графики которых можно построить.
2. Построить графики функции f(x) и g(x).
3. Определить точки пересечения построенных графиков.
4. Определить абсциссы найденных точек. Они и дадут множество решений исходного уравнения.
5. Записать ответ.

Замечание. Преимущество данного метода заключается в том, что он позволяет легко определить число корней уравнения. Недостаток – в том, что корни, в общем случае, определяются приближенно.

Пример 1. 2 х = -х 2 +3

К этому уравнению нельзя применить стандартные приемы решения. Если построим эскиз графиков функции у =2 х и у = -х 2 +3, то увидим, что уравнение имеет два корня, один из них равен 1 (проверяем), а значение другого корня -1,7 (точное значение не можем определить).

Пример 2. Что можно сказать о корнях уравнения ?

Обе функции — убывающие на своих областях определения. Хотя бы два корня можно угадать: и . Остается вопрос: есть ли другие корни и сколько их, какому промежутку они принадлежат?

Построим графики функции .

По рис.1 мы видим, что на некотором промежутке графики функции

« сливаются», по рисунку 2 можем определить только промежуток, которому принадлежат корни уравнения [0;1] , а о количестве корней ничего не можем сказать (рисунки отличаются по масштабу).

После решения несколько таких уравнений, я понял, что умения строить графики различных функций и знание их свойств является важным условием решения нестандартных уравнений и неравенства.

Исследование посвящено проблеме совершенствования умений и навыков построения графиков сложных функций. Актуальность этой проблемы определяется тем, что нестандартные уравнения и неравенства часто решаются функционально – графическим методом. В заданиях ЕГЭ (и в части В, и в части С) имеются задания, при решении которых используется функционально – графический метод, свойства функций. Многие задачи с параметрами невозможно решить другим методом. ( В.П.Моденов. Задачи с параметрами. Координатно – параметрический метод. М: «Экзамен»,2006).

В пособие для поступающих (Е.М.Родионов, С.Л. Синякова. Математика. Пособие для поступающих в вузы. Учебный центр «Ориентир» МГТУ им.Н.Э.Баумана,2003) много заданий на построение графиков функций..

Поскольку в школьном курсе математики на эту тему «Построение графика сложной функции» отводится мало времени, то я решил изучить методы построения сложных функций (без производной).

Построение графиков элементарных функций не составляет труда, в школьном курсе математики они достаточно хорошо описаны. Я предположил: если знаем свойства элементарных функций и умеем строить их графики, то сможем построить и графики сложных функций.

— выявить способы построения графиков сложных функций.

— изучить основные методы построения элементарных функций и приемы их преобразования;

— выделить способы построения графиков сложных функций, опираясь на графики элементарных функций, и научиться их строить.

Объектом исследования является сложная функция, а предметом исследования — графики сложных функций.

(Сложную функцию y=f(v(x)) называют также композицией двух функций )

Построение графиков функций одна из интереснейших тем в школьной математике.

Методы построения элементарных функций

Умения строить графики функций и их читать, т.е. определять промежутки монотонности и другие характеристики функции по их графику, — важный элемент математической культуры. Во многих задачах график является лишь вспомогательным элементом решения. Поэтому необходимо владеть простыми приемами построения графиков. Перечислим эти приемы:

1. График функции у = f(x)+b получается из графика функции у = f(x) (рис.1) на вектор (0,b) вдоль оси ординат (рис.2).

1. График функции у = f(x+b) получается из графика функции у = f(x) на вектор (-b,0) вдоль оси абсцисс (рис.3).

График функции у = f(x) Графики функции у = f(x)+b и у = f(x+b)

1. График функции у = -f(x) получается симметрией графика функции у = f(x) относительно оси абсцисс (рис.4).

1. График функции у = f(аx) получается сжатием графика функции

у = f(x) к оси ординат в а раз, если a > 1, и растяжением от оси ординат в раз, если

1. График функции у = f(-x) получается симметрией графика функции у = f(x) относительно оси ординат (рис.6).

1. График функции у = аf(x) получается умножением каждой ординаты графика функции у = f(x) на а, т.е. растяжением от оси абсцисс в а раз, если a > 1, и сжатием к оси абсцисс в раз, если 0

1. График функции у = совпадает с графиком функции у = f(x) там, где f(x) 0, и получается из него симметрией относительно оси абсцисс там, где f(x)

1. График функции у = при x 0 совпадает с графиком функции у = f(x) , при x

Например, при построении графика функции у = 2sin( ) используются приемы 4, 2, 8, 6 (рис.10)

Прием 4. Прием 2.

2. Построение графика функции y=f(v(x))

Посмотрим схему построения графиков сложных функции вида y=f(v(x)) без использования производной.

Пусть нам нужно построить график y=f(v(x)). Обязательно на бумаге или мысленно нужно построить оба графика: график внутренней функции у = v(x) и график внешней функции у = f(v).

Если удобно строить график внешней функции по контрольным точкам, то лучше, для большой наглядности, построив график внутренней точки, разметить ось ординат контрольными значениями аргумента для внешней функции, а затем построить прямо по графику, в каких точках внутренняя функция принимала эти значения.

1. Построить график функции у = arctg2 x .

Решение. Данная функция является композицией двух функции v=2 x и y= arctgv. Функцию v = v(x) назовем внутренней, y = y(v) – внешней. Внутренняя функция является строго возрастающей: при возрастании х от — ∞ до + ∞ v(x) возрастает от 0 до + ∞. По графику внешней функции определяем, что такому возрастанию v соответствует возрастание у от 0 до /2, т.е. при возрастании х от — ∞ до + ∞ у возрастает от 0 до /2

График функции v=2 x График функции y(v)= arctgv.

График функции у = arctg2 x имеет вид:

Контрольная точка: при х=0 у = π /4

Пример 2. Построить график функции у =

Решение. Построим графики функции у = и f(v)=

Выделяем промежутки монотонности функции у = : (- ∞;0) и (0; + ∞). При возрастании х на промежутке (- ∞ ;0) v(x) убывает от 0 до — ∞. Такому изменению v соответствует убывание у от 1 до 0. Если х возрастает от 0 до + ∞, то v(x) убывает от +∞ до 1.

Для более точного построения графика следует использовать контрольные точки, выбирая те значения аргумента х, при которых легко вычислять значения у(х).

Таким образом, построение графика сложной функции y=f(v(x)) в некоторых случаях можно выполнить по следующему алгоритму:

1. Начертить графики внутренней и внешней функций.
2. Определить промежутки монотонности внутренней функции y=v(x) и отметить их на оси Ох плоскости хОу.
3. На каждом промежутке определить границы изменения v=v(x) и выбрать те значения, которые попадают в область определения функции y=f(v).
4. По графику внешней функции у = f(v) найти характер изменения функции у.
5. В системе координат хОу начертить график у = у(х).

Такая работа позволяет по графику следить за изменением функции при изменении аргумента и, наоборот, по заданному изменению функции строить ее график.

Использование схемы построения графика функции у = у(х) помогает сложиться умению представлять сложную функцию в виде композиции двух функции, — внутренней и внешней, овладеть навыком «видеть» эти две функции. На мой взгляд, это поможет ученику не только при прохождении тем сложной функции, построения функций и тому подобных, но еще и при проведении различных алгебраических преобразований выражений. Умение проводить операции анализа-синтеза значительно уменьшает трудности учеников при выборе способа тождественного преобразования выражения.

3. Построить график функции у = .

Решение. Построим графики внутренней и внешней функций.

Если х возрастает от 0 до + ∞, то v(x) возрастает от 1 до + ∞. Этому изменению v соответствует убывание у от 1 до 0. Изобразим график функции у = у(х) при х 0, а затем используем четность данной функции.

4.Построить график функции у = ln(x 2 – 3x +2).

Решение. Построим графики функций y= x 2 – 3x +2 и y = lnv.

Если х возрастает от — ∞ до 1, то v(x) убывает + ∞ до 0, а у при этом убывает от + ∞ до — ∞. При х [1; 2] v(x) 0 и при этих значениях х функция не определена. Если х возрастает от 2 до + ∞, то v(x) возрастает от 0 до + ∞, а у при этом возрастает от + ∞

5.Построить график функции .

Решение. (Алгоритм построения графика этой функции и функции у = log 2 sinx дан в учебнике 11 класса «Алгебра и начала анализа» С.М.Никольский и др.)

Данная функция является композицией двух функции v = sinx и y = 2 v

Область определения функции — множество всех действительных чисел. Поскольку функция v = sinx периодическая с главным периодом 2 , то функция также периодическая с главным периодом 2 . На промежутке [- ; ] функция v = sinx возрастает от -1 до 1, значит, функция y = 2 v возрастает на этом промежутке от до 2.

На промежутке [ ; ] функция v = sinx убывает от 1 до -1, функция y = 2 v убывает на этом промежутке от 2 до .

Перечисленные свойства позволяют построить схематический график на отрезке [- ; ], затем продолжить его периодически.

1. Построить график функции .

Решение. Предложенная схема применима и тогда, когда сложная функция является композицией не двух, а большего числа функций, графики которых известны. Данная функция является композицией трех функций. Аналогично рассуждая, получаем следующие графики функций: u = x 2 – 4x +3, v =1/u, y= 2 v .

Решение. Предложенная схема применима и тогда, когда сложная функция является композицией не двух, а большего числа функций, графики которых известны. Данная функция является композицией трех функций. Аналогично рассуждая, получаем следующие графики функций: u = x 2 – 4x +3, v =1/u, y= 2 v .

Графики этих функций:

u = x 2 – 4x +3 v =1/u

При построении графиков сложных функций надо использовать все элементарные средства: переносы, отражения, сложение графиков т.д.

1. Построить график функции .

8. Построить график функции y = arctg(lnx).

9. Построить график функции y = arctgx 2

3. Метод построения функции у = f(x) + g(x)

Для построения графика функции у = f(x)+g(x), если известны графики функции у = f(x) и у = g(x), надо произвести алгебраическое сложение соответствующих ординат функций. Применение такого способа целесообразно, например, когда слагаемые являются основными элементарными функциями разных типов.

Пример. Построить график функции у = х + sinx.

Строим графики функции у = х и у = sinx и получаем график заданной функции путем сложения соответствующих ординат.

При построении следует обратить внимание на два обстоятельства:

1) , а потому имеет смысл провести прямые у = х+1 и у = х-1, параллельные прямой у = х, между этими двумя прямыми располагается график функции у = х + sinx.

2) В тех точках, где sinx = 0 у = х ( соответствующе точки графика заданной функции лежат на прямой у = х).

В тех точках, где sinx = -1 у = х-1 (соответствующе точки графика заданной функции лежат на прямой у = х).

Пример 2. Построить график функции у = .

Так как существует лишь при х > 0 (sinx существует на всей числовой оси), то областью существования для заданной функции является промежуток (0; + ∞). Модули не могут быть отрицательными, то у 0. Строим графики функции только при х>0 производим сложение графиков . При этом обращаем внимание на то, что значение второй функции равно нулю только в одной точке х = 1. Наибольшее значение первой функции достигается в точках , в этих точках у = .

4, Метод построения функции у = f(x)∙g(x )

Для построения графика функции у = f(x) ∙ g(x), если известны графики функции у = f(x) и у = g(x), надо перемножить соответствующие ординаты функций. Применение такого способа целесообразно, например, когда множителями являются основными элементарными функциями разных типов.

Пример. Построить график функции у = х ∙ sinx.

Строим графики функции у = х и у = sinx и получаем график заданной функции путем умножения соответствующих ординат.

Построение производим при х 0, а затем отражаем полученный график относительно оси ординат, так как у = х ∙ sinx является четной функции. При этом учитываем, что в точках с координатами х=k , sinx = 0 произведение х ∙ sinx=0. Наибольшее значение функции у = sinx равно 1 при . В этих точках соответствующе точки графика заданной функции лежат на прямой у = х. Наименьшее значение функции у = sinx равно -1 при . В этих точках соответствующе точки графика заданной функции лежат на прямой у = -х. Значит, график колеблется между прямыми у = х и у = — х.

Я провел работу по построению графика сложной функции и сделал следующие выводы:

1.Графики функций y=f(v(x)), у = f(x)+g(x), у = f(x) ∙ g(x) можно построить без использования производных, особенно этот метод особенно подходит, если f(x) и g(x),v(x) – функции разные элементарные функции.

2.Для построения графиков нужно знать свойства функции, уметь читать графики полученных функции, исследовать поведение графиков в бесконечности.

3. Построение графиков, как и всевозможные другие способы геометрической интерпретации, является весьма эффективным средством для решения алгебраических задач, в том числе и задач с параметрами. Поэтому научиться строить графики функции, в том числе и сложных, для решения задач просто необходимо. При выполнении этой работы, я выяснил, что есть класс уравнений и неравенств, при решении которых требуется умения и навыки построения графиков функций и умения их читать. (Многие уравнения неравенства с параметрами решаются функционально — графическим методом).

Итак, в результате графических и компьютерных экспериментов, я убедился, что графики сложных функций можно строить не только с помощью производных, но и путём исследования внутренних и внешних функций, преобразованиями элементарных функций, поведения графиков функции при х  ±∞, преобразованиями элементарных функций.

При выполнении этой работы:

— повторил и углубил знания свойств и методов построения графиков элементарных функций;

— приобрел опыт построения графиков таких функций, как:

y=f(v(x)); у = f(x)+g(x),у = f(x) ∙ g(x);

— научился работать с дополнительной литературой и материалами, производить отбор научных сведений; приобрел опыт выполнения графических работ на компьютере;

— узнал, что тема « Методы построения графиков функций», очень объемная и интересная, рассмотреть все методы сразу невозможно, т.е. есть можно дальше продолжать работу по данной теме.

По моему мнению, умение проводить такие преобразования (построения) графиков функций позволяет ученикам:

1) научиться читать графики различных функций и использовать их при решении уравнений и неравенств;

2) освоить свойства функций;

3) лучше различать графики различных функций.

Поэтому, на мой взгляд, использование этих способов в педагогической практике целесообразно (хотя бы факультативно), ведь их в тематическом плане нет, а это поможет успешно и эффективно подготовится к выпускным и вступительным экзаменам.

При построении графиков функций я использовал систему компьютерной математики Maple 8.

Строим график функции, заданный системой уравнений, в EXCEL

history 8 января 2018 г.

Группы статей
• Контрольные работы и задания
• Диаграммы и графики

Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.

Пусть дана система уравнений

Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.

Решение (1 ряд данных)

Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.

СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL . О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL .

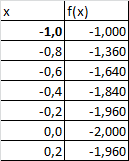
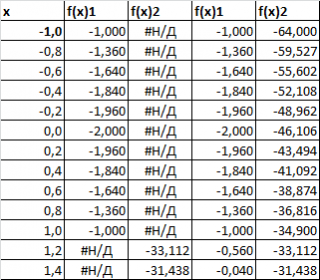
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):

Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.

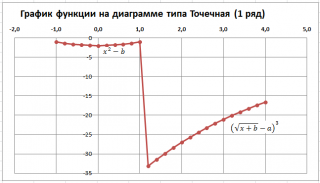
Чтобы построить диаграмму типа Точечная:

• выделите любую ячейку таблицы;
• во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .

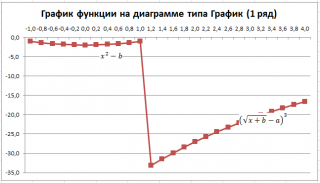
Чтобы построить диаграмму типа График:

• выделите любую столбец f(x) вместе с заголовком;
• во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .

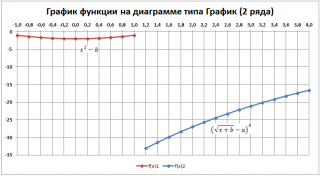
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных .

Решение (2 ряда данных)

Создадим другую таблицу с исходными данными в файле примера, лист График :

Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.

У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.

Решение (3 ряда данных)

Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .

Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).

Решение уравнений с помощью графиков

Решение линейных уравнений

Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.

Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.

Сейчас же я покажу тебе, как это сделать графическим способом.

Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)

Как его решить?

Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:

Иными словами, у нас будет:

Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:

Наш ответ: ( displaystyle x=6)

Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!

Вариант 1. Напрямую

Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)

Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:

Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:

И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).

Ты знаешь, что парабола симметрична относительно своей вершины, например:

Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:

Возвращаемся к нашей параболе.

Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?

Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).

Как ты думаешь, что является решением уравнения?

Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).

И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).

Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!

Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.

Что у тебя получилось? То же самое?

Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!

Решение смешанных неравенств

Теперь перейдем к более сложным неравенствам!

Как тебе такое:

Первое, с чего мы начнем, – это с построения двух графиков:

Расписал? Теперь строй два графика.

Сравним наши рисунки?

У тебя так же? Отлично!

Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).

Смотри, что получилось в итоге:

А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!

На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).

Это и есть ответ!

Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!

Графики сложных функций

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

К написанию данной исследовательской работы подвиг интерес к построению графиков функций. Это один из интереснейших разделов в математике. Построение графиков функций дает возможность их прочитать, то есть определить различные характеристики по их графикам. Решение задач с помощью функций стало сегодня неотъемлемой частью нашей жизни, но не все задачи можно решить аналитическим, алгебраическим способом, большинство задач можно решить только графическим способом. Поэтому хотелось узнать, как будет вести себя график функции, если над ним осуществлять разные преобразования. В школьном курсе изучаются лишь элементарные функции и элементарные преобразования над ними. Встретив функцию, которую нельзя было отнести ни к одному из видов элементарных функций, возникла проблема построения графика подобных функций.

Появляется гипотеза: если знать и применять свойства элементарных функций, использовать операции над графиками функций, то можно составить алгоритмы построения графиков сложных функций.

Цель данной работы – выявление алгоритмов построения графиков сложных функций.

В ходе исследования необходимо выполнить следующие задачи: изучить основные методы построения элементарных функций и приемы их преобразования, выявить алгоритмы построения графиков сложных функций, опираясь на графики элементарных функций, и научиться их строить.

Для изучения данного вопроса было изучена литература, основными источниками для работы стали: Гурский И.П. «Графики сложных функций», статья Дворянинова С.В. «О построении графиков сложных функций» опубликованная в журнале «Математика в школе», Дорофеев Г.В. «Пособие по математике для поступающих в ВУЗы».

Объектом исследования является графики сложных функций, а предметом исследования – алгоритмы построения графиков сложных функций.

В ходе работы были использованы следующие методы: анализ, сравнение, моделирование, систематизация, чтение учебной, научно-популярной и справочной литературы по исследуемой теме, поиск информации в глобальных компьютерных сетях. Работа рассматривает лишь один из аспектов проблемы, исследование в этом направлении может быть продолжено, это могло бы быть изучение не только построения графиков сложных функций, но и подбор и систематизация различных задач, решаемых графическим способом с использованием алгоритмов, рассмотренных в этой работе. Результаты исследования могут быть полезны учащимся школ, которые увлекаются изучением математики, так же, для учителей при подготовке к урокам.

Основная часть

Глава №1. Построение графиков элементарных функций

1. Линейная функция.

Линейной функцией называется функция, задаваемая формулой у = kx + m, где х – аргумент, у – функция, k и m – произвольные действительные числа, Графиком линейной функции является прямая.

Стандартный алгоритм построения прямой:

1) Найти две произвольные точки, принадлежащие функции, методом подстановки аргумента х в уравнение функции;

2) Провести прямую по найденным точкам.

Для такого метода обязательно нужна линейка. А что делать, если приходится рисовать график «от руки»?

Рассмотрим график функции y = kx. Можно заметить, что с каждым последующим увеличением аргумента х на 1 значение функции у изменяется на угловой коэффициент k, в данном случае: на 1; на 2; на -3:

y = x См.рис:1 y = 2x См.рис:2 y = -3x См.рис:3

Из этого можно сделать вывод, что скорость возрастания функции зависит от углового коэффициента k, и вывести последовательность: f(x) = f(x-1) + k. Проще говоря, для отыскания каждой следующей точки нужно увеличивать значение аргумента х на единицу, а значение функции у – на коэффициент k. Если мы имеем коэффициент k, который по модулю меньше единицы, то для отыскания точек с целыми значениями координат нужно подставлять в значение аргумента формулу х = 1/k*n (n– натуральное число, обозначающее порядковый номер точки с целыми значениями координат, принадлежащей графику, начиная от начала координат); то есть, при увеличении значения y на единицу аргумент x будет увеличиваться на 1/k: y = х См.рис:4 Преобразования графика линейной функции, не влияющие на закономерность роста функции. – [у = k(x+b)] – свободный член b влияет на перемещение графика функции у = kx на вектор (-b,0) вдоль оси абсцисс; y = (x+3) – 2 См.рис:5

– [у = kx+ m] – свободный член m влияет на перемещение графика функции у = kx на вектор (0; m) вдоль оси ординат. y = -0,5(x-1) + 5 См.рис:6

В итоге, алгоритм построения линейной функции сводится к следующему: 1) Найти произвольную точку, принадлежащую функции, методом подстановки аргумента х в уравнение функции (обычно проще всего подставить в функцию 0); 2) Пользуясь арифметической прогрессией, отыскать другие точки: – взять координаты известной нам точки; – к значению аргумента х прибавить/отнять единицу, а к значению у прибавить/отнять угловой коэффициент k. 3) Провести по этим точкам прямую.

Преобразования графика линейной функции вида у = k|x|+ m и у = |kx+m|

При попадании kх под модуль часть графика, находящаяся слева от оси Y, симметрично отражается по этой оси от части, находящейся справа: у = -2х + 2 См.рис:7 у = -2|х|+ 2 См.рис:8. Если же под модулем оказывается вся функция, то часть графика, находящаяся снизу от оси Х, отражается симметрично этой оси: у = 3х+2 См.рис:9 у = |3x+2| См.рис:10

2. Квадратичная функция.

Квадратичной функцией называется функция, представленная формулой y = ax² + bx + c (а ), где х – аргумент, у – функция, a, bи c – произвольные действительные числа, являющиеся коэффициентами квадратичной функции. График квадратичной функции – парабола. Стандартный алгоритм построения: 1) Выяснить направление ветвей параболы: если коэффициент a>0, то ветви направлены вверх, а если a<0 – вниз; 2) Определить координаты вершины параболы. Чтобы определить абсциссу вершины параболы пользуются формулой , для отыскания ординаты вершины нужно подставить найденный х в уравнение функции;

3) Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси Y;

4) Найти точки пересечения с осями координат, если они есть;

5) Найти координаты произвольной точки A(x;y), которая принадлежит параболе. Затем найти координаты точки А₁(-х;у), пользуясь свойством параболы – её чётностью ();

6) Соединить полученные точки на графике плавной линией и продолжить график. Такой способ полезен для случаев, когда нужно найти координаты точек при пересечении с осями Х и Y. Но нередко возникают случаи, когда графическим методом нужно найти пересечение нескольких функций.

Рассмотрим простейший вариант квадратичной функции y = x²: См.рис:11 y = x²На рисунке хорошо видно, что значение функции увеличивается в определенной закономерности: разность между двумя значениями y по целым значениям аргумента х постоянно возрастает на 2. На основании этого можно выразить следующую арифметическую последовательность: f(x)= f(x-1)+ (2n-1), где n – натуральное число, обозначающее расстояние до вершины параболы по оси абсцисс.То есть, для отыскания следующей точки нужно прибавлять к х единицу, а к у – 1; 3; 5; 7 и т.д.

Рассмотрим варианты функции y = ax²: См.рис:12 y = -2x² См.рис:13 y = 0,5x² В данных случаях разность между значениями y зависит от старшего коэффициента а, поэтому разность прогрессии нужно дополнить таким образом: f(x)= f(x-1)+ a(2n-1).

Преобразования графика квадратичной функции, не влияющие на закономерность роста функции : – [y = ax² + bx] – от второго коэффициента b зависит точка нахождения вершины параболы; См.рис:14 y = x² + 2x + 3. – [y = ax² + bx + с] – свободный член с влияет на перемещение графика функции у = ax² на вектор (0; с) вдоль оси ординат. См.рис:15 y = -2x² + 4х + 5 См.рис:16 у = 3x² + 6x + 2. Суммируя вышесказанное, алгоритм построения функции сводится к следующему: 1) Определить координаты вершины параболы. Чтобы определить абсциссу вершины параболы пользуются формулой , для отыскания ординаты вершины нужно подставить найденный х в уравнение функции; 2) Пользуясь арифметической прогрессией, отыскать точки, принадлежащие параболе, то есть:

прибавить к аргументу xпредыдущей точки A(x; y) единицу, а к значению y– разность прогрессии a(2n-1) и получить точку

B( x+1; y+a(2n-1) );

найти точку В₁ (-(х+1); y+a(2n-1)), используя свойство – чётность параболы;

3) Соединить полученные точки на графике плавной линией и продолжить график. Преобразования графика квадратичной функции вида y = аx² -|bx |+ c и y = |аx² – bx + c|. Если bx находится под модулем, то часть графика, находящаяся слева от оси Y, симметрично отражается относительно этой оси от части, находящейся справа:

См.рис:17 y = x² – 4x + 2 См.рис:18 y = x² -|4x |+ 2

Если под модулем находится вся функция, то часть графика, находящаяся снизу от оси Х, отражается симметрично этой оси : См.рис:19 у = -2x² – 8x + 2 См.рис:20 y = |-2x² – 8x + 2|

3. Функция квадратного корня.

Функция называется графиком функции квадратного корня, где х – аргумент, у – функция, а и с – произвольные действительные числа. Графиком такой функции является ветвь параболы, «лежащая» на оси Х.

Стандартный алгоритм построения:

Найти вершину графика функции:

2) Методом подбора отыскать точки, принадлежащие графику;

3) Соединить полученные точки на графике плавной линией и продолжить график за крайние точки до конца координатной плоскости.

Однако, такой метод не всегда удобен в работе с различными преобразованиями функции квадратного корня – для отыскания целых значений координат методом подбора может уйти много времени. Рассмотрим функцию вида у = a√х: См.рис:21 у = См.рис:22 у = -2 . По рисункам 21 и 22 видно, что закономерность роста функции аналогична квадратичной функции, однако в данном случае закономерно возрастает (убывает) не значение функции, а её аргумент х, поэтому закономерность изменения х можно выразить последовательностью х_n = x_n-1 + (2n – 1), где n– натуральное число, обозначающее порядковый номер точки с целыми значениями координат, принадлежащей графику, начиная от первой точки с целыми значениями координат от вершины графика. Значение функции у в данном случае зависит от коэффициента а и выражается последовательностью y_n = y_n-1 + a. Рассмотрим функцию вида у = a√kх, где k – коэффициент, произвольное действительное число: См.рис:23 y = См.рис:24 y = 2 . По рисункам 23 и 24 можно заметить, что коэффициент k влияет как на значение аргумента x, так и на значение функции y, поэтому его нужно включить в обе выведенные закономерности: y_n = y_n-1 + a*k; х_n = x_n-1 + k(2n – 1).

Для нахождения точек, принадлежащих функции, с целыми значениями нужно каждое последующее значение функции у нужно увеличивать на а*k, а значение аргумента х – на k(2n – 1).

2) Преобразования графика функции, не влияющие на закономерность роста функции: – [у = а√(x + b)] – коэффициент b влияет на перемещение графика функции у = а√x на вектор (-b,0) вдоль оси абсцисс; См.рис:25 ; – [у = a√х + с] – Коэффициент с не влияет на закономерность роста функции, так как влияет на смещение графика функции у = a√х на вектор (0; с) вдоль оси ординат. См.рис:26 y = 0,5√x – 2. Учитывая всё выше сказанное, новый алгоритм построения функции будет выглядеть таким образом:

1) Найти вершину графика функции: – значение функции находится по формуле у = с; – значение аргумента находится подстановкой найденного значения функции в уравнение функции. 2) Отыскать точки, имеющие целые значения координат и принадлежащие графику, по следующим последовательностям: х_n = x_n-1 + k(2n – 1); y_n = y_n-1 + a*k. То есть, для отыскания следующей точки, принадлежащей графику, нужно к значению у прибавить a*k, а к значению х – k(2n – 1); 3) Соединить полученные точки на графике плавной линией и продолжить график за крайние точки до конца координатной плоскости.

Преобразования графика функции квадратного корня вида y = а√|x| + с и у =|а√x + с|. Если подкоренное выражение находится под модулем, то график функции симметрично отражается относительно оси, параллельной оси Y и проходящей через вершину графика функции квадратного корня: Если вся функция находится под модулем, то часть графика, находящаяся ниже оси абсцисс, симметрично отображается относительно этой оси:

4. Функция обратной пропорциональности Функцию, которую можно задать формулой вида называют обратной пропорциональностью. Две кривые (ветви), симметричные друг другу относительно начала координат являются графиком функции и в совокупности называются гиперболой. Алгоритм построения:

1) Установить расположение графика в четвертях координат : Если k>0, то ветви гиперболы расположены в I и III координатных четвертях, если k<0 – во II и IV четвертях.

2) Построить ветвь графика на промежутке (0, +∞) методом подстановки значений;

3) Соединить полученные точки плавной линией и продолжить график за пределы координатной плоскости; 4) Симметрично отразить ветвь графика относительно начала координат. Рассмотрим варианты функции вида : См. рис:30 По рисункам можно заметить, что коэффициент k влияет на отдаленность ветвей от начала координат.

2) Преобразования графика функции, не влияющие на закономерность роста функции: – [ + с] – Коэффициент с не влияет на закономерность роста функции, так как влияет на смещение графика функции на вектор (0; с) вдоль оси ординат:

(О – точка симметрии двух ветвей, которая также смещается на вектор (0; с) вдоль оси ординат.) ; – [ ] – где b – свободный член, который влияет на перемещение графика функции на вектор (-b; 0) вдоль оси абсцисс: (О – точка симметрии двух ветвей, которая также смещается на вектор (-b;с).)

Преобразования графика гиперболы вида y = и y = | | Если х находится под знаком модуля, то ветвь гиперболы, находящаяся в III или IV четверти, симметрично переносится относительно оси абсцисс или прямой, параллельной ей, в I или II четверть соответственно:

Если вся функция находится под знаком модуля, то часть графика, находящаяся ниже оси абсцисс, симметрично отображается относительно неё:

Вывод: в этой главе мы изучилиразновидности элементарных функций, их графики и преобразования над ними.Составлены авторские алгоритмы построения функций. Подводя итоги вышесказанному необходимо отметить следующее, что для того чтобы выполнить преобразование над элементарными функциями нужно знать некоторые правила.

Глава №2 Построение графиков сложных функций.Посмотрим схему построения графиков сложных функции вида y=f(v(x)) без использования производной. Пусть нам нужно построить график y=f(v(x)). Обязательно на бумаге или мысленно нужно построить оба графика: график внутренней функции у = v(x) и график внешней функции у = f(v). Если удобно строить график внешней функции по контрольным точкам, то лучше, для большой наглядности, построив график внутренней точки, разметить ось ординат контрольными значениями аргумента для внешней функции, а затем построить прямо по графику, в каких точках внутренняя Алгоритм для построения графиков сложной функции y=f(v(x)) :

Начертить графики внутренней и внешней функций.

Определить промежутки монотонности внутренней функции y=v(x) .

На каждом промежутке определить границы изменения v=v(x) и выбрать те значения, которые попадают в область определения функции y=f(v).

По графику конечной у = f(v) найти характер изменения функции у.

В системе координат хОу начертить график у = у(х).

Такая работа позволяет по графику следить за изменением функции при изменении аргумента и, наоборот, по заданному изменению функции строить ее график.

Также мы вывели алгоритм построения общей точки для композиции функций.

Берём точку на оси Ох с абсциссой х1;

Находим ординату v(x1);

Переносим её на прямую y=x и делаем абсциссой;

Находим ординату f(v(x1));

Переносим её на прямую x=x1.

Для построения графиков функций, мы опирались на следующую теорему:

Пусть функция v(x) определена и монотонна на промежутке I1, её областью значений является промежуток I2, а функция. Тогда суперпозиция h(x)=f(v(x)) определена и монотонна на промежутке I1, причём, если обе функции возрастают или обе функции убывают, то h(x) возрастает, а если одна из функций возрастает, а другая убывает, то h(x) убывает.¹

Далее рассмотрим пример:

1.Построить график функции у =

Решение. Построим графики внутренней и внешней функций. Функция v(x)=x²²+1 определена и возрастает на промежутке I1=[0; +∞), а её областью значений является промежуток I2=[1; +∞). Функция f(x)=1/х определена на промежутке I2 и убывает. Следовательно, h(x)=убывает на промежутке [0; +∞). Аналогично, v(x) определена и убывает на промежутке (-∞,0 ], а её областью значений при х (-∞,0 ] также является промежуток =[1; +∞). Функция h(x)= возрастает на промежутке (-∞,0 ]. Таким образом, функция , h(x)=возрастает на промежутке (-∞,0 ], убывает на промежутке [0; +∞) и имеет точку максимума х=0. См рис: 39(а,б,в.)

2.Построить график функции:

Построим графики внутренней и внешней функций. Область определения (-∞, +∞), Область значений (-1, +∞). Если х возрастает (2, +∞), у (-1,+∞), убывает (- ∞,2), у (+∞,-1). Изобразим график функции у = у(х). См рис:40(аб) 3.Построить график функции:

Построим графики внутренней и внешней функций. Область определения (-∞,+∞), Область значений (-∞,+∞). Если х возрастает (-6,-2), у (-∞,16), убывает (-2,2), у (16,-∞). Изобразим график функции у = у(х). См рис: 41(аб)

4.Построить график функции:

Построим графики внутренней и внешней функций. Область определения (1, 5), область значений (0,+∞). На каждом промежутке является убывающей, по х (-∞,+∞)., по у (+∞,-∞). Изобразим график функции у = у(х). См рис: 42(аб)

Сложение, разность, произведение и частное функций. ²

Над функциями, как и над числами, можно производить арифметические действия, т.е. определять сумму (разность). График функции y=f(x)+-g(x) можно получить, используя правила сложения (вычитания) графиков функции y=f(x) и y=g(x). Особенно эффективным этот метод бывает в том случае, когда f(x) и g(x) являются элементарными функциями. Заметим, что осуществлять арифметические действия можно над функциями, имеющими общую область определения или общую часть областей определения. При этом частное двух функций определено, если знаменатель отличен от нуля. Суммой двух функций f(x) и g(x) называется функция h(x) с областью определения, являющейся общей частью областей определения f(x) и g(x), при этом значения функции h(x) равны f(x)+g(x). Ординаты графика суммы функций получаются путём сложения ординат графиков складываемых функций для каждого значения аргумента (для каждой абсциссы) из областей определения суммы. Другими словами, чтобы построить график функции h(x)=f(x)+g(x). Нужно построить график функции y=f(x) и y=g(x) в одной и той же системе координат, а затем в каждой точке к отрезку, изображающему ординату первого графика, пристроить отрезок, изображающий ординату второго графика, при этом второй отрезок откладывать вверх, если g=(x)>0, и вниз, если g(x)<0. Аналогично определяется разность, произведение двух функций и строится её график. При построении графика частного двух функций сначала строим график y=1/g(x) ( разделить единицу на ординаты графика функции g(x)). Строим график произведения f(x)*1/g(x).При построении графика разности можно поступить иначе: построить график функции y=f(x) и y=g(x), затем график функции y=g(x) отобразить симметрично относительно оси Ох, тем самым получится график функции y=-g(x), и, наконец, складываются графики функций y=f(x) и y=g(x). Обобщив информацию, мы вывели общий алгоритм построения функций

1.Находим общую область определения. 2.Слаживаем или вычитаем (если это разность), умножаем или делим ординаты первой и второй функции по соответствующим абсциссам. 3.Отмечаем полученные точки на графике.

4.Соединяем эти точки.

5.Получаем искомую функцию.

Заключение

В процессе написания работы был приобретен ценный опыт. Думаю, что полученные знания позволят избежать ошибок в заданиях на построение различных функций. Результаты исследования заставили задуматься о продолжении данной работы. Больше всего сложностей вызвало создание алгоритма построения функций. Исследование в корне изменило мое представление о видах функций и их преобразованиях.

В перспективе было бы интересно изучить тригонометрические, логарифмическую, показательную функции, а так же сложные функции, полученные различными преобразованиями с ними и узнать, как строить графики этих функций. Также подобрать и систематизировать различные задачи, решаемых графическим способом с использованием алгоритмов, рассмотренных в этой работе.

Список использованной литературы:

Данкова И.Н. Элективный курс по математике: учебное пособие/ И.Н. Данкова, Т.Е. Бондаренко, Л.Л. Емелина — М: 5 за знания, 2006. — 128 с.

Гурский И.П. Графики сложных функций: пособие для учителей/ И.П Гурский. — М: Просвещение, 1968г – 215с.

Дворянинов С. В. О построении графиков сложных функций на основе свойства монотонности/ С. В. Дворянинов// Математика в школе. – 2009. – № 05. – с. 32.

Дорофеев Г.В. Для чего нам нужны графики функций/ Г.В. Дорофеев// Математика в школе. – 2007. – № 07. – с. 50.

Дорофеев Г.В. Пособие по математике для поступающих в ВУЗы: учебное пособие / Г.В. Дорофеев, М.К. Потапов, Н.Х. Розов – М: Дрофа , 2007. – 666с

Приложение

Рис 39 а б в

Рис 40 а б рис41 а

Рис 41 б Рис 42 а б

Рис 43 а б в

Рис 44 а б в

рис 45 а б в

Рис 46 а б в

Рис 47 а б в

рис 48 а б в

рис 49 а б в

Рис 50 а б в

Рис 51 а б в

Рис 52 а б в

Рис 53 а б в

Рис 54 а б в

Рис 55а б в

Рис56 а б в

1Данкова И.Н. Элективный курс по математике: учебное пособие / И.Н. Данкова, Т.Е. Бондаренко, Л.Л. Емелина — М: 5 за знания, 2006. — 128 с.

2 Опираясь на: Гурский И.П. Графики сложных функций: пособие для учителей/ И.П Гурский. — М: Просвещение, 1968г – 215с.

Просмотров работы: 7047

Скачать материал

без ожидания

Скачать материал

без ожидания

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Построение графиков сложных функций
  Михеева Людмила Александровна, учитель математики
  .
  МБОУ НиколаевскаяСОШ, Зейский район

• 

  2 слайд

  Введение
  Цели и задачи
  Основная часть
  Основные результаты
  Список используемых ресурсов

  Содержание

• 

  3 слайд

  Умение строить графики функций и их читать, т. е. определять промежутки монотонности, экстремальные значения и другие характеристики функции по её графику,- важный элемент математической культуры. Во многих задачах график является лишь вспомогательным элементом решения.
  Построение графика сложной функции вида
  y = f(φ(x)) без использования производной можно осуществлять элементарными способами по некоторой схеме.
  Введение

• 

  4 слайд

  Схема построения графика сложной функции
  Построение графиков функций вида

  Построение графиков функций вида

  Построение графиков функций вида
  Основная часть

• 

  5 слайд

  Овладеть умением представлять сложную функцию в виде композиции двух функций
  Освоить приём построения эскиза графика функции без применения производной
  Показать возможность использования схемы построения графиков сложных функций вида y = f(φ(x))
  Цели и задачи

• 

  6 слайд

  Для построения графика функции любой сложности необходимо знать и применять свойства элементарных функций (область определения, нули функции, четность и нечетность, периодичность и т. д.).
  График сложной функции y = f(φ(x)) можно построить с помощью упрощенной схемы, если использовать операции над графиками (понимая под этим выполнение операций над соответствующими координатами).
  Основные результаты

• 

  7 слайд

  Гусев В.А., Мордкович А.Г. Математика: Справочные материалы. – М.: Просвещение, 1988
  Гурский И. П. Графики сложных функций
  Дворянинов С. В. О построении графиков сложных функций на основе свойства монотонности. Журнал «Математика в школе»
  Дорофеев Г.В. Пособие по математике для поступающих в вузы. – М.: Наука, 1972
  Костюкова Н.К. Научно-исследовательская работа учащихся. – М.: Математика в школе №5, 1999
  Райхмист Р.Б. Графики функций: задачи и упражнения. – М.: Школа – Пресс, 1997
  Рывкин А.А. Справочник по математике – М.: Высшая школа, 1987
  Факультативный курс по математике – М.: Просвещение, 1991
  http://mathem.by.ru/diff1.html
  Список ресурсов:

• 

  8 слайд

  Построение графиков функций вида

• 

  9 слайд

  Построение графиков функций вида

• 

  10 слайд

  Построение графиков функций вида

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

  30 слайд

  Найти область определения исследуемой сложной функции, а также граничные значения функции.
  Построить график функции у1 = φ(х). Отметить на этом графике характерные точки, т. е. нули и точки разрыва, найти граничные точки, одну – две промежуточные точки; (при выборе характерных точек функции φ(х) приходиться учитывать не только её свойства, но и свойства f(φ )).
  Произвести заданные операции над ординатами выбранных точек.
  Нанести полученные точки и предельные значения на рисунок, помещённый под графиком функции у1 = φ(х) так, чтобы у1 была продолжением оси у. Затем соединить полученные точки сплошной линией в тех промежутках, в которых функция непрерывна, и учесть (если она имеется) симметрию графика относительно точки или прямой.
  Схема построения графика сложной функции у = f(φ(x))

• 

  31 слайд

  Проблемный вопрос
  Можно ли построить графики сложных функций элементарными способами?

  вернуться

• 

  32 слайд

  В работе рассматриваются функции вида y = f(φ(x)), где φ(x) – любая из основных элементарных функций, а f – любая из следующих операций над ними: прибавление к функции какого-либо числа, умножение функции на число, деление единицы на функцию, возведение функции в положительную степень, извлечение корня из функции, нахождение показательной функции от функции, логарифмирование функции, нахождение модуля функции, нахождение тригонометрических функций от функции.
  Все указанные операции можно проводить непосредственно над графиками основных элементарных функций(понимая под этим выполнение операций над соответствующими координатами), поскольку эти графики известны. Как правило, график функции
  y = f(φ(x)) трудно, а порой и просто невозможно построить, используя общую схему исследования функции. В то же время эскиз такого графика легко нарисовать с помощью упрощенной схемы исследования, если использовать операции над графиками.

Краткое описание документа:

Умение строить графики функций и их читать, т. е. определять промежутки монотонности, экстремальные значения и другие характеристики функции по её графику,- важный элемент математической культуры. Во многих задачах график является лишь вспомогательным элементом решения. Построение графика сложной функции вида y = f(φ(x)) без использования производной можно осуществлять элементарными способами по некоторой схеме. Цели и задачи урок: овладеть умением представлять сложную функцию в виде композиции двух функций;

*  Освоить приём построения эскиза графика функции без применения производной;

*  Показать возможность использования схемы построения графиков сложных функций вида  y = f(φ(x)) 

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 257 666 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Сложные функции в задачах ЕГЭ

В преддверии очередного экзамена по математике на семинарах
учителей нередко речь заходит о том, на что следует обратить особое внимание
выпускников при подготовке к итоговой аттестации. Ответ на этот вопрос
непременно должен включать упоминание сложных функций и их графиков. Анализ
заданий ЕГЭ минувшего года показывает, что сложные функции служат основой многих
задач ЕГЭ. Для подтверждения этого тезиса рассмотрим задачи из одного реального
варианта ЕГЭ-2008.

С1. Найдите наибольшее значение функции

f (x) = 18(0,5x – 2)² – (0,5x
– 2)⁴ при | x – 5 | ≤ 3.

Решение. Данная функция является композицией двух
квадратичных функций — внутренней функции n(x)
= (0,5x – 2)² и внешней функции f(n)
= 18n
– n².

По условию первая функция рассматривается на отрезке 2
≤ x
≤ 8.
По графику этой квадратичной функции находим множество ее значений на отрезке
[2; 8]. Множество значений функции n(x) —
это отрезок 0 ≤ n ≤
4. На этом отрезке теперь рассмотрим функцию f(n).
Читая ее график, устанавливаем, что на отрезке [0; 4] эта функция монотонно
возрастает, поэтому ее множество значений — это отрезок [f(0); f(4)]
= [0; 56]. Отсюда получаем ответ: наибольшее значение данной функции равно 56.

Разумеется, предложенное решение не отменяет стандартное
решение этой задачи с использованием производной.

В4. Решите уравнение

Конечно, это уравнение заменой сводится к квадратному, у
которого следует найти неотрицательные корни. Но и здесь следует привлечь
внимание учащихся к функциональной стороне задачи.

График функции получается из графика в результате двух
преобразований. Следовательно, функция n(x)
является возрастающей. Сложная функция является возрастающей как суперпозиция
возрастающих функций.

Отсюда следует, что сумма двух возрастающих функций является
функцией возрастающей. Поэтому уравнение может иметь только один корень. Хорошо
известно, что в подобных случаях корень можно найти с любой степенью точности.
Для этого следует рассматривать отрезки, на концах которых выражение принимает
значения разных знаков. Разумеется, на экзамене это не самый быстрый способ
решения, но он безусловно важен при обучении математике.

С3. Найдите все значения a, при каждом из которых
неравенство

не имеет решения.

Естественный способ решения этой задачи такой. На плоскости
xOa следует изобразить множество точек, координаты которых удовлетворяют
этому неравенству. Это множество называется графиком этого неравенства. При этом
необходимо использовать свойства двух функций:

и

Своеобразной подсказкой к тому, чтобы рассмотреть эти две
функции, выступают в условии задачи четыре скобки (с формальных позиций эти
скобки являются абсолютно лишними!).

В учебнике [1] на с. 53 приведен график функции Если
представить эту функцию в виде то можно сказать, что ее график получается из
синусоиды y = sin x сжатием по оси x (при | x |
≤ 1)
или растяжением (при | x | ≥ 1)
с переменным коэффициентом

Аналогичным образом можно сказать, что график функции
получается из графика функции y = cos x сжатием или растяжением с
переменным коэффициентом

Заметим, что при решении этой задачи В4 не требуется столь
детального построения графика (хотя это и возможно). Достаточно знать множество
значений функции a₁(x) — отрезок [–6; –2].

Функция является суперпозицией двух функций:

внутренней n(x)
= log₂ x, где x [4; + ∞),

внешней где n [2; + ∞).

На экзамене, конечно, функцию a₂(ν)
следует исследовать с помощью производной, и затем график сложной функции a₂(x)
строится по методу из [3].

При обучении математике исследовать функцию a₂(ν)
и построить ее график можно без производной (см. [2] ).

При исследовании функции a₂(ν)
элементарными методами (без производной) полезно ее представление в виде

Графики функций a₁(x) и a₂(x)
делят плоскость xOa на три части. Данное неравенство задает на плоскости
точки (x; a), лежащие выше графика a₁(x)
(включая точки графика), и точки, лежащие ниже графика a₂(x).
Все такие точки образуют график неравенства. Ответ задачи составляют все те
значения параметра a, при каждом из которых соответствующая
горизонтальная прямая не пересекает график неравенства. В итоге получаем ответ —
промежуток

В пользу освоения выпускниками такого графического решения
задач с параметром говорит и задача В8 в демонстрационном варианте ЕГЭ-2009.
Рассмотрим ее аналог.

В8.  При каком значении параметра a уравнение имеет ровно три корня?

Уравнение равносильно совокупности

Отсюда

Объединение графиков этих двух функций на плоскости xOa
является графиком данного уравнения. Для решения задачи следует найти те
горизонтальные прямые, которые пересекают график уравнения в трех точках. В
итоге получаем ответ: a = –1.

С5 из рассматриваемого варианта ЕГЭ-2008 основана на
свойствах функции f(x), где

при x ≥ 5.

Дробно-линейная функция в 10-м классе служит хорошим
средством для повторения преобразований графиков. Кроме того, существует
доступный большинству учащихся практический способ рисования графика этой
функции по двум асимптотам и одной пробной точке (см. [5]).

Функция является суперпозицией возрастающей функции и
возрастающей
при x ≥ 5 дробно-линейной функции следовательно, функция f₁ также
возрастает.

Функция является суперпозицией возрастающей функции и
возрастающей при x ≥ 5 дробно-линейной функции следовательно, функция f₂ также
возрастает.

Отсюда следует, что сумма f₁ + f₂
является возрастающей при x ≥ 5 функцией.

В итоге график кусочной функции f(x), которая
лежит в основе данной задачи, может быть построен. Решение задачи получается в
результате чтения этого графика.

Итак, в четырех задачах одного варианта заданий ЕГЭ-2008
решение основано на использовании свойств функций и их графиков. По нашему
мнению, учитель математики должен учитывать это обстоятельство. А к нашим
ученикам, перефразируя классика, мы можем обратиться с таким призывом: «Любите
функции и их графики — основу решения многих сложных задач на ЕГЭ!»

Литература

1. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Алгебра и начала анализа: учеб. для 11 кл. общеобразоват.
учреждений: базовый и профильный уровни. — 6-е изд. — М.: Просвещение, 2007.
2. Дворянинов С.В., Розов Н.Х. Дробно-квадратичная
функция в школьном курсе математики // Математика в школе, 1997, № 4, с. 50–58.

3. Дворянинов С.В. Рисунок как графическое
представление свойств функции // Математика, 2007, № 8, с. 1–7.
4.  Дворянинов С.В. Как находить множество значений
функции // Математика, 2005, № 13, с. 23–25.
5. Дворянинов С.В. Дробно-линейная функция в
школьном курсе математики // Математика, 2000, № 5, с. 4–6.

Дворянинов С.