Цели урока:
- Проверка практических умений и навыков решения задач на составление
уравнения. - Активизация учебной деятельности учащихся путём общения в динамических
парах, когда каждый учит каждого. - Воспитывать ответственное отношение к учебному труду, развивать
логическое мышление, любознательность, умение проверять и оценивать
выполненную работу.
Коллективным способом обучения (А. Г. Ривин и В.К. Дьяченко) является такая
его организация, при которой обучение осуществляется путём общения в
динамических парах, когда каждый учит каждого.
Ход урока
I. Работа начинается с ввода или так называемого “запуска” раздела.
Обобщение и систематизация знаний по теме “ Задачи, решаемые с помощью
уравнения”.
Примеры задач:
1. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против
течения. Найдите собственную скорость теплохода, если скорость течения реки 2
км/ч.
Пусть собственная скорость теплохода – Х км/ч. Заполним таблицу значений трёх
величин.
| Скорость (км/ч) | Время (ч) | Расстояние (км) | |
| По течению | Х + 2 | 9 | 9(Х + 2) |
| Против течения | Х – 2 | 11 | 11(Х – 2) |
На основании условия задачи составим уравнение:
9(Х + 2) = 11(Х – 2), которое имеет единственный корень 20.
Собственная скорость теплохода 20 км/ч.
2. Увеличив среднюю скорость с 250 до300 м/мин, спортсменка стала пробегать
дистанцию на 1 мин быстрее. Какова длина дистанции?
Пусть Х мин – время, за которое спортсменка пробегала дистанцию со скоростью 300
м/мин, тогда Х +1 мин – время, за которое спортсменка пробегала дистанцию со
скоростью 250 м/мин. Составим уравнение:
250(Х + 1) = 300Х , которое имеет единственный корень 5.Найдём длину дистанции
300Х = 300×5 = 1500 м.
3. В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую.
Каждый час работы первая бригада расходовала 150 кг раствора, а вторая – 200кг.
Через 3 ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во
второй. Сколько раствора привезли в каждую бригаду?
Пусть в первую бригаду привезли Х кг раствора, тогда во вторую – Х + 50 кг.
Заполним таблицу значений величин для двух бригад:
| Привезли(кг) | Расход(кг)за 1 час | Время (ч) | Осталось раствора(кг) | |
| 1-я бригада | Х | 150 | 3 | Х – 450 |
| 2-я бригада | Х + 50 | 200 | 3 | Х + 50 – 600 |
По условию задачи в первой бригаде осталось раствора в 1,5 раза больше, чем
во второй. Составим уравнение:
Х – 450 = (Х + 50 – 600)×1,5 , имеющее единственный корень 750. 750 кг
раствора привезли в первую бригаду, а во вторую привезли 750 + 50 = 800 кг.
4. (Задача Э.Безу) По контракту работникам причитается 48 франков за каждый
отработанный день, а за каждый неотработанный день с них вычитается по 12
франков. Через 30 дней выяснилось, что работникам ничего не причитается. Сколько
дней они отработали в течение этих 30 дней?
Пусть работники отработали Х дней, тогда они не работали (30 – Х) дней. Составим
уравнение:
48Х – 12 (30 – Х) = 0.
Решив это уравнение, получим Х = 6, то есть они отработали 6 дней.
5. Книгу в 296 страниц ученик прочитал за три дня. Во второй день он прочитал
на 20% больше, чем в первый, а в третий – на 24 страницы больше, чем во второй.
Сколько страниц прочитал ученик в первый день?
Пусть в первый день ученик прочитал Х страниц, тогда во второй день ученик
прочитал Х + 0,2Х = 1,2Х страниц, а в третий день прочитал 1,2Х + 24. Составим
уравнение:
Х + 1,2Х +1,2Х + 24 = 296. Решив это уравнение, получим Х = 80, то есть ученик
прочитал в первый день 80 страниц.
6. На солнышке грелось несколько кошек. У них лап на 10 больше, чем ушей.
Сколько кошек грелось на солнышке?
Пусть грелось Х кошек, тогда у этих кошек 2Х ушей и 4Х лап. Составим уравнение:
4Х – 2Х = 10. Решив это уравнение, получим Х = 5,то есть 5 кошек грелось на
солнышке.
II. Самостоятельная работа учащихся.
Каждый ученик получает индивидуальную карточку с задачами. Правильность
решения проверяет преподаватель, при необходимости он оказывает помощь в
решении. После проверки ученику выставляется в оценочный лист плюс или оценка.
Примеры карточек для первой группы:
Карточка № 1.
1. (Старинная задача.) Послан человек из Москвы в Вологду и велено ему
проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан
другой человек и велено ему проходить по 45 вёрст в день. Через сколько дней
второй догонит первого?
2. Чтобы сделать вовремя заказ, артель стеклодувов должна была изготовлять в
день по 40 изделий. Однако она изготовляла ежедневно на 20 изделий больше и
выполнила заказ на 3 дня раньше срока. Каков был срок выполнения заказа?
Ответ: № 1 – 8 дней, № 2 – 9 дней.
Карточка № 2.
1. Кооператив наметил изготовить партию мужских сорочек за 8 дней. Выпуская в
день на 10 сорочек больше, чем предполагалось, он выполнил план за один день до
срока. Сколько сорочек в день должен был выпускать кооператив?
2. На ферме 1000 кроликов и кур, у них 3150 ног. Сколько кроликов и сколько
кур на ферме?
Ответ: № 1 – 70 сорочек, № 2 – 575 кроликов и 425 кур..
Карточка № 3.
1. Из пункта А вышла грузовая машина со скоростью 60км/ч. Через 2 ч вслед за
ней из пункта А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии
от пункта А легковая машина догонит грузовую?
2. Чтобы выполнить задание в срок, токарь должен изготавливать по 24 детали в
день. Однако он ежедневно перевыполнял норму на 15 деталей и уже за 6дней до
срока изготовил 21 деталь сверх плана. Сколько деталей изготовил токарь?
Ответ: № 1 – 360 км, № 2 – 408 деталей.
Карточка № 4.
1. От турбазы до привала туристы шли со скоростью 4,5км/ч, а возвращались на
турбазу со скоростью 4км/ч, затратив на обратный путь на 15 мин больше. На каком
расстоянии от турбазы был сделан привал?
2. На одном складе было 185 т угля, а на другом – 237 т. Первый склад стал
отпускать ежедневно по 15 т угля, а второй – по 18 т. Через сколько дней на
втором складе угля будет в полтора раза больше, чем на первом?
Ответ: № 1 – 9 км, № 2 – 9 дней.
Примеры карточек для второй группы:
Карточка № 5.
1. Из пункта А выехал велосипедист. Одновременно вслед за ним из пункта В ,
отстоящего от пункта А на расстоянии 60 км/ч, выехал мотоциклист. Велосипедист
ехал со скоростью 12 км/ч, а мотоциклист – со скоростью 30 км/ч. На каком
расстоянии от пункта А мотоциклист догонит велосипедиста?
2. Три бригады изготовили 65 деталей. Первая бригада изготовила на 10 деталей
меньше, чем вторая, а третья – 30% того числа деталей, которые изготовили первая
и вторая детали вместе. Сколько деталей изготовила каждая бригада?
Ответ: № 1 – 40 км, № 2 – 20, 30, 15 деталей.
Карточка № 6.
1. Расстояние между пристанями М и N равно 162 км. От пристани М отошёл
теплоход со скоростью 45 км/ч. Через 45 мин от пристани N навстречу ему отошёл
другой теплоход, скорость которого 36 км/ч. Через сколько часов после
отправления первого теплохода они встретятся?
2. Бригада рабочих должна была изготовить определённое количество деталей за
20 дней. Однако она ежедневно изготавливала на 70 деталей больше, чем
планировалось первоначально. Поэтому уже за 7 дней до срока ей осталось
изготовить 140 деталей. Сколько деталей должна была изготовить бригада?
Ответ: № 1 – 2
![]() ч, № 2 –
ч, № 2 –
3000 деталей.
Карточка № 7.
1. От пристани А отошел теплоход со скоростью 40 км/ч. Через 1
![]() ч вслед за
ч вслед за
ним отошёл другой теплоход со скоростью 60 км/ч. Через сколько часов после
своего отправления и на каком расстоянии от А второй теплоход догонит первый?
2. В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе
19 голов и 46 ног?
Ответ: № 1 – 2 ,5 ч; 150 км, № 2 – 4 овцы и15 кур.
Карточка № 8.
1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было
монет по 2 р.?
2. За 4 ч катер проходит по течению расстояние, в 2,4 раза большее, чем за 2
ч против течения. Какова скорость катера в стоячей воде, если скорость течения
1,5 км/ч?
Ответ: № 1 – 7 монет, № 2 – 16,5 км/ч.
Примеры карточек для третьей группы:
Карточка № 9.
1. Со станции М и N, расстояние между которыми 380 км, одновременно навстречу
друг другу вышли два поезда. Скорость поезда, отправившегося со станции N, была
больше скорости другого поезда на 5 км/ч. Через 2 ч после отправления поездам
оставалось пройти до встречи 30 км. Найдите скорость поездов.
2. В одном резервуаре 380 м³ воды, а в другом 1500 м³. В первый резервуар
каждый час поступает 80 м³ воды, а из второго каждый час выкачивают 60 м³. Через
сколько часов воды в резервуаре станет поровну?
Ответ: № 1 – 85 и 90км/ч, № 2 – 56 ч.
Карточка № 10.
1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было
монет по 2 р.?
2. Скашивая ежедневно по 60 га вместо 50 га, бригада сумела скосить луг на
один день быстрее, чем планировалось. Какова площадь луга?
Ответ: № 1 – 7 монет, № 2 – 300 га.
Карточка № 11.
1. (Старинная задача.) Летели галки, сели на палки: по две сядут – одна палка
лишняя, по одной сядут – одна галка лишняя. Сколько было галок и сколько палок?
2. Турист рассчитал, что если он будет идти к железнодорожной станции со
скоростью 4км/ч, то опоздает к поезду на полчаса, а если он будет идти со
скоростью 5км/ч, то придёт на станцию за 6 мин до отправления поезда. Какое
расстояние должен пройти турист?
Ответ: № 1 – 4 галки и 3 палки, № 2 – 12 км.
Карточка № 12.
1. (Задача С.А. Рачинского.) Я дал одному ученику 3 ореха, а всем остальным
по 5 . Если бы я всем дал по 4 ореха, у меня осталось бы 15. Сколько было
орехов?
2. К числу приписали справа нуль. Число увеличилось на 405. Найдите первое
число.
Ответ: № 1 – 83 ореха, № 2 – 45.
Раздел считается введённым в работу, если каждая карточка с заданиями
выполнена хотя бы одним учеником.
III. Работа в группах.
Затем работа классного коллектива выглядит так: организуется 3–4 группы по 4
человека (можно до 7 человек). В группе у каждого ученика своя карточка, за
которую ученик уже получил плюс или оценку в оценочный лист. Каждый в группе
выбирает партнёра, и они меняются карточками. Школьники работают в парах (решают
карточку своего партнера полностью), затем пары в группе меняются. Если
необходима помощь, то происходит взаимообучение. Если помощь не нужна, то после
выполнения задания происходит взаимопроверка и делается отметка в оценочный
лист. Потом пары меняются, и процесс продолжается до тех пор, пока каждый ученик
не выполнит задания других учеников группы. Затем подводится итог, и
выставляется общая оценка.
Оценочный лист.
| №1 | №2 | №3 | №4 | Итоговая оценка | |
| Лаптева Алина | 5 | ||||
| Борзенков Егор | 3 | ||||
| Мартышин Сергей | 4 | ||||
| Казакова Виктория | 3 |
По диагонали оценка выставлена учителем. За выполнение карточки № 1оценка
выставляется Лаптевой А., № 2 – Борзенковым Е., № 3 – Мартышиным С., № 4 –
Казаковой В..
Алгебра
7 класс
Урок № 44
Решение задач с помощью линейных уравнений
Перечень рассматриваемых вопросов:
• Линейные уравнения.
• Корень уравнения.
• Решение линейных уравнений.
• Текстовые задачи.
Тезаурус:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.
Решить уравнение – значит найти все его корни или установить, что их нет.
Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.
Математическая модель – математическое представление реальности, один из вариантов модели как системы, исследование которой позволяет получать информацию о некоторой другой системе.
Выражение – это совокупность чисел и букв, соединенных между собой различными знаками.
Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.
Свободный член – член уравнения, не содержащий неизвестного.
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
Решить уравнение – значит найти все его корни или установить, что их нет.
Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.
Математическая модель – математическое представление реальности, один из вариантов модели как системы, исследование которой позволяет получать информацию о некоторой другой системе.
Выражение – это совокупность чисел и букв, соединенных между собой различными знаками.
Линейное уравнение – уравнение вида ax = b, где x – переменная, a, b – некоторые числа.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Мы уже рассматривали примеры функциональных зависимостей между величинами как математические модели реальных процессов. Теперь рассмотрим текстовые задачи, математическими моделями которых являются линейные уравнения и уравнения, сводящиеся к линейным.
Решить задачу можно с помощью системы уравнений, а можно с помощью одного уравнения. Рассмотрим на примере задачи.
Задача 1.
Из города А в город В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 15 км/ч, а вторую половину пути – со скоростью 90 км/ч, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 54 км/ч. Ответ дайте в км/ч.
При решения текстовых задач эффективно построение схем и составление таблиц.
Используя сравнение скоростей, указанное в задаче, и обозначая скорость первого автомобиля икс, запишем скорость второго автомобиля на протяжении всего пути:
Скорость первого автомобиля: x, скорость второго автомобиля: x – 15x – 15/
Теперь заполним вспомогательную таблицу.

Условие, что автомобили прибыли в пункт назначения одновременно, используем для составления уравнения. Выражаем время первого автомобиля, которое он затратил на весь путь, через x.
Время первого автомобиля:

Время второго автомобиля:


Сократим на S ≠ 0 и умножим на 2.

Умножим обе части на 90x(x – 15), получим:

Решением уравнения будут корни:
x1 = 60, x2 = 45.
Условию уравнения удовлетворяет только x = 60
Ответ: 60 км/ч – скорость первого автомобиля.
Составим алгоритм решения текстовых задач при помощи уравнений.
Решать задачу с помощью уравнения следует в такой последовательности:
1) обозначить переменной одну из неизвестных величин;
2) другие неизвестные величины (если они есть) выразить через введенную переменную;
3) по условию задачи установить соотношение между неизвестными и известными значениями величин и составить уравнение;
4) решить полученное уравнение;
5) проанализировать решение уравнения и найти неизвестную величину, а при необходимости и значения остальных неизвестных величин;
6) записать ответ к задаче.
Дополнительный материал.
Решите задачу двумя способами.
В первый день со склада было отпущено 20% имевшихся груш. Во второй день 180% от того количества груш, которое было отпущено в первый день. В третий день ‑ оставшиеся 88 кг. Сколько кг груш было на складе первоначально?
Разберем 2 способа решения этой задачи.
Для первого способа составим вспомогательную таблицу:
Значит, первоначально было 200 кг груш.
2 способ.
Составим вспомогательную аблицу:


Ответ: 200 кг груш.
Разбор заданий тренировочного модуля.
Задание 1. Запишите выражение для нахождения цены 1 кг сахара (в руб.), если n тонн сахара стоят m рублей.
Решение:
Для решения задачи, вспомним, сколько килограммов содержится в одной тонне:
1 т = 1000 кг.
Следовательно, получаем:
n т = 1000n кг
Так как стоимость n тонн сахара = m рублей, то, чтобы найти, сколько стоит 1 кг сахара, нужно стоимость разделить на количество:
m : 1000n
Ответ:

Задание 2.
Цена персиков на 30 р. выше, чем цена абрикосов. Для консервирования компота купили 5 кг персиков и 7 кг абрикосов. По какой цене покупали фрукты, если вся покупка обошлась 850 рублей?
Решение:
Пусть цена абрикосов – x рублей. Тогда x + 20x + 20 – цена персиков.
Всего купили персиков: 5(x + 30) и абрикосов 7x.
Так как на всю покупку затратили 850 руб., имеем выражение:
5(x + 30) + 7x = 850
Раскроем скобки: 5x + 150 + 7x = 850
Перенесем слагаемые, не содержащие переменной, в правую часть, меняя знак на противоположный:
5x + 7x = 850 – 150
Приведём подобные слагаемые:
12x = 700
Поделим обе части уравнения на 12:

Получаем: цена абрикосов равна:

Следовательно, цена персиков равна:

Проверим полученное решение:

850 = 850
Ответ:
цена абрикосов равна:

цена персиков равна:

Следовательно, полученное решение верно.
Онлайн. Глава 1. Линейное уравнение с одной переменной. § 3. Решение задач с помощью уравнений. Упражнения №№ 3.1 — 3.53. Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф (Российский учебник). Электронная ознакомительная версия для покупки пособия. Цитаты из книги использованы в учебных целях.
Алгебра 7 класс Мерзляк, Поляков (угл.изуч.)
Предыдущая тема ОГЛАВЛЕНИЕ Следующая тема
§ 3. Решение задач с помощью уравнений.
Вам неоднократно приходилось решать задачи с помощью составления уравнений. Разнообразие решённых задач является лучшим подтверждением эффективности и универсальности этого метода. В чём же заключается секрет его силы?
Дело в том, что условия непохожих друг на друга задач удаётся записать математическим языком. Полученное уравнение — это результат перевода условия задачи с русского языка на математический.
Часто условие задачи представляет собой описание какой–то реальной ситуации. Составленное по условию уравнение называют математической моделью ситуации.
Конечно, чтобы получить ответ, уравнение надо решить. Для этого в алгебре разработаны различные методы и приёмы. С некоторыми из них вы уже знакомы, многие другие вам ещё предстоит изучить.
Найденный корень уравнения — это ещё не ответ задачи. Следует выяснить, не противоречит ли полученный результат реальной ситуации, описанной в условии задачи.
Рассмотрим, например, такие задачи.
1) За 4 ч собрали 6 кг ягод, причём каждый час собирали одинаковое по массе количество ягод. Сколько ягод собирали за один час?
2) Несколько мальчиков собрали 6 кг ягод. Каждый из них собрал по 4 кг. Сколько мальчиков собирали ягоды?
По условию этих задач можно составить одно и то же уравнение 4х = б, корнем которого является число 1,5. Но в первой задаче ответ «полтора килограмма ягод за час» является приемлемым, а во второй ответ «ягоды собирали полтора мальчика» — нет. Поэтому вторая задача не имеет решений.
При решении задач на составление уравнений удобно придерживаться такой последовательности действий.
⊕ ⇒ 1. По условию задачи составить уравнение (сконструировать математическую модель задачи).
2. Решить полученное уравнение.
3. Выяснить, соответствует ли найденный корень смыслу задачи, и записать ответ.
Эту последовательность действий, состоящую из трёх шагов, можно назвать алгоритмом решения текстовых задач.
ПРИМЕР 1. Рабочий должен был выполнить заказ за 8 дней. Однако, изготавливая ежедневно 12 деталей сверх нормы, он уже за б дней работы не только выполнил заказ, но и изготовил дополнительно 22 детали. Сколько деталей ежедневно изготавливал рабочий?
Решение. Пусть рабочий изготавливал ежедневно х деталей. Тогда по плану он должен был изготавливать ежедневно (х– 12) деталей, а всего их должно было быть изготовлено 8(х– 12). На самом деле он изготовил 6х деталей.
Так как по условию значение выражения 6х на 22 больше значения выражения 8(х – 12), то получаем уравнение:
6х – 22 = 8(х – 12).
Тогда 6х – 22 = 8х – 96;
6х – 8х = –96 + 22;
—2х = –74;
х = 37.
Ответ: 37 деталей. ■
ПРИМЕР 2. Велосипедист проехал 65 км за 5 ч. Часть пути он ехал со скоростью 10 км/ч, а оставшийся путь — со скоростью 15 км/ч. Сколько времени он ехал со скоростью 10 км/ч и сколько — со скоростью 15 км/ч?
Решение. Пусть велосипедист ехал х ч со скоростью 10 км/ч. Тогда со скоростью 15 км/ч он ехал (5 – х) ч. Первая часть пути составляет 10х км, а вторая — 15(5 – х) км. Всего велосипедист проехал 10х + 15(5 – х) км. Поскольку весь путь составил 65 км, то получаем уравнение:
10х + 15(5 – х) = 65.
Отсюда 10х + 75 – 15х = 65;
–5х = –10; х = 2.
Следовательно, со скоростью 10 км/ч он ехал 2 ч, а со скоростью 15 км/ч — 3 ч.
Ответ: 2 ч, 3 ч. ■
Предыдущая тема ОГЛАВЛЕНИЕ Следующая тема
Вы смотрели: Ознакомительная версия для принятия решения о покупке книги: Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник). 3. Решение задач с помощью уравнений.
Алгоритм решения задачи с помощью системы линейных уравнений
- Обозначить неизвестные величины переменными («от смысла к буквам»).
- По условию задачи записать уравнения, связывающие обозначенные переменные.
- Решить полученную систему уравнений.
- Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Например:
Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.
Шаг 1
«От смысла к буквам»:
Пусть x и y – задуманные числа.
Шаг 2
Уравнения по условию задачи::
${left{ begin{array}{c} x-y = 10 \ x+2y = 91 end{array} right.}$
Шаг 3
Решение системы уравнений:
$(-) {left{ begin{array}{c} x-y = 10 \ x+2y = 91 end{array} right.} Rightarrow {left{ begin{array}{c} -3y = -81 \ x = y+10 end{array} right.} Rightarrow$
$ Rightarrow {left{ begin{array}{c} x = 37 \ y = 27 end{array} right.} $
Шаг 4
«От букв к смыслу»:
Задуманы числа 37 и 27.
Примеры
Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.
Найдите стороны прямоугольника.
Пусть a и b – длина и ширина прямоугольника.
По условию:
$$ {left{ begin{array}{c} P = 2(a+b) = 48 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} a+b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} 3b+b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} 4b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} a = 18 \ b = 6 end{array} right.} $$
Ответ: длина прямоугольника 18 см, ширина 6 см.
Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?
Пусть x – ежедневное количество строк для 1-го программиста, y- для 2-го.
По условию:
$$ {left{ begin{array}{c} 70x+100y = 100500 |:10 \ 30x-30y = 5550 |:30 end{array} right.} (-) Rightarrow {left{ begin{array}{c} 7x+10y = 10050 \ x-y=185 | times 10 end{array} right.}$$
$$ Rightarrow (+) {left{ begin{array}{c} 7x+10y = 10050 \ 10x-10y = 1850 end{array} right.} Rightarrow {left{ begin{array}{c} 17x = 11900 \ y = x-185 end{array} right.} Rightarrow {left{ begin{array}{c} x = 700 \ y = 515 end{array} right.} $$
Ответ: 700 строк и 515 строк
Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?
Пусть x – цена за 1 кг конфет, y – за 1 кг печенья.
По условию:
$$ {left{ begin{array}{c} 2x+3y = 1540 \ 2y-x = 210 | times 2 end{array} right.} Rightarrow (+) {left{ begin{array}{c} 2x+3y = 1540 \ -2x+4y = 420 end{array} right.} Rightarrow {left{ begin{array}{c} 7y = 1960 \ x = 2y-210 end{array} right.} Rightarrow {left{ begin{array}{c} x = 350 \ y = 280 end{array} right.} $$
Ответ: 1 кг конфет – 350 руб. и 1 кг печенья – 280 руб.
Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.
Пусть v – скорость катера (км/ч), u – скорость течения (км/ч).
По условию:
$$ {left{ begin{array}{c} 3(v-u)+2(v+u) = 73 \ 4(v+u)-3(v-u) = 29 end{array} right.} Rightarrow {left{ begin{array}{c} 3v-3u+2v+2u = 73 \ 4v+4u-3v+3u = 29 end{array} right.}$$
$$ Rightarrow {left{ begin{array}{c} 5v-u = 73 \ v+7u = 29 end{array} right.} Rightarrow {left{ begin{array}{c} 5(29-7u)-u = 73 \ v = 29-7u end{array} right.} Rightarrow {left{ begin{array}{c} 145-35u-u = 73 \ v = 29-7u end{array} right.} Rightarrow$$
$$ Rightarrow {left{ begin{array}{c} -36u = -72 \ v = 29-7u end{array} right.} Rightarrow {left{ begin{array}{c} v = 15 \ u = 2 end{array} right.} $$
Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч
Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.
Пусть x – первоначальная цена карандаша, y – тетрадки.
По условию:
$$ {left{ begin{array}{c} 5x+3y = 170 \ 3cdot0,8x+5cdot1,3y = 284 end{array} right.} Rightarrow {left{ begin{array}{c} 5x+3y = 170 |times frac{2,4}{5} \ 2,4x+6,5y = 284 end{array} right.} Rightarrow (-) {left{ begin{array}{c} 2,4x+1,44y = 81,6 \ 2,4x+6,5y = 284 end{array} right.} $$
$$ Rightarrow {left{ begin{array}{c} (6,5-1,44)y = 284-81,6 \ x = frac{170-3y}{5} end{array} right.}Rightarrow {left{ begin{array}{c} y = 202,4:5,06 = 40 \ x = frac{170-120}{5} = 10 end{array} right.} $$
Ответ: карандаш сначала стоил 10 руб., тетрадка – 40 руб.
Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.
Пусть v – обычная скорость велосипедиста (км/ч), t – обычное время (ч).
Расстояние между А и В неизменно, и по условию равно:
$$ s_{AB} = vt = (v+3)(t-1) = (v-2)(t+1) $$
Получаем систему:
$$ {left{ begin{array}{c} vt = (v+3)(t-1) \ vt = (v-2)(t+1) end{array} right.} Rightarrow (-) {left{ begin{array}{c} vt = vt-v+3t-3 \ vt = vt+v-2t-2 end{array} right.} Rightarrow (+) {left{ begin{array}{c} v-3t = -3 \ -v+2t = -2 end{array} right.} Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} -t = -5 \ v = 2t+2 end{array} right.} Rightarrow {left{ begin{array}{c} t = 5 \ v = 12 end{array} right.} $$
Ответ: обычная скорость 12 км/ч, время 5 ч
Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.
Пусть x – объём первой бочки (л), y – объём второй (л).
Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:
$$ (+) {left{ begin{array}{c} 12+a = x \ 32-a = frac{1}{2} y end{array} right.} Rightarrow x+ frac{1}{2} y = 44 $$
Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:
$$ (+) {left{ begin{array}{c} 32+b = y \ 12-b = frac{1}{6} x end{array} right.} Rightarrow frac{1}{6}x+y = 44 $$
Получаем систему:
$$ {left{ begin{array}{c} x+ frac{1}{2} y = 44 | times 2 \ frac{1}{6} x+y = 44 end{array} right.} Rightarrow (-) {left{ begin{array}{c} 2x+y = 88 \ frac{1}{6} x+y = 44 end{array} right.} Rightarrow (+) {left{ begin{array}{c} 1frac{5}{6} x = 44 \ y = 88-2x end{array} right.} Rightarrow $$
$$ {left{ begin{array}{c} x = 44: frac{11}{6} = 44cdot frac{6}{11} = 24 \ y = 88-2cdot24 = 40 end{array} right.} $$
Ответ: первая бочка 24 л, вторая – 40 л
Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?
Пусть s – расстояние между домом и школой, v – скорость автобуса, u – скорость школьника, t – искомое время, потраченное на дорогу туда и обратно пешком.
По условию задачи:
$$ {left{ begin{array}{c} 1,5 = frac{s}{v} + frac{s}{u} \ 0,5 = frac{2s}{v} \ t = frac{2s}{u} end{array} right.} $$
Из второго уравнения $ frac{s}{v} = frac{0,5}{2} = 0,25 $. Подставляем в первое уравнение:
$$ frac{s}{u} = 1,5-frac{s}{v} = 1,5-0,25 = 1,25 $$
И тогда искомое время:
$$ t = frac{2s}{v} = 2cdot1,25 = 2,5 (ч) $$
Ответ: 2,5 ч
Решение задачи обычно свóдится к тому, чтобы путем логических рассуждений и вычислений найти значение какой-нибудь величины. Например, найти скорость, время, расстояние, массу какого-нибудь предмета или количество чего-то.
Такую задачу можно решить с помощью уравнения. Для этого искомое значение обозначают через переменную, затем путем логических рассуждений составляют и решают уравнение. Решив уравнение, производят проверку на то, удовлетворяет ли решение уравнения условиям задачи.
Запись выражений, содержащих неизвестное
Решение задачи сопровождается составлением уравнения к этой задаче. На начальном этапе изучения задач желательно научиться составлять буквенные выражения, описывающие ту или иную жизненную ситуацию. Этот этап не является сложным и его можно изучать в процессе решения самой задачи.
Рассмотрим несколько ситуаций, которые можно записать с помощью математического выражения.
Задача 1. Возраст отца x лет. Мама на два года младше. Сын младше отца в 3 раза. Запишите возраст каждого с помощью выражений.
Решение:
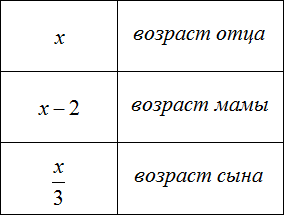
Задача 2. Возраст отца x лет, мама на 2 года младше отца. Сын младше отца в 3 раза, дочь младше матери в 3 раза. Запишите возраст каждого с помощью выражений.
Решение:
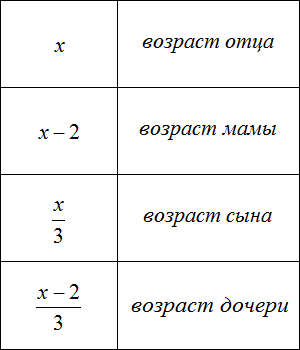
Задача 3. Возраст отца x лет, мама на 3 года младше отца. Сын младше отца в 3 раза, дочь младше матери в 3 раза. Сколько лет каждому, если общий возраст отца, мамы, сына и дочери составляет 92 года?
Решение:
В данной задаче помимо записи выражений, необходимо вычислить возраст каждого члена семьи.
Сначала запишем возраст каждого члена семьи с помощью выражений. За переменную x примем возраст отца, и далее пользуясь этой переменной составим остальные выражения:
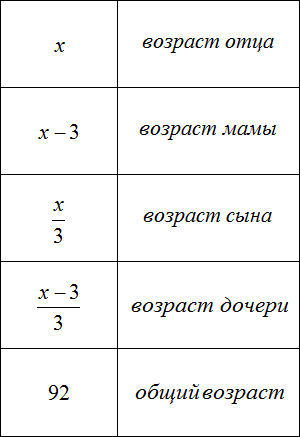
Теперь определим возраст каждого члена семьи. Для этого нам нужно составить и решить уравнение. Все компоненты уравнения у нас уже готовы. Осталось только собрать их воедино.
Общий возраст в 92 года получился путем сложения возрастов папы, мамы, сына и дочери:
![]()
Для каждого возраста мы составили математическое выражение. Эти выражения и будут компонентами нашего уравнения. Давайте соберем наше уравнение согласно данной схеме и таблице, которая была приведена выше. То есть слова папа, мама, сын, дочь заменим на соответствующее им в таблице выражение:
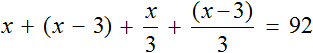
Выражение, отвечающее за возраст мамы x − 3, для наглядности было взято в скобки.
Теперь решим получившееся уравнение. Для начала можно раскрыть скобки там, где это можно:
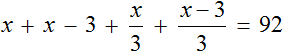
Чтобы освободить уравнение от дробей, умножим обе части на 3
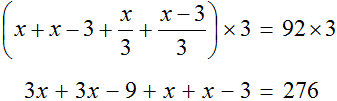
Решим получившееся уравнение, пользуясь известными тождественными преобразованиями:
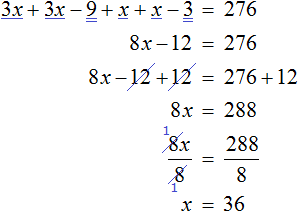
Мы нашли значение переменной x. Эта переменная отвечала за возраст отца. Значит возраст отца составляет 36 лет.
Зная возраст отца, можно вычислить возрасты остальных членов семьи. Для этого нужно подставить значение переменной x в те выражения, которые отвечают за возраст конкретного члена семьи.
В задаче было сказано, что мама на 3 года младше отца. Ее возраст мы обозначили через выражение x−3. Значение переменной x теперь известно, и чтобы вычислить возраст мамы, нужно в выражении x − 3 вместо x подставить найденное значение 36
x − 3 = 36 − 3 = 33 года маме.
Аналогично определяется возраст остальных членов семьи:
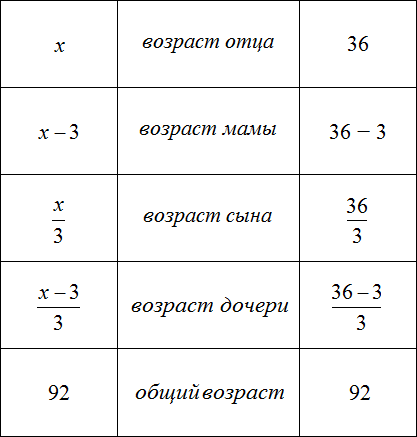
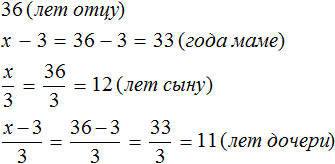
Проверка:
![]()
Задача 4. Килограмм яблок стоит x рублей. Запишите выражение, вычисляющее сколько килограмм яблок можно купить на 300 рублей.
Решение
Если килограмм яблок стоит x рублей, то на 300 рублей можно купить ![]() килограмм яблок.
килограмм яблок.
Пример. Килограмм яблок стоит 50 рублей. Тогда на 300 рублей можно купить ![]() , то есть 6 килограмм яблок.
, то есть 6 килограмм яблок.
Задача 5. На x рублей было куплено 5 кг яблок. Запишите выражение, вычисляющее сколько рублей стоит один килограмм яблок.
Решение
Если за 5 кг яблок было уплачено x рублей, то один килограмм будет стоит ![]() рублей
рублей
Пример. За 300 рублей было куплено 5 кг яблок. Тогда один килограмм яблок будет стоит ![]() , то есть 60 рублей.
, то есть 60 рублей.
Задача 6. Том, Джон и Лео на перемене пошли в столовую и купили по бутерброду и по кружке кофе. Бутерброд стоит x рублей, а кружка кофе — 15 рублей. Определите стоимость бутерброда, если известно, что за всё было уплачено 120 рублей?
Решение
Конечно, данная задача проста как три копейки и ее можно решить не прибегая к уравнению. Для этого из 120 рублей нужно вычесть стоимость трех кружек кофе (15 × 3), и полученный результат разделить на 3
![]()
Но наша цель — составить уравнение к задаче и решить это уравнение. Итак, стоимость бутерброда x рублей. Куплено их всего три. Значит увеличив стоимость в три раза, мы получим выражение описывающее сколько рублей было уплачено за три бутерброда
3x — стоимость трех бутербродов
А стоимость трех кружек кофе можно записать как 15 × 3. 15 это стоимость одной кружки кофе, а 3 множитель (Том, Джон и Лео), увеличивающий эту стоимость в три раза.
По условию задачи за все уплачено 120 рублей. У нас уже появляется примерная схема, что нужно делать:

Выражения, описывающие стоимость трех бутербродов и трех кружек кофе, у нас уже готовы. Это выражения 3x и 15 × 3. Пользуясь схемой составим уравнение и решим его:
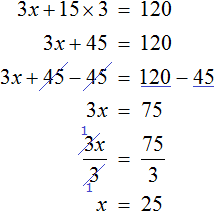
Итак, стоимость одного бутерброда составляет 25 рублей.
Задача решается верно только в том случае, если уравнение к ней составлено правильно. В отличие от обычных уравнений, по которым мы учимся находить корни, уравнения для решения задач имеют своё конкретное применение. Каждый компонент такого уравнения может быть описан в словесной форме. Составляя уравнение, обязательно нужно понимать для чего мы включаем в его состав тот или иной компонент и зачем он нужен.
Также необходимо помнить, что уравнение это равенство, после решения которого левая часть должна будет равняться правой части. Составленное уравнение не должно противоречить этой идее.
Представим, что уравнение это весы с двумя чашами и экраном, показывающим состояние весов.
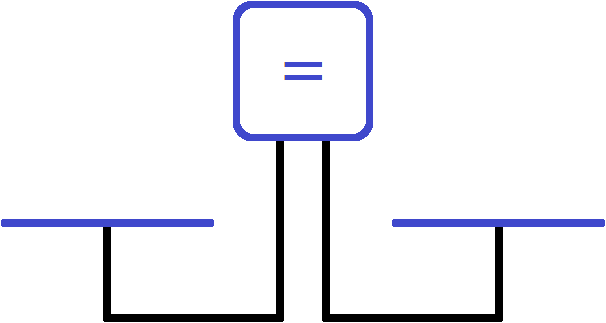
В данный момент экран показывает знак равенства. Понятно почему левая чаша равна правой чаше — на чашах ничего нет. Состояние весов и отсутствие на чашах чего-либо запишем с помощью следующего равенства:
0 = 0
Положим на левую чашу весов арбуз:
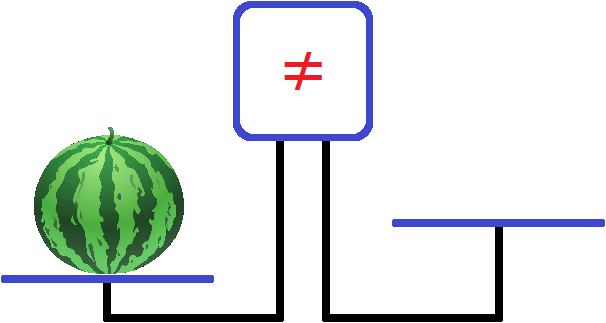
Левая чаша перевесила правую чашу и экран забил тревогу, показав знак не равно ( ≠ ). Этот знак говорит о том, что левая чаша не равна правой чаше.
Теперь попробуем решить задачу. Пусть требуется узнать сколько весит арбуз, который лежит на левой чаше. Но как это узнать? Ведь наши весы предназначены только для проверки равна ли левая чаша правой.
На помощь приходят уравнения. Вспомним, что уравнение по определению есть равенство, содержащее в себе переменную значение которой требуется найти. Весы в данном случае играют роль этого самого уравнения, а масса арбуза это переменная, значение которой нужно найти. Наша цель правильно составить это уравнение. Понимай, выровнять весы так, чтобы можно было вычислить массу арбуза.
Чтобы выровнять весы, на правую чашу можно положить какой-нибудь тяжелый предмет. Например, положим туда гирю массой 7 кг.
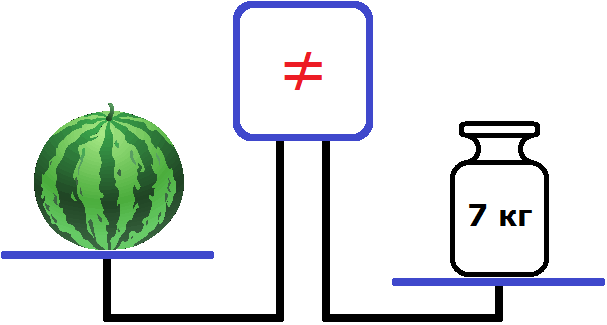
Теперь наоборот правая чаша перевесила левую. Экран по прежнему показывает, что чаши не равны.
Попробуем на левую чашу положить гирю массой 4 кг
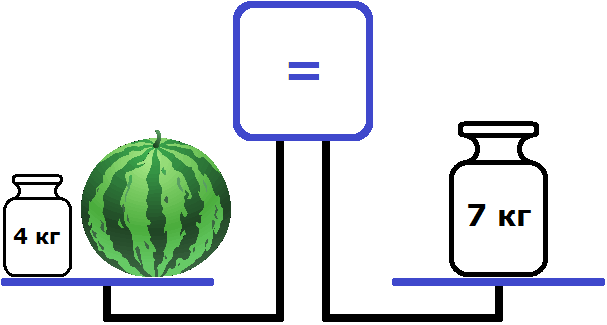
Теперь весы выровнялись. На рисунке видно, что левая чаша на уровне правой чаши. А экран показывает знак равенства. Этот знак говорит о том, что левая чаша равна правой чаше.
Таким образом мы получили уравнение — равенство, содержащее неизвестное. Левая чаша — это левая часть уравнения, состоящая из компонентов 4 и переменной x (массы арбуза), а правая чаша — это правая часть уравнения, состоящая из компонента 7.
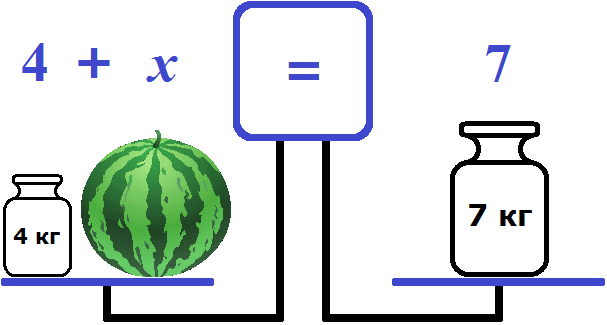
Ну и нетрудно догадаться, что корень уравнения 4 + x = 7 равен 3. Значит масса арбуза равна 3 кг.
Аналогично дела обстоят и с другими задачами. Чтобы найти какое-нибудь неизвестное значение, к левой или к правой части уравнения добавляют различные элементы: слагаемые, множители, выражения. В школьных задачах эти элементы бывают уже даны. Остается только правильно структурировать их и построить уравнение. Мы же в данном примере занимались подбором, пробуя гири разной массы, чтобы вычислить массу арбуза.
Естественно, те данные которые даны в задаче сначала нужно привести к виду, при котором их можно включить в уравнение. Поэтому, как говорят «хочешь не хочешь, а думать придётся».
Рассмотрим следующую задачу. Возраст отца равен возрасту сына и дочери вместе. Сын вдвое старше дочери и на двадцать лет моложе отца. Сколько лет каждому?
Возраст дочери можно обозначить через x. Если сын вдвое старше дочери, то его возраст будет обозначаться как 2x. В условии задачи сказано, что вместе возраст дочери и сына равен возрасту отца. Значит возраст отца будет обозначаться суммой x + 2x
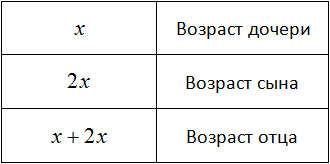
В выражении ![]() можно привести подобные слагаемые. Тогда возраст отца будет обозначаться как 3x
можно привести подобные слагаемые. Тогда возраст отца будет обозначаться как 3x
Теперь составим уравнение. Нам нужно получить равенство в котором можно найти неизвестное x. Воспользуемся весами. На левую чашу положим возраст отца (3x), а на правую чашу возраст сына (2x)
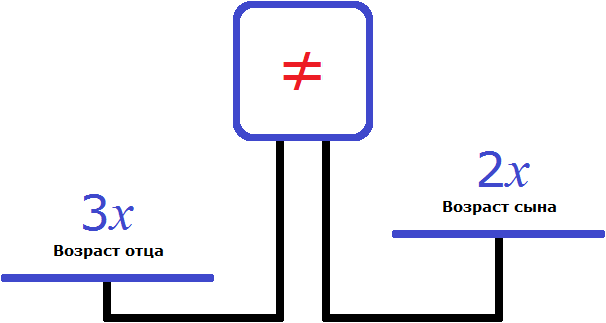
Понятно почему левая чаша перевесила правую и почему экран показывает знак ( ≠ ). Ведь логично, что возраст отца больше возраста сына.
Но нам нужно уравнять весы, чтобы можно было вычислить неизвестное x. Для этого к правой чаше нужно прибавить какое-нибудь число. Какое именно число указано в задаче. В условии было сказано, что сын моложе отца на 20 лет. Значит 20 лет это то самое число, которое нужно положить на весы.
Весы выровнятся, если мы эти 20 лет добавим на правую чашу весов. Иными словами, вырастим сына до возраста отца
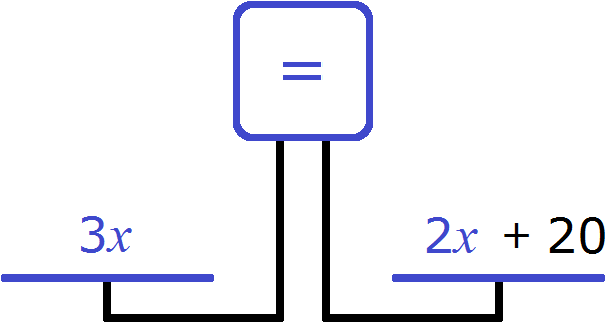
Теперь весы выровнялись. Получилось уравнение ![]() , которое решается легко:
, которое решается легко:
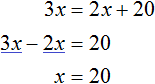
В начале решения данной задачи через переменную x мы обозначили возраст дочери. Теперь мы нашли значение этой переменной. Дочери 20 лет.
Далее было сказано, что сын двое старше дочери, значит сыну (20 × 2), то есть 40 лет.
Ну и наконец вычислим возраст отца. В задаче было сказано, что он равен сумме возрастов сына и дочери, то есть (20 + 40) лет.
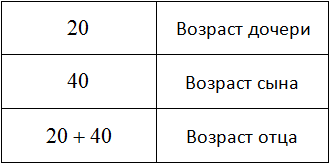
Вернемся к середине задачи и обратим внимание на один момент. Когда мы положили на весы возраст отца и возраст сына, левая чаша перевесила правую

Но мы решили эту проблему, добавив на правую чашу еще 20 лет. В результате весы выровнялись и мы получили равенство ![]()

Но можно было не добавлять к правой чаше эти 20 лет, а вычесть их из левой. Мы получили бы равенство и в таком случае
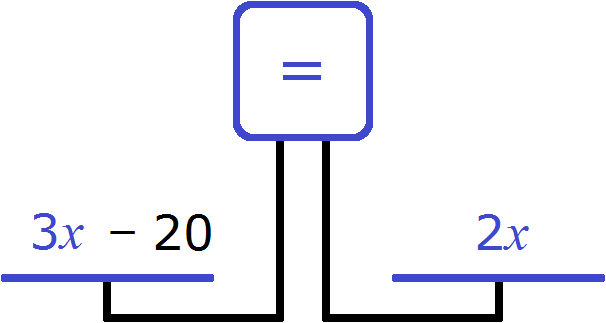
В этот раз получается уравнение ![]() . Корень уравнения по прежнему равен 20
. Корень уравнения по прежнему равен 20
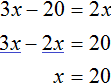
То есть уравнения ![]() и
и ![]() являются равносильными. А мы помним, что у равносильных уравнений корни совпадают. Если внимательно посмотреть на эти два уравнения, то можно увидеть что второе уравнение получено путем переноса числа 20 из правой части в левую с противоположным знаком. А это действие, как было указано в предыдущем уроке, не меняет корней уравнения.
являются равносильными. А мы помним, что у равносильных уравнений корни совпадают. Если внимательно посмотреть на эти два уравнения, то можно увидеть что второе уравнение получено путем переноса числа 20 из правой части в левую с противоположным знаком. А это действие, как было указано в предыдущем уроке, не меняет корней уравнения.
Также нужно обратить внимание на то, что в начале решения задачи возрасты каждого члена семьи можно было обозначить через другие выражения.
Скажем возраст сына обозначить через x и поскольку он двое старше дочери, то возраст дочери обозначить через ![]() (понимай сделать её младше сына в два раза). А возраст отца поскольку он является суммой возрастов сына и дочери обозначить через выражение
(понимай сделать её младше сына в два раза). А возраст отца поскольку он является суммой возрастов сына и дочери обозначить через выражение ![]() . Ну и напоследок для построения логически правильного уравнения, к возрасту сына нужно прибавить число 20, ведь отец старше на двадцать лет. В итоге получается совсем другое уравнение
. Ну и напоследок для построения логически правильного уравнения, к возрасту сына нужно прибавить число 20, ведь отец старше на двадцать лет. В итоге получается совсем другое уравнение ![]() . Решим это уравнение
. Решим это уравнение
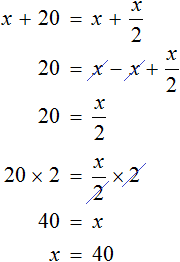
Как видно ответы к задаче не поменялись. Сыну по прежнему 40 лет. Дочери по прежнему ![]() лет, а отцу 40 + 20 лет.
лет, а отцу 40 + 20 лет.
Другими словами, задача может решаться различными методами. Поэтому не следует отчаиваться, что не получается решить ту или иную задачу. Но нужно иметь ввиду, что существует наиболее простые пути решения задачи. К центру города можно доехать различными маршрутами, но всегда существует наиболее удобный, быстрый и безопасный маршрут.
Примеры решения задач
Задача 1. В двух пачках всего 30 тетрадей. Если бы из первой пачки переложили во вторую 2 тетради, то в первой пачке стало бы вдвое больше тетрадей, чем во второй. Сколько тетрадей было в каждой пачке?
Решение
Обозначим через x количество тетрадей, которое было в первой пачке. Если всего тетрадей было 30, а переменная x это количество тетрадей из первой пачке, то количество тетрадей во второй пачке будет обозначаться через выражение 30 − x. То есть от общего количества тетрадей вычитаем количество тетрадей из первой пачки и тем самым получаем количество тетрадей из второй пачки.

Далее сказано, что если переложить 2 тетради из первой пачки во вторую, то в первой пачке окажется вдвое больше тетрадей. Итак, снимем с первой пачки две тетради
![]()
и добавим эти две тетради во вторую пачку
![]()
Выражения из которых мы будем составлять уравнение теперь принимают следующий вид:

Попробуем составить уравнение из имеющихся выражений. Положим на весы обе пачки тетрадей
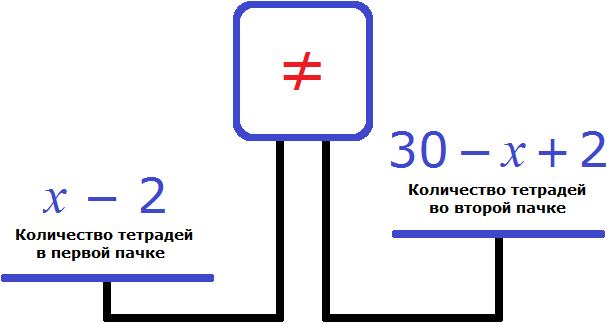
Левая чаша тяжелее правой. Это потому, что в условии задачи сказано, что после того как из первой пачки взяли две тетради и положили их во вторую, количество тетрадей в первой пачке стало вдвое больше, чем во второй.
Чтобы выровнять весы и получить уравнение, увеличим правую часть вдвое. Для этого умножим её на 2
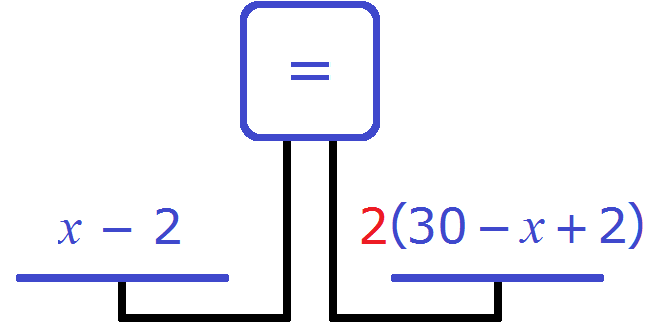
Получается уравнение ![]() . Решим данное уравнение:
. Решим данное уравнение:
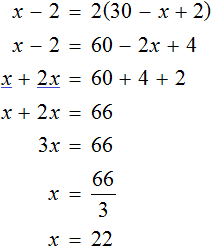
Первую пачку мы обозначали через переменную x. Теперь мы нашли её значение. Переменная x равна 22. Значит в первой пачке было 22 тетради.
А вторую пачку мы обозначали через выражение 30 − x и поскольку значение переменой x теперь известно, то можно вычислить количество тетрадей во второй пачке. Оно равно 30 − 22, то есть 8 шт.
Задача 2. Два человека чистили картофель. Один очищал в минуту две картофелины, а второй — три картофелины. Вместе они очистили 400 шт. Сколько времени работал каждый, если второй проработал на 25 минут больше первого?
Решение
Обозначим через x время работы первого человека. Поскольку второй человек проработал на 25 минут больше первого, то его время будет обозначаться через выражение ![]()
Первый рабочий в минуту очищал 2 картофелины, и поскольку он работал x минут, то всего он очистил 2x картофелин.
Второй человек в минуту очищал три картофелины, и поскольку он работал ![]() минут, то всего он очистил
минут, то всего он очистил ![]() картофелин.
картофелин.
Вместе они очистили 400 картофелин

Из имеющихся компонентов составим и решим уравнение. В левой части уравнения будут картофелины, очищенные каждым человеком, а в правой части их сумма:
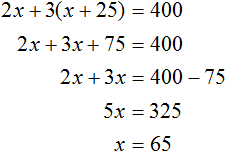
В начале решения данной задачи через переменную x мы обозначили время работы первого человека. Теперь мы нашли значение этой переменной. Первый человек работал 65 минут.
А второй человек работал ![]() минут, и поскольку значение переменной x теперь известно, то можно вычислить время работы второго человека — оно равно 65 + 25, то есть 90 мин.
минут, и поскольку значение переменной x теперь известно, то можно вычислить время работы второго человека — оно равно 65 + 25, то есть 90 мин.
Задача из Учебника по алгебре Андрея Петровича Киселева. Из сортов чая составлена смесь в 32 кг. Килограмм первого сорта стоит 8 руб., а второго сорта 6 руб. 50 коп. Сколько килограммов взято того и другого сорта, если килограмм смеси стоит (без прибыли и убытка) 7 руб. 10 коп.?
Решение
Обозначим через x массу чая первого сорта. Тогда масса чая второго сорта будет обозначаться через выражение 32 − x

Килограмм чая первого сорта стоит 8 руб. Если эти восемь рублей умножить на количество килограмм чая первого сорта, то можно будет узнать во сколько рублей обошлись x кг чая первого сорта.
А килограмм чая второго сорта стоит 6 руб. 50 коп. Если эти 6 руб. 50 коп. умножить на 32 − x, то можно узнать во сколько рублей обошлись 32 − x кг чая второго сорта.
В условии сказано, что килограмм смеси стоит 7 руб. 10 коп. Всего же было приготовлено 32 кг смеси. Умножим 7 руб. 10 коп. на 32 мы сможем узнать сколько стоит 32 кг смеси.
Выражения из которых мы будем составлять уравнение теперь принимают следующий вид:

Попробуем составить уравнение из имеющихся выражений. Положим на левую чашу весов стоимость смесей чая первого и второго сорта, а на правую чашу положим стоимость 32 кг смеси, то есть общую стоимость смеси, в составе которой оба сорта чая:
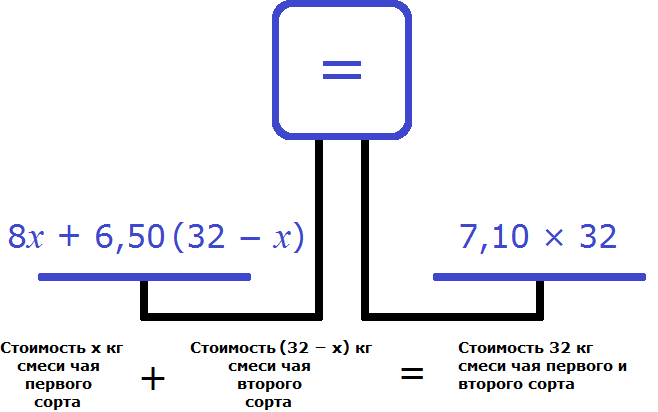
Получили уравнение ![]() . Решим его:
. Решим его:
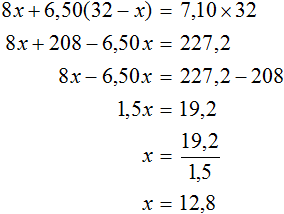
В начале решения данной задачи через переменную x мы обозначили массу чая первого сорта. Теперь мы нашли значение этой переменной. Переменная x равна 12,8. Значит для приготовления смеси было взято 12,8 кг чая первого сорта.
А через выражение 32 − x мы обозначили массу чая второго сорта и поскольку значение переменой x теперь известно, то можно вычислить массу чая второго сорта. Оно равно 32 − 12,8 то есть 19,2. Значит для приготовления смеси было взято 19,2 кг чая второго сорта.
Задача 3. Велосипедист проехал некоторое расстояние со скоростью 8 км/ч. Возвратиться он должен был другой дорогой, которая была на 3 км длиннее первой, и, хотя возвращаясь, ехал со скоростью 9 км/ч, он употребил времени на ![]() минут более. Как длинны были дороги?
минут более. Как длинны были дороги?
Решение
Некоторые задачи могут затрагивать темы, которые человек возможно не изучал. Данная задача относится к такому кругу задач. В ней затрагиваются понятия расстояния, скорости и времени. Соответственно, чтобы решить подобную задачу, нужно иметь представление о тех вещах, о которых говорится в задаче. В нашем случае, надо знать что представляет собой расстояние, скорость и время.
В задаче нужно найти расстояния двух дорог. Мы должны составить уравнение, которое позволит вычислить эти расстояния.
Вспомним, как взаимосвязаны расстояние, скорость и время. Каждая из этих величин может быть описана с помощью буквенного уравнения:
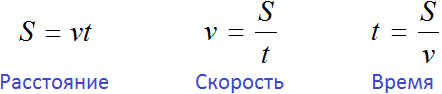
Правую часть одного из этих уравнений мы будем использовать для составления своего уравнения. Чтобы узнать какую именно, нужно вернуться к тексту задачи и обратить внимание на следующий момент:

Следует обратить внимание на момент, где велосипедист на обратном пути употребил времени на ![]() минут более. Эта подсказка указывает нам, что можно воспользоваться уравнением
минут более. Эта подсказка указывает нам, что можно воспользоваться уравнением ![]() , а именно его правой частью. Это позволит нам составить уравнение, которое содержит переменную S.
, а именно его правой частью. Это позволит нам составить уравнение, которое содержит переменную S.
Итак, обозначим длину первой дороги через S. Этот путь велосипедист проехал со скоростью 8 км/ч. Время за которое он преодолел этот путь будет обозначаться выражением ![]() , поскольку время это отношение пройденного расстояния к скорости
, поскольку время это отношение пройденного расстояния к скорости

Обратная дорога для велосипедиста была длиннее на 3 км. Поэтому её расстояние будет обозначаться через выражение S + 3. Эту дорогу велосипедист проехал со скоростью 9 км/ч. А значит время за которое он преодолел этот путь будет обозначаться выражением ![]() .
.
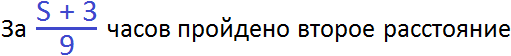
Теперь составим уравнение из имеющихся выражений
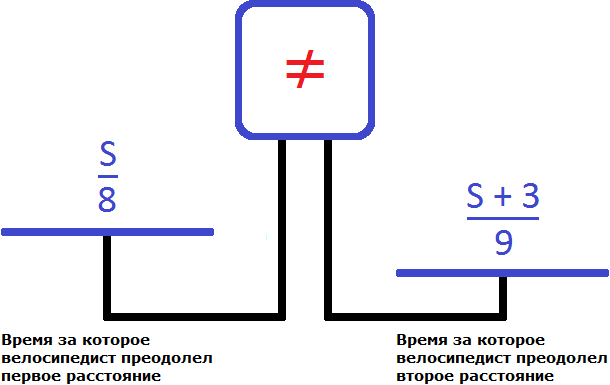
Правая чаша тяжелее левой. Это потому, что в задаче сказано, что на обратную дорогу велосипедист затратил времени на ![]() больше.
больше.
Чтобы уравнять весы прибавим к левой части эти самые ![]() минут. Но сначала переведем минуты в часы, поскольку в задаче скорость измеряется в километрах в час, а не в метрах в минуту.
минут. Но сначала переведем минуты в часы, поскольку в задаче скорость измеряется в километрах в час, а не в метрах в минуту.
Чтобы ![]() минут перевести в часы, нужно разделить их на 60
минут перевести в часы, нужно разделить их на 60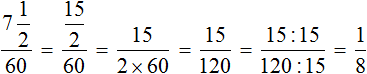
![]() минут составляют
минут составляют ![]() часа. Прибавляем эти
часа. Прибавляем эти ![]() часа к левой части уравнения:
часа к левой части уравнения:
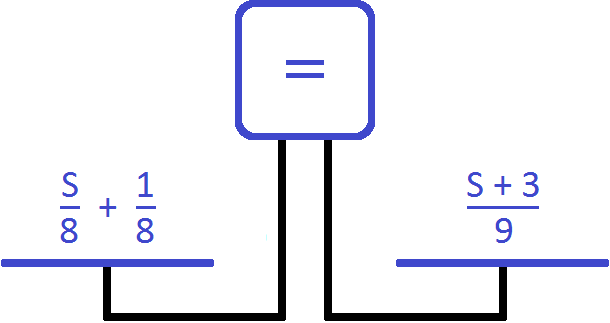
Получается уравнение ![]() . Решим данное уравнение. Чтобы избавиться от дробей, обе части части можно умножить на 72. Далее пользуясь известными тождественными преобразованиями, найдем значение переменной S
. Решим данное уравнение. Чтобы избавиться от дробей, обе части части можно умножить на 72. Далее пользуясь известными тождественными преобразованиями, найдем значение переменной S
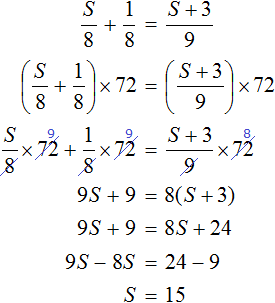
Через переменную S мы обозначали расстояние первой дороги. Теперь мы нашли значение этой переменной. Переменная S равна 15. Значит расстояние первой дороги составляет 15 км.
А расстояние второй дороги мы обозначили через выражение S + 3, и поскольку значение переменной S теперь известно, то можно вычислить расстояние второй дороги. Это расстояние равно сумме 15 + 3, то есть 18 км.
Задача 4. По шоссе идут две машины с одной и той же скоростью. Если первая увеличит скорость на 10 км/ч, а вторая уменьшит скорость на 10 км/ч, то первая за 2 ч пройдет столько же, сколько вторая за 3 ч. С какой скоростью идут автомашины?
Решение
Обозначим через v скорость каждой машины. Далее в задаче приводятся подсказки: скорость первой машины увеличить на 10 км/ч, а скорость второй — уменьшить на 10 км/ч. Воспользуемся этой подсказкой
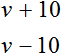
Далее говорится, что при таких скоростях (увеличенных и уменьшенных на 10 км/ч) первая машина пройдет за 2 часа столько же расстояния сколько вторая за 3 часа. Фразу «столько же» можно понимать как «расстояние, пройденное первой машиной, будет равно расстоянию, пройденному второй машиной».
Расстояние как мы помним, определяется по формуле ![]() . Нас интересует правая часть этого буквенного уравнения — она позволит нам составить уравнение, содержащее переменную v.
. Нас интересует правая часть этого буквенного уравнения — она позволит нам составить уравнение, содержащее переменную v.
Итак, при скорости v + 10 км/ч первая машина пройдет 2(v+10) км, а вторая пройдет 3(v − 10) км. При таком условии машины пройдут одинаковые расстояния, поэтому для получения уравнения достаточно соединить эти два выражения знаком равенства. Тогда получим уравнение ![]() . Решим его:
. Решим его:
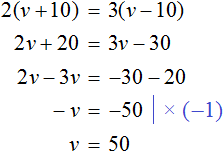
В условии задачи было сказано, что машины идут с одинаковой скоростью. Мы обозначили эту скорость через переменную v. Теперь мы нашли значение этой переменной. Переменная v равна 50. Значит скорость обеих машин составляла 50 км/ч.
Задача 5. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.
Решение
Обозначим через v собственную скорость теплохода. Скорость течения реки равна 2 км/ч. По течению реки скорость теплохода будет составлять v + 2 км/ч, а против течения — (v − 2) км/ч.
В условии задачи сказано, что за 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Фразу «тот же путь» можно понимать как «расстояние, пройденное теплоходом по течению реки за 9 часов, равно расстоянию, пройденному теплоходом против течения реки за 11 часов». То есть расстояния будут одинаковыми.
Расстояние определяется по формуле ![]() . Воспользуемся правой частью этого буквенного уравнения для составления своего уравнения.
. Воспользуемся правой частью этого буквенного уравнения для составления своего уравнения.
Итак, за 9 часов по течению реки теплоход пройдет 9(v + 2) км, а за 11 часов против течения — 11(v − 2) км. Поскольку оба выражения описывают одно и то же расстояние, приравняем первое выражение ко второму. В результате получим уравнение ![]() . Решим его:
. Решим его:
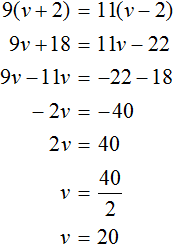
Значит собственная скорость теплохода составляет 20 км/ч.
При решении задач полезной привычкой является заранее определить на каком множестве ищется для неё решение.
Допустим, что в задаче требовалось найти время, за которое пешеход преодолеет указанный путь. Мы обозначили время через переменную t, далее составили уравнение, содержащее эту переменную и нашли её значение.
Из практики мы знаем, что время движения объекта может принимать как целые значения, так и дробные, например 2 ч, 1,5 ч, 0,5 ч. Тогда можно сказать, что решение данной задачи ищется на множестве рациональных чисел Q, поскольку каждое из значений 2 ч, 1,5 ч, 0,5 ч может быть представлено в виде дроби.
Поэтому после того, как неизвестную величину обозначили через переменную, полезно указать к какому множеству эта величина принадлежит. В нашем примере время t принадлежит множеству рациональных чисел Q
t ∈ Q
Ещё можно ввести ограничение для переменной t, указав что она может принимать только положительные значения. Действительно, если объект затратил на путь определенное время, то это время не может быть отрицательным. Поэтому рядом с выражением t ∈ Q укажем, что её значение должно быть больше нуля:
t ∈ R, t > 0
Если решив уравнение, мы получим отрицательное значение для переменной t, то можно будет сделать вывод, что задача решена неправильно, поскольку это решение не будет удовлетворять условию t ∈ Q, t > 0.
Ещё пример. Если бы мы решали задачу в которой требовалось найти количество человек для выполнения той или иной работы, то это количество мы обозначили бы через переменную x. В такой задаче решение искалось бы на множестве натуральных чисел
x ∈ N
Действительно, количество человек является целым числом, например 2 человека, 3 человека, 5 человек. Но никак не 1,5 (один целый человек и половина человека) или 2,3 (два целых человека и еще три десятых человека).
Здесь можно было бы указать, что количество человек должно быть больше нуля, но числа входящие во множество натуральных чисел N сами по себе являются положительными и большими нуля. В этом множестве нет отрицательных чисел и числа 0. Поэтому выражение x > 0 можно не писать.
Задача 6. Для ремонта школы прибыла бригада в которой было в 2,5 раза больше маляров, чем плотников. Вскоре прораб включил в бригаду еще четырех маляров, а двух плотников перевел на другой объект. В результате маляров в бригаде оказалось в 4 раза больше чем плотников. Сколько маляров и сколько плотников было в бригаде первоначально
Решение
Обозначим через x плотников, прибывших на ремонт первоначально.
Количество плотников является целым числом, большим нуля. Поэтому укажем, что x принадлежит множество натуральных чисел
x ∈ N
Маляров было в 2,5 раза больше, чем плотников. Поэтому количество маляров будет обозначаться как 2,5x.

Далее говорится, что прораб включил в бригаду еще четырех маляров, а двух плотников перевел на другой объект. Сделаем для своих выражений тоже самое. Уменьшим количество плотников на 2
![]()
А количество маляров увеличим на 4
![]()
Теперь количество плотников и маляров будут обозначаться через следующие выражения:

Попробуем составить уравнение из имеющихся выражений:
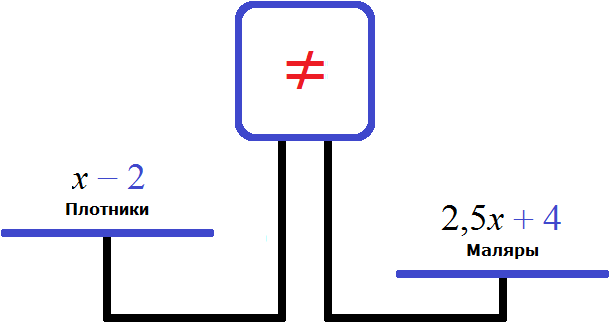
Правая чаша больше, поскольку после включения в бригаду ещё четырёх маляров, и перемещения двух плотников на другой объект, количество маляров в бригаде оказалось в 4 раза больше чем плотников. Чтобы уравнять весы, нужно левую чашу увеличить в 4 раза:
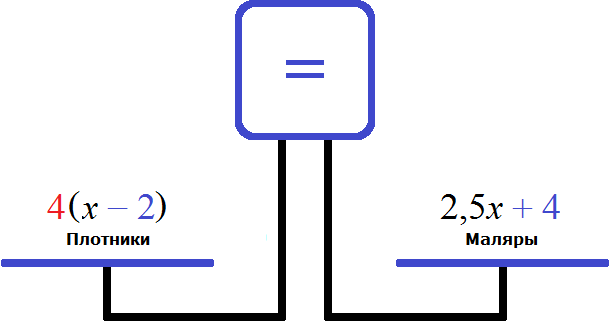
Получили уравнение ![]() . Решим его:
. Решим его:
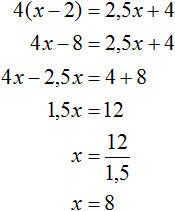
Через переменную x было обозначено первоначальное количество плотников. Теперь мы нашли значение этой переменной. Переменная x равна 8. Значит 8 плотников было в бригаде первоначально.
А количество маляров было обозначено через выражение 2,5x и поскольку значение переменной x теперь известно, то можно вычислить количество маляров — оно равно 2,5 × 8, то есть 20.
Возвращаемся к началу задачи и удостоверяемся, что соблюдается условие x ∈ N. Переменная x равна 8, а элементы множества натуральных чисел N это все числа, начинающиеся с 1, 2, 3 и так далее до бесконечности. В это же множество входит число 8, которое мы нашли.
8 ∈ N
Тоже самое можно сказать о количестве маляров. Число 20 принадлежит множеству натуральных чисел:
20 ∈ N
Для понимания сути задачи и правильного составления уравнения, вовсе необязательно использовать модель весов с чашами. Можно использовать и другие модели: отрезки, таблицы, схемы. Можно придумать свою модель, которая хорошо описывала бы суть задачи.
Задача 9. Из бидона отлили 30% молока. В результате в нем осталось 14 л. Сколько литров молока было в бидоне первоначально?
Решение
Искомое значение это первоначальное число литров в бидоне. Изобразим число литров в виде линии и подпишем эту линию как X
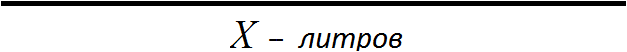
Сказано, что из бидона отлили 30% молока. Выделим на рисунке приблизительно 30%
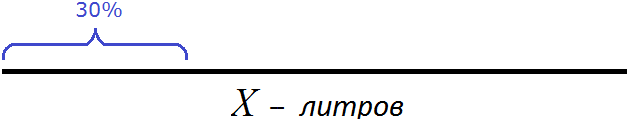
Процент по определению есть одна сотая часть чего-то. Если 30% молока отлили, то остальные 70% остались в бидоне. На эти 70% приходятся 14 литров, указанные в задаче. Выделим на рисунке оставшиеся 70%
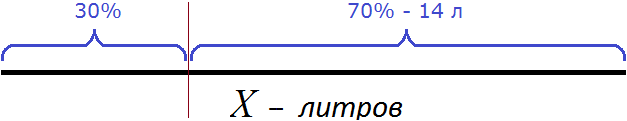
Теперь можно составить уравнение. Вспомним, как находить процент от числа. Для этого общее количество чего-то делят на 100 и полученный результат умножают на искомое количество процентов. Замечаем, что 14 литров, составляющих 70% можно получить таким же образом: первоначальное число литров X разделить на 100 и полученный результат умножить на 70. Всё это приравнять к числу 14
![]()
Или получить более простое уравнение: 70% записать как 0,70, затем умножить на X и приравнять это выражение к 14
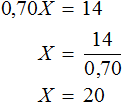
Значит первоначально в бидоне было 20 литров молока.
Задача 9. Взяли два сплава золота и серебра. В одном количество этих металлов находится в отношении 1 : 9, а в другом 2 : 3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золото и серебро относилось бы как 1 : 4?
Решение
Попробуем сначала узнать сколько золота и серебра будет содержáться в 15 кг нового сплава. В задаче сказано, что содержание этих металлов должно быть в отношении 1 : 4, то есть на одну часть сплава должно приходиться золото, а на четыре части — серебро. Тогда всего частей в сплаве будет 1 + 4 = 5, а масса одной части будет 15 : 5 = 3 кг.
Определим сколько золота будет содержáться в 15 кг сплава. Для этого 3 кг умножим на количество частей золота:
3 кг × 1 = 3 кг
Определим сколько серебра будет содержáться в 15 кг сплава:
3 кг × 4 = 12 кг
Значит сплав массой 15 кг будет содержать 3 кг золота и 12 кг серебра. Теперь вернёмся к исходным сплавам. Использовать нужно каждый из них. Обозначим через x массу первого сплава, а массу второго сплава можно обозначить через 15 − x

Выразим в процентах все отношения, которые даны в задаче и заполним ими следующую таблицу:
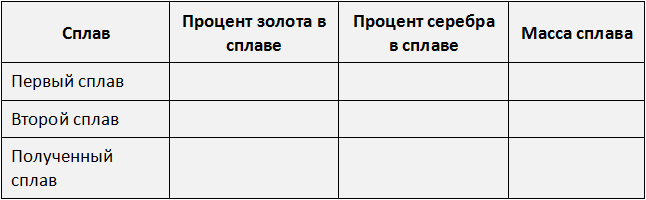
В первом сплаве золото и серебро находятся в отношении 1 : 9. Тогда всего частей будет 1 + 9 = 10. Из них золота будет ![]() , а серебра
, а серебра ![]() .
.
Перенесём эти данные в таблицу. 10% занесём в первую строку в графу «процент золота в сплаве», 90% также занесём в первую строку графу «процент серебра в сплаве», а в последнюю графу «масса сплава» занесём переменную x, поскольку так мы обозначили массу первого сплава:
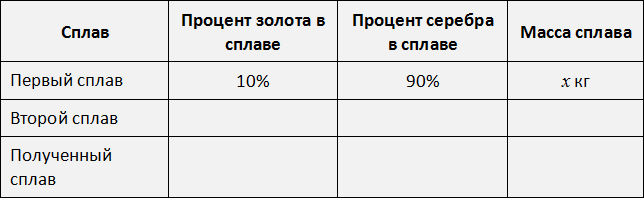
Аналогично поступаем со вторым сплавом. Золото и серебро в нём находятся в отношении 2 : 3. Тогда всего частей будет 2 + 3 = 5. Из них золота будет ![]() , а серебра
, а серебра ![]() .
.
Перенесём эти данные в таблицу. 40% занесем во вторую строку в графу «процент золота в сплаве», 60% также занесём во вторую строку графу «процент серебра в сплаве», а в последнюю графу «масса сплава» занесём выражение 15 − x, поскольку так мы обозначили массу второго сплава:
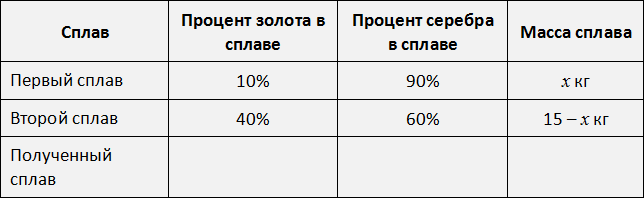
Заполним последнюю строку. Полученный сплав массой 15 кг будет содержать 3 кг золота, что составляет ![]() сплава, а серебра будет
сплава, а серебра будет ![]() сплава. В последнюю графу записываем массу полученного сплава 15
сплава. В последнюю графу записываем массу полученного сплава 15
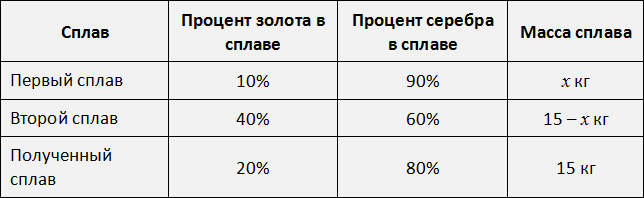
Теперь по данной таблице можно составить уравнения. Вспоминаем задачи на концентрацию, сплавы и смеси. Если мы отдельно сложим золото обоих сплавов и приравняем эту сумму к массе золота полученного сплава, то сможем узнать чему равно значение x.
Далее для удобства проценты будем выражать в десятичной дроби.
В первом сплаве золота было 0,10x, а во втором сплаве золота было 0,40(15 − x). Тогда в полученном сплаве масса золота будет суммой масс золота первого и второго сплавов и эта масса составляет 20% от нового сплава. А 20% от нового сплава это 3 кг золота, вычисленные нами ранее. В результате получаем уравнение 0,10x + 0.40(15 − x) = 3. Решим это уравнение:
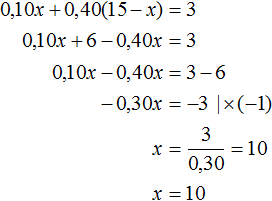
Изначально через x мы обозначили массу первого сплава. Теперь мы нашли значение этой переменной. Переменная x равна 10. А массу второго сплава мы обозначили через 15 − x, и поскольку значение переменной x теперь известно, то можно вычислить массу второго сплава, она равна 15 − 10 = 5 кг.
Значит для получения нового сплава массой 15 кг в котором золото и серебро относились бы как 1 : 4, нужно взять 10 кг первого и 5 кг второго сплава.
Уравнение можно было составить, воспользовавшись и вторым столбцом получившейся таблицы. Тогда мы получили бы уравнение 0,90x + 0.60(15 − x) = 12. Корень этого уравнения тоже равен 10
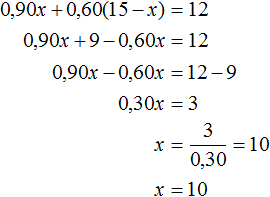
Задача 10. Имеется руда из двух пластов с содержанием меди в 6% и 11%. Сколько надо взять бедной руды, чтобы получить при смешивании с богатой 20 тонн с содержанием меди 8%?
Решение
Обозначим через x массу бедной руды. Поскольку нужно получить 20 тонн руды, то богатой руды будет взято 20 − x. Поскольку содержание меди в бедной руде составляет 6%, то в x тоннах руды будет содержáться 0,06x тонн меди. В богатой руде содержание меди составляет 11%, а в 20 − x тоннах богатой руды будет содержáться 0,11(20 − x) тонн меди.
В получившихся 20 тоннах руды содержание меди должно составлять 8%. Значит в 20 тоннах руды меди будет содержáться 20 × 0,08 = 1,6 тонн.
Сложим выражения 0,06x и 0,11(20 − x) и приравняем эту сумму к 1,6. Получим уравнение 0,06x + 0,11(20 − x) = 1,6

Решим данное уравнение:
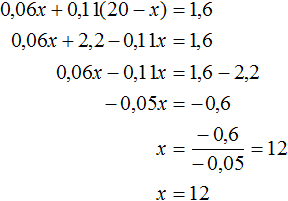
Значит для получения 20 тонн руды с содержанием меди 8%, нужно взять 12 тонн бедной руды. Богатой же будет взято 20 − 12 = 8 тонн.
Задача 11. Увеличив среднюю скорость с 250 до 300 м/мин спортсменка стала пробегать дистанцию на 1 мин быстрее. Какова длина дистанции?
Решение
Длину дистанции (или расстояние дистанции) можно описать следующим буквенным уравнением:
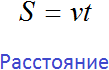
Воспользуемся правой частью этого уравнения для составления своего уравнения. Изначально спортсменка пробегала дистанцию со скоростью 250 метров в минуту. При такой скорости длина дистанции будет описываться выражением 250t
Затем спортсменка увеличила свою скорость до 300 метров в минуту. При такой скорости длина дистанции будет описываться выражением 300t
Заметим, что длина дистанции это величина постоянная. От того, что спортсменка увеличит скорость или уменьшит её, длина дистанции останется неизменной.
Это позволяет нам приравнять выражение 250t к выражению 300t, поскольку оба выражения описывают длину одной и той же дистанции
250t = 300t
Но в задаче сказано, что при скорости 300 метров в минуту спортсменка стала пробегать дистанцию на 1 минуту быстрее. Другими словами, при скорости 300 метров в минуту, время движения уменьшится на единицу. Поэтому в уравнении 250t = 300t в правой части время нужно уменьшить на единицу:
![]()
Получилось простейшее уравнение. Решим его:
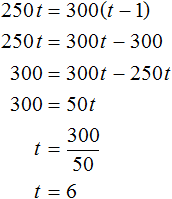
При скорости 250 метров в минуту спортсменка пробегает дистанцию за 6 минут. Зная скорость и время, можно определить длину дистанции:
S = 250 × 6 = 1500 м
А при скорости 300 метров в минуту спортсменка пробегает дистанцию за t − 1, то есть за 5 минут. Как было сказано ранее длина дистанции не меняется:
S = 300 × 5 = 1500 м
Задача 12. Всадник догоняет пешехода, находящегося впереди него на 15 км. Через сколько часов всадник догонит пешехода, если каждый час первый проезжает по 10 км, а второй проходит только по 4 км?
Решение
Данная задача является задачей на движение. Её можно решить, определив скорость сближения и разделив изначальное расстояние между всадником и пешеходом на эту скорость.
Скорость сближения определяется вычитанием меньшей скорости из большей:
10 км/ч − 4 км/ч = 6 км/ч (скорость сближения)
С каждым часом расстояние в 15 километров будут сокращаться на 6 км. Чтобы узнать, когда оно сократится полностью (когда всадник догонит пешехода), нужно 15 разделить на 6
15 : 6 = 2,5 ч
2,5 ч это два целых часа и половина часа. А половина часа это 30 минут. Значит всадник догонит пешехода через 2 часа 30 минут.
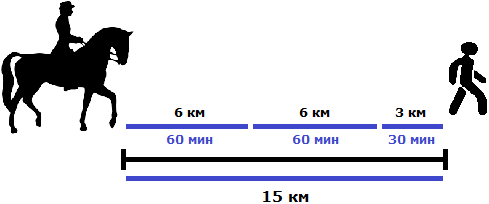
Решим эту задачу с помощью уравнения.
Будем считать, что пешеход и всадник вышли в путь из одного и того же места. Пешеход вышел раньше всадника и успел преодолеть 15 км
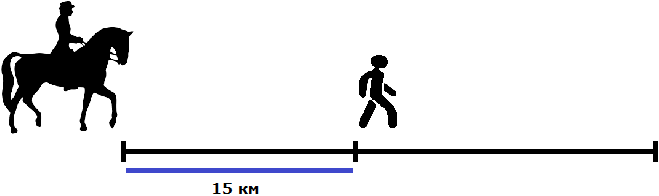
После этого вслед за ним в путь вышел всадник со скоростью 10 км/ч. А скорость пешехода составляет только 4 км/ч. Это значит, что всадник через некоторое время догонит пешехода. Это время нам нужно найти.
Когда всадник догонит пешехода это будет означать, что они вместе прошли одинаковое расстояние. Расстояние, пройденное всадником и пешеходом описывается следующим уравнением:
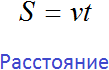
Воспользуемся правой частью этого уравнения для составления своего уравнения.
Расстояние, пройденное всадником, будет описываться выражением 10t. Поскольку пешеход вышел в путь раньше всадника и успел преодолеть 15 км, то расстояние пройденное им будет описываться выражением 4t + 15.
На момент, когда всадник догонит пешехода, оба они пройдут одинаковое расстояние. Это позволяет нам приравнять расстояния, пройденные всадником и пешеходом:
![]()
Получилось простейшее уравнение. Решим его:
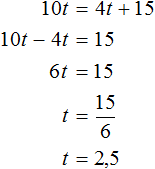
Задачи для самостоятельного решения
Задача 1. Из одного города в другой пассажирский поезд приезжает на 45 мин быстрее товарного. Вычисли расстояние между городами, если скорость пассажирского поезда 48 км/ч, а товарного 36 км/ч.
Решение
Скорости поездов в данной задаче измеряются в километрах в час. Поэтому 45 мин, указанные в задаче, переведем в часы. 45 мин это 0,75 ч
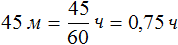
Обозначим время, за которое товарный поезд приезжает в город, через переменную t. Поскольку пассажирский поезд приезжает в этот город на 0,75 ч быстрее, то время его движения будет обозначаться через выражение t − 0,75
Пассажирский поезд преодолел 48(t − 0.75) км, а товарный 36t км. Поскольку речь идет об одном и том же расстоянии, приравняем первое выражение ко второму. В результате получим уравнение 48(t − 0.75) = 36t. Решим его:
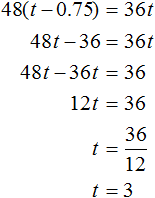
Теперь вычислим расстояние между городами. Для этого скорость товарного поезда (36 км/ч) умножим на время его движения t. Значение переменной t теперь известно — оно равно трём часам
36 × 3 = 108 км
Для вычисления расстояния можно воспользоваться и скоростью пассажирского поезда. Но в этом случае значение переменной t необходимо уменьшить на 0,75 поскольку пассажирский поезд затратил времени на 0,75 ч меньше
48 × (3 − 0,75) = 144 − 36 = 108 км
Ответ: расстояние между городами равно 108 км.
Задача 2. Из двух городов, расстояние между которыми 150 км, одновременно навстречу друг другу выехали два автомобиля. Скорость одного автомобиля 65 км/ч, а второго 60 км/ч. Через сколько часов они встретились?
Решение
Пусть t время через которое автомобили встретились. Тогда первый автомобиль на момент встречи проедет 65t км, а второй 60t км. Сложим эти расстояния и приравняем к 150. Получим уравнение 65t + 60t = 150
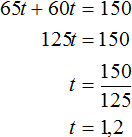
Значение переменной t равно 1,2. Значит автомобили встретились через 1,2 часа.
Ответ: автомобили встретились через 1,2 часа.
Задача 3. В трех цехах завода всего 685 рабочих. Во втором цехе рабочих в три раза больше, чем в первом, а в третьем — на 15 рабочих меньше, чем во втором цехе. Сколько рабочих в каждом цехе?
Решение
Пусть x рабочих было в первом цехе. Во втором цехе было в три раза больше, чем в первом, поэтому количество рабочих во втором цехе можно обозначить через выражение 3x. В третьем цехе было на 15 рабочих меньше, чем во втором. Поэтому количество рабочих в третьем цехе можно обозначить через выражение 3x − 15.
В задаче сказано, что всего рабочих было 685. Поэтому можно сложить выражения x, 3x, 3x − 15 и приравнять эту сумму к числу 685. В результате получим уравнение x + 3x + (3x − 15) = 685
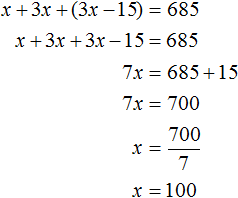
Через переменную x было обозначено количество рабочих в первом цехе. Теперь мы нашли значение этой переменной, оно равно 100. Значит в первом цехе было 100 рабочих.
Во втором цехе было 3x рабочих, то есть 3 × 100 = 300. А в третьем цехе было 3x − 15, то есть 3 × 100 − 15 = 285
Ответ: в первом цехе было 100 рабочих, во втором — 300, в третьем — 285.
Задача 4. Две ремонтные мастерские в течение недели должны отремонтировать по плану 18 моторов. Первая мастерская выполнила план на 120%, а вторая — на 125%, поэтому в течение недели отремонтировали 22 мотора. Какой план по ремонту моторов на неделю имела каждая мастерская?
Решение
Пусть x моторов должна была отремонтировать первая мастерская. Тогда вторая мастерская должна была отремонтировать 18 − x моторов.
Поскольку первая мастерская выполнила свой план на 120%, это означает что она отремонтировала 1,2x моторов . А вторая мастерская выполнила свой план на 125%, значит она отремонтировала 1,25(18 − x) моторов.
В задаче сказано, что было отремонтировано 22 мотора. Поэтому можно сложить выражения 1,2x и 1,25(18 − x) , затем приравнять эту сумму к числу 22. В результате получим уравнение 1,2x + 1,25(18 − x) = 22
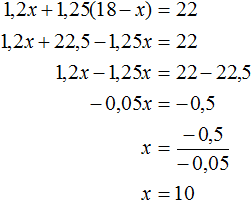
Через переменную x было обозначено количество моторов, которые должна была отремонтировать первая мастерская. Теперь мы нашли значение этой переменной, она равна 10. Значит первая мастерская должна была отремонтировать 10 моторов.
А через выражение 18 − x было обозначено количество моторов, которые должна была отремонтировать вторая мастерская. Значит вторая мастерская должна была отремонтировать 18 − 10 = 8 моторов.
Ответ: первая мастерская должна была отремонтировать 10 моторов, а вторая — 8 моторов.
Задача 5. Цена товара повысилась на 30% и составляет теперь 91 руб. Сколько стоил товар до повышения цены?
Решение
Пусть x рублей стоил товар до повышения цены. Если цена увеличилась на 30% это означает, что она увеличилась на 0,30x рублей. После повышения цены товар начал стоить 91 руб. Сложим x с 0,30x и приравняем эту сумму к 91. В результате получим уравнение x + 0.30x = 91
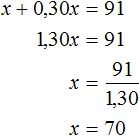
Значит до повышения цены товар стоил 70 рублей.
Ответ: до повышения цены товар стоил 70 рублей.
Задача 6. Число увеличили на 25%. На сколько процентов надо уменьшить новое число, чтобы получилось исходное?
Решение
Пусть x — исходное число. Увеличим его на 25%. Получим выражение x + 0,25x. Приведем подобные слагаемые, получим x + 0,25x = 1.25x.
Узнаем какую часть исходное число x составляет от нового числа 1,25x
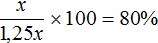
Если новое число 1,25x считать за 100%, а исходное число x составляет от него 80%, то уменьшив новое число на 20% можно получить исходное число x

Ответ: чтобы получить исходное число, новое число нужно уменьшить на 20%.
Задача 7. При увеличении числа на 20% получилось 144. Найти первоначальное значение числа.
Решение
Пусть x — первоначальное число. Увеличим его на 20%. Получим выражение x + 0,20x. Приравняем эту сумму к числу 144, получим уравнение x + 0,20x = 144

Ответ: первоначальное значение числа равно 120.
Задача 8. При уменьшении числа на 10% получилось 45. Найти первоначальное значение числа.
Решение
Пусть x — первоначальное число. Уменьшим его на 10%. Получим выражение x − 0,10x. Приравняем эту разность к числу 45, получим уравнение x − 0,10x = 45
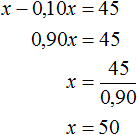
Ответ: первоначальное значение числа равно 50.
Задача 9. Цена альбома была снижена сначала на 15%, потом еще на 15 руб. Новая цена альбома после двух снижений 19 руб. Определить его первоначальную цену.
Решение
Пусть x рублей — первоначальная цена альбома. Снизим эту цену на 15%, получим x − 0,15x. Снизим цену ещё на 15 руб., получим x − 0,15x − 15. После этих снижений альбом стал стоить 19 руб. Приравняем выражение x − 0,15x − 15 к числу 19, получим уравнение x − 0,15x − 15 = 19
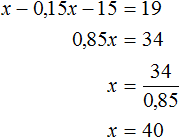
Ответ: первоначальная цена альбома составляет 40 руб.
Задача 10. Трава при сушке теряет 80% своей массы. Сколько тонн травы нужно накосить, чтобы получить 4 т сена?
Решение
Если 80% массы теряется, то на оставшиеся 20% будут приходиться 4 т сена. Пусть x тонн травы требуется для получения 4 т сена. Если 4 т будут составлять 20% травы, то можно составить уравнение:

Ответ: для получения 4 т сена, нужно накосить 20 т травы.
Задача 11. Сколько килограммов 20%-го раствора соли нужно добавить к 1 кг 10%-го раствора, чтобы получить 12%-й раствор соли?
Решение
Пусть x кг 20%-го раствора соли нужно добавить к 1 кг 10%-го раствора.
В 1 кг 10%-го раствора соли содержится 0,1 кг соли. А в x кг 20%-го раствора соли содержится 0,20x кг соли.
После добавления x кг 20%-го раствора в новом растворе будет содержáться 0,12(1 + x) кг соли. Сложим выражения 0,1 и 0,20x, затем приравняем эту сумму к выражению 0,12(1 + x). В результате получим уравнение 0,1 + 0,20x = 0,12(1 + x)
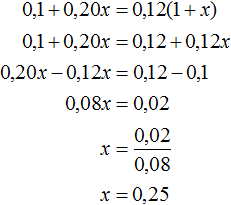
Ответ: чтобы получить 12%-й раствор соли, нужно к 1 кг 10%-го раствора добавить 0,25 кг 20%-го раствора.
Задача 12. Даны два раствора соли в воде, концентрации которых равны 20% и 30%. Сколько килограммов каждого раствора нужно смешать в одном сосуде, чтобы получить 25 кг 25,2%-го раствора?
Решение
Пусть x кг первого раствора нужно взять. Поскольку требуется приготовить 25 кг раствора, то массу второго раствора можно обозначить через выражение 25 − x.
В первом растворе будет содержáться 0,20x кг соли, а втором — 0,30(25 − x) кг соли. В полученном растворе содержание соли будет 25 × 0,252 = 6,3 кг. Сложим выражения 0,20x и 0,30(25 − x), затем приравняем эту сумму к 6,3. В результате получим уравнение
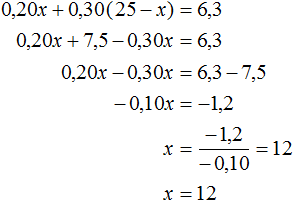
Значит первого раствора нужно взять 12 кг, а второго 25 − 12 = 13 кг.
Ответ: первого раствора нужно взять 12 кг, а второго 13 кг.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


