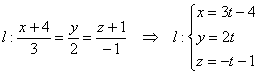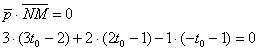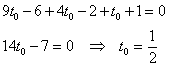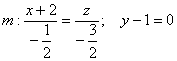Как составить уравнение прямой через вектор перпендикулярно - Сайт, где вы сможете решить свои вопросы

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

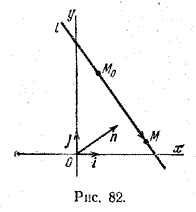
Пусть дана некоторая точка М₀ и вектор n. Проведем через точку М₀ прямую l перпендикулярно вектору n (рис. 82).

Пусть M — произвольная точка. Точка M лежит на прямой l в том и только в том случае, когда вектор (overrightarrowM>) перпендикулярен вектору n, а для этого необходимо и достаточно, чтобы скалярное произведение векторов n и (overrightarrowM>) равнялось нулю:

Чтобы выразить последнее равенство в координатах, введем прямоугольную декартову систему координат. Пусть точки M₀ и M имеют координаты (x₀ ; у₀ ) и (x; у).

Тогда (overrightarrowM>) = (x — x₀; у — у₀). Обозначим координаты нормального вектора n через (А; В). Теперь равенство (1) можно записать так:

Уравнение (2) есть уравнение прямой l, проходящей через данную точку М₀ (x₀; у₀) перпендикулярно данному вектору n = (А; В).

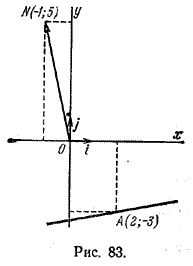
Задача 1. Составить уравнение прямой, проходящей через точку А (2; -3) перпендикулярно вектору n = (-1;5) (рис.83).

Пользуясь формулой (2), находим уравнение данной прямой:

— 1 • (x-2) + 5 • (у + 3) = 0

или, окончательно, x — 5у — 17 = 0.

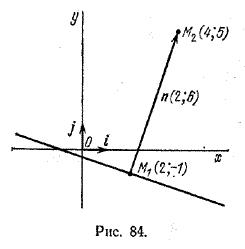
Задача 2. Даны точки M₁(2; -1) и M₂(4; 5). Написать уравнение прямой, проходящей через точку М₁ перпендикулярно вектору (overrightarrowM_<2>>).

Нормальный вектор искомой прямой n = (overrightarrowM_<2>>) имеет координаты (2; 6) (рис. 84).

Следовательно, по формуле (2) получим уравнение

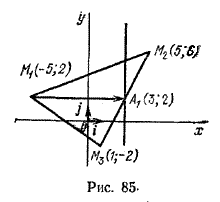
Задача 3. В треугольнике с вершинами в точках M₁(-5; 2), M₂(5; 6) и M₃(1; -2) проведена медиана M₁А₁. Требуется составить уравнение прямой, проходящей через точку А₁ перпендикулярно медиане M₁A₁ (рис. 85).

За нормальный вектор искомой прямой можно принять вектор n = (overrightarrowA_<1>>). Определим его координаты. Точка A₁ — середина отрезка M₂M₃, поэтому, если (x₁; y₁) — ее координаты, то ( x_1 = frac<5+1><2>=3, ;;а ;; y_1=frac<6-2><2>=2 ).

Тогда нормальный вектор n = (overrightarrowA_<1>>) имеет координаты (8; 0). Следовательно, искомое уравнение прямой имеет вид

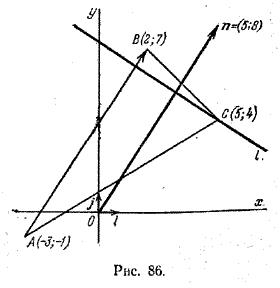
Задача 4. Дан треугольник с вершинами в точках А(-3; -1), В(2; 7) и С(5; 4). Требуется составить уравнение прямой, проходящей через вершину С перпендикулярно стороне AB (рис. 86).

За нормальный вектор искомой прямой можно взять вектор n = (overrightarrow).

Так как n = (2-(-3); 7 — (-1)) = (5; 8), то, подставляя координаты точки С и координаты вектора n в формулу (2), получим

или, окончательно, 5х + 8у — 57 = 0.

Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой

В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

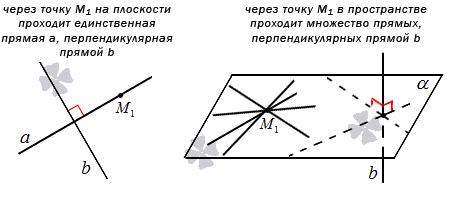
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.

Если плоскость α проходит через заданную точку М 1 перпендикулярно к заданной прямой b , то прямые, лежащие в этой плоскости, в том числе и проходящая через М 1 являются перпендикулярными заданной прямой b .

Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.

Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Если на плоскости с системой координат О х у z имеем прямую b , то ей соответствует уравнение прямой на плоскости, задается точка с координатами M 1 ( x 1 , y 1 ) , а необходимо составить уравнение прямой a , которая проходит через точку М 1 , причем перпендикулярно прямой b .

По условию имеем координаты точки М 1 . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a , или координаты нормального вектора прямой a , или угловой коэффициент прямой a .

Необходимо получить данные из заданного уравнения прямой b . По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a . Отсюда получим, что угловые коэффициенты обозначаются как k b и k a . Они связаны при помощи соотношения k b · k a = — 1 .

Получили, что направляющий вектор прямой b имеет вид b → = ( b x , b y ) , отсюда нормальный вектор — n a → = ( A 2 , B 2 ) , где значения A 2 = b x , B 2 = b y . Тогда запишем общее уравнение прямой, проходящее через точку с координатами M 1 ( x 1 , y 1 ) , имеющее нормальный вектор n a → = ( A 2 , B 2 ) , имеющее вид A 2 · ( x — x 1 ) + B 2 · ( y — y 1 ) = 0 .

Нормальный вектор прямой b определен и имеет вид n b → = ( A 1 , B 1 ) , тогда направляющий вектор прямой a является вектором a → = ( a x , a y ) , где значения a x = A 1 , a y = B 1 . Значит осталось составить каноническое или параметрическое уравнение прямой a , проходящее через точку с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) , имеющее вид x — x 1 a x = y — y 1 a y или x = x 1 + a x · λ y = y 1 + a y · λ соответственно.

После нахождения углового коэффициента k b прямой b можно высчитать угловой коэффициент прямой a . Он будет равен — 1 k b . Отсюда следует, что можно записать уравнение прямой a , проходящей через M 1 ( x 1 , y 1 ) с угловым коэффициентом — 1 k b в виде y — y 1 = — 1 k b · ( x — x 1 ) .

Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.

Решение примеров

Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.

Записать уравнение прямой а, которая проходит через точку с координатами M 1 ( 7 , — 9 ) и перпендикулярна прямой b , которое задано каноническим уравнением прямой x — 2 3 = y + 4 1 .

Из условия имеем, что b → = ( 3 , 1 ) является направляющим вектором прямой x — 2 3 = y + 4 1 . Координаты вектора b → = 3 , 1 являются координатами нормального вектора прямой a , так как прямые a и b взаимно перпендикулярны. Значит, получаем n a → = ( 3 , 1 ) . Теперь необходимо записать уравнение прямой, проходящее через точку M 1 ( 7 , — 9 ) , имеющее нормальный вектор с координатами n a → = ( 3 , 1 ) .

Получим уравнение вида: 3 · ( x — 7 ) + 1 · ( y — ( — 9 ) ) = 0 ⇔ 3 x + y — 12 = 0

Полученное уравнение является искомым.

Ответ: 3 x + y — 12 = 0 .

Составить уравнение прямой, которая проходит через начало координат системы координат О х у z , перпендикулярно прямой 2 x — y + 1 = 0 .

Имеем, что n b → = ( 2 , — 1 ) является нормальным вектором заданной прямой. Отсюда a → = ( 2 , — 1 ) — координаты искомого направляющего вектора прямой.

Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором a → = ( 2 , — 1 ) . Получим, что x — 0 2 = y + 0 — 1 ⇔ x 2 = y — 1 . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой 2 x — y + 1 = 0 .

Ответ: x 2 = y — 1 .

Записать уравнение прямой, проходящей через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 .

Из уравнения y = — 5 2 x + 6 угловой коэффициент имеет значение — 5 2 . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение — 1 — 5 2 = 2 5 . Отсюда делаем вывод, что прямая, проходящая через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 , равна y — ( — 3 ) = 2 5 · x — 5 ⇔ y = 2 5 x — 5 .

Прямая линия. Уравнение прямой.

Свойства прямой в евклидовой геометрии.

Через любую точку можно провести бесконечно много прямых.

Через любые две несовпадающие точки можно провести единственную прямую.

Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются

параллельными (следует из предыдущего).

В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:

прямые пересекаются;

прямые параллельны;

прямые скрещиваются.

Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия

задается на плоскости уравнением первой степени (линейное уравнение).

Общее уравнение прямой.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим

уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

• А = 0, В ≠0, С ≠0 — прямая параллельна оси Ох

• В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу

• В = С = 0, А ≠0 – прямая совпадает с осью Оу

• А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных

Уравнение прямой по точке и вектору нормали.

Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В)

перпендикулярен прямой , заданной уравнением

Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С

подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно

С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.

Уравнение прямой, проходящей через две точки.

Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой,

проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На

плоскости записанное выше уравнение прямой упрощается:

Дробь = k называется угловым коэффициентом прямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение. Применяя записанную выше формулу, получаем:

Уравнение прямой по точке и угловому коэффициенту.

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется

уравнением прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору.

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание

прямой через точку и направляющий вектор прямой.

Определение. Каждый ненулевой вектор (α₁, α₂), компоненты которого удовлетворяют условию

Аα₁ + Вα₂ = 0 называется направляющим вектором прямой.

Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,

коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.

при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:

Уравнение прямой в отрезках.

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:

или , где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения

прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется

нормирующем множителем, то получим

xcosφ + ysinφ — p = 0 – нормальное уравнение прямой.

Знак ± нормирующего множителя надо выбирать так, чтобы μ * С Что-то не нашли? Ошибка? Предложения? Сообщите нам

источники:

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-prjamoj-prohodjaschej-cherez-zadannuju-t/

http://www.calc.ru/1437.html

Источник

Уравнения прямой, проходящей через точку перпендикулярно вектору

Общее уравнение прямой

Ненулевой вектор vec{n} , перпендикулярный заданной прямой, называется нормальным вектором (или, короче, нормалью) для этой прямой.

Пусть на координатной плоскости Oxy (в прямоугольной системе координат) заданы точка M_0(x_0,y_0) и ненулевой вектор vec{n}=Acdotvec{i}+Bcdotvec{j} (рис. 3.5, а). Требуется составить уравнение прямой, проходящей через точку перпендикулярно вектору vec{n} .

Выберем на плоскости произвольную точку M(x,y) . Обозначим vec{r}=overrightarrow{OM}=xvec{i}+vec{y}vec{j} и $vec{r}_0=overrightarrow{OM_0}=x_0vec{i}+vec{y}_0vec{j}$ — радиус-векторы точек M(x,y) и M_0(x_0,y_0) . Точка принадлежит заданной прямой тогда и только тогда, когда векторы $overrightarrow{M_0M}$ и vec{n} перпендикулярны (рис. 3.5, б). Условие ортогональности запишем при помощи скалярного произведения $bigllangleoverrightarrow{M_0M},, vec{n}bigrrangle=0$ . Учитывая, что $overrightarrow{M_0M}=vec{r}-vec{r}_0$ , получаем векторное уравнение прямой:

$langlevec{r}-vec{r}_0,,vec{n}rangle=0.$

(3.5)

Это уравнение можно записать в другой форме. Преобразуем левую часть $langlevec{r}-vec{r}_0,, vec{n}rangle= langlevec{r}, vec{n}rangle- langlevec{r}_0,vec{n}rangle$ , используя свойства скалярного произведения. Обозначая $c=langlevec{r}_0, vec{n}rangle$ , получаем уравнение

langlevec{r},vec{n}rangle-c=0quad Leftrightarrow quad langlevec{r}, vec{n}rangle=c,

(3.6)

выражающее постоянство проекций на нормаль vec{n} радиус-векторов точек, принадлежащих прямой.

Векторное и общее уравнения прямой на плоскости

Получим координатную форму записи векторного уравнения прямой (3.5). Так как $vec{r}-vec{r}_0=(x-x_0)vec{i}+(y-y_0)vec{j}$ и vec{n}=Avec{i}+Bvec{j} , по формуле (1.9) находим $langlevec{r}-vec{r}_0,,vec{n}rangle=(x-x_0)A+(y-y_0)B$ или

Acdot(x-x_0)+Bcdot(y-y_0)=0.

(3.7)

Полученное соотношение (3.7) позволяет по координатам точки M_0(x_0,y_0) и координатам A,,B нормали vec{n} записать уравнение прямой без промежуточных вычислений.

Обозначив C=-Acdot x_0-Bcdot y_0 , получим общее уравнение прямой на плоскости

{color{red}boxed{{color{black}Acdot x+Bcdot y+C=0}}}

(3.8)

Поскольку коэффициенты и не равны нулю одновременно (это координаты ненулевого вектора vec{n} ), уравнение (3.8) является алгебраическим уравнением первой степени, т.е. линейным уравнением с двумя неизвестными. Следовательно, прямая является алгебраической линией первого порядка.

Проводя рассуждения в обратном порядке, делаем вывод о том, что линейное уравнение (3.8) задает на координатной плоскости прямую. Полученные выводы сделаны для прямоугольной системы координат, но, учитывая теорему 3.1, они переносятся (без изменений) и на любую аффинную систему координат.

Теорема (3.2) об алгебраической линии первого порядка. Всякое уравнение первой степени с двумя неизвестными задает в аффинной системе координат прямую, и наоборот, всякая прямая в любой аффинной системе координат может быть задана уравнением первой степени с двумя неизвестными. Другими словами, алгебраическая линия первого порядка есть прямая.

Замечания 3.2

1. При составлении общего уравнения прямой нормаль выбирается неоднозначно: можно выбрать любую, отличную от нуля, длину нормали vec{n} , а также одно из двух возможных направлений (противоположный вектор ( -vec{n} ) также является нормалью). Например, вместо нормали vec{n} можно взять нормаль -7vec{n} , что соответствует умножению обеих частей уравнения (3.8) на число .

2. Если один из коэффициентов уравнения прямой (3.8) равен нулю, общее уравнение прямой (3.8) принимает один из следующих частных видов:

а) если A=0 , уравнение (3.8) имеет вид By+C=0 или $y=-frac{C}{B}$ уравнение прямой, параллельной оси абсцисс (рис.3.6.a); при C=0 прямая y=0 совпадает с осью ;

б) если B=0 , уравнение (3.8) имеет вид Ax+C=0 или $x=-frac{C}{A}$ уравнение прямой, параллельной оси ординат (рис.3.6,б); при C=0 прямая x=0 совпадает с осью ;

в) если C=0 , уравнение (3.8) имеет вид Ax+By=0 – уравнение прямой, проходящей через начало координат (рис.3.6,в).

Уравнения прямой параллельные и перпендикулярные осям координат

3. Нормаль vec{n}=Avec{i}+Bvec{j} к прямой Ax+By+C=0 совпадает с градиентом функции f(x,y)=Ax+By+C :

$operatorname{grad}f(x,y)=nabla f(x,y)=frac{partial f(x,y)}{partial x}cdotvec{i}+frac{partial f(x,y)}{partial y}cdotvec{j}=Acdotvec{i}+Bcdotvec{j}=vec{n}.$

В курсе математического анализа доказывается, что градиент направлен в сторону наискорейшего возрастания функции в данной точке.

4. Прямая Ax+By+C=0 разбивает плоскость на две полуплоскости (рис.3.7,а): положительную, координаты всех точек которой удовлетворяют неравенству Ax+By+Cgeqslant0 , и отрицательную, для точек которой Ax+By+Cleqslant0 . Нормаль vec{n}=Avec{i}+Bvec{j} , приложенная к любой точке прямой, принадлежит положительной полуплоскости. Другими словами, нормаль, приложенная к произвольной точке прямой, указывает на положительную полуплоскость (рис.3.7,а).

Действительно, обозначим через p(x,y)=Ax+By+C — многочлен первой степени от двух переменных и . Тогда для любой точки M_0(x_0,y_0) , принадлежащей прямой (3.8), справедливо равенство p(x_0,y_0)=0 . Представим значение многочлена p(x,y) в произвольной точке $M^{ast}(x^{ast},y^{ast})$ плоскости в виде скалярного произведения:

$begin{aligned} p(x^{ast},y^{ast})&= p(x^{ast},y^{ast})-underbrace{p(x_0,y_0)}_{=0}=Acdot x^{ast}+Bcdot y^{ast}+C-underbrace{(Acdot x_0+Bcdot y_0+C)}_{=0}=\[3pt] &=Acdot(x^{ast}-x_0)+Bcdot(y^{ast}-y_0)=leftlangleoverrightarrow{M_0M^{ast}},,vec{n}rightrangle= left|overrightarrow{M_0M^{ast}}right|cdot|vec{n}|cdotcosvarphi, end{aligned}$

где $vec{n}=begin{pmatrix}A&Bend{pmatrix}^T$ — нормаль к прямой Ax+By+C=0 ; M_0(x_0,y_0) — точка, принадлежащая этой прямой. Знак выражения p(x,y) определяется величиной угла varphi между нормалью vec{n} и вектором $overrightarrow{M_0M^{ast}}$ . Например, для точки M_1(x_1,y_1) угол varphi_1 острый (рис.3.7,б), поэтому p(x_1,y_1)>0 , а для точки M_2(x_2,y_2) угол varphi_2 тупой (рис.3.7,б), поэтому p(x_1,y_1)<0 . Следовательно, координаты любой точки $M^{ast}(x^{ast},y^{ast})$ , принадлежащей полуплоскости, на которую указывает нормаль, удовлетворяют неравенству $Ax^{ast}+By^{ast}+Cgeqslant0$ , а координаты точек $M^{ast}(x^{ast},y^{ast})$ другой полуплоскости- неравенству $Ax^{ast}+By^{ast}+Cleqslant0$ .

Прямая и положительная и отрицательная полуплоскости

5. Абсолютное значение |Ax+By+C| пропорционально расстоянию от точки M(x,y) до прямой Ax+By+C=0 , т.е. отношение расстояний от точек M_1(x_1,y_1) и M_2(x_2,y_2) до прямой равно отношению $frac{|Ax_1+By_1+C|}{|Ax_2+By_2+C|}$ .

Действительно, в пункте 3 получено представление значений линейного трехчлена p(x,y)=Ax+By+C в виде скалярного произведения, которое можно выразить через алгебраическое значение длины ортогональной проекции:

$p(x^{ast},y^{ast})= leftlangle overrightarrow{M_0M^{ast}},,vec{n}rightrangle=operatorname{pr}_{vec{n}}overrightarrow{M_0M^{ast}}cdot|vec{n}|.$

Запишем отношение значений линейного трехчлена p(x,y) для двух точек M_1(x_1,y_1) и M_2(x_2,y_2) :

$frac{p(x_1,y_1)}{p(x_2,y_2)}= frac{operatorname{pr}_{vec{n}}overrightarrow{M_0M_1}cdot|vec{n}|}{operatorname{pr}_{vec{n}}overrightarrow{M_0M_2}cdot|vec{n}|}=frac{operatorname{pr}_{vec{n}}overrightarrow{M_0M_1}}{operatorname{pr}_{vec{n}}overrightarrow{M_0M_2}}.$

Учитывая, что абсолютная величина $bigl|operatorname{pr}_{vec{n}}overrightarrow{M_0M^{ast}},bigr|$ равна расстоянию от точки $M^{ast}$ до прямой, получаем искомое отношение

$frac{|operatorname{pr}_{vec{n}}overrightarrow{M_0M_1}|}{|operatorname{pr}_{vec{n}}overrightarrow{M_0M_2}|}=frac{|p(x_1,y_1)|}{p(x_2,y_2)}=frac{|Ax_1+By_1+C|}{|Ax_2+By_2+C|}.$

6. В аффинной системе координат $Ovec{e}_1vec{e}_2$ линейное уравнение ах a_1x_1+a_2x_2+a_3=0 задает, согласно теореме 3.2, прямую. Выводы, полученные в пунктах 2,3,4,5, остаются справедливыми с тем лишь исключением, что вектор $vec{n}=a_1vec{e}_1+a_2vec{e}_2$ не является нормалью.

Пример 3.5. На координатной плоскости Oxy (в прямоугольной системе координат) заданы точки K(1;2) и L(5;0) . Составить уравнение серединного перпендикуляра к отрезку (рис.3.8).

Уравнение серединного перпендикуляра к отрезку

Решение. Серединный перпендикуляр, по определению, проходит перпендикулярно отрезку через его середину. Находим координаты середины отрезка :

$M!left(frac{1+5}{2};,frac{2+0}{2}right)$ то есть M(3;1) .

Вектор overrightarrow{KL} можно взять в качестве нормали для серединного перпендикуляра. Находим координаты этого вектора, вычитая из координат его конца соответствующие координаты его начала:

$overrightarrow{KL}=begin{pmatrix}5\0end{pmatrix}-begin{pmatrix}1\2end{pmatrix}=begin{pmatrix}4\-2end{pmatrix}=begin{pmatrix}A\Bend{pmatrix}=vec{n}$

Следовательно, уравнение (3.8) искомой прямой имеет вид 4x-2y+C=0 . Осталось найти величину свободного члена . Поскольку точка M(3;1) принадлежит прямой, то ее координаты x=3,~y=1 должны удовлетворять уравнению этой прямой, следовательно, 4cdot3-2cdot1+C=0 . Отсюда C=10 . Таким образом, серединный перпендикуляр задается уравнением

4x-2y-10=0 quad Leftrightarrow quad 2x-y-5=0.

Уравнение этой прямой можно было получить в виде (3.7), подставляя координаты нормали $vec{n}=begin{pmatrix}4&-2end{pmatrix}^T$ и точки M(3;1)colon4(x-3)-2(y-1)=0 .

Решение задачи получено аналитически без использования графического изображения (рис.3.8). Чертеж в аналитической геометрии служит, как правило, лишь иллюстрацией к решению.

Расстояние от точки до прямой

Пусть заданы на плоскости прямая, описываемая общим уравнением (3.8) Ax+By+C=0 , и точка $M(x^{ast},y^{ast})$ . Требуется найти расстояние от точки до прямой.

Искомое расстояние равняется длине ортогональной проекции вектора $overrightarrow{M_0M^{ast}}$ на направление нормали vec{n} (рис.3.9):

$d=left|operatorname{pr}_{vec{n}}overrightarrow{M_0M^{ast}}right|=frac{|langlevec{n},,overrightarrow{M_0M^{ast}}rangle|}{|vec{n}|}$ , где M_0(x_0,y_0) — любая точка на заданной прямой.

Запишем правую часть в координатной форме, выражая скалярное произведение и длину через координаты векторов $vec{n}=begin{pmatrix}A&Bend{pmatrix}^T$ , $overrightarrow{M_0M^{ast}}=begin{pmatrix}x^{ast}-x_0&y^{ast}-y_0end{pmatrix}^T$ :

$d=frac{|Acdot (x^{ast}-x_0)+Bcdot (y^{ast}-y_0)|}{sqrt{A^2+B^2}}=frac{|Ax^{ast}+By^{ast}-(Ax_0+By_0)}{sqrt{A^2+B^2}|}.$

Поскольку координаты точки M_0(x_0,y_0) удовлетворяют уравнению (3.8), то Ax_0+By_0=-C . Подставляя это выражение, получаем формулу расстояния от точки $M^{ast}(x^{ast},y^{ast})$ до прямой Ax+By+C=0

$d=frac{|Acdot x^{ast}+Bcdot y^{ast}+C|}{sqrt{A^2+B^2}},.$

(3.9)

Пример 3.6. На координатной плоскости Oxy (в прямоугольной системе координат) заданы точки K(1;2) и L(5;0) . Требуется найти, в каком отношении прямая mcolon 3x-4y-10=0 делит отрезок .

Прямая, делящая отрезок в отношении

Решение. Найдем значения линейного трехчлена p(x,y)=3x-4y-10 в точках K(1;2) и L(5;0) : p(1;2)=3cdot1-4cdot2-10=-15 ; p(5;0)=5 . Получили значения разных знаков. Следовательно, точки и лежат по разные стороны от прямой (согласно пункту 4 замечаний 3.2, эти точки лежат в разных полуплоскостях), т.е. прямая действительно пересекает отрезок (в точке на рис.3.10). Так как эти значения по абсолютной величине пропорциональны расстояниям от точек и до прямой , то

$frac{KM}{ML}=frac{|p(1;2)|}{|p(5;0)|}=frac{|-15|}{|5|}=frac{3}{1}.$

Этот же результат можно получить по формуле (3.9). Находим расстояния d_K и d_L от точек и до прямой :

$d_k=frac{|3cdot1-4cdot2-10|}{sqrt{3^2+(-4)^2}}=frac{15}{5}=3;qquad d_L=frac{|3cdot5-4cdot0-10|}{sqrt{3^2+(-4)^2}}=frac{5}{5}=1$

Следовательно, $frac{KM}{ML}=frac{d_k}{d_L}=frac{3}{1}$ .

Нормированное уравнение прямой

Преобразуем общее уравнение прямой AX+By+C=0 следующим образом. Если свободный член C<0 , то разделим обе части на длину нормали $|vec{n}|=sqrt{A^2+B^2}$ , а если Cgeqslant0 , то разделим на $-|vec{n}|=-sqrt{A^2+B^2}$ . Получим уравнение

$frac{A}{pmsqrt{A^2+B^2}}cdot x+frac{B}{pmsqrt{A^2+B^2}}cdot y+frac{C}{pmsqrt{A^2+B^2}}=0,$

в котором свободный член $frac{C}{pmsqrt{A^2+B^2}}$ , в силу описанного выбора знака, неположительный. Обозначим его через $-rho=frac{C}{pmsqrt{A^2+B^2}}$ . Коэффициенты при неизвестных являются координатами единичного вектора $frac{1}{|vec{n}|}cdotvec{n}$ или $-frac{1}{|vec{n}|}cdotvec{n}$ , и равны направляющим косинусам:

$cosalpha=frac{A}{pmsqrt{A^2+B^2}}, qquad cosbeta=frac{B}{pmsqrt{A^2+B^2}}.$

Тогда уравнение принимает вид (3.10) и называется нормированное уравнение прямой

xcdotcosalpha+ycdotcosbeta-rho=0, quad rhogeqslant0,

(3.10)

Замечания 3.3

1. Свободный член rho нормированного уравнения (3.10) равен расстоянию от начала координат до прямой.

Действительно, по формуле (3.9) находим расстояние от начала координат O(0;0) до прямой, описываемой уравнением (3.10):

Нормированное уравнение прямой

$d=frac{|0cdotcosalpha+0cdotcosbeta-rho|}{sqrt{cos^2alpha+cos^2beta}}=frac{rho}{1}=rho.$

2. Нормированное уравнение прямой (3.10) можно записать в виде (3.7): langlevec{r},vec{n}rangle=rho , если в качестве нормали л выбрать единичный вектор vec{n}=cosalphacdotvec{i}+cosbetacdotvec{j} , так как xcosalpha+ycosbeta=langlevec{r},vec{n}rangle . Из двух возможных единичных нормалей условию rho>0 отвечает нормаль vec{n} , направленная к прямой (рис.3.11), если вектор vec{n} приложить к началу координат. При выборе противоположного вектора (-vec{n}) получилось бы отрицательное значение rho , которое не допускается в уравнении (3.10).

3. Коэффициенты общего уравнения прямой (3.8) определяются неоднозначно в силу неоднозначного выбора нормали. При составлении нормированного уравнения (3.10) прямой такого произвола нет. Здесь все коэффициенты определены однозначно (при rho>0 ) или с точностью до знака (при rho=0 ).

4. Нормированное уравнение прямой имеет смысл только в прямоугольной системе координат.

Пример 3.7. На координатной плоскости Oxy (в прямоугольной системе координат) заданы вершины P(1;2),~Q(13;-3),~R(5;5) треугольника (рис.3.12). Требуется:

а) составить общее и нормированное уравнения прямой, содержащей высоту ;

б) найти расстояние от начала координат до прямой ;

в) найти расстояние от точки до прямой .

Решение. а) Вектор overrightarrow{RQ} , перпендикулярный прямой , является нормалью для этой прямой. Находим координаты вектора vec{n}=overrightarrow{RQ} , вычитая из координат конца координаты его начала:

Вершины треугольника на координатной плоскости

$vec{n}=begin{pmatrix}13\-3end{pmatrix}-begin{pmatrix}5\5end{pmatrix}=begin{pmatrix}8\-8end{pmatrix}.$

Коэффициенты при неизвестных в общем уравнении прямой равны координатам нормали, поэтому A=8 и B=-8 , т.е. уравнение имеет вид 8x-8y+C=0 . Подберем свободный член так, чтобы прямая проходила через точку . Для этого подставим координаты x=1 и y=2 точки в уравнение: 8cdot1-8cdot2+C=0 . Отсюда C=8 . Таким образом, искомое общее уравнение имеет вид: x-y+1=0 .

Преобразуем общее уравнение x-y+1=0 . Поскольку в этом уравнении A=1,~B=-1,~C=1>0 , разделим его на $-sqrt{A^2+B^2}=-sqrt{1^2+(-1)^2}=-sqrt{2}$ . Получим нормированное уравнение прямой $PHcolon-frac{x}{sqrt{2}}+frac{y}{sqrt{2}}-frac{1}{sqrt{2}}=0$ . Сравнивая с (3.10), находим направляющие косинусы $cosalpha=-frac{1}{sqrt{2}},~cosbeta=frac{1}{2}$ и параметр $rho=frac{1}{sqrt{2}}$ .

б) Из пункта 1 замечаний 3.3 следует, что искомое расстояние от начала координат до прямой равно $rho=frac{1}{sqrt{2}}$ .

в) Расстояние от точки Q(13;-3) до прямой PHcolon x-y+1=0 находим по формуле (3.9):

$d=frac{|1cdot13+(-1)cdot(-3)+1|}{sqrt{1^2+(-1)^2}}=frac{17}{sqrt{2}}.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Типы уравнений прямой.

Название
уравнения определяется названием
постоянных величин, определяющих
положение прямой линии в системе
координат.

Уравнение
прямой линии, проходящей через данную
точку
,
перпендикулярно данному вектору

имеет вид:

(1)

Оно
вытекает из условия того, что скалярное
произведение взаимно перпендикулярных
векторов равно нулю.

Действительно,
возьмем на прямой произвольную точку
.
Образуем текущий вектор,
направленный из точкив точку.
Этот вектор будет иметь координаты,
и направлен он будет вдоль прямой. Второй
вектор – это данный вектор.
Скалярное произведение этих векторов
равно нулю, отсюда и вытекает уравнение
прямой.

Общее
уравнение прямой линии:

(2)

где
коэффициенты при неизвестных
суть координаты нормального вектора
прямой. Действительно, раскроем скобки
в предыдущем уравнении:

Теорема
1.
Всякая
прямая на плоскости имеет уравнение
первой степени, и всякое уравнение
первой степени является уравнением
некоторой прямой.

Следствия.

a)
– уравнение прямой, параллельной оси(,
уравнение оси),

б)

– уравнение прямой, параллельной оси(,
уравнение оси),

в)
– прямая линия, проходящая через начало
координат.

Замечание.
При переменном коэффициенте
– это будут уравнения пучка прямых,
проходящих через начало координат.

Уравнение
прямой линии, проходящей через данную
точку
,
параллельно данному вектору(каноническое):

(3)

Вектор
вдоль прямой
коллинеарен вектору,
отсюда это условие.

Уравнение
прямой, проходящей через данную точку
в заданном направлении:

(4)

Замечание.
При переменном коэффициентеуравнение называется уравнением пучка
прямых линий, проходящих через точку.

Уравнение
прямой линии с угловым коэффициентом
(рис. 4):

(5)

Здесь

.
К этому виду нельзя привести прямую,
параллельную оси
.

Уравнение
прямой, проходящей через две данные
точки:

(6)

Действительно,
пусть даны две точки
и,
через которые должна пройти наша прямая.
На этой прямой возьмем текущую точкуи образуем два вектора:и.
Эти два вектора коллинеарные, отсюда и
вытекает уравнение.

Замечание.
Если
,то
уравнение прямой
;
если,
то.

3. Угол между двумя прямыми. Условие параллельности и перпендикулярности.

1) Пусть
прямые линии заданы общими уравнениями:

где
нормальные векторы:

и
₂,

– угол между векторами
и
,
т.е. угол между прямыми. Тогда:

(7)

Условие
параллельности прямых эквивалентно
условию коллинеарности их нормальных
векторов:

(8)

Условие
перпендикулярности прямых – ортогональность
векторов
и:

(9)

2) Пусть
прямые линии заданы с угловыми
коэффициентами(рис.
5):,

где

.
Тогда

Это
вытекает из формулы тангенса суммы
углов.
,,,,(*).

За
принимаем угловой коэффициент той
прямой, которую надо вращать против
хода часовой стрелки, чтобы обойти уголдо совмещения со второй прямой.

Условие
параллельности прямых:

Условие
перпендикулярности прямых:

Расстояние
точки
от прямойопределяется формулой:

(10)

Доказательство
смотри в другом файле.

Замечания.

1.
Если две прямые
изаданы в каноническом виде, то угол
между ними можно рассматривать как угол
между их направляющими векторами,
а значит,

(11)

Пример
1.

Даны
точки
,,.

Найти:

1)
Уравнение прямой
.

Согласно
уравнению (6) (уравнение прямой, проходящей
через две точки), запишем:

,
или
.

2)
Уравнение прямой
,
проходящей через точку,
параллельно прямой.

Согласно
уравнению (1), (уравнение прямой, проходящей
через точку параллельно данному вектору)
точка
это точка,
параллельно прямойзначит перпендикулярно ее нормальному
вектору.
Следовательно, запишем

3) Уравнение
прямой
,
проходящей через точку,
перпендикулярно прямой.

Перпендикулярно
прямой, значит параллельно ее нормальному
вектору, в нашем случае
. Точкаэто точка.
Согласно уравнению (3), запишем

4)
Уравнение медианы
треугольника.

На
медиане
образуем текущий вектор.

Найдем
координаты точки
– середины стороны:

Образуем
вектор
,
расположенный параллельно текущему
вектору.
Тогда, в силу условия параллельности
векторов, получим уравнение медианы:

,
или
.

5)
Уравнение высоты
.

На
высоте
возьмем текущую точкуи образуем текущий вектор.
Так как,
где,
то условие перпендикулярности этих
векторов порождает уравнение прямой(скалярное произведение векторов равно
нулю):

или

6)
Длину высоты
.

Заметим,
что длина высоты
равна расстоянию от точкидо прямой.
Чтобы воспользоваться формулой (10),
сначала найдем уравнение прямой.

На
стороне
образуем текущий вектор.

Запишем
условие параллельности векторов
,
где:

,
или в общем виде
.

Теперь,
подставляя известные данные в формулу
(10), имеем:

Пример
2. Дана
прямая
:и точка.

Найти:

1)
Для прямой
уравнение
с угловым коэффициентом, угловой
коэффициент
,
отрезок, отсекаемый по оси ординат.

Разрешив
уравнение прямой
относительно,
получаем уравнение с угловым коэффициентом:

.
Отсюда,.

Нормаль
и
направляющий векторпрямой–.

Коэффициенты
при переменных
в общем уравнении прямой,
есть координаты нормального вектора,
то есть.

Поскольку
направляющий вектор
прямой– это любой ненулевой вектор, параллельный
этой прямой, то выполняется условие
(перпендикулярность векторов):

где

Дадим
величине
какое-нибудь значение. Пусть, например,,
тогда,
то есть

.
Получаем направляющий вектор
.

Каноническое
уравнение прямой
.

Для
составления канонического уравнения
(3) прямой
нам необходимо знать точку,
лежащую на,
и направляющий вектор.
Так как координаты векторабыли получены нами ранее в задание 2,
осталось найти координаты точки.

Зафиксируем
произвольное значение, например,
и подставим его в уравнение прямой.
Получим.
Следовательно,.

Воспользовавшись
теперь каноническим уравнением прямой
(10), находим:

Уравнение
прямой
,
параллельной–и проходящей через точку.

Прежде
всего, заметим, что точка
не лежит на прямой,
поскольку ее координаты не удовлетворяют
уравнению этой прямой. Поэтому можно
построить прямую,
проходящую черезпараллельно,
но не совпадающую с.

Пусть
– текущая точка прямой.
Так как текущий векторперпендикулярен вектору нормалипрямой,
то.
Отсюда получаем уравнение прямой:

или

уравнение
прямой
,
перпендикулярной–

и проходящей через точку.

Пусть
– текущий вектор прямой.
Из условия параллельностии нормалипрямой,
получаем уравнение:

Пример
3.

Проверить, являются ли прямые линии

Параллельными.

Прямые

ибудут параллельны, если их нормали.
Из общего уравнения прямойнайдем нормаль.
Чтобы найти нормаль
₂
приведем уравнение прямой
к общему виду:.
Отсюда
.

Поскольку
условие параллельности векторови
₂не
выполняется, так как
,
стало быть,и

не параллельны.

б)
Перпендикулярными.

Прямые
ибудут
перпендикулярны, если
₂.
Но условие перпендикулярности для
векторов
и
₂не
выполняется, так как
.
Следовательно,не перпендикулярна.

в)
Найти угол
междуи.

Угол
между прямыми равен углу между их
нормалями. Поэтому, используя формулу
угла между двумя векторами, получим

Так
как
,
,

,
то
.

Соседние файлы в папке Лекц.Мат-ка Базов

Источник

5.5.6. Как найти прямую, перпендикулярную данной?

Обращаю внимание, что для скрещивающихся прямых таких прямых можно провести бесконечно много, а вот для

пересекающихся – задача имеет единственное решение:

Задача 157

а) Составить уравнения прямой, проходящей через точку перпендикулярно

прямой (прямые пересекаются).

б) Найти расстояние от точки до прямой , в) симметричную точку .

а) Решение: обозначим неизвестную прямую через :

И начинаем

раскручивать задачу: что нам известно об этой прямой?

Известна её точка . Неплохо бы найти направляющий вектор. В качестве

такого вектора вполне подойдёт вектор . Но мы не знаем точку . Вот ей-то и займёмся

План есть, и мы счастливы:

1) Вытащим из уравнений прямой «эль» её направляющий вектор , а сами

уравнения перепишем в параметрической форме:

И вот уже в третий раз используем тот же самый фокус. Рассмотрим точку с пока ещё неизвестными координатами. Поскольку точка , то её

координаты удовлетворяют параметрическим уравнениям прямой «эль» и им

соответствует конкретное значение параметра :
, или в строчку:

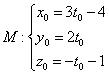
Тогда:

2) По условию прямые должны быть перпендикулярны, следовательно, их направляющие векторы – ортогональны. А если векторы ортогональны, то их скалярное

произведение равно нулю:

Что получилось? Простейшее линейное уравнение с одной неизвестной:

3) Значение параметра известно, находим точку:

И направляющий вектор: .

4) Уравнения прямой составим по точке и вектору… избавимся-ка мы от дробей и возьмём направляющий вектор :

Ответ:

Но, разумеется, тут можно было взять и вектор :

Проверка состоит из двух этапов:

1) проверяем направляющие векторы прямых на ортогональность;

2) подставляем координаты точки в уравнения каждой прямой, они должны «подойти» и там и там.

Об этих действиях говорилось много, поэтому я выполнил проверку на черновике.

5.5.7. Как найти расстояние от точки до прямой?

5.5.5. Пересекающиеся прямые в пространстве

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

Решение примеров

Прямая линия. Уравнение прямой.

Уравнения прямой, проходящей через точку перпендикулярно вектору

Общее уравнение прямой

Расстояние от точки до прямой

Нормированное уравнение прямой

Типы уравнений прямой.

3. Угол между двумя прямыми. Условие параллельности и перпендикулярности.

5.5.6. Как найти прямую, перпендикулярную данной?

Вам также может понравиться

Как составить закон распределения дискретной случайной величины примеры

Как найти номер владельца по вин номеру

Как найти эонакса в вов

Добавить комментарий Отменить ответ