Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой (общее уравнение прямой на плоскости и его исследование). Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и его исследование, как осуществлять переходы от общего уравнения к другим типам уравнений прямой (неполного уравнения, полного уравнения). Всю теорию закрепим иллюстрациями и решением практических задач на уравнения.
Общее уравнение прямой: основные сведения
Как найти уравнение прямой? Пусть на плоскости задана прямоугольная система координат Oxy.
Любое уравнение первой степени, имеющее вид Ax+By+C=0, где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид Ax+By+C=0 при некотором наборе значений А, В, С.
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение Ax+By+C=0 определяет на плоскости прямую.
Пусть существует некоторая точка М0(x0, y0), координаты которой отвечают уравнению Ax+By+C=0. Таким образом: Ax0+By0+C=0. Вычтем из левой и правой частей уравнений Ax+By+C=0 левую и правую части уравнения Ax0+By0+C=0, получим новое уравнение, имеющее вид A(x-x0)+B(y-y0)=0. Оно эквивалентно Ax+By+C=0.
Полученное уравнение A(x-x0)+B(y-y0)=0 является необходимым и достаточным условием перпендикулярности векторов n→=(A, B) и M0M→=(x-x0, y-y0). Таким образом, множество точек M(x, y) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n→=(A, B). Можем предположить, что это не так, но тогда бы векторы n→=(A, B) и M0M→=(x-x0, y-y0) не являлись бы перпендикулярными, и равенство A(x-x0)+B(y-y0)=0 не было бы верным.

Следовательно, уравнение A(x-x0)+B(y-y0)=0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение Ax+By+C=0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени Ax+By+C=0.
Зададим в прямоугольной системе координат на плоскости прямую a; точку M0(x0, y0), через которую проходит эта прямая, а также нормальный вектор этой прямой n→=(A, B).
Пусть также существует некоторая точка M(x, y) – плавающая точка прямой. В таком случае, векторы n→=(A, B) и M0M→=(x-x0, y-y0) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n→, M0M→=A(x-x0)+B(y-y0)=0
Перепишем уравнение Ax+By-Ax0-By0=0, определим C: C=-Ax0-By0 и в конечном результате получим уравнение Ax+By+C=0.
Так, без какой-либо помощи онлайн мы смогли доказать и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид Ax+By+C=0 – это общее уравнение прямой на плоскости в прямоугольной системе координат Oxy (уравнение прямой параллельной оси ox).
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой Ax+By+C=0.
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2x+3y-2=0, которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n→= (2, 3). Изобразим заданную прямую линию из уравнения с вектором на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2x+3y-2=0, поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ·Ax+λ·By+λ·C=0, умножив обе части общего уравнения прямой на число λ, не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой Ax+By+C=0, в котором числа А, В, С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А=0, В≠0, С≠0, общее уравнение принимает вид By+C=0. Такое неполное общее уравнение задает в прямоугольной системе координат Oxy прямую, которая параллельна оси Ox, поскольку при любом действительном значении x переменная y примет значение -CB . Иначе говоря, общее уравнение прямой Ax+By+C=0, когда А=0, В≠0, задает геометрическое место точек (x, y), координаты которых равны одному и тому же числу -CB.
- Если А=0, В≠0, С=0, общее уравнение принимает вид y=0. Такое неполное уравнение определяет ось абсцисс Ox.
- Когда А≠0, В=0, С≠0, получаем неполное общее уравнение Ax+С=0, задающее прямую, параллельную оси ординат.
- Пусть А≠0, В=0, С=0, тогда неполное общее уравнение примет вид x=0, и это есть уравнение координатной прямой Oy.
- Наконец, при А≠0, В≠0, С=0, неполное общее уравнение принимает вид Ax+By=0. И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел (0, 0) отвечает равенству Ax+By=0, поскольку А·0+В·0=0.
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Известно, что заданная прямая параллельна оси ординат и проходит через точку 27, -11. Необходимо написать общее уравнение заданной прямой. Попробуем его составить.
Решение
Решение лежит на поверхности. Прямая, параллельная оси ординат, задается уравнением вида Ax+C=0, в котором А≠0. Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения Ax+C=0, т.е. верно равенство:
A·27+C=0
Из него возможно определить C, если придать A какое-то ненулевое значение, к примеру, A=7. В таком случае получим: 7·27+C=0⇔C=-2. Нам известны оба коэффициента A и C, подставим их в уравнение Ax+C=0 и получим требуемое уравнение прямой: 7x-2=0
Ответ: 7x-2=0
На чертеже изображена прямая, необходимо записать ее уравнение. Как будем это находить?

Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси Ox и проходит через точку (0, 3).
Прямую, которая будет являться параллельной оси абсцисс, определяет неполное общее уравнение By+С=0. Найдем значения B и C. Координаты точки (0, 3), поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой By+С=0, тогда справедливым является равенство: В·3+С=0. Зададим для В какое-то значение, отличное от нуля. Допустим, В=1, в таком случае из равенства В·3+С=0 можем найти С: С=-3. Используем известные значения В и С, получаем требуемое уравнение прямой: y-3=0.
Ответ: y-3=0.
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М0(x0, y0), тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: Ax0+By0+C=0. Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A(x-x0)+B(y-y0)+C=0, это уравнение эквивалентно исходному общему, проходит через точку М0(x0, y0) и имеет нормальный вектор n→=(A, B).
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М0(-3, 4), через которую проходит прямая, и нормальный вектор этой прямой n→=(1, -2). Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А=1, В=-2, x0=-3, y0=4. Тогда:
A(x-x0)+B(y-y0)=0⇔1·(x-(-3))-2·y(y-4)=0⇔⇔x-2y+22=0
Задачу можно решать иначе. Как она будет решаться? Общее уравнение прямой имеет вид Ax+By+C=0. Заданный нормальный вектор (векторная прямая) позволяет получить значения коэффициентов A и B в уравнении прямой, тогда:
Ax+By+C=0⇔1·x-2·y+C=0⇔x-2·y+C=0
Теперь найдем значение С, используя заданную условием задачи точку М0(-3, 4), через которую проходит прямая. Координаты этой точки отвечают уравнению x-2·y+C=0, т.е. -3 – 2·4+С=0. Отсюда С=11. Требуемое уравнение прямой принимает вид: x – 2·y + 11=0.
Ответ: x – 2·y + 11=0.
Задана прямая 23x-y-12=0 и точка М0, лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна -3. Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М0 как x0 и y0. В исходных данных указано, что x0=-3. Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
23×0-y0-12=0
Определяем y0: 23·(-3)-y0-12=0⇔-52-y0=0⇔y0=-52
Ответ: -52
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида Ax+By+C=0 к каноническому уравнению x-x1ax=y-y1ay.
Если А≠0, тогда переносим слагаемое By в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: Ax+CA=-By.
Это равенство возможно записать как пропорцию: x+CA-B=yA .
В случае, если В≠0, оставляем в левой части общегь уравнения только слагаемое Ax, прочие переносим в правую часть, получаем: Ax=-By-C. Выносим –В за скобки, тогда: Ax=-By+CB.
Перепишем равенство в виде пропорции: x-B=y+CBA .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3y-4=0. Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3y-4=0. Далее действуем по алгоритму: в левой части остаётся слагаемое 0x; а в правой части выносим -3 за скобки; получаем: 0x=-3y-43.
Запишем полученное равенство как пропорцию: x-3=y-430. Так, мы получили уравнение канонического вида.
Ответ: x-3=y-430.
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Перед нами задание. Прямая задана уравнением 2x-5y-1=0. Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2x-5y-1=0⇔2x=5y+1⇔2x=5y+15⇔x5=y+152
Теперь примем обе части полученного канонического уравнения равными λ, тогда:
x5=λy+152=λ⇔x=5·λy=-15+2·λ, λ∈R
Ответ: x=5·λy=-15+2·λ, λ∈R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y=k·x+b, но только тогда, когда В≠0. Для перехода в левой части оставляем слагаемое By, остальные переносятся в правую. Получим: By=-Ax-C. Разделим обе части полученного равенство на B, отличное от нуля: y=-ABx-CB.
Задано общее уравнение прямой: 2x+7y=0. Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2x+7y=0⇔7y-2x⇔y=-27x
Ответ: y=-27x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида xa+yb=1. Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на –С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y:
Ax+By+C=0⇔Ax+By=-C⇔⇔A-Cx+B-Cy=1⇔x-CA+y-CB=1
Необходимо преобразовать общее уравнение прямой x-7y+12=0 в уравнение прямой в отрезках.
Решение
Перенесем 12 в правую часть: x-7y+12=0⇔x-7y=-12.
Разделим на -1/2 обе части равенства: x-7y=-12⇔1-12x-7-12y=1.
Преобразуем далее в необходимый вид: 1-12x-7-12y=1⇔x-12+y114=1.
Ответ: x-12+y114=1.
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
xa+yb⇔1ax+1by-1=0⇔Ax+By+C=0y=kx+b⇔y-kx-b=0⇔Ax+By+C=0
Каноническое уравнение преобразуется к общему по следующей схеме:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax(y-y1)⇔⇔ayx-axy-ayx1+axy1=0⇔Ax+By+C=0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔Ax+By+C=0
Заданы параметрические уравнения прямой x=-1+2·λy=4. Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x=-1+2·λy=4⇔x=-1+2·λy=4+0·λ⇔λ=x+12λ=y-40⇔x+12=y-40
Перейдем от канонического к общему:
x+12=y-40⇔0·(x+1)=2(y-4)⇔y-4=0
Ответ: y-4=0
Задано уравнение прямой в отрезках x3+y12=1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x3+y12=1⇔13x+2y-1=0
Ответ: 13x+2y-1=0.
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A(x-x0)+B(y-y0)=0. Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2x-3y+33=0. Также известна точка M0(4, 1), через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n→=(2, -3): 2x-3y+33=0. Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A(x-x0)+B(y-y0)=0⇔2(x-4)-3(y-1)=0⇔2x-3y-5=0
Ответ: 2x-3y-5=0.
Заданная прямая проходит через начало координат перпендикулярно прямой x-23=y+45. Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x-23=y+45.
Тогда n→=(3, 5). Прямая проходит через начало координат, т.е. через точку О(0, 0). Составим общее уравнение заданной прямой:
A(x-x0)+B(y-y0)=0⇔3(x-0)+5(y-0)=0⇔3x+5y=0
Ответ: 3x+5y=0.
Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.
Здесь будет калькулятор
Уравнение прямой с угловым коэффициентом
y=kx+by=kx+b,
где kk — угловой коэффициент, а bb — свободный коэффициент.
Уравнения данного вида составляются следующим образом по формуле:
y−y0=k(x−x0)y-y_0=k(x-x_0),
где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.
Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.
Решение
Подставляем значения в формулу:
y−y0=k(x−x0)y-y_0=k(x-x_0)
y−2=1⋅(x−1)y-2=1cdot(x-1)
Приводим подобные слагаемые:
y=x+1y=x+1
Ответ
y=x+1y=x+1
Общее уравнение прямой
Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:
y−x−1=0y-x-1=0
Уравнение прямой по двум точкам
Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},
где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.
Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).
Решение
x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}
x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}
x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}
x−4=−y−12x-4=frac{-y-1}{2}
y+1=2⋅(4−x)y+1=2cdot(4-x)
y=8−2x−1y=8-2x-1
y=−2x+7y=-2x+7
Ответ
y=−2x+7y=-2x+7
Уравнение прямой при помощи точки и вектора нормали
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.
Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).
Решение
x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,
x−7+40−5y=0x-7+40-5y=0
x−5y=−40+7x-5y=-40+7
x−5y=−33x-5y=-33
5y=x+335y=x+33
y=x5+335y=frac{x}{5}+frac{33}{5}
Проверка
Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.
8=75+3358=frac{7}{5}+frac{33}{5}
8=88=8 — верно, ответ правильный.
Ответ
y=x5+335y=frac{x}{5}+frac{33}{5}
Прямая в пространстве
Уравнение прямой, заданной в пространстве имеет такой вид:
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.
Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).
Решение
x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Проверка
Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:
1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.
Такой вид уравнения прямой называется каноническим.
Ответ
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Тест по теме “Составление уравнения прямой”
Загрузить PDF
Загрузить PDF
В тригонометрии есть задачи, в которых нужно найти уравнение прямой. При этом даны либо координаты одной точки и угловой коэффициент, либо координаты двух точек, которые лежат на прямой. В любом случае найти уравнение прямой довольно легко, если использовать соответствующие формулы.
-

1
Подставьте значение углового коэффициента «k» в альтернативное уравнение прямой y-y1 = k(x-x1). С помощью этого уравнения, в котором присутствуют координаты точки, которая лежит на прямой, можно найти координаты точки пересечения прямой с осью Oy. Данное значение углового коэффициента «k» подставьте вместо «k» в уравнении y-y1= k(x-x1).[1]
- Например, угловой коэффициент k = 2, тогда уравнение запишется так: y-y1= 2 (x-x1).
-

2
Вместо x1 и y1 подставьте координаты данной точки, чтобы записать окончательное уравнение прямой.[2]
- Например, если дана точка с координатами (4,3), уравнение запишется так: y-3 = 2(x-4).
-

3
Изолируйте «y», чтобы записать уравнение прямой в конечном виде. Чтобы раскрыть скобки, примените свойство дистрибутивности, а затем следуйте определенному порядку выполнения математических операций.
- Раскрыв скобки, вы получите: y-3 = 2x-8.
- Теперь прибавьте 3 к каждой стороне уравнения, чтобы изолировать «y».
- Окончательное уравнение прямой, которая проходит через точку с координатами (4, 3) и имеет угловой коэффициент 2, запишется так: y = 2x-5.
Реклама
-

1
Вычислите угловой коэффициент по формуле k = (y2-y1)/(x2-x1). Вам будут даны две пары координат; каждая пара координат записывается так: (x, y). Первую пару координат обозначьте как (x1, y1), а вторую как (x2, y2). Подставьте числа в формулу k = (y2-y1)/(x2-x1) и вычислите угловой коэффициент k.[3]
- Например, даны две точки с координатами (3, 8) и (7, 12). Тогда формула запишется так: k = (12-8)/(7-3) = 4/4 = 1. В этом примере угловой коэффициент k = 1.
-

2
Подставьте найденное значение углового коэффициента k в стандартное уравнение прямой. Уравнение прямой имеет следующий вид: y = kx + b, где k — угловой коэффициент, b — координата «y» точки пересечения прямой с осью Oy. В уравнение прямой подставьте найденное значение углового коэффициента вместо «k».[4]
- В нашем примере уравнение прямой запишется так: y = 1x + b или y = x + b.
-

3
Вместо «x» и «y» подставьте координаты одной из данных точек, чтобы найти «b». Координаты подставьте в уравнение прямой — вместо «х» подставьте координату «х», а вместо «y» координату «y».[5]
- В нашем примере возьмем точку с координатами (3, 8). Тогда уравнение прямой запишется так: 8 = 1(3) + b.
- Используйте координаты одной из двух данных точек, но никогда не смешивайте координаты сразу двух точек.
-

4
Вычислите «b». Сделайте это, когда в уравнение прямой подставите значения «k», «х» и «у». Изолируйте «b» на одной стороне уравнения, следуя определенному порядку выполнения математических операций.[6]
- В нашем примере уравнение приняло вид 8 = 1(3) + b. Умножьте 1 на 3 и получите 8 = 3 + b. Теперь вычтите 3 из каждой стороны уравнения, чтобы изолировать «b». Вы получите 5 = b, или b = 5.
-

5
Подставьте найденные значения «k» и «b» в уравнение прямой, чтобы записать его в окончательном виде.
- В нашем примере уравнение прямой, которая проходит через точки с координатами (3, 8) и (7, 12), запишется так: y = 1x + 5 или просто y = x + 5.
Реклама
Об этой статье
Эту страницу просматривали 31 161 раз.
Была ли эта статья полезной?
Как составить уравнение прямой, если дана только одна точка?
Ученик
(109),
на голосовании
3 года назад
Голосование за лучший ответ
Остерегайтесь Любительских научных исследований
Профи
(590)
3 года назад
Я тоже не изучал эту тему, но вот
4.Видишь там значок перпендикуляра? Это ведь наверняка должно значить что у любой другой точки этой линии будет такая же координата по игрику
5. а тут наоборот будет одинаковая координата по иксу
6.а тут точка пересекает начало координат, что значит вторая точка может быть (0;0)
Знаешь вот эту формулку? Это уравнение прямой по двум точкам. Х1- координата х первой точки Х2 – координата х второй точки. Так же и с игриками. У двух точек 4 координаты. Подставляй их и получишь зависимость от х и у, которое и называется уравнением прямой.
2.2.2. Как составить уравнение прямой
по точке и направляющему вектору?
Если известна некоторая точка ![]() , принадлежащая прямой, и направляющий вектор
, принадлежащая прямой, и направляющий вектор ![]() этой прямой
этой прямой ![]() , то уравнение данной прямой можно составить по формуле:
, то уравнение данной прямой можно составить по формуле:
![]()
Иногда его называют каноническим уравнением прямой.
Что делать, когда одна из координат ![]() равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты равняться нулю не могут, так как нулевой вектор не задаёт конкретного направления.
равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты равняться нулю не могут, так как нулевой вектор не задаёт конкретного направления.
Задача 61
Составить уравнение прямой по точке ![]() и направляющему вектору
и направляющему вектору ![]() .
.
Решение: Используем формулу ![]() . В данном случае:
. В данном случае:
![]()
С помощью свойств пропорции* (Школьные материалы) избавляемся от дробей:
![]() (* технически здесь также можно умножить обе части на 2)
(* технически здесь также можно умножить обе части на 2)
и приводим уравнение к общему виду:
![]()
Ответ: ![]()
Чертежа в таких примерах делать не нужно, но понимания ради:
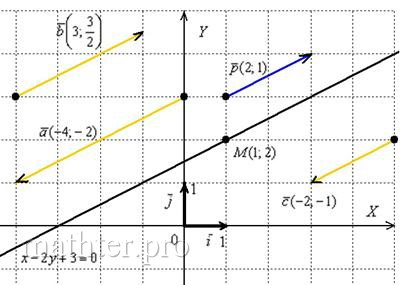
На чертеже мы видим исходную точку ![]() , исходный направляющий вектор
, исходный направляющий вектор ![]() (его можно отложить от любой точки плоскости) и построенную прямую
(его можно отложить от любой точки плоскости) и построенную прямую ![]() .
.
Как отмечалось в начале параграфа, у прямой бесконечно много направляющих векторов, и все они коллинеарны. Для примера я нарисовал три таких вектора: ![]() . Какой бы направляющий вектор мы ни выбрали, в результате всегда получится одно и то же уравнение прямой
. Какой бы направляющий вектор мы ни выбрали, в результате всегда получится одно и то же уравнение прямой ![]() .
.
Составим уравнение прямой по точке ![]() и, например, направляющему вектору
и, например, направляющему вектору ![]() :
:
![]()
разруливаем пропорцию:
![]()
Делим обе части на –2 и получаем знакомое уравнение:
![]()
Желающие могут аналогичным образом протестировать векторы ![]() или любой другой коллинеарный вектор.
или любой другой коллинеарный вектор.
Теперь решим обратную задачу:
 2.2.3. Как найти направляющий вектор по общему уравнению прямой?
2.2.3. Как найти направляющий вектор по общему уравнению прямой?
 2.2.1. Общее уравнение и направляющий вектор прямой
2.2.1. Общее уравнение и направляющий вектор прямой
| Оглавление |
Автор: Aлeксaндр Eмeлин
