В прошлом материале мы рассмотрели основные моменты, касающиеся темы уравнения прямой на плоскости в математике. Теперь же перейдем к изучению определенного уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости. Будем считать, что это большой ликбез для “чайников”.
Определение уравнения прямой на плоскости
Допустим, что есть прямая линия, котору. можно задавать в прямоугольной декартовой системе координат Oху. Дадим определение прямой.
Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе Oxy, будет являться общим уравнением прямой на плоскости.
Фактически, уравнением прямой линии на плоскости будем называть уравнение с двумя переменными, которые обозначаются как x и y. Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии (линейной точки).
Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости (поверхности). Этому будет посвящен весь следующий раздел нашей статьи. Сколько существует вариантов записи? Отметим, что существует несколько вариантов записи уравнения прямой, которые можно сделать. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.
Общее уравнение прямой линии
Первым делом познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости (пространстве) в декартовой системе координат Oxy и с ее понятием.
Уравнение вида Ax+By+C=0 , где x и y – переменные, а А, В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат Oxy. В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида Ax+By+C=0 .
Таким образом, общее уравнение прямой на плоскости имеет вид Ax+By+C=0 .
Поясним смысл некоторых важных разных аспектов темы.
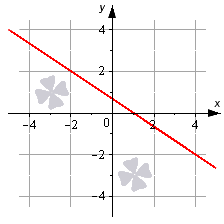
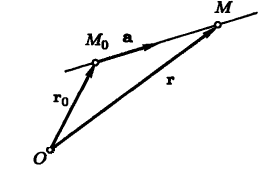
Попробуем это нарисовать. Посмотрите на рисунок.
Линию на чертеже стоит определять уравнением вида 2x+3y-2=0, так как координаты любой точки, которые будут составлять эту прямую (составляющие), удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2x+3y-2=0, дают нам прямую линию, которую мы видим на рисунке.
Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А, В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида Ax+By=0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение Ax+By+C=0 задает прямую, расположенную параллельно оси абсцисс Ox. Если B равно нулю, то можно говорить о параллельности линия оси ординат Oy.
Можно вывести: при некотором наборе значений чисел А, В и C с помощью общего уравнения прямой можно написать любую прямую линию на плоскости в прямоугольной системе координат Oху.
Прямая, заданная уравнением вида Ax+By+C=0 , имеет нормальный вектор прямой с координатами A, B .
Все приведенные уравнения прямых, которые мы по порядку рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.
Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале лекции мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.
Уравнение прямой в отрезках
Уравнение прямой в отрезках имеет вид xa+yb=1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.
Благодаря уравнению построение прямой линии на чертеже будет простым делом. Для этого необходимо отметить в прямоугольной системе координат точки a, 0 и 0, b , а затем начертить прямую линию, которая будет через них проходить.
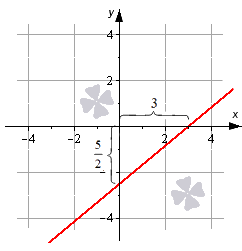
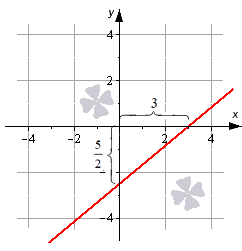
Построим прямую, которая задана формулой x3+y-52=1. Отмечаем на графике прямой две точки 3, 0, 0, -52, соединяем их между собой. Как это рисовать.
Что еще можно дополнить? Рекомендуем ознакомиться с аналитическим материалом, изложенным в статье «Уравнение прямой в отрезках».
Уравнение прямой с угловым коэффициентом
Эти уравнения, имеющие вид y=k·x+b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x.
Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси Ox.
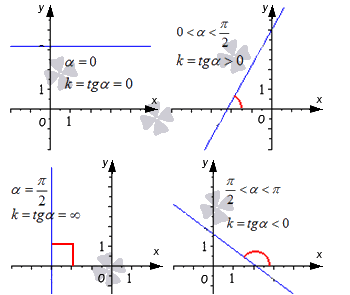
Для обозначения угла наклона прямой к положительному направлению оси Ox в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси Ox или совпадает с ней.
Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывать это будем следующим образом k=tg α. Для прямой, которая располагается параллельно оси Oy или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).
Прямая, которая задана уравнением y=k·x+b, проходит через точку 0, b на оси ординат – это будет означать, что уравнение прямой с угловым коэффициентом y=k·x+b задает на плоскости прямую линию, которая проходит через точку 0, b и образует угол α с положительным направлением оси Ox, причем k=tg α .
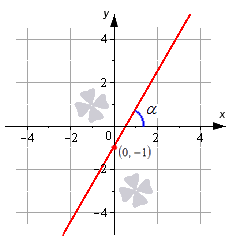
Изобразим прямую линию, которая определяется уравнением вида y=3·x-1.
Записываться это будет так. Эта вертикальная линия должна пройти через точку (0, -1) . Угол наклона α=arctg 3=π3 равен 60 градусов к положительному направлению оси Ox. Угловой коэффициент равен 3
Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции прямой в точке.
Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.
Каноническое уравнение прямой на плоскости
Данный вид уравнения имеет вид x-x1ax=y-y1ay, где x1, y1, ax, ay- это некоторые действительные числа, из которых ax и ay не равны нулю.
Прямая линия, заданная каноническим уравнением прямой, проходит через точку M1(x1, y1) . Числа ax и ay в знаменателях дробей представляют собой координаты вектора прямой линии, который будет направлять. Это значит, что каноническое уравнение прямой линии x-x1ax=y-y1ay в декартовой системе координат Oxy соответствует линии, проходящей через точку M1(x1, y1) и имеющей направляющий вектор a→=(ax, ay) .
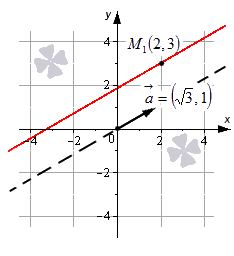
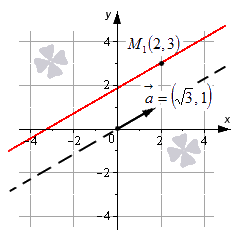
Изобразим в системе координат Oxy прямую линию, которая задается уравнением x-23=y-31. Точка M1(2, 3) будет иметь принадлежность прямой, вектор a→(3, 1) является направляющим вектором этой прямой линии.
Каноническое уравнение прямой линии вида x-x1ax=y-y1ay может быть использовано в случаях, когда ax или ay равно нулю. Наличие ноля в знаменателе делает запись x-x1ax=y-y1ay условной. Уравнение можно писать следующим образом ay(x-x1)=ax(y-y1).
В том случае, когда ax=0 , каноническое уравнение прямой принимает вид x-x10=y-y1ay и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.
Каноническое уравнение прямой при условии, что ay=0, принимает вид x-x1ax=y-y10. Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.
Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд задач и как их нужно решать, а также многочисленные примеры с решениями, которые позволяют на высоком уровне овладеть темой (и ни в коем случае не путать прямую с кривой).
Параметрические уравнения прямой на плоскости
Данные уравнения имеют вид x=x1+ax·λy=y1+ay·λ , где x1, y1, ax, ay – это некоторые действительные числа, из которых ax и ay не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.
Назначение параметрического уравнения в том, чтобы устанавливать неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .
Числа x, y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .
Предположим, что λ=0 .
Тогда x=x1+ax·0y=y1+ay·0⇔x=x1y=y1 , т. е. точка с координатами (x1, y1) принадлежит прямой.
Обращаем ваше внимание на то, что коэффициенты ax и ay при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.
Рассмотрим параметрические уравнения прямой линии вида x=2+3·λy=3+λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку (x1, y1) и имеет направляющий вектор a→=(3, 1) .
Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».
Нормальное уравнение прямой
Нормальное уравнение прямой имеет вид ,Ax+By+C=0, где числа А, В, и C таковы, что длина вектора n→=(A, B) равна единице, а C≤0 .
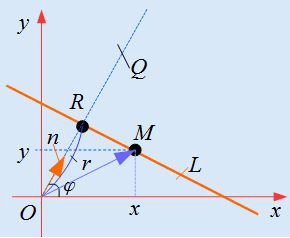
Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат Oху, является вектор n→=(A, B) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n→=(A, B) .
Еще одним вариантом записи нормального уравнения прямой линии является cos α·x+cos β·y-p=0 , где cos α и cos β – это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n→=(cos α, cos β) , справедливо равенство n→=cos2 α + cos2 β=1 , величина p≥0 и равна расстоянию от начала координат до прямой.
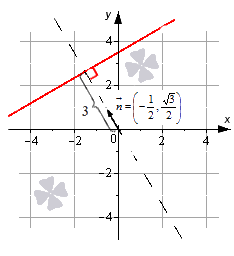
Рассмотрим общее уравнение прямой -12·x+32·y-3=0. Это общее уравнение прямой является нормальным уравнением прямой, так как n→=A2+B2=-122+32=1 и C=-3≤0 .
Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты -12, 32 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n→=-12, 32 .
Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.
Если в общем уравнении прямой Ax+By+C=0 числа А, В и С таковы, что уравнение Ax+By+C=0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».
В данном материале рассмотрим, что такое уравнение прямой. Проанализируем каждый вид данного уравнения. Изучим основные формулы и графики. Применим весь рассмотренный материал на практике, в виде решения задач и уравнений.
Данное уравнение — характеризуется, как уравнение двух переменных значений.
Значения в математики, чаще всего обозначают буквами x и y. Это самое распространенное обозначение, однако можно встретить и другие буквенные обозначения. Например: z, n и другие значения.
Определение прямой линии- фигура, состоящая из множества простых точек. Каждая точка, имеет собственные, определенные координаты, относительно осей абсцисс и ординат.
Уравнение прямой на плоскости — уравнение, характеризующее взаимосвязь координатных значений точек на прямой.
Для решения уравнений необходимо помнить ряд важным математических функций, правил, значений.
Все их мы будем рассматривать подробно в каждом разделе на примерах решения.
Общее уравнение прямой линии системы координат
Рассмотрим соответствующую теорему, которая отражает уравнение прямой на плоскости в системе координат Oxy.
Подробно исследуем следующее уравнение: ax+by+c=0.
Значения х и y, являются переменными данными со значениями.
a и b — действительные простые числа. Обязательное условие, которых неравенство нулю.
Следовательно, прямая линия задается вышеупомянутым уравнением данного вида: ax+by+c=0.
Рассмотрим на примере изученную теорему:
На данном рисунке, мы рассмотрим красную линию и запишем уравнение для нее.
2x+3y-2=0.
Координаты на данной прямой удовлетворяют составленному уравнению.
Уравнение может быть также полным и неполным. Рассмотрим случаи:
- Полное уравнение.
Все действительные числа, имеют любое значение, но не равные нулю. Поэтому такое определение относится к данному типу уравнений.
- Неполное уравнение.
Все числа в уравнении имеют любое значение. Характерно, также значения отрицательных знаков.
Уравнение прямой в отрезках прямой
Для отрезков уравнение будет иметь следующей вид:
[frac{x}{a}+frac{y}{b}=1]
Данные в знаменателе, являются действительными значениями, не равными нулевому значению. Величины действительных данных равняются отрезку. Он отсоединяется линией на оси координат. Протяженность начинает свой отсчет от начала координатной прямой.
Пример:
Нужно начертить прямую линию, которая задается формулой.
[frac{x}{3}+frac{y}{-frac{5}{2}}=1]
Обозначим на графике две точки ( 3 ; 0 ) , (0; [-frac{5}{2}]). Далее необходимо их соединить между собой.
Уравнение прямой с угловым коэффициентом
Записываем уравнение вида: [mathrm{y}=mathrm{k} cdot x+b];
x — значение, которое принимается, как переменное;
к — простое действительное число, является показателем углового коэффициента;
b — действительное число.
Угол наклона на плоскости в системе координат — угол, который берет свой отсчет значений от направления с положительным знаком до прямой, которая направлена против хода часовой стрелки.
Угол будут считать нулевым, если прямая линии, имеют параллельное расположение относительно оси абсцисс либо совпадает с ней по расположению. Угол принимает значения, согласно интервалу (0, [pi]).
Формула
[text { Формула обозначения коэффициента: } k=operatorname{tg} alpha .]
Угловой коэффициент — значение тангенса угла наклона этой же прямой линии.
В случае, когда прямая линия параллельная другой оси, ординат, то принято считать, что угловой коэффициент не определяется. И соответствует интервалу бесконечности.
График функции будет возрастать, если значение коэффициента имеет положительное значение. Следовательно, убывание будет наблюдаться в противоположном значение, а именно с отрицательным значением.
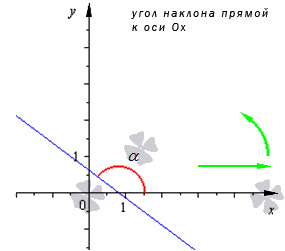
На графиках показаны значения угловых коэффициентов и угол наклона. Когда есть разное расположение относительно осей.
На примерах рассмотрим нахождение углового коэффициента. Для этого из прошлых тем, вспомним определение тангенса и его вычисление.
Пример №1:
Угол наклона прямой равен 120 градусов, относительно оси ох.
Нам нужно определить угловой коэффициент.
Применим известные нам формулы и подставим данные.
[alpha=120^{circ}, mathrm{k}=operatorname{tg} alpha=120=-sqrt{3}]
Следовательно правильный ответ задачи будет равняться [k=-sqrt{3}]
Пример №2:
В этом примере нам уже известно значение углового коэффициента.
Нужно определить угол наклона, относительно прямой. Для этого, нужно обязательно учитывать знак известного коэффициента. Если к>0, следует что угол будет острый и определяться как [alpha=operatorname{arctg} k].
Когда к<0, то угол будет характеризоваться как тупой. его значение определяется функцией: [alpha=pi-operatorname{arctg}|k|].
Например, угловое значение равно 3.
Значение коэффициента является положительным, значит угол будет острый. Вычисляться он будет по формуле: [alpha=operatorname{arctg} k=3]
Ответ задачи: [operatorname{arctg}=3].
Пример №3:
Значение углового коэффициента имеет отрицательное число в виде дроби. И равняется следующему значению: [-frac{1}{sqrt{3}}]
Для определения угла наклона, выполнить следующие действия: обозначим все значения. Угол наклона относительно оси имеет положительное значение. Следовательно формула для решения запишется следующим образом: [mathrm{k}=-frac{1}{sqrt{3}}<0 Rightarrow alpha=pi-operatorname{arctg}|k|].
Подставим данные, которые заданы в условии задания:
[alpha=pi-operatorname{arctg}left|-frac{1}{sqrt{3}}right|=pi-operatorname{arctg} frac{1}{sqrt{3}}=pi-frac{pi}{6}=frac{5 pi}{6} Rightarrow]ответ будет [frac{5 pi}{6}].
Пример №4:
Необходимо определить, относятся ли точки координат к прямой. Они равны: [m_{1}(3 ; 0) text { и } m_{2}(2 ;-2)]. Уравнение прямой задано следующее: [y=frac{1}{3} x-1].
Известные нам значения точек подставляем, в заданное уравнение прямой.
И получаем следующий вид формулы: [0=frac{1}{3} cdot 3-1 Leftrightarrow 0=0]. Так после вычисления, мы получаем равенство, которое считается верным. Можно утверждать, что точка принадлежит прямой.
Далее подставляем значения второй точки в уравнение.
[-2=frac{1}{3} cdot 2-1 Leftrightarrow-2=-frac{1}{3}] следовательно точка [m_{2}] не относится к прямой и не лежит на ней.
Вывод решения: только первая точка относится к прямой и лежит на ней, а вторая равная (2;-2) — нет.
Пример №5:
Нужно найти уравнение прямой, которая проходит через значение точки [m_{1}(4 ; 1)]. Значение углового коэффициента — (-2).
Запишем условие : [x_{1}=4, y_{1}=-1, k=-2]
Следовательно необходимое уравнение прямой равно: [y-y_{1}=k].
[left(x-x_{1}right) text { следовательно } y-(-1)=-2 cdot(x-4) Leftrightarrow y=-2 x+7]
Искомое уравнение: [y=-2 x+7]
Пример №6:
Составить уравнение прямой, проходящей через значение (-2;4). Угол наклона положительного направления равен [frac{3 pi}{4}].
Решение необходимо начать с определения коэффициента угла.
[k=operatorname{tg} alpha frac{3 pi}{4}=-1]
Определив угловое значение, можно составить искомое уравнение вида: [y-y_{1}=k cdotleft(x-x_{1}right) text { из этого следует } y-4=-1 cdot(x-(-2) Leftrightarrow y=-x+2]
Каноническое уравнение прямой на плоскости
Определение канонического уравнения — это уравнение следующего вида [frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}}].
Данное уравнение задает на плоскости в прямоугольной системе прямую линию. Она, в свою очередь проходит через точку [m_{1}(x ; y)], которая имеет вектор направления, обозначающийся как [underline{alpha}=left(alpha_{x} ; a_{y}right)]
Запишем несколько примеров для данного вида уравнения.
[frac{x-2}{sqrt{3}}=frac{y-3}{1}]
Приведенное уравнение — это уравнение прямой для канонического вида. Прямая его будет проходить через значения точек [m_{1}(2 ; 3)]. Вектор направляющий равен [sqrt{3}, 1].
Важные моменты, которые следует помнить, при решении задач с каноническим уравнением.
Отметим следующие важные факты:
- если вектор является прямым и прямая линия проходит через точку, то ее уравнение имеет вид : [frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}}]
- когда вектор прямой по направлению, то любой из векторов может быть направляющим вектором прямой. И уравнение записывается следующим образом: [frac{x-x_{1}}{mu cdot alpha_{x}}=frac{y-y_{1}}{mu cdot alpha_{y}}]
Пример №1:
Прямая в системе координат проходит через точки (2;-4) и вектор направляющий равен (1;-3). Составьте и напишите каноническое уравнение, применяя известные нам данные.
[frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}}]
[x_{1}=2, y_{1}=2, alpha_{x}=1, alpha_{y}=-3]
Следовательно уравнение записывается следующим образом: [frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}} Leftrightarrow frac{x-2}{1}=frac{y-(-4)}{-3} Leftrightarrow frac{x-2}{1}=frac{y+4}{-3}]
[frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}} Leftrightarrow frac{x-2}{1}=frac{y-(-4)}{-3} Leftrightarrow frac{x-2}{1}=frac{y+4}{-3}] — окончательное искомое уравнение.
Пример №2:
Составить каноническое уравнение, проходящее через точки [sqrt[3]{2} ; quad-frac{1}{7}]
Прямая является параллельной относительно оси координат. Направляющий вектор принимается [underline{j}=(0 ; 1)]. Учитывая значение точек, через которые проходит прямая, записываем уравнение:
[frac{x-sqrt[3]{2}}{0}=frac{y-left(-frac{1}{7}right)}{1} Leftrightarrow frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}]
[text { Ответ: } frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}]
Пример №3:
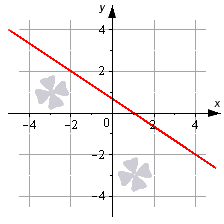
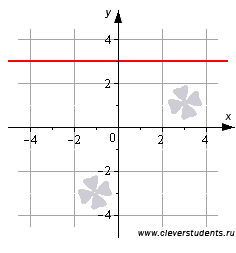
Составим уравнение, руководствуясь графиком, приведенным ниже.
Из рисунка видно, что прямая проходит через точки со значениями (0;3). Расположена параллельно относительно оси x (ось абсцисс). Координатный вектор [underline{i}=(1,0)] — направляющий вектор, для данной системы.
Собрав все данные, преобразовав их. можно записать уравнение:
[frac{x-0}{1}=frac{y-3}{0} Leftrightarrow frac{x}{1}=frac{y-3}{0}]
Нет времени решать самому?
Наши эксперты помогут!
Параметрическое уравнение на плоскости и его характеристики
Уравнение такого типа записываются в следующем виде:
[x=x_{1}+alpha_{x} cdot lambda]
[mathrm{y}=y_{1}+alpha_{y} cdot lambda]
[x_{1} y_{1} alpha_{x} alpha_{y} text { — действительные простые значения. }]
[alpha_{x} alpha_{y} text{ — значения, которые математически возможны равняться нулю.}]
[lambda text { — параметр, значение которого может быть различным. }]
Уравнение параметрического вида предназначено, для установления не очевидного взаимодействия между координатами точек системы. Для определения этого свойства и вводится параметр [lambda].
Пример №1:
Задана система уравнения:
[{x=-3-1 / 2 cdot lambda}]
[{y=3 cdot lambda}]
[{z=2 / 3}]
Необходимо определить все координаты, каждой направляющей системы.
[{x=-3-1 / 2 cdot lambda}]
[{y=3 cdot lambda}]
[{z=2 / 3} Leftrightarrow]
[Leftrightarrow{x=-3-1 / 2 cdot lambda}]
[{y=0+3 cdot lambda}]
[{z=2 / 3+0 cdot lambda}]
Коэффициенты перед значение [lambda] имеют соответствующие значения координат направляющего вектора и равняются: [underline{alpha}=(-1 / 2,3,0)] — для прямой по заданию.
Соответственно запишем все координаты направляющих векторов:
[left(-frac{1}{2} cdot mu, 3 cdot mu, 0 cdot muright)=left(-frac{1}{2} cdot mu, 3 cdot mu, 0 cdot muright), mu in R, mu neq 0 ]
[left(-frac{1}{2} cdot mu, 3 cdot mu, 0 cdot muright), mu in R, mu neq 0]
Пример №2
Составить параметрическое уравнение в пространстве:
[underline{alpha}=left(2 ;-frac{1}{sqrt{3}}, 0right)-text { вектор направляющий.}]
Точки (7, -1, 0) — значения точки на прямой координат.
[x_{1}=7, y_{1}=-1, z_{1}=0, alpha_{x}=2, alpha_{y}=-frac{1}{sqrt{3}}, alpha_{z}=0]
Полученные данные подставляем систему уравнения.
[x=x_{1}+alpha_{x} cdot lambda]
[mathrm{y}=y_{1}+alpha_{y} cdot lambda]
[z=z_{1}+alpha_{z} cdot lambda]
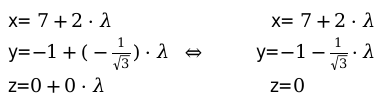
Особые моменты данного типа уравнений:
Имея любое значение [lambda], можно определить три числа (z, y,x).
К примеру точки [M_{1}left(x_{1} text { и так далее }right) text { находятсся в параметрах уравнения в системе. }]
[mathrm{x}=chi_{1}+alpha_{x} cdot lambda]
[mathrm{y}=y_{1}+alpha_{y} cdot lambda]
[z=z_{1}+alpha_{z} cdot lambda]
где значение [lambda]=0.
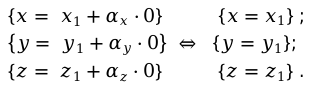
Пример №3:
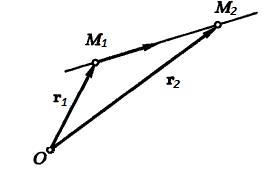
Любые значения точек находятся на прямой, для определенной заданной системы координат.
[M_{1}(4 ; 3 ;-2)]
[N_{1}(-2 ; 3 ;-1)]
Запишем систему параметрических уравнение:
[x=2+2 cdot lambda]
[y=3 cdot lambda]
[z=-1-lambda]
Поставляя данные первой точки, получаем уравнения:
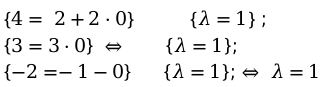
Следовательно значение [lambda=1 text {, для } M_{1}(4 ; 3 ;-2)]. следовательно она находится на прямой координат.
Аналогичные действия проводим для второй координаты точек.
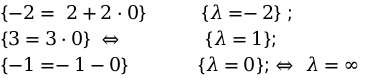
Выполнив вычисления, мы видим, что параметра для [lambda] не существует.
Нормальное уравнение для координатной прямой
Формула
Нормальное уравнение можно выразить в виде уравнения:
[A_{x}+B_{y}+C=0]
Где числа А, В, и C имеют такие значения, что, вектор [underline{n}=(mathrm{A}, quad mathrm{B})] равняется единице, [C leq 0].
Вектор [underline{n}=(mathrm{A}, quad mathrm{B})], будет является нормальным в системе координат.
Так же есть еще один способ записать нормальный вид уравнения, применяя для этого значения тригонометрических функций.
[cos alpha cdot x+cos beta cdot y-rho=0]
[cos alpha cos beta] — это действительные простые числа. Следовательно, они представлены направляющими косинусами. А также нормального вектора и единичной прямой.
Отсюда следует [underline{n}=left(begin{array}{lll} cos alpha & cos beta end{array}right)] равняется равенству: [underline{n}=cos ^{2} alpha+cos ^{2} beta=1]
Значение [rho geq 0]
Данное значение определяет длину расстояния от прямой линии до начала координатной прямой.
Пример №1:
В задаче имеется уравнение прямой для общего случая.
2x-3y+4=0
Нужно используя вышеуказанное уравнение составить простое уравнение для координатной прямой.
Для начала запишем А=2; В=-3; С=4.
Неизвестное значение t, сможем вычислить из равенства используя известные значения.
[mathrm{t}=pm frac{1}{sqrt{A^{2}+B^{2}}}=pm frac{1}{sqrt{13}}]
t- будет отрицательным значение, так как С>0.
[t=-frac{1}{sqrt{13}}]
Перемножим уравнение:
[frac{2}{sqrt{13}} x+frac{3}{sqrt{13}} y-frac{4}{sqrt{13}}=0]
Вывод решения: [frac{2}{sqrt{13}} x+frac{3}{sqrt{13}} y-frac{4}{sqrt{13}}=0]
Значение [frac{4}{sqrt{13}}] — будет являться, тем самым значение, которое показывает расстояние от начала до прямой координат прямой.
Пример №2.
Определим и составим нужное уравнение имея следующие известные нам данные: угол [varphi=60 text { градусов }]
Расстояние до прямой от начала координат равняется 4.
Используя данные решим задачу.
[cos varphi=cos left(60^{circ}right)=frac{1}{2}]
[sin varphi=sin left(60^{circ}right)=frac{sqrt{3}}{2}]
[frac{1}{2} x+frac{sqrt{3}}{2} y-4=0]
[text { Ответ: } frac{1}{2} x+frac{sqrt{3}}{2} y-4=0]
Пример №3:
Имея данные значения решим задачу согласно задания. Где угол [varphi=90 text { градусов }]
Расстояние до прямой от начала координат равняется 3.
Используя данные решим задачу.
[cos varphi=cos left(90^{circ}right)=0]
[sin varphi=sin left(90^{circ}right)=1]
[1 x+0 y-3=-2]
Ответ: [0 x+-1 y-3=-2] координата не лежит на прямой, так как имеет отрицательное значение.
Выводы по материалу:
Рассмотрев типы уравнения, для прямой в плоскости. Перечислив их категории и основные характеристики. Можно сказать, что это одна из составляющих математики.
В ней переплетаются все основные значения и функции этой технической науки.
Для решения задач, необходимо обладать следующими навыками:
- вспомнить весь изученный материал по работе с тригонометрическими функциями: косинус, синус. тангенс и другие.
- вычисление отрицательных значений и их правила;
- решение уравнений с дробными числами;
- помнить правило возведения числа в степень.
Учитывая все, рекомендации, процесс работы с материалом по данной теме значительно облегчит процесс.
Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.
Здесь будет калькулятор
Уравнение прямой с угловым коэффициентом
y=kx+by=kx+b,
где kk — угловой коэффициент, а bb — свободный коэффициент.
Уравнения данного вида составляются следующим образом по формуле:
y−y0=k(x−x0)y-y_0=k(x-x_0),
где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.
Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.
Решение
Подставляем значения в формулу:
y−y0=k(x−x0)y-y_0=k(x-x_0)
y−2=1⋅(x−1)y-2=1cdot(x-1)
Приводим подобные слагаемые:
y=x+1y=x+1
Ответ
y=x+1y=x+1
Общее уравнение прямой
Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:
y−x−1=0y-x-1=0
Уравнение прямой по двум точкам
Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},
где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.
Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).
Решение
x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}
x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}
x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}
x−4=−y−12x-4=frac{-y-1}{2}
y+1=2⋅(4−x)y+1=2cdot(4-x)
y=8−2x−1y=8-2x-1
y=−2x+7y=-2x+7
Ответ
y=−2x+7y=-2x+7
Уравнение прямой при помощи точки и вектора нормали
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.
Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).
Решение
x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,
x−7+40−5y=0x-7+40-5y=0
x−5y=−40+7x-5y=-40+7
x−5y=−33x-5y=-33
5y=x+335y=x+33
y=x5+335y=frac{x}{5}+frac{33}{5}
Проверка
Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.
8=75+3358=frac{7}{5}+frac{33}{5}
8=88=8 — верно, ответ правильный.
Ответ
y=x5+335y=frac{x}{5}+frac{33}{5}
Прямая в пространстве
Уравнение прямой, заданной в пространстве имеет такой вид:
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.
Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).
Решение
x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Проверка
Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:
1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.
Такой вид уравнения прямой называется каноническим.
Ответ
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Тест по теме “Составление уравнения прямой”
Содержание
- Уравнение прямой на плоскости
- Уравнения прямой на плоскости в координатной форме
- Общее уравнение прямой
- Параметрическое уравнение прямой
- Параметрическое уравнение прямой в канонической форме
- Уравнение прямой, проходящей через две точки
- Уравнения прямой на плоскости в векторной форме
- Векторное уравнение прямой в параметрической форме
- Нормальное векторное уравнение прямой
- Векторное уравнение прямой, проходящей через две точки
- Уравнения прямой на плоскости в координатной форме
- Уравнение прямой в пространстве
- Уравнения прямой в пространстве в координатной форме
- Параметрические уравнения прямой
- Параметрические уравнения прямой в канонической форме
- Уравнение прямой, проходящей через две точки
- Прямая как пересечение двух плоскостей
- Уравнения прямой в пространстве в векторной форме
- Векторное уравнение прямой в параметрической форме
- Векторные уравнения прямой
- Векторное уравнение прямой, проходящей через две точки
- Уравнения прямой в пространстве в координатной форме
Уравнение прямой на плоскости
Уравнения прямой на плоскости в координатной форме
Любую прямую линию на плоскости можно задать общим уравнением прямой в декартовой системе координат:
то есть числа одновременно не равны нулю.
Прямая линия на плоскости может быть задана параметрическим уравнением прямой:
где числа не равны нулю одновременно. Числа
являются компонентами направляющего вектора прямой — ненулевого вектора, лежащего на прямой.
Если
то после исключения из уравнений прямой в параметрической форме параметра
уравнение прямой приводятся к канонической форме:
Уравнение прямой, проходящей через две точки и
:
При или
это уравнение принимает соответственно вид
или
Уравнения прямой на плоскости в векторной форме
Векторное уравнение прямой в параметрической форме:
где — направляющий вектор прямой,
— радиус-вектор некоторой точки прямой.
Нормальное векторное уравнение прямой:
где — вектор нормали к прямой.
Это уравнение также можно записать в форме
причём если вектор — единичный, то величина
есть расстояние от точки
до прямой. Вообще говоря, это уравнение имеет следующий смысл: проекция радиус-вектора любой точки прямой на нормаль к этой прямой постоянна.
Векторное уравнение прямой, проходящей через две различные точки:
где и
— радиус-векторы данных точек.
Это уравнение легко получается из векторного уравнения прямой в параметрической форме, если в качестве направляющего вектора прямой взять вектор
Уравнение прямой в пространстве
Уравнение прямой в пространстве в координатной форме
Прямая линия в пространстве может быть задана параметрическими уравнениями:
Числа являются компонентами направляющего вектора прямой.
Исключением параметра параметрические уравнения прямой приводятся к канонической форме:
Если, например, то канонические уравнения принимают вид
Аналогично для любой другой компоненты направляющего вектора.
Если два параметра равны нулю, например, то канонические уравнения имеют вид
Аналогично для любых других пар компонент направляющего вектора.
Уравнение прямой в пространстве, проходящей через две точки и
:
Если, например, то уравнения прямой принимают вид
Если к тому же то уравнения прямой записываются в виде
Аналогично для любых двух пар совпадающих координат точек.
Прямая в пространстве может быть задана как пересечение двух непараллельных плоскостей:
Уравнение прямой в пространстве в векторной форме
Прямая линия в пространстве может быть задана уравнением в параметрической форме:
где — направляющий вектор прямой,
— радиус-вектор некоторой точки прямой. Это уравнение совпадает с параметрическим векторным уравнением прямой на плоскости.
Прямую в пространстве можно задать векторными уравнениями:
или
Векторное уравнение прямой в пространстве, проходящей через две различные точки:
где и
— радиус-векторы двух точек прямой.