Как составить уравнение прямой проходящей через точку перпендикулярно двум прямым

Задача 43106 Составить уравнение прямой, проходящей…

Условие

Составить уравнение прямой, проходящей через точку А(1,-3,2) перпендикулярно двум прямым (x-2)/3 = y/-2 = z/1 и x/1 = (y+1)/4 = (z+3)/-5

математика ВУЗ
7181

Решение

★

Каноническое уравнение прямой

(x-2)/3=y/(-2)=z/1 –
это уравнение прямой, проходящей через точку
M_(1)(2;0;0)
с направляющим вектором vector{s_(1)}=(2;-2;1)

Каноническое уравнение прямой

x/1=(y+1)/4=(z+3)/(-5) –
это уравнение прямой, проходящей через точку
M_(2)(0;-1;-3)
с направляющим вектором vector{s_(2)}=(1;4;-5)

Находим вектор vector{s}= vector{s_(1)} × vector{s_(2)}=[m]begin{vmatrix} i & j & k\ 2 & -2 &1 \ 1 & 4 & -5 end{vmatrix}[/m]=6[i]i[/i]+11[i]j[/i]+10[i]k[/i]

vector{s} ⊥ vector{s_(1)} и vector{s} ⊥ vector{s_(2)}

vector{s} – направляющий вектор искомой прямой:

Уравнение прямой, проходящей через точку (x_(o);y_(o);z_(o) с заданным направляющим вектором vector{s}={m;n;k)имеет вид:

[m]frac{x-x_{o}}{m}=frac{y-y_{o}}{n}=frac{z-z_{o}}{k}[/m]

Подставляем известные значения и получаем ответ

Написать комментарий

Источник

Сообщения без ответов | Активные темы

Автор

Сообщение

Заголовок сообщения: Уравнение прямой через точку и перпендикулярно двум прямым

Добавлено: 23 ноя 2011, 13:36

Начинающий

Зарегистрирован:
26 фев 2011, 21:36
Сообщений: 34
Cпасибо сказано: 17
Спасибо получено:
0 раз в 0 сообщении
Очков репутации: 2

Сижу ломаю голову, который час.
Составить уравнение прямой, проходящей через точку [math][M(1; – 2;3)][/math] и перпендикулярно прямым [math][frac{{x – 5}}{3} = frac{{y – 4}}{1} = frac{{z – 3}}{{ – 2}}[/math] и [math][frac{{x + 2}}{2} = frac{{y + 4}}{{ – 5}} = frac{{z – 1}}{4}][/math]

Записываю условия перпендикулярности через направляющие вектора, но чего-то мне не хватает для решения задачи. Помогите пожалуйста!

Вернуться к началу

dolby	Заголовок сообщения: Re: Уравнение прямой через точку и перпендикулярно двум прямым Добавлено: 23 ноя 2011, 14:51
	Если представить искомую прямую в виде уравнения, то получим [math][frac{{x – 1}}{m} = frac{{y + 2}}{n} = frac{{z – 3}}{p}][/math] Исходя из условия [math][begin{gathered} m1 = 3 hfill \ n1 = 1 hfill \ p1 = – 2 hfill \ hfill \ m2 = 2 hfill \ n2 = – 5 hfill \ p2 = 4 hfill \ end{gathered} ][/math] Условие перпендикулярности прямых [math][mm1 + nn1 + p*p1 = 0][/math] Аналогично, для второй прямой. Получается система уравнений [math][left{ begin{gathered} 3m + n – 2p = 0 hfill \ 2m – 5n + 4p = 0 hfill \ end{gathered} right.][/math] А что дальше я не знаю
Вернуться к началу

dolby	Заголовок сообщения: Re: Уравнение прямой через точку и перпендикулярно двум прямым Добавлено: 23 ноя 2011, 15:09
	arkadiikirsanov писал(а): Положите р=1 и найдите 2 других неизвестных. А почему p = 1 ?
Вернуться к началу

dolby	Заголовок сообщения: Re: Уравнение прямой через точку и перпендикулярно двум прямым Добавлено: 24 ноя 2011, 23:30
	Yurik писал(а): Ещё один способ. Векторное произведение направляющих векторов заданных прямых будет направляющим вектором искомой прямой. Спасибо, решила этим способом =)
Вернуться к началу

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Уравнение прямой через точку перпендикулярно к прямой в форуме Аналитическая геометрия и Векторная алгебра	hanna	7	858	10 май 2014, 19:26
Уравнение прямой проходящей через точку перпендикулярно плос в форуме Аналитическая геометрия и Векторная алгебра	Olena88	2	148	10 ноя 2021, 00:53
Уравнение прямой, проходящей через точку в форуме Аналитическая геометрия и Векторная алгебра	NervTokyo3	2	666	21 окт 2013, 18:36
Уравнение прямой проходящей через точку в форуме Аналитическая геометрия и Векторная алгебра	pirab	3	385	29 окт 2017, 17:27
Записать уравнение прямой, проходящей через точку в форуме Аналитическая геометрия и Векторная алгебра	focus	2	370	27 мар 2017, 19:22
Через точку провести прямую и найти уравнение прямой в форуме Аналитическая геометрия и Векторная алгебра	lanvandance	3	464	30 окт 2018, 16:08
Составить уравнение прямой и плоскости через точку и вектора в форуме Аналитическая геометрия и Векторная алгебра	Morgan031	7	257	22 дек 2020, 16:23
Найти уравнение прямой, которая проходит через точку в форуме Аналитическая геометрия и Векторная алгебра	RAFA	1	448	08 июн 2013, 19:56
Уравнение прямой проходящей через точку паралельно вектору в форуме Аналитическая геометрия и Векторная алгебра	Safinika	1	286	20 ноя 2017, 14:20
Уравнение прямой, перпендикулярной двум заданным в форуме Аналитическая геометрия и Векторная алгебра	Tsvirotka	4	816	12 окт 2018, 19:50

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 3

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

Уравнение перпендикуляра к двум прямым — это уравнение прямой, перпендикулярной к каждой из прямых, задаётся системой равенств нулю смешанных произведений соответствующего вектора-разности радиусов-векторов точек, направляющего вектора и векторного произведения направляющих векторов.

Обозначения[править]

Введём обозначения:

— радиус-вектор точки перпендикуляра;

${displaystyle {bar {r}}_{1}=(x_{1},y_{1},z_{1})}$ — радиус-вектор точки первой прямой;

${displaystyle {bar {r}}_{2}=(x_{2},y_{2},z_{2})}$ — радиус-вектор точки второй прямой;

${displaystyle {bar {s}}_{1}=(l_{1},m_{1},n_{1})}$ — направляющий вектор первой прямой;

${displaystyle {bar {s}}_{2}=(l_{2},m_{2},n_{2})}$ — направляющий вектор второй прямой;

${displaystyle {frac {x-x_{1}}{l_{1}}}={frac {y-y_{1}}{m_{1}}}={frac {z-z_{1}}{n_{1}}}}$ — уравнение первой прямой;

${displaystyle {frac {x-x_{2}}{l_{2}}}={frac {y-y_{2}}{m_{2}}}={frac {z-z_{2}}{n_{2}}}}$ — уравнение второй прямой.

Формулы:[править]

Векторная форма:

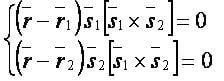
Координатная форма:

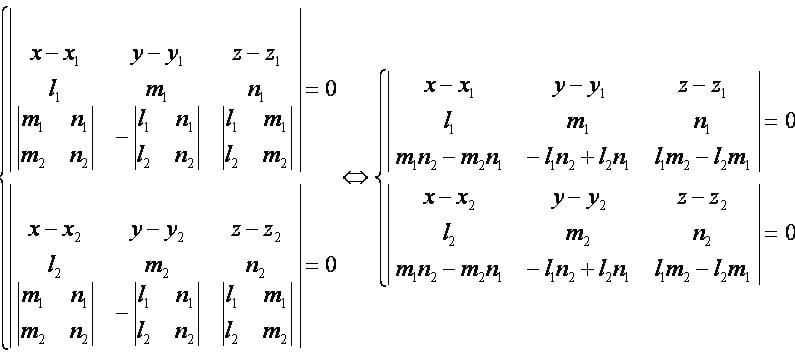
Заметим, что формулы верны только для скрещивающихся прямых.

Пример[править]

Даны две прямые:

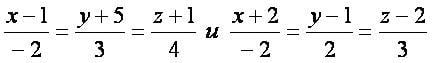
Найти уравнение перпендикуляра к этим прямым.

Решение.

Уравнения прямой:[править]

уравнение прямой, проходящей через две точки;
уравнение прямой, равноудалённой от трёх точек;
уравнение прямой, проходящей через точку в направлении вектора;
уравнение прямой, проходящей через точку параллельно прямой;
уравнение прямой, проходящей через точку перпендикулярно плоскости;
уравнение прямой, образованной пересечением двух плоскостей;
уравнение проекции прямой на плоскость;
уравнение перпендикуляра из точки к прямой в трёхмерном пространстве;
уравнение перпендикуляра из точки к плоскости;
уравнение перпендикуляра к двум прямым.

Литература[править]

Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.
Выгодский М. Я. Справочник по высшей математике — М.: Наука, 1964, стр.192.

Ссылки[править]

Участник:Logic-samara

Источник

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α₁ и α₂, заданные соответственно уравнениями:

Под углом
между двумя плоскостями будем понимать один из двугранных углов, образованных
этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α₁
и α₂ равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.

Условие параллельности двух плоскостей.

Две плоскости α₁ и α₂
параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда
коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны
тогда и только тогда, когда их нормальные векторы перпендикулярны, а
следовательно, или .

Таким образом, .

Примеры.

Составить уравнение плоскости, проходящей через точку
M(-2; 1; 4) параллельно
плоскости 3x+2y-7z+8=0.

Уравнение плоскости будем искать в виде Ax+By+Cz+D=0. Из условия
параллельности плоскостей следует, что: . Поэтому можно положить A=3, B=2, C=-7. Поэтому уравнение плоскости
принимает вид3x+2y-7z+D=0.

Кроме того, так какMÎ α, то-6+2-28+D=0, D=32.

Итак, искомое уравнение 3x+2y-7z+32=0.
Составить уравнение
плоскости, проходящей через точки M₁(1;
1; 1), M₂(0;
1; –1) перпендикулярно плоскости x+y+z=0.

Так как M₁Î α, то
используя уравнение плоскости, проходящей через заданную точку, будем иметь A(x-1)+B(y-1)+C(z-1)=0.

Далее, так как M₂Î α, то
подставив координаты точки в выписанное уравнение, получим равенство -A-2C=0 или A+2C=0.

Учтем, что заданная плоскость перпендикулярна искомой. Поэтому A+B+C=0.

Выразим коэффициенты Aи
Bчерез C: A=-2C, B=C и подставим их в исходное уравнение: -2C(x-1)+C(y-1)+C(z-1)=0.

Окончательно получаем -2x+y+z=0.
Составить уравнение
плоскости, проходящей через точку M(-2; 3; 6) перпендикулярно
плоскостям 2x+3y-2z-4=0 и 3x+5y+z=0.

Так как MÎ α, то A(x+2)+B(x-3)+C(z-6)=0.

По условию задачи , поэтому

Итак уравнение плоскости принимает вид
13(x+2)-8(y-3)+z-6=0 или 13x-8y+z+44=0.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Положение прямой в пространстве вполне определяется заданием какой-либо её
фиксированной точки М₁ и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М₁(x₁, y₁, z₁), лежащую
на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z)
на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t, что ,
где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М₁ и
М соответственно через и ,
получаем .
Это уравнение называется векторным уравнением прямой. Оно
показывает, что каждому значению параметра t соответствует радиус-вектор
некоторой точки М, лежащей на прямой.

Запишем это уравнение в координатной форме.
Заметим, что ,
и отсюда

Полученные уравнения называются параметрическими
уравнениями прямой.

При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Пусть М₁(x₁, y₁, z₁) – точка,
лежащая на прямой l, и –
её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты
должны быть пропорциональны, следовательно,

– канонические
уравнения прямой.

Замечание 1. Заметим, что канонические
уравнения прямой можно было получить из параметрических,исключив параметр t. Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим ,
отсюда x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Замечание 2. Пусть прямая
перпендикулярна одной из координатных осей, например оси Ox. Тогда
направляющий вектор прямой перпендикулярен
Ox,
следовательно, m=0. Следовательно,
параметрические уравнения прямой примут вид

Исключая из уравнений параметр t, получим уравнения прямой в виде

Однако и в этом случае условимся формально
записывать канонические уравнения прямой в виде.
Таким образом, еслив знаменателе одной
из дробей стоит нуль, то это означает, что прямая
перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz.

Примеры.

Составить канонические и параметрические уравнения прямой,
проходящей через точку М₁(1;0;-2) параллельно вектору .

Канонические уравнения: .

Параметрические уравнения:
Составить уравнения прямой,
проходящей через две точки М₁(-2;1;3), М₂(-1;3;0).

Составим канонические уравнения прямой. Для
этого найдем направляющий вектор . Тогда l: .

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые
две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения
любых двух таких плоскостей, рассматриваемые совместно представляют собой
уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой
достаточно найти любые две ее точки. Проще всего выбрать точки пересечения
прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений
прямой, полагая z= 0:

Решив эту систему, найдем точку M₁(1;2;0).

Аналогично, полагая y= 0, получим точку
пересечения прямой с плоскостью xOz:

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти
какую-либо точку М₁ на прямой и направляющий вектор прямой.

Координаты точки
М₁
получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания
направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к
обоим нормальным векторам и .
Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

Пример. Привести общие уравнения прямой
к каноническому виду.

Найдём точку,
лежащую на прямой. Для этого выберем произвольно одну
из координат, например, y= 0 и
решим систему уравнений:

Нормальные векторы
плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор
прямой будет

.
Следовательно, l: .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом
между прямыми в пространстве будем называть любой из смежных углов, образованных
двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими
векторами и . Так как , то по формуле для косинуса угла между векторами получим

Условия параллельности и
перпендикулярности двух прямых равносильны условиям параллельности и
перпендикулярности их направляющих векторов и :

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l₁ параллельна l₂ тогда и только тогда, когда параллелен .

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна
нулю: .

Примеры.

Найти угол между прямыми и .
Найти уравнения прямой проходящей через точку М₁(1;2;3) параллельно прямой l₁:

Поскольку
искомая прямая l параллельна l₁, то в качестве
направляющего вектора искомой прямой l можно взять направляющий вектор прямой l₁.
Составить уравнения прямой,
проходящей через точку М₁(-4;0;2) и перпендикулярной прямым: и .

Направляющий
вектор прямой l можно найти как векторное произведение
векторов и :

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Углом между прямой и плоскостью
будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

Рассмотрим векторы и .
Если угол между ними острый, то он будет ,
где φ – угол между прямой и плоскостью. Тогда .

Если
угол между векторами и тупой,
то он равен .
Следовательно .
Поэтому в любом случае .
Вспомнив формулу вычисления косинуса
угла между векторами, получим .

Условие перпендикулярности
прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда
направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т.е. .

Условие параллельности прямой и плоскости.
Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.

Примеры.

Написать уравнение плоскости, проходящей через точку М₁(2;-3;4) параллельно прямым и .
Так как M₁Î α, то уравнение плоскости
будем искать в виде

.

Применяя
условие параллельности прямой и плоскости, получим систему линейных уравнений

Отсюда

Итак,
или .
Найти угол между прямой и плоскостью .
Направляющий
вектор прямой .
Нормальный вектор плоскости .
Следовательно,
Найдите точку, симметричную данной М(0;-3;-2) относительно прямой .

Составим уравнение плоскости α перпендикулярной l. MÎ α, .
Следовательно, или
.

Найдём точку пересечения прямой l и α:

Итак,
N(0.5;-0.5;0.5). Пусть
искомая точка М₁ имеет
координаты М₁(x,y,z). Тогда очевидно равенство
векторов ,
т.е. (0,5;2,5;2,5)=(х-0.5;у+0.5;z-0.5). Откуда x=1,
y=2, z=3 или М₁(1;2;3)..

Источник

Макеты страниц

Рис. 178

Рис. 179

Искомый перпендикуляр представляется уравнениями

или после упрощений

Точку пересечения общего перпендикуляра с прямой (3) найдем из системы (3)-(6). Получим . Аналогично получим Длина общего перпендикуляра равна

Пример 2. Найти уравнения общего перпендикуляра к прямым

Прямые параллельны: Направляющий вектор общего перпендикуляра или, умножая на За начальную точку примем произвольную точку прямой (7). Получим уравнение общего перпендикуляра