Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.
Понятие канонического уравнения прямой
Допустим, что у нас есть декартова (прямоугольная) система координат, в которой задана прямая. Нам известны координаты произвольно взятой точки этой прямой M1(x1, y1), а также ее направляющего вектора a→=(ax, ay). Попробуем составить уравнение, которое описывало бы эту прямую.
Возьмем плавающую точку M(x, y). Тогда вектор M1M→ можно считать направляющим для исходной прямой. Его координаты будут равны x-x1, y-y1 (если нужно, повторите материал о том, как правильно вычислять координаты вектора с помощью координат отдельных его точек).
Множество произвольно взятых точек M(x, y) будут определять нужную нам прямую с направляющим вектором a→=(ax, ay) только в одном случае – если векторы M1M→ и a→=(ax, ay) будут коллинеарны по отношению друг к другу. Посмотрите на картинку:
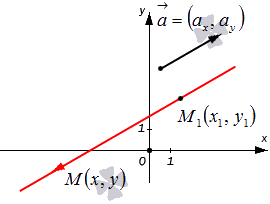
Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:
M1M→=λ·a→, λ∈R
Если преобразовать полученное равенство в координатную форму, то мы получим:
x-x1=λ·axy-y1=λ·ay
При условии, что ax≠0 и ay≠0, получим:
x-x1=λ·axy-y1=λ·ay⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay
Итог наших преобразований и будет каноническим уравнением прямой на плоскости. Запись вида x-x1ax=y-y1ay также называют уравнением прямой в каноническом виде.
Таким образом, с помощью уравнения x-x1ax=y-y1ay можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор a→=(ax, ay) и проходит через точку M1(x1, y1).
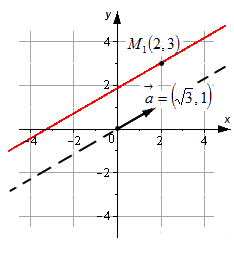
Примером уравнения подобного типа является, например, x-23=y-31. Прямая, которая задана с его помощью, проходит через M1(2, 3) и имеет направляющий вектор a→=3, 1. Ее можно увидеть на рисунке:
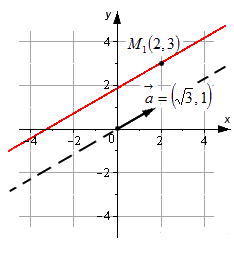
Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:
1. Если прямая, имеющая направляющий вектор a→=(ax, ay), проходит через две точки – M1(x1, y1) и M2(x2, y2), то уравнение для нее может быть записано как в виде x-x1ax=y-y1ay, так и x-x2ax=y-y2ay.
2. Если заданная прямая имеет направляющий вектор с координатами a→=(ax, ay), то множество всех ее векторов можно обозначить как μ·a→=(μ·ax, μ·ay), μ∈R, μ≠0. Таким образом, любое уравнение прямой в каноническом виде x-x1μ·ax=y-y1μ·ay будет соответствовать этой прямой.
Разберем важный пример задачи на нахождение канонического уравнения.
В прямоугольной системе координат на плоскости задана прямая, которая проходит через точку M1(2, -4) и имеет направляющий вектор с координатами a→=(1, -3). Запишите каноническое уравнение, описывающее данную прямую.
Решение
Для начала вспомним общий вид нужного нам канонического уравнения – x-x1ax=y-y1ay. Подставим в него имеющиеся значения x1=2, y1=-4, ax=1, ay=-3 и подсчитаем:
x-x1ax=y-y1ay⇔x-21=y-(-4)-3⇔x-21=y+4-3
Получившееся в итоге равенство и будет нужным ответом.
Ответ: x-21=y+4-3
Канонические уравнения прямой на плоскости с ax или ay, равными нулю
Если значение хотя бы одной переменной a является нулевым, то уравнение плоскости используют в первоначальном виде. Сразу две переменные нулевыми не могут быть по определению, поскольку нулевой вектор не бывает направляющим. В таком случае мы можем считать запись x-x1ax=y-y1ay условной и понимать ее как равенство ay(x-x1)=ax(y-y1).
Разберем случаи канонических уравнений на плоскости с одним нулевым a более подробно. Допустим, что x-x10=y-y1ay при ax=0, а исходная прямая будет проходить через M1(x1, y1). В таком случае она является параллельной оси ординат (если x1=0, то она будет с ней совпадать). Докажем это утверждение.
Для этой прямой вектор a→=(0, ay) будет считаться направляющим. Этот вектор является коллинеарным по отношению к координатному вектору j→=(0,1).
Если же нулевым является значение второго параметра, то есть ay=0, то мы получаем равенство вида x-x1ax=y-y10. Это уравнение описывает прямую, проходящую через M1(x1, y1), которая расположена параллельно оси абсцисс. Это утверждение верно, поскольку a→=(ax, 0) является для этой прямой направляющим вектором, а он в свою очередь является коллинеарным по отношению к координатному вектору i→=(1, 0).
Проиллюстрируем два частных случая канонического уравнения, описанные выше:
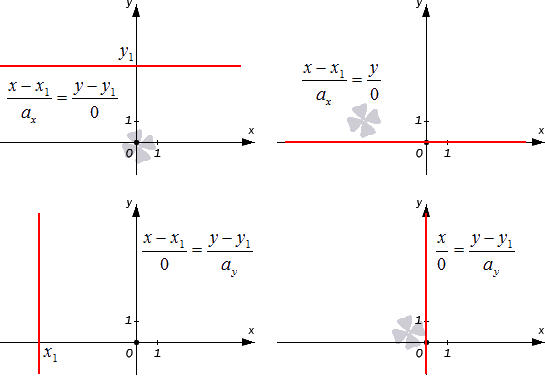
На плоскости задана прямая, параллельная оси Oy. Известно, что она проходит через точку M123, -17. Запишите каноническое уравнение для нее.
Решение
Если прямая по отношению оси ординат является параллельной, то мы можем взять координатный вектор j→=(0, 1) в качестве направляющего для нее. В таком случае искомое уравнение выглядит следующим образом:
x-230=y–171⇔x-230=y+171
Ответ: x-230=y+171
На рисунке изображена прямая. Запишите ее каноническое уравнение.
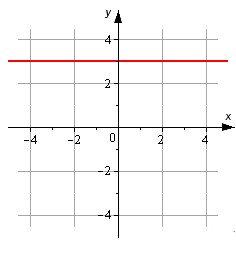
Решение
Мы видим, что исходная прямая проходит параллельно оси Ox через точку M1(0, 3). Мы берем координатный вектор i→=(1, 0) в качестве направляющего. Теперь у нас есть все данные, чтобы записать нужное уравнение.
x-01=y-30⇔x1=y-30
Ответ: x1=y-30
Преобразование канонического уравнения прямой в другие виды уравнений
Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.
Стандартной форме записи канонического уравнения x-x1ax=y-y1ay можно поставить в соответствие систему параметрических уравнений на плоскости x=x1+ax·λy=y1+ay·λ. Чтобы преобразовать один вид уравнения в другой, нам надо приравнять правую и левую часть исходного равенства к параметру λ. После этого надо выполнить разрешение получившихся равенств относительно переменных x и y:
x-x1ax=y-y1ay⇔x-x1ax=y-y1ay=λ⇔⇔x-x1ax=λy-y1ay=λ⇔x=x1+ax·λy=y1+ay·λ
Покажем на примере, как именно выполняется это действие с конкретными числами.
У нас есть прямая, заданная на плоскости с помощью канонического уравнения x+23=y-111. Запишите параметрические уравнения исходной прямой.
Решение
Сначала поставим знак равенства между отдельными частями уравнения и переменной λ и получим x+23=λy-111=λ.
Далее можно перейти к формулированию необходимых параметрических уравнений:
x+23=λy-111=λ⇔x+2=3·λy-1=11·λ⇔x=-2+3·λy=1+11·λ
Ответ: x=-2+3·λy=1+11·λ
Из канонического уравнения можно получить не только параметрические, но и общие уравнения прямой. Вспомним понятие пропорции: запись ab=cd можно представить в виде a·d=b·c с сохранением смысла. Значит, что x-x1ax=y-y1ay⇔ay(x-x1)=ax(y-y1)⇔ayx-axy-ayx1+axy1=0.
Это и есть общее уравнение прямой. Это станет более очевидно, если мы добавим в него значения параметров ay=A, -ax=B, -ayx1+axy1=C.
Прямая на плоскости описана с помощью канонического уравнения x-12=y+40. Вычислите общее уравнение этой прямой.
Решение
Делаем указанные выше действия по порядку.
x-12=y+40⇔0·(x-1)=2·(y+4)⇔y+4=0
Ответ: y+4=0 .
Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.
На плоскости задана прямая с помощью уравнения x+33=y-22. Запишите уравнение этой же прямой в отрезках.
Решение
Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.
x+33=y-22⇔2·(x+3)=3·(y-2)⇔2x-3y+6+23=0
Далее переходим к формулировке уравнения прямой в отрезках.
2x-3y+6+23=0⇔2x-3y=-6+23⇔⇔2-(6+23)x-3-(6+23)y=1⇔x-6+232+y6+233=1⇔x-3+3+y33+2=1
Ответ: x-3+3+y33+2=1
Достаточно легко решить и задачу, обратную этой, т.е. привести уравнение прямой на плоскости обратно к каноническому. Допустим, у нас есть общее уравнение прямой в стандартной формулировке – Ax+By+C=0. При условии A≠0 мы можем перенести By вправо с противоположным знаком. Получим Ax+C=-By. Теперь выносим A за скобки и преобразуем равенство так:
Ax+CA=-By
Получившееся уравнение мы записываем в виде пропорции: x+CA-B=yA.
У нас получилось нужное нам каноническое уравнение прямой на плоскости.
А как сделать преобразование, если B≠0? Переносим все слагаемые, кроме Ax, вправо с противоположными знаками. Получаем, что Ax=-By-C. Выносим -B за скобки:
Ax=-By+CB
Формируем пропорцию: x-B=y+CBA
Есть общее уравнение прямой x+3y-1=0. Перепишите его в каноническом виде.
Решение
Оставим с левой стороны только одну переменную x. Получим:
x=-3y+1
Теперь вынесем -3 за скобки: x=-3y-13. Преобразуем равенство в пропорцию и получим необходимый ответ:
x-3=y-131
Ответ: x-3=y-131
Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.
Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x=x1+ax·λy=y1+ay·λ и приравнять обе части равенств. Схема решения выглядит так:
x=x1+ax·λy=y1+ay·λ⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay
Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.
Прямая на плоскости описана с помощью системы параметрических уравнений x=3+0·λy=-2-4·λ. Запишите каноническое уравнение для этой прямой.
Решение
Для начала преобразуем исходные уравнения в систему x=3+0·λy=-2-4·λ. Следующим шагом будет выражение параметра в каждом уравнении:
x=3+0·λy=-2-4·λ⇔λ=x-30λ=y+2-4
Ставим знак равенства между получившимися частями и получаем нужное нам каноническое уравнение: x-30=y+2-4
Ответ: x-30=y+2-4
Как решать задачи на составление канонических уравнений
В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.
На плоскости задана прямая, каноническое уравнение которой имеет вид x-12=y+12-3. Выясните, лежат ли на ней точки M13, -312 и M2(5, -4).
Решение
Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.
3-12=-312+12-2⇔1=1
Результат говорит нам, что точка M13, -312 принадлежит исходной прямой.
Точно так же поступим и с координатами второй точки:
5-12=-4+12-3⇔2=76
Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.
Ответ: первая точка лежит на заданной прямой, а вторая нет.
Есть две точки M1(2, 4) и M2(-1, 3). Будет ли прямая, которая задана в той же плоскости с помощью уравнения x-20=y-32, проходить через них?
Решение
Вспомним, что запись x-20=y-32 можно понимать как 2·(x-2)=0·(y-3)⇔x-2=0. Подставим координаты заданных точек в это равенство и проверим.
Начнем с первой точки M1(2, 4) : 2-2=0⇔0=0
Равенство верное, значит, эта точка расположена на заданной прямой.
Подставляем данные второй точки: -1-2=0⇔-3=0.
Равенство неверное, значит, точка M2(-1, 3) не лежит на исходной прямой.
Ответ: через точку M1(2, 4) прямая проходит, а через M2(-1, 3) нет.
Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.
Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.
Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.
Прямая на плоскости проходит через точку M1(0, -3) и через точку M2(2, -2). Сформулируйте для этой прямой канонической уравнение.
Решение
Eсли у нас есть координаты двух точек, то мы можем вычислить по ним координаты вектора M1M2→=2, 1. По отношению к прямой, чье уравнение мы составляем, он будет направляющим вектором. После этого мы можем записать следующее:
x-02=y-(-3)1⇔x2=y+31
Также можно использовать координаты второй точки. Тогда мы получим: x-22=y-(-2)1⇔x-22=y+21
Ответ: x2=y+31
Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.
Известно, что точка M1(1, 3) принадлежит некоторой прямой, которая параллельна второй прямой, заданной с помощью уравнения x2=y-5. Запишите каноническое уравнение первой прямой.
Решение
Для первой прямой можно определить направляющий вектор a→=2, -5. Его можно рассматривать и в качестве направляющего для второй прямой, что следует из самого определения направляющих векторов. Это позволяет нам получить всю информацию, нужную для записи искомого уравнения: x-12=y-3-5
Ответ: x-12=y-3-5
Через точку M1(-1, 6) проходит прямая, которая является перпендикулярной другой прямой, определенной на плоскости с помощью уравнения 2x-4y-7=0. Запишите каноническое уравнение первой прямой.
Решение
Из данного уравнения мы можем взять координаты нормального вектора второй прямой – 2, 4. Мы знаем, что этот вектор является направляющим по отношению к первой. Тогда мы можем записать искомое уравнение:
x-(-1)2=y-64⇔x+11=y-62
Ответ: x+11=y-62
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Существует несколько различных типов уравнений, описывающих кривую первого порядка, называемую прямой. Каждый из них оптимален для какой-то своей цели. Давайте познакомимся с ними поближе.
Каноническое уравнение прямой в пространстве
Определение 1
Канонический вид уравнения прямой в пространстве выглядит как следующее равенство:
$frac{x – x_0}{α} = frac{y – y_0}{β} = frac{z – z_0}{γ}$,
где буквы $(x_0, y_0, z_0)$ используются для обозначения координат любой точки, возлежащей на данной прямой, а $(α, β, γ)$ — координаты направляющего эту прямую вектора, как несложно догадаться, они не могут быть нулевыми.
Не во всех случаях удобно и практично пользоваться каноническим уравнением, поэтому частенько возникает надобность использовать какое-то другое, например, можно прибегнуть к параметрическому.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Для каких прямых не представляется возможным или нельзя написать каноническое уравнение?
Глядя на это уравнение, видно, что его возможно использовать только в том случае, если координаты направляющих векторов исследуемых прямых не равны нулю, для таких прямых стоит воспользоваться параметрическими уравнениями.
Определение 2
Параметрический вид уравнений прямой в пространстве такой:
$begin{cases} x = x_1 + α cdot λ \ y = y_1 + β cdot λ \ z = z_1 + γ cdot λ \ end{cases}$,
где $x_1, y_1, z_1$ — координаты некоторой точки, находящейся на описываемой прямой, $α, β, γ$ — координаты параллельного или лежащего на данной прямой вектора, $λ$ — произвольное число-коэффициент, иногда для его обозначения используют слово “параметр”.
Параметрическое уравнение как раз удобно применять если одна из координат направляющего вектора равна нулю.
Чтобы произвести переход от параметрического вида уравнения к каноническому виду уравнения прямой в пространстве, осуществите вывод канонического уравнения прямой из параметрического.
«Каноническое уравнение прямой в пространстве» 👇
Для этого следует в к каждом уравнении перенести $λ$ в левую часть, а затем приравнять уравнения. Никакой магии, а только самая что ни на есть пресловутая арифметика:
$begin{cases} λ = frac{x – x_1}{ α} \ λ = frac{y – y_1}{β} \ λ = frac{z – z_1}{γ} \ end{cases}$
$frac{x – x_0}{α} = frac{y – y_0}{β} = frac{z – z_0}{γ}$
Уравнение прямой, образуемой пересечением двух плоскостей
Рисунок 1. Связь канонического и общего уравнения прямой
Для того чтобы составить каноническое уравнение прямой в пространстве, заданной пересечением плоскостей, необходимо познакомиться поближе с 2 исследуемыми плоскостями.
Любую плоскость, находящуюся в пространстве, можно описать с помощью равенства:
$Ax + By + Cz + D = 0$,
где $A, B, C$ и $D$ – постоянные, причём $A, B, C$ не могут быть одновременно все нулевыми.
Соответственно, не нужно быть гением, чтобы понять, что если две плоскости пересечены между собой, то на их общей части будет возлежать некая прямая. Чтобы её найти, нужно получить общее решение следующей системы уравнений:
$begin{cases} A_1x + B_1y + C_1z + D_1 = 0 \ A_2x + B_2y + C_2z + D_2 = 0 \ end{cases}$
С помощью же частного решения этой системы уравнений можно узнать, принадлежит ли какая-либо точка трёхмерной системы координат описанным уравнениями плоскостям и, конечно же, нашей прямой. Для этого нужно просто подставить её икс, игрек и зет в систему.
Приведённая система уравнений является своеобразной “формулой”, служащей для нахождения общего уравнения прямой в пространстве.
Иногда в каких-либо практических задачах требуется получить из уравнения прямой в пространстве в общем виде параметрические или канонические уравнения, тогда в первую очередь вам стоит узнать координаты её направляющего вектора и какую-либо точку, находящуюся на изучаемой прямой.
Ну что ж, давайте решать нашу задачу. На первом этапе вычислим $x, y, z$ для направляющего вектора.
Найдём нормальные вектора для плоскостей. Если кто забыл, нормальный вектор — это такой вектор, который является перпендикулярным (ортогональным) к данной плоскости или прямой.
Для этого из нашего очаровательного примера системы уравнений необходимо взять коэффициенты из уравнений. В итоге для 1-ой плоскости вектор-нормаль будет выглядеть как $(A_1; B_1; C_1)$, а для второй как $(A_2; B_2; C_2)$.
Теперь необходимо перемножить оба вектора и получить их произведение, здесь $(i, j, k)$ – координаты единичного вектора.
$overline{a} = [overline{n} cdot overline{n}] = left| begin{array}{ccc} overline{i} & overline{j} & overline{k} \ A_1 & B_1 & C_1 \ A_2 & B_2 & C_2 \ end{array} right| = overline{i} cdot left| begin{array}{cc}\B_1 & C_1 \ B_2 & C_2\ end{array} right| – overline{j} cdot left| begin{array}{cc}\ A_1 & C_1 \ A_2 & C_2 \ end{array} right| + overline{k} cdot left| begin{array}{cc} \ A_1 & B_1 \ A_2 & B_2 \ end{array} right| $
$|overline{n} cdot overline{n}| = overline{i} cdot (B_1 cdot C_2 – C_1 cdot B_2) – overline{j} cdot (A_1 cdot C_2 – A_2 cdot C_1) + overline{k} cdot (A_1 cdot B_2 – A_2 cdot B_1)$
Следующим этапом выполняем поиск координат точки, возлежащей на искомой прямой.
Для выполнения этого наиболее “сложного” пункта необходимо выбрать одну наиболее нравящуюся вам координату $x, y$ или $z$ и вместо неё подставить в систему уравнений, описывающую плоскости, нулевое значение.
Пример 1
Составьте каноническое уравнение прямой, получаемой из системы уравнений, описывающей пару пересечённых плоскостей:
$begin{cases} 2x – y + 3z + 4 = 0 \ x + 5y – 3z – 7 = 0 \ end{cases}$
Найдём направляющий вектор, для этого сначала запишем вектора нормалей плоскостей:
$overline{n_1}(2;-1;3), overline{n_2}(1;-5;-3)$
Ну а сейчас пора вычислить сам направляющий вектор:
$overline{a} = left| begin{array}{ccc} overline{i} & overline{j} & overline{k} \ 2 & -1 & 3 \ 1 & 5 & -3 \ end{array} right| = overline{i} cdot left| begin{array}{cc}\ -1 & 3 \ 5 & -3\ end{array} right| – overline{j} cdot left| begin{array}{cc}\ 2 & 3 \ 1 & -3 \ end{array} right| + overline{k} cdot left| begin{array}{cc} \ 2 & -1 \ 1 & 5 \ end{array} right| $
$overline{a} = (3 – 15) cdot overline{i} – (-6-3) cdot overline{j} + (10 +1) cdot overline{k} = -12 overline{i} + 9 overline{j} + 11 overline{k}$
Найдём точку, находящуюся на нашей прямой, тут всё просто, приравняем $y$ к нулю и внедрим в нашу систему уравнений:
$begin{cases} 2x + 3z + 4 = 0 \ x – 3z – 7 = 0 \ end{cases}$
Решение вышеприведённой системы уравнений будет: $x = 1, z = -2$, то есть координаты точки, возлежащей на нашей прямой, будут $(1; 0; -2)$.
Подставим все полученные нами цифры и получим следующее уравнение:
$frac{x-1}{-12} = frac{y}{9} = frac{z+2}{11}$
Составление канонического уравнения прямой по координатам двух точек
На практике это очень распространённая и любимая во многих вузах и других учебных заведениях задача — нужно найти уравнение прямой в пространстве, проходящей через 2 точки. Примем заранее, что эти две точки не обладают одинаковыми $x, y, z$.
Для того чтобы написать уравнение прямой в пространстве, проходящей через 2 точки, воспользуйтесь координатами ваших точек и внедрите их в следующее уравнение:
$frac{x – x_1}{x2 – x_1} = frac{y – y_1}{y_2 – y_1} = frac{z – z_1}{z_2 – z_1}$
Это уравнение можно вывести из параметрического уравнения прямой.
Допустим, у нас есть две точки с координатами $(x_1; y_1; z_1)$, и для второй $(x_2; y_2; z_2)$.
Найти направляющий вектор для изучаемой прямой при наличии пары точек несложно, вектор с координатами $(x_2 – y_1; y_2 – y_2;z_2 – z_2)$ и будет желаемой частью результата.
Придумаем точку, находящуюся на нашей прямой, пусть она будет обладать координатами $(x_1;y_1;z_1)$.
Помещаем обнаруженные нами координаты вектора и точки в каноничное уравнение прямой в пространстве и получим уравнение прямой, проходящей через 2 точки.
Если же необходимо выразить именно параметрические уравнения из координат двух точек, через которые проведена некая одна прямая, то тут тоже всё довольно просто и без неожиданностей:
$begin{cases} x = x_1 + (x_2 – x_1) cdot λ \ y = y_1 + (y_2 – y_1)cdot λ \ z = z_1 + (z_2 – z_1) cdot λ \ end{cases}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Понятие канонического уравнения прямой
Чтобы разобраться, что такое каноническое уравнение, нужно рассмотреть следующий пример. Дана прямоугольная система координат, в которой задана некая произвольная прямая. Известны координаты произвольной точки на отрезке [M_{1}left(x_{1}, y_{1}right)] и координаты направляющего вектора [bar{a}=left(a_{x^{prime}} a_{y}right)]. Используя все имеющиеся данные составим и запишем уравнение, которое будет описывать данную заданную прямую.
Рассмотрим точку [mathrm{M}(x, y)]. Вектор [overline{M_{1} M}] можно отнести к направляющим исходной линии в координатной плоскости. Координатами вектора будут точки [left(x-x_{1}, y-y_{1}right)]. Чтобы правильно определить векторные координаты, необходимо вспомнить основное правило решения векторов.
Произвольные точки [M(x, y)] будут являться основой для необходимой прямой с направляющим вектором [bar{a}=left(a_{x}, a_{y}right)], только тогда, когда вектора [overline{M_{1} M}] и [bar{a}=left(a_{x}, a_{y}right)] будут являться коллинеарными по отношению друг к другу.
Исходя из этого можно составить формулу коллинеарности двух векторов.
Формула
[overline{M_{1} M}=lambda cdot overline{mathrm{a}}, lambda in R]
Где:
После преобразования данного равенства в координатную форму, можно получить следующее уравнение:
[begin{aligned}
&x-x_{1}=lambda cdot a_{x} \
&y-y_{1}=lambda cdot a_{y}
end{aligned}]
Однако, обязательно выполнение главных условий: [a_{x} neq 0] и [a_{y} neq 0].
При выполнении вышеперечисленных условий, получаем следующие равенства:
[begin{aligned}
&x-x_{1}=lambda cdot a_{x} Rightarrow lambda=frac{x-x_{1}}{a_{x}} \
&y-y_{1}=lambda cdot a_{y} Rightarrow lambda=frac{x-x_{1}}{a_{x}} \
&Leftrightarrow frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}
end{aligned}]
Все выполненные преобразования привели к тому, что мы получили окончательную формулу канонического уравнения на плоскости [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}].
Иначе такое равенство, еще называют уравнением прямой канонического вида.
Используя данную запись [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}], можно в прямоугольной системе координат задать прямую, которой будет характерен направляющий вектор [bar{a}=left(a_{x}, a_{y}right)]. Также данная линия будет проходить через заданную точку [M_{1}left(x_{1}, y_{1}right)].
Например: задано уравнение [frac{x-2}{sqrt{3}}=frac{y-3}{1}]. Задается линия, которая будет проходить через точки [M_{1}(2,3)]. Ее направляющий вектор имеет координатные точки: [bar{a}=(sqrt{3}, 1)].
Когда любая прямая в системе координат проходит через две любые точки [M_{1}left(x_{1}, y_{1}right)] и [M_{2}left(x_{2}, y_{2}right)] и имеет направляющий вектор [bar{a}=left(a_{x}, a_{y}right)], множество всех векторов можно записать как [mu cdot overline{mathrm{a}}=left(mu cdot mathrm{a}{x^{prime}} mu cdot a{y}right), mu in R, mu neq 0].
Таким образом, каждое уравнение прямой канонического вида [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}], будет соответствовать заданной прямой на плоскости.
Пример 1
В системе координат задана прямая, которая проходит через точки [M_{1}(2,4)], и имеет направляющий вектор [bar{a}=(1,-3)].
Решение задачи:
Составим и запишем общий вид канонического уравнения [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}].
Далее подставим в него заданные значения [x_{1}=2, y_{1}=-4, a_{x}=1, a_{y}=-3].
Проведем необходимый расчет и получим следующую запись:
[frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}} Leftrightarrow frac{x-2}{1}=frac{y-(-4)}{-2} Leftrightarrow frac{x-2}{1}=frac{y+4}{-3}].
Ответ: [frac{x-2}{1}=frac{y+4}{-3}]
Каноническое уравнение на плоскости с точками ax и ay равными нулевому значению
При условии, что одно из значений переменной является нулю, будет использоваться первоначальный вид уравнения. Две переменные нулевыми быть не могут, так как это невозможно по определению. Направляющий вектор не может быть нулевым.
В такой ситуации выражение [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}] считается условным, и его нужно понимать как равенство [a_{y}left(x-x_{1}right)=a_{x}left(y-y_{1}right)].
Если [frac{x-x_{1}}{0}=frac{y-y_{1}}{a_{y}}] при [a_{x}=0], а заданная прямая проходит через точки [M_{1}left(x_{1}, y_{1}right)]. В данном случае она является параллельной относительно оси ординат. Если [x_{1}=0], то прямая будет совпадать с осью координат.
Утверждение необходимо доказать. Для заданной прямой вектор [bar{a}=left(a_{x}, a_{y}right)] является направляющим. Также данный вектор будет являться коллинеарным по отношению к координатному вектору [bar{j}=(0.1)].
Если второй параметр является нулевым значением, то [a_{y}=0] и мы получим равенство [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{0}]. Данное уравнение характеризует прямую, которая проходит через точку [M_{1}left(x_{1}, y_{1}right)] и располагается параллельно оси абсцисс. Это утверждение будет правдивым, так как [bar{a}=left(a_{x^{prime}} 0right)], и является для прямой направляющим вектором. А вектор, в свою очередь, коллинеарен по отношению к вектору координат [bar{j}=(0.1)].
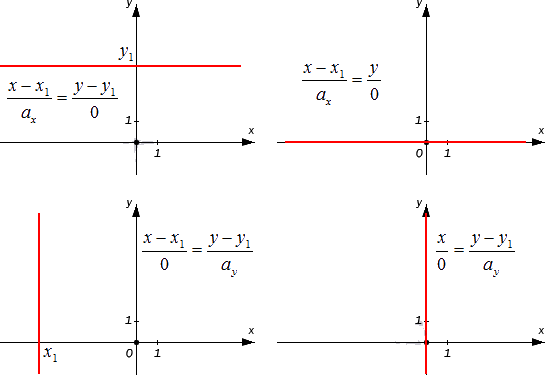
Примеры 2 — 3
На координатной плоскости задана прямая, которая расположена параллельно оси Oy. Она проходит через точку
[M_{1}left(sqrt[3]{2},-frac{1}{7}right)].
Необходимо составить каноническое уравнение для заданной прямой, используя исходные данные.
Решение:
Так как прямая по отношению к координатной оси является параллельной, можно использовать координатный вектор
[bar{j}=(0.1)]. Данный вектор будет служить, как направляющий.
Искомое уравнение будет выглядеть в следующем виде:
[frac{x-sqrt[3]{2}}{0}=frac{y-left(-frac{1}{7}right)}{1} Leftrightarrow
frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}].
Ответ: [frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}].
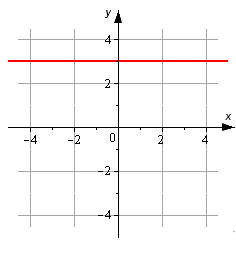
Согласно графику, нужно составить каноническое уравнение прямой.
Решение:
Исходя из графика можно сказать, что линия параллельна оси Ox и проходит через точку [M_{1}(0,3)].
Используем координатный вектор как направляющий.
Записываем каноническое уравнение: [frac{x-0}{1}=frac{y-3}{0} Leftrightarrow
frac{x}{1}=frac{y-3}{0}].
Ответ: [frac{x}{1}=frac{y-3}{0}].
Преобразование канонического уравнения прямой в уравнение другого вида
Стандартную форму канонического уравнения [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}] можно поставить в систему параметрических уравнений для плоскости.
Для преобразования одного вида уравнения в другой необходимо одну часть уравнения приравнять к другой.
[begin{aligned}
&frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}} Leftrightarrow frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}=lambda Leftrightarrow frac{x-x_{1}}{a_{y}}=lambda Rightarrow \
&frac{y-y_{1}}{a_{y}}=lambda Leftrightarrow x=x_{1}+a_{x} cdot lambda Rightarrow y=y_{1}+a_{y} cdot lambda
end{aligned}]
Примеры 4 — 5
Задана прямая на плоскости в виде канонического уравнения [frac{x+2}{3}=frac{y-1}{11}].
Необходимо записать параметрическое уравнение для прямой.
Принцип решения задачи:
Нужно поставить знак равенства между отдельными частями уравнения и переменной [lambda]. Получается
следующий вид уравнения: [frac{x+2}{3}=lambda] и [frac{y-1}{11}=lambda].
Далее можно записать необходимы уравнения параметрического вида:
[frac{x+2}{3}=lambda] и [frac{y-1}{11}=lambda.].
[Leftrightarrow x+2=3 cdot lambda] и
[y-1=11 cdot lambda Leftrightarrow x=-2+3 cdot lambda] и [y=1+11 cdot lambda]
Ответ: [x=-2+3 cdot lambda] и [y=1+11 cdot lambda].
Задана на плоскости прямая при помощи канонического уравнения [frac{x-1}{2}=frac{y+4}{0}].
Необходимо составить общей вид канонического уравнения для данной прямой.
Решение:
Аналогичным образом решаем задачу, как в предыдущем примере:
[frac{x-1}{2}=lambda] и [frac{y+4}{0}=lambda].
[Leftrightarrow x-1=2 cdot lambda] и [y+4=0
cdot lambda Leftrightarrow x=-2+1 cdot lambda] и [y=-4+0 cdot lambda]
[Leftrightarrow 0
cdot(x-1)=2 cdot(y+4) Leftrightarrow y+4=0]
Ответ: [y+4=0].
Нет времени решать самому?
Наши эксперты помогут!
Принцип решения задач на составление канонических уравнений
Первым делом канонические уравнения применяется для тех задач, где необходимо вычислить принадлежность точки к заданному отрезку на плоскости.
Рассмотрим несколько вариантов задач, и подробно опишем их решение.
Примеры 6 — 8
Задана линия, каноническое уравнение которой выглядит следующим образом:
[frac{x-1}{2}=frac{y+frac{1}{2}}{-3}].
Нужно определить принадлежат ли две точки [M_{1}left(3,-3 frac{1}{2}right)] и [M_{2}(5,-4)]
прямой.
Решение:
Для того чтобы проверить принадлежность прямой, нужно подставить заданные координаты точек в каноническое
уравнение.
Выполнив данное действие получим верное равенство: [frac{3-1}{2}=frac{-3 frac{1}{2}+frac{1}{2}}{-2}
Leftrightarrow 1=1].
Согласно результату, можно сказать что точка [M_{1}left(3,-3 frac{1}{2}right)] принадлежит заданному
отрезку.
Аналогичным образом нужно поступить и с другой точкой.
[frac{5-1}{2}=frac{-4 frac{1}{2}+frac{1}{2}}{-3} Leftrightarrow 2=frac{7}{6}]
Полученное в ходе решения равенство не является верным, следовательно, точка [M_{2}(5,-4)] не будет ей
принадлежать.
Ответ: прямой принадлежат координаты точки [M_{1}left(3,-3 frac{1}{2}right)], координаты точки
[M_{2}(5,-4)] нет.
Заданы координаты двух точек [M_{1}(2,4)] и [M_{2}(-1,3)]. Нужно определить, будет ли заданная прямая на
плоскости с помощью уравнения [frac{x-2}{0}=frac{y-3}{2}], проходить через заданные координаты.
Решение:
Уравнение [frac{x-2}{0}=frac{y-3}{2}] можно преобразовать, и записать как [2 cdot(x-2)=0 cdot(y-3)
Leftrightarrow x-2=0].
Заданные координаты точек подставим преобразованное уравнение, и произведем проверку.
Для точки [M_{1}(2,4) 2-2=0 Leftrightarrow 0=0].
Так как равенство верное, можно сделать вывод, что точка принадлежит прямой.
Аналогичным образом проводится проверка второй точки: [M_{2}(-1,3)]
[-1-2=0 Leftrightarrow-3=0].
Равенство неверное, поэтому точка [M_{2}(-1,3)] не принадлежит прямой.
Ответ: через точку [M_{1}(2,4)] прямая будет проходить, так как равенство верное, через точку
[M_{2}(-1,3)] нет.
Задачи, в которых заданы точки с координатами, будут являться наиболее простыми по отношению нахождения
канонического уравнения прямой.
Наиболее сложнее решаются задачи, когда предварительно необходимо определить координаты точек, через которые
проходит прямая.
Наиболее распространенной является тип задач, где нужно доказать прохождение прямой, через заданные точки.
Задана прямая, которая проходит через точки [M_{1}(0,-3)] и [M_{2}(2,-2)] в прямоугольной системе координат. Согласно условию задачи, необходимо составить каноническое уравнение.
Решение:
Вычислим координаты вектора [overline{M_{1} M_{2}}=(2.1)], по уже известной методике решения, используя заданные точки. По отношению к прямой данный вектор будет направляющим.
[frac{x-0}{2}=frac{y-(-3)}{1} Leftrightarrow frac{x}{2}=frac{y+3}{1}]
Ответ: [frac{x-0}{2}=frac{y-(-3)}{1} Leftrightarrow frac{x}{2}=frac{y+3}{1}].
Уравнения прямых в пространстве
Уравнение прямой как линии пересечения двух плоскостей
Пусть в координатном пространстве (в прямоугольной системе координат) две плоскости заданы общими уравнениями
в которых коэффициенты при неизвестных непропорциональны, т.е. . Это условие означает, что плоскости
и
пересекаются (см. условие (4.25)), поскольку их нормали
и
неколлинеарны (рис.4.25). Тогда линия пересечения плоскостей описывается системой уравнений
(4.31)
Система (4.31) называется общим уравнением прямой в пространстве.
Пример 4.13. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис.4.26). Требуется составить уравнение прямой, содержащей высоту
треугольника.
Решение. Прямая является линией пересечения двух плоскостей: плоскости
, треугольника
и плоскости
, проходящей через точку
перпендикулярно вектору
(рис.4.26). По формуле (4.21) составим уравнение плоскости
проходящей через три точки
По формуле (4.14) составим уравнение плоскости , проходящей через точку
перпендикулярно вектору
Следовательно, общее уравнение (4.31) прямой имеет вид
Параметрическое уравнение прямой в пространстве
Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.
Пусть в координатном пространстве заданы точка
и ненулевой вектор
(рис.4.27). Требуется составить уравнение прямой, коллинеарной вектору
и проходящей через точку
.
Выберем на прямой произвольную точку . Обозначим
— радиус-векторы точек
и
(рис.4.28).
Точка принадлежит заданной прямой тогда и только тогда, когда векторы
и
коллинеарны. Запишем условие коллинеарности:
, где
— некоторое действительное число (параметр). Учитывая, что
, получим векторное параметрическое уравнение прямой в пространстве:
(4.32)
где — направляющий вектор прямой, а
— радиус-вектор заданной точки
принадлежащей прямой.
Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве
(4.33)
где — координаты направляющего вектора
прямой. Параметр
в уравнениях (4.32),(4.33) имеет следующий геометрический смысл: величина
пропорциональна расстоянию от заданной точки
до точки
. Физический смысл параметра
в параметрических уравнениях (4.32),(4.33) — это время при равномерном и Прямолинейном движении точки
по прямой. При
точка
совпадает с заданной точкой
. При возрастании параметра
движение происходит в направлении направляющего вектора.
Каноническое уравнение прямой в пространстве
Выразим параметр из каждого уравнения системы (4.33):
, а затем исключим этот параметр:
(4.34)
Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты не равны нулю одновременно, так как это координаты направляющего вектора прямой.
Замечания 4.6.
1. Если один или два из трех знаменателей дробей в (4.34) равны нулю, то считается, что соответствующий числитель дроби равен нулю. Например:
а) каноническое уравнение — это уравнение
прямой, параллельной оси аппликат (рис.4.29,а);
б) каноническое уравнение — это уравнение
прямой, параллельной координатной плоскости
(рис.4.29,б).
2. Направляющий вектор прямой определяется неоднозначно. Например, любой ненулевой вектор
, где
, также является направляющим вектором для той же прямой.
Переход от общего уравнение к каноническому
3. Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:
1) найти любое решение системы
определяя тем самым координаты точки
, принадлежащей прямой;
2) найти направляющий вектор прямой как векторное произведение нормалей
заданных плоскостей:
3) записать каноническое уравнение (4.34) с учетом пунктов 1 и 2.
4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы
и привести подобные члены.
5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):
6. Если в каноническом уравнении (4.34) прямой фиксировать координаты точки
, а коэффициентам
придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке
, т.е. совокупность всех прямых, проходящих через точку
.
7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.
Пример 4.14. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис. 4.30). Требуется:
а) составить каноническое уравнение прямой, содержащей высоту треугольника;
б) составить общее уравнение прямой, содержащей биссектрису треугольника.
Решение. а) Общее уравнение прямой получено в примере 4.13:
Перейдем от общего уравнения к каноническому.
1) Найдем любое решение системы, например,
(это координаты точки
).
2) Найдем направляющий вектор прямой как векторное произведение нормалей
заданных плоскостей
3) Запишем каноническое уравнение (4.34): .
б) Сначала составим каноническое уравнение прямой . Для этого нужно найти направляющий вектор
этой прямой. Учитывая, что диагональ ромба является биссектрисой,
, где
и
— единичные векторы, одинаково направленные с векторами
и
соответственно. Находим
Составляем каноническое уравнение прямой .
Записывая двойное равенство в виде системы, получаем общее уравнение прямой
Расстояние от точки до прямой в пространстве
Найдем расстояние от точки
до прямой
, заданной каноническим уравнением (рис.4.31)):
Искомое расстояние равно высоте параллелограмма, построенного на векторах
и
, то есть.
(4.35)
Уравнение прямой, проходящей через две заданные точки
Пусть в координатном пространстве заданы две точки
и
. Требуется составить уравнение прямой, проходящей через заданные точки.
Как показано в разд., точка принадлежит прямой
тогда и только тогда, когда ее радиус-вектор
удовлетворяет условию (рис.4.32):
, где
— некоторое действительное число (параметр). Это уравнение, а также его координатную форму
(4.36)
будем называть аффинным уравнением прямой, проходящей через две точки и
.
Выражая параметр из каждого уравнения системы (4.36), получаем:
. Исключая параметр
, приходим к уравнению прямой, проходящей через две точки
и
:
(4.37)
Уравнение (4.37) можно получить из канонического уравнения (4.34), выбирая в качестве направляющего вектора вектор
т.е. подставляя
Пример 4.15. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис.4.33). Требуется:
а) составить уравнение прямой ;
б) составить уравнение прямой, содержащей медиану треугольника;
в) найти высоту треугольника, опущенную на сторону
.
Решение. а) Записываем уравнение (4.37) прямой, проходящей через точки
б) Находим координаты середины стороны
. Составляем уравнение (4.37) прямой
в) Искомую высоту находим по формуле (4.35), полагая
и
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.
Прямая – это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнения прямой, проходящей через две точки могут быть следующих видов:
- каноническое уравнение,
- параметрическое уравнение,
- общее уравнение прямой,
- уравнение прямой с угловым коэффициентом,
- уравнение прямой в полярных координатах и другие.
Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.
Каноническое уравнение прямой на плоскости
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
xa и ya – координаты первой точки A,
xb и yb – координаты второй точки B
Параметрическое уравнение прямой на плоскости
{begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases}}
xa, ya – координаты точки, лежащей на прямой,
{l;m} – координаты направляющего вектора прямой,
t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой в пространстве
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a} = dfrac{z-z_a}{z_b-z_a}}
xa, ya и za – координаты первой точки A,
xb, yb и zb – координаты второй точки B
Параметрическое уравнение прямой в пространстве
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a \ z=n cdot t + z_a end{cases} }
xa, ya и za – координаты точки, лежащей на прямой,
{l;m;n} – координаты направляющего вектора прямой,
t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Пример нахождения уравнения прямой, проходящей через две точки
Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).
Каноническое уравнение прямой
Каноническое уравнение прямой, проходящей через две точки имеет вид {dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
Подставим в формулу координаты точек A и B: {dfrac{x-1}{3-1} = dfrac{y-2}{8-2}}
Получаем каноническое уравнение прямой: {dfrac{x-1}{2} = dfrac{y-2}{4}}
Уравнение прямой с угловым коэффициентом
Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}
Параметрическое уравнение прямой
Параметрическое уравнение прямой имеет вид:
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases} }
где {x_a, y_b} – координаты точки, лежащей на прямой, {{l;m}} – координаты направляющего вектора прямой, t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.
Найдем координаты направляющего вектора:
overline{AB} = {x_b – x_a; y_b – y_a} = {3-1; 8-2} = {2; 6}
Получаем параметрическое уравнение:
begin{cases} x=2 t + 1 \ y=6 t + 2 end{cases}
Используем калькулятор для проверки полученного ответа.


