При
переходе к трехмерному пространству с
заданной декартовой прямоугольной
системой координат происходит естественное
обобщение уравнений прямой на плоскости
на трехмерный случай. Запишем основные
виды уравнений прямой
![]() в трехмерном пространстве,
в трехмерном пространстве,
|
Название |
Вид |
Геометрический |
|
Уравнение |
|
|
|
Каноническое |
|
|
|
Параметрическое |
|
Геометрический |
Обратим
внимание на то, что все, приведенные в
таблице, виды уравнений прямой могут
быть представлены как системы уравнений
двух плоскостей.
Например, уравнение
прямой, проходящей через две заданные
точки:


В
уравнении плоскости
![]() :
:![]() ,
,![]() ,
,![]() ;
;
координата![]() отсутствует,
отсутствует,
следовательно, плоскость![]()
![]() или, что то же самое,
или, что то же самое,![]()
![]() .
.
Аналогично для плоскости![]() :
:
![]()
![]() или
или
![]()
![]() ;
;![]() ,
,![]() ,
,![]() .
.
Также
и остальные уравнения прямой можно
представить как системы уравнений двух
плоскостей, параллельных координатным
плоскостям. В общем случае плоскости ,
линией пересечения которых является
прямая
![]() ,
,
могут быть расположены произвольно
относительно системы координат. Систему
уравнений двух плоскостей называютобщим
уравнением прямой. Общее
уравнение прямой – это уравнение линии
пересечения данных плоскостей:
|
|
(6.17) |
В
заключение приведем векторное
уравнение прямой:
|
|
(6.18) |
где
![]() =
=![]() –
–
радиус-вектор произвольной точки,
лежащей на прямой,![]() =
=![]() – радиус-вектор известной, фиксированной
– радиус-вектор известной, фиксированной
точки этой прямой,![]() – направляющий вектор прямой. Векторное
– направляющий вектор прямой. Векторное
уравнение прямой, лежащей в плоскости,
имеет вид (6. ), но все векторы, входящие
в него, имеют лишь по две координаты.
6.5. Преобразование координат
Рассматривая
уравнения плоскости и прямой, мы
подчеркивали их связь с выбранным
репером. В этом разделе рассмотрим, как
меняются эти уравнения при переходе от
одного репера к другому.
Будем
рассматривать геометрические пространства
с ортонормированными базисами, то есть
базисами состоящими из единичных
векторов, попарно перпендикулярных
друг другу. Реперы с такими базисами
могу отличаться друг от друга (а) точкой
приложения базиса, (б) направлениями
базисных векторов.
Пусть
точки приложения базиса (![]() ,
,![]() )
)
– точки![]() и
и![]() .
.
Точка![]() имеет
имеет
радиусы-векторы![]() в репере
в репере![]() ,
,
и![]() в
в
репере![]() .
.
Точка![]() в репере
в репере![]() имеет радиус-вектор
имеет радиус-вектор![]() .
.
|
|
Так
где |
Равенства
(6.19) можно записать более компактно:
|
|
(6.20) |
где
![]() – радиус вектор точки
– радиус вектор точки![]() в репере
в репере![]() ,
,![]() – радиус вектор той же точки в репере
– радиус вектор той же точки в репере![]() ,
,![]() – радиус-вектор «нового» начала координат
– радиус-вектор «нового» начала координат
в «старом» репере.
|
|
Пусть
= |
Следовательно,
имеем:
 ,
,
или
в матричной форме:
|
|
(6.21) |
где
![]()
![]() – столбец координат точки
– столбец координат точки![]() в
в
репере![]() ,
,![]() =
= матрица перехода от репера
матрица перехода от репера![]() к реперу
к реперу![]() ,
,
столбцами которой являются координаты
векторов![]() и
и![]() в репере
в репере![]() ,
,![]() =
=![]() – столбец координат точки
– столбец координат точки![]() в репере
в репере![]() .
.
Если
найти матрицу
![]() ,
,
обратную матрице![]() ,
,
то можно выразить![]() через
через![]() :
:
|
|
(6.22) |
Столбцы
матрицы
![]() – это координаты векторов
– это координаты векторов![]() и
и![]() в репере
в репере![]() .
.
В
случае трехмерного геометрического
пространства будут справедливы равенства
(6.21 ) и (6.22), но векторы
![]() и
и![]() будут содержать по три координаты, а
будут содержать по три координаты, а
матрицы![]() и
и![]() иметь три строки и три столбца.
иметь три строки и три столбца.
Таким
образом, переход от одного репера к
другому удобно выполнять в два шага:
Шаг
1. Выполнить
перенос начала координат, пользуясь
формулой:
![]() .
.
Шаг
2. Выполнить
поворот осей координат, пользуясь
формулой:![]() .
.
Пример.
Прямая
![]() задана своим общим уравнением:
задана своим общим уравнением:
![]() :
:
 .
.
Записать
уравнение этой прямой в системе координат,
начало которой является какая-либо
точка прямой
![]() ,
,![]() сонаправлена вектору нормали плоскости
сонаправлена вектору нормали плоскости![]() ,
,
ось![]() проходит по прямой
проходит по прямой![]() ,
,
базис является левой тройкой векторов.
Решение.
1.Найдем
какую-либо точку лежащую на прямой
![]() и перенесем в нее начало координат.
и перенесем в нее начало координат.
Пусть
![]() .
.
Новое
начало координат:
![]() .
.
Пользуясь формулами ,
,
запишем уравнение прямой в системе
координат с началом в точке![]() :
:

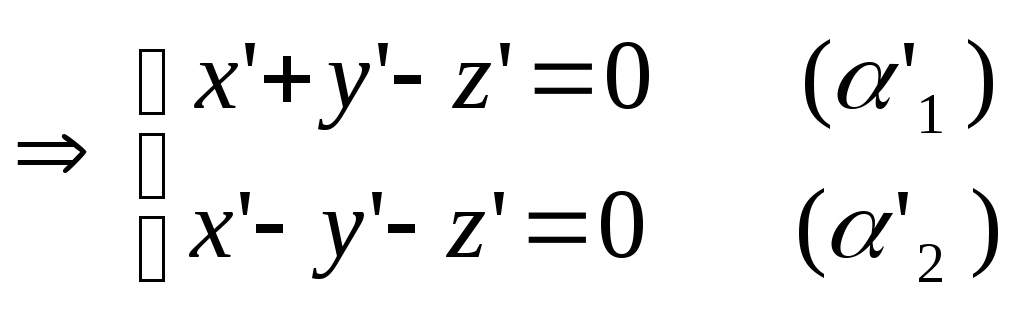 .
.
2.
Найдем векторы, сонаправленные новым
координатным осям, и, нормировав их,
получим новый базис.
Вектор
нормали плоскости
![]() :
:![]() .
.
Напомним, что координаты вектора нормали
к плоскости – это коэффициенты перед
переменными в ее уравнении.![]() .
.
Вектор,
сонаправленный прямой
![]() ,
,
можно найти как векторное произведение
векторов нормалей к плоскостям![]() и
и![]() :
:
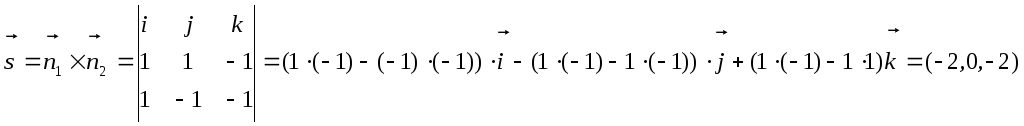 .
.
![]() ,
,
![]()
Вектор,
сонаправленный
![]() найдем, вычислив векторное произведение
найдем, вычислив векторное произведение![]() и
и![]() .
.
Напомним, что тройка (![]() –
–
левая. (см. стр. ).
![]()
 =
=![]() )=
)=
(2,-4,-2)=-2(1,-2,-1),![]() .
.
Итак,
матрица
![]() перехода от базиса
перехода от базиса![]() к базису
к базису![]() имеет
имеет
вид:
![]() =
=
![]() =
=
–
(Вычисление
элементов матрицы
![]() выполните самостоятельно).
выполните самостоятельно).
3.
Умножим нормальные векторы плоскостей
![]() и
и![]() на матрицу
на матрицу![]() :
:

![]()
![]() =
=
–

![]() =(0,0,-
=(0,0,-![]() ),
),
![]()
![]() =
=
–

![]() =(0,-
=(0,-![]() ,-
,-![]() ).
).
Уравнения
плоскостей
![]() ,
,![]() и общее уравнение прямой
и общее уравнение прямой![]() в репере
в репере![]() имеет вид:
имеет вид:
![]()

 .
.
Обратим
внимание на следующий факт:
![]() ,
,
то есть,чтобы
найти матрицу, обратную матрице перехода
от одного ортонормированного базиса к
другому, достаточно ее транспонировать.
1Вектор, перпендикулярный плоскости,
называютнормалью к этой плоскости.
112
Соседние файлы в папке Математика
- #
- #
- #
- #
- #
- #
- #
Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.
В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через 2 заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.
Что такое каноническое уравнение прямой в пространстве
О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.
Допустим, у нас есть прямоугольная система координат Oxyz, в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой a, а точку M, то можно записать, что M1(x1, y1, z1) лежит на прямой a и направляющим вектором этой прямой будет a→=(ax, ay, az). Чтобы множество точек M(x, y, z) определяло прямую a, векторы M1M→ и a→ должны быть коллинеарными,
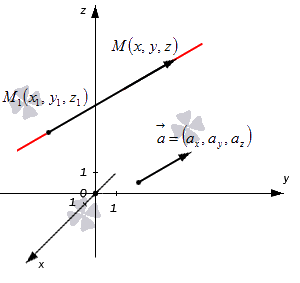
Если мы знаем координаты векторов M1M→ и a→, то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты a→. Для того чтобы получить координаты M1M→, нам необходимо вычислить разность между M(x, y, z) и M1(x1, y1, z1). Запишем:
M1M→=x-x1, y-y1, z-z1
После этого нужное нам условие мы можем сформулировать так: M1M→=x-x1, y-y1, z-z1 и a→=(ax, ay, az): M1M→=λ·a→⇔x-x1=λ·axy-y1=λ·ayz-z1=λ·az
Здесь значением переменной λ может быть любое действительное число или ноль. Если λ=0, то M(x, y, z) и M1(x1, y1, z1)совпадут, что не противоречит нашим рассуждениям.
При значениях ax≠0, ay≠0, az≠0 мы можем разрешить относительно параметра λ все уравнения системы x-x1=λ·axy-y1=λ·ayz-z1=λ·az
Между правыми частями после этого можно будет поставить знак равенства:
x-x1=λ·axy-y1=λ·ayz-z1=λ·az⇔λ=x-x1axλ=y-y1ayλ=z-z1az⇔x-x1ax=y-y1ay=z-z1az
В итоге у нас получились уравнения x-x1ax=y-y1ay=z-z1az, с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.
Такая запись используется даже при нулевых значениях одного или двух параметров ax, ay, az, поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны 0, поскольку направляющий вектор a→=(ax, ay, az) нулевым не бывает.
Если один-два параметра a равны 0, то уравнение x-x1ax=y-y1ay=z-z1az носит условный характер. Его следует считать равным следующей записи:
x=x1+ax·λy=y1+ay·λz=z1+az·λ, λ∈R.
Частные случаи канонических уравнений мы разберем в третьем пункте статьи.
Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.
1) если исходная прямая будет проходить через две точки M1(x1, y1, z1) и M2(x2, y2, z2), то канонические уравнения примут следующий вид:
x-x1ax=y-y1ay=z-z1az или x-x2ax=y-y2ay=z-z2az.
2) поскольку a→=(ax, ay, az) является направляющим вектором исходной прямой, то таковыми будут являться и все векторы μ·a→=μ·ax, μ·ay, μ·az, μ∈R, μ≠0. Тогда прямая может быть определена с помощью уравнения x-x1ax=y-y1ay=z-z1az или x-x1μ·ax=y-y1μ·ay=z-z1μ·az.
Вот несколько примеров таких уравнений с заданными значениями:
x-32=y+1-12=zln 7
Тут x1=3, y1=-1, z1=0, ax=2, ay=-12, az=ln 7.
x-40=y+21=z+10
Тут M1(4, -2, -1), a→=(0, 1, 0).
Как составить каноническое уравнение прямой в пространстве
Мы выяснили, что канонические уравнения вида x-x1ax=y-y1ay=z-z1az будут соответствовать прямой, проходящей через точку M1(x1, y1, z1), а вектор a→=(ax, ay, az) будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.
Разберем пару конкретных задач.
У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x+14=y2=z-3-5. Запишите координаты всех направляющих векторов для нее.
Решение
Чтобы получить координаты направляющего вектора, нам надо просто взять значения знаменателей из уравнения. Мы получим, что одним из направляющих векторов будет a→=(4, 2, -5), а множество всех подобных векторов можно сформулировать как μ·a→=4·μ, 2·μ, -5·μ. Здесь параметр μ – любое действительное число (за исключением нуля).
Ответ: 4·μ, 2·μ, -5·μ, μ∈R, μ≠0
Запишите канонические уравнения, если прямая в пространстве проходит через M1(0, -3, 2) и имеет направляющий вектор с координатами -1, 0, 5.
Решение
У нас есть данные, что x1=0, y1=-3, z1=2, ax=-1, ay=0, az=5. Этого вполне достаточно, чтобы сразу перейти к записи канонических уравнений.
Сделаем это:
x-x1ax=y-y1ay=z-z1az⇔x-0-1=y-(-3)0=z-25⇔⇔x-1=y+30=z-25
Ответ: x-1=y+30=z-25
Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.
Канонические уравнения с одним или двумя a, равными нулю
Ранее мы уже говорили, что одно-два значения параметров ax, ay, az в уравнениях могут иметь нулевые значения. При этом запись x-x1ax=y-y1ay=z-z1az=λ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при λ∈R):
x=x1+ax·λy=y1+ay·λz=z1+az·λ
Рассмотрим эти случаи подробнее. Допустим, что ax=0, ay≠0, az≠0, ax≠0, ay=0, az≠0, либо ax≠0, ay≠0, az=0. В таком случае нужные уравнения мы можем записать так:
- В первом случае:
x-x10=y-y1ay=z-z1az=λ⇔x-x1=0y=y1+ay·λz=z1+az·λ⇔x-x1=0y-y1ay=z-z1az=λ -
Во втором случае:
x-x1ax=y-y10=z-z1az=λ⇔x=x1+ax·λy-y1=0z=z1+az·λ⇔y-y1=0x-x1ax=z-z1az=λ -
В третьем случае:
x-x1ax=y-y1ay=z-z10=λ⇔x=x1+ax·λy=y1+ay·λz-z1=0⇔z-z1=0x-x1ax=y-y1ay=λ
Получается, что при таком значении параметров нужные прямые находятся в плоскостях x-x1=0, y-y1=0 или z-z1=0, которые располагаются параллельно координатным плоскостям (если x1=0, y1=0 либо z1=0). Примеры таких прямых показаны на иллюстрации.
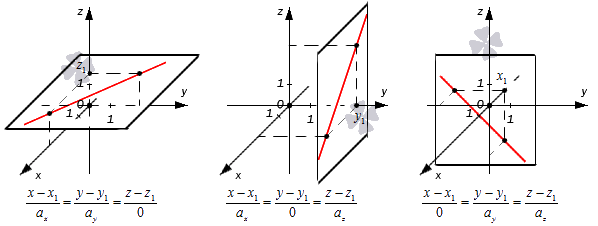
Следовательно, мы сможем записать канонические уравнения немного иначе.
- В первом случае: x-x10=y-y10=z-z1az=λ⇔x-x1=0y-y1=0z=z1+az·λ, λ∈R
- Во втором: x-x10=y-y1ay=z-z10=λ⇔x-x1=0y=y1+ay·λ, λ∈Rz-z1=0
- В третьем: x-x1ax=y-y10=z-z10=λ⇔x=x1+ax·λ, λ∈Ry=y1=0z-z1=0
Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: x1=0y1=0, x1=0z1=0, y1=0z1=0. Их направляющие векторы имеют координаты 0, 0, az, 0, ay, 0, ax, 0, 0. Если обозначить направляющие векторы координатных прямых как i→, j→, k→, то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:
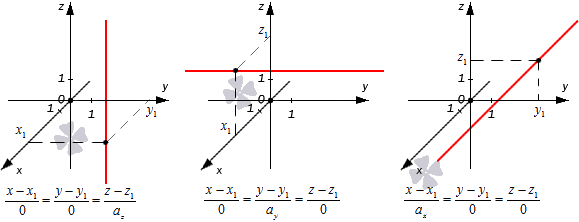
Покажем на примерах, как применяются эти правила.
Найдите канонические уравнения, с помощью которых можно определить в пространстве координатные прямые Oz, Ox, Oy.
Решение
Координатные векторы i→=(1, 0, 0), j→=0, 1, 0, k→=(0, 0, 1) будут для исходных прямых направляющими. Также мы знаем, что наши прямые будут обязательно проходить через точку O(0, 0, 0), поскольку она является началом координат. Теперь у нас есть все данные, чтобы записать нужные канонические уравнения.
Для прямой Ox: x1=y0=z0
Для прямой Oy: x0=y1=z0
Для прямой Oz: x0=y0=z1
Ответ: x1=y0=z0, x0=y1=z0, x0=y0=z1.
В пространстве задана прямая, которая проходит через точку M1(3, -1, 12). Также известно, что она расположена параллельно оси ординат. Запишите канонические уравнения этой прямой.
Решение
Учитывая условие параллельности, мы можем сказать, что вектор j→=0, 1, 0 будет для нужной прямой направляющим. Следовательно, искомые уравнения будут иметь вид:
x-30=y-(-1)1=z-120⇔x-30=y+11=z-120
Ответ: x-30=y+11=z-120
Как записать каноническое уравнение прямой, которая проходит через две заданные точки
Допустим, что у нас есть две несовпадающие точки M1(x1, y1, z1) и M2(x2, y2, z2), через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?
Для начала примем вектор M1M2→ (или M2M1→) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:
M1M2→=x2-x1, y2-y1, z2-z1
Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:
x-x1x2-x1=y-y1y2-y1=z-z1z2-z1x-x2x2-x1=y-y2y2-y1=z-z2z2-z1
Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:
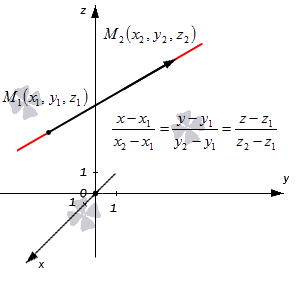
Приведем пример решения задачи.
в пространстве есть две точки с координатами M1(-2, 4, 1) и M2(-3, 2, -5), через которые проходит прямая. Запишите канонические уравнения для нее.
Решение
Согласно условиям, x1=-2, y1=-4, z1=1, x2=-3, y2=2, z2=-5. Нам требуется подставить эти значения в каноническое уравнение:
x-(-2)-3-(-2)=y-(-4)2-(-4)=z-1-5-1⇔x+2-1=y+46=z-1-6
Если мы возьмем уравнения вида x-x2x2-x1=y-y2y2-y1=z-z2z2-z1, то у нас получится: x-(-3)-3-(-2)=y-22-(-4)=z-(-5)-5-1⇔x+3-1=y-26=z+5-6
Ответ: x+3-1=y-26=z+5-6 либо x+3-1=y-26=z+5-6.
Преобразование канонических уравнений прямой в пространстве в другие виды уравнений
Иногда пользоваться каноническими уравнениями вида x-x1ax=y-y1ay=z-z1az не очень удобно. Для решения некоторых задач лучше использовать запись x=x1+ax·λy=y1+ay·λz=z1+az·λ. В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0. Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.
Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру λ и разрешим эти уравнения относительно других переменных. В итоге получим:
x-x1ax=y-y1ay=z-z1az⇔x-x1ax=y-y1ay=z-z1az⇔⇔x-x1ax=λy-y1ay=λz-z1az=λ⇔x=x1+ax·λy=y1+ay·λz=z1+az·λ
Значение параметра λ может быть любым действительным числом, ведь и x, y, z могут принимать любые действительные значения.
В прямоугольной системе координат в трехмерном пространстве задана прямая, которая определена уравнением x-23=y-2=z+70. Запишите каноническое уравнение в параметрическом виде.
Решение
Сначала приравниваем каждую часть дроби к λ.
x-23=y-2=z+70⇔x-23=λy-2=λz+70=λ
Теперь разрешаем первую часть относительно x, вторую – относительно y, третью – относительно z. У нас получится:
x-23=λy-2=λz+70=λ⇔x=2+3·λy=-2·λz=-7+0·λ⇔x=2+3·λy=-2·λz=-7
Ответ: x=2+3·λy=-2·λz=-7
Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).
Равенство x-x1ax=y-y1ay=z-z1az нужно для начала представить в виде системы уравнений:
x-x1ax=y-y1ayx-x1ax=z-z1axy-y1ay=z-z1az
Поскольку pq=rs мы понимаем как p·s=q·r, то можно записать:
x-x1ax=y-y1ayx-x1ax=z-z1azy-y1ay=z-z1az⇔ay·(x-x1)=ax·(y-y1)az·(x-x1)=ax·(z-z1)az·(y-y1)=ay·(z-z1)⇔⇔ay·x-ax·y+ax·y1-ay·x1=0az·x-ax·z+ax·z1-az·x1=0az·y-ay·z+ay·z1-az·y1=0
В итоге у нас вышло, что:
x-x1ax=y-y1ay=z-z1az⇔ay·x-ax·y+ax·y1-ay·x1=0az·x-ax·z+ax·z1-az·x1=0az·y-ay·z+ay·z1-az·y1=0
Выше мы отмечали, что все три параметра a не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен 2, поскольку ay-ax0az0-ax0az-ay=0 и один из определителей второго порядка не равен 0:
ay-axaz0=ax·az, ay0az-ax=ax·ay, -ax00-ax=ax2ay-ax0az=ay·az, ay00-ay=-ay2, -ax0az-ay=ax·ayaz00az=az2, az-ax0-ay=-ay·az, 0-axaz-ay=ax·az
Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать 3 неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.
Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.
Прямая задана каноническим уравнением x-12=y0=z+20. Напишите для нее уравнение пересекающихся плоскостей.
Решение
Начнем с попарного приравнивания дробей.
x-12=y0=z+20⇔x-12=y0x-12=z+20y0=z+20⇔⇔0·(x-1)=2y0·(x-1)=2·(z+2)0·y=0·(z+2)⇔y=0z+2=00=0
Теперь исключаем из расчетов последнее уравнение, потому что оно будет верным при любых x, y и z. В таком случае x-12=y0=z+20⇔y=0z+2=0.
Это и есть уравнения двух пересекающихся плоскостей, которые при пересечении образуют прямую, заданную с помощью уравнения x-12=y0=z+20
Ответ: y=0z+2=0
Прямая задана уравнениями x+12=y-21=z-5-3, найдите уравнение двух плоскостей, пересекающихся по данной прямой.
Решение
Приравниваем дроби попарно.
x+12=y-21=z-5-3⇔x+12=y-21x+12=z-5-3y-21=z-5-3⇔⇔1·(x+1)=2·(y-2)-3·(x+1)=2·(z-5)-3·(y-2)=1·(z-5)⇔x-2y+5=03x+2z-7=03y+7-11=0
Получаем, что определитель основной матрицы полученной системы будет равен 0:
1-20302031=1·0·1+(-2)·2·0+0·3·3-0·0·0-1·2·3-(-2)·3·1=0
Минор второго порядка нулевым при этом не будет: 1-230=1·0-(-2)·3=6. Тогда мы можем принять его в качестве базисного минора.
В итоге мы можем вычислить ранг основной матрицы системы x-2y+5=03x+2z-7=03y+z-11=0. Это будет 2. Третье уравнение исключаем из расчета и получаем:
x-2y+5=03x+2z-7=03y+z-11=0⇔x-2y+5=03x+2z-7=0
Ответ: x-2y+5=03x+2z-7=0
4. Аналитическая геометрия в трехмерном пространстве
4.4 Прямая в трехмерном пространстве
Фиксировать прямую в трехмерном пространстве можно, задавая точку $M_0$, через которую проходит прямая, и направляющий вектор прямой $textbf {a}$. Пусть точке $M_0$ соответствует вектор $ textbf {r}_0$, текущей точке прямой $M$ соответствует вектор $textbf {r}$, тогда вектора $textbf {r}-textbf {r}_0$ и $textbf {a}=(a_1,, a_2, ,a_3)^T$ отличаются только множителем,
begin{equation}
textbf {r}-textbf {r}_0=textbf {a}t. (36)
label{pryam_3}
end{equation}
Это уравнение называется векторным уравнением прямой, см. рис. ref{pryam33}. Когда параметр $t$ пробегает значения от $-infty$ до $infty$, точка $M$ пробегает прямую.
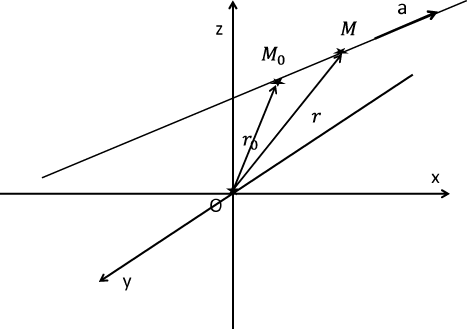
Рис 15: Прямая в трехмерном пространстве задается фиксированной точкой $M_0$ и направляющим вектором $textbf {a}$.
Записывая это уравнение в координатах, получаем:
[
x-x_0=a_1t, quad y-y_0=a_2t, quad z-z_0=a_3t.
]
Этот набор уравнений называется параметрическим описанием прямой в трехмерном пространстве. Исключая $t$ из этих уравнений, находим:
begin{equation}
frac{x-x_0}{a_1}=frac{y-y_0}{a_2}=frac{z-z_0}{a_3}. (37)
label{pryam31}
end{equation}
Эти уравнения называются координатными уравнениями прямой. Заметим, что по знаменателям в этом соотношении можно восстановить вектор $textbf {a}=(a_1,, a_2, ,a_3)^T$.
Выпишем уравнение прямой, проходящей через две заданные точки, $M_0=(x_0,, y_0, ,z_0)$, $M_1=(x_1,, y_1, ,z_1)$. Подставляя вторую точку в уравнение (37) и затем разделив (37) на результат подстановки, получим искомое уравнение:
begin{equation}
frac{x-x_0}{x_1-x_0}=frac{y-y_0}{y_1-y_0}=frac{z-z_0}{z_1-z_0}. (38)
label{pryam32}
end{equation}
Далее, в трехмерном пространстве прямую можно представить как результат пересечения двух плоскостей, т.е. как результат совместного решения уравнений
begin{equation}
A_1x+B_1y+C_1z+D_1=0, quad A_2x+B_2y+C_2z+D_2=0. (39)
label{pryam34}
end{equation}
Заметим, что уравнения прямой (37), (38) можно трактовать как уравнения вида (39).
Пример.
Контрольный вопрос.
Решение типовых задач.
Задачи.
Уравнения прямых в пространстве
Уравнение прямой как линии пересечения двух плоскостей
Пусть в координатном пространстве (в прямоугольной системе координат) две плоскости заданы общими уравнениями
в которых коэффициенты при неизвестных непропорциональны, т.е. . Это условие означает, что плоскости
и
пересекаются (см. условие (4.25)), поскольку их нормали
и
неколлинеарны (рис.4.25). Тогда линия пересечения плоскостей описывается системой уравнений
(4.31)
Система (4.31) называется общим уравнением прямой в пространстве.
Пример 4.13. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис.4.26). Требуется составить уравнение прямой, содержащей высоту
треугольника.
Решение. Прямая является линией пересечения двух плоскостей: плоскости
, треугольника
и плоскости
, проходящей через точку
перпендикулярно вектору
(рис.4.26). По формуле (4.21) составим уравнение плоскости
проходящей через три точки
По формуле (4.14) составим уравнение плоскости , проходящей через точку
перпендикулярно вектору
Следовательно, общее уравнение (4.31) прямой имеет вид
Параметрическое уравнение прямой в пространстве
Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.
Пусть в координатном пространстве заданы точка
и ненулевой вектор
(рис.4.27). Требуется составить уравнение прямой, коллинеарной вектору
и проходящей через точку
.
Выберем на прямой произвольную точку . Обозначим
— радиус-векторы точек
и
(рис.4.28).
Точка принадлежит заданной прямой тогда и только тогда, когда векторы
и
коллинеарны. Запишем условие коллинеарности:
, где
— некоторое действительное число (параметр). Учитывая, что
, получим векторное параметрическое уравнение прямой в пространстве:
(4.32)
где — направляющий вектор прямой, а
— радиус-вектор заданной точки
принадлежащей прямой.
Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве
(4.33)
где — координаты направляющего вектора
прямой. Параметр
в уравнениях (4.32),(4.33) имеет следующий геометрический смысл: величина
пропорциональна расстоянию от заданной точки
до точки
. Физический смысл параметра
в параметрических уравнениях (4.32),(4.33) — это время при равномерном и Прямолинейном движении точки
по прямой. При
точка
совпадает с заданной точкой
. При возрастании параметра
движение происходит в направлении направляющего вектора.
Каноническое уравнение прямой в пространстве
Выразим параметр из каждого уравнения системы (4.33):
, а затем исключим этот параметр:
(4.34)
Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты не равны нулю одновременно, так как это координаты направляющего вектора прямой.
Замечания 4.6.
1. Если один или два из трех знаменателей дробей в (4.34) равны нулю, то считается, что соответствующий числитель дроби равен нулю. Например:
а) каноническое уравнение — это уравнение
прямой, параллельной оси аппликат (рис.4.29,а);
б) каноническое уравнение — это уравнение
прямой, параллельной координатной плоскости
(рис.4.29,б).
2. Направляющий вектор прямой определяется неоднозначно. Например, любой ненулевой вектор
, где
, также является направляющим вектором для той же прямой.
Переход от общего уравнение к каноническому
3. Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:
1) найти любое решение системы
определяя тем самым координаты точки
, принадлежащей прямой;
2) найти направляющий вектор прямой как векторное произведение нормалей
заданных плоскостей:
3) записать каноническое уравнение (4.34) с учетом пунктов 1 и 2.
4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы
и привести подобные члены.
5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):
6. Если в каноническом уравнении (4.34) прямой фиксировать координаты точки
, а коэффициентам
придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке
, т.е. совокупность всех прямых, проходящих через точку
.
7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.
Пример 4.14. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис. 4.30). Требуется:
а) составить каноническое уравнение прямой, содержащей высоту треугольника;
б) составить общее уравнение прямой, содержащей биссектрису треугольника.
Решение. а) Общее уравнение прямой получено в примере 4.13:
Перейдем от общего уравнения к каноническому.
1) Найдем любое решение системы, например,
(это координаты точки
).
2) Найдем направляющий вектор прямой как векторное произведение нормалей
заданных плоскостей
3) Запишем каноническое уравнение (4.34): .
б) Сначала составим каноническое уравнение прямой . Для этого нужно найти направляющий вектор
этой прямой. Учитывая, что диагональ ромба является биссектрисой,
, где
и
— единичные векторы, одинаково направленные с векторами
и
соответственно. Находим
Составляем каноническое уравнение прямой .
Записывая двойное равенство в виде системы, получаем общее уравнение прямой
Расстояние от точки до прямой в пространстве
Найдем расстояние от точки
до прямой
, заданной каноническим уравнением (рис.4.31)):
Искомое расстояние равно высоте параллелограмма, построенного на векторах
и
, то есть.
(4.35)
Уравнение прямой, проходящей через две заданные точки
Пусть в координатном пространстве заданы две точки
и
. Требуется составить уравнение прямой, проходящей через заданные точки.
Как показано в разд., точка принадлежит прямой
тогда и только тогда, когда ее радиус-вектор
удовлетворяет условию (рис.4.32):
, где
— некоторое действительное число (параметр). Это уравнение, а также его координатную форму
(4.36)
будем называть аффинным уравнением прямой, проходящей через две точки и
.
Выражая параметр из каждого уравнения системы (4.36), получаем:
. Исключая параметр
, приходим к уравнению прямой, проходящей через две точки
и
:
(4.37)
Уравнение (4.37) можно получить из канонического уравнения (4.34), выбирая в качестве направляющего вектора вектор
т.е. подставляя
Пример 4.15. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис.4.33). Требуется:
а) составить уравнение прямой ;
б) составить уравнение прямой, содержащей медиану треугольника;
в) найти высоту треугольника, опущенную на сторону
.
Решение. а) Записываем уравнение (4.37) прямой, проходящей через точки
б) Находим координаты середины стороны
. Составляем уравнение (4.37) прямой
в) Искомую высоту находим по формуле (4.35), полагая
и
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.
Параметрическое и каноническое уравнение прямой в пространстве
Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку
параллельно направляющему вектору
.
Пусть, – произвольная точка прямой, тогда векторы
и
коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:
(1)
это и есть канонические уравнения прямой.
Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:
(2)
Уравнение прямой в пространстве, которая проходит через две заданные точки
Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.
Итак, через две точки и
можно не только геометрично провести линию, но и сложить её уравнения.
За направляющий вектор возьмём , тогда по формуле (1) у нас получается:
(3)
уравнение прямой в пространстве, которые проходят через две заданные точки.
Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Общее уравнение прямой – переход к каноническому уравнению
Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.
Пусть известны их уравнения:
(4)
Тогда система (4) называется общим уравнением прямой.
Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку
этой прямой.
Точку находим, как один из решений системы (4). Например, положив в (4)
находим
, тогда и точку
. Направляющий вектор
, который параллелен к каждой из плоскостей
и
и перпендикулярен к их нормальным векторам
и
, то есть
,
. (см. рис. 1). Поэтому вектор
можно найти при помощи векторного произведения
и
=
x
=
Найдены координаты и
подставим в каноническое уравнение (1).
Например, от общих уравнений прямой:
Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём
. Нормальные векторы
и
. Тогда направляющий вектор
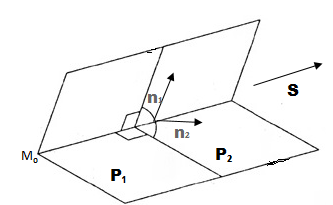
Рис. 1
x
=
,
и канонические уравнения станут:
Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Угол между двумя прямыми :
и
равен углу между их направляющими векторами и
, поэтому
=
(5)
Условия параллельности и перпендикулярности прямых соответственно запишутся:
и
.
(6)
Примеры решения задач
Давайте рассмотрим первый пример, где можно двумя способами построить прямую:
Задача
При точке и направляющем векторе
необходимо:
- составить каноническое уравнение прямой;
- построить эту прямую.
Решение
1) По формуле (1) запишем каноническое уравнение прямой :
=
.
2) Рассмотрим два способа построения прямой .
Первый способ
В системе координат строим вектор
и точку
и проводим через точку
прямую параллельную вектору
.
Второй способ
По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:
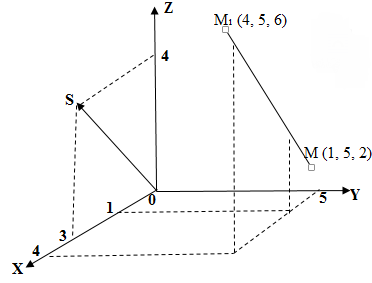
На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой
. Так при
находим координаты
. Через две точки
и
проводим прямую
.
Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:
Задача
Найти острый угол между прямыми:
,
(7)
Решение
По формуле (7) получаем:
=
=
=
Так как , тогда угол
тупой,
, а острый угол
.
Ответ
.
Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.
Задача
Составить уравнение прямой , которая проходит через точку
и параллельна прямой
.
Решение
От параметрического уравнения переходим к каноническому При условии параллельности прямых
то есть направляющим вектором новой прямой может служить известный вектор
и по формуле (1) у нас получается:
.
Ответ
.

 .
.
 или
или ,
,
