Как составить уравнение прямой параллельной данной прямой и проходящей через данную точку?
Пусть y = k1x+b1 — данная прямая. С учётом условия параллельности прямых уравнение прямой, параллельной данной, имеет вид y = k1x+b2.
Так как эта прямая проходит через точку M(xo; yo), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение xo и yo, мы найдем b:
yo= k1∙xo+ b2, откуда b2 = yo — k1∙xo.
Примеры.
1) Составить уравнение прямой, которая проходит через точку A(4;21) и параллельна прямой y=3x-8.
Решение:
Так как угловые коэффициенты у параллельных прямых равны, то k2=k1=3 и уравнение прямой, параллельной прямой y=3x-8, имеет вид y=3x+b. Так как искомая прямая проходит через точку A(4;21), подставляем в уравнение прямой координаты A (x=4; y=21):
21=3·4+b, откуда находим b: b= 21-12= 9.
Итак, уравнение прямой, параллельной прямой y=3x-8, проходящей через точку A(4;21) — y=3x+9.
Ответ: y=3x+9.
2) Написать уравнение прямой, параллельной прямой x=5, проходящей через точку B(-3; 5).
Решение:
Так как прямая x=5 параллельна оси Oy, то и параллельная ей прямая также параллельна Oy, а значит, уравнение этой прямой имеет вид x=a.
Так как эта прямая проходит через точку B(-3; 5), то её абсцисса удовлетворяет уравнению прямой: a= -3.
Итак, уравнение прямой, параллельной прямой x=5 и проходящей через точку B(-3; 5) — x= -3.
Ответ: x= -3.
3) Написать уравнение прямой, параллельной прямой y= -11, проходящей через точку K(2; 4).
Решение:
Так как прямая y= -11 параллельна оси Ox, то и параллельная ей прямая также параллельна оси Ox. Поэтому уравнение прямой имеет вид y=b.
Поскольку эта прямая проходит через точку K(2; 4), то её ордината удовлетворяет уравнению прямой: b=4.
Уравнение прямой, параллельной прямой y= -11 и проходящей через точку K(2; 4) — y=4.
Ответ: y=4.
Уравнение параллельной прямой
Альтернативная формула:
Прямая, проходящая через точку M1(x1; y1) и параллельная прямой Ax+By+C=0 , представляется уравнением
назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).
Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника 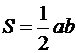 , где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
, где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
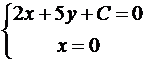
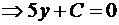
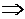
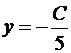 ;
;
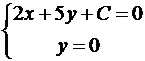
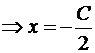 .
.
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: 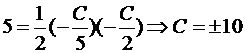 . Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .
. Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .
Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /7x – 4 /7 (здесь a = 5 /7). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .
Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.
Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).
2.5.2. Как найти прямую, параллельную данной?
За незнание этой простейшей задачи сурово наказывает Соловей-Разбойник.
Задача 75
Прямая задана уравнением  . Составить уравнение параллельной прямой, которая проходит через точку
. Составить уравнение параллельной прямой, которая проходит через точку  .
.
Решение: обозначим неизвестную прямую буквой  . Что о ней сказано в условии? Прямая
. Что о ней сказано в условии? Прямая  проходит через точку
проходит через точку  . А если прямые параллельны, то очевидно, что направляющий вектор прямой «цэ» подойдёт и для построения прямой «дэ».
. А если прямые параллельны, то очевидно, что направляющий вектор прямой «цэ» подойдёт и для построения прямой «дэ».
Вытаскиваем направляющий вектор из уравнения  :
: 
Уравнение искомой прямой  составим по точке
составим по точке  и направляющему вектору
и направляющему вектору  :
: 
Ответ: 
Геометрия задачи выглядит незатейливо: 
Аналитическая же проверка состоит в следующих шагах:
1) Проверяем, что у прямых  один и тот же направляющий вектор (если уравнения не упрощены должным образом, то векторы будут коллинеарны). Да что тут векторы?! – посмотрим на коэффициенты:
один и тот же направляющий вектор (если уравнения не упрощены должным образом, то векторы будут коллинеарны). Да что тут векторы?! – посмотрим на коэффициенты: 
– параллельность прямых понятна без всякого чертежа!
2) Проверяем, удовлетворяет ли точка  полученному уравнению
полученному уравнению  . И это тоже устный пункт!
. И это тоже устный пункт!
Примеры для самостоятельного решения сегодня будут творческими. Потому что вам ещё придётся тягаться с Бабой-Ягой, а она, знаете, любительница всяких загадок.
Задача 76
Составить уравнение прямой, проходящей через точку  , параллельную прямой
, параллельную прямой  , если
, если 
Существует рациональный и не очень рациональный способ решения. Самый короткий путь в конце книги.
С параллельными прямыми немного поработали и к ним ещё вернёмся. Случай совпадающих прямых малоинтересен, поэтому перейдём к задаче, которая хорошо знакома вам из школьной программы:
Уравнение прямой, проходящей через заданную точку параллельно заданной прямой.
Эта статья является развернутым ответом на вопрос: «Как составить уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой»? Сначала приведена необходимая теория, после чего разобраны решения характерных задач. В заключении разобрано нахождение уравнений прямой, проходящей через заданную точку трехмерного пространства параллельно заданной прямой.
Навигация по странице.
Уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой.
Чтобы составление уравнения прямой, проходящей через заданную точку плоскости параллельно заданной прямой, не вызвало затруднений, вспомним важные факты.
Аксиома параллельных прямых гласит: на плоскости через точку, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Таким образом, мы можем определить конкретную прямую a на плоскости, указав прямую линию b , которой параллельна прямая a , и точку М1 , не лежащую на прямой b , через которую проходит прямая a .
Поставим перед собой следующую задачу.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy . Пусть в этой системе координат задана точка и прямая b , которой соответствует некоторое уравнение прямой на плоскости. Требуется написать уравнение прямой a , которая проходит через точку М1 и параллельна прямой b .
Решим поставленную задачу.
Из условия мы знаем координаты точки М1 , через которую проходит прямая a . Этих данных не достаточно, чтобы написать уравнение прямой a .
Нам еще нужно знать
Как же их найти?
По условию прямая a параллельна прямой b , тогда, на основании необходимого и достаточного условия параллельности двух прямых на плоскости, в качестве направляющего вектора прямой a мы можем принять направляющий вектор прямой b , в качестве нормального вектора прямой a мы можем взять нормальный вектор прямой b , а угловой коэффициент прямой a равен угловому коэффициенту прямой b (или они оба бесконечны).
Таким образом, чтобы в прямоугольной системе координат на плоскости написать уравнение прямой a , проходящей через заданную точку параллельно заданной прямой b , нужно определить
- или координаты направляющего вектора прямой b (),
- или координаты нормального вектора прямой b (),
- или угловой коэффициент прямой b (),
принять их соответственно в качестве
- координат направляющего вектора прямой a (),
- координат нормального вектора прямой a (),
- углового коэффициента прямой a (),
и записать требуемое уравнение прямой a соответственно в виде
- или ,
- ,
- .
Внесем ясности – приведем примеры с подробными решениями на каждый случай.
Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку параллельно прямой .
Из параметрических уравнений прямой нам сразу видны координаты ее направляющего вектора . Этот вектор является направляющим вектором прямой, уравнение которой нам требуется составить. Уравнение прямой, проходящей через точку и имеющей направляющий вектор с координатами , имеет вид .
Это и есть искомые уравнения прямой, проходящей через заданную точку параллельно заданной прямой .
.
Иногда требуется составить уравнение прямой определенного вида, проходящей через заданную точку плоскости параллельно заданной прямой. В этом случае сначала записываем уравнение прямой, которое проще всего получить, после чего приводим его к нужному виду.
Составьте уравнение прямой в отрезках, если эта прямая в прямоугольной системе координат Oxy проходит через точку плоскости с координатами параллельно прямой .
Очевидно, нормальным вектором прямой, общее уравнение которой имеет вид , является вектор . Этот вектор также является нормальным вектором прямой, уравнение которой мы ищем. Общее уравнение прямой, проходящей через точку с координатами и имеющей нормальный вектор имеет вид . Это общее уравнение прямой, проходящей через точку с координатами параллельно прямой . Осталось перейти от полученного уравнения прямой к требуемому уравнению прямой в отрезках: .
.
Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку и параллельна прямой .
Мы знаем, что угловые коэффициенты параллельных прямых равны (или бесконечны), тогда – угловой коэффициент прямой, уравнение которой нам требуется составить. По условию эта прямая проходит через точку , следовательно, ее уравнение имеет вид .
.
Итак, уравнение прямой a , проходящей через заданную точку плоскости M1 параллельно заданной прямой b , проще всего записывать в таком виде, в котором записано уравнение заданной прямой b .
Уравнения прямой, проходящей через заданную точку пространства параллельно заданной прямой.
В трехмерном пространстве через точку М1 , не лежащую на прямой b , проходит единственная прямая a , параллельная прямой b . Таким образом, прямую в пространстве можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана прямая b некоторыми уравнениями прямой в пространстве и точка . Требуется написать уравнения прямой a , проходящей через точку M1 параллельно прямой b .
Направляющим вектором прямой a является направляющий вектор прямой b . Таким образом, по известным уравнениям прямой b мы можем определить координаты ее направляющего вектора, а, следовательно, и координаты направляющего вектора прямой a . После этого мы можем записать канонические уравнения прямой a в пространстве и параметрические уравнения прямой a в пространстве, так как известны координаты точки, лежащей на прямой a , и координаты направляющего вектора прямой a .
Рассмотрим решения примеров.
Напишите уравнения прямой, которая проходит через начало прямоугольной системы координат Oxyz в трехмерном пространстве параллельно прямой .
Очевидно, направляющим вектором прямой является вектор с координатами . Этот же вектор является направляющим вектором прямой, уравнение которой мы составляем. По условию эта прямая проходит через точку , следовательно, ее канонические уравнения имеют вид .
.
От канонических уравнений прямой a при необходимости можно будет перейти к уравнениям двух плоскостей, пересекающихся по прямой a .
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы три точки . Напишите уравнения двух плоскостей, которые пересекаются по прямой, проходящей через точку С параллельно прямой АВ .
Направляющим вектором прямой, проходящей через точку С параллельно прямой АВ , является вектор . По координатам точек В и А мы можем вычислить координаты вектора (при необходимости смотрите статью вычисление координат вектора по координатам точек конца и начала вектора): . Канонические уравнения прямой, проходящей через точку и имеющей направляющий вектор , запишутся как .
Осталось получить уравнения двух пересекающихся плоскостей, задающих эту прямую:
.
[spoiler title=”источники:”]
http://mathter.pro/angem/2_5_2_kak_nayti_parallelnuyu_pryamuyu.html
http://www.cleverstudents.ru/line_and_plane/line_passes_through_point_parallel_to_line.html
[/spoiler]
Как построить прямую, параллельную данной?
Пример
Прямая
задана уравнением ![]()
.
Составить уравнение параллельной
прямой, которая проходит через точку ![]()
.
Решение:
Обозначим неизвестную прямую буквой ![]()
.
Прямая
проходит
через точку ![]()
.
А если прямые параллельны, то очевидно,
что направляющий вектор прямой c
подойдёт и для
построения прямой d.
Направляющий
вектор берем из уравнения
:
![]()
Уравнение
прямой
составим
по точке
и
направляющему вектору
:

Ответ: ![]()
Иллюстрация
примера:
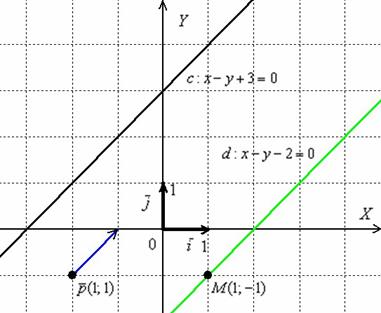
Как найти точку пересечения двух прямых?
Если
прямые
пересекаются
в точке ![]()
,
то её координаты являются решением
СЛАУ:
![]()
Как
найти точку пересечения прямых? Решить
систему.
Геометрический
смысл системы двух линейных уравнений
с двумя неизвестными –
это две пересекающиеся (чаще всего)
прямые на плоскости.
Пример
Найти
точку пересечения прямых ![]()
Решение:
Существуют два способа решения –
графический и аналитический.
Графический
способ состоит в том, чтобы просто
начертить данные прямые и узнать точку
пересечения непосредственно из
чертежа:
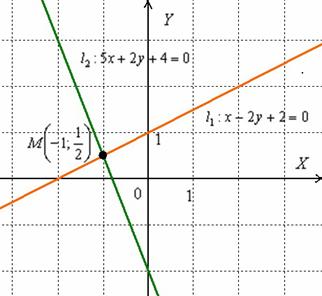
Получилась
точка ![]()
.
Для проверки следует подставить её
координаты в каждое уравнение прямой,
они должны подойти и там, и там. Иными
словами, координаты точки
являются
решением системы ![]()
.
Точку
пересечения ![]()
целесообразнее
искать аналитическим методом. Решим
систему:

Ответ:
Как построить прямую, перпендикулярную данной?
Пример
Прямая
задана уравнением ![]()
.
Составить уравнение перпендикулярной
прямой ![]()
,
проходящей через точку ![]()
.
Решение:
По условию известно, что ![]()
.
Надо найти направляющий вектор прямой
Из
уравнения
находим
вектор нормали: ![]()
,
который будет направляющим вектором
прямой
.
Уравнение
прямой
составим
по точке
и
направляющему вектору
:

Ответ: ![]()
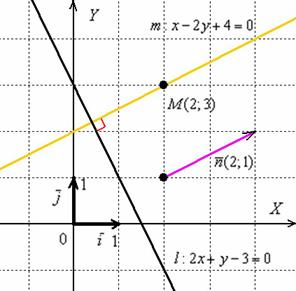
Расстояние от точки до прямой
Расстояние
от точки до прямой – это длина
перпендикулярного отрезка.
Расстояние
в геометрии традиционно обозначают
греческой буквой «ро», например: ![]()
–
расстояние от точки «эм» до прямой «дэ».
Расстояние
от точки ![]()
до
прямой ![]()
выражается
формулой
![]()
Пример
Найти
расстояние от точки ![]()
до
прямой ![]()
Решение:
![]()
Ответ: ![]()
Как найти угол между двумя прямыми?
Существуют
две формулы.
Первый
способ.
Рассмотрим
две прямые, заданные уравнениями в общем
виде:
Если
прямые не
перпендикулярны, то
угол ![]()
между
ними можно вычислить с помощью формулы:

Рассмотрим
знаменатель – это скалярное произведение
направляющих векторов прямых:
![]()
Если ![]()
,
то знаменатель формулы обращается в
ноль, а векторы будут ортогональны и
прямые перпендикулярны. Именно поэтому
сделана оговорка о неперпендикулярности
прямых в формулировке.
Второй
способ.
Если
прямые заданы уравнениями с угловым
коэффициентом ![]()
и не
перпендикулярны,
то угол
между
ними можно найти с помощью формулы:
![]()
Условие
перпендикулярности прямых выражается
равенством ![]()
,
откуда следует полезная взаимосвязь
угловых коэффициентов перпендикулярных
прямых: ![]()
,
которая используется в некоторых
задачах.
Пример
Найти
угол между прямыми ![]()
Решение первым
способом
Решение
удобно оформить в два этапа:
1)
Вычислим скалярное произведение
направляющих векторов прямых:
![]()
,
значит, прямые не перпендикулярны.
2)
Угол между прямыми найдём по формуле:
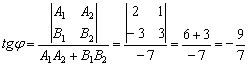
С
помощью обратной функции легко найти
и сам угол. При этом используем нечётность
арктангенса:
![]()
Ответ: ![]()
Решение
вторым способом
Алгоритм
решения похож на предыдущий пункт. Но
сначала перепишем прямые в нужном
виде:
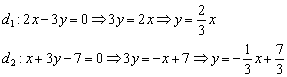
Таким
образом, угловые коэффициенты: ![]()
1)
Проверим, будут ли прямые перпендикулярны:
![]()
,
значит, прямые не перпендикулярны.
2)
Используем формулу:

Ответ:
13
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2.5.2. Как найти прямую, параллельную данной?
За незнание этой простейшей задачи сурово наказывает Соловей-Разбойник.
Задача 75
Прямая задана уравнением ![]() . Составить уравнение параллельной прямой, которая
. Составить уравнение параллельной прямой, которая
проходит через точку ![]() .
.
Решение: обозначим неизвестную прямую буквой ![]() . Что о ней
. Что о ней
сказано в условии? Прямая ![]() проходит через точку
проходит через точку ![]() . А если прямые параллельны, то очевидно, что направляющий вектор прямой «цэ» подойдёт и для
. А если прямые параллельны, то очевидно, что направляющий вектор прямой «цэ» подойдёт и для
построения прямой «дэ».
Вытаскиваем направляющий вектор из уравнения ![]() :
:
![]()
Уравнение искомой прямой ![]() составим по точке
составим по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:

Ответ: ![]()
Геометрия задачи выглядит незатейливо:

Аналитическая же проверка состоит в следующих шагах:
1) Проверяем, что у прямых ![]() один и тот же направляющий вектор (если
один и тот же направляющий вектор (если
уравнения не упрощены должным образом, то векторы будут коллинеарны). Да что тут векторы?! – посмотрим на коэффициенты: ![]()
– параллельность прямых понятна без всякого чертежа!
2) Проверяем, удовлетворяет ли точка ![]() полученному уравнению
полученному уравнению ![]() . И это тоже устный пункт!
. И это тоже устный пункт!
Примеры для самостоятельного решения сегодня будут творческими. Потому что вам ещё придётся тягаться с Бабой-Ягой, а она, знаете, любительница
всяких загадок.
Задача 76
Составить уравнение прямой, проходящей через точку ![]() , параллельную прямой
, параллельную прямой ![]() , если
, если ![]()
Существует рациональный и не очень рациональный способ решения. Самый короткий путь в конце книги.
С параллельными прямыми немного поработали и к ним ещё вернёмся. Случай совпадающих прямых малоинтересен, поэтому перейдём к задаче, которая
хорошо знакома вам из школьной программы:
 2.5.3. Как найти точку пересечения прямых?
2.5.3. Как найти точку пересечения прямых?
 2.5.1. Взаимное расположение двух прямых
2.5.1. Взаимное расположение двух прямых
| Оглавление |
Автор: Aлeксaндр Eмeлин
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой (общее уравнение прямой на плоскости и его исследование). Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и его исследование, как осуществлять переходы от общего уравнения к другим типам уравнений прямой (неполного уравнения, полного уравнения). Всю теорию закрепим иллюстрациями и решением практических задач на уравнения.
Общее уравнение прямой: основные сведения
Как найти уравнение прямой? Пусть на плоскости задана прямоугольная система координат Oxy.
Любое уравнение первой степени, имеющее вид Ax+By+C=0, где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид Ax+By+C=0 при некотором наборе значений А, В, С.
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение Ax+By+C=0 определяет на плоскости прямую.
Пусть существует некоторая точка М0(x0, y0), координаты которой отвечают уравнению Ax+By+C=0. Таким образом: Ax0+By0+C=0. Вычтем из левой и правой частей уравнений Ax+By+C=0 левую и правую части уравнения Ax0+By0+C=0, получим новое уравнение, имеющее вид A(x-x0)+B(y-y0)=0. Оно эквивалентно Ax+By+C=0.
Полученное уравнение A(x-x0)+B(y-y0)=0 является необходимым и достаточным условием перпендикулярности векторов n→=(A, B) и M0M→=(x-x0, y-y0). Таким образом, множество точек M(x, y) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n→=(A, B). Можем предположить, что это не так, но тогда бы векторы n→=(A, B) и M0M→=(x-x0, y-y0) не являлись бы перпендикулярными, и равенство A(x-x0)+B(y-y0)=0 не было бы верным.

Следовательно, уравнение A(x-x0)+B(y-y0)=0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение Ax+By+C=0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени Ax+By+C=0.
Зададим в прямоугольной системе координат на плоскости прямую a; точку M0(x0, y0), через которую проходит эта прямая, а также нормальный вектор этой прямой n→=(A, B).
Пусть также существует некоторая точка M(x, y) – плавающая точка прямой. В таком случае, векторы n→=(A, B) и M0M→=(x-x0, y-y0) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n→, M0M→=A(x-x0)+B(y-y0)=0
Перепишем уравнение Ax+By-Ax0-By0=0, определим C: C=-Ax0-By0 и в конечном результате получим уравнение Ax+By+C=0.
Так, без какой-либо помощи онлайн мы смогли доказать и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид Ax+By+C=0 – это общее уравнение прямой на плоскости в прямоугольной системе координат Oxy (уравнение прямой параллельной оси ox).
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой Ax+By+C=0.
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2x+3y-2=0, которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n→= (2, 3). Изобразим заданную прямую линию из уравнения с вектором на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2x+3y-2=0, поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ·Ax+λ·By+λ·C=0, умножив обе части общего уравнения прямой на число λ, не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой Ax+By+C=0, в котором числа А, В, С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А=0, В≠0, С≠0, общее уравнение принимает вид By+C=0. Такое неполное общее уравнение задает в прямоугольной системе координат Oxy прямую, которая параллельна оси Ox, поскольку при любом действительном значении x переменная y примет значение -CB . Иначе говоря, общее уравнение прямой Ax+By+C=0, когда А=0, В≠0, задает геометрическое место точек (x, y), координаты которых равны одному и тому же числу -CB.
- Если А=0, В≠0, С=0, общее уравнение принимает вид y=0. Такое неполное уравнение определяет ось абсцисс Ox.
- Когда А≠0, В=0, С≠0, получаем неполное общее уравнение Ax+С=0, задающее прямую, параллельную оси ординат.
- Пусть А≠0, В=0, С=0, тогда неполное общее уравнение примет вид x=0, и это есть уравнение координатной прямой Oy.
- Наконец, при А≠0, В≠0, С=0, неполное общее уравнение принимает вид Ax+By=0. И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел (0, 0) отвечает равенству Ax+By=0, поскольку А·0+В·0=0.
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Известно, что заданная прямая параллельна оси ординат и проходит через точку 27, -11. Необходимо написать общее уравнение заданной прямой. Попробуем его составить.
Решение
Решение лежит на поверхности. Прямая, параллельная оси ординат, задается уравнением вида Ax+C=0, в котором А≠0. Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения Ax+C=0, т.е. верно равенство:
A·27+C=0
Из него возможно определить C, если придать A какое-то ненулевое значение, к примеру, A=7. В таком случае получим: 7·27+C=0⇔C=-2. Нам известны оба коэффициента A и C, подставим их в уравнение Ax+C=0 и получим требуемое уравнение прямой: 7x-2=0
Ответ: 7x-2=0
На чертеже изображена прямая, необходимо записать ее уравнение. Как будем это находить?

Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси Ox и проходит через точку (0, 3).
Прямую, которая будет являться параллельной оси абсцисс, определяет неполное общее уравнение By+С=0. Найдем значения B и C. Координаты точки (0, 3), поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой By+С=0, тогда справедливым является равенство: В·3+С=0. Зададим для В какое-то значение, отличное от нуля. Допустим, В=1, в таком случае из равенства В·3+С=0 можем найти С: С=-3. Используем известные значения В и С, получаем требуемое уравнение прямой: y-3=0.
Ответ: y-3=0.
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М0(x0, y0), тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: Ax0+By0+C=0. Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A(x-x0)+B(y-y0)+C=0, это уравнение эквивалентно исходному общему, проходит через точку М0(x0, y0) и имеет нормальный вектор n→=(A, B).
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М0(-3, 4), через которую проходит прямая, и нормальный вектор этой прямой n→=(1, -2). Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А=1, В=-2, x0=-3, y0=4. Тогда:
A(x-x0)+B(y-y0)=0⇔1·(x-(-3))-2·y(y-4)=0⇔⇔x-2y+22=0
Задачу можно решать иначе. Как она будет решаться? Общее уравнение прямой имеет вид Ax+By+C=0. Заданный нормальный вектор (векторная прямая) позволяет получить значения коэффициентов A и B в уравнении прямой, тогда:
Ax+By+C=0⇔1·x-2·y+C=0⇔x-2·y+C=0
Теперь найдем значение С, используя заданную условием задачи точку М0(-3, 4), через которую проходит прямая. Координаты этой точки отвечают уравнению x-2·y+C=0, т.е. -3 – 2·4+С=0. Отсюда С=11. Требуемое уравнение прямой принимает вид: x – 2·y + 11=0.
Ответ: x – 2·y + 11=0.
Задана прямая 23x-y-12=0 и точка М0, лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна -3. Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М0 как x0 и y0. В исходных данных указано, что x0=-3. Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
23×0-y0-12=0
Определяем y0: 23·(-3)-y0-12=0⇔-52-y0=0⇔y0=-52
Ответ: -52
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида Ax+By+C=0 к каноническому уравнению x-x1ax=y-y1ay.
Если А≠0, тогда переносим слагаемое By в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: Ax+CA=-By.
Это равенство возможно записать как пропорцию: x+CA-B=yA .
В случае, если В≠0, оставляем в левой части общегь уравнения только слагаемое Ax, прочие переносим в правую часть, получаем: Ax=-By-C. Выносим –В за скобки, тогда: Ax=-By+CB.
Перепишем равенство в виде пропорции: x-B=y+CBA .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3y-4=0. Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3y-4=0. Далее действуем по алгоритму: в левой части остаётся слагаемое 0x; а в правой части выносим -3 за скобки; получаем: 0x=-3y-43.
Запишем полученное равенство как пропорцию: x-3=y-430. Так, мы получили уравнение канонического вида.
Ответ: x-3=y-430.
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Перед нами задание. Прямая задана уравнением 2x-5y-1=0. Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2x-5y-1=0⇔2x=5y+1⇔2x=5y+15⇔x5=y+152
Теперь примем обе части полученного канонического уравнения равными λ, тогда:
x5=λy+152=λ⇔x=5·λy=-15+2·λ, λ∈R
Ответ: x=5·λy=-15+2·λ, λ∈R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y=k·x+b, но только тогда, когда В≠0. Для перехода в левой части оставляем слагаемое By, остальные переносятся в правую. Получим: By=-Ax-C. Разделим обе части полученного равенство на B, отличное от нуля: y=-ABx-CB.
Задано общее уравнение прямой: 2x+7y=0. Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2x+7y=0⇔7y-2x⇔y=-27x
Ответ: y=-27x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида xa+yb=1. Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на –С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y:
Ax+By+C=0⇔Ax+By=-C⇔⇔A-Cx+B-Cy=1⇔x-CA+y-CB=1
Необходимо преобразовать общее уравнение прямой x-7y+12=0 в уравнение прямой в отрезках.
Решение
Перенесем 12 в правую часть: x-7y+12=0⇔x-7y=-12.
Разделим на -1/2 обе части равенства: x-7y=-12⇔1-12x-7-12y=1.
Преобразуем далее в необходимый вид: 1-12x-7-12y=1⇔x-12+y114=1.
Ответ: x-12+y114=1.
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
xa+yb⇔1ax+1by-1=0⇔Ax+By+C=0y=kx+b⇔y-kx-b=0⇔Ax+By+C=0
Каноническое уравнение преобразуется к общему по следующей схеме:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax(y-y1)⇔⇔ayx-axy-ayx1+axy1=0⇔Ax+By+C=0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔Ax+By+C=0
Заданы параметрические уравнения прямой x=-1+2·λy=4. Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x=-1+2·λy=4⇔x=-1+2·λy=4+0·λ⇔λ=x+12λ=y-40⇔x+12=y-40
Перейдем от канонического к общему:
x+12=y-40⇔0·(x+1)=2(y-4)⇔y-4=0
Ответ: y-4=0
Задано уравнение прямой в отрезках x3+y12=1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x3+y12=1⇔13x+2y-1=0
Ответ: 13x+2y-1=0.
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A(x-x0)+B(y-y0)=0. Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2x-3y+33=0. Также известна точка M0(4, 1), через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n→=(2, -3): 2x-3y+33=0. Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A(x-x0)+B(y-y0)=0⇔2(x-4)-3(y-1)=0⇔2x-3y-5=0
Ответ: 2x-3y-5=0.
Заданная прямая проходит через начало координат перпендикулярно прямой x-23=y+45. Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x-23=y+45.
Тогда n→=(3, 5). Прямая проходит через начало координат, т.е. через точку О(0, 0). Составим общее уравнение заданной прямой:
A(x-x0)+B(y-y0)=0⇔3(x-0)+5(y-0)=0⇔3x+5y=0
Ответ: 3x+5y=0.
