
Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.
При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат
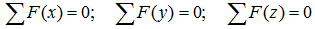
что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы
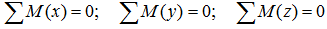
из условия отсутствия ее вращения относительно указанных осей.
Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.
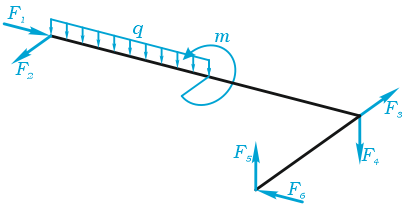
Пример составления уравнений равновесия
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F1-F6, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.
Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.
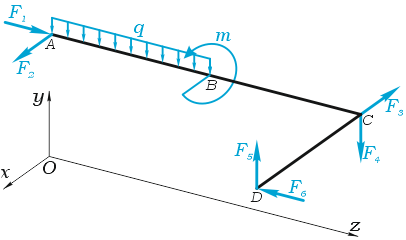
Суммы проекций сил
Сумма проекций всех сил на ось x (с учетом правила знаков для сил):
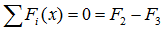
— на ось z:
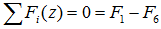
Суммы моментов
Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):
Определение момента от распределенной нагрузки рассмотрено здесь.
Из полученных шести уравнений можно определить не более шести неизвестных усилий.
- Примеры решения задач на равновесие
- Составление уравнений равновесия
- для балки
- для рамы
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Содержание
Физика ( Справочник )
-
-
Уравнения равновесия
-
Уравнения равновесия
Проекция силы на ось – характеризует действие этой силы вдоль этой оси.
То есть Проекция силы на ось Ох ($ P_x = sum X_i $ ) характеризует действие этой силы вдоль оси Ох.
А проекция силы на ось Оу ($ P_y = sum Y_i $ ) характеризует действие этой силы вдоль оси Оу.
И если сумма проекций всех сил на ось Ох равна нулю ($ sum X_i = 0 $ )– значит действие этих сил вдоль этой оси Ох нет ,
силы вдоль этой оси друг друга уравновешивают.
И если сумма проекций всех сил на ось Оу равна нулю ($ sum Y_i = 0 $ )- значит действие этих сил вдоль этой оси Оу нет , силы друг друга вдоль этой оси Оу уравновешивают.
Вращательное действие силы относительно точки О характеризует момент этой силы относительно этой точки О ($ M_0(P)=0 $) .
И если сумма моментов всех сил относительно точки О равно нулю ($ sum M_O =0 $), то вращательного действия всех этих сил на тело относительно точки О нет, они его не производят, или их вращательные действия их взаимно уравновешены.
Теперь – если проекции всех сил на оси Ох и Оу равны нулю , и сумма моментов всех сил относительно любой – какой угодно – точки равны нулю, то тело находится в равновесии.
$$ sum X=0 \ sum Y=0 \ sum M_A=0 $$
Это и есть условия равновесия тела под действием произвольной плоской системы тел:
Система сил, действующих на тело, называется сходящейся, если линии действия этих сил пересекается в одной точке.
Условие равновесия системы сходящихся сил
Для того, чтобы система сходящихся сил была уравновешенной, то есть под действием ее тело будет находится в равновесии –
условие равновесия системы сходящихся сил,
может быть записано :
$$ sum X_i = 0
\ sum Y_i = 0
$$
Или другими словами – для плоской системы сходящихся сил, лежащих в плоскости Oxy,
соответствующие уравнения равновесия примут вид:
$$ sum X_i = 0
\ sum Y_i = 0
$$
Проекция силы на ось
Определение. Проекцией силы $vec{Р}$ на ось Ox называется взятая с знаком $pm$
длина отрезка этой оси, заключенная между проекциями на неё начала и конца
вектора силы.
Эту проекцию обычно обозначают как Рx или X. В соответствии с
определением она равна:
$$ P_x = X = |vec{Р}| cdot cos (vec{Р}, vec{i}) = P cdot cos alpha $$
$$ P_y = Y = |vec{Р}| cdot cos (vec{Р}, vec{j}) = P cdot sin alpha $$
, где $vec{i}$ – единичный вектор оси /Ox/, а $alpha$ – угол между ним и силой $vec{Р}$ (Рис.1).
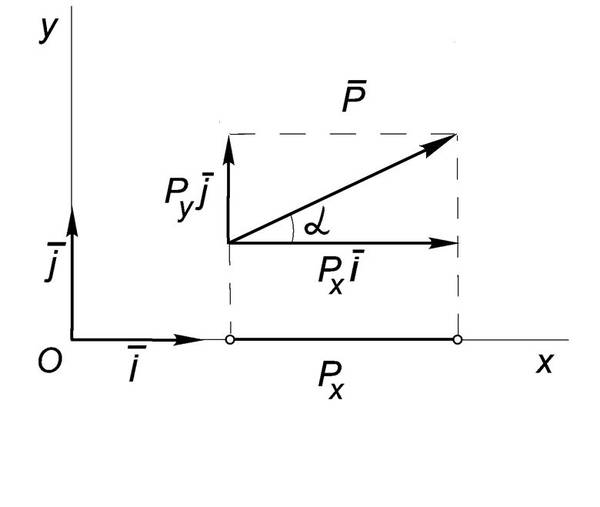
Рис.1
Таким образом:
$$ P_x > 0text{, если }0 leq alpha < frac{pi}{2} $$
$$ P_x = 0text{, если } alpha = frac{pi}{2} $$
$$ P_x < 0text{, если } frac{pi}{2} < alpha leq pi $$
Проекция силы на ось равна нулю, если сила перпендикулярно оси.
Аналогично находится проекция силы Р на ось Oy.
Вектор $ vec{Р} $ может быть выражен:
$$vec{Р} = P_x cdot vec{i} + P_y cdot vec{j} = X cdot vec{i} + Y cdot vec{j}$$
А равнодействующая плоской системы двух
сходящихся сил равна диагонали параллелограмма, построенного на
этих силах, как на сторонах.
Модуль и направление искомого вектора силы Р можно найти по
формулам:
$$ P = sqrt{X^2 + Y^2}
\ cos (vec{Р}, vec{i}) = frac{X}{P}
\ cos (vec{Р}, vec{j}) = frac{Y}{P}
$$
Момент силы относительно центра
Приложим в точке А силу P и выясним – чем определяется момент силы относительно точки О, который характеризует
вращательное действие этой силы относительно точки О(Рис.1).
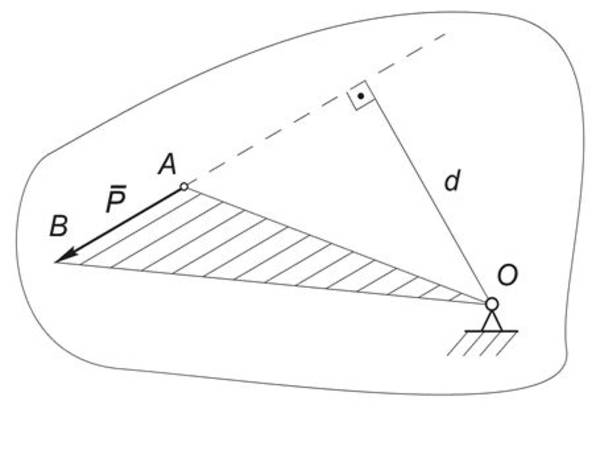
Рис.1
Очевидно, что воздействие силы на тело будет зависеть не только от ее
величины, но и от того, как она направлена, и в конечном итоге будет
определяться ее моментом относительно центра О.
Рассмотренное определение момента силы подходит только для плоской
системы сил.
Определение 1. Моментом силы Р относительно центра О называется
взятое со знаком $pm$ произведение модуля силы на ее плечо – то есть длину
перпендикуляра, опущенного из моментной точки на линию действия силы.
Правило знаков: момент силы считается положительным, если сила
стремится повернуть тело против хода часовой стрелки и отрицательным, если
она вращает тело по ходу часовой стрелки.
В соответствии с данным определением момент силы численно равен
удвоенной площади треугольника OAB, построенного на векторе силы P с
вершиной в моментной точке: $M_0(P) = Pcdot d = 2SDelta_{OAB}$ .
Отметим, что момент силы относительно точки О равен нулю, если линия
действия силы проходит через моментную точку.
Уравнения равновесия плоской системы сил
Уравнения равновесия плоской системы сил,
которые можно записать в трех различных формах:
-
Первая форма:
$$ sum X=0 \ sum Y=0 \ sum M_A=0 $$ -
Вторая форма:
$$ sum M_A=0 \ sum M_B=0 \ sum Y=0 $$ , где ось Oy не перпендикулярна отрезку АВ -
Третья форма:
$$ sum M_A=0 \ sum M_B=0 \ sum M_C=0 $$ , где точки А, В и С не лежат на одной прямой.
Таким образом, любая из этих трех форм эквивалентна условию равновесия плоской системы сил и наоборот.
Центр тяжести
Центр тяжести – точка, через которую проходит равнодействующая сил тяжести при любом пространственном расположении тела.
Если тело имеет ось или центр симметрии, то центр тяжести лежит там.
Центр тяжести квадрата и прямоугольника – точка пересечения его диагоналей.
Центр тяжести круга – в его центре.
Центр тяжести треугольника – в точке пересечения медиан.
Задачи и опыты
Задачи
Опыты с пояснением – физика 9 кл.
Центр тяжести
☆ Закон рычага ☆
Момент силы
✘☆ Вращающий момент ☆✘
Золотое правило механики
Балка на двух опорах
Рекомендуем

47
две силы R′ и R1 уравновешиваются, так как R′ = – R1 , и рассматриваемая система сил приводится только к одной силе R, равной главному вектору R′ и приложенной в точке А. Эта сила является равнодействующей заданной системе сил (рис. 6. 3, в).
Таким образом, если силы, произвольно расположенные на плоскости, не уравновешиваются, то их можно привести или к одной силе или к паре сил.
Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия:
|
R′ = 0; |
М0 = 0 |
(6. 1) |
|||||||
|
Эти условия можно получить в трех различных формах. |
|||||||||
|
1. Основная форма уравнений равновесия. |
|||||||||
|
Величины |
′ и М0 определяются равенствами: |
||||||||
|
R |
|||||||||
|
____________ |
|||||||||
|
R′ = √ (Rх′)2 + (Rу′)2 |
; |
М0 = ∑ М0 ( |
Рi) = 0 , |
где Rх′ = ∑ Хi , R у′ = ∑ Уi . Но R′ может равняться нулю только тогда, когда одновременно Rх′ = 0 и Rу′= 0. Следовательно, условия (6. 1) будут выполнены, если:
|
∑ Хi = 0 ; |
∑ Уi = 0 ; |
∑ М0 (Рi) = 0 |
(6. 2) |
||
|
Таким образом, |
для равновесия |
плоской системы |
сил необходимо и |
достаточно, чтобы сумма проекций всех сил на каждую из двух координатных осей в плоскости их действия и сумма моментов всех сил относительно любой точки на плоскости равнялись нулю. Так как оси прямоугольных координат выбираются произвольно и точка О – любая точка плоскости, то для полученной системы уравнений равновесия (6. 1) ограничения отсутствуют. Поэтому такая система уравнений равновесия является основной.
2. Вторая форма уравнений равновесия.
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех этих сил относительно любых двух точек А, В на плоскости и сумма их проекций на ось ОХ, не перпендикулярную к прямой АВ, были равны нулю:
|
∑ МА (Рi |
) = 0 ; ∑ МВ (Рi) = 0 ; ∑ Хi = 0 |
(6. 3) |
3. Третья форма уравнений равновесия.
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех точек А, В, С на плоскости, не лежащих на одной прямой, были равны нулю:
|
∑ МА (Рi) = 0 ; ∑ МВ (Рi) = 0 ; ∑ МС (Рi) = 0 |
(6. 4) |
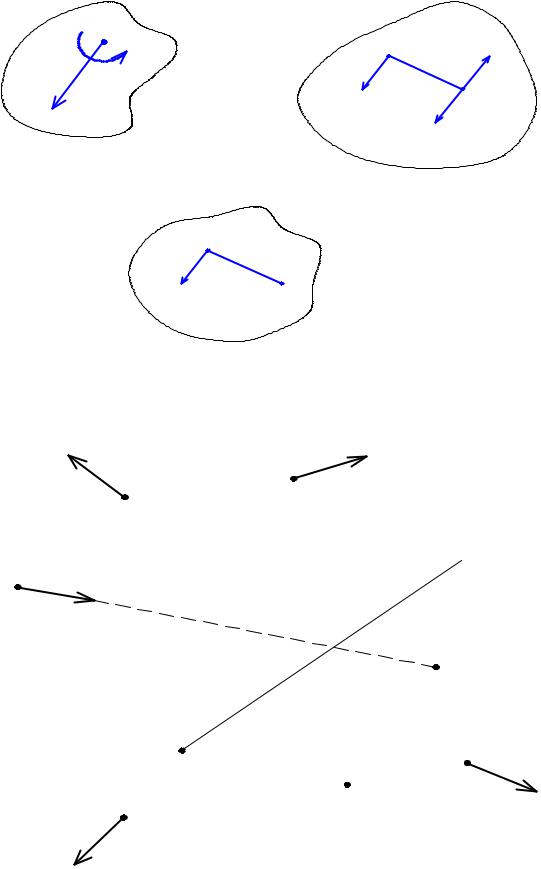
48
|
a. |
б. |
|||
|
0 |
A |
|||
|
M0 |
d |
_ |
||
|
_ |
R1 |
|||
|
R |
O |
|||
|
_ |
||||
|
R’ |
_ |
|||
|
R’ |
в.
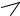 X
X
B
Рис. 6.4
49
Докажем справедливость уравнений равновесия (6. 2), (6. 3), (6. 4). Рассмотрим систему уравнений (6. 3).
Если имеет место уравнение ∑ МА (Рi) = 0, то главный момент системы сил, когда за центр приведения выбрана точка А, равен нулю и система сил или находится в равновесии или приводится к равнодействующей R′, линия действия которой должна проходить через точку А.
Из уравнения ∑ МА (Рi) = 0 следует, что главный момент системы сил равен нулю, а если равнодействующая R′ отлична от нуля, то ее линия действия должна проходить через центр приведения – точку В.
При выполнении двух первых уравнений системы следует, что система сил или находится в равновесии, или приводится к равнодействующей, причем ее линия действия должна проходить по прямой АВ.
Из третьего уравнения системы ∑Хi = 0 следует, что проекция равнодействующей Rх′ = 0, и если ось Х не перпендикулярна АВ, то это возможно лишь только в том случае, когда равнодействующая R′ = 0.
Таким образом, система уравнений является системой уравнений равновесия.
Рассмотрим систему уравнений (6. 4).
При выполнении двух первых уравнений системы (как было показано) следует, что система сил или находится в равновесии или приводится к равнодействующей R′, линия действия которой совпадает с прямой АВ. Из третьего уравнения системы ∑МС(Рi) = 0 следует, что момент равнодействующей R′ относительно точки С должен равняться нулю. Это возможно лишь в том случае, когда равнодействующая R′ = 0 (мы предположили, что точка С не должна лежать на прямой АВ).
Таким образом, полученные выражения являются системой уравнений равновесия для сил, произвольно расположенных на плоскости (при принятом ограничении выбора моментных точек).
6. 5. Уравнения равновесия плоской системы параллельных сил
Систему n параллельных сил (Р1, Р2, … Рn), лежащих в одной плоскости, можно рассматривать как частный случай плоской произвольной системы сил. Выбрав одну из осей прямоугольных координат (например, ось у) параллельной линии действия сил рассматриваемой системы, из уравнений равновесия (6. 2) получаем только два уравнения равновесия:
|
∑ Уi = 0 ; |
∑ МС ( |
(6. 5) |
||||
|
Рi) = 0 . |
||||||
|
Другой вид уравнений равновесия системы параллельных сил на |
||||||
|
плоскости: |
||||||
|
∑ МА (Рi) = 0 ; |
∑ МВ (Рi) = 0 |
(6. 6) |
причем прямая АВ не должна быть параллельна линии действия сил.

50
6.6. Теорема Вариньона о моменте равнодействующей плоской системы сил
Докажем, что если плоская система сил приводится к равнодействующей, то момент равнодействующей относительно любой точки, лежащей в плоскости действия данных сил, равен алгебраической сумме моментов составляющих сил относительно той же точки.
Определим момент равнодействующей силы R′, приложенной в точке А, относительно произвольно выбранного центра приведения О (рис. 6. 3, в).
М0
|
М0 (Ri) = R . d , но R = R′ |
и d = —— |
|||||
|
М0 |
R′ |
|||||
|
Тогда |
М0 |
(R) |
= R′ . —— = М0 = |
∑ М0 (Рi) |
||
|
R′ |
Из этой теоремы следует, что главный момент плоской системы сил относительно любой точки, лежащей на линии действия ее равнодействующей, равен нулю.
6. 7. Статически определимые и статически неопределимые задачи
Различают задачи статически определимые, которые можно решать методами статики твердого тела, и задачи статически неопределимые, которые могут быть решены, если принять во внимание упругие свойства тела и возникающие в нем деформации. Но так как решение последних задач выходит за пределы статики абсолютно твердого тела, то эти задачи рассматриваются в курсах сопротивления материалов и строительной механики.
Статически определимыми будем называть задачи, в которых число неизвестных не превышает числа уравнений равновесия статики для данной системы сил.
При равновесии плоской системы произвольно расположенных сил, приложенных к твердому телу, можно составить три уравнения равновесия, а для уравновешенной системы параллельных сил только два уравнения равновесия. В первом случае задача будет статически определимой, если число неизвестных не превышает трех, во втором случае число неизвестных задачи не должно быть больше двух.
В противном случае задача становится статически неопределимой, так как число уравнений равновесия статики окажется меньше числа неизвестных.
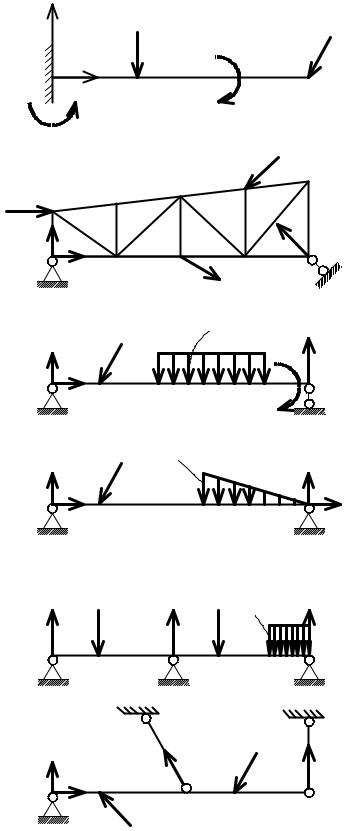
Балка (рис. 6. 5, а) имеет связь в виде жесткой заделки. Реакции заделки представляют собой силы, которые приводятся к силе RА (препятствующей перемещению балки) и реактивной паре сил с моментом МА (препятствующей вращению балки вокруг закрепленного конца). Так как неизвестна RА, то ее заменяем составляющими ХА и УА. Таким образом, неизвестными,
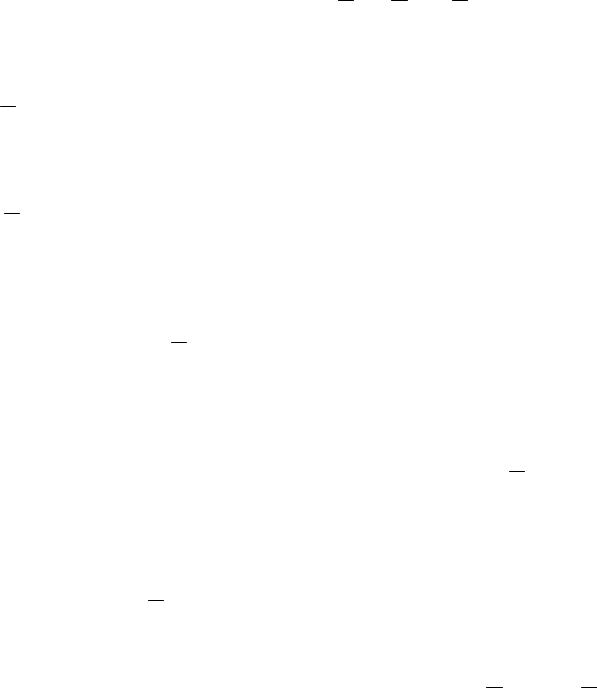
51
подлежащими определению, являются ХА , УА и МА. Для определения неизвестных имеем 3 уравнения равновесия статики. Число неизвестных равно числу уравнений равновесия, следовательно, задача является статически определимой.
Ферма (рис. 6.5, б) имеет шарнирно неподвижную связь А. Линия действия RА неизвестна. Поэтому при решении задачи ее заменяем двумя взаимно перпендикулярными составляющими ХА и УА. Связь В выполнена шарнирно подвижной. Линия действия реакции RВ известна, она пройдет перпендикулярно плоскости катания.
Таким образом, число неизвестных, подлежащих определению, равно трем (ХА, УА и RВ), что соответствует числу уравнений равновесия статики. Следовательно, задача является статически определимой.
Балка, показанная на рис. 6. 5, в, также является статически определимой на основании рассуждений, приведенных для фермы (рис. 6. 5, б).
Балка (рис. 6. 5, г) имеет шарнирно неподвижные опорные связи А и В. Так как линия действия реакций RА и RВ заранее неизвестны, то их заменяем
составляющими ХА , УА и ХВ, УВ. Число уравнений равновесия статики равно трем. Так как число неизвестных превышает число уравнений равновесия, задача является статически неопределимой.
Балка (рис. 6. 5, д) имеет три шарнирно неподвижные связи. На балку действует система параллельных сил. Поэтому горизонтальные составляющие опорных реакций ХА , ХВ и ХС будут заведомо равны нулю. Неизвестными
будут только вертикальные составляющие УА = RА, УВ = RВ, УС = RС . Таким образом, число неизвестных, подлежащих определению, равно трем. Для системы параллельных сил имеем два уравнения равновесия статики. Число неизвестных превышает число уравнений равновесия, следовательно, задача является статически неопределимой.
Балка (рис. 6. 5, е) имеет шарнирно неподвижную связь А. Так как линия действия реакции RА неизвестна, то ее заменяем двумя составляющими ХА и УА. В точке В и С балка закреплена двумя стержнями. Стержень шарнирно закреплен с балкой и основанием. Линия действия реакции таких связей проходит по линии, соединяющей шарниры. Таким образом, число неизвестных, подлежащих определению, равно четырем (ХА , УА и Т1, Т2). Число уравнений равновесия для определения неизвестных равно трем. Число неизвестных превышает число уравнений равновесия статики, следовательно, задача является статически неопределимой.
52
|
а. |
_ |
||||
|
yA |
_ |
||||
|
_ |
P |
_ |
|||
|
A |
xA |
P1 |
|||
|
M |
|||||
|
MA |
|||||
|
б. |
_ |
||||
|
P2 |
|||||
|
_ |
|||||
|
P1 |
_ |
||||
|
_ |
_ |
||||
|
B |
|||||
|
yA |
R |
||||
|
xA |
B |
||||
|
A |
_ |
||||
|
P3 |
|||||
|
в. |
_ |
q |
|||
|
_ |
_ |
||||
|
P |
|||||
|
yA |
_ |
||||
|
B |
|||||
|
xA |
R |
||||
|
A |
|||||
|
B |
|||||
|
M |
|||||
|
г. _ |
_ |
q |
_ |
||
|
yA |
_ |
P |
yB _ |
||
|
A |
xA |
xB |
|||
|
B |
|||||
|
д. |
_ |
||||
|
_ |
_ |
_ |
_ |
||
|
RA |
1 |
RB |
P2 q |
RC |
|
|
P |
|||||
|
A |
B |
C |
|||
|
е. |
|||||
|
_ |
_ |
_ |
|||
|
yA |
_ |
_ |
|||
|
1 |
2 |
||||
|
xA |
T |
P2 |
T |
||
A_
P1
Рис.6.5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статика — раздел механики, изучающий условия равновесия тел.
Виды равновесия
Устойчивое равновесие |
|
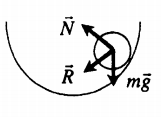 |
Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (Ep min). |
Неустойчивое равновесие |
|
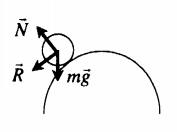 |
Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (Ep max). |
Безразличное равновесие |
|
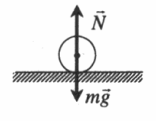 |
При выведении тела из положения безразличного равновесия дополнительных сил не возникает. |
Момент силы
Определение
Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:
M = Fd
M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).
Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?
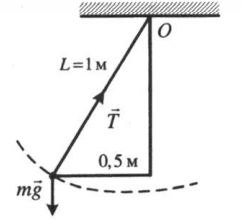
Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:
M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)
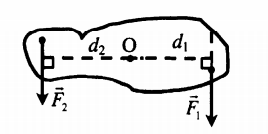
Момент силы может быть положительным и отрицательным.
Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:
M1 = F1d1
Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:
M2 = F2d2
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
∑Mi=0
Иначе правило моментов можно сформулировать так:
Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.
∑Mпо час. стр.=∑Mпр. час. стр.
Условия равновесия тел
| Тело не участвует в поступательном движении: |
∑→Fi=0; →vo=0 |
| Тело не участвует во вращательном движении: |
∑Mi=0; ω0=0 |
| Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении) |
∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0 |
Простые механизмы
Определение
Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.
Наклонная плоскость |
|
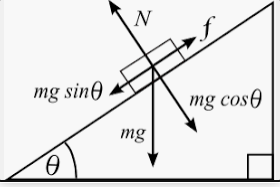 |
Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsinθ<mg |
Рычаг |
|
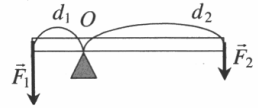 |
Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2=d2d1 |
Неподвижный блок |
|
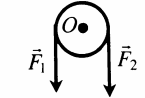 |
Изменяет направление действия силы. Модули и плечи сил при этом равны: F1 = F2 M1 = M2 |
Подвижный блок |
|
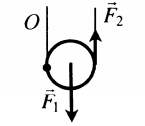 |
Дает выигрыш в силе в 2 раза:
d1 = R d2 = 2R F1 = 2F2 |
Клин |
|
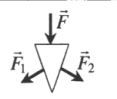 |
Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2 |
Золотое правило механики
При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.
Задание EF22660
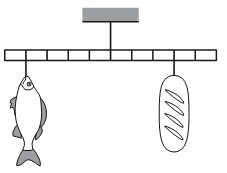 Мальчик взвесил рыбу на самодельных весах с коромыслом из лёгкой рейки (см. рисунок). В качестве гири он использовал батон хлеба массой 0,8 кг. Определите массу рыбы.
Мальчик взвесил рыбу на самодельных весах с коромыслом из лёгкой рейки (см. рисунок). В качестве гири он использовал батон хлеба массой 0,8 кг. Определите массу рыбы.
Алгоритм решения
1.Записать исходные данные.
2.Записать правило моментов и выполнить решение в общем виде.
3.Подставить известные данные и вычислить искомую величину.
Решение
Известна лишь масса батона: m1 = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:
d1 = 0,3
d2 = 0,4
Запишем правило моментов:
F1 d1 = F2 d2
Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:
m1gd1 = m2gd2
m1d1 = m2d2
Отсюда масса рыбы равна:
m2=m1d1d2=0,8·0,30,4=0,6 (кг)
Ответ: 0,6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18706
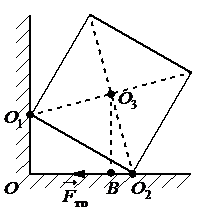 Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения Fтр относительно оси, проходящей через точку О3 перпендикулярно плоскости чертежа, равно…
Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения Fтр относительно оси, проходящей через точку О3 перпендикулярно плоскости чертежа, равно…
Ответ:
а) 0
б) О2О3
в) О2В
г) О3В
Алгоритм решения
- Сформулировать определение плеча силы.
- Найти плечо силы трения и аргументировать ответ.
Решение
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 9.5k
