Как составить уравнение равновесия плоской системы сходящихся сил

Содержание:

Система сходящихся сил:

Рассмотрим одну из важных систем сил — систему сходящихся сил. Для этой системы сил следует рассмотреть приведение ее к простейшему виду и установить условия равновесия.

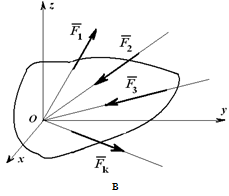
Системой сходящихся сил (или пучком сил) называют такую систему сил, линии действия которых пересекаются в одной точке — центре пучка. Сходящиеся системы сил могут быть пространственными и плоскими, т. е. расположенными в одной плоскости.

Приведение к равнодействующей силе

Рассмотрим общий случай пространственной системы сходящихся сил. Так как сила, действующая на твердое тело, есть вектор скользящий, то можно считать, что силы системы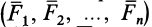

Применяя к первым двум силам пучка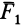

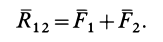
Затем по правилу параллелограмма складываем силы 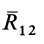и и 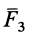получаем их равнодействующую:

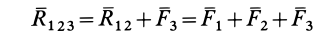
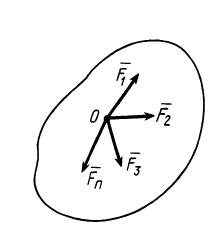
Рис. 12

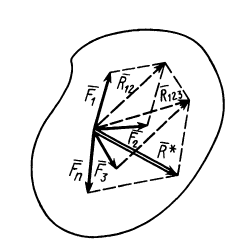
Рис. 13

и т. д. Продолжая процесс векторного сложения сил для всех 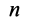сил, получим

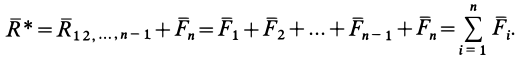
Таким образом, система 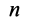сходящихся сил эквивалентна одной силе 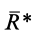, которая и является равнодействующей этой системы сил.

Процесс последовательного применения к силам правила параллелограмма, или их векторного сложения, приводит к построению силового многоугольника из заданных сил. В силовом многоугольнике конец одной из сил служит началом другой (рис. 14). Равнодействующая сила 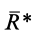в силовом многоугольнике соединяет начало первой силы с концом последней, т. е. изображается замыкающей силового многоугольника, который в общем случае является незамкнутым. Силы в силовом многоугольнике можно изображать в любой последовательности. От этого изменится форма силового многоугольника, а замыкающая не изменится; следовательно, не изменится и равнодействующая сила.

Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской— плоской. Для плоской системы сходящихся сил равнодействующую силу можно определить графически путем построения замыкающей силового многоугольника в выбранном для сил масштабе. Для пространственной системы сходящихся сил пришлось бы силовой многоугольник строить в пространстве из стержней.

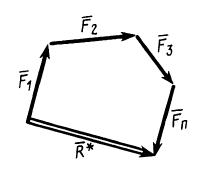
Рис. 14

Итак, система сходящихся сил в общем случае приводится к одной силе—равнодействующей этой системы сил, которая изображается замыкающей силового многоугольника, построенного на силах системы. Линия действия равнодействующей силы проходит через центр пучка параллельно замыкающей силового многоугольника.

Для аналитического определения равнодействующей силы следует выбрать систему прямоугольных осей координат и воспользоваться известной из геометрии теоремой о том, что проекция замыкающей любого многоугольника на какую-либо ось равна алгебраической сумме проекций составляющих его сторон на ту же ось.

Так как равнодействующая сила 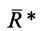является замыкающей силового многоугольника, или векторной суммой сил, то

Проецируя векторы векторного равенства на прямоугольные оси координат, согласно теореме о проекции замыкающей получим

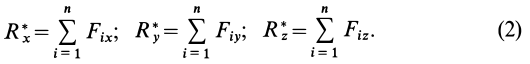
По проекциям определяем модуль равнодействующей силы и косинусы углов ее с осями координат по формулам

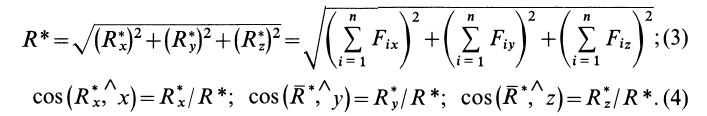
В формуле (3) перед квадратным корнем всегда берут знак плюс, так как определяется модуль равнодействующей силы.

В случае плоской системы сходящихся сил одну из координатных осей, обычно , выбирают перпендикулярной силам, тогда каждая из сил пучка даст проекцию на эту ось, равную нулю, а следовательно, будет равна нулю и проекция равнодействующей силы на эту ось, т. е.

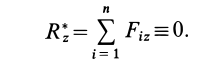
Условия равновесия системы сходящихся сил

Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпасть с началом первой силы. Такой силовой многоугольник называют замкнутым (рис. 15). Получено условие равновесия сходящихся сил в геометрической форме: для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил.

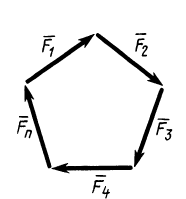
Рис. 15

Для определения неизвестных сил при равновесии более предпочтительным является использование условий равновесия системы сходящихся сил в аналитической форме. Так как при равновесии системы сходящихся сил равнодействующая сила должна быть равна нулю (силовой многоугольник замкнут), то из этого следует, что равно нулю подкоренное выражение в (3), состоящее из суммы положительных величин. Таким образом, равны нулю квадраты каждой из величин подкоренного выражения, а следовательно, равны нулю и сами величины. Получаем условия равновесия пространственной системы сходящихся сил в аналитической форме:

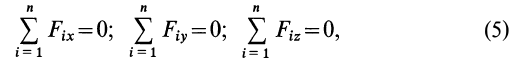
т. е. для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны нулю.

В случае плоской системы сходящихся сил одну из осей координат, обычно 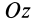, выбирают перпендикулярной силам, а две другие оси—соответственно в плоскости сил. Тогда третье условие из (5) превратится в тождество 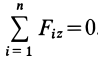. Отбрасывая его, получаем

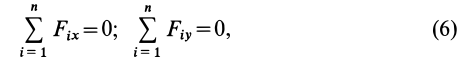
т. е. для равновесия плоской системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координатных осей, лежащих в плоскости сил, были равны нулю.

Проецирование силы на оси координат

Если дана сила 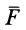, то ее проекции на прямоугольные оси координат вычисляются по формулам

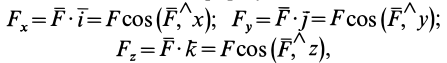
где 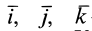— единичные векторы, направленные по осям координат. Косинусы углов силы с осями координат удовлетворяют условию

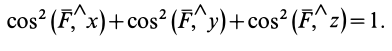
Из трех углов независимыми являются только два.

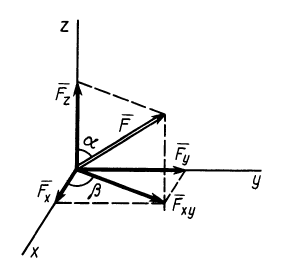
Рис. 16

При проецировании силы на прямоугольные оси координат целесообразно использовать тоже два угла. Для этого предварительно силу разлагают на две взаимно перпендикулярные составляющие, одна из которых параллельна какой-либо оси координат, например , а другая находится в координатной плоскости двух других осей, в нашем случае — координатной плоскости (рис. 16). Получаем

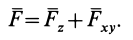
Проецируя векторы векторного равенства на координатные оси, имеем

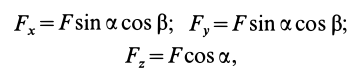
так как

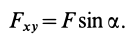
При проецировании использованы только два угла: 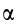и .

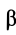Векторные величины 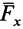, , 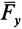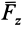называются составляющими силы 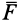по осям координат. Скалярные величины 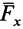, , 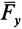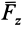являются проекциями силы 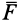на оси координат. Таким образом, силу на оси координат проецируют обычно в два приема. Сначала ее проецируют на одну из осей и на координатную плоскость двух других осей. Проекция силы на плоскость является вектором. Этот вектор затем проецируют на оси координат, расположенные в плоскости.

Пример 1.

Подъемный кран, имеющий вертикальную ось вращения 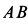, состоит из стержней, скрепленных шарнирами. Ось крана закреплена с помощью подпятника 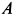и подшипника 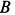(рис. 17, а). Считая стержни и весь кран невесомыми, определить силы реакций в подпятнике и в подшипнике, усилия в стержнях 1, 2, 3, 4, если известны размеры 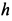и 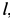, а также углы 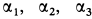. Стержни 2 и 5 горизонтальны. Кран с помощью троса 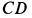удерживает груз, сила тяжести которого равна .

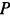Решение. Считая кран твердым телом, освободим его от связей, которыми являются подпятник и подшипник, заменив их силами реакций связей. Сила реакции подшипника (цилиндрический шарнир) перпендикулярна его оси. Направление силы реакции подпятника заранее не известно и подлежит определению. На весь кран, находящийся в равновесии, действуют три силы: 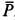, , 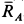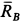(рис. 17,6). Линии действия этих сил должны пересекаться в одной точке, т. е. линия действия силы 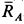должна пройти через точку 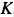, в которой пересекаются линии действия сил 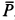и 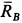. Три силы должны образовывать также замкнутый силовой треугольник. Отложим силу 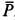в выбранном масштабе и проведем через ее начало и конец линии, параллельные силам 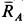и 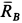. В полученном силовом треугольнике три силы должны быть направлены друг за другом (рис. 17, в). Из полученного прямоугольного треугольника находим

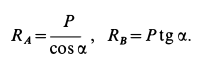
Рис. 17

Из геометрического треугольника

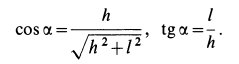
Для определения усилий в стержнях 1 и 2 применим метод вырезания узлов. Для этого рассмотрим равновесие отдельного шарнира или узла С. На этот узел действуют сила Р через трос и силы реакций стержней 1 и 2, которые следует мысленно отбросить. Силы реакций стержней на узел должны быть направлены по стержням, так как на эти стержни между их шарнирами другие силы не действуют. Стержни являются шарнирными. (Условимся силы реакций стержней направлять от узла (рис. 17, г) и знак вектора у сил на рисунке не ставить, чтобы не увеличивать без необходимости число обозначений для одинаковых по числовому значению сил.)

Выбрав в точке 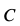оси координат, составим условия равновесия для плоской системы сходящихся сил, действующих на узел :

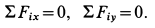
Эти условия в рассматриваемом случае принимают форму в проекциях на оси:

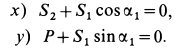
Из полученных уравнений получаем:

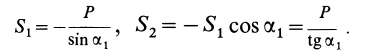
Знак 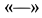у 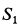показывает, что направление этой силы противоположно принятому, т. е. направлено к узлу. Рассматривая равновесие отдельного стержня 1, убеждаемся, что на него действуют только две силы со стороны узлов и 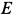. Эти силы должны быть при равновесии равны по модулю и противоположны по направлению. Узел действует на стержень 1 с силой 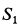, противоположной по направлению силе действия стержня на узел 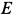(рис.17, д). Таким образом, получаем, что при рассмотрении равновесия узла , когда 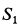имеет отрицательное значение, стержень 1 будет сжат; 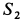получили с плюсом. Следовательно, стержень 2 будет испытывать растяжение.

На узел действуют три силы, и они поэтому должны образовывать замкнутый силовой треугольник. Построение силового треугольника следует начать с известной силы 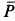, проводя через ее концы линии, параллельные неизвестным по значению силам реакций стержней (рис. 17, е). Из силового треугольника можно определить силы 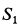и .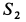

Из уравнений равновесия или силового треугольника можно определить только две неизвестные силы. Поэтому при дальнейшем решении задачи следует переходить к рассмотрению равновесия узла, на который действуют не более двух неизвестных сил. Таким узлом является узел 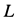. На узел 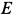действуют три неизвестные силы. При рассмотрении равновесия узла 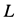будем направлять силы реакций стержней опять от этого узла (рис. 17,ж) независимо от ранее полученных знаков для них. В уравнения равновесия уже известную силу 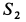следует подставить со знаком плюс, полученным для нее ранее. Условия равновесия сил, действующих на узел 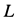, имеют форму:

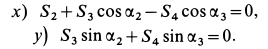
Из этих уравнений находим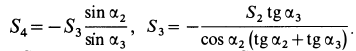

Подставляя в выражение для 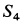полученное значение 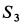, получим

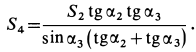
Усилие 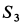при положительном 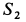отрицательно. Следовательно, стержень 3 сжат. Усилие 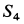положительно. Поэтому стержень 4 растянут.

Для узла 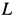можно построить также замкнутый силовой треугольник и решить задачу нахождения неизвестных сил геометрически.

Пример 2.

Груз с силой тяжести 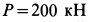прикреплен с помощью троса к шарниру 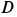, который крепится к вертикальной стене тремя стержнями, два из которых расположены в горизонтальной плоскости, а третий — в вертикальной, с помощью шарниров. Сила сопротивления груза от ветра 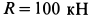горизонтальна и параллельна стене. Определить силу натяжения троса и усилия в стержнях, считая стержни невесомыми, если 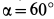, 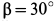(рис. 18, а).

Решение. На находящийся в равновесии груз 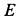действует система трех сходящихся сил, расположенных в вертикальной_ плоскости, параллельной стене. Это сила тяжести 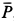, сила сопротивления 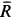и сила натяжения троса 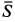, направленная по нему (рис. 18,6). Сила 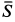должна уравновесить равнодействующую сил 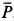и 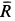. Следовательно,

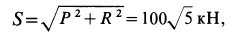
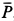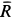так как силы и перпендикулярны. Сила 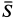составляет с вертикалью угол 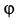, для которого

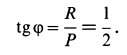
Рассмотрим равновесие шарнира 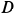, на который действуют силы реакции трех стержней 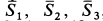, направленные по стержням, и сила натяжения троса, равная 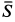(рис. 18, в). Имеем пространственную систему сходящихся сил, условия равновесия которой имеют форму

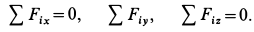
В рассматриваемом случае для выбранных осей координат имеем:

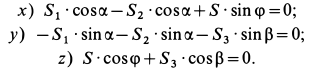
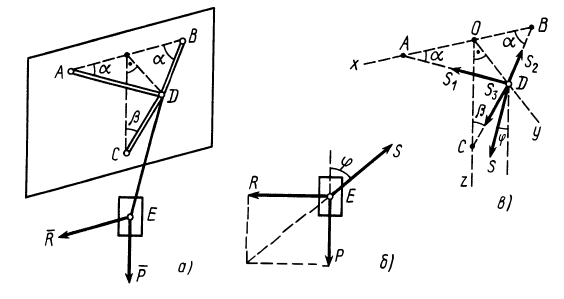
Рис. 18

Так как

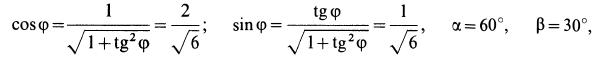
то система уравнений принимает форму

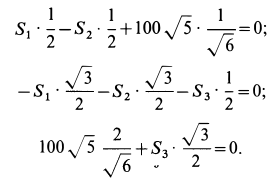
Решая эту систему уравнений, получаем:

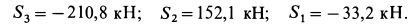
Усилия в стержнях направляли от рассматриваемого узла и получил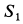и и 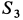со знаком минус, a 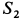— со знаком плюс. Это служит указанием, что стержни 1 и 3 подвергаются сжатию, а стержень 2 — растяжению.

Силы, сходящиеся в одной точке

Если на точку А действуют n сил, расположенных в одной плоскости (рис. 22), то эти силы можно сложить геометрически, построив многоугольник векторов, который в нашем случае называется многоугольником сил.

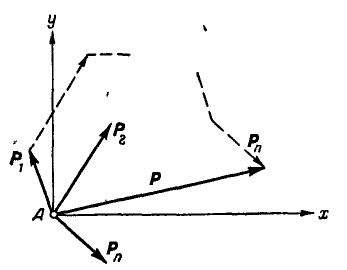
Рис. 22.

Обозначая равнодействующую сил через Р, можем написать:

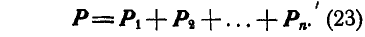
Проектируя равнодействующую и составляющие на координатные оси, проведенные через точку А, по формуле (3) имеем:

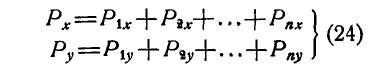
Величину равнодействующей находим по формуле (7):

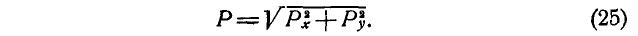
Направление равнодействующей определяем по формулам (6):

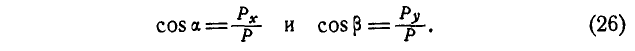
Может оказаться, что при построении многоугольника сил конец последней силы совпадет с началом первой; в этом случае многоугольник сил получается замкнутым, равнодействующая сила равна нулю и силы находятся в равновесии. Таким образом, геометрическое условие равновесия сил, приложенных к точке, заключается в том, что многоугольник этих сил должен быть замкнут.

В этом случае Р=0, а поэтому и 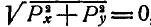, а это может быть при условии, когда 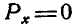и 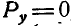, что возможно, если:

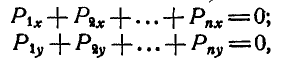
или сокращенно:

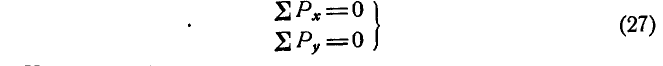
Уравнения (27) называются уравнениями равновесия сил, приложенных к точке, и выражают аналитические условия равновесия этих сил.

Рассмотрим равновесие трех сил 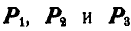, действующих на тело (рис. 23).

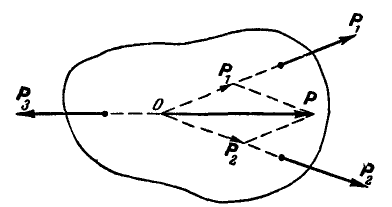
Рис. 23.

Пусть в точке О пересекаются линии действия любых двух сил, например 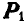и 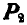, тогда эти силы можно перенести в точку О и по правилу параллелограмма заменить одной силой Р.

Теперь на тело уже действуют две силы Р и А, равновесие которых по аксиоме 2 возможно, если они будут направлены по одной прямой.

Отсюда заключаем, что три силы, действующие на тело, и расположенные в одной плоскости, могут находиться в равновесии только тогда, когда их линии действия пересекаются в одной точке.

Заказать решение задач по теоретической механике

Задача 1.

К точке В шарнирного кронштейна АВС (рис. 24, а) подвешен груз Q = 100 кГ. Определить усилия 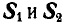в стержнях ВА и ВС.

Решение. Для определения усилия 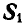в стержне ВА, который является связью для точки В, освободимся от связи и введем реакцию стержня, которая, согласно аксиоме 6, будет равна и прямо цретивоположна искомому усилию 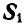(рис. 24, б). Теперь точка В находится в равновесии под действием двух сил 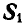и 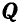и имеет возможность двигаться по дуге окружности радиуса ВС (рис. 24, б). Поэтому равновесие точки В возможно будет только тогда, когда равнодействующая этих двух сил 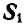и 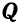пойдет по направлению оси стержня ВС. Но это равносильно тому, что проекция ее на направление 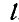, перпендикулярное к стержню ВС, будет равна нулю, или, что то же, сумма проекций составляющих на это направление равна нулю: 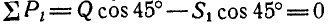, откуда .

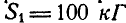Для нахождения усилия 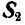в стержне ВС поступаем аналогично. Устраняем связь ВС и взамен ее вводим реакцию 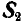(рис. 24, в); тогда точка В должна находиться в равновесии под действием двух сил 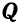и 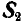. Проектируя эти силы на направление у возможного движения точки В, получим условие равновесия точки В в виде: 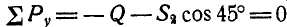, откуда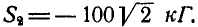

При решении этой задачи можно было бы освободиться одновременно от обеих связей ВА и ВС, вводя взамен их реакции связе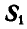й и 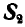(рис. 24,г).

Тогда для свободной точки В можно написать два уравнения равновесия (27) в виде:

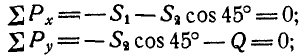
отсюда находим, что 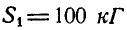и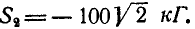

Знак минус у 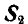указывает на то, что направление реакции нами выбрано неправильно и это направление следует изменить на обратное. На рисунке 24, д дано правильное направление стрелок реакций связей.

Рис. 24.

При неподвижной точке В реакция направленная от узла, будет растягивать стержень, а реакция 58, направленная к узлу, будет сжимать стержень, что ясно видно из чертежа.

Решим теперь эту задачу геометрическим способом. Все силы, заданные и реактивные, действующие на точку В, взаимно уравновешиваются, а поэтому многоугольник этих сил должен быть замкнут. На этом основании проводим вектор, равный силе 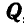, и из начала и конца этого вектора проводим направления, параллельные линиям действия реакций связей ВА и ВС (рис. 24, е или 24, ж); в пересечении этих направлений получаем точку О или О’.

Так как многоугольник сил, действующих на точку В, должен быть замкнут, то стрелки всех сил в полученном многоугольнике сил, в нашем случае – треугольнике (рис. 24, е или 24, ж), должны быть расположены в одном направлении. Исходя из заданного направления силы , получим правильное направление стрелок реактивных сил 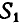и 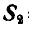(рис. 24, з или 24, м).

Выбрав один из полученных треугольников сил, замечаем, что сила 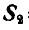, перенесенная параллельно самой себе на стержень 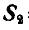(рис. 24, а или 24, д), будет направлена к узлу В, следовательно, стержень ВС — сжат, а сила 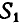направленная от узла В, будет растягивать стержень ВА. Из полученного треугольника сил (рис. 24, з или 24, и) имеем:

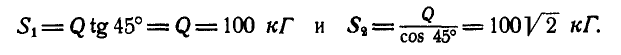
При решении дальнейших задач аналитическим способом стрелки неизвестных реакций стержней будём направлять всегда от рассматриваемого нами узла; тогда знак минус у модуля реакции какого-либо стержня будет указывать на то, что рассматриваемый нами стержень сжат.

Задача 2.

Определить усилия в стержнях АВ и ВС при действии в шарнире В силы Q=100 кГ, если АВ = ВС =5 м, BD = 0,5 м и шарниры А и С расположены на одной горизонтали (рис. 25, а).

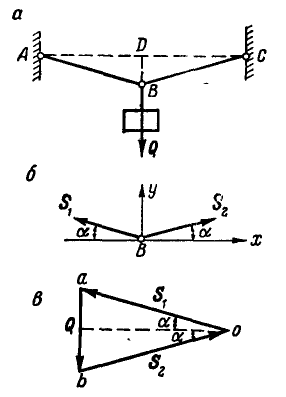
Рис. 25.

Решение. Решим сначала задачу аналитическим способом, для чего рассмотрим равновесие точки В, находящейся под действием трех сил: заданной силы 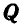и реакций связе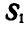й и 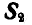(рис. 25, б).

Применяя уравнения равновесия (27), имеем:

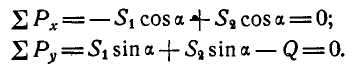
Из первого уравнения находим: 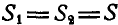; тогда второе уравнение примет вид: 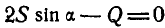, откуда 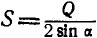. Из ΔABD имеем: 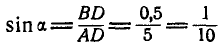, поэтому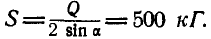

Знак плюс у S указывает на то, что оба стержня ВА и ВС растянуты.

Для решения этой задачи геометрическим способом, построим треугольник равновесия 0ab (рис. 25,в), из которого сразу находим правильное направление реакци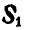и и 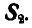. Далее 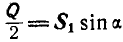, или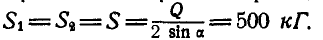

Задача 3.

Однородный цилиндр (рис. 26,а) весом 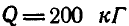опирается на гладкую плоскость, наклоненную под 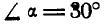к горизонту и удерживается в равновесии горизонтальным канатом 0С. К оси цилиндра О приложена сила Р=400 кГ, направленная параллельно плоскости. Найти реакцию N плоскости и натяжение Т каната ОС.

Рис. 26.

Решение. Решим задачу аналитическим способом. Освободившись от связей (рис. 26,6) и составляя для точки О уравнения равновесия (27), имеем:

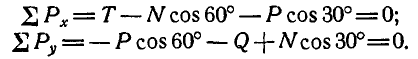
Подставляя вместо Р и Q их значения и решая полученные уравнения, находим неизвестные силы:

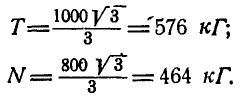
Задача 4.

Жесткое колено ABCD (рис. 27,а), могущее вращаться вокруг шарнира В, опирается в точке D на гладкий уступ. Пренебрегая весом колена, определить реакции связей в точках В и D, если в точке А колена приложена сила Р=100 кГ.

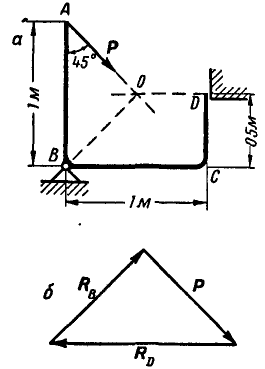
Рис. 27.

Решение. Так как колено находится в равновесии, то три силы, действующие в точках А, В и D, должны пересекаться в одной точке. Продолжаем линию действия силы Р и реакции в точке D, направленной перпендикулярно к плоскости уступа, до взаимного пересечения в точке О; тогда линия действия реакции шарнира В пройдет обязательно через точку О. На рисунке 27, б дано построение треугольника равновесия трех сил 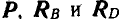, из которого следует, что 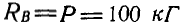и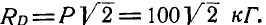

Задача 5.

При подъеме плуга на стоянке (рис. 30) поворачивают коленчатый рычаг АВС, вращая рукоятку силой Р. Какова при этом должна быть величина силы Р, если вес части плуга, передающейся на коленчатый рычаг, вращающийся вокруг шарнира В, равен Q = 30 кГ, длина рукоятки АВ = 0,6 м и радиус колеса плуга г = 0,25 м.

Рис. 30.

Решение. Строим для сил, приложенных к коленчатому рычагу, треугольник равновесия. Из подобия треугольника равновесия и соответствующего треугольника на чертеже находим силу Р.

Ответ: Р = 11 кГ.

Моменты силы относительно точки и оси
Теория пар сил
Приведение системы сил к простейшей системе
Условия равновесия системы сил
Аксиомы и теоремы статики
Приведение системы сил к простейшему виду
Плоское движение тела
Принцип виртуальных перемещений

Источник

Сходящаяся система сил находится в равновесии в случае замкнутости силового многоугольника. Величина равнодействующей при этом равна нулю (R = 0).

Проекции равнодействующей системы сходящихся сил на координатные оси равны суммам проекций составляющих сил на те же оси, т. е.

Модуль равнодействующей определится по формуле:

Оба слагаемых, стоящих под знаком корня, во всех случаях положительны как величины, возведенные в квадрат. Поэтому R = 0 только при выполнении условий:

Таким образом, равнодействующая плоской системы сходящихся сил равна нулю только в том случае, когда алгебраические суммы проекций ее слагаемых на каждую из двух координатных осей равны нулю.

Формулы Σх=0 (сумма проекций всех сил на ось Х равна нулю), Σy=0 (сумма проекций всех сил на ось Y равна нулю) называют уравнениями равновесия плоской системы сходящихся сил и используют при аналитическом решении задач.

Следовательно, для решения задач на равновесие плоской системы сходящихся сил мы имеем два уравнения. Эти уравнения позволяют определить две неизвестные величины.

Если же задача содержит неизвестные в количестве, превышающем число уравнений равновесия, то эту задачу нельзя решить методами статики абсолютно твердого тела. Задачи подобного типа называют статически неопределимыми. Их решение возможно только при отказе от допущения об абсолютной твердости тел; помимо уравнений равновесия для решения их составляют дополнительные уравнения, основанные на рассмотрении деформаций тел. Методы решения таких задач рассматриваются в курсе сопротивления материалов.

Источник

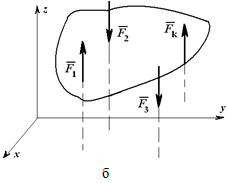
Равновесие системы сходящихся сил

Система сходящихся
сил – это
силы, сходящиеся в одной точке (рис.
2.6).

Геометрическое
условие равновесия.
Для равновесия системы сходящихся сил
необходимо и достаточно, чтобы силовой
многоугольник, построенный на этих
силах, был замкнут.

Рис. 2.6

налитические условия равновесия.
Для равновесия пространственной системы
сходящихся сил необходимо и достаточно,
чтобы суммы проекций этих сил на каждую
из трех координатных осей были равны
нулю.

F_kx
= 0; F_ky
= 0; F_kz
= 0.

Теорема о трех
силах. Если
свободное твердое тело находится в
состоянии равновесия под действием
трех непараллельных сил, лежащих в одной
плоскости, то линии действия этих сил
пересекаются в одной точке.

₁
+ F₂
+ F₃
= 0

Системы статически определимые и статически неопределимые

Задача статики
может быть решена лишь в том случае,
когда для нее число неизвестных реакций
связей не превышает число уравнений
равновесия, содержащих эти реакции.
Такие задачи называют статически
определенные, а система тел, для которых
это имеет место – статически определимыми
системами.

Задачи, в которых
число неизвестных реакций связей больше
числа уравнений равновесия, содержащих
эти реакции, называются статически
неопределенные, а система тел для которых
это имеет место – статически неопределимыми
системами.

Рис. 2.7

римером для статически неопределенной
системы может служить груз, подвешенный
на трех нитях, лежащих в одной плоскости
(рис. 2.7). В этой задаче три неизвестные
силы натяжения нити T₁,
T₂,
T₃,
а уравнений равновесия в случае плоской
системы сходящихся сил можно составить
только два.

Решение задач статики

Для решения задач
статики необходимо:

Выбрать тело,
равновесие которого должно быть
рассмотрено.
Освобождение тела
от связей и изображение действующих
на него заданных сил и реакций отброшенных
связей.
Составление
уравнений равновесия.
Определение
искомых величин, проверка правильности
решения и исследование полученных
результатов.

Для решения задач
на равновесие тела под действием
сходящихся сил можно использовать
следующие способы:

)
Геометрический способ. Применяется
если число сил, действующих на тело
равно трем. При равновесии треугольник,
построенный на этих силах, должен быть
замкнутым.

б) Аналитический
способ. Применяется при любом количестве
сил, действующих на тело. В случае плоской
системы сходящихся сил составляется
два уравнения равновесия, а в случае
пространственной системы сил – три.

Рис. 2.8а

ример
№3. К вертикальной гладкой стене АВ
подвешен на тросе АС однородный шар.
Трос составляет со стеной угол ,
сила тяжести шара Р. Определить силу
натяжения троса Т и давление шара на
стену Q.
Шар находится в равновесии под действием
этих трех сил (рис. 2.8а).

Решение.

ассмотрим
решение задачи геометрическим
(графическим) способом. Так как шар
находится в равновесии под действием
трех сил, то эти силы сходящиеся. Точка,
в которой сходятся эти силы, является
геометрическим центром шара (точка О).
Построим силовой треугольник (рис.
2.8б). Построение начинают с известной
силы Р.

Силовой треугольник
должен быть замкнут. В данном случае
это прямоугольный треугольник. Тогда:

;

Рис. 2.8б

твет:

;

а)

б)

в)

Рис. 2.9

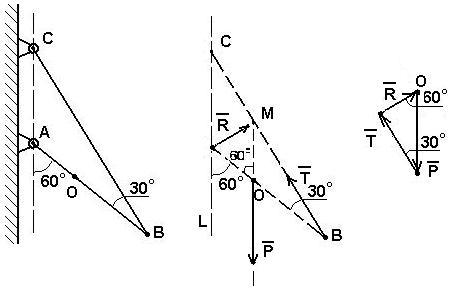
ример №4. Однородный стержень АВ
прикреплен к стенке посредством шарнира
А и удерживается под углом 60⁰
к вертикали при помощи троса ВС,
образующего с ним угол 30⁰
(рис. 2.9а). Определить величину и направление
реакции R
шарнира, если известно, что вес стержня
равен 20Н.

Решение:

Определим силы,
действующие на данную конструкцию:

Р – сила тяжести
стержня АВ, так как стержень однородный,
то сила приложена к его геометрическому
центру (точка О).

Т – натяжение
троса СВ, направлено вдоль СВ.

R
– реакция в шарнире А (направление
неизвестно) (рис. 2.9б).

Согласно принципу
освобождаемости от связей, заменим
связи соответствующими реакциями.

Так как система
находится в равновесии под действием
трех сил, то эти силы должны сходиться,
а поэтому сила реакции R
направлена от А к М (точка пересечения
сил Р и Т).

Построим силовой
треугольник. Для этого выберем произвольную
точку О и отложим от нее известную силу
Р, сохраняя ее направление. Из конца
вектора Р под углом 30⁰проведем
луч, который соответствует направлению
силы Т (рис. 2.9в).

Так как <LAO
= <AOM
(как накрест лежащие углы), то угол <MOB
= 180⁰–
60⁰
= 120⁰,
тогда <OMB
= 180⁰
– (120⁰
+ 30⁰)
= 30⁰,
т.е. треугольник ОМВ равнобедренный:
сторона ОМ = ОВ. Поэтому ОМ = ОВ = ОА, так
как О является серединой АВ, а угол <АOM
= 60⁰,
то треугольник АОМ является равносторонним.
Поэтому <OАM
= 60⁰
= <AMO.
Из точки О проводим луч под углом 60⁰
к направлению силы Р до пересечения с
направлением силы Т. Полученный
треугольник прямоугольный, поэтому R
= Psin30⁰
= 20/2 = 10H.

Ответ: R
= 10H.

Пример №5. Три
груза А, В и С массой 10, 20, и 60 кг
соответственно лежат на плоскости,
наклоненной под углом 
к горизонту (рис. 2.10). Грузы соединены
тросами, как показано на рисунке.
Коэффициенты трения между грузами и
плоскостью равны _А
= 0,1, _В
= 0,25, _С
= 0,5 соответственно.

Определить угол
,
при котором тела равномерно движутся
вниз по плоскости. Найти также натяжение
тросов Т_АВ
и Т_ВС.

Р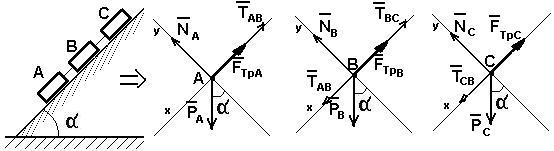
ешение:

а)

б)

в)

г)

Рис. 2.10

ассмотрим, какие силы действуют на
каждое тело и запишем условие равновесия,
так как тела движутся равномерно, то

умма
всех сил, действующих на тело равна
нулю. На тело А действует сила тяжести
Р_А,
сила реакции опоры N_А,
сила трения F_трА
и сила натяжения троса Т_АВ(рис. 2.10б).
Условие равновесия: Р_А
+ N_А
+ F_трА + Т_АВ
= 0.

Выберем систему
координат и спроектируем силы на оси:

Ось ОХ Р_Аsin
– Р_Аcos
– Т_АВ
= 0.

Подставляя численные
значения получим: 10sin
– cos
– Т_АВ
= 0.

ассмотрим,
какие силы действуют на тело В: Р_В
– сила тяжести, F_трВ
– сила трения, Т_ВА–
сила натяжения троса со стороны груза
А, Т_ВС
– сила натяжения троса со стороны груза
С, N_В
– сила реакции опоры (рис. 2.10в). Тогда
условие равновесия будет: Р_В
+ N_В
+ F_трВ + Т_ВА
+ Т_ВС
= 0.

Проектируя это
уравнение на ось ОХ, получим:

Р_Вsin
– F_трВ + Т_ВА
– Т_ВС
= 0; учитывая, что Т_ВА
= Т_АВ:

Р_Вsin
– Р_Вcos*_В + Т_ВА
– Т_ВС
= 0;

30sin
– 30cos*0.25 + Т_ВА
– Т_ВС
= 0;

а
тело С действуют следующие силы: Р_С
– сила тяжести, F_трС
– сила трения, Т_СВ–
сила натяжения троса со стороны груза
В, N_С
– сила реакции опоры (рис. 2.10г). Тогда
условие равновесия при проектировании
на ось ОХ будет:

Р_Сsin
– Р_Сcos*_С
– Т_СВ
= 0; так как Т_ВС
= Т_СВ,

60sin
– 60*0,5cos
– Т_ВС
= 0.

Получим систему
из трех уравнений с тремя неизвестными:

Так как неизвестные
силы перпендикулярны оси y,
то на эту ось силы не проектируем.

1
0sin
– cos
– Т_АВ
= 0 (1);

30sin
– 7,5cos
+ Т_ВА
– Т_ВС
= 0 (2);

60sin
– 30cos
– Т_ВС
= 0 (3).

Отсюда:
Т_АВ
= 10sin
– cos;
Т_ВС
= 60sin
– 30cos.

Подставляя выражения
Т_АВ
и Т_ВС
в уравнение (2), получим:

100sin
= 38.5cos;
tg
= 0.385; 
= arctg0.385;

= 21⁰.

Из уравнения (1)
получим: Т_АВ
= 10sin21⁰
– cos21⁰
= 10*0,358 – 0,93 = 2,67Н.

Т_АВ
= 2,67Н.

Подставляя численные
данные в уравнение (3), получим:

Т_ВС
= 60sin21⁰
– 30cos21⁰
= 60*0,358 – 30*0,93 = 6,42Н;

Т_ВС
= 6,42Н.

Ответ: 
= 21⁰;
Т_АВ
= 2,67Н; Т_ВС
= 6,42Н.

Соседние файлы в папке теормех

Источник

Методика решения задач плоской системы сходящихся сил

1. Число неизвестных в данных задачах не превышает двух.

2. Рассматриваем точку, находящуюся в равновесии.

3. Определяем наличие активных сил.

4. Освобождаемся от связей и заменяем их реакциями.

5. Выбираем оси координат и располагаем в этих осях имеющиеся активные и реактивные силы.

6. Решаем уравнения равновесия относительно неизвестных.

7. Выполняем проверку.

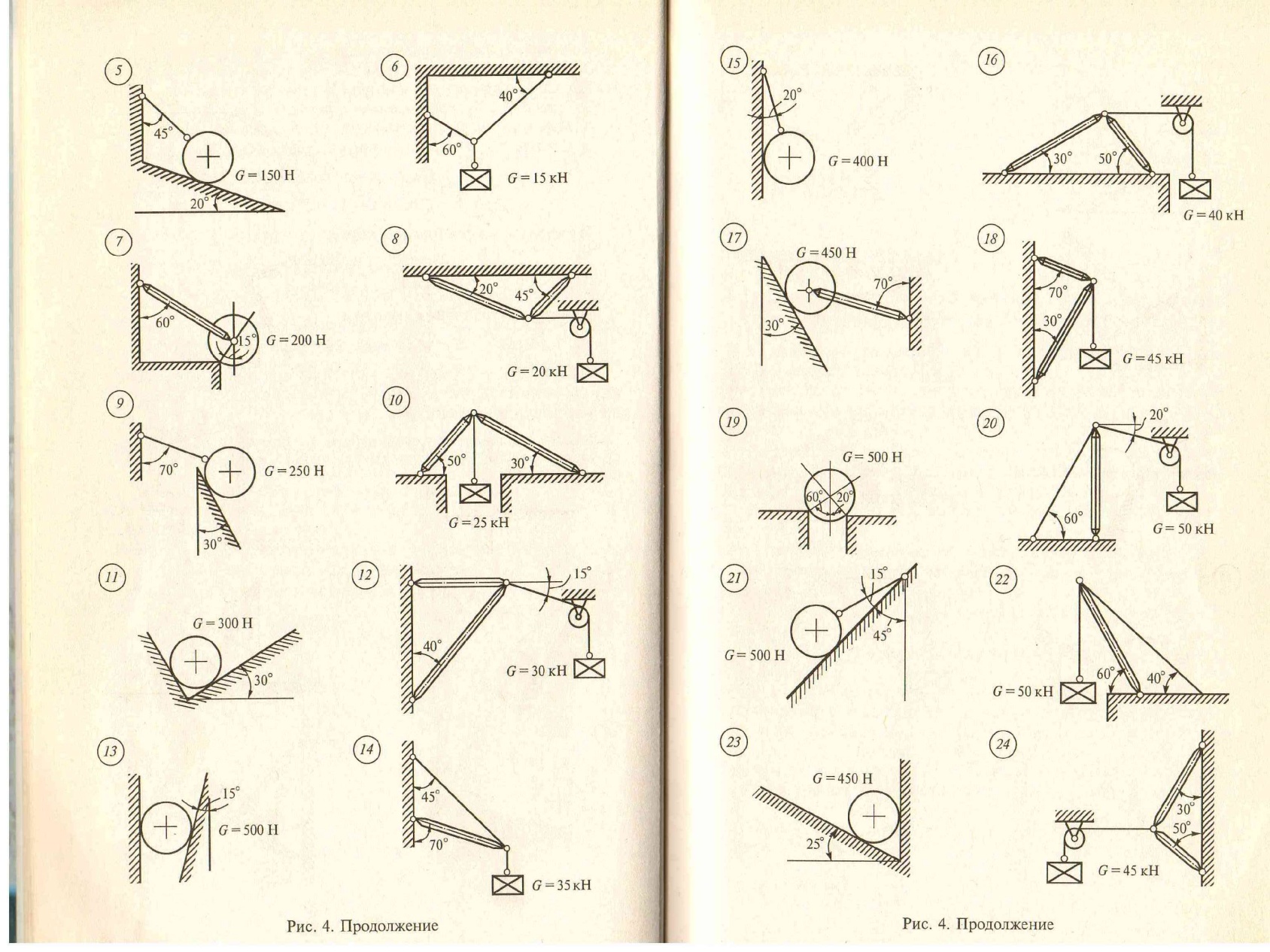
Пример.Груз, силой тяжести F1=10Н удерживается в равновесии с помощью связей –гладких поверхностей . Определить реакции связи аналитически и графически.

Решение.

I. Аналитическое решение

1. Освобождаемся от связей, заменяя их реакциями. Получаем систему трех сходящихся в точке О сил.

2. Выбираем систему координат хОу и составляем таблицу, уравнения равновесия.

силы	=0	=0
R₁
R₂
F₁

3. Составляем систему уравнения и решаем.

Проверка: + =4,7·0,5 +8,46 ·0,9- 10=0

II. Графическое решение.

1. Выбираем масштаб 1:20 и из точки О откладываем вектор силы тяжести F₁.

2. Полученная система сил находится в равновесии, поэтому силовой многоугольник должен быть замкнут, R₁+R₂+F₁=0. Поэтому, из конца и начала вектора F проводим прямые параллельные векторам R₁ и R₂ до их пересечения.

3. Определяем реакции связей R₁ и R₂ , умножая полученные результате графического построения отрезки на масштаб.

4. Проверка: Заключается в сравнении значений векторов R₁ и R₂ , найденных аналитическим и графическим способами. r1 = (R_1а – R_1б)/ R_1а; r1 = (R_2а – R_2б)/ R_2а;

Задания для выполнения работы

Груз, силой тяжести G удерживается в равновесии с помощью связей. Определить реакции связей, удерживающих груз аналитически и графически.

Контрольные вопросы:

1. В чем отличие между осью и проекцией?

2. Сколько уравнений равновесия Вы составляли при решении задачи?

3. Методика решения задач ПССС.

4. Дайте определение плоской системе сходящихся сил.

5. Какой величиной является проекция силы на координатную плоскость?

Литература:

1. Вереин Л.И. Техническая механика – М: Академия, 2006.

2. Мовнин М.С. Основы технической механики – СПБ: Политехника, 2003.

3. Молчанова Е.В., Шурыгина Г.Н. Статика и сопротивление материалов – Томск, 2008.

Практическая работа №3

Тема урока: Определение реакций в опорах с вертикальными нагрузками

Тип урока:закрепление полученных знаний.

Цель урока:Научиться определять реакции в опорах с вертикальными нагрузками

Обеспечивающие средства:

1. методическое руководство по выполнению работы;

3.тетрадь для практических работ;

4.карандаш, линейка, ластик, авторучка;

Технология работы:

1.Внимательно изучите методические указания, предложенный теоретический материал.

2.В соответствие с вариантом, выполнить задание по методике представленной ниже.

3.Сделайте выводы о проделанной работе.

4.Ответить на контрольные вопросы.

Теоретический материал

Плоская система произвольно-расположенных сил – это система, в которой все силы лежат в одной плоскости, но линии их действия не пресекаются в одной точке.

Момент силы относительно точки

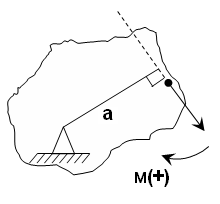
Момент –способность силы создавать вращение (М).

Единица измерения М [ Н * м] 1кНм = 10 3 Нм, 1мНм = 10 6 Нм

Момент силы относительно точки равен произведению силы на перпендикуляр, опущенный из точки вращения на линию действия силы.

а – плечо, перпендикуляр или кратчайшее расстояние между точкой вращения и линией действия силы.

Если вращение тела происходит по часовой стрелке, то момент положительный.

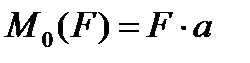
Момент отрицательный, если вращение тела против часовой стрелки.

Момент силы относительно точки равен нулю, если линия действия силы проходит через точку вращения, т.к. плеча равно нулю, нет вращения.

Пример. Для двух опорной балки, нагруженной силами F₁, F₂ , определить реакции в опорах R_А и R_В. Силами тяжести балки АВ пренебречь. Опора А шарнирно-подвижная, опора В шарнирно-неподвижная.

Решение.

1. Определяем связи, заменяем их реакциями.

2. Определяем оси координат Х, У.

3. Составляем таблицу уравнения равновесия.

R_BX =0 т.к. все силы располагаются параллельно балке R_B =R_BY

Силы	=0	=0	=0
R_А	6R_A	R_A
R_BY	-6R_BY	R_BY
F₁	2F₁	-4F₁	-F₁
F₂	-4F₂	2F₂	F₂

4. Составляем уравнение по II-ому виду

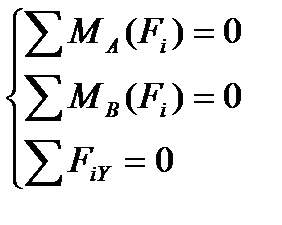
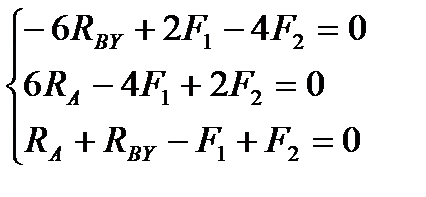
Из 1-го уравнения находим R_BY

Из 2-го уравнения находим R_A

5. Проверка: по 3-му уравнению 4,7+1,3-8+2=0

Техническая механика

Плоская система сходящихся сил

Геометрический способ определения равнодействующей плоской системы сходящихся сил

Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.

Теорема

Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.

Пусть дана плоская система трех сил F₁ , F₂ и F₃ , линии действия которых сходятся в точке А (см. рисунок а) .
На основании следствия из аксиом III и IV перенесем эти силы вдоль линий их действия в точку А . Сложив первые две силы F₁ и F₂ по правилу параллелограмма, получим их равнодействующую R (см. рисунок а) :
R = F₁ + F₂ .

Пользуясь той же аксиомой параллелограмма, сложим равнодействующую R с силой F₃ :

где F_Σ – равнодействующая данной системы трех сил.

Аналогичные рассуждения можно провести для любого количества сходящихся сил, в результате чего получим:
F_Σ = F₁ + F₂ + F₃ +…+ F_n .
Сокращенно это равенство можно записать так:
F_Σ = ΣF_i , где i – все целые числа от единицы до n .

Очевидно, что построения, выполненные на рисунке a , можно заменить более простым, как показано на рисунке b . Многоугольник АВСD называют силовым многоугольником. Сторона AD , соединяющая начало первого с концом последнего вектора, называется замыкающей стороной.

Необходимо помнить, что стрелки векторов слагаемых сил образуют определенное направление обхода по контуру силового многоугольника, а замыкающая сторона, определяющая модуль и направление равнодействующей, имеет стрелку, направленную против обхода (см. рисунок b) .

Если определить равнодействующую из силового многоугольника с помощью геометрии и тригонометрии, то такой способ будет называться геометрическим.

Если сделать чертеж силового многоугольника в определенном масштабе, то равнодействующая определится простым измерением замыкающей стороны с последующим умножением на масштаб. Такой способ нахождения равнодействующей называется графическим.

Порядок сложения векторов при построении силового многоугольника на величину равнодействующей не влияет, так как векторная сумма от перемены мест слагаемых не меняется.

Геометрическое условие равновесия плоской системы сходящихся сил

При построении силового многоугольника возможен случай, когда конец последнего вектора совпадает с началом первого. В этом случае замыкающей стороны не будет, и такой силовой многоугольник называется замкнутым.

Очевидно, что равнодействующая F_Σ системы сходящихся сил, образующих замкнутый силовой многоугольник, равна нулю, т. е. система сил находится в равновесии. Отсюда вытекает условие, при котором плоская система сходящихся сил будет находиться в равновесии. Это условие выражается равенством:

и формулируется так: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.

Условия равновесия, записанные в виде равенств, содержащих неизвестные величины, называются уравнениями равновесия.

Применяя геометрическое условие равновесия, удобно решать задачи, в которых на тело действуют три силы, так как в этом случае замкнутый силовой многоугольник представляет собой треугольник.

Решение большинства задач статики проводят в три этапа:
– выбирают тело, равновесие которого будет рассматриваться;
– отбрасывают связи, заменяя их реакциями, и устанавливают, какая система сил действует на тело;
– пользуясь условиями равновесия, находят неизвестные величины.

При решении задач статики следует строго соблюдать правило: размерности и единицы величин всех слагаемых и обеих частей равенства должны быть одинаковыми.

В сомнительных случаях целесообразно использовать это правило для проверки правильности хода решения задач, для чего следует подставить в слагаемые проверяемого равенства единицы всех входящих в них величин и, произведя возможные сокращения, сравнить полученные единицы правой и левой частей.

Пример решения задачи

В качестве примера решения задачи с использованием изложенных выше методов, определим натяжение веревки F и силу давления шара P на стену, если сила тяжести шара равна G .

Рассмотрим условие равновесия шара. Применив принцип освобождаемости, отбросим связи и заменим их реакциями. Реакция N гладкой стены перпендикулярна стене и проходит через центр шара (так как шар однородный, его геометрический центр совпадает с центром тяжести).
Реакция F веревки направлена вдоль линии натяжения веревки и тоже проходит через центр шара (согласно теореме о равновесии трех непараллельных сил). Применим к системе сил уравнение равновесия:

ΣF_i = 0 , или G + N + R = 0.

Строим замкнутый силовой треугольник, начиная с изображения в произвольном масштабе вектора известной силы G (см. рисунок) . Направление обхода треугольника (т. е. направление стрелок) определяется направлением этой силы. Из построенного силового треугольника получим соотношения:

N = G tg α ; R = G/cos α

Искомая сила давления P шара на стену, согласно аксиоме взаимодействия, по модулю равна реакции N стены, но направлена в противоположную сторону.
Натяжение веревки F равно по модулю ее реакции R .

Эту же задачу можно решить, разложив силу тяжести шара G по реальным направлениям (направлениям реакций) на составляющие P (сила давления шара на стену) и F (натяжение веревки) , причем согласно аксиоме взаимодействия:

Из построенного параллелограмма (см. рисунок) легко определить искомые величины.
Такой метод решения задачи называют методом разложения силы.

Проекция силы на оси координат

В тех случаях, когда на тело действует более трех сил, а также когда неизвестны направления некоторых сил, удобнее при решении задач пользоваться не геометрическим, а аналитическим условием равновесия, которое основано на методе проекций сил на оси координат.

Проекцией силы на ось называют отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.

На приведенном ниже рисунке видно, что проекции силы P на оси x и y можно определить при помощи тригонометрических функций:
P_x = Pcos α, P_y = Psin α .

Проекция силы на ось есть величина алгебраическая, которая может быть положительной или отрицательной, что устанавливается по направлению проекции – проекция, направленная в положительном направлении оси считается положительной, в противном случае – отрицательной.
Возможны два частных случая:
– если сила перпендикулярна оси, то ее проекция равна нулю (сила проецируется в точку) ;
– если сила параллельна оси, то она проецируется на ось в натуральную величину.

Зная проекции силы на координатные оси, можно определить ее величину (модуль) , используя теорему Пифагора, учитывая, что проекции являются катетами прямоугольного треугольника, а сама сила – гипотенузой.
Направляющий тангенс угла между вектором силы P и осью x можно определить из отношения:
tgα = P_y/P_x .

Отметим, что силу P можно представить, как равнодействующую двух составляющих сил P_x и P_y , параллельных осям координат, но эти составляющие не будут являться проекциями силы по определению, поскольку сила (в т. ч. и составляющая силы) есть величина векторная, а проекция – алгебраическая.

Аналитический способ определения равнодействующей плоской системы сил

Пусть дана плоская система сходящихся сил F₁, F₂, F₃, F₄. F_n .
Равнодействующая этой системы F_Σ = ΣF_i .

В плоскости действия данной системы сил выберем ось координат и спроецируем данные силы и их равнодействующую на эту ось. Из математики известно свойство проекции векторной суммы, на основании которого можно утверждать, что проекция равнодействующей на ось равна алгебраической сумме проекций составляющих сил на ту же ось, т. е. F_Σx = ΣF_ix .
Правую часть этого равенства можно представить упрощенно: F_Σx = ΣX .

Для того чтобы определить равнодействующую любой плоской системы сходящихся сил, спроецируем их на оси координат x и y , алгебраически сложим проекции всех сил и найдем таким образом проекции равнодействующей:

Зная проекции, определим модуль и направление равнодействующей:
Модуль равнодействующей:

F_Σ = √(F_Σx 2 + F_Σy 2 ) (здесь и далее √ – знак корня);

Направляющий тангенс угла между вектором F_Σ и осью x :

Линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.

Аналитические условия равновесия плоской системы сходящихся сил

Если данная плоская система сходящихся сил находится в равновесии, то равнодействующая такой системы, а значит и проекции равнодействующей на оси координат равны нулю.
Математически это выражение можно записать так:

Учитывая, что F_Σx = ΣX; F_Σy = ΣY , получаем равенства, выражающие аналитические условия равновесия плоской системы сходящихся сил:

Формулируется это условие следующим образом: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций этих сил на каждую из двух координатных осей равнялась нулю.

С помощью уравнений равновесия можно определить два неизвестных элемента данной системы сил, например модуль и направление одной силы или модули двух сил, направления которых известны и т. п.

Выведенные условия равновесия справедливы для любой системы координат, но для упрощения расчетов рекомендуется оси координат по возможности выбирать перпендикулярными неизвестным силам, чтобы каждое уравнение равновесия содержало одно неизвестное.
Когда направление искомой силы неизвестно, ее можно разложить на две составляющие по заданным направлениям, обычно по направлениям координатных осей; по найденным двум составляющим легко определяется неизвестная сила.

Если при решении задач аналитическим способом искомая реакция получается отрицательной, то это означает, что действительное ее направление противоположно направлению, принятому при расчетах.

iSopromat.ru

Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:

Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия: R=0, M_O=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

Формы условий равновесия

Первая форма

Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:

причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.

Вторая форма

Уравнения равновесия могут быть записаны иначе:

Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.

Третья форма

Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.

Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.

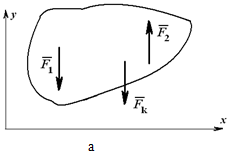
Другие условия равновесия

При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):

Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:

Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:

и два уравнения для плоской системы:

В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

[spoiler title=”источники:”]

http://k-a-t.ru/tex_mex/11-statika_plosk_sily/

Условия равновесия произвольной системы сил

[/spoiler]

Источник

Если система уравновешена, то получаем условия равновесия: R=0, M_O=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

∑x_i =0, ∑M_ix=0;
∑y_i =0, ∑M_iy=0; (1.20)
∑z_i =0, ∑M_iz=0.