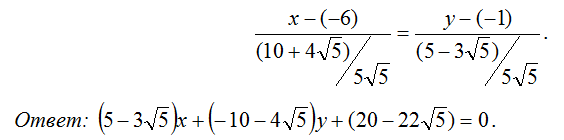Как составить уравнение стороны если известны вершины

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.



2.9. Типовая задача с треугольником

Многие помнят из школы признаки равенства треугольников, признаки подобия треугольников и мучительное заучивание доказательств теорем. Как в

сердцАх сказал один мой одноклассник, «не понимаю, на### доказывать равенство треугольников, если и так видно, что они одинаковые». Мы тоже не

будем ничего доказывать, поскольку аналитическая геометрия рассматривает треугольник совсем с другой стороны.

Типовая задача, как правило, формулируется так: Даны три вершины треугольника. Требуется найти… много чего требуется

найти…. Повезёт, если будет пункта 3-4, но чаще всего их 5-6 и даже больше. И вам повезло – разберём всё! Или почти всё:

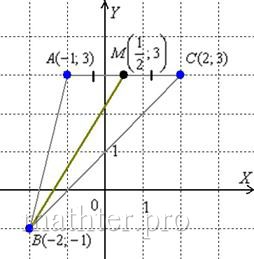
Задача 95

Даны вершины треугольника . Требуется:

1) составить уравнения сторон  и найти их угловые коэффициенты;
2) найти длину стороны ;
3) найти ;
4) составить прямой , проходящей через точку  параллельно прямой ;
5) составить уравнение высоты и найти её длину;
6) вычислить площадь треугольника ;
7) составить уравнение медианы ;
8) найти точку пересечения .
и для особо опасных энтузиастов:
9) найти уравнение биссектрисы ;
10) найти центр тяжести  треугольника;
11) составить систему линейных неравенств, определяющих треугольник.

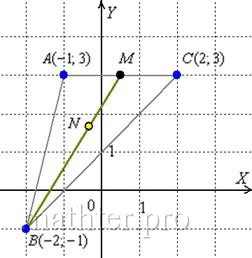
С чего начать решение? Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и

самопроверки всегда строим чертёж на черновике, не устану это рекомендовать:

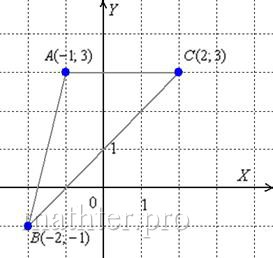
Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1

см (2 тетрадные клетки). Всё хорошо видно, и расстояния удобно измерять линейкой.

Вперёд без страха и сомнений:

1) Составим уравнения сторон  и найдём их угловые

коэффициенты.
Поскольку известны вершины треугольника, то уравнения каждой стороны составим по двум

точкам.

Составим уравнение стороны  по точкам :

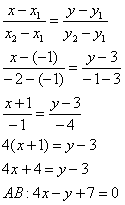
Для проверки мысленно либо на черновике подставляем координаты каждой точки в полученное уравнение.

Теперь

найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом:

Таким образом, угловой коэффициент:

Самостоятельно разбираемся со сторонами  и сверяемся, что

получилось:

2) Найдём длину стороны .  Используем соответствующую формулу для точек :

Сторону легко измерить обычной линейкой, хотя это не сильно строгая проверка 🙂

3) Найдём . Это Задача 31, повторим:

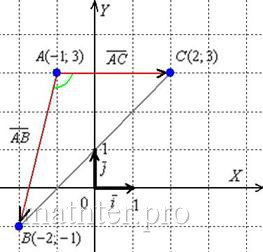
Используем формулу .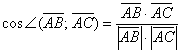
Найдём векторы:

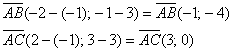
Таким образом:
, и сам угол:
, ну что же, похоже на правду, желающие могут приложить транспортир, у кого

он есть.

Внимание! При выполнении этого пункта лучше не использовать формулы ориентированного угла

между прямыми, так как они всегда дают острый угол.

4) Составим уравнение прямой , проходящей через точку  параллельно прямой . Это стандартная задача, и мы ленимся отработать её вновь!

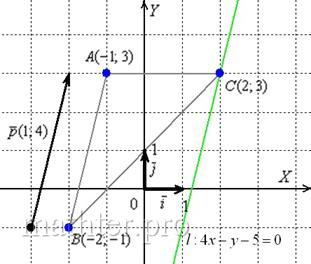
Из общего уравнения прямой  вытащим направляющий вектор .

Составим уравнение прямой  по точке  и направляющему вектору :

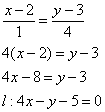
5) Составим уравнение высоты и найдём её длину.
Первую часть задания мы тоже решали:

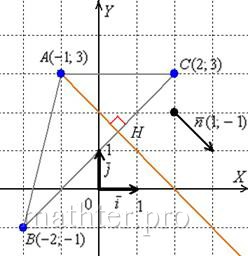
Из уравнения стороны  снимаем вектор нормали . Уравнение высоты

 составим по точке  и направляющему вектору :

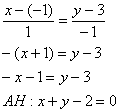
Обратите внимание, что координаты точки  нам не известны.

Иногда уравнение высоты находят из соотношения угловых коэффициентов перпендикулярных прямых: . В данном случае , тогда: . Уравнение высоты  составим по точке  и угловому коэффициенту :

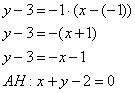
Длину высоты можно найти двумя способами.

Существует окольный путь:

а) находим  – точку

пересечения высоты и стороны ;

б) находим длину отрезка  по двум

известным точкам.

Но зачем? – ведь есть удобная формула расстояния от точки  до прямой :

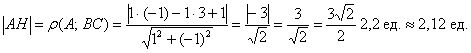
6) Вычислим площадь треугольника. Используем «школьную» формулу:

7) Уравнение медианы  составим в два шага:

а) Найдём точку  – середину стороны . Используем формулы координат середины отрезка.

Известны концы , и тогда середина:

б) Уравнение медианы  составим по точкам :

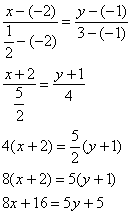
 – для проверки подставим координаты точек .

8) Найдём точку пересечения  высоты и медианы:
      в

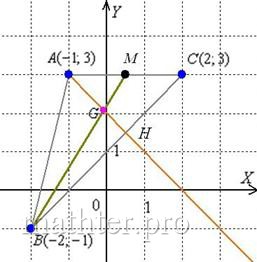
Первое уравнение умножили на 5, складываем их почленно:
 – подставим в первое уравнение:

9) Биссектриса делит угол пополам:

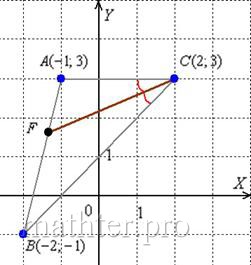
Из свойств биссектрисы внутреннего угла следует соотношение длин следующих отрезков:

Длины сторон уже найдены в предыдущих пунктах: .

Таким образом, . Координаты точки  найдём по формулам деления отрезка в данном отношении. Да,

параметр «лямбда» получился просто сказочным, ну а кому сейчас легко? Точки  известны и понеслась нелёгкая:

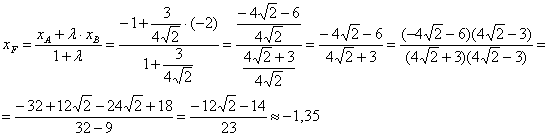
Примечание: на последнем шаге я умножил числитель и знаменатель на сопряжённое выражение  – чтобы использовать формулу  и

избавиться от иррациональности в знаменателе.

Разбираемся со второй координатой:

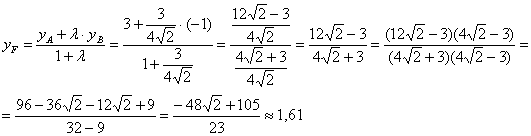
аким образом: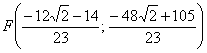  

И предчувствие вас не обмануло, уравнение биссектрисы  составим по точкам 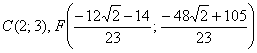 по формуле :

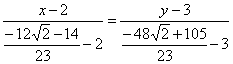
обратите внимание на технику упрощений:

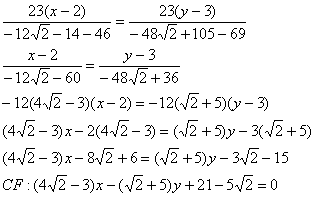
Проверил, всё сходится. На практике, конечно, вычисления почти всегда будут проще. Никого не хотел запугать, так уж получилось =)

10) Найдём центр тяжести треугольника.

Но сначала поймём, что такое центр тяжести плоской фигуры. Мысленно вырежьте из тонкого однородного картона любую фигуру. …Почему-то фигура зайца

в голову пришла. Так вот: если слегка насадить данную фигуру центром тяжести (какой же я изверг =)) на вертикально расположенную иголку, то

теоретически фигура не должна свалиться.

Центром тяжести треугольника является точка пересечения его медиан. В треугольнике три медианы и пересекаются они в одной точке.

Из пункта 7 нам уже известна одна из медиан: .  Как решить задачу?

Напрашивается очевидный алгоритм: можно найти уравнение второй медианы (любой из двух оставшихся) и точку пересечения этих медиан. Но есть путь

короче! Нужно только знать полезное свойство:

Точка пересечения медиан делит каждую из медиан в

отношении , считая от вершины треугольника. Поэтому справедливо

отношение
Нам известны концы отрезка – точки  и .
По формулам деления отрезка в данном отношении:

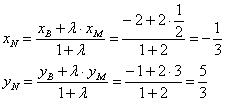
Таким образом, центр тяжести треугольника:
И заключительный пункт задачи, для освоения которого нужно уметь решать недавно разобранные линейные

неравенства:

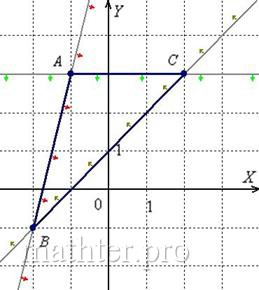
11) Составим систему линейных неравенств, определяющих треугольник.

Для удобства я перепишу найденные уравнения сторон:

Рассмотрим прямую . Треугольник лежит в полуплоскости, где находится

вершина . Составим вспомогательный многочлен  и вычислим его значение в точке : . Поскольку сторона  принадлежит треугольнику, то неравенство будет нестрогим:

Внимание! Если вам не понятен этот алгоритм, то обратитесь к

Задаче 90.

Рассмотрим прямую . Треугольник расположен ниже данной прямой, поэтому

очевидно неравенство .

И, наконец, для  составим многочлен , в который подставим координаты точки : .
Таким образом, получаем третье неравенство: .

Итак, треугольник  определяется следующей системой линейных

неравенств:

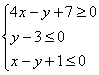
Готово.

Какой можно сделать вывод?

Многие задачи аналитической геометрии прозрачны и просты,
главное, не допустить вычислительных ошибок.

Следует отметить, что по настоящему трудные задачи в аналитической геометрии встречаются редко, и вы справитесь практически с любой из них!

Главное, придерживаться методики решения и проявить маломальское упорство.

Ну что, может ещё задачку? Да ладно, не надо стесняться, я же по глазам вижу, что хотите =) 

Но сейчас на очереди другая увлекательная тема, продолжаем изучать геометрию плоскости:

3.1. Алгебраическая линия и её порядок

2.8. Как научиться решать задачи по геометрии?

| Оглавление |



Автор: Aлeксaндр Eмeлин

По известным координатам вершин треугольника  А(4;4), В(-6;-1), С(-2;-4) записать для его сторон уравнения в общем виде и уравнение в общем виде биссектрисы угла АВС. 

Решение

Так как нам известны координаты вершин, то проще всего получить уравнение стороны в канонической форме – формула, от которого легко перейти к уравнению в общей форме. Для канонического уравнения нам нужны координаты точки, принадлежащей стороне и координаты направляющего вектора (параллельного рассматриваемому).

1. Найдем уравнение стороны АВ. В качестве точки прямой можно взять точку А с заданными координатами, а в качестве направляющего вектора – вектор АВ. Найдем координаты вектора АВ:

2. Тогда каноническое уравнение стороны АВ запишется:

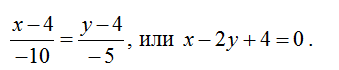
3. Аналогично можно получить уравнения остальных сторон треугольника: для стороны ВС: координаты вектора 

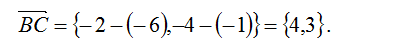
4. Откуда каноническое уравнение: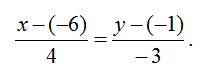

Следовательно, общее уравнение: 3x+4y+22=0.

5. Для стороны CА: координаты направляющего вектора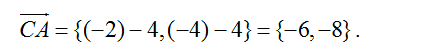

6. Каноническое уравнение: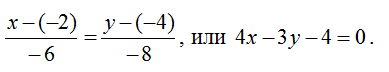 

7. Выведем общее уравнение для биссектрисы. Известно, что биссектриса делит угол пополам. Если на сторонах АВ и ВС треугольника отложить орты (соответственно a и b) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов a и b).

8. Для нахождения орта a необходимо знать координаты вектора BA:

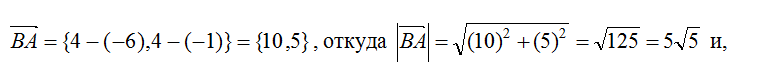
соответственно a определится как:

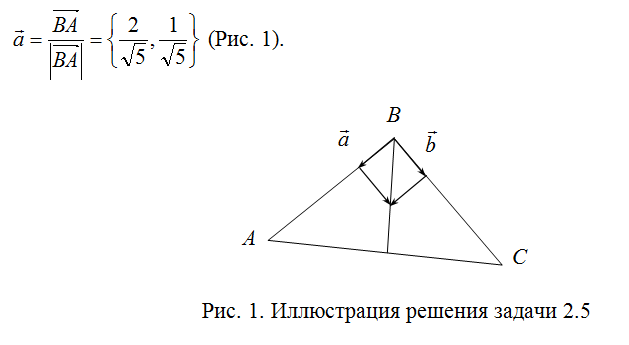
9. Аналогично определим орт b:

Теперь определим их сумму:

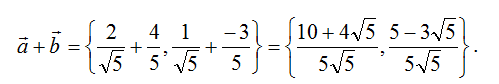
10. Тогда каноническое уравнение биссектрисы: