Как составить уравнение трех медиан треугольника

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

1. Найти координаты середины отрезка по координатам его концов.
2. Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Пример.

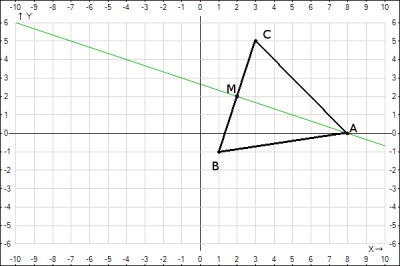
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Решение:

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

1) По формулам координат середины отрезка

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы  BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

C(-3;-7), C(4,5;-1), y=kx+b:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

Медиана равна половине гипотенузы прямоугольного треугольника!

Почему??? При чём тут прямой угол?

Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник.

Ты заметил, что наш треугольник ( displaystyle ABC) – ровно половина этого прямоугольника?

Проведём диагональ ( displaystyle BD):

Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам?

Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, ромб…»

Но одна из диагоналей – ( displaystyle AC) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы ( displaystyle Delta ABC).

Она называлась у нас ( displaystyle M).

Значит, половина второй диагонали – наша медиана ( displaystyle BM). Диагонали равны, их половинки, конечно же, тоже. Вот и получим ( displaystyle BM=MA=MC)

Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.

Более того, так бывает только в прямоугольном треугольнике!

Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.

Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника?

Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.

Решение задач на свойства медианы в прямоугольном треугольнике

Давай посмотрим, как это свойство помогает решать задачи.

Найти ( displaystyle AB), если ( displaystyle AB=2CN).

Рисуем:

Сразу вспоминаем, это если ( displaystyle CN=frac{AB}{2}), то ( displaystyle angle ACB=90{}^circ )!

Ура! Можно применить теорему Пифагора!

Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!

Применяем теорему Пифагора:

( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})

( A{{B}^{2}}={{5}^{2}}+{{12}^{2}}=169)

Ответ: ( AB=13)

А в следующей задаче пусть у нас будет не одна, а целых три медианы! Как же они себя ведут?

Запомни очень важный факт:

Три медианы в треугольнике (любом!) пересекаются в одной точке и делятся этой точкой в отношении ( 2:1), считая от вершины.

Сложно? Смотри на рисунок:

Медианы ( displaystyle AM), ( displaystyle BN) и ( displaystyle CK) пересекаются в одной точке.

Запомни:

• ( displaystyle AO) – вдвое больше, чем ( displaystyle OM);
• ( displaystyle BO) – вдвое больше, чем ( displaystyle ON);
• ( displaystyle CO) – вдвое больше, чем ( displaystyle OK).

Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении ( displaystyle 2:1 ), считая от вершины.

Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил?

1. Медианы треугольника пересекаются в одной точке.

2. Точкой пересечения медианы делятся в отношении ( displaystyle 2:1 ), считая от вершины.

Давай попробуем разгадать секрет этой теоремы, то есть доказать ее.

Доказательство теоремы о трех медианах треугольника

Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой ( displaystyle E).

Соединим точки ( displaystyle N) и ( displaystyle K). Что получилось?

Конечно, ( displaystyle NK) – средняя линяя ( displaystyle triangle ABC). Ты помнишь, что это значит?

• ( displaystyle NK) параллельна ( displaystyle AC);
• ( displaystyle NK=frac{AC}{2}).

А теперь проведем ещё одну среднюю линию: отметим середину ( displaystyle AE) – поставим точку ( displaystyle F), отметим середину ( displaystyle EC) — поставим точку ( displaystyle G).

Теперь ( displaystyle FG) – средняя линия ( displaystyle triangle AEC). То есть:

• ( displaystyle FG) параллельна ( displaystyle AC);
• ( displaystyle FG=frac{AC}{2}).

Заметил совпадения? И ( displaystyle NK) , и ( displaystyle FG) – параллельны ( displaystyle AC). И ( displaystyle NK=frac{AC}{2}), и ( displaystyle FG=frac{AC}{2}).

Что из этого следует?

• ( displaystyle NK) параллельна ( displaystyle FG);
• ( displaystyle NK=FG)

Посмотри теперь на четырехугольник ( displaystyle NKGF). У какого четырехугольника противоположные стороны (( displaystyle NK) и ( displaystyle FG)) параллельны и равны?

Конечно же, только у параллелограмма!

Значит, ( displaystyle NKGF) – параллелограмм. Ну и что?

А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам.

Снова смотрим на рисунок.

Получилось что:

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике по треугольникам

Лучше всего смотреть это видео с ручкой и тетрадкой в руках. То есть ставьте видео на паузу и решайте задачи самостоятельно.

Помните, понимать и уметь решать — это два, совершенно разных навыка. Очень часто вы понимаете как решить задачу, но не можете это сделать. Или допускаете ошибки, или просто теряетесь и не можете найти ход решения.

Как с этим справиться?

Нужно решать много задач. Другого способа нет. Вы должны совершить свои ошибки, чтобы научиться их не допускать.

ЕГЭ №6 Равнобедренный треугольник, произвольный треугольник

В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и «обычные» треугольники.

ЕГЭ №6 Прямоугольный треугольник, теорема Пифагора, тригонометрия

ЕГЭ №16. Подобие треугольников. Задачи н доказательство

Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!

Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.

В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.

Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.

Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.

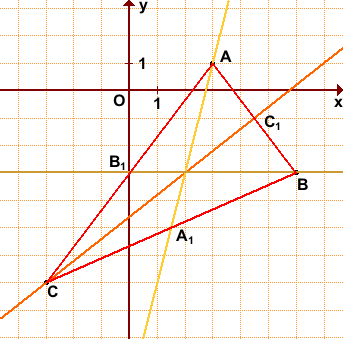
Задача эта рассмотрена на многих сайтах. Но я пишу свой подход к решению этой задачи. Рассматривая рисунок 1, находим, как построить треугольник из частей медиан, для чего делаем дополнительные построения.

Задача.

Пусть даны величины трёх медиан треугольника АВС: АМ3; ВМ1; СМ2.

Построить треугольник АВС.

Казалось бы , что тут особенного, есть 3 величины в треугольнике, вот и стройте его. Но вопрос – как строить, как пристраивать эти медианы. Воспользуемся чертежом треугольника, и посмотрим, как медианы соотносятся друг с другом в треугольнике. А поможет нам замечательная точка треугольника – точка пересечения медиан.

Кроме рисунков в статье понять построение можно из видео.

Применяем одно из свойств медианы: медианы в треугольнике – точка деления делит каждую из медиан в отношении 2 к 1.

Деление отрезка медианы на 3 части. Вспомогательное построение.

Вспомним метод деление любого отрезка на части, в частности на 3 части.

Для того, чтобы разделить любой отрезок (МВ1) на 3 части, нужно –

1) построить произвольный отрезок (МК) около него , предварительно построив на нём 3 равных отрезка : ММ1 = М1К1 = К1К.

2) Из конца отрезка МК, М провести линию к точке В отрезка М1В.

3) Проводим параллельные линии МВ∥К1О∥М1К. Таким образом, получаем отрезки медианы ВМ1, ВО и ОМ1Ю которые разделены в отношении 2 к 1.

И так, другие медианы делим в отношении 2 к 1, чтобы воспользоваться для дальнейшего построения треугольника из частей медиан треугольника. А точнее – из 2/3 частей каждой медианы.

После построения треугольника ОВ1С, стороны которого есть 2/3 часть каждой медианы, остаётся только достроить. А именно – продлить каждую эту часть медианы на её треть, соответственно и получить точки медиан М1, М2, и М3.

Продлить ОМ1 на 2 части этой седины, и получить точку В – вершину..

Также поступить с двумя другими медианами, и получить точки А ю С.

Далее – соединить точки А, В, С, и треугольник АВС построен. Подробности в видео, желательно смотреть на Ютуб канале.

Поделитесь данной статьёй в соцсетях. Подписывайтесь на наш канал.

Спасибо за просмотр.

Лучший ответ

0 Голосов

Posted Декабрь 5, 2013 by Вячеслав Моргун 1. Вычислить длину медианы АМ. Для нахождения длины медианы найдем координату точки M, зная координаты точки A найдем расстояние между этими точками, которое рассчитывается по формуле  $$d = sqrt{(x_2-x_1)^2+(y_2-y_1)^2} quad (1)$$Найдем координаты точки M, которая находится по середине между точками B(1;-1) и  C(3;5), координаты рассчитываются по формуле $$M(frac{x_B+x_C}{2};frac{y_B+y_C}{2})$$ подставляем значения координат и получаем $$M(frac{1+3}{2};frac{-1+5}{2}) => M(2;2)$$ Найдем длину медианы, подставим координаты точек в формулу (1) $$d_{AM} = sqrt{(8-2)^2+(0-2)^2} = 2sqrt{10}$$ 2. Уравнение медианы AM. Известны две точки A и M через которые проходит медиана. Для составления уравнения медианы, воспользуемся формула уравнения прямой, проходящей через две заданные точки $$frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}$$ Подставляем координаты точек и получаем уравнение медианы$$frac{x-8}{2-8}=frac{y-0}{2-0} => y = -frac{1}{3}x+frac{8}{3}$$ 3. Наносим полученные точки и уравнение прямой на декартовую систему координат.

Другие ответы