Как составить уравнение в отрезках проходящее через 3 точки

Уравнением
прямой в отрезках называется
уравнение
вида

(4)

где
а
и b
– абсцисса и ордината точек пересечения
прямой с осями Ох
и Оу,
т.е. длины

отрезков,
отсекаемых прямой на координатных осях,
взятые с соответствующими знаками.

Пример
4. Общее
уравнение прямой 2х
– 3у
– 6 = 0 привести к уравнению в отрезках.

Решение:
запишем данное уравнение в виде 2х
– 3у=6
и разделим обе его части на свободный
член:
.
Это и есть уравнение данной прямой в
отрезках.

Пример
5. Через
точку А (1;2)
провести прямую, отсекающую на
положительных полуосях координат равные
отрезки.

Решение:
Пусть уравнение искомой прямой имеет
вид

По условию а=b.
Следова-тельно, уравнение принимает
вид х +
у =
а.
Так как точка А (1; 2) принадлежит этой
прямой, значит ее координаты удовлетворяют
уравнению х
+ у =
а;
т.е. 1 + 2 = а,
откуда а
= 3. Итак, искомое уравнение записывается
следующим образом: х
+ у = 3, или
х + у – 3
= 0.

Пример
6. Для прямой


написать
уравнение в отрезках. Вычислить площадь
треугольника, образованного этой прямой
и осями координат.

Решение:
Преобразуем данное уравнение следующим
образом:
,
или

.

В
результате получим уравнение
,
которое и
является уравнением данной прямой в
отрезках. Треугольник, образованный
данной прямой и осями координат, является
прямоугольным треугольником с катетами,
равными 4 и 3, поэтому его площадь равна

S
=
(кв.
ед.)

26

2.1.4 Уравнение прямой, проходящей через точку в данном направлении

Уравнение
прямой, проходящей через т.у А(х_а;
у_а)
и имеющей
угловой коэффициент k,
записывается в виде

у
– у_а=k
(x
– x_a).
(5)

Пример 7.
Составить уравнение прямой, проходящий
через точку (–2; 5) и образующей с осью

Ох
угол 45º.

Решение:
Угловой коэффициент искомой прямой k=
tg
45º = 1. Поэтому, воспользовавшись уравнением
(5), получаем у
– 5 = x
– (–2), или
х – у + 7
= 0.

2.1.5 Уравнение прямой, проходящей через две точки

Уравнение
прямой, проходящей через две точки т.
А (х₁;
у₁)
и т.В (х₂;
у₂),
имеет вид

(6)

Пример
8. Составить
уравнение прямой, проходящей через
точки А(–3;
5) и
В(7;
–2).

Решение:
Воспользуемся уравнением (6):

,
или
,
откуда 7х
+ 10у
– 29 = 0.

2.1.6 Нормальное уравнение прямой

Пусть
дана прямая С, проходящая через данную
точку Мо(Хо; Уо) и перпендикулярная
вектору

(А;В). Любой вектор
,
перпендикулярный данной прямой
,
называется ее нормальным
вектором.

Выберем
на прямой произвольную т. М(х;у).
Тогда
,
а значит их скалярное произведение
.
Это равенство можно записать в координатах

А(
х-х_о
)+В( у-у_о
)=0
(7)

Уравнение
(7) называется нормальным
уравнением прямой.

Пример
9.
Даны точки М₁
(2;-1) и М₂(4;
5). Написать уравнение прямой, проходящей
через

точку
М₁
перпендикулярно
вектору

Решение:
Нормальный вектор искомой прямой
имеет
координаты (2;6), следовательно по формуле
(7) получим уравнение 2(х-2)+6(у+1)=0
или х+3у
+1=0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уравнения плоскости, проходящей через три точки

Пусть в координатном пространстве заданы три точки не лежащие на одной прямой (рис.4.17). Требуется составить уравнение плоскости, проходящей через заданные точки.

Как было показано ранее (формула (1.23)), точка принадлежит плоскости, проходящей через точки тогда и только тогда, когда ее радиус-вектор удовлетворяет условию:

где – некоторые действительные числа (параметры). Это уравнение, а также его координатную форму

будем называть аффинным уравнением плоскости, проходящей через точки

Используя векторы

и

в качестве направляющих векторов плоскости, составим уравнение вида (4.18):

которое называется уравнением плоскости, проходящей через три заданные точки.

Уравнение плоскости “в отрезках”

Пусть на координатных осях заданы точки и , причем (рис.4.18). Требуется составить уравнение плоскости, проходящей через эти три точки.

Подставляя в уравнение (4.21) координаты заданных точек , получаем:

Разделив уравнение на , получаем уравнение

которое называется уравнением плоскости “в отрезках”. Говорят, что плоскость, проходящая через точки и , отсекает на координатных осях “отрезки”: на оси абсцисс, на оси ординат и на оси аппликат. Разумеется, длины отрезков и равны и соответственно.

Замечания 4.5.

1. Перейти от общего уравнения плоскости (4.15) к уравнению “в отрезках” (4.22) можно при условии, что все коэффициенты общего уравнения отличны от нуля. Для этого нужно перенести свободный член в правую часть уравнения: , а затем разделить обе части уравнения на

Обозначив получим уравнение в отрезках (4.22):

2. Уравнения (4.21), (4.22), полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним, однако величины и в общем случае не равны длинам отсекаемых отрезков и .

Пример 4.9. В координатном пространстве (в прямоугольной системе координат) заданы точки

Требуется:

а) составить общее уравнение плоскости треугольника ;

б) составить уравнение в “отрезках” для плоскости треугольника ;

в) определить точки пересечения этой плоскости с координатными осями.

Решение. а) Составим уравнение (4.21):

Раскрывая определитель и приводя подобные члены, получаем

б) Переносим свободный член общего уравнения плоскости (см. пункт “а”) в правую часть и делим уравнение на 12, получаем уравнение плоскости в “отрезках”:

в) По уравнению плоскости в “отрезках” заключаем, что плоскость (см. пункт “б”) проходит через точки на координатных осях.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.

Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:

Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.

Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.

Допустим, у нас имеется прямоугольная система координат. Обозначим ее Oxyz. В ней лежат три точки M с координатами M1 (x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3), которые нельзя соединить прямой линией. Исходя из этих условий, мы можем записать уравнение необходимой нам плоскости. Есть два подхода к решению этой задачи.

1. Первый подход использует общее уравнение плоскости. В буквенном виде оно записывается как A(x-x1)+B(y-y1)+C(z-z1)=0. С его помощью можно задать в прямоугольной системе координат некую плоскость альфа, которая проходит через первую заданную точку M1(x1, y1, z1). У нас получается, что нормальный вектор плоскости α будет иметь координаты A, B, C. 

Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.  

Из этого мы и будем исходить в дальнейшем.

Таким образом, согласно условиям задачи, мы имеем координаты искомой точки (даже трех), через которую проходит плоскость. Чтобы найти уравнение, нужно вычислить координаты ее нормального вектора. Обозначим его n→.

Вспомним правило: любой не равный нулю вектор данной плоскости является перпендикулярным нормальному вектору этой же плоскости. Тогда мы имеем, что n→ будет перпендикулярным по отношению к векторам, составленным из исходных точек M1M2→ и M1M3→. Тогда мы можем обозначить n→ как векторное произведение видаM1M2→·M1M3→.

Поскольку M1M2→=(x2-x1, y2-y1, z2-z1) а M1M3→=x3-x1, y3-y1, z3-z1 (доказательства этих равенств приведены в статье, посвященной вычислению координат вектора по координатам точек), тогда получается, что:

n→=M1M2→×M1M3→=i→j→k→x2-x1y2-y1z2-z1x3-x1y3-y1z3-z1

Если мы вычислим определитель, то получим необходимые нам координаты нормального вектора n→. Теперь мы можем записать нужное нам уравнение плоскости, проходящей через три заданные точки.

2. Второй подход нахождения уравнения, проходящей через M1 (x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3), основан на таком понятии, как компланарность векторов.

Если у нас есть множество точек M (x, y, z), то в прямоугольной системе координат они определяют плоскость для заданных точек M1 (x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) только в том случае, когда векторы M1M →=(x-x1, y-y1, z-z1), M1M2 →=(x2-x1, y2-y1, z2-z1) и M1M3 →=(x3-x1, y3-y1, z3-z1) будут компланарными.

На схеме это будет выглядеть так:

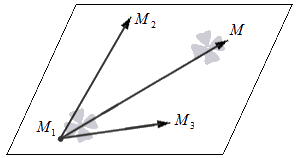
Это будет означать, что смешанное произведение векторов M1M→, M1M2→, M1M3→ будет равно нулю: M1M→·M1M2→· M1M3→=0, поскольку это является основным условием компланарности: M1M →=(x-x1, y-y1, z-z1), M1M2 →=(x2-x1, y2-y1, z2-z1) и M1M3 →=(x3-x1, y3-y1, z3-z1).

Запишем полученное уравнение в координатной форме:

x-x1y-y1z-z1x2-x1y2-y1z2-z1x3-x1y3-y1z3-z1=0

После того, как мы вычислим определитель, мы сможем получить нужное нам уравнение плоскости для трех не лежащих на одной прямой точек M1 (x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3).

От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.

В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.

Примеры задач на составление уравнения плоскости, проходящих через 3 точки

Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.

А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.

Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги:

1. Записать уравнение прямой М1М2, М1М3 или М2М3 (при необходимости посмотрите материал об этом действии).

2. Взять точку M4(x4, y4, z4), которая не лежит на прямой М1М2.

3. Записать уравнение плоскости, которая проходит через три различных точки М1, М2 и M4, не лежащих на одной прямой.  

Уравнение прямой в отрезках

В данной статье мы рассмотрим уравнение прямой в отрезках. Представим методы преобразования уравнения прямой в отрезках в уравнение прямой в общем виде и обратно. Рассмотрим численные примеры.

Уравнение прямой в отрезках представляется следующей формулой:

где a и b числа, отличные от нуля.

Отметим, что числа a и b в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает прямая на осях Ox и Oy (Рис.1).

Действительно. Подставляя в (1) y=0, получим x=a, если же подставить в (1) x=0, то получим y=b. Таким образом прямая L проходит через точки M₁(a, 0) и M₂(0, b).

Пример 1. Составить уравнение прямой, которая пересекает оси Ox и Oy в точках −1 и 3, соответственно.

Решение. Подставляя значения a=−1 и b=3 в (1), получим:

Ответ:

Приведение уравнения прямой в отрезках к общему виду

Левая часть уравнения (1) приведем к общему знаменателю:

Далее, умножив обе части уравнения на ab, получим:

или

Пример 2. Уравнение прямой в отрезках представлено следующим уравнением:

Перевести уравнение к общему виду.

Решение. Приведем левую часть уравнения к общему знаменателю:

Умножив обе части уравнения на −20, получим:

или

Ответ:

Приведение общего уравнения прямой на плоскости к уравнению прямой в отрезках

Пусть задано общее уравнение прямой на плоскости:

где A, B, C − отличные от нуля числа.

Сделаем следующие преобразования. Переведем свободный член C на правую часть уравнения и разделим обе части уравнения на −C:

Уравнение (2) можно переписать в следующем виде:

Сделаем следующие обозначения:

Тогда получим уравнение прямой в отрезках (1).

Пример 3. Привести общее уравнение прямой

к уравнению прямой в отрезках.

Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение прямой в отрезках. Воспользуемся формулой (3). Имеем: A=5, B=8, C=−3. Подставив эти значения в формулу (3), получим:

или

Ответ: